Color crosstalk is challenging for color fringe projection profilometry, which will cause color imbalance and phase-shift deviation, thus resulting in phase error. To address this challenge, this paper presents a blind crosstalk correction method for color phase-shifting fringe projection profilometry without crosstalk calibration. Three channels of the color fringe are firstly normalized to resolve color imbalance. The phase error induced by phase-shift deviation between three channels doubles the frequency of the color fringe. Therefore, the original cosine color fringe is shifted by quarter period to generate another sine color fringe to compensate the periodic phase error. Both simulations and experiments were carried out, and their results confirmed the effectiveness and accuracy of the proposed method.

1. Introduction

Fringe projection profilometry (FPP) based on triangulation principle is one of the most commonly used methods in optical three-dimensional (3D) shape measurement due to its low cost, fast speed, and high-resolution capabilities [1–6]. Normally, a FPP system contains a computer, a projector, and a camera. The projector and the camera are directed along different directions to the measured objects, all of which are controlled by the computer. Firstly, the fringe patterns should be designed and generated by the computer. Then, these patterns are projected onto the measured objects by the projector; at the same time, the deformed patterns are recorded by the camera. Finally, these captured images are transferred to the computer and analyzed by phase extraction algorithms to obtain the geometric information of the measured objects [7]. There are several phase extraction algorithms, including Fourier transform [8], wavelet transform [9], and phase-shifting profilometry (PSP) [10]. Among them, PSP is the most popular method, because it can achieve pixel-wise phase extraction, which can reconstruct the measured objects with abrupt changes more robustly. However, it generally requires more fringe patterns (normally at least three) than transform methods [11].

In order to overcome this problem, color phase-shifting technique has been developed [12–19]. Three phase-shifting patterns are assigned to red, green, and blue channels, respectively. Thus, only one color fringe pattern is required to reconstruct 3D shapes. However, the spectra of red, green, and blue channels are usually made to have some overlaps so that there would be no color-blind areas on the spectrum [20–22]. Thence, phase error will be introduced if conventional phase-shifting algorithms are employed directly. To suppress the phase error caused by color crosstalk, Huang et al. [23] proposed a method to compensate the coupling effects between channels. Since the degrees of overlaps are fixed, they projected pure red, green, and blue fringe patterns onto a white-painted flat board to calculate the degrees of coupling effects between three channels and then compensated it. This method has been explored when different numbers of fringes are projected on each channel by Zhang [24]. On the other hand, Wan et al. [25] presented an active phase error suppression method based on hue precorrection. The hue is precorrected to be linear by measuring the function of the combined effect and modifying the computer-generated hue according to the source-distorted relationship. Then, the new modified color fringe pattern can be generated for measuring objects. However, all these techniques need preprocessing before measurement, which makes it inconvenient to use. Hu et al. [26] proposed an algorithm for estimating the color remixing matrix based on the color fringe patterns captured from the reference plane or the surface of objects. Ma et al. [27] proposed a blind phase error suppression approach based on isotropic n-dimensional fringe pattern normalization [28] and carrier squeezing interferometry [29]. Wu et al. [30] proposed a point-to-point compensation method for color coupling and imbalance. The proposed method achieves point-to-point compensation based on the correspondence between camera pixels and projector pixels. Recently, Wang et al. [31] found the phase error introduced by crosstalk is approximately twice the frequency of color fringe. Therefore, Hilbert transform was applied on the color fringe to compensate the phase error. However, due to the fact that Hilbert transform belongs to frequency domain methods, this approach cannot handle the measured objects that contain discontinuities or separations well.

In this paper, we present a blind crosstalk correction method for color phase-shifting fringe projection profilometry. Due to the fact that phase error introduced by color crosstalk is twice the frequency of color fringe, the other color fringe with phase-shift is used to compensate the phase error. In addition, the fringe normalization was also designed to resolve the color imbalance problem. We describe the principle of this method in Section 2. Simulations and experiments are illustrated in Sections 3 and 4, respectively. Finally, Section 5 summarizes this work.

2. Principle

2.1. Color Phase-Shifting Fringe

Phase-shifting algorithms are widely used in optical metrology because of their high accuracy, among which three-step phase-shifting algorithm is the most commonly chosen algorithm since it requires the least number of patterns. Three phase-shifting patterns can be separately encoded into three channels of one color fringe. Ideally, the three channels of the color fringe can be written as

(1)

where (x, y) denotes the image pixel, A₀(x, y) is the average intensity, B₀(x, y) is the intensity modulation, and ϕ(x, y) is the wrapped phase. Simultaneously solving the above equations will lead to

(2)

The arctangent function gives the wrapped phase ranging from −π to +π with 2π phase jumps. Therefore, phase unwrapping should be performed to recover the absolute phase map. The relationship between the wrapped phase ϕ(x, y) and the absolute phase Φ(x, y) can be described as

(3)

where k(x, y) represents the fringe order, which can be determined by phase unwrapping algorithms.

2.2. Color Crosstalk Model

Most color cameras and projectors are designed to have spectrum overlaps between three channels to avoid color-blind regions in the spectrum. As a result, it is difficult to completely separate the three encoded fringes because of color crosstalk. In general, the linear color crosstalk can be described as [32]

(4)

where

are the RGB channels of the captured fringe pattern, M represents the crosstalk matrix, and m_ij(i, j = 1, 2, 3) are crosstalk factors. In general, the crosstalk between red and blue channels is smaller than that between red and green channels or between blue and green channels. Thus, crosstalk factors generally satisfy the following constraints:

(5)

Taking the red channel as an example,

can be further expressed as

(6)

(7)

The above equations can be rewritten as

(8)

(9)

Since X_R > −Y_R > 0, ε_R is positive and usually very small. The phase-shift deviations of green channel and blue channel can be analyzed in the equivalent way; ε_G and ε_B are also usually very small and ε_B is negative. As a result, the green channel

and the blue channel

can be further expressed as

(10)

(11)

Through above analysis, it can be known that the values of A_R, A_G, and A_B are different (the same for B_R, B_G, and B_B), which will cause color imbalance between three channels of color fringe. To avoid introducing phase error caused by color imbalance, fringe normalization should be performed, which will be discussed in Section 2.5. After fringe normalization, the three channels of the color fringe can be rewritten as

(12)

2.3. Phase Error Analysis

Although the color imbalance problem is addressed after fringe normalization, there are still phase-shift deviations between three channels of color fringe due to the existence of ε_R, ε_G, ε_B. If we continue to calculate the phase as

(13)

Then, phase error will be introduced, which can be expressed as

(14)

where n = R, G, B and θ_n = 2δ_n + ε_n; δ_n = −2π/3, 0, +2π/3. It can be seen that Δϕ^′ highly relates to 2ϕ. To simplify the above equation, we assume that ε_G = 0 and ε_B = −ε_R = ε⟶0⁻. Based on this assumption, Δϕ^′ will be simplified as

(15)

(16)

Therefore, Equation (15) can be further approximated as [29]

(17)

This indicates that the phase error approximately doubles the frequency of the color fringe.

2.4. Phase Error Compensation

Based on this observation, if the original phase map is shifted by quarter period or π/2, the shifted phase map can be used to compensate the quasisine phase error by averaging it with the original phase map. Therefore, the other color fringe with π/2 phase shift to the original one is also obtained as

(18)

Then, we can calculate the carried phase as

(19)

The phase error can be expressed as

(20)

Clearly, Δϕ^′ and Δϕ^″ have the same amplitude but opposite distributions. Thence, we can compensate the phase error as

(21)

2.5. Fringe Normalization

As mentioned above, two color fringes with π/2 phase shift are used to compensate the phase error which caused by phase-shift deviation. And the color crosstalk matrix of two color fringes can be considered the same. Namely, for the same channel, the values of A_n and B_n of two color fringes are equal. Thus, a background pattern is utilized to obtain the values of A_n. By subtracting A_n of each channel, the fringe intensities of two color fringes can be rewritten as

(22)

Then, they can be normalized by the following equations:

(23)

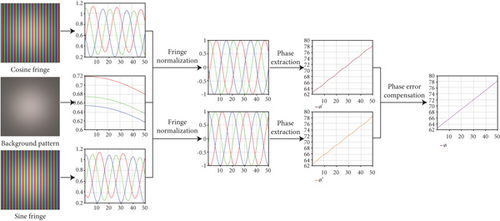
As shown in Figure 1, the framework of the proposed method contains three steps. Firstly, a background pattern is used to remove color imbalance in different channels of cosine and sine fringes. Then, two phase maps with phase errors caused by phase-shift deviation are extracted, respectively. Finally, the phase error caused by phase-shift deviation is compensated by averaging two phase maps.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Framework of the proposed method.

3. Simulations

In this section, simulations were carried out to verify the performance of the proposed method. The first simulated object is called peaks function in MATLAB, and its resolution is 400 × 400 pixels. The fringe pitch of the patterns we used is 20 pixels. As mentioned in Section 2.2, the crosstalk matrix should satisfy Equation (5). Therefore, we choose the crosstalk matrix as

(24)

Meanwhile, to simulate the uneven illumination, a 2D Gaussian function G(x, y) with a size of 400 × 400 pixels and a standard deviation of 100 pixels was applied on the simulated patterns. And the uneven illumination can be expressed as

(25)

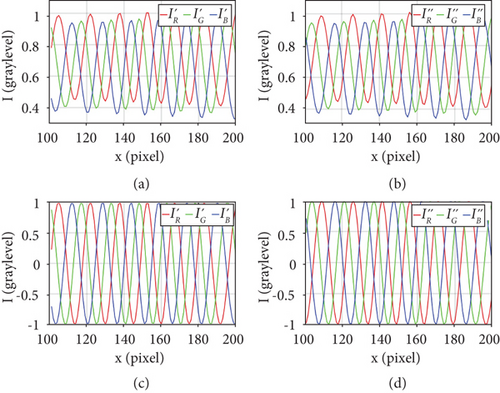
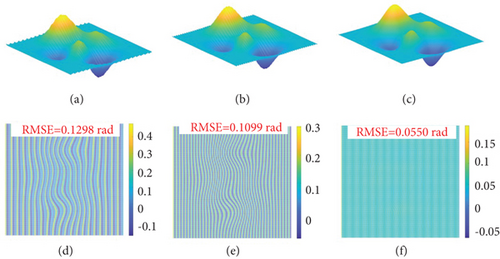
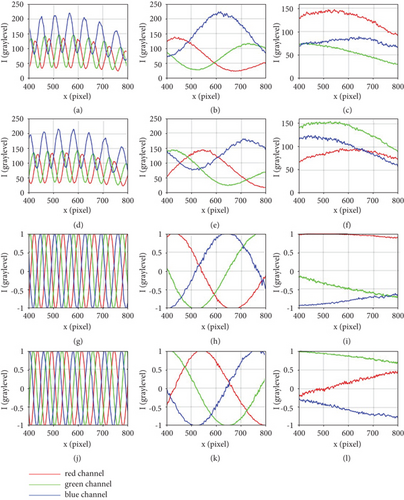
Figures 2(a) and 2(b) plot the 300th cross sections of cosine and sine fringes before fringe normalization, respectively. Obviously, the problem of color imbalance was existing in different channels. Then, the color imbalance problem was eliminated by fringe normalization, and the fringes after fringe normalization are shown in Figures 2(c) and 2(d). Figure 3(a) shows the 3D shape obtained before fringe normalization; periodic errors can be seen clearly. As shown in Figure 3(b), these errors were decreased after fringe normalization, but the errors caused by phase-shift deviation were still existing. Figure 3(c) shows the 3D shape retrieved after phase error compensation. Apparently, periodic errors were effectively suppressed by the proposed method. The reconstructed surface is very smooth, with almost no visible errors. In addition, their corresponding root mean square errors (RMSE) are shown in Figures 3(d)–3(f). Before fringe normalization, the RMSE in Figure 3(d) is 0.1298 rad. Figure 3(e) shows that the RMSE was reduced to 0.1099 rad after fringe normalization. And the RMSE, as shown in Figure 3(f), was reduced to 0.0550 rad after phase error compensation. This simulation illustrates the effectiveness of the proposed method.

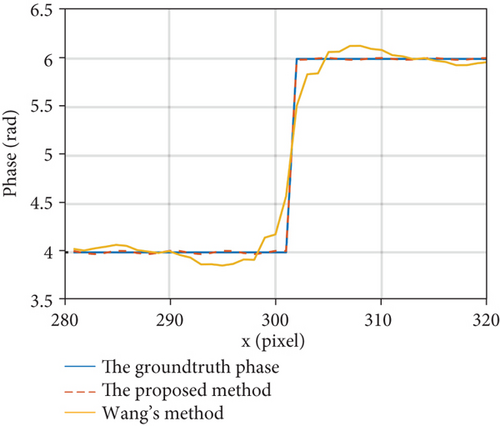
To compare the proposed method with Wang’s method [31] which uses frequency domain method, a staircase with four steps was simulated. The 3D shapes reconstructed by the proposed method and Wang’s method are shown in Figures 4(a) and 4(b), respectively. Obviously, Wang’s method performed worse than the proposed method because it uses frequency domain method, which is not suitable for processing objects with abrupt surfaces. Figure 5 illustrates a part of the 300th cross section, which contains the abrupt change between the third and fourth steps. The third and fourth stairs are marked in green and yellow in Figure 4, respectively. The distortion of the abrupt change retrieved by Wang’s method is more serious than the proposed method. This simulation demonstrates that the proposed method can handle objects with abrupt surfaces well.

4. Experiments

To further verify the proposed method, a FPP system was set up comprising a digital-light-processing (DLP) projector (Light-Crafter 4500) and a complementary-metal-oxide-semiconductor (COMS) camera (Point grey Chameleon3). The resolution of the camera is 1280 × 1024 pixels, and the optical lens (Kowa LM16JCM) mounted on the camera has a focal length of 16 mm. The resolution of the projector is 912 × 1140 pixels. It is well known that high-frequency fringes can effectively resist noise and provide high-precision measurement [10]. However, using high-frequency fringes also introduces phase ambiguities in the reconstruction process that need to be addressed by means of phase unwrapping. In these experiments, three-frequency method [7] was employed to unwrap the wrapped phase. Here, T_h, T_m, and T_l represent periods of high-, medium-, and low-frequency fringes, respectively. And they satisfy the following equation:

(26)

where N is a constant. Corresponding wrapped phases of three frequency are ϕ_h, ϕ_m, and ϕ_l. In addition, T_l is usually greater than the projector’s horizontal and vertical resolution to ensure complete elimination of phase ambiguity, which means the wrapped phase of low-frequency fringes has no phase ambiguity. It can be mathematically expressed as

(27)

where Φ_l is the absolute phase of low-frequency fringes. Then, the fringe order k_m and absolute phase Φ_m of medium-frequency fringes can be calculated as

(28)

where round( ) returns the closest integer. After determining Φ_m, the fringe order k_h and absolute phase Φ_h of high-frequency fringes can be obtained similarly:

(29)

Certainly, the errors caused by noise will inevitably be introduced in the actual measurement. Let us assume that the noise errors of low- and medium-frequency fringes are ΔΦ_l and ΔΦ_m, respectively. Then, the actual fringe orders obtained are

(30)

Obviously, if the value of N is too large, the fringe orders of medium- and high-frequency fringes will be calculated wrong, which will result in unwrapping errors. In our measurement system, N = 8 is a suitable value. As mentioned above, the period of low-frequency fringes should be greater than the projector’s horizontal and vertical resolution. Therefore, the period of high-frequency fringes should satisfy

(31)

In this paper, we choose T_h = 18 pixels. Thus, T_m = NT_h = 144 pixels and T_l = N²T_h = 1152 pixels.

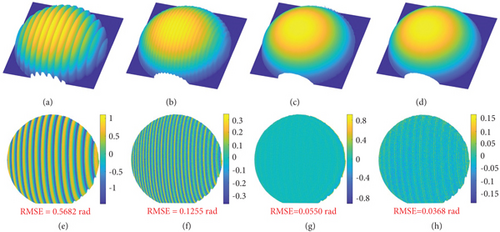
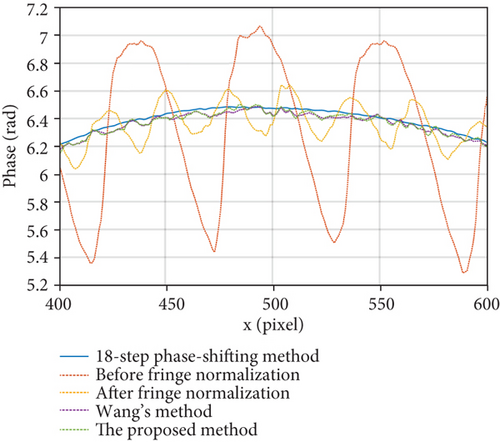
In the first experiment, a ball was measured. Total seven patterns were projected onto the ball and captured by the camera, as shown in Figure 6. Figures 6(a)–6(c) show the deformed cosine fringe patterns with periods of 18, 144, and 1152 pixels, respectively. Their corresponding sine fringe patterns are shown in Figures 6(d)–6(f). Figure 6(g) shows the background pattern that is used for fringe normalization. Before phase error compensation, we need to normalize these fringes to address the color imbalance problem. Figure 7 shows the 500th cross sections of six color patterns. Obviously, the imbalance problem existing in Figures 7(a)–7(f) was effectively resolved after fringe normalization, and the normalized fringes are shown in Figures 7(g)–7(l). Afterwards, the reconstructed 3D shapes are shown in Figure 8. Among them, Figure 8(a) shows the 3D shape reconstruction before fringe normalization; periodic phase errors are clearly visible. Then, the fringe normalization method was employed, and the 3D shape retrieved after fringe normalization is shown in Figure 8(b). The phase errors caused by color imbalance were suppressed, but the phase errors caused by phase-shift deviation were still existing. Thus, Wang’s [31] and the proposed methods were both applied to compensate these errors, and the reconstructions obtained are shown in Figures 8(c) and 8(d), respectively. Visually, both Wang’s and the proposed methods effectively suppressed the phase errors in the center of the ball. However, the frequency domain method used by Wang caused large errors in the edge areas, especially the upper edge of the ball. In order to quantify errors, we also used 18-step phase-shifting method [8] to measure this ball and compared the measurement result with the above four processing results. The corresponding deviation maps are shown in Figures 8(e)–8(h). The RMSE of the reconstruction before fringe normalization is 0.5682 rad, and it is reduced to 0.1255 rad after fringe normalization. As shown in Figures 8(g) and 8(h), after phase error compensation, the RMSEs of Wang’s and the proposed methods are 0.0550 and 0.0368 rad, respectively. And the maximum phase error of Wang’s method reaches 0.8 rad in edge areas which is 5.3 times that of the proposed method. In addition, Figure 9 plots the 800th cross section of the center of the ball. This experiment shows that both Wang’s method and the proposed method are reliable in processing smooth object, but the proposed method handles edge areas better than Wang’s method.

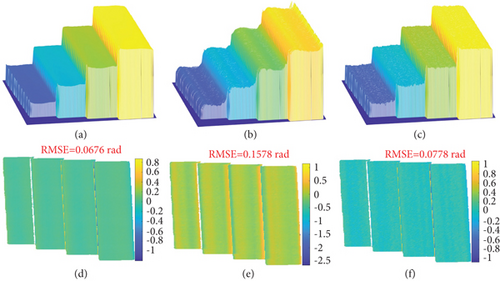
In order to further compare the proposed method with Wang’s method in dealing with object with abrupt surface, a staircase with four steps was measured. All captured patterns are shown in Figure 10. Similarly, the 18-step phase-shifting method was used as a reference. Figures 11(a)–11(c) show the 3D reconstructions recovered by 18-step phase-shifting, Wang’s, and the proposed methods, respectively. Visually, the 18-step phase-shifting method performed best while Wang’s method worked the worst. Due to the application of frequency domain method, the abrupt changes between steps were smoothed, resulting in incorrect measurement. The abrupt changes between steps reconstructed by the proposed method are obviously better than Wang’s method. Furthermore, we performed plane fitting on each step of the reconstruction retrieved by 18-step phase-shifting method. Figures 11(d)–11(f) show the deviation maps between the three reconstructions and the fitting results. Markedly, the accuracy of the proposed method is similar to that of the 18-step phase-shifting method, with only a difference of 0.01 rad. However, the RMSE of Wang’s method is approximately twice that of the proposed method. Figure 12 plots the 800th cross section of the staircase. The proposed method almost coincides with 18-step phase-shifting method, while Wang’s method performs poorly. This experiment confirms that the proposed method is more robust and accurate than Wang’s method in dealing with object with abrupt surfaces.

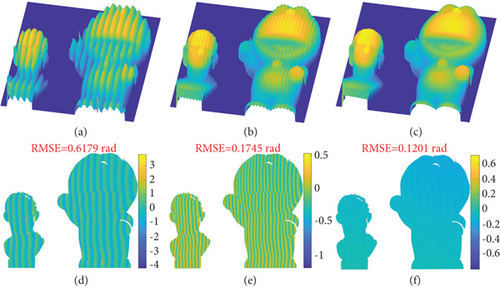
Two isolated sculptures were also measured to verify the actual measurement effect of the proposed method. All captured images are shown in Figure 13. Figure 14 shows the reconstructed 3D shapes, and the reconstruction in Figure 14(c) is significantly better than that in Figures 14(a) and 14(b). Figures 14(d)–14(f) show their corresponding deviation maps. Compared with the result before fringe normalization, the proposed method significantly improved the measurement accuracy, and the RMSE of the proposed method is only one-fifth of that before fringe normalization. This experiment demonstrates that the proposed method has sufficient robustness and accuracy in the actual measurement.

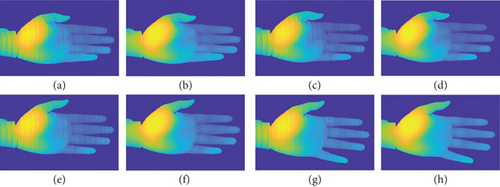
To further validate the dynamic measurement performance of the proposed method, one moving hand was measured. Figures 15(a)–15(d) show the 3D shapes reconstructed without color crosstalk compensation, and phase errors can be seen clearly. In contrast, the corresponding frames processed by the proposed method have no obvious errors, as shown in Figures 15(e)–15(h). This experimental result further confirms that the proposed method can effectively compensate the phase errors and improve measurement accuracy in dynamic measurement.

5. Conclusion

This paper presents an effective color crosstalk correction method for color FPP without crosstalk calibration. Due to the fact that phase error induced by color crosstalk is approximately twice the frequency of color fringe, the other sine color fringe was used to compensate the phase error. Both simulations and experiments confirmed the effectiveness of the proposed method. Experimental data shows that the proposed method has the ability to deal with objects with abrupt surfaces, and phase error caused by color crosstalk can be reduced to one-fifth after applying the proposed method.

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Su X. and Zhang Q., Dynamic 3-D shape measurement method: a review, Optics and Lasers in Engineering. (2010) 48, no. 2, 191–204, https://doi.org/10.1016/j.optlaseng.2009.03.012, 2-s2.0-70449527574.
10.1016/j.optlaseng.2009.03.012
Web of Science® Google Scholar
2 Zhang S., High-speed 3D shape measurement with structured light methods: a review, Optics and Lasers in Engineering. (2018) 106, 119–131, https://doi.org/10.1016/j.optlaseng.2018.02.017, 2-s2.0-85042855516.
10.1016/j.optlaseng.2018.02.017
Web of Science® Google Scholar
3 Zhang S., Absolute phase retrieval methods for digital fringe projection profilometry: a review, Optics and Lasers in Engineering. (2018) 107, 28–37, https://doi.org/10.1016/j.optlaseng.2018.03.003, 2-s2.0-85046039201.
10.1016/j.optlaseng.2018.03.003
Web of Science® Google Scholar
4 Wang Y., Liu L., Wu J., Chen X., and Wang Y., Enhanced phase-coding method for three-dimensional shape measurement with half-period codeword, Applied Optics. (2019) 58, no. 27, https://doi.org/10.1364/AO.58.007359, 2-s2.0-85072390689.
10.1364/AO.58.007359
Google Scholar
5 Deng J., Li J., Feng H., Ding S., Xiao Y., Han W., and Zeng Z., Efficient intensity-based fringe projection profilometry method resistant to global illumination, Optics Express. (2020) 28, no. 24, 36346–36360, https://doi.org/10.1364/OE.408835, 33379730.
10.1364/OE.408835
PubMed Web of Science® Google Scholar
6 Deng J., Li J., Ding S., Feng H., Xiao Y., Han W., and Zeng Z., Fringe projection decamouflaging, Optics and Lasers in Engineering. (2020) 134, article 106201, https://doi.org/10.1016/j.optlaseng.2020.106201.
10.1016/j.optlaseng.2020.106201
Google Scholar
7 Zuo C., Huang L., Zhang M., Chen Q., and Asundi A., Temporal phase unwrapping algorithms for fringe projection profilometry: a comparative review, Optics and Lasers in Engineering. (2016) 85, 84–103, https://doi.org/10.1016/j.optlaseng.2016.04.022, 2-s2.0-84965025483.
10.1016/j.optlaseng.2016.04.022
Web of Science® Google Scholar
8 Takeda M., Fourier fringe analysis and its application to metrology of extreme physical phenomena a review, Applied Optics. (2012) 52, 20–29.
10.1364/AO.52.000020
Google Scholar
9 Zhong J. and Weng J., Spatial carrier-fringe pattern analysis by means of wavelet transform wavelet transform profilometry, Applied Optics. (2004) 43, no. 26, 4993–4998, https://doi.org/10.1364/AO.43.004993, 2-s2.0-4944257336, 15468699.
10.1364/AO.43.004993
PubMed Web of Science® Google Scholar
10 Zuo C., Feng S., Huang L., Tao T., Yin W., and Chen Q., Phase shifting algorithms for fringe projection profilometry: a review, Optics and Lasers in Engineering. (2018) 109, 23–59, https://doi.org/10.1016/j.optlaseng.2018.04.019, 2-s2.0-85047072247.
10.1016/j.optlaseng.2018.04.019
Web of Science® Google Scholar
11 Wang Y., Liu L., Wu J., Song X., Chen X., and Wang Y., Dynamic three-dimensional shape measurement with a complementary phase-coding method, Optics and Lasers in Engineering. (2020) 127, https://doi.org/10.1016/j.optlaseng.2019.105982.
10.1016/j.optlaseng.2019.105982
Google Scholar
12 Kinell L., Multichannel method for absolute shape measurement using projected fringes, Optics and Lasers in Engineering. (2004) 41, no. 1, 57–71, https://doi.org/10.1016/S0143-8166(02)00148-3, 2-s2.0-0141504276.
10.1016/S0143-8166(02)00148-3
Google Scholar
13 Li B., Fu Y., Zhang J., Wu H., Xia G., and Jiang G., A fast three-dimensional shape measurement method based on color phase coding, Optik. (2016) 127, no. 3, 1011–1015, https://doi.org/10.1016/j.ijleo.2015.10.036, 2-s2.0-84959375932.
10.1016/j.ijleo.2015.10.036
Google Scholar
14 Wan Y.-Y., Cao Y.-P., Chen C., and Peng K., An online triple-frequency color-encoded fringe projection profilometry for discontinuous object, Journal of Modern Optics. (2016) 63, no. 14, 1420–1427, https://doi.org/10.1080/09500340.2016.1149628, 2-s2.0-84959045165.
10.1080/09500340.2016.1149628
CAS Google Scholar
15 Ding Y., Xi J., Yu Y., Deng F., and Cheng J., Recovering the absolute phase maps of three selected spatial-frequency fringes with multi-color channels, Neurocomputing. (2017) 252, 17–23, https://doi.org/10.1016/j.neucom.2016.04.074, 2-s2.0-85017423242.
10.1016/j.neucom.2016.04.074
Google Scholar
16 Yee C. K. and Yen K. S., Single frame profilometry with rapid phase demodulation on colour-coded fringes, Optics Communications. (2017) 397, 44–50, https://doi.org/10.1016/j.optcom.2017.03.064, 2-s2.0-85016466302.
10.1016/j.optcom.2017.03.064
CAS Google Scholar
17 Wan Y., Cao Y., Liu X., Tao T., and Kofman J., High-frequency color-encoded fringe-projection profilometry based on geometry constraint for large depth range, Optics Express. (2020) 28, no. 9, 13043–13058, https://doi.org/10.1364/OE.388579, 32403786.
10.1364/OE.388579
PubMed Google Scholar
18 Wang J., Zhou Y., and Yang Y., Rapid 3D measurement technique for colorful objects employing RGB color light projection, Applied Optics. (2020) 59, no. 7, 1907–1915, https://doi.org/10.1364/AO.382302, 32225707.
10.1364/AO.382302
PubMed Google Scholar
19 Chen X., Lu C., Ma M., Mao X., and Mei T., Color-coding and phase-shift method for absolute phase measurement, Optics Communications. (2013) 298-299, 54–58, https://doi.org/10.1016/j.optcom.2013.02.013, 2-s2.0-84876138175.
10.1016/j.optcom.2013.02.013
CAS Google Scholar
20 Huang P. S., Color phase-shifting technique for three-dimensional shape measurement, Optical Engineering. (2006) 45, no. 1, https://doi.org/10.1117/1.2151160, 2-s2.0-33748591130.
10.1117/1.2151160
Google Scholar
21 Ma S., Quan C., Tay C. J., Zhu R., and Li B., Phase error correction for digital fringe projection profilometry, Physics Procedia. (2011) 19, 227–232, https://doi.org/10.1016/j.phpro.2011.06.153, 2-s2.0-84863148340.
10.1016/j.phpro.2011.06.153
Google Scholar
22 Song L., Li Z., Chen C., Xi J., Guo Q., and Li X., A correction method of color projection fringes in 3D contour measurement, Opyoelectronics Letters. (2015) 11, no. 4, 303–306, https://doi.org/10.1007/s11801-015-5050-x, 2-s2.0-84937907165.
10.1007/s11801-015-5050-x
Google Scholar
23 Huang P. S., Hu Q., Jin F., and Chiang F.-P., Color-encoded digital fringe projection technique for high-speed three-dimensional surface contouring, Optical Engineering. (1999) 38, no. 6, 1065–1071, https://doi.org/10.1117/1.602151, 2-s2.0-0032628769.
10.1117/1.602151
Web of Science® Google Scholar
24 Zhang Z., Time efficient color fringe projection system for 3D shape and color using optimum 3-frequency selection, Optics Express. (2006) 14, no. 14, 6444–6455, https://doi.org/10.1364/OE.14.006444, 2-s2.0-33745859403, 19516822.
10.1364/OE.14.006444
PubMed Web of Science® Google Scholar
25 Wan Y., Cao Y., Chen C., Wang Y., Fu G., Wang L., and Li C., Active phase error suppression for color phase-shifting fringe projection based on hue pre-correction, Optics & Laser Technology. (2019) 118, 102–108, https://doi.org/10.1016/j.optlastec.2019.05.014, 2-s2.0-85065537499.
10.1016/j.optlastec.2019.05.014
Web of Science® Google Scholar
26 Hu Y., Xi J., Chicharo J., and Yang Z., Blind color isolation for color-channel-based fringe pattern profilometry using digital projection, Journal of the Optical Society of America. A. (2007) 24, no. 8, 2372–2382, https://doi.org/10.1364/JOSAA.24.002372, 2-s2.0-38849207549, 17621340.
10.1364/JOSAA.24.002372
PubMed Google Scholar
27 Ma S., Zhu R., Quan C., Li B., Tay C. J., and Chen L., Blind phase error suppression for color-encoded digital fringe projection profilometry, Optics Communications. (2012) 285, no. 7, 1662–1668, https://doi.org/10.1016/j.optcom.2011.12.027, 2-s2.0-84856211817.
10.1016/j.optcom.2011.12.027
CAS Google Scholar
28 Antonio Quiroga J. and Servin M., Isotropic n -dimensional fringe pattern normalization, Optics Communications. (2003) 224, no. 4-6, 221–227, https://doi.org/10.1016/j.optcom.2003.07.014, 2-s2.0-0042191623.
10.1016/j.optcom.2003.07.014
Google Scholar
29 Li B., Chen L., Tuya W., Ma S., and Zhu R., Carrier squeezing interferometry suppressing phase errors from the inaccurate phase shift, Optics Letters. (2011) 36, no. 6, 996–998, https://doi.org/10.1364/OL.36.000996, 2-s2.0-79952844949, 21403754.
10.1364/OL.36.000996
PubMed Web of Science® Google Scholar
30 Wu M., Wu G., Zhang S., Wu Y., Liu F., and Fan N., Point-to-point compensation method for color coupling and imbalance in color-fringe pattern profilometry, Journal of Optics. (2020) 22, no. 9, https://doi.org/10.1088/2040-8986/aba3b5.
10.1088/2040-8986/aba3b5
Google Scholar
31 Wang Y., Liu L., Wu J., Chen X., and Wang Y., Hilbert transform-based crosstalk compensation for color fringe projection profilometry, Optics Letters. (2020) 45, no. 21, 6110–6113, https://doi.org/10.1364/OL.392061, 33137081.
10.1364/OL.405768
CAS PubMed Google Scholar
32 Caspi D., Kiryati N., and Shamir J., Range imaging with adaptive color structured light, IEEE Transactions on Pattern Analysis and Machine Intelligence. (1998) 20, no. 5, 470–480, https://doi.org/10.1109/34.682177, 2-s2.0-0032069591.
10.1109/34.682177
Web of Science® Google Scholar

Citing Literature

All articles

Blind Crosstalk Correction for Color Fringe Projection Profilometry Combining the Sine and Cosine Phase-Shifting Patterns

Abstract

1. Introduction