International Journal of Differential Equations
Volume 2022, Issue 1 7331913
Research Article
Open Access

Existence of Strong Solutions for Nonlinear Systems of PDEs Arising in Convective Flow

Khaled Bouazzaoui, 

Corresponding Author

Khaled Bouazzaoui

Département de Mathématiques, Laboratoire d’Analyse Mathématiques et Applications (LAMA), Faculté des Sciences Exactes et Appliquées, Université Oran 1 Ahmed Ben Bella, Oran, Algeria

Search for more papers by this author
Mohammed Aiboudi, 

Mohammed Aiboudi

Département de Mathématiques, Laboratoire d’Analyse Mathématiques et Applications (LAMA), Faculté des Sciences Exactes et Appliquées, Université Oran 1 Ahmed Ben Bella, Oran, Algeria

Search for more papers by this author
Sameh Elsayed Ahmed, 

Sameh Elsayed Ahmed

Department of Mathematics, Faculty of Sciences, South Valley University Qena, Qena 83523, Egypt uss.rnu.tn

Search for more papers by this author
First published: 10 January 2022
https://doi.org/10.1155/2022/7331913
Academic Editor: Sining Zheng

Abstract

In this paper, we will study the existence of strong solutions for a nonlinear system of partial differential equations arising in convective flow, modeling a phenomenon of mixed convection created by a heated and diving plate in a porous medium saturated with a fluid. The main tools are Schäfer’s fixed-point theorem, the Fredholm alternative, and some theorems on second-order elliptic operators.

1. Introduction

In recent years, many authors have studied the case of the semi-infinite vertical plane plate immersed in a porous medium saturated with a fluid. The following problem is derived from this phenomenon:
(1)
with mixed boundary conditions
(2)
where (x, y) is the rectangular Cartesian coordinates system. The constants k and λ depend on the density, the viscosity, and the thermal expansion coefficient of the fluid. They also depend on the permeability and the thermal diffusivity of the saturated porous medium.

In the framework of boundary layer approximations, by introducing similarity variables, we can transform the system of partial differential equations into a system of ordinary differential equations of the third order with appropriate boundary values (see [1], p.3). These two-point boundary value problems can be studied by using a shooting method (see for example [2, 3]). For the auxiliary dynamical system, we refer the reader to [4]. For an integral equation, we refer the reader to [5]. For nonstandard analysis techniques, we refer the reader to [6]. For numerical method, we refer the reader to [7]. The second natural way of dealing with this problem, which is the framework of this paper, is straightly related to the coupled partial differential equations (see [1, 8, 9]).

The aim of this paper is to generalize the existence of strong solutions of the problem introduced in [1, 8, 9]. More precisely, we will give new results about the existence of strong solutions, in particular, without assuming that is small (as in [8], Theorem 4). We choose the data (the function K) in the larger space inspired by other works, and we will give conditions which make each solution in .

Let us introduce now the problem in which we are interested. Let Ω be a bounded domain of ℝ2 whose boundary Γ = ∂Ω is sufficiently smooth and divided into two parts Γ1 and Γ2 such that meas(Γ1) ≠ 0 and
(3)
On Ω, we consider the boundary value problem defined by
(4)
(5)
with boundary conditions
(6)
(7)
where λ is a strictly positive constant, ν is the unit outward normal vector on ∂Ω, and ∇Ψ⊥ = (∂yΨ, −∂xΨ).

2. Preliminaries

In this section, we will introduce the notations, definitions, and preliminary facts which are used throughout the paper.

2.1. Sobolev Spaces and Notations

For a positive integer k and for 1 ≤ p ≤ ∞, the Sobolev space is defined as follows:
(8)
where Dα(u) is the α-derivative of u in the sense of distributions. For p = 2, we denote by Hk(Ω) the space Wk,2(Ω). The boundary space is defined as
(9)
1 < p < ∞, equipped with the norm
(10)
Throughout the paper, we use the following notations:
  • (i)

    Wk,2(Ω) = Hk(Ω), Bk−(1/2),2(∂Ω) = Hk−(1/2)(∂Ω), and C is Poincaré’s constant of Ω

  • (ii)

  • (iii)

    , and

  • (iv)

    ‖⋅‖p,  1 ≤ p ≤ ∞, is the norm of Lp(Ω) (or the norm of Lp(Ω) × Lp(Ω))

  • (v)

    ‖⋅‖ is the norm of L(E, F), i.e., the space of linear operators from E into F (normed spaces)

2.2. Variational Formulation

Let us assume
(11)
Then, from the existence and uniqueness theorem for the Dirichlet problem for strong solutions (see [10], Theorem 5.13), there exists a unique function Θ ∈ H2(Ω) satisfying
(12)
Furthermore, Θ ∈ L∞(Ω) and . For the coefficient K = (k1, k2), it is supposed that
(13)
where
(14)
Let us notice that is dense in (see [11], Proposition 3.57). Let us set H = T − Θ. Then, (Ψ, T) is the solution of problem (5)–(7) if and only if (Ψ, H) is the solution of the problem
(15)
(16)
with boundary conditions
(17)
(18)
Let us assume that is a solution of problem (15)–(18). Multiplying equation (15) by a function and equation (16) by a function , integrating on Ω, and using Green’s formula, we yield
(19)
where
(20)

3. Main Results

We start with the following lemma which plays a key role in our main results.

Lemma 1. Let Ψ ∈ W1,4(Ω). The function H ≡ 0 is the unique solution of problem

(21)
in the space .

Proof. It is clear that H ≡ 0 is the solution of problem (21). Then, if satisfies λΔH − ∇H · ∇Ψ⊥ = 0, multiplying the members of this equation by H, we get

(22)

By integration on Ω, we get

(23)

On the other hand, we have

(24)
because div(∇Ψ⊥) = 0, in the sense of distributions. Since ∇H · ∇Ψ⊥ ∈ L2(Ω), div(H∇Ψ⊥) ∈ L2(Ω), and hence, by the density of D(Ω) in (when Ω is at least a Lipschitz open set), we have
(25)
that is, ‖∇H‖2 = 0. Thus, H = 0.

Remark 1. From the proof of the previous lemma, we observe that for all and Ψ ∈ W1,4(Ω), we have

(26)

Thus, by the density of D(Ω) in and by the embedding H1(Ω)↬L4(Ω), we can easily show that for all and Ψ ∈ W1,4(Ω), we have

(27)

Now, we will prove the following proposition which plays an important role in proving our main results.

Proposition 1. Let us assume that ∂Ω is of class C1,1 and Ψ ∈ W1,4(Ω). Then, for all f ∈ L2(Ω), the equation

(28)
has exactly one solution H in the space .

Proof. Let us consider

(29)
defined by
(30)
where the operator is defined by
(31)

Then, it is clear that for all , we have

(32)

From the existence and uniqueness theorems for the Dirichlet problem for strong solutions (see [12], Theorem 9.15, Lemma 9.17, problem 9.8) combined with the open mapping theorem (see [13], Corollary 2.7), the operator T is invertible. On the other hand, we can write TΨ = φ2∘φ1 where

(33)
defined by
(34)
with j as the operator from into defined by j(H) = ∇H and , where ic : H1(Ω)↬L4(Ω), and
(35)
defined by
(36)

Then, TΨ is compact. Indeed, φ1 is continuous because ic and j are continuous, and the operator ic is compact (Rellich–Kondrachov theorem); it is clear that φ2 is continuous. Now, it is easy to show that for all , (32) holds, if and only if

(37)
holds. By Lemma (21), H ≡ 0 is the unique solution of equation
(38)
in the space . Hence, from the Fredholm alternative, equation (28) has exactly one solution . Besides
(39)
as needed.

Lemma 2. Under the assumptions of the previous proposition, the mapping L from W1,4(Ω) into is defined by L(Ψ) = H where

(40)
is continuous. Moreover, there exists R > 0 such that for all Ψ ∈ W1,4(Ω), if L(Ψ) = H,
(41)

Proof. Let Ψ ∈ W1,4(Ω) and let be the unique solution of problem (40). Let be a sequence of elements in converging to Ψ in W1,4(Ω). Then, there exists a sequence of elements in satisfying

(42)

Then, for all n ∈ ℕ,  Hn + Θ is the solution of the problem

(43)

By the weak maximum principle theorem (see [12], Theorem 8.1), for all n ∈ ℕ, we have

(44)
and by variational formulation (system (19)), we have
(45)

Replacing v by H − Hn and using Remark 1, we give

(46)

On the other hand, for W = H − Hn, we have

(47)

Similarly, . We replace the previous inequality in inequality (46), and we use Remark 1, to get

(48)

Thus,

(49)
with
(50)

Then, there exists a subsequence of the sequence converging almost everywhere to H. That is,

(51)

From inequality (49), we get, for all Ψ1, Ψ2 ∈ W1,4(Ω),

(52)
where C″ > 0 depends only on Ω, R, and λ, as needed.

Remarks 2.

  • (1)

    The main advantage of Proposition 1 (particularly, Fredholm’s alternative) is the generalization of the results ([8], Theorem 1 and Theorem 4, and [1], Theorem 4), and more precisely, it leads us to show that there exist strong solutions to problem (15)–(18) without assuming that is bounded by certain constants and without assuming that ‖K · ∇Θ‖2 is quite small.

  • (2)

    The previous lemma is similar to Lemma 3.1 in [8], but in this paper, we have seen a new technique for its proof (it is proved by a weak maximum principle).

The following proposition is useful.

Proposition 2. Let us assume, in addition to assumptions (11)–(13), that ∂Ω is of class C1,1, Γ1 = ∂Ω, and . Then, problem (15)–(18) have at least one solution (Ψ, H) in the space .

Proof. For all , we have K · ∇(H + Θ) ∈ L2(Ω). Then, from the existence and uniqueness theorem for the Dirichlet problem for strong solutions ([12], Theorem 9.15), the problem

(53)
has exactly one solution Ψ ∈ H2(Ω). Besides, there exists such that
(54)
(see [12], Lemma 9.17). Let us denote by Λ the application from into H2(Ω) defined by Λ(H) = Ψ, and let us consider the application defined by
(55)
with L given in Lemma 2 and i : H2(Ω)↬W1,4(Ω). Then, we have
(56)
that is, the set of the solutions of problem (15)–(18) is
(57)

Then, J is continuous and compact. Indeed, L and Λ are continuous because for Ψi = Λ(Hi),  i = 1,2, we have

(58)
and the continuity of L has been proved in Lemma 2. By the Rellich–Kondrachov theorem, we can easily show that i is compact. Now, let H be in the set
(59)

Then, there exists ε ∈ [0,1] such that

(60)

By the variational formulation, the previous problem is equivalent to

(61)

From the first equation in system (61), we have

(62)
with R′ = R′(Θ, Ω). Hence,
(63)

Now, from the second equation in system (61), since (H∇H, ∇Ψ⊥) = 0 (see Remark 1) and (H∇Θ, ∇Ψ⊥) = −(Θ∇H, ∇Ψ⊥) (the same method as the one used to get inequality (47)), we have

(64)

From inequalities (63) and (64), we deduce that , i.e., A is bounded. From Schäfer’s fixed-point theorem (see [14], Theorem 11.1, p.59), we deduce that J has at least one fixed point . That is, (Λ(H), H) is the strong solution of problem (15)–(18). Furthermore, K · ∇(H + Θ) ∈ L4(Ω). Thus, Ψ ∈ W2,4(Ω), i.e., . Hence, H ∈ W2,4(Ω), as needed.

Remark 3. From the previous proof, it is observed that under the assumptions

(65)
the previous result (the previous proposition) is still valid, which is the generalization of ([8], Theorem 1 and Theorem 4). In addition, Proposition 1 helps us to generalize the previous result in the case where .

Now, we are going to generalize the previous result in the case where . To this end, we start with the following remark.

Remark 4. Let be a solution of the problem

(66)

Then, from the first equation with boundary conditions, for all , we have

(67)

Now, from the second equation in system (66) with boundary conditions, for all , we have

(68)

On the other hand, we have

(69)
the same method as the one used to get inequality (47). Then, we have
(70)

Thereby, if is a solution of problem (66), then for all , we have

(71)
(72)

Now, we will prove the following result.

Theorem 1. Let us assume, in addition to assumptions (11)–(13), that ∂Ω is of class C1,1 and Γ1 = ∂Ω. Then, problem (15)–(18) have at least one solution (Ψ, H) in the space .

Proof. Let be a sequence converging to K in . Then, from Proposition 2, there exists which is bounded in and satisfying

(73)

By the compactness of the embedding H1(Ω)↬Lp(Ω),  p ≥ 2, there exists a subsequence of the sequence converging weakly in and strongly in Lp(Ω),  p ≥ 2, to an element denoted (Ψ∗, H∗), and we have H∗ ∈ L∞(Ω). Now, we shall complete the proof in three steps.

Step 1. converges in H1 to (Ψ∗, H∗). Indeed, from Remark 4, for all u ∈ D(Ω), we have

(74)

Then, for , we have

(75)

By Lemma 2 and the fact that is convergent in , we get that there are strictly positive constants C1, C2, and C3, such that

(76)

That is, converges strongly to Ψ∗. On the other hand, for all , we have

(77)

By the same process as the one used to obtain inequality (52), we have

(78)
that is, converges strongly to H∗.

Step 2. (Ψ∗, H∗) satisfies systems (71) and (72). Indeed, for all u ∈ D(Ω), we have

(79)

For all u ∈ D(Ω), we have

(80)

Taking the limit as k⟶∞ in (71) when gives

(81)

Now, for all , we have

(82)
because
(83)
By the dominated convergence theorem, we have
(84)

Obviously,

(85)

Taking the limit in (77) as k⟶∞ yields

(86)

Step 3. . Indeed

(87)

Since , we have K · ∇(H∗ + Θ) ∈ L4/3(Ω). Then, from the existence and uniqueness theorems for the Dirichlet problem for strong solutions and since the application

(88)
is continuous and coercive, we deduce that Ψ∗ ∈ W2,(4/3)(Ω). Thus, in which W1,(4/3)(Ω)↬L4(Ω) (see [11], Theorem 2.72), that is, . Then, from Proposition 1, there exists a unique satisfying
(89)

On the other hand, from Remark 1, the bilinear form

(90)
is continuous and coercive. Thus, from the Lax–Milgram theorem, we deduce that H = H∗. Hence, K · ∇H∗ ∈ L2(Ω), that is, K · ∇(H∗ + Θ) ∈ L2(Ω), and thereby, from the existence and uniqueness theorems for the Dirichlet problem for strong solutions ([12], Theorem 9.15, problem 9.8) and from the Lax–Milgram theorem, Ψ∗ is the unique function in obeying
(91)

By the same method as the one used in the previous proposition, we get

(92)

This completes the proof.

Remark 5. Notice that in Step 3 of the previous proof, Proposition 1 is necessary. Also, we need Lemma 1 and Remark 1, particularly, (H∇H, ∇Ψ⊥) = 0 for and Ψ ∈ W1,4(Ω) which is a different result from ([8], Lemma 2.1) and it is proved by the generalized Green formula.

In addition to the previous results, we will study the existence of solutions in Cn(Ω),  n ≥ 3.

Theorem 2. Let us assume, in addition to the hypotheses of the previous theorem, that ∂Ω is of class Cn, Tω ∈ Hn−(1/2)(∂Ω), and K ∈ Wn−2,4(Ω) with n ≥ 2. Then, problem (15)–(18) have at least one solution (Ψ, H) in the space Hn(Ω) × Hn(Ω).

Proof. Let us assume n ≥ 3, and let be a solution of problem (15)–(18). Then, we have

(93)

On the other hand, from (12) and by the regularity theorem of elliptic problem ([12], Theorem 8.13), Θ is in Hn(Ω). It then follows that

(94)

Since , we have

(95)

From the regularity theorem of elliptic problem ([12], Theorem 8.13), we deduce that Ψ is in H3(Ω). Hence,

(96)
that is, H ∈ H3(Ω). Continuing the above process, we obtain, after n − 2 steps, .

Let us denote by γ0 the trace operator on ∂Ω. Then, we have the following result.

Corollary 1. Let us assume, in addition to the hypotheses of the previous theorem, that ∂Ω is of class C∞ and and there exists such that γ0(φ) = Tω. Then, problem (15)–(18) have at least one solution (Ψ, H) in the space .

Remark 6. If Γ1 and Γ2 are closed and open subsets and Ω is sufficiently smooth (being able to apply Poincaré’s inequality), then by applying Theorem 2.24 given in ([15], p. 132) or Theorem 5.8 given in ([16], p. 146), we can prove that the previous results of the existence of strong solutions are still valid in the general case where Γ2 ≠ ∅.

4. Conclusion

In this paper, we study a problem given by two strongly coupled partial differential equations in a two-dimensional bounded domain, modeling a phenomenon of convective flow created by a heated and diving plate in a porous medium saturated with a fluid. We have established the existence of strong solutions without assuming that is bounded by a certain constant (nor ‖K∇Θ‖2 is small enough) and by choosing K in . Besides, we have added a new result (which does not exist in the literature) which is the existence of solutions of class Cn,  n ≥ 3 (particularly, solutions of class C∞).

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Appendix

Numerical Example

Let us consider a semi-infinite vertical permeable or impermeable flat plate embedded in a fluid-saturated porous medium at the ambient temperature Tb. The rectangular Cartesian co-ordinates system is applied with the origin fixed at the leading edge of the vertical plate. The x-axis is directed upward along the plate, and the y-axis normal to it. It is assumed that the porous medium is homogeneous and isotropic where all the properties of the fluid and the porous medium are constants except the density. Also, the flow is incompressible and follows the Darcy–Boussinesq law. Based on these assumptions, the following governing equations are introduced:
(A.1)
(A.2)
with boundary conditions
(A.3)
(A.4)
with m ∈ ℝ, A, b > 0, λ = 1 and K ≡ (1,0). The parameter ω ∈ ℝ is the mass transfer coefficient where ω = 0 refers to the impermeable wall. Also, the permeable surface is represented by ω < 0 for the fluid suction and ω > 0 for the fluid injection.
Now, a brief discussion for the similarity solutions is given. Assuming that the convection takes place in a thin layer around the plate (we can neglect ∂2Ψ/∂x2 and ∂2T/∂y2) and hence the boundary layer approximation is obtained:
(A.5)
(A.6)
with same boundary conditions (A.3)-(A.4).
For the case of prescribed heat, we introduce the new dimensionless similarity variables
(A.7)
where
(A.8)
is the local Rayleigh number; equations (A.1) and (A.2) with boundary conditions (A.3) and (A.4) lead to the third-order ordinary differential equation
(A.9)
on [0, b) subjected to
(A.10)
where
(A.11)
In the case of prescribed heat flux, we introduce the new dimensionless similarity variables:
(A.12)
where the Rayleigh number is
(A.13)
Equations (A.5) and (A.6) with boundary conditions (A.3) and (A.4) lead to the third-order ordinary differential equation
(A.14)
on [0, b) subjected to
(A.15)

In order to show the effectiveness of main results, numerical results are presented in this part and discussed. Here, the transformed equations governing the case of prescribed constant heat and the prescribed heat flux at γ = 0.5 are solved, numerically, using the fourth-order Runge–Kutta method based on the shooting technique. The obtained data are presented in Figures 1 and 2 for f′(η), as well as values of f″(0) and f′(0) are included in Tables 1 and 2. It is seen that a strong solution is existed and the behaviors of f′(η) for all values of m are asymptotic. In addition, the growth in the power index m has negative impacts on the values of f′(η), f″(0), and f′(0) due to the decrease in the temperature distributions at the surface and thickness of the thermal boundary layers.

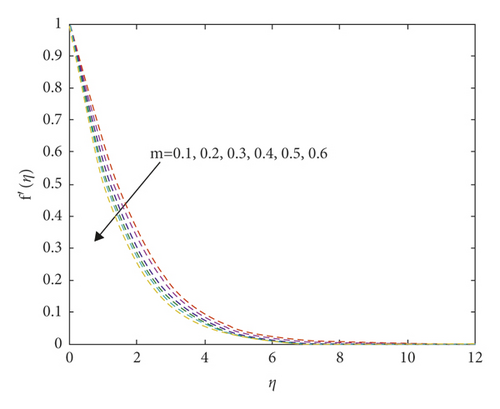
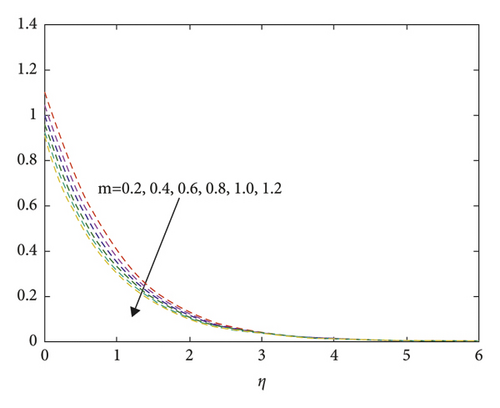
Details are in the caption following the image
Details are in the caption following the image
1. Values of f″(0) for the case of prescribed heat at γ = 0.5.
M f″(0)
0.1 −0.383276439
0.2 −0.446235343
0.3 −0.501716988
0.4 −0.551568992
0.5 −0.597004528
0.6 −0.638866144
2. Values of f′(0) for the case of prescribed heat flux at γ = 0.5.
M f′(0)
0.2 1.109186225
0.4 1.047023594
0.6 0.998565092
0.8 0.959474627
1.0 0.927113207
1.2 0.899773212

Data Availability

No external data were used to support the study in this paper.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.