Soft Substructures in Quantales and Their Approximations Based on Soft Relations
Abstract
The aim of this research article is to derive a new relation between rough sets and soft sets with an algebraic structure quantale by using soft binary relations. The aftersets and foresets are utilized to define lower approximation and upper approximation of soft subsets of quantales. As a consequence of this new relation, different characterization of rough soft substructures of quantales is obtained. To emphasize and make a clear understanding, soft compatible and soft complete relations are focused, and these are interpreted by aftersets and foresets. Particularly, in our work, soft compatible and soft complete relations play an important role. Moreover, this concept generalizes the concept of rough soft substructures of other structures. Furthermore, the algebraic relations between the upper (lower) approximation of soft substructures of quantales and the upper (lower) approximation of their homomorphic images with the help of soft quantales homomorphism are examined. In comparison with the different type of approximations in different type of algebraic structures, it is concluded that this new study is much better.
1. Introduction
Quantale theory was proposed by Mulvey[1]. It is based on defining an algebraic structure on a complete lattice. Since quantale was defined on a complete lattice, there must be a correlation between linear logic and quantale theory which was studied by Yetter, in his study. He presented a new class of models for linear intuitionistic logic [2]. In recent years, quantale is applied in vast research areas, such as algebraic theory [3], rough set theory [4–7], topological theory [8], theoretical computer science [9], and linear logic [10].
In 1982, Pawlak developed the famous rough set theory [11], which is a mathematization of inadequate knowledge. The rough set deals with the categorization and investigation of inadequate information and knowledge. After Pawlak’s work, Zhu [12] provided some new views on the rough set theory. In [13], Ali et al. studied some properties of generalized rough sets. Nowadays, rough sets are applied in many different areas, such as cognitive sciences, machine learning, pattern recognition, and process control.
There are many problems that arise in different fields such as engineering, economics, and social sciences in which data have some sort of uncertainty. Well-known mathematical tools have so many limitations because these tools are introduced for particular circumstances. There are many theories to overcome uncertainty such as fuzzy set theory, probability theory, rough sets, and vague sets, but these are limited due to its design.
In 1998, Molodtsov present the idea of soft set theory, which is a mathematical tool to overcome the adversities affecting the above theories [14]. Many authors like Maji et al. present different operations on soft sets and try to consolidate the algebraic aspects of soft sets [15]. A new and different idea of operations was presented by Ali et al. [16]. Many soft algebraic structures such as soft modules [17], soft groups [18], soft rings [19], and soft ordered semigroups [20] were studied. The basic theme and purpose of soft sets are to create the idea of parametrization, and this idea has been utilized to find soft binary relation (SBR) which is a parameterized collection of binary relations on a universe under consideration. This puts forward the consideration for complicated objects that may be perceived from different points of view. In [21–23], Feng et al. presented the relationship between soft, rough, and fuzzy sets and produced rough soft sets, soft rough sets, and soft-rough fuzzy sets.
By using aftersets and foresets notions associated with SBR, a new approximation space is widely utilized these days. By using generalized approximation space based on SBR, different soft substructures in semigroups were approximated by Kanawal and Shabir [24]. Motivated by the idea in [24], soft substructures in quantales are defined, and the aftersets and foresets are employed to construct the lower approximation and upper approximation of soft substructures. Since we are dealing with the approximation of soft subsets of quantale, further soft substructures are employed for further characterization.
There are several authors who introduced rough sets theory in algebraic structures and soft algebraic structures. Iwinski analyzes algebraic properties of rough sets [25]. Qurashi and Shabir present the idea of roughness in Q- module [5]. Idea of the generalized rough quantales (subquantales) was presented by Xiao and Li [6]. Rough prime (semiprime and primary) ideals in quantales were investigated by Yang and Xu [7]. Fuzzy ideals (prime, semiprime, and primary) in quantales were introduced by Luo and Wang [4]. Generalized roughness of fuzzy substructures in quantale is studied by Qurashi et al. [26]. In [27], Yamak et al. proposed the idea of set-valued mappings as the basis of the generalized upper (lower) approximations of a ring with the help of ideals. Rough prime bi Γ-hyper ideals of Γ-semihypergroups were proposed by Yaqoob et al. [28, 29]. Rough substructures of semigroups were studied by Kuroki [30].
The following scheme is designed for the rest of the paper. Some essential explanations related to quantales, its substructures, soft substructures, and their corresponding sequels are connected in Section 2. Notion of approximations of soft sets over quantale generated by soft binary relations is discussed in Section 3. In Section 4, by using these ideas, generalized soft substructures are defined and investigated further fundamental algebraic characteristics of these phenomena. Additionally, we extend this study to define the relationship between homomorphic images and their approximation by soft binary relation in Section 5.
2. Preliminaries
The Ψ − Lappr of R in Θ is the greatest definable in Θ contained in R. The Ψ − Uappr of R in Θ is the least definable set in Θ containing R. For any nonempty subset R in Θ, is called rough set with respect to Ψ or simply a Ψ-rough subset of P(Θ) × P(Θ) if , where P(Θ) denotes the set of all subsets of Θ.
Definition 1 (see [31].)Let Θ be a complete lattice. Define an associative binary relation ∘ on Θ satisfying
Let T1, T2, TI ⊂ Θ, i ∈ I. We define some notions as follows:
Throughout the paper, quantales are denoted by Θ1 and Θ2.
Let ∅≠W⊆Θ. Then, W is called a subquantale of Θ if the following holds:
- (1)
w1°w2 ∈ W, ∀w1, w2 ∈ W.
- (2)
∨i∈Iwi, ∈W, ∀wi, ∈W.
That is, Θ closed under ∘ and arbitrary supremum.
Definition 2 (see [32].)Let Θ be a quantale, ∅≠I⊆Θ is called left (right) ideal if the following satisfied:
- (1)
u, v ∈ I implies u∨v ∈ 1
- (2)
p ∈ Θ, u ∈ I such that p ≤ u implies p ∈ I
- (3)
q ∈ Θ and u ∈ I implies q°u ∈ I(u°q ∈ I)
A nonempty subset I⊆Θ is called ideal of Θ if it is left as well as right ideal.
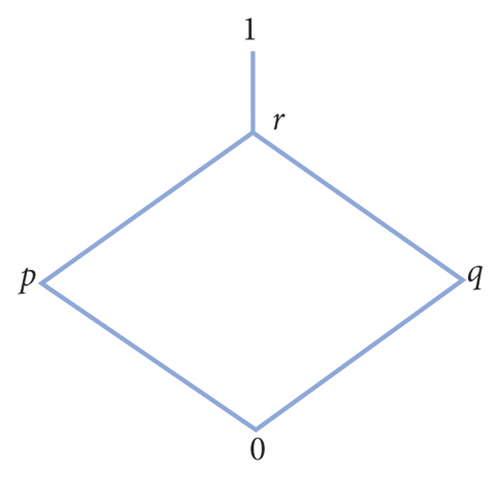
Example 1. Let Θ={0, p, q, r, 1} complete lattices are shown in Figure 1. We define ∘ be the associative binary operation on Θ as shown in Table 1.
Then, Θ is a quantale. Then, {0}, {0, p}, {0, q}, {0, p, q, r}, and Θ are all I of quantale Θ.
| ∘1 | 0 | p | q | r | 1 |
|---|---|---|---|---|---|
| 0 | 0 | p | q | r | 1 |
| p | 0 | p | q | r | 1 |
| q | 0 | p | q | r | 1 |
| r | 0 | p | q | r | 1 |
| 1 | 0 | p | q | r | 1 |
Definition 3 (see [32].)Let ∅≠I⊆Θ be an ideal. I is called prime ideal if, ∀u, v ∈ Θ, u°v ∈ I⇒u ∈ I or v ∈ I. I is called semiprime I if, ∀ u ∈ Θ, u°u ∈ I⇒u ∈ II is called primary I if, ∀u, v ∈ Θ, u°v ∈ I and u ∉ I implies vn ∈ I for some n ∈ Ν.
Definition 4 (see [14].)A pair (Ψ, C) is called a soft set over Θ if Ψ : C⟶P(Θ) where C is a subset of E (the set of parameters).
Definition 5 (see [16].)Let (F, C1) and (H, C2) be two soft sets over Θ. Then, (F, C1) soft subset (H, C2) if the following conditions are fulfilled:
- (1)
C1⊆C2
- (2)
F(c)⊆H(c), ∀ c ∈ C1
Definition 6 (see [33].)Let (Ψ, C) be a soft set over Θ × Θ, that is, Ψ : C⟶P(Θ × Θ). Then, (Ψ, C) is called a soft binary relation (SBR) over Θ × Θ. A SBR over Θ1 × Θ2 is a soft set (Ψ, C) over Θ1 × Θ2. That is, Ψ : C⟶P(Θ1 × Θ2).
Definition 7. Let (Ψ, C) be a soft set over quantale Θ. Then,
- (1)
(Ψ, C) is called soft subquantale over Θ iff Ψ(c) is a subquantale of Θ, ∀ c ∈ C
- (2)
(Ψ, C) is called soft ideal over Θ iff Ψ(c) is an ideal of Θ, ∀ c ∈ C
- (3)
(Ψ, C) is called soft prime ideal over Θ iff Ψ(c) is a prime ideal of Θ, ∀ c ∈ C
- (4)
(Ψ, C) is called soft semiprime ideal over Θ iff Ψ(c) is a semiprime ideal of Θ, ∀ c ∈ C
- (5)
(Ψ, C) is called soft primary ideal over Θ iff Ψ(c) is a primary ideal of Θ, ∀ c ∈ C
3. Approximation of Soft Sets over Quantale by Soft Binary Relation
In this section, we present some important aspects regarding to the approximation of soft sets in quantale Θ by SBR. We utilized aftersets and foresets to approximate soft sets.
Definition 8 (see [34].)Let (Ψ, C) be a SBR over Θ1 × Θ2, where C⊆E (parametric set). Then, Ψ : C⟶P(Θ1 × Θ2). For a soft set (F, C) over Θ2, the Lappr and Uappr of (F, C) w.r.t the afterset are essentially two soft sets over Θ1, which is defined as
And for a soft set (H, C) over Θ1, the Lappr and Uappr of (H, C) w.r.t the foreset are actually two soft sets over Θ2, which is defined as
For all c ∈ C, where q1Ψ(c)={q2 ∈ Θ2 : (q1, q2) ∈ Ψ(c)} is called the afterset of q1 and Ψ(c)q2={q1 ∈ Θ1 : (q1, q2) ∈ Ψ(c)} is called the foreset of q2.
Remark 1.
- (1)
For each soft set (F, C) over Θ2, and
- (2)
For each soft set (H, C) over Θ1, and
Definition 9. Let (Ψ, C) be a SBR over Θ1 × Θ2, that is, Ψ : C⟶P(Θ1 × Θ2). Then, (Ψ, C) is called soft compatible relation (SCPR) if for all p, r, ji ∈ Θ1 and q, s, ki ∈ Θ2(i ∈ I), we have
- (1)
(p, q), (r, s) ∈ Ψ(c)⇒(p∘1r, q∘2s)∈Ψ(c)
- (2)
(ji, ki) ∈ Ψ(c)⇒(∨i∈Iji, ∨i∈Iki)∈Ψ(c)
Definition 10. A SCPR (Ψ, C) over Θ1 × Θ2 is called soft complete relation (SCTR) with respect to the afterset if, for all p, r, ∈ Θ1, we have
- (1)
pΨ(c)∨rΨ(c)=(p∨r)Ψ(c)
- (2)
pΨ(c)∘2rΨ(c)=(p∘1r)Ψ(c)
A SCPR (Ψ, C) is called ∨-complete w.r.t the aftersets if it satisfies only condition (1). A SCPR (Ψ, C) is called °-complete w.r.t the aftersets if it satisfies only condition (2).
A SCPR (Λ, C) over Θ1 × Θ2 is called soft complete relation (SCTR) with respect to the foreset if for all q, s ∈ Θ2, and we have
- (1)
Λ(c)q∨Λ(c)s=Λ(c)(q∨s)
- (2)
Λ(c)q∘1Λ(c)s=Λ(c)(q∘2s)
A SCPR (Λ, C) is called ∨-complete w.r.t the foresets if it satisfies only condition (1).
A SCPR (Λ, C) is called °-complete w.r.t the foresets if it satisfies only condition (2).
Theorem 1. Let (Ψ, C) be a SCPR with respect to the afterset over Θ1 × Θ2. Then, for any two soft sets (F1, C) and (F2, C) over Θ2, we have
- (1)
- (2)
Proof. For arbitrary c ∈ C, let Then, x=y1∘1y2 for some and . This implies that y1Ψ(c)∩F1(c) ≠ ∅ and y2Ψ(c)∩F2(c) ≠ ∅, so there exist elements l, m ∈ Θ2 such that l ∈ y1Ψ(c)∩F1(c) and m ∈ y2Ψ(c)∩F2(c). Thus, l ∈ y1Ψ(c), m ∈ y2Ψ(c), l ∈ F1(c) and m ∈ F2(c). So (y1, l) ∈ Ψ(c) and (y2, m) ∈ Ψ(c) imply (y1∘1y2, l∘2m) ∈ Ψ(c); that is, (l∘2m) ∈ (y1∘1y2)Ψ(c). Also, l∘2m∈F1(c)∘2F2(c); therefore, l∘2m ∈ y1∘1y2Ψ(c)∩F1(c)∘2F2(c). This shows that
Now, for arbitrary c ∈ C, let Then, x=y1∨y2 for some and . This implies that y1Ψ(c)∩F1(c) ≠ ∅ and y2Ψ(c)∩F2(c) ≠ ∅, so there exist elements l, m ∈ Θ2 such that l ∈ y1Ψ(c)∩F1(c) and m ∈ y2Ψ(c)∩F2(c). Thus, l ∈ y1Ψ(c), m ∈ y2Ψ(c), l ∈ F1(c), and m ∈ F2(c). So (y1, l) ∈ Ψ(c) and (y2, m) ∈ Ψ(c) imply (y1∨y2, l∨m) ∈ Ψ(c); that is, (l∨m) ∈ (y1∨y2)Ψ(c). Also, l∨m ∈ F1(c)∨F2(c); therefore, l∨m ∈ y1∨y2Ψ(c)∩F1(c)∨F2(c). This shows that
Theorem 2. Let (Ψ, C) be a SCPR with respect to the foreset over Θ1 × Θ2. Then, for any two soft sets (L1, C) and (L2, C) over Θ1, we have
- (1)
- (2)
Proof. The proof is simple.
Theorem 3. Let (Ψ, C) be a SCTR w.r.t the afterset over Θ1 × Θ2. Then, for any two soft sets (F1, C) and (F2, C) over Θ2, we have
- (1)
- (2)
Proof. For arbitrary c ∈ C, if at least one of and is empty, then (1) is obvious. Now, for arbitrary c ∈ C, consider that and . Then, . So, let . Then, x=y1°1y2 for some and . This implies that ∅≠y1Ψ(c)⊆F1(c) and ∅≠y2Ψ(c)⊆F2(c). As (y1°1y2)Ψ(c)=y1Ψ(c)°2Ψ(c)⊆F1(c)°2F2(c). This shows that . Hence, (1) is proved.
For arbitrary c ∈ C, if at least one of and is empty, then (2) is obvious. Now, for arbitrary c ∈ C, consider that and . Then, . So, let . Then, x=y1∨y2 for some and . This implies that ∅≠y1Ψ(c)⊆F1(c) and ∅≠y2Ψ(c)⊆F2(c). As (y1∨y2)Ψ(c)=y1Ψ(c)∨y2Ψ(c)⊆F1(c)∨F2(c). This shows that . Hence, (2) is proved.
Theorem 4. Let (Ψ, C) be a SCTR with respect to the foreset over Θ1 × Θ2. Then, for any two soft sets (L1, C) and (L2, C) over Θ1, we have
- (1)
- (2)
Proof. The proof is obvious.
4. Approximation of Soft Substructures in Quantales
In this section, we consider two quantales Θ1 and Θ2 and approximate different soft substructures of quantales by using different SBR over Θ1 × Θ2. We will show that Uappr of a soft substructure of quantales by using SCPR is again a soft substructure of quantales and provide counter examples to support the argument that the converse is not true. Also, we will show that Lappr of a soft substructure of quantales by using SCTR is again a soft substructure of quantales and provide a counter example to support the argument that the converse is not true.
Throughout this section, we consider (Ψ, C) to be the SBR over Θ1 × Θ2 and xΨ(c) ≠ ∅ for all x ∈ Θ1, c ∈ C, and Ψ(c)y ≠ ∅ for all y ∈ Θ2, c ∈ C unless otherwise specified.
Definition 11. Let (Ψ, C) be a SBR over Θ1 × Θ2 and (F, C) be a soft set over Θ2. If Uappr. is a soft subquantale of Θ1, then (F, C) is called generalized upper soft (GUpS) subquantale of Θ1 w.r.t the aftersets. If Uappr is a soft ideal (prime ideal, semiprime ideal, and primary ideal) of Θ1, then (F, C) is called GUpS ideal (prime ideal, semiprime ideal, and primary ideal) of Θ1 w.r.t the aftersets.
Definition 12. Let (Ψ, C) be a SBR over Θ1 × Θ2 and (L, C) be a soft set over Θ1. If Uappr is a soft subquantale of Θ2, then (L, C) is called generalized upper soft (GUpS) subquantale of Θ2 w.r.t the foresets. If Uappr is a soft ideal (prime ideal, semiprime ideal, and primary ideal) of Θ2, then (L, C) is called GUpS ideal (prime ideal, semiprime ideal, and primary ideal) of Θ2 w.r.t the foresets.
Theorem 5. Let (Ψ, C) be a SCPR over Θ1 × Θ2. If (F, C) is a soft subquantale of Θ2, then (F, C) is a GUpS subquantale of Θ1 w.r.t the aftersets.
Proof. Suppose that (F, C) is a soft subquantale, then for any c ∈ C. Let , i ∈ I. Then, piΨ(c)∩F(c) ≠ ∅. So, there exists qi ∈ piΨ(c)∩F(c). Thus, qi ∈ piΨ(c) and qi ∈ F(c) since (Ψ, C) is a SCPR. Therefore, (pi, qi) ∈ Ψ(c), i ∈ I implies (∨i∈Ipi, ∨i∈Iqi) ∈ Ψ(c). This implies that ∨i∈Iqi ∈ ∨i∈IpiΨ(c). Also, ∨i∈Iqi ∈ F(c) (as (F, C) is a soft subquantale). So, ∨i∈Iqi ∈ ∨i∈Ipi ∈ Ψ(c)∩F(c). Hence, .
Let . Then, p1Ψ(c)∩F(c) ≠ ∅ and . So, there exists q1 ∈ p1Ψ(c)∩F(c) and q2 ∈ p2Ψ(c)∩F(c). Thus, q1 ∈ p1Ψ(c), q1 ∈ F(c), q2 ∈ p2Ψ(c), and q2 ∈ F(c) since (Ψ, C) is a SCPR. Therefore, (p1, q1), (p2, q2) ∈ Ψ(c) implies (p1°1q1), (p2°2q2) ∈ Ψ(c). This implies that q1°2q2 ∈ p1°p2Ψ(c). Also, q1°2q2 ∈ (c) (as (F, C) is a soft subquantale). So, q1°2q2 ∈ p1°p2Ψ(c)∩F(c). Hence, . This completes the proof.
With the same arguments, the next Theorem 6 can be achieved.
Theorem 6. Let (Ψ, C) be a SCPR over Θ1 × Θ2. If (L, C) is a soft subquantale of Θ1, then (L, C) is a GUpS subquantale of Θ2 w.r.t the foresets.
Theorem 7. Let (Ψ, C) be a soft ∨-complete relation over Θ1 × Θ2 w.r.t the aftersets. If (F, C) is a soft left (right) ideal of Θ2, then (F, C) is a GUpS left (right) ideal of Θ1 w.r.t the aftersets.
Proof. Suppose that (F, C) is a soft left ideal of Θ2, then for any c ∈ C. Let . Then, u1Ψ(c)∩F(c) ≠ ∅ and u2Ψ(c)∩F(c) ≠ ∅. So, there exists v1 ∈ u1Ψ(c)∩F(c) and v2 ∈ u2Ψ(c)∩F(c). Thus, v1 ∈ u1Ψ(c), v1 ∈ F(c), v2 ∈ u2Ψ(c), and v2 ∈ F(c) since (Ψ, C) is a SCPR. Therefore, (u1∨u2, v1∨v2) ∈ Ψ(c); that is, v1∨v2 ∈ (u1∨u2)Ψ(c). Also, v1∨v2 ∈ F(c) (as (F, C) is a soft left ideal). So, v1∨v2 ∈ (u1∨u2)Ψ(c)∩F(c). Hence, .
Now, let u1, u2 ∈ Θ1 such that u1 ≤ u2 and . So, . Since , so there exist v2 ∈ u2Ψ(c)∩F(c). Thus, v2 ∈ u2Ψ(c) and v2 ∈ F(c). Since (Ψ, C) is a soft ∨-complete relation, therefore, v2 ∈ u2Ψ(c)=u1∨u2Ψ(c)=u1Ψ(c)∨u2Ψ(c). This implies that v2=s∨t, for some s ∈ u1Ψ(c) and t ∈ u2Ψ(c). Thus, s ≤ v2 and v2 ∈ F(c) imply s ∈ F(c) (as F(c) is ideal). So, s ∈ u1Ψ(c)∩F(c). Hence, .
Let p, x ∈ Θ1 and . Then, xΨ(c)∩F(c) ≠ ∅. So, there exist q ∈ xΨ(c)∩F(c). Thus, q ∈ xΨ(c) and q ∈ F(c). Since (F, C) is a soft left ideal so, y∘2q ∈ F(c) for any y ∈ pΨ(c)⊆Θ2. This implies that (p, y) ∈ Ψ(c). So, (p∘1x, y∘2q) ∈ Ψ(c); that is, y∘2q ∈ p∘1xΨ(c). So, y∘2q ∈ p∘1xΨ(c)∩F(c). Hence, . Similarly, we can show that .
Theorem 8. Let (Ψ, C) be a SCTR over Θ1 × Θ2 w.r.t the aftersets. If (F, C) is a soft prime ideal of Θ2, then (F, C) is a GUpS prime ideal of Θ1 w.r.t the aftersets.
Proof. Assume that (F, C) is a soft prime ideal of Θ2, then for any c ∈ C. Then, by Theorem 5, (F, C) is generalized upper soft ideal of Θ1. Let p1, p2 ∈ Θ1 such that . Then, (p1∘1p2)Ψ(c)∩F(c) ≠ ∅. So, there exist q ∈ (p1∘1p2)Ψ(c)∩F(c). This implies that q ∈ (p1∘1p2)Ψ(c) and q ∈ F(c). Since (Ψ, C) is a SCTR, q ∈ (p1∘1p2)Ψ(c)=p1Ψ(c)∘2p2Ψ(c). Thus, q=c∘2d for some c ∈ p1Ψ(c) and d ∈ p2Ψ(c). Thus, c∘2d ∈ F(c) and (F, C) is a soft prime ideal of Θ2 so, c ∈ F(c) or d ∈ F(c). Thus, c ∈ p1Ψ(c)∩F(c) or d ∈ p2Ψ(c)∩F(c). Hence, or .
Theorem 9. Let (Ψ, C) be a SCTR over Θ1 × Θ2 w.r.t the aftersets. If (F, C) is a soft semiprime ideal of Θ2, then (F, C) is a GUpS semiprime ideal of Θ1 w.r.t the aftersets.
Proof. Assume that (F, C) is a soft semiprime ideal of Θ2, then for any c ∈ C. Then, by Theorem 5, (F, C) is generalized upper soft ideal of Θ1. Let p1 ∈ Θ1 such that . Then, (p1∘1p1)Ψ(c)∩F(c) ≠ ∅. So, there exist q ∈ (p1∘1p1)Ψ(c)∩F(c). This implies that q ∈ (p1∘1p1)Ψ(c) and q ∈ F(c). Since (Ψ, C) is a SCTR, q ∈ (p1∘1p1)Ψ(c)=p1Ψ(c)∘2 p1Ψ(c). Thus, q=c ∘2 c for some c ∈ p1Ψ(c). Thus, c∘2c ∈ F(c) and (F, C) is a soft semiprime ideal of Θ2 so, c ∈ F(c). Thus, c ∈ p1Ψ(c)∩F(c). Hence, .
Theorem 10. Let (Ψ, C) be a SCTR over Θ1 × Θ2 w.r.t the aftersets. If (F, C) is a soft primary ideal of Θ2, then (F, C) is a GUpS primary ideal of Θ1 w.r.t the aftersets.
Proof. Assume that (F, C) is a soft primary ideal of Θ2, then for any c ∈ C. Then, by Theorem 5, (F, C) is generalized upper soft ideal of Θ1. Let p1, p2 ∈ Θ1 such that p1∘1p2∈ and . Then, (p1∘1p2)Ψ(c)∩F(c) ≠ ∅. So, there exist q ∈ (p1∘1p2)Ψ(c)∩F(c). This implies that q ∈ (p1∘1p2)Ψ(c) and q ∈ F(c). Since (Ψ, C) is a SCTR, q ∈ (p1∘1p2)Ψ(c)=p1Ψ(c)∘2p2Ψ(c). Thus, q=c∘2d for some c ∈ p1Ψ(c) and d ∈ p2Ψ(c). Thus, c∘2d ∈ F(c) and (F, C) is a soft primary ideal of Θ2 so dn ∈ F(c) for some n ∈ ℕ. Also, for n ∈ ℕ. Thus, . Hence, .
Remark 2. In general, the converse of the above theorem is not true. We will present examples to justify our claim as follows.
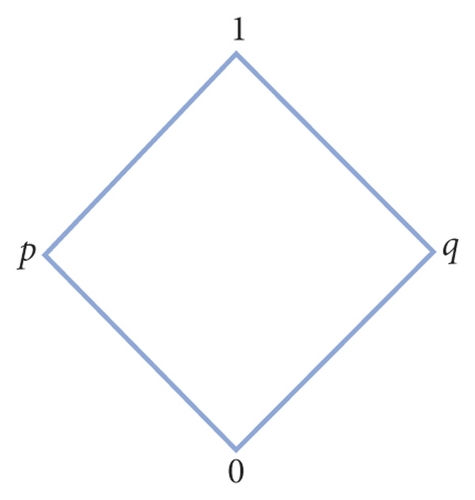
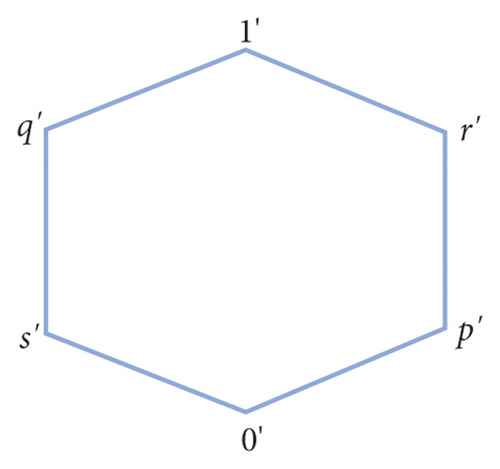
Example 2. Let Θ1={0, p, q, 1} and Θ2={0′, s′, q′, p′, 1′, r′} be two complete lattices described in Figures 2 and 3, respectively.
We define ∘1 and ∘2 the associative binary operation on Θ1 and Θ2, respectively, as shown in Tables 2 and 3. Then, and are quantales.
- (1)
Let C={c1, c2} and define SBR (Ψ, C) over Θ1 × Θ2 by the rule
(8) -
Then, (Ψ, C) is SCPR. The aftersets with respect to Ψ(c1) and Ψ(c2) are given as follows:
(9) -
Define soft set (F, C) over Θ2 by the rule
(10) -
Then, (F, C) is not a soft subquantale of Θ2. But and are subquantale of Θ1. So (F, C) is a GUpSSΘ of Θ1 w.r.t the aftersets.
-
Foresets with respect to Ψ(c1) and Ψ(c2) are given as follows:
(11) -
Define soft set (L, C) over Θ1 by the rule
(12) -
Then, (L, C) is not a soft subquantale of Θ1. But and are subquantale of Θ2. So, (L, C) is a GUpS subquantale of Θ2 w.r.t the foresets.
- (2)
Now, let C={c1, c2} and define SBR (Ψ, C) over Θ1 × Θ2 by the rule
Aftersets with respect to Ψ(c1) and Ψ(c2) are given as follows:
Then, (Ψ, C) is ∨-complete relation over Θ1 × Θ2 w.r.t the aftersets. Define soft set (F, C) over Θ2 by the rule
Then, (F, C) is not a soft ideal of Θ2. But and are ideal of Θ1. So, (F, C) is a GUpS ideal of Θ1 w.r.t the aftersets.
Now, define SBR (Ψ, C) over Θ1 × Θ2 by the rule
Foresets with respect to Ψ(c1) and Ψ(c2) are given as follows:
Then, (Ψ, C) is soft ∨-complete relation over Θ1 × Θ2 w.r.t the foresets. Define soft set (L, C) over Θ1 by the rule
Then, (L, C) is not a soft ideal of Θ1. But and are ideal of Θ2. So, (L, C) is a GUpS ideal of Θ2 w.r.t the foresets.
Similar examples can be presented to justify that converse of Theorems 11 to 13 is not true.
| O1 | 0 | p | q | 1 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| p | 0 | p | 0 | p |
| q | 0 | 0 | q | q |
| 1 | 0 | p | q | 1 |
| O2 | 0′ | s′ | p′ | q′ | r′ | 1′ |
|---|---|---|---|---|---|---|
| 0′ | 0′ | s′ | p′ | q′ | r′ | 1′ |
| s′ | 0′ | s′ | p′ | q′ | r′ | 1′ |
| p′ | 0′ | s′ | p′ | q′ | r′ | 1′ |
| q′ | 0′ | s′ | p′ | q′ | r′ | 1′ |
| r′ | 0′ | s′ | p′ | q′ | r′ | 1′ |
| 1′ | 0′ | s′ | p′ | q′ | r′ | 1′ |
Definition 13. Let (Ψ, C) be a SBR over Θ1 × Θ2. Consider the soft set (M, C) over Θ2, if Lappr is a soft subquantale of Θ1, then (M, C) is called generalized lower soft (GLWS) subquantale of Θ1 w.r.t the aftersets. If Lappr is a soft ideal (prime ideal, semiprime ideal, and primary ideal) of Θ1, then (M, C) is called GUpS ideal (prime ideal, semiprime ideal, and primary ideal) of Θ1 w.r.t the aftersets.
Definition 14. Let (Ψ, C) be a SBR over Θ1 × Θ2. Consider the soft set (L, C) over Θ1, if Lappr is a soft subquantale of Θ2, then (L, C) is called GLWS subquantale of Θ2 w.r.t the foresets. If Lappr is a soft ideal (prime ideal, semiprime ideal, and primary ideal) of Θ2, then (L, C) is called GUpS ideal (prime ideal, semiprime ideal, and primary ideal) of Θ2 w.r.t the foresets.
Theorem 11. Let (Ψ, C) be a SCTR over Θ1 × Θ2 w.r.t the aftersets. If (M, C) is a soft subquantale of Θ2, then (M, C) is a GLWS subquantale of Θ1 w.r.t the aftersets.
Proof. Suppose that (M, C) is a soft subquantale of Θ2 and for any c ∈ C. Let . Then, uiΨ(c)⊆M(c). Since (Ψ, C) is a SCTR, therefore, ∨i∈I(uiΨ(c))=(∨i∈Iui)Ψ(c)⊆M(c). Hence, .
Now, let . Then, u1Ψ(c)⊆M(c) and u2Ψ(c)⊆M(c). Since (Ψ, C) is a SCTR and (M, C) is a soft subquantale, therefore, u1Ψ(c)∘2u2Ψ(c)⊆M(c)∘2M(c) implies (u1∘1u2)Ψ(c)⊆M(c). Hence, .
With the same arguments, next Theorem 12 can be achieved.
Theorem 12. Let (Ψ, C) be a SCTR over Θ1 × Θ2 w.r.t the foresets. If (L, C) is a soft subquantale of Θ1, then (L, C) is a GLWS subquantale of Θ2 w.r.t the foresets.
Theorem 13. Let (Ψ, C) be a SCTR over Θ1 × Θ2 w.r.t the aftersets. If (M, C) is a soft ideal of Θ2, then (M, C) is a GLWS ideal of Θ1 w.r.t the aftersets.
Proof. Suppose that (M, C) is a soft ideal of Θ2 and for any c ∈ C. Let . Then, u1Ψ(c)⊆M(c) and u2Ψ(c)⊆M(c). Since (Ψ, C) is a SCTR and (M, C) is a soft ideal of Θ2 so u1Ψ(c)∨u2Ψ(c)=(u1∨u2)Ψ(c)⊆M(c)∨M(c); that is, (u1∨u2)Ψ(c)⊆M(c) Hence, .
Now, let u1, u2 ∈ Θ1 such that u1 ≤ u2 and . So, . Let, v1 ∈ u1Ψ(c) and v2 ∈ u2Ψ(c)⊆M(c). So, v1∨v2 ∈ (u1∨u2)Ψ(c), that is, v1∨v2 ∈ u2Ψ(c)⊆M(c). Since M(c) is ideal so v1 ≤ v1∨v2 ∈ M(c) implies v1 ∈ M(c). Thus, u1Ψ(c)⊆M(c). Hence, .
Now, let u, y ∈ Θ1 and . Then, ∅≠yΨ(c)⊆M(c). Consider v1∈(u∘1y)Ψ(c) since (Ψ, C) is a SCTR so v1 ∈ u Ψ(c)∘2yΨ(c). Thus, v1=c∘2d for some c ∈ uΨ(c) and d ∈ yΨ(c). But yΨ(c)⊆M(c) so d ∈ M(c) and (M, C) is a soft ideal of Θ2; therefore, c∘2d ∈ M(c), that is, v1 ∈ M(c). Thus, (u∘1y)Ψ(c)⊆M(c). Hence, . Similarly, we can show that .
Theorem 14. Let (Ψ, C) be a SCTR over Θ1 × Θ2 w.r.t the aftersets. If (M, C) is a soft prime ideal of Θ2, then (M, C) is a GLWS prime ideal of Θ1 w.r.t the aftersets.
Proof. Assume that (M, C) is a soft prime ideal of Θ2 and for any c ∈ C. Then, by Theorem 4.19, (M, C) is GLWS ideal of Θ1. Let u1, u2 ∈ Θ1 such that . Then, (u1∘1u2)Ψ(c)⊆M(c). Consider v ∈ (u1∘1u2)Ψ(c)⊆M(c). Since (Ψ, C) is a SCTR, v ∈ (u1∘1u2)Ψ(c)=u1Ψ(c)∘2u2Ψ(c). Thus, v=c∘2d for some c ∈ u1Ψ(c) and d ∈ u2Ψ(c). This implies that v=c∘2d ∈ M(c). As (M, C) is a soft prime ideal so, c ∈ M(c) or d ∈ M(c). Thus, c ∈ u1Ψ(c)⊆M(c) or d ∈ u2Ψ(c)⊆M(c). Hence, or .
Theorem 15. Let (Ψ, C) be a SCTR over Θ1 × Θ2 w.r.t the aftersets. If (M, C) is a soft semiprime ideal of Θ2, then (M, C) is a GLWS semiprime ideal of Θ1 w.r.t the aftersets.
Proof. Assume that (M, C) is a soft semiprime ideal of Θ2 and for any c ∈ C. Then, by Theorem 14,(M, C) is GLWS ideal of Θ1. Let u ∈ Θ1 such that . Then, (u∘1u)Ψ(c)⊆M(c). Let v ∈ uΨ(c). As (Ψ, C) is a SCTR so v∘2v ∈ (u∘1u)Ψ(c)⊆M(c). Since (M, C) is a soft semiprime ideal, v∘2v ∈ M(c) implies v ∈ M(c). Thus, uΨ(c)⊆M(c). Hence, .
Theorem 16. Let (Ψ, C) be a SCTR over Θ1 × Θ2 w.r.t the aftersets. If (M, C) is a soft primary ideal of Θ2, then (M, C) is a GLWS primary ideal of Θ1 w.r.t the aftersets.
Proof. Suppose that (M, C) is a soft primary ideal of Θ2 and for any c ∈ C. Then, by Theorem 4.19., (M, C) is a GLWS ideal of Θ1. Let u1, u2 ∈ Θ1 such that and . Then, (u1∘1u2)Ψ(c)⊆M(c). Let v ∈ (u1∘1u2)Ψ(c). Since (Ψ, C) is a SCTR, v ∈ u1Ψ(c)∘2u2Ψ(c). Thus, v=c∘2d for some c ∈ u1Ψ(c) and d ∈ u2Ψ(c). Thus, for some n ∈ ℕ. Also, c∘2d ∈ M(c). As (M, C) is a soft primary ideal, c ∉ M(c) and dn ∈ M(c). Thus, . Hence, for some n ∈ ℕ.
5. Relationship between Soft Quantale Homomorphism and Their Approximation
In this section, we define soft weak quantale homomorphism (SWQH), and then, we established the relationship between homomorphic images and their approximation by SBR.
Definition 15 (see [4].)A function η : Θ1⟶Θ2 is called weak quantale homomorphism (WQH) if η(p∘1q)=η(p)∘2η(q) and η(p∨q)=η(p)∨η(q), where (Θ1, ∘1) and (Θ2, ∘2) are quantales. If η is one-one, then η is monomorphism. If η is onto, then η is called epimorphism, and if η is bijective, then η is called isomorphism between (Θ1, ∘1) and (Θ2, ∘2).
Definition 16. Let (H, C1) be a soft quantale over Θ1 and (F, C2) be a soft quantale over Θ2. Then, (H, C1) is said to soft weak homomorphic to (F, C2) if there exist ordered pair of functions (η, ζ) satisfies the following
- (1)
η : Θ1⟶Θ2 is onto WQH, that is, η(p∘1q)=η(p)∘2η(q) and η(p∨q)=η(p)∨η(q)
- (2)
ζ : C1⟶C2 is surjective
- (3)
η(H(c1))=F(ζ(c1)), ∀c1 ∈ C1
The ordered pair (η, ζ) of functions is SWQH. If in ordered pair (η, ζ) both η and ζ are one-to-one functions, then (H, C1) is said to soft weak isomorphic to (F, C2) and (η, ζ) is called SWQI.
Lemma 1. Let (H, C1) be soft weak homomorphic to (F, C2) with SWQH (η, ζ). Let (Ψ2, C3) be a SBR over Θ2 and . Define Ψ1(c3)={}(x, y)∈Θ1 × Θ1:(η(x), η(y)) ∈ Ψ2(c3){} be a SBR over Θ1. Then, the following holds:
- (1)
(Ψ1, C3) is SCPR if (Ψ2, C3) is SCPR
- (2)
If (η, ζ) is SWQI and (Ψ2, C3) is SCPR w.r.t the aftersets (w.r.t the foresets), then (Ψ1, C3) is SCPR w.r.t the aftersets (w.r.t the foresets)
- (3)
- (4)
⊆ and if (η, ζ) is SWQI, then
- (5)
Let (η, ζ) be a SWQI. Then, and ⇔
Proof.
- (1)
and (2) are obvious
- (3)
Suppose and for any c3 ∈ C3, for some z ∈ Θ2. Then, there exist a ∈ Θ1 such that and η(a)=z. Thus, . So, (a, x) ∈ Ψ1(c3) and . Thus, (η(a), η(x)) ∈ Ψ2(c3), that is, η(x) ∈ η(a)Ψ2(c3). Also, . So, η(a)Ψ2(c3)∩≠∅. This implies that . Hence, .
-
Now, let . Then, wΨ2(c3)∩. This implies that . Thus, y ∈ wΨ2(c3) and . This implies that there exists and x1 ∈ Θ1 such that η(x)=y and η(x1)=w. So, (w, y)=(η(x1), η(x))∈Ψ2(c3). This implies that (x1, x) ∈ Ψ1(c3). So, . Thus, . So, . Hence, . Consequently, .
- (4)
Suppose and for any c3 ∈ C3, for some z ∈ Θ2. Then, there exist a ∈ Θ1 such that and η(a)=z. Thus, . Let x ∈ zΨ2(c3). Then, there exist y ∈ Θ1 such that η(y)=x. So, η(y) ∈ η(a)Ψ2(c3), that is, (η(a), η(y)) ∈ Ψ2(c3). So, (a, y) ∈ Ψ1(c3), that is, y ∈ aΨ1(c3). Thus, η(y)∈. So, η(a)Ψ2(c3)⊆. Thus, . Hence, .
-
Now, let . Then, there exist unique a ∈ Θ1 such that η(a)=z and . Let x ∈ aΨ1(c3), that is, (a, x) ∈ Ψ1(c3). Then, (η(a), η(x)) ∈ Ψ2(c3). Then, . So, . This implies that . So, . Then, . So, . Hence, . Consequently, .
- (6)
Let for any c3 ∈ C3. Then, . Conversely, suppose that . As η is bijection so . Similarly, we can show that ⇔.
Remark 4. With a similar technique, Lemma 1 can be proved but for the foresets.
Theorem 17. Let (H, C1) be soft weak isomorphic to (F, C2) with SWQI (η, ζ). Let (Ψ2, C3) be a SCPR over Θ2 and . Define Ψ1(c3)={}(x, y)∈Θ1 × Θ1:(η(x), η(y))∈Ψ2(c3){} for any c3 ∈ C3. Then, the following holds:
- (1)
is an ideal of Θ1 iff is an ideal of Θ2 for all c3 ∈ C3
- (2)
is a subquantale of Θ1 iff is a subquantale of Θ2 for all c3 ∈ C3
- (3)
is a prime ideal of Θ1 iff is a prime ideal of Θ2 for all c3 ∈ C3
- (4)
is a semiprime ideal of Θ1 iff is a semiprime ideal of Θ2 for all c3 ∈ C3
- (5)
is a primary ideal of Θ1 iff is a primary ideal of Θ2 for all c3 ∈ C3
Proof.
- (1)
Let be an ideal of Θ1 for any c3 ∈ C3. We will show that is an ideal of Θ2. By Lemma 1 (3), we have
Let . Then, there exist such that η(u)=p and η(v)=q. Since is ideal and (η, ζ) is SWQI so p∨q=η(u)∨η(v)=η(u∨v)∈.
Now, let p, q ∈ Θ2 such that p ≤ q and . Then, there exist u ∈ Θ1 and such that η(u)=p and η(v)=q. So, η(u) ≤ η(v) implies η(u∨v)=η(u). This implies that . This implies that u ≤ v and are ideal so . Thus, .
Finally, let p ∈ Θ2 and . Then, there exist u ∈ Θ1 and such that η(u)=p and η(v)=q. Since ideal, . Thus, η(u∘1v). Similarly, . Hence, is ideal of Θ2.
Conversely, suppose that = be an ideal of Θ2 for any c3 ∈ C3. We will show that is ideal of Θ1.
Let . Then, η(u), η(v)∈. Since is ideal so . Then, by Lemma 5.2(5), .
Now, let u, v ∈ Θ1 such that u ≤ v and . Then, . Thus, η(u∨v)=η(u)∨η(v)=η(v)∈. This implies that η(u) ≤ η(v). Since is ideal . Then, by Lemma 5.2(5), . Finally, let u ∈ Θ1 and . Then, η(u) ∈ Θ2 and . Since is ideal, , that is, . Thus, u∘1v∈. In a similar way, we can show that . This completes the proof.
The proof of (2)–(5) is similar to the proof of (1).
Remark 5. Theorem 17with a similar technique can be proved but for the foresets.
With the same arguments, the next Theorem 18 can be achieved.
Theorem 18. Let (H, C1) be soft weak isomorphic to (F, C2) with SWQI (η, ζ). Let (Ψ2, C3) be a SCTR over Θ2 and . Define Ψ1(c3)={}(x, y)∈Θ1 × Θ1:()η(x), η()y∈Ψ2(c3){} for any c3 ∈ C3. Then, the following holds:
- (1)
is an ideal of Θ1 iff is an ideal of Θ2 for all c3 ∈ C3
- (2)
is a subquantale of Θ1 iff is a subquantale of Θ2 for all c3 ∈ C3
- (3)
is a prime ideal of Θ1 iff is a prime ideal of Θ2 for all c3 ∈ C3
- (4)
is a semiprime ideal of Θ1 iff is a semiprime ideal of Θ2 for all c3 ∈ C3
- (5)
is a primary ideal of Θ1 iff is a primary ideal of Θ2 for all c3 ∈ C3
6. Comparison
Yang and Xu [7] introduced rough approximations in quantale which is a kind of partially ordered algebraic structure with an associative binary operation. The main idea of work in [7] is based on equivalence relation equipped with congruence relation in quantale. In fact, the generalization of Pawlak’s space is discussed in [7]. Further approximation of fuzzy substructures of quantale in crisp atmospheric space was discussed in [4]. Sometimes, it is difficult to find out an equivalence relation and then congruence while finding rough substructures in quantale. To remove this hurdle, soft binary relations are utilized in this paper. Since suitable soft binary relations are easy to find out, it is an easy approach to apply soft rough properties to approach different characterizations of soft rough structures in quantale with the help of aftersets and foresets.
7. Conclusion
The new combined effect of an algebraic structure quantale with rough and soft sets is presented by using soft binary relation, in this paper. The soft substructures of quantales like soft subquantale and soft ideal are discussed. The approximation w.r.t aftersets and foresets of these substructures by SBR which is an extended notion of Pawlak’s rough approximation space are presented. The more generalized version of approximation space implied from SBR over Θ1 × Θ2 is employed. This new relation over Θ1 × Θ2 enables us to use the concept of aftersets and foresets to express the lower and upper approximation. Important results regarding to the approximation of soft substructures of quantales under SBR with some essential algebraic conditions such as compatible and complete relations are introduced. To emphasize and make a clear understanding, soft compatible and soft complete relations are focused, and these are interpreted by aftersets and foresets. Particularly, in our work, soft compatible and soft complete relations play an important role. Crux of these results is that whenever we approximate a soft algebraic structure of quantale, corresponding upper and lower approximations, are again the same kind of soft algebraic structure. Furthermore, we presented the soft quantale homomorphism and established the relationship of soft homomorphic images with their approximation under SBR.
In future, one can use this work and generalize it to different soft algebraic structures such as soft quantale modules, soft hypergroups, soft hyperquantales, and soft hyperrings. One can take motivation from our generalized approximation space and define new approximation spaces.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Open Research
Data Availability
No data were used to support this study.




