Let ξ be a simple connected graph. The first Gourava index of graph ξ is defined as GO₁(ξ) = ∑_μη∈E(ξ)[d(μ) + d(η) + d(μ)d(η)], where d(μ) indicates the degree of vertex μ. In this paper, we will find the upper bound of GO₁(ξ) for trees of given diameter, order, size, and pendent nodes, by using some graph transformations. We will find the extremal trees and also present an ordering of these trees having this index in decreasing order.

1. Introduction

Topological index is very basic tool in chemical modeling. In molecular graph, atoms are considered as vertices and chemical bonds as edges. In short, the graph is a combination of vertices and edges. First chemical index was Wiener index introduced by Wiener [1] in 1947 to compare the boiling points of few alkanes isomers; he revealed that this index is highly agreed with the boiling point of molecules of alkanes. Later study on QSAR manifested that this index is also helpful to correlate with other quantities like density, critical point, and surface tension. The mathematical formula of this index is given as

(1)

where d_ξ(μ, η) indicates the distance between the vertices μ and η in ξ. The most studied degree-based indices, i.e., Zagreb indices introduced by Gutman and Das [2], are defined as follows

(2)

Some properties about these indices are depicted in [3, 4]. The 1^st and 2^nd reformulated Zagreb indices were regenerated by Mili

evic^′ et al. [5] in terms of edge degree, defined as

(3)

The 1^st and 2^nd Gourava indices were presented by V. R. Kulli in 2017 [6]. These indices are defined as

(4)

A topological index is a mathematical formula, which has significant applications in chemical graph theory, because it is used as a molecular descriptor to investigate physical as well as chemical properties of chemical structure. Therefore, it is a powerful technique in avoiding high-cost and long-term laboratory experiments. There are 3,000 topological invariants registered till now. All these indices have their applications in chemical graph theory. In these molecular descriptors, Gourava and hyper-Gourava invariants are used to find out the physical and chemical properties (such as entropy, acentric factor, and DHAVP) of octane isomers. The 1^st and 2^nd Gourava invariants highly correlate with entropy and acentric factor, respectively.

In [7], the graph operations for Gourava index are presented. In our present study, we considered that all graphs are simple and connected. For any graph, the degree of a vertex is defined as the number of edges attached to it. The smallest degree of graph ξ is represented by δ(ξ). The vertex in a graph whose degree is one is known as pendent vertex. The neighborhood of a vertex μ is the set of all nodes attached with μ, represented by N(μ). There are two types of neighborhood, open neighborhood and closed neighborhood. If N(μ) includes all the other nodes except μ, then it is called open neighborhood, but if it includes the node μ, then it is called closed neighborhood. Closed neighborhood is defined as N[μ] = N(μ) ∪ {μ} (for further notations in graph theory, we refer [8]).

Some bounds of reformulated Zagreb indices are given in [9]. In 2012, Xu and Das [10] established some graph transformations that maximize or minimize the multiplicative sum Zagreb index of graphs and used these graph transformations to determine the extremal graphs among trees, unicyclic, and bicyclic graphs for multiplicative sum Zagreb index. Two years later, in 2014, Ji et al. [11] extended the work of Xu and Das [10] for the 1^st reformulated Zagreb index. In 2017, Gao et al. [12] used the same graph transformations as given in [11] to compute the similar results as computed in [11] but for the hyper-Zagreb index.

Tomescu and Kanwal [13] in 2013 introduced some graph transformations to compute the general sum-connectivity index for acyclic connected graphs of given diameter, order, and pendant vertices and determined the corresponding extremal trees and gave the ordering of trees with minimum general sum-connectivity index. Ilic^′ et al. in 2011 [14] used some graph transformations to find the bounds for unicyclic and bicyclic graphs with respect to degree distance index. Liu et al. [15] analyzed the newly introduced chemical invariant termed as Mostar invariant for tree-like phenylenes and provided a detailed discussion for the obtained results. Liu et al. [16], provided an ordering of acyclic, bicyclic, and tricyclic structures with respect to recently introduced invariants Sombor and reduced Sombor invariants. In [17], Liu et al. determined some degree-based chemical invariants for octahedron networks. Qi et al. [18] put forward computations of several degree-based chemical invariants for rhombus-type silicate and oxide structures. In [19], the authors investigated several degree-based invariants for planar octahedron networks and made comparison of obtained numerical results. Hu et al. [20] analyzed certain distance-based invariants for chemical interconnection networks and analyzed their behavior.

In this work, we are aimed to determine the acyclic structures having maximum values of first Gourava invariant and put forward acyclic structures attaining first five greatest values of first Gourava invariant. Plan of work and methodology behind attaining main results of this work is to apply certain edge swapping transformations to acyclic graphs and observe the behavior of first Gourava invariant. We will see that it increased for the resultant graph and eventually leads us to acyclic structures with the first five bigger values of above-mentioned invariant.

2. Gourava Index and Graph Transformations

In this section, we use certain graph transformations presented by Ji et al. [11]. Further, we will notice that these transformations increase the GO₁ for trees. These transformations are narrated below.

In B₁-transformation, let ξ be a nontrivial connected graph having vertices η, μ ∈ ξ, such that N(η₁) = μ₁, η_1,1, η_1,2, ⋯, η_1,h and N(μ₁) = η₁, μ_1,1, μ_1,2, ⋯, μ_1,f, where η₁ and μ₁ have no common neighbors in ξ, f ≥ 0 and h ≥ 1.

Let ξ^′ be the graph obtained after applying B₁ − transformation, such that ξ^′ = ξ − η₁η_1,1, η₁η_1,2, ⋯, η₁η_1,h + μ₁η_1,1, μ₁η_1,2, ⋯, μ₁η_1,h as explained in Figure 1.

Lemma 1. Let ξ be a connected graph with no cycle and ξ^′ be a graph obtained after applying B₁-transformation (as shown in Figure 1), and then, GO₁(B₁(ξ)) = GO₁(ξ^′) > GO₁(ξ) for any f, h ≥ 1.

Proof. From Figure 1, d_ξ′ = f + h + 1 and . We can easily guess that degree of μ₁ increases, while degree of η₁ decreases after applying transformation, and all other vertices preserve their degrees.

(5)

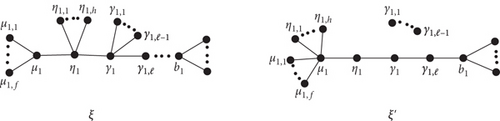
Lemma 2. Let ξ be an acyclic graph, and ξ^′ is obtained after applying B₂-transformation (as shown in Figure 2) where d_ξ(γ₁, b₁) ≥ 1; then,

(6)

for any f > 1 and h, ℓ ≥ 1.

Proof. Here , and , and after transformation, and .

(7)

Lemma 3. Let ξ be an acyclic graph and B₃(ξ) = ξ^′ is obtained after applying B₃-transformation (as shown in Figure 3), where and . If f > 1, h, ℓ ≥ 1, then,

(8)

Proof. Like the previous lemma, we have

(9)

Lemma 4. Let ξ be acyclic connected graph, and ξ^′ = B₄(ξ) is obtained after applying B₄-transformation(as shown in Figure 4) for any f > (ℓ − 1); we have GO₁(B₄(ξ)) = GO(ξ^′) > GO₁(ξ).

Proof. Since d_ξ(μ₁, γ₁) ≥ 1, and if d_ξ(μ₁, γ₁) ≥ 2, then d_ξ′(μ₁) + d_ξ′(γ₁) = (f + 1) + (ℓ + 1) = d_ξ(μ₁) + d_ξ(γ₁); now by using definition of GO₁(ξ), we have

(10)

If d_ξ(μ₁, γ₁) = 1, then

(11)

Details are in the caption following the image — Open in figure viewer PowerPoint

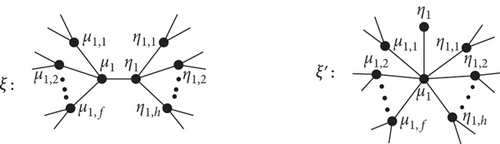
3. Ordering Trees Having Maximum GO₁

In this section, we identify the trees having maximum first Gourava index, and also, we give a sequence of these trees having first five largest values of GO₁.

Theorem 5. Let T^∗ be a set of trees having order λ and diameter d^∗, where λ ≥ 3 and 2 ≤ d^∗ ≤ λ − 1. Then, GO₁ is maximum value for .

Proof. First, we apply B₁-transformation to those vertices of T^∗ which are other than diametral path, and we observe that maximum value of GO₁ is obtained for . Then, we apply all those transformations which are explained above, and we conclude that the maximum value is acquired only for for .

Corollary 6. (a) Let T^∗ denotes the set of trees with order λ. Then,

(12)

where 2 ≤ ℓ ≤ m^′ ≤ λ − 1.

(b) Let the order of set of trees of T^∗ be λ with diameter 3 ≤ d^∗ ≤ λ − 2; then the greatest value of GO₁(T^∗) for these graphs is in the following order: MS(λ − d^∗, 0, ⋯, 0, 1), MS(λ − d^∗ − 1, 0, ⋯, 0, 2), ⋯, MS(⌈λ − d^∗ + 1/2⌉, 0, ⋯, 0, ⌊λ − d^∗ + 1/2⌋).

Proof. We can achieve MS(λ − ℓ, 0, ⋯, 0, 1) from MS(λ − m^′, 0, ⋯, 0, 1) by repeated use of first transformation (as described in Lemma 1).

(b) We use first three transformations (as explained in Lemmas 1 to 3, and then, we use the fourth transformation to multistars MS(g₁, 0, ⋯, 0, g₂) with order λ where g₁ + g₂ = λ − d^∗ + 1.

Theorem 7. For λ > 10, the trees having the greatest 1^st Gourava index can be given in the following order (shown in Figure 5):

(13)

Proof. In the family of trees having diameter 2, the star K_1,λ−1 is the only tree which by above corollary possesses the greatest 1^st Gourava index. The second maximum value of 1^st Gourava index reaches for for the trees having diameter 3. The third maximum value of this sequence can be obtained for BS(λ − 4, 2) which also belongs to the class of trees having diameter 3. For λ = 5, the BS(λ − 4, 2) coincides with BS(λ − 3, 1). The next graph in the class of trees with diameter 3 is BS(λ − 5, 3). The next maximum value is obtained by which has diameter 4. We obtain

(14)

Applying τ₁-transform to

, we obtain BS(λ − 4, 2). It follows that for λ ≥ 6, the order of trees possessing maximum value is GO₁(K_1,λ−1) > GO₁(BS(λ − 3, 1)) > GO₁(BS(λ − 4, 2)). For the fourth term of this series, we have

(15)

This implies that

for λ > 10. So for λ > 10, the fourth member in the above constructed sequence is

. For next member, we calculate

(16)

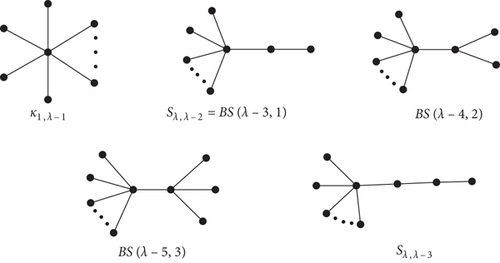
For λ > 4, MS(λ − 5, 0, 2) gets the 2^nd maximum value of GO₁ in the set of trees of diameter 4. Applying 1^st transformation (as described earlier) to MS(λ − 5, 0, 2), we get MS(λ − 5, 0, 0, 1) which attains maximum value of 1^st Gourava index in the set of trees of diameter 5 and MS(λ − 5, 0, 0, 1) < MS(λ − 5, 0, 2) which terminates the proof.

For example, for λ = 12, we see that

(17)

which as a result verifies our main result of this work.

(18)

Hence proved

(19)

Table 1 provides certain trees of order λ, along with their value of GO₁.

Theorem 8. Let T^∗ be a tree having order λ ≥ 5 with α-leaf nodes, where 3 ≤ α ≤ λ − 2. Then,

(20)

Equality holds if .

Proof. First under the supposition of theorem, we prove that if x^′ is a pendant node attached to a vertex y^′, then

(21)

Equality holds for and for d(y^′) = α. Here, we notice that there exist a vertex ℓ₀ ∈ N(y^′)\{x^′} such that d(ℓ₀) ≥ 2 since otherwise T^∗ would be a star, which is against the supposition of theorem. Now,

(22)

Since d(ℓ₀ ≥ 2, we have

(23)

For the remaining d(y^′) − 2 nodes ℓ ∈ N(y^′)\{x^′, ℓ₀}, we conclude that

(24)

This implies that

(25)

Since d(y^′) ≤ α,

(26)

Equality holds if d(y^′) = α, one neighbor of y^′ has degree two, while all the neighbor are leaf nodes, i.e., .

Now, the proof follows by induction on λ. For λ = 5, we obtain α = 3, and is a single tree of order 5 having three pendant nodes.

Let α ≥ 6 and suppose that the theorem is true for all the trees of order λ − 1 having α-leaf nodes where 3 ≤ α ≤ λ − 3. Let x^′ be the pendant node that is attached to node y^′. Here, we examine two subcases:

(a)
When d(y^′) = 2
(b)
When d(y^′) ≥ 3
(a)
For d(y^′) = 2, we have
(27)

Equality holds for d(ℓ) = 2. If α = λ − 2, then T − x^′ has λ − 1 nodes and λ − 2 pendent nodes, i.e., T^∗ − x^′ = κ_1,λ−2 and .

(b)
For d(y^′) ≥ 3, then T^∗ − x^′ has λ − 1 nodes and α − 1 leaf nodes. Then, by induction, we obtain
(28)

Equality holds if and d(y^′) = α, i.e., .

1. Comparison of different values of

for λ = 14.


κ_1,13	351
BS(11, 1)	318
BS(10, 2)	291
S_14,11	278
BS(9, 3)	270

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

The data used to support the findings of this study are cited at relevant places within the articles in references.

References

1 Wiener H., Structural determination of paraffin boiling points, Journal of the American Chemical Society. (1947) 69, no. 1, 17–20, https://doi.org/10.1021/ja01193a005, 2-s2.0-8544254107, 20291038.
10.1021/ja01193a005
CAS PubMed Web of Science® Google Scholar
2 Gutman I. and Das K. C., The first Zagreb index 30 years after, MATCH Communications in Mathematical and in Computer Chemistry. (2004) 50, no. 1, 83–92.
CAS Google Scholar
3 Gutman I. and Trinajstić N., Graph theory and molecular orbitals. Total ϕ-electron energy of alternant hydrocarbons, Chemical Physics Letters. (1972) 17, no. 4, 535–538.
10.1016/0009-2614(72)85099-1
CAS Web of Science® Google Scholar
4 Das K. C. and Gutman I., Some properties of the second Zagreb index, MATCH Communications in Mathematical and in Computer Chemistry. (2004) 52, no. 1.
Google Scholar
5 Miličević A., Nikolić S., and Trinajstić N., On reformulated Zagreb indices, Molecular Diversity. (2004) 8, 393–399.
10.1023/B:MODI.0000047504.14261.2a
CAS PubMed Web of Science® Google Scholar
6 Kulli V. R., The Gourava indices and coindices of graphs, Annals of Pure and Applied Mathematics. (2017) 14, no. 1, 33–38.
10.22457/apam.v14n1a4
Google Scholar
7 Kulli V. R., The Gourava index of four operations on graphs, Mathematical Combinatorics. (2018) 4, 65–67.
Google Scholar
8 Bondy J. A. and Murty U. S. R., Graph Theory, 2008, Springer, New York, https://doi.org/10.1007/978-1-84628-970-5.
10.1007/978-1-84628-970-5
Google Scholar
9 De N., Some bounds of reformulated Zagreb indices, Applied Mathematical Sciences. (2012) 6, no. 101, 5005–5012.
Google Scholar
10 Xu K. and Das K. C., Trees, unicyclic, and bicyclic graphs extremal with respect to multiplicative sum Zagreb index, MATCH Communications in Mathematical and in Computer Chemistry. (2012) 68, 257–272.
Web of Science® Google Scholar
11 Ji S., Li X., and Huo B., On reformulated Zagreb indices with respect to acyclic, unicyclic and bicyclic graphs, MATCH Communications in Mathematical and in Computer Chemistry. (2014) 72, 723–732.
Web of Science® Google Scholar
12 Gao W., Jamil M. K., Javed A., Farahani M. R., Wang S., and Liu J. B., Sharp bounds of the hyper- Zagreb index on acyclic, unicyclic and bicycli, Discrete Dynamics in Nature and Society. (2017) 2017, 5, https://doi.org/10.1155/2017/6079450, 2-s2.0-85013308914, 6079450.
10.1155/2017/6079450
Google Scholar
13 Tomescu I. and Kanwal S., Ordering trees having small general sum- connectivity index, MATCH Communications in Mathematical and in Computer Chemistry. (2013) 69, 535–548.
Web of Science® Google Scholar
14 Ilić A., Stevanović D., Feng L., Yu G., and Dankelmann P., Degree distance of unicyclic and bicyclic graphs, Discrete Applied Mathematics. (2011) 159, 779–788.
10.1016/j.dam.2011.01.013
Web of Science® Google Scholar
15 Liu H., Chen H., Tang Z., and You L., Ordering tree-like phenylenes by their Mostar indices, 2021, https://arxiv.org/abs/2103.04018.
Google Scholar
16 Liu H., You L., and Huang Y., Ordering chemical graphs by Sombor indices and its applications, MATCH Communications in Mathematical and in Computer Chemistry. (2022) 87, no. 1, 5–22, https://doi.org/10.46793/match.87-1.005L.
10.46793/match.87-1.005L
Web of Science® Google Scholar
17 Liu J. B., Ali H., Shafiq M. K., Dustigeer G., and Ali P., On topological properties of planar octahedron networks, Polycyclic Aromatic Compounds. (2021) 42, 1–17.
Google Scholar
18 Qi R., Ali H., Babar U., Liu J. B., and Ali P., On the Sum of Degree-Based Topological Indices of Rhombus-Type Silicate and Oxide Structures, Journal of Mathematics. (2021) 2021, 16, https://doi.org/10.1155/2021/1100024, 1100024.
10.1155/2021/1100024
Web of Science® Google Scholar
19 Zhen W., Ali P., Ali H., Dustigeer G., and Liu J. B., On Computation Degree-Based Topological Descriptors for Planar Octahedron Networks, Journal of Mathematics. (2021) 2021, 12, https://doi.org/10.1155/2021/4880092, 4880092.
10.1155/2021/4880092
Web of Science® Google Scholar
20 Hu M., Ali H., Binyamin M. A., Ali B., Liu J. B., and Fan C., On Distance-Based Topological Descriptors of Chemical Interconnection Networks, Journal of Mathematics. (2021) 2021, 10, https://doi.org/10.1155/2021/5520619, 5520619.
10.1155/2021/5520619
Web of Science® Google Scholar

Citing Literature

All articles

[Retracted] On Acyclic Structures with Greatest First Gourava Invariant

Retraction(s) for this article

Retracted: On Acyclic Structures with Greatest First Gourava Invariant

Abstract

1. Introduction

2. Gourava Index and Graph Transformations

3. Ordering Trees Having Maximum GO₁

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

[Retracted] On Acyclic Structures with Greatest First Gourava Invariant

Retraction(s) for this article

Retracted: On Acyclic Structures with Greatest First Gourava Invariant

Abstract

1. Introduction

2. Gourava Index and Graph Transformations

3. Ordering Trees Having Maximum GO1

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

3. Ordering Trees Having Maximum GO₁