Volume 2022, Issue 1 5966274

Research Article

Open Access

Effect of Welding Sequence and Constraint on the Residual Stress and Deformation of Thick Welded Butt Joint Made of Q345qD Steel

Yi Zhang,

Yi Zhang

China Construction Third Bureau First Engineering Co., Ltd, Wuhan, Hubei 430040, China

Search for more papers by this author

Wenxue Su,

Wenxue Su

School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan, Hubei 430070, China whut.edu.cn

Search for more papers by this author

Hua Dong,

Hua Dong

China Construction Third Bureau First Engineering Co., Ltd, Wuhan, Hubei 430040, China

Search for more papers by this author

Tao Li,

Corresponding Author

Tao Li

[email protected]

orcid.org/0000-0001-6161-7352

School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan, Hubei 430070, China whut.edu.cn

Search for more papers by this author

Hongyou Cao,

Hongyou Cao

School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan, Hubei 430070, China whut.edu.cn

Search for more papers by this author

Yi Zhang,

Yi Zhang

China Construction Third Bureau First Engineering Co., Ltd, Wuhan, Hubei 430040, China

Search for more papers by this author

Wenxue Su,

Wenxue Su

School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan, Hubei 430070, China whut.edu.cn

Search for more papers by this author

Hua Dong,

Hua Dong

China Construction Third Bureau First Engineering Co., Ltd, Wuhan, Hubei 430040, China

Search for more papers by this author

Tao Li,

Corresponding Author

Tao Li

[email protected]

orcid.org/0000-0001-6161-7352

School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan, Hubei 430070, China whut.edu.cn

Search for more papers by this author

Hongyou Cao,

Hongyou Cao

School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan, Hubei 430070, China whut.edu.cn

Search for more papers by this author

First published: 24 September 2022

https://doi.org/10.1155/2022/5966274

Citations: 4

Academic Editor: Wenjun Zhu

Share a link

Email
Wechat
Bluesky

Abstract

In this paper, the residual stress and deformation of 32 mm thick welded butt joints made of Q345qD steel using gas metal arc welding (GMAW) are studied by using the thermoelastic-plastic finite element analysis (FEA). Element birth and death technique is used to simulate the deposition of the welding consumables, and the volume heat source in double-ellipsoidal distribution is used. An in-house python code is developed to enable the volume heat source movement. After the finite element model was verified against the experimental results, the effects of five welding sequences and two types of boundary constraint conditions on the residual stress and deformation of the thick welded butt joints were investigated. Results of the experimental measurement and the numerical simulation are in good agreement. The transverse residual stress and the vertical deformation can be significantly reduced by increasing the alternating times of the welding beads in two halves of the weld. The transverse residual stress and the vertical deformation can be reduced by 21.4% and 87.4%, respectively. In addition, the residual stress and deformation of the thick welded butt joints are significantly affected by the applied constraints. Increasing the constraint significantly increases the overall level of the transverse residual stress but can decrease the maximum longitudinal residual stress by 51.8% and the vertical deformation by 65.9%.

1. Introduction

Welding is a common connection method in the modern industry and is widely used in many engineering fields [1]. Most welding methods involve local heating and, thus, welding residual stress and deformation are generated for welded structures. Welding residual stress and deformation affect many mechanical properties of welded structures, such as the fatigue performance, stiffness, and compressive stability. In addition, welding deformation is unfavourable to the fabrication accuracy and dimensional stability of welded structures. Therefore, it is very necessary to minimize the welding residual stress and deformation by optimizing the welding process.

The welding residual stress and deformation of welded structures produced by using different welding processes can be measured through the experimental testing. However, usually only the stress data at several points of a welded structure will be measured because it is difficult to measure the residual stress distribution of the entire structure. Numerical methods can be used to simulate and optimize the welding process [2]. Compared to experimental testing, it is much more convenient and cost-effective to optimize the welding process via numerical simulation to reduce welding deformation and residual stress.

In the early 1970s, Ueda and Hibbit et al. [3, 4] proposed the thermoselastic-plastic finite element analysis (FEA) to simulate the welding temperature field, residual stress, and deformation. Nowadays, many scholars use finite element analyses to simulate the welding process so as to study the welding residual stress distribution and deformation of welded joints. For instance, Fu et al. [5] studied the effect of welding sequences on the welding residual stress distribution of tube sheet joints made of the 6061 thin-walled aluminum alloy. It was found that the optimized welding sequence can effectively reduce the residual stress of the welded joints investigated. Azad et al. [6] studied the influence of welding sequences on the deformation of ship deck and analysed the influence of eight different welding sequences on the deformation of six wire plates. Results show that different welding sequences affect both the shape and the size of the welding deformation. Zhu et al. [7] studied the influence of welding sequences on the deformation and transverse residual stress of fillet welded T-joints. Results show that, for the fillet welded T-joints, opposite-direction welding for the two welding beads leads to less angular deflection compared to the same-direction welding. The transverse residual stresses on the side of the first weld bead were lower according to the thermoelasto-plastic FEA results. Fahlström et al. [8] studied the influence of welding sequences on the welding deformation of ultrathin and ultrahigh strength steel U-beams. Results show that the welding direction has an insignificant influence on the welding deformation, and the welding deformation appears to mainly depend on the welding consumable volume. Carrizalez-Vazque and Pérez-Medina [9] simulated the welding process of butt joints made of DP600 steel thin plate considering different welding sequences. It was found that the welding residual stress and deformation caused by the segmented continuous welding were much smaller compared to the single-pass welding under the same heat input. Fu et al. [10] studied the influence of welding sequences on the residual stress and deformation of welded T-joints. Results show that the welding deformation generated in the single-side welding is larger compared to the double-side welding. Wang et al. [11] studied the influence of welding sequences on the residual stress distribution and deformation of Q345 steel H-beam butt joints. Results show that welding deformations of the welded joints are nearly the same for three different welding sequences, and the residual stress of the welded joints with the web welded before the flange is the smallest. Woo et al. [12] introduced an effective method to determine the optimal welding sequence leading to the minimum deformation of a general ship side panel. Results show that the optimal welding sequence can be determined by properly dividing the groups of the welding lines. Taraphdar et al. [13] analysed the influence of different welding sequences on the residual stress of equal double V-groove weld. Results show that the residual stress generated in weld bead alternative welding is smaller. In contrary, weld bead unidirectional welding causes a higher tensile residual stress level in the weld area. Yang et al. [14] studied the effect of three welding sequences on the residual stress of SA738Gr.B thick plate. It was found that the transverse stress of double-sided alternating symmetrical welding is 17% lower compared to the nonalternating welding.

In addition to the welding sequence, the constraint applied to the welded joints also has a significant effect on the welding residual stress and deformation of the joints. For instance, Kohandehghan and Serajzadeh [15] analysed the effect of the clamp and the welding sequences on the distribution and magnitude of welding residual stress of butt joints welded using the gas tungsten arc welding. It was found that the maximum transverse residual stress of the welded joint with the clamp is increased by about 76%, and the optimal welding sequence reduces the maximum longitudinal residual stress by about 44%. Aalami-aleagha and Eslampanah [16] studied the effect of four types of constraint on the welding residual stress and deformation of fillet welded T-joints. It was found that increasing mechanical constraints could reduce the deformation but increase the residual stress. The maximum residual stress increased as the constraint level increased. Deng et al. [17] analysed the influence of external constraints on the welding deformation of welded thin plate joints based on experimental and numerical results and discussed the mechanism of out-of-plane deformation of the investigated joints. Results show that external constraints can not only reduce the in-plane and out-of-plane deformation but also change the mode of the out-of-plane deformation. Besides, external constraints can reduce the welding deformation of thin plate welded joints to a very small level but cannot eliminate it completely. Venkatkumar and Ravindran [18] studied the effect of five constraint conditions on the welding residual stress and deformation of 316 stainless steel welded butt joints. It was found that the welding residual stress and deformation are significantly affected by the constraint conditions. In the case of complete constraint, the residual stress in the longitudinal direction is higher than that without any constraint. Liu and Zhang [19] analysed the influence of external constraint on the welding residual stress and compared the numerical results of the displacement constraint model to the multibody coupling model. It was found that the transverse residual stress at the welding centreline is significantly changed with the constraint increase, and the transverse residual stress obtained from the displacement constraint model is larger than that of the multibody coupling model. Heinze et al. [20] studied the effect of the transverse shrinkage constraint on the welding residual stress. It was found that, under the transverse shrinkage-constraint condition, the transverse residual stress near the weld reaches 400 MPa. Wang and Yi [21] analysed the influence of the welding sequence and the tack welding clamping constraint on the welding deformation. It was concluded that the optimized welding sequence can reduce the out-of-plane welding deformation by about 38%, while the clamping constraint can decrease by 56%. Tomków et al. [22] reported that using more tack welds leads to a larger angular deformation of AISI 441 steel fillet welded joints.

As mentioned above, many scholars have studied the influence of the welding sequences and boundary constraints on the welding residual stress and deformation of welded joints using numerical simulation, but there are few studies that focus on thick-plate welded butt joints made of Q345qD steel, which is normally used for constructing steel bridges in China. To optimize the welding process of thick-plate welded butt joints made of Q345qD steel, in this paper, the effects of five welding sequences and two types of constraint on the welding residual stress and deformation of thick-plate welded butt joints made of Q345qD steel are investigated through experimental testing and FEA.

2. Experiment

2.1. Materials and Welding Process

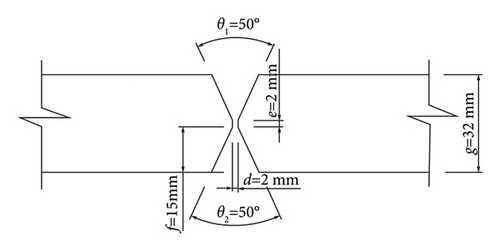
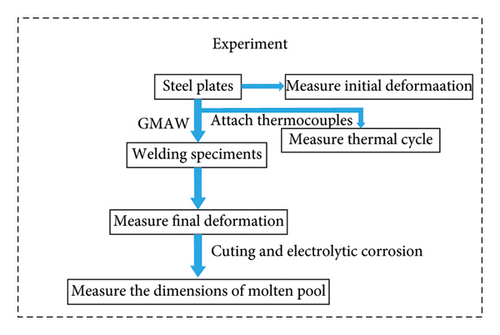
Three welded butt joint specimens were fabricated in this study. The material of the three specimens is Q345qD steel, and its chemical compositions provided by the manufacturer are shown in Table 1. The geometry and dimensions of three specimens are shown in Figures 1(a)–1(c), and the groove parameter values are shown in Figure 1(c). For the three specimens, manual gas metal arc welding (GMAW) was adopted using the type ER50-6 welding wire with the diameter of 1.2 mm. The chemical compositions of the ER50-6 welding wire provided by the manufacturer are shown in Table 2, and the shielding gas is CO₂. The welding parameters including the current used for fabricating the three butt joint specimens are shown in Table 3. The cooling time between different weld beads is 120 s for the welded joints. The diagram of the experimental system is shown in Figure 2. Tack welding was used to facilitate welding the specimens as shown in Figure 3(a).

1. Chemical composition of Q345qD steel (mass fraction, %).

C	Si	Mn	P	S	Cr	Ni	Cu
0.20	0.55	1.60	0.025	0.025	0.30	0.30	0.40

Details are in the caption following the image — Open in figure viewer PowerPoint

2. Chemical composition of ER50-6 welding wire (mass fraction, %).

C	Mn	Si	P	S	Ni	Cr	Mo	V	Cu
0.06	1.40	0.80	0.025	0.025	0.15	0.15	0.15	0.03	0.05

3. Welding parameters.

Pass	Current I (A)	Voltage V (V)	Welding speed v (mm/s)	Heat input Q (kJ/mm)
1–12	140	23	4	0.805

2.2. Thermal Cycle Measurement

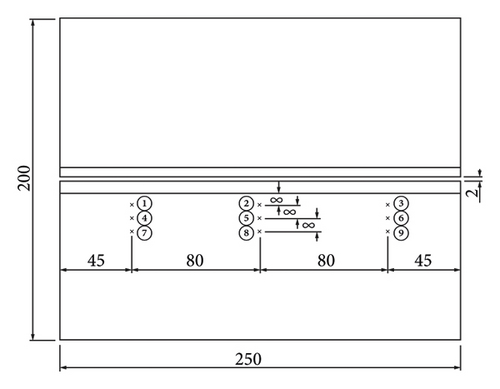
To monitor the thermal history during the welding process, nine K-type thermocouples (measurement range 0–1000°C with an accuracy of ±1°C) were attached to the upper surface of each welded specimen as shown in Figure 3(a). Positions of all measuring points are shown in Figure 3(b), and the other end of the thermocouples is connected to the R7100 paperless recorder (16 channels, accuracy 0.1°C) for data collection.

2.3. Deformation Measurement

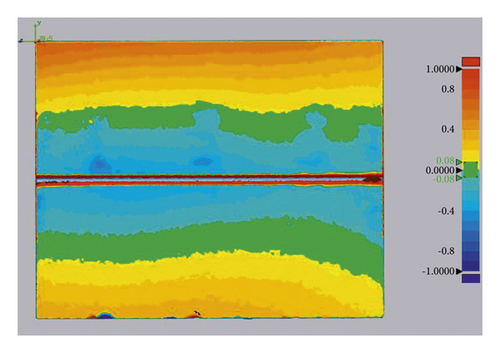
The deformation of each welded joint was measured by using a laser portable 3D scanner (FreeScan UE, with an accuracy of 0.02 mm). The two plates of each specimen with marked points were scanned before welding and the scanned model is displayed in the FreeScan UE software as shown in Figure 4. After welding, each specimen was scanned again. The scanned data is processed in the Geomagic Control 2014 and Geomagic Control X 2018 software to form the deformation cloud diagram shown in Figure 5. Finally, the extracted cloud point data is imported and plotted to show the angular deformation of each specimen.

3. Finite Element Modelling

3.1. Geometric Model and Mesh Generation

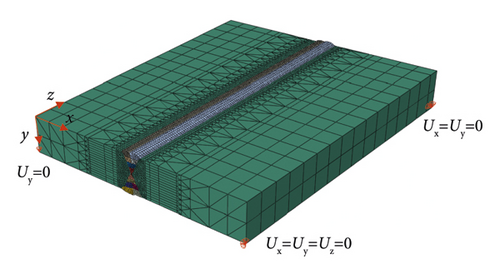
To ensure calculation accuracy and save calculation time, fine mesh was used around the weld bead (inclusive) and coarse mesh was used at other regions [23]. The mesh model is shown in Figure 6. The welding simulation adopts the thermoelastic-plastic sequential coupling method in which the thermal analysis is completed first and then the obtained temperature data is inputted into the mechanical analysis as thermal load. The element types for the thermal and the mechanical analysis are DC3D6 and C3D6, respectively, and the numbers of elements and nodes are 92067 and 49010, respectively.

3.2. Thermal Analysis

In the thermal analysis, the three-dimensional transient heat transfer model uses the following control differential equation to simulate the welding process [6]:

(1)

where k is the conductivity coefficient, ρ is the material density, c_s is the specific heat capacity, and Q_in is the internal heat generation rate.

The double-ellipsoidal heat source model shown in Figure 7 is adopted [24], and the heat input in welding is applied to the numerical models using the moving volumetric heat flux. As shown in Figure 7, the front and rear parts of the heat source model are in two different ellipsoid quadrants. The power density distribution of the front part is

(2)

The power density distribution of the rear part is

(3)

where x, y, and z are the local coordinates of the moving heat source and Q is the heat input expressed as

(4)

where η is the welding efficiency, V is the voltage, and I is the current. For GMAW, η is usually in the range of 50%–70% [25]. In the study, η is taken as 70%. Parameters b, c, a_f, and a_r are the dimensions of the two semiellipsoids shown in Figure 7 and their values are listed in Table 4. Parameter b is the width of the heat source, c is the depth of the heat source, a_f is the length of the front ellipsoid, and a_r is the length of the rear ellipsoid. Parameters f_f and f_r are the heat input proportional coefficients of the front part and the rear part, respectively. Goldak [24] proposed

(5)

4. Heat source parameters.

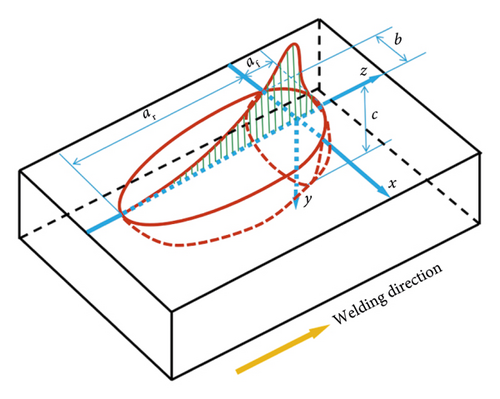
b (mm)	C (mm)	a_f (mm)	a_r (mm)
5.25	5.90	2.00	5.00

In the heating and cooling process of welding, the Stephen-Boltzmann law is used to calculate the heat loss q_r due to the radiation at high temperature, and Newton’s law is used to calculate the heat loss q_c due to the heat convection. Expressions of q_c and q_r are as follows [6]:

(6)

where T₀, ε, σ_s, and h_c are the initial temperature, the emissivity of the material surface, the Stefan-Boltzmann constant, and the convective heat transfer coefficient, respectively. T₀ is taken as 20°C in this study. Due to limited experimental data, three other parameters are usually taken as the constant in numerical simulation [10], h_c is assumed to be 10Wm⁻²K⁻¹, ε is 0.8, and σ_s is 5.67×10⁻⁸Wm⁻²K⁻⁴.

3.3. Mechanical Analysis

In the mechanical analysis, temperature data obtained from the thermal analysis is inputted into the mechanical model as the thermal load. The mechanical analysis uses the same mesh model as in the thermal analysis. To prevent the rigid body movement of the model, the mechanical boundary conditions shown in Figure 6 are adopted, where U_x, U_y, and U_z represent the displacement constraint in the x-, y-, and z-direction, respectively. Different constraints are applied to three nodes at the corners shown in Figure 6. The welding thermal stress field analysis is regarded as a transient problem of nonlinear materials, and, hence, the elastoplastic mechanical model is calculated using incremental theory. Other necessary assumptions used in this study are as follows: material follows the von-Mises yielding criterion; material behaviour in the plastic zone of the welded specimen follows the law of plastic flow and isotropic hardening; elastic-plastic strain and thermal strain are inseparable; the temperature-dependent thermal properties and the stress strain change linearly in small time increments. Since the strain caused by the phase transformation has minor contribution to the total strain of the low carbon steel [26], it is ignored in the mechanical analysis. Because the high temperature time in the welding thermal cycle is very short, the creep strain is small and can be ignored as well. The total strain can then be decomposed into the three following components [27]:

(7)

where ε_th, ε_e, and ε_pl are the thermal strain, elastic strain, and plastic strain, respectively. Figure 8 is the flow chart of the mechanical analysis for predicting the welding deformation and residual stress [28, 29] of the welded butt joints in the present study, where σ is the stress vector and D is the stiffness matrix.

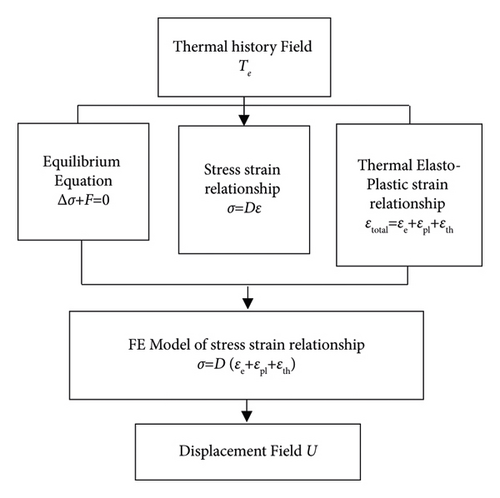
3.4. Steel Material Properties

The thermophysical properties of steel are related to temperature [30]; therefore, the material properties of Q345qD steel incorporating the effect of temperature must be used. The specific parameters [31] are shown in Table 5. In the FEA, the influence of the latent heat of phase transformation is considered. The latent heat of fusion is 270000 J/kg, and the steel is fused between the solid phase temperature of 1460°C and the liquid phase temperature of 1530°C [32].

5. Material properties of Q345qD steel as a function of temperature.

Temperature (°C)	Thermal conductivity (W/mm·K)	Density (kg/mm³)	Coefficient of expansion (×10⁻⁵/°C)	Elastic modulus (N/mm²)	Yield stress (N/mm²)	Specific heat capacity (J/kg·K)	Poisson’s ratio
20	50 × 10⁻³	7850 × 10⁻⁹	1.10	2.05 × 10⁵	3.15 × 10²	460	0.28
100	49 × 10⁻³	7850 × 10⁻⁹	1.05	1.97 × 10⁵	3.1 × 10²	465	0.28
250	47 × 10⁻³	7850 × 10⁻⁹	1.22	1.87 × 10⁵	2.75 × 10²	480	0.29
500	40 × 10⁻³	7850 × 10⁻⁹	1.39	1.5 × 10⁵	2.4 × 10²	575	0.31
750	27 × 10⁻³	7850 × 10⁻⁹	1.48	7.0 × 10⁴	40	625	0.35
1000	30 × 10⁻³	7850 × 10⁻⁹	1.35	2.0 × 10⁴	20	675	0.40
1500	35 × 10⁻³	7850 × 10⁻⁹	1.33	1.0 × 10²	1	650	0.45
2000	145 × 10⁻³	7850 × 10⁻⁹	1.31	1	1	820	0.49

3.5. Element Birth and Death Technique

In Abaqus software, the element birth and death technique is used to simulate the addition of deposited metal to the base metal [33, 34]. When adding materials to the base metal, related elements must be activated by using the element birth and death technique. All elements of the weld are disabled before welding, and elements for each welding pass will be activated in an appropriate loading step. In this study, an in-house Python code is developed to set the loading steps to apply element birth and death technique.

4. Verification of the Finite Element Model

4.1. Molten Pool

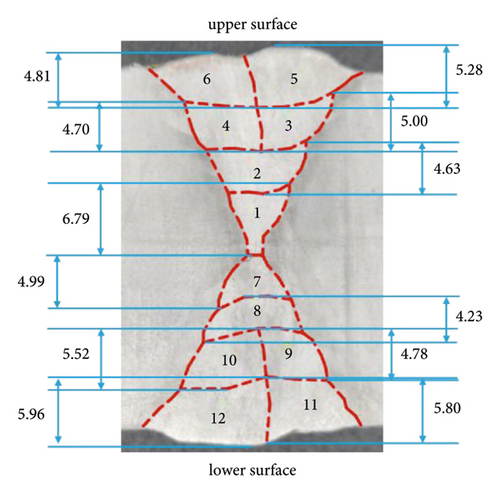
The three specimens were cut through at the middle perpendicular to the weld line and a digital tool measuring microscope with 2k resolution was used to measure the dimensions of the molten pool. According to the report of Tomków et al. [35], cold cracks were observed in the HAZ of wet welded high-strength low-alloy steel. For the three specimens fabricated in this study, no cracks were observed at the HAZ region. The experimental and numerically simulated molten pool contours are in good agreement as shown in Figure 9. The predicted and measured dimensions of the molten pool of one welded joint are shown in Table 6. The differences of the height and width of the molten pool between the FEA and experimental measurement are 1.02% and 5.62%, respectively. The above comparison shows that the thermal analysis model used for predicting the temperature field of the butt joint is reliable.

6. Geometry dimensions of the molten pool.

	h (mm)	w (mm)
Experimental results	5.90	10.50
Numerical results	5.84	9.91
Error (%)	1.02	5.62

4.2. Thermal Cycle

The thermal history at points 1, 2, 5 and 9 shown in Figure 2 is investigated to verify the FEA. Thermocouple at point 3 was damaged during testing, and, hence, no valid data was measured. The comparison between the experimental data and the numerical results is shown in Figures 10(a)–10(d). Temperature at the measured points was about 20°C before welding. Every time the heat source approaches, temperature at the measured point rises rapidly and then enters the cooling and heat dissipation stage. After all welding passes are completed, the whole weldment enters the cooling state, and temperature at the measured point continues decreasing to the room temperature. When the heat source of the weld bead 5 passes by, temperatures at the measured points 1 and 2 reach the peak value. The maximum temperatures at the measured point 1 obtained from the experimental test and FEA are 300°C and 311°C, respectively. At the measured point 2, temperatures measured and obtained from the FEA are identical and reach 313°C. It also can be observed that peak temperature is lower at the measured point further away from the molten pool, such as the measured point 9. The maximum temperature obtained from the FEA is 2909°C. Comparison in Figure 10 shows that the thermal analysis model used in this study is accurate and reliable.

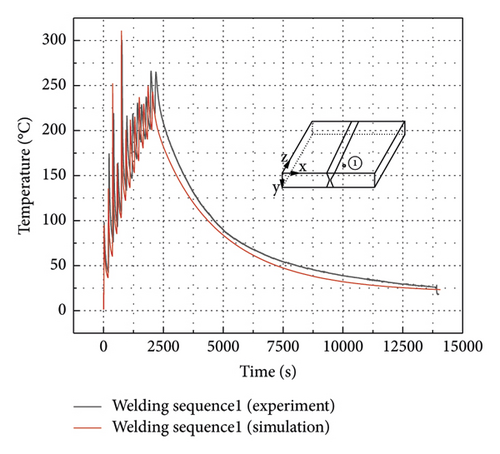
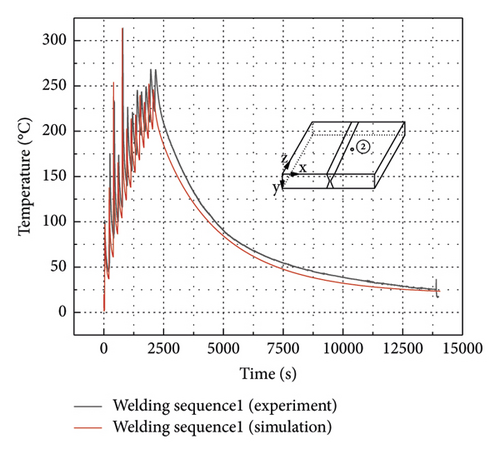
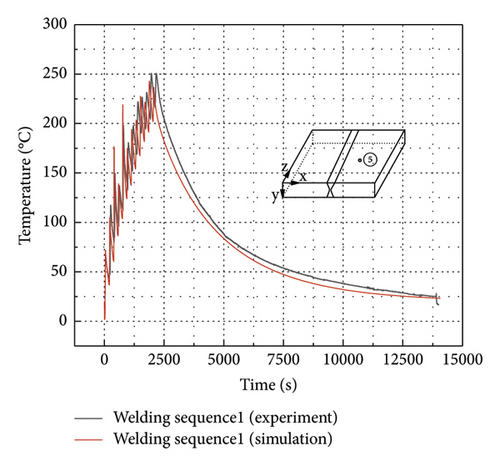
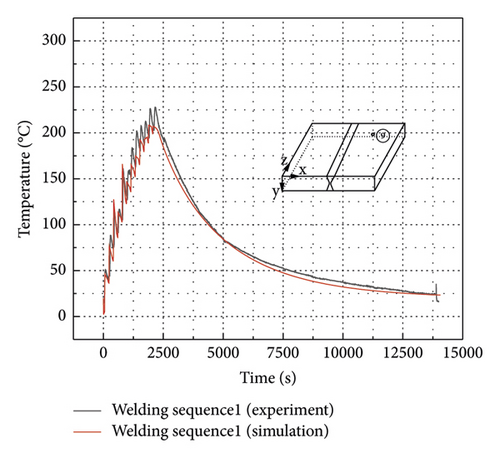
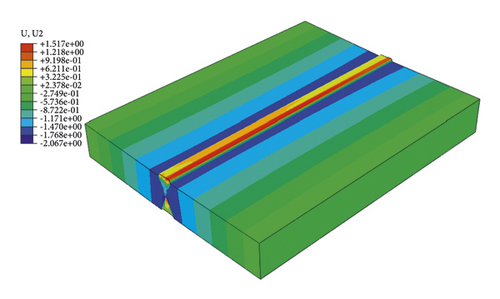
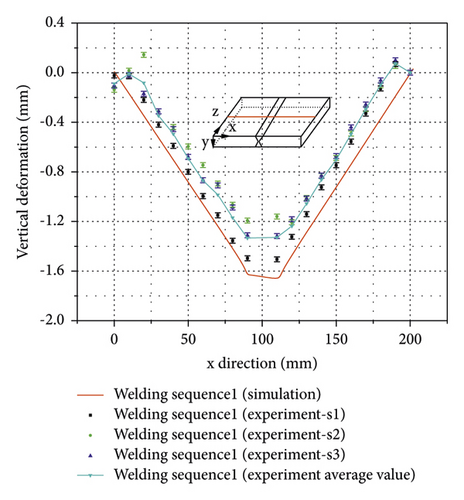
Figure 11 shows the cloud map distribution of the vertical deformation of specimen s1, and the deformation scaling factor is 1. Figure 12 shows the comparison of the vertical deformation of three specimens between the measured values and the results obtained from FEA. For the three specimens, the vertical deformations of 21 points on the red line highlighted in Figure 12 were measured. The red line is 120 mm offset from the welding start position and perpendicular to the weld line. From Figure 12, it can be found that the experimental measurement and the numerical simulation results are in good agreement. Deformation curves of the experimental testing and the FEA have the same trend, and the curves are in a V-shape. The measured maximum vertical deformations for three specimens are 1.51 mm, 1.21 mm, and 1.32 mm, respectively, and the FE result is 1.67 mm. The difference of the maximum vertical deformation between the FE and the experimental results is in the range of 10.60%–38.01%. It can be seen from Figure 12 that the measured vertical deformation curves of the three specimens are also discrete, and the maximum vertical deformation difference among three specimens is 24.79%. The above results show that the established mechanical analysis model could be reliable.

5. Finite Element Analysis

5.1. Welding Sequence and Constraint Scheme

The weldment of each specimen is divided into eight layers and twelve welding beads, and the schematic diagrams of each weld layer and welding bead are shown in Figures 13(a) and 13(b). In the figures, numbers 1–12 represent the numbering of weld beads. To investigate the effects of the alternating welding and the reverse welding on the residual stress and the deformation, five welding sequences are investigated in this study as follows:

(1)
Unidirectional welding: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
(2)
Unidirectional welding: 1, 7, 2, 8, 3, 9, 4, 10, 5, 11, 6, 12
(3)
Reverse welding: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
(4)
Reverse welding: 1, 7, 2, 8, 3, 9, 4, 10, 5, 11, 6, 12
(5)
Unidirectional welding: 1, 2, 3, 7, 8, 10, 4, 5, 6, 9, 12, 11

Unidirectional welding means that all weld beads are welded along the same direction, while reverse welding means that the adjacent weld beads are welded in the opposite direction. Three butt joint specimens were welded using the welding sequence 1.

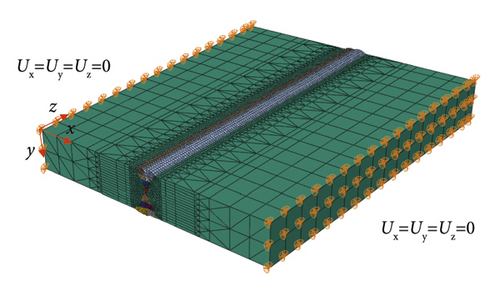
In the mechanical analysis, the two types of constraints applied to the finite element models are investigated. The first type of constraint is shown in Figure 6, in which six degrees of freedom of the three nodes at the corner of the finite element model are constrained. The first type of boundary condition applies minimal constraints to the welded butt joints to prevent rigid body movement [36]. Figure 14 shows the second type of constraint applied to the welded joints, in which all nodes on the two sides of the finite element model are constrained in three translate directions.

5.2. Influence of the Welding Sequence on the Residual Stress

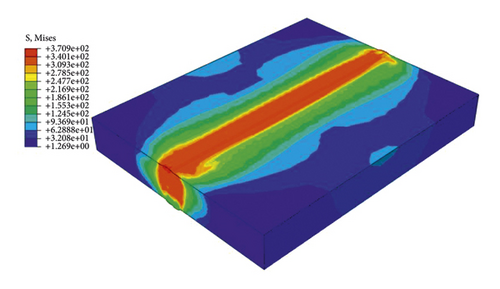
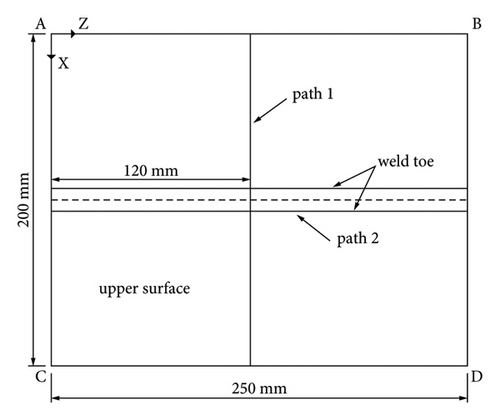
Figure 15 shows the residual stress (von-Mises) distribution of a specimen welded using the welding sequence 1. It can be found that the weldment and the heat affected zone (HAZ) are in the places where the residual stress is higher, with the maximum reaching 370.9 MPa. The residual stress away from the HAZ is smaller. Figure 16 shows two paths where the residual stress is investigated in this study. Path 2 refers to one weld toe and path 1 is perpendicular to the weld line. In this study, longitudinal and transverse directions refer to the welding direction and the one perpendicular to the weld, respectively.

The residual stress curves are plotted for nodes on path 1 and path 2. As shown in Figures 17(a), 17(b), 18(a), and 18(b), the residual stress curves of welding sequences 1 and 3 are very close. Also, the residual stress curves of welding sequences 2 and 4 almost overlap with each other. Therefore, changing the welding direction of the weld bead has minor effect on the residual stress distribution.

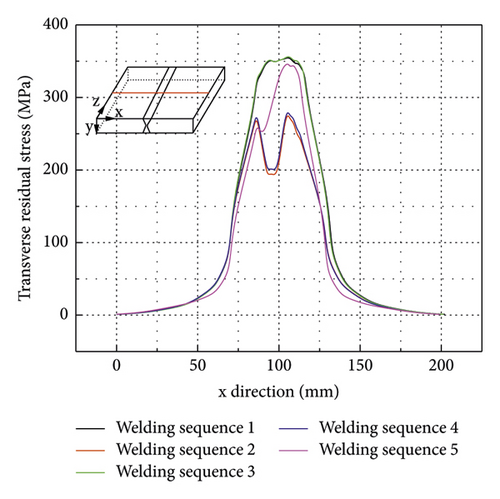
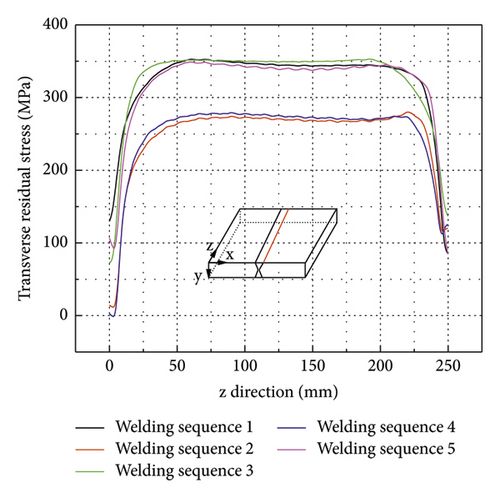
As shown in Figure 17(a), the transverse residual stress is the largest near the weld toe and decreases quickly as it gets away from the weldment. The transverse residual stress curves of welding sequences 2 and 4 are M-shaped, while the transverse residual stress curves of welding sequences 1, 3, and 5 are inverted U-shaped. Compared to welding sequence 1, the maximum transverse residual stress of the FE model using welding sequence 2 decreases from 355 MPa to 279 MPa, decreasing by about 21.4%, and the maximum transverse residual stress of the FE model using welding sequence 5 decreases from 355 MPa to 347 MPa, decreasing by about 2.3%. This means that alternating welding such as welding sequences 2 can significantly reduce the transverse residual stress at the weldment and the HAZ.

As shown in Figure 17(b), the transverse residual stress curves along the weld toe are flat in the middle segment (from −100 to 100 mm region). At the welding start and end regions (about 25 mm from the start and end point of the weldment), the transverse residual stress decreases rapidly. From the comparison of five curves, it can be concluded that alternating welding can significantly reduce the transverse residual stress at the weld toe in the middle segment. Compared to welding sequence 1, the maximum transverse residual stress at the weld toe using welding sequence 2 decreases from 353 MPa to 281 MPa, decreasing by about 20.4%, and the maximum transverse residual stress at the weld toe using welding sequence 5 decreases slightly, from 353 MPa to 349 MPa.

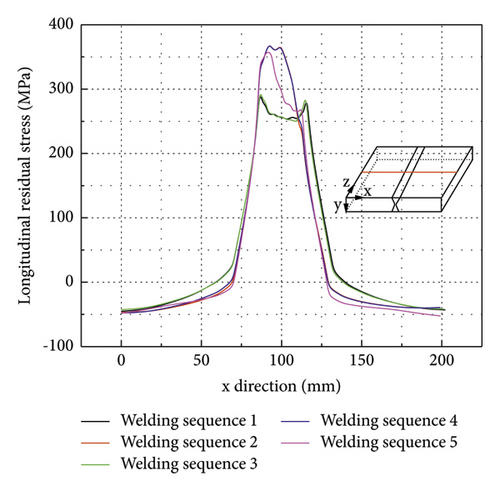
As shown in Figure 18(a), the longitudinal residual stress is the largest near the weld toe along path 1, and it decreases as it gets further away from the weldment and becomes compressive stress near the two edges of the FE models. The residual stress curves of welding sequences 1 and 3 are M-shaped, while the residual stress curves of welding sequences 2, 4, and 5 are inverted U-shaped. Compared to welding sequence 1, the maximum longitudinal residual stress of the FE model along path 1 using welding sequence 2 increases from 301 MPa to 368 MPa, increasing by about 22.3%, and the maximum longitudinal residual stress of the FE model along path 1 using welding sequence 5 increases from 301 MPa to 358 MPa, increasing by about 18.9%. It means that alternating welding such as welding sequence 2 can significantly increase the longitudinal residual stress at the weldment and the HAZ.

As shown in Figure 18(b), the longitudinal residual stress distribution along path 2 appears in an inverted U-shape. At the welding start and end regions, the longitudinal residual stress decreases rapidly to the minimum. Compared to welding sequence 1, the maximum longitudinal residual stress of the FE model along path 2 using welding sequence 2 increases from 255 MPa to 312 MPa, increasing by about 22.4%, and the maximum longitudinal residual stress of the FE model along path 2 using welding sequence 5 increases from 255 MPa to 271 MPa, increasing by about 6.3%. This means that alternating welding such as welding sequence 2 can significantly increase the maximum longitudinal residual stress at the weld toe.

From the above analyses, it can generally be concluded that alternating welding can reduce the transverse residual stress but increase the longitudinal residual stress at the weldment and the HAZ regions. In engineering practice, it is better to choose a reasonable welding process according to the design requirement. For example, if the welded butt joint was subjected to fatigue loading, it would be preferable to use alternating welding such as welding sequence 2. However, too many alternating welding times generally lead to a higher cost and lower productivity. Therefore, it is recommended to use the welding sequence with less alternating times.

Influence of the welding sequence on the welding deformation: as shown in Figure 16, in this study, the transverse shrinkage is defined as the relative displacement between nodes on lines CD and AB, while the longitudinal shrinkage is defined as the relative displacement between nodes on lines AC and BD. The vertical deformation is defined as the Y-direction displacement of nodes on path 1 shown in Figure 16.

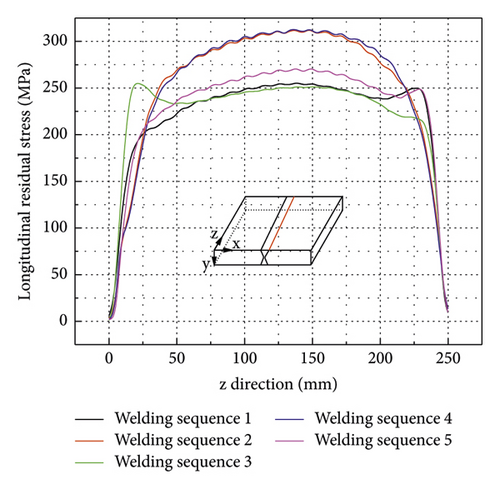
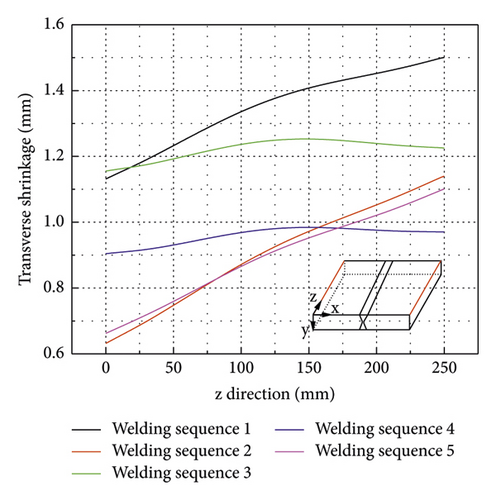
As shown in Figure 19, the transverse shrinkage (relative displacement between nodes on lines CD and AB in Figure 16) is larger on one side and smaller on the other due to the asymmetry constraints applied (refer to Figure 6). Transverse shrinkage curves of FE models using reverse welding sequence 3 and 4 are flatter compared to others. In addition, alternative welding such as welding sequences 2, 4, and 5 leads to a smaller transverse shrinkage. The transverse shrinkage of FE model using welding sequence 1 is between 1.13 and 1.5 mm, and the average is about 1.32 mm.

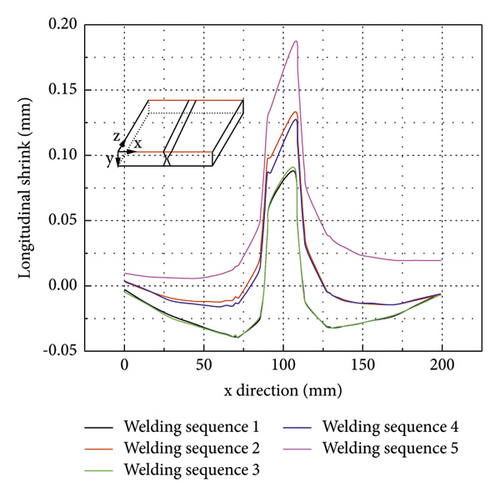
As shown in Figure 20, the longitudinal shrinkage (relative displacement between nodes on lines AC and BD in Figure 16) distribution of the welded thick plate is W-shaped. The longitudinal shrinkage at the weldment and the HAZ are much larger compared to other regions. Overall, the longitudinal shrinkage is much smaller compared to the transverse shrinkage using different welding sequences. The longitudinal shrinkage curves of welding sequences 1 and 3 are very close. Also, the longitudinal shrinkage curves of welding sequences 2 and 4 are almost overlapping with each other. Therefore, alternative welding has a minor effect on the longitudinal shrinkage distribution of the welded thick plate. Compared to others, welding sequence 1 produces the smallest longitudinal shrinkage and the maximum at the weldment is only 0.09 mm.

As shown in Figure 21, the vertical deformation curves of welding sequences 1 and 3 are V-shaped, while the vertical deformation curves of welding sequences 2, 4, and 5 are very flat. Compared to the FE model using welding sequence 1, the maximum vertical deformations of FE models using alternative welding sequences including welding sequences 2, 4, and 5 are much smaller. This implies that alternative welding can effectively reduce the vertical deformation of welded thick plate. For example, the maximum vertical deformation of FE model using welding sequence 5 decreases by about 87.4% compared to the one using welding sequence 1.

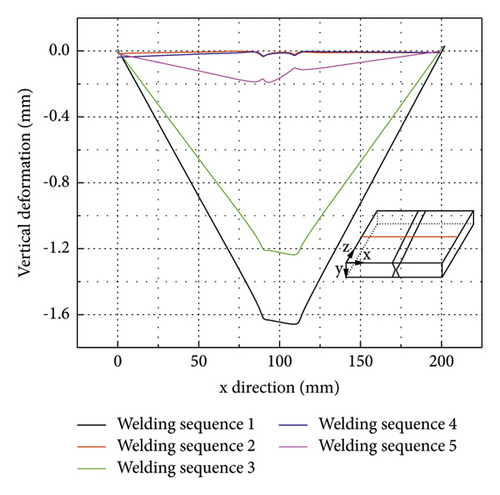
From the above analyses, it can be concluded that, generally, alternating welding can significantly reduce the transverse shrinkage and vertical deformation but increase the longitudinal shrinkage. As the magnitude of the longitudinal shrinkage is much smaller, it is recommended to use the alternative welding to control the transverse shrinkage and the vertical deformation of the welded thick butt joint. Considering the welding productivity and cost, it is recommended to use the alternative welding with limited alternating times such as welding sequence 5. Besides, changing welding direction of adjacent weld beads has less effect to the welding deformation compared to the welding sequences of different weld beads.

5.3. Influence of the Constraint Condition on the Residual Stress

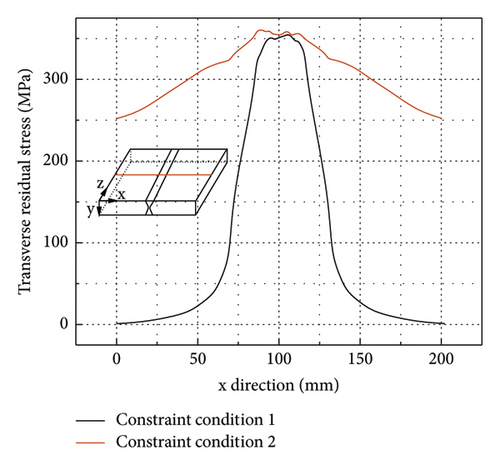
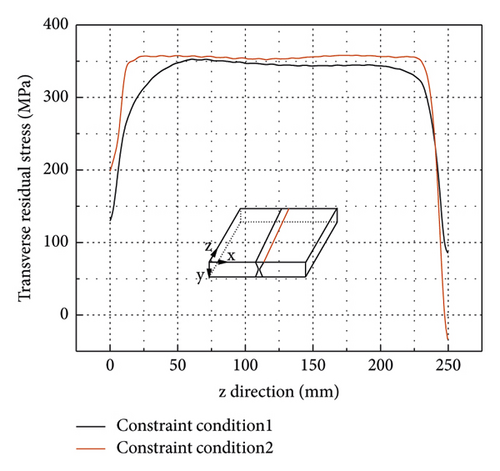
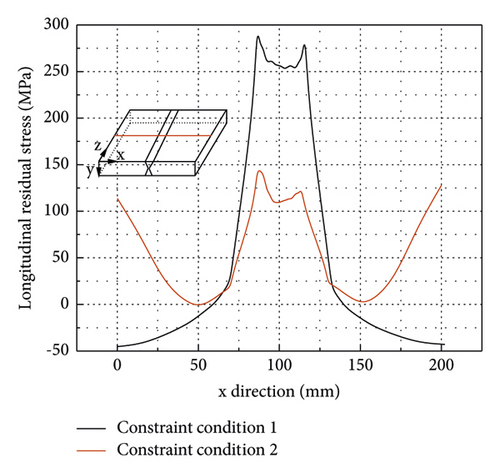
The welding residual stress and deformation of the welded thick butt joint using welding sequence 1 are analysed to investigate the effect of the constraint conditions. Constraint conditions 1 and 2 investigated in this study are shown in Figures 6 and 14, respectively. Figures 22(a) and 22(b) show the effects of the constraint conditions on the transverse residual stresses along path 1 and path 2 (weld toe) shown in Figure 16. It can be seen that constraint conditions have an ignorable effect on the maximum transverse residual stress at the weldment along path 1. Also, constraint conditions have a negligible effect on the transverse residual stress at the weld toe. It can be concluded that the constraint conditions have a negligible effect on the transverse residual stress at the weldment and the HAZ regions. However, a stronger constraint (constraint condition 2) applied to the welded thick butt joint can significantly reduce the longitudinal residual stress at the weldment and the HAZ regions as shown in Figures 23(a) and 23(b). For example, the maximum longitudinal residual stress for the FE model applying constraint condition 2 decreases from 289 MPa (for constraint condition 1) to 145 MPa at the weldment and the HAZ regions as shown in Figure 23(a).

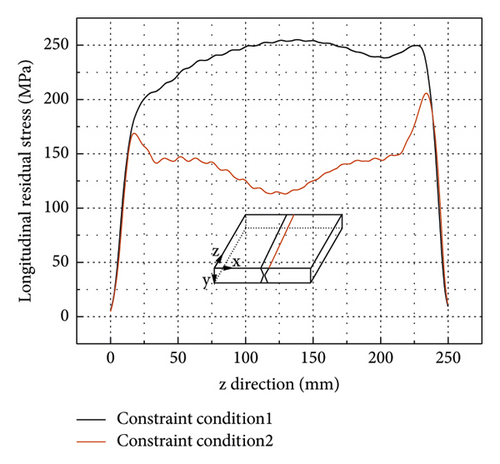
Theoretically, constraint condition 2 can completely omit the transverse shrinkage of the welded thick butt joint because it forbids any movement of all nodes on lines AB and CD. The longitudinal shrinkage and vertical deformation of the welded thick butt joints analysed are shown in Figures 24 and 25, respectively. As shown in Figure 24, a stronger constraint (constraint condition 2) applied to the FE model can significantly increase the longitudinal shrinkage. However, the longitudinal shrinkage under constraint condition 2 is still very small and less than 0.37 mm.

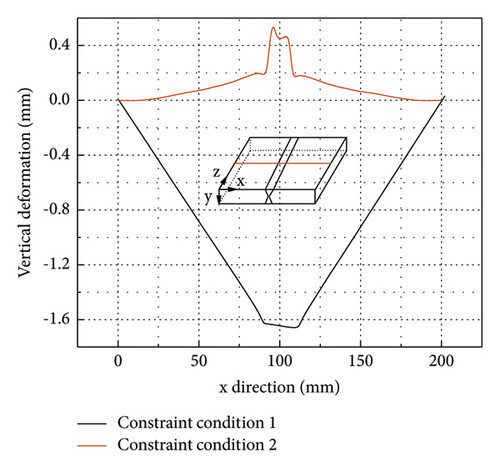
As shown in Figure 25, the vertical deformation curve under constraint condition 1 is V-shaped, while the curve under constraint condition 2 is inverted V-shaped. By increasing the constraints, the maximum vertical deformation decreased from 1.67 mm to 0.57 mm, decreasing by about 65.9%. Change of constraint conditions may not only affect the deformation magnitude but also change the deformation mode. However, a very strong constraint like constraint condition 2 cannot eliminate the vertical deformation at the weldment.

6. Conclusions

The residual stress and deformation of 32 mm thick welded butt joints made of Q345qD steel using gas metal arc welding are studied by using the thermoelastic-plastic FEA in this study. After the FE model was verified against the experimental results, the effects of five welding sequences and two types of boundary constraint conditions on the residual stress and deformation of the thick welded butt joints are investigated. Based on the FE results, the following conclusions can be drawn:

(1)
Generally, alternating welding (welding sequences 2, 4, and 5 in this study) can reduce the transverse residual stress by 20.4% but increase the longitudinal residual stress by 22.4% at the weld toe for the thick welded butt joints investigated. In engineering practice, it is better to choose a reasonable welding process according to the design requirement. For example, if the welded butt joints were subjected to fatigue loading, it would be preferable to use alternating welding such as welding sequence 2. However, too many alternating welding times generally lead to a higher cost and lower productivity. Therefore, it is recommended to use the welding process with limited welding alternating times.
(2)
Alternating welding can significantly reduce the transverse shrinkage by about 24%–46.9% (comparison between results of welding sequences 1 and 2 in Figure 19) and the vertical deformation by 87.4%; however, it can increase the longitudinal shrinkage. As the magnitude of the longitudinal shrinkage is much smaller, it is recommended to use alternative welding to control the transverse shrinkage and the vertical deformation of the welded thick butt joint. Considering the welding productivity and cost, it is recommended to use alternative welding with limited alternating times.
(3)
Generally, reverse welding, that is, changing the welding direction of adjacent weld beads, has a negligible effect on the transverse residual stress, longitudinal residual stress, and longitudinal shrinkage of the thick welded butt joints investigated. However, it may significantly reduce the transverse shrinkage and the vertical deformation.
(4)
A strong boundary constraint such as the one shown in Figure 14 may slightly increase the transverse residual stress but significantly reduce the longitudinal stress at the weld toe for the thick welded butt joints investigated.
(5)
The strong boundary constraint shown in Figure 14 can completely omit the transverse shrinkage for the thick welded butt joint investigated. Meanwhile, the strong constraint can minimize the longitudinal shrinkage and the vertical deformation.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The authors appreciate the financial support provided by the National Natural Science Foundation of China (no. 51908437), the Fundamental Research Funds for the Central Universities of China (WUT: 2019IVA024 and 2020IVB0090), and the research fund provided by China Construction Third Bureau First Engineering CO. LTD.

Open Research

Data Availability

The data used to support the findings of this study can be obtained from the corresponding author upon request.

References

1 Xue S., Wang B., Zhang L., and Weimin L., Development of green welding technology in China during the past decade, Materials Reports. (2019) 33, no. 9, 2813–2830.
Google Scholar
2 Wu Y. G., Li W. S., Feng L. Z., and Zou H. J., State-of-the-art of numerical simulation in welding, Transactions of the China Welding Institute. (2002) 23, no. 3, 89–92.
Google Scholar
3 Ueda Y. and Yamakawa T., Analysis of thermal elastic-plastic stress and strain during welding by finite element method, Transactions of Japan Welding Society. (1971) 2, no. 2, 186–196.
Google Scholar
4 Hibbitt H. D. and Marcal P. V., A numerical, thermo-mechanical model for the welding and subsequent loading of a fabricated structure, Computers & Structures. (1973) 3, no. 5, 1145–1174, https://doi.org/10.1016/0045-7949(73)90043-6, 2-s2.0-0015660667.
10.1016/0045-7949(73)90043-6
Google Scholar
5 Fu D. F., Zhou C. Q., Li C., Wang G., and Li L., Effect of welding sequence on residual stress in thin-walled octagonal pipe–plate structure, Transactions of Nonferrous Metals Society of China. (2014) 24, no. 3, 657–664, https://doi.org/10.1016/s1003-6326(14)63108-3, 2-s2.0-84898445704.
10.1016/S1003-6326(14)63108-3
CAS Web of Science® Google Scholar
6 Azad N., Iranmanesh M., and Rahmati Darvazi A., A study on the effect of welding sequence on welding distortion in ship deck structure, Ships and Offshore Structures. (2020) 15, no. 4, 355–367, https://doi.org/10.1080/17445302.2019.1619898, 2-s2.0-85067690221.
10.1080/17445302.2019.1619898
Web of Science® Google Scholar
7 Zhu J., Khurshid M., and Barsoum Z., Accuracy of computational welding mechanics methods for estimation of angular distortion and residual stresses, Welding in the World. (2019) 63, no. 5, 1391–1405, https://doi.org/10.1007/s40194-019-00746-9, 2-s2.0-85067672268.
10.1007/s40194-019-00746-9
CAS Web of Science® Google Scholar
8 Fahlström K., Andersson O., Melander A., Karlsson L., and Svensson L. E., Correlation between laser welding sequence and distortions for thin sheet structures, Science and Technology of Welding & Joining. (2017) 22, no. 2, 150–156, https://doi.org/10.1080/13621718.2016.1207046, 2-s2.0-84978705979.
10.1080/13621718.2016.1207046
Web of Science® Google Scholar
9 Carrizalez-Vazquez M. A. and Pérez-Medina G. Y., Effect of laser welding sequences on residual stresses and distortion of DP600 steel joints, MRS Advances. (2019) 4, no. 63, 3441–3451, https://doi.org/10.1557/adv.2019.415.
10.1557/adv.2019.415
CAS Web of Science® Google Scholar
10 Fu G. M., Lourenço M. I., Duan M. L., and Estefen S. F., Influence of the welding sequence on residual stress and distortion of fillet welded structures, Marine Structures. (2016) 46, 30–55, https://doi.org/10.1016/j.marstruc.2015.12.001, 2-s2.0-84951808528.
10.1016/j.marstruc.2015.12.001
Web of Science® Google Scholar
11 Wang Y. F., Feng G. J., Pu X. W., and Deng D., Influence of welding sequence on residual stress distribution and deformation in Q345 steel H-section butt-welded joint, Journal of Materials Research and Technology. (2021) 13, 144–153, https://doi.org/10.1016/j.jmrt.2021.04.059.
10.1016/j.jmrt.2021.04.059
Web of Science® Google Scholar
12 Woo D. H., Kitamura M., and Takezawa A., Method to systemically order welding sequence to efficiently mitigate welding displacement of a general ship grillage structure, Ships and Offshore Structures. (2020) 15, no. 7, 753–768, https://doi.org/10.1080/17445302.2019.1681865.
10.1080/17445302.2019.1681865
Web of Science® Google Scholar
13 Taraphdar P. K., Kumar R., Giri A., Pandey C., Mahapatra M., and Sridhar K., Residual stress distribution in thick double-V butt welds with varying groove configuration, restraints and mechanical tensioning, Journal of Manufacturing Processes. (2021) 68, 1405–1417, https://doi.org/10.1016/j.jmapro.2021.06.046.
10.1016/j.jmapro.2021.06.046
Web of Science® Google Scholar
14 Yang X. Y., Yan G. Z., Xiu Y. F., Yang Z., Wang G., Liu W., Li S., and Jiang W., Welding temperature distribution and residual stresses in thick welded plates of SA738Gr.B through experimental measurements and finite element analysis, Materials. (2019) 12, no. 15, https://doi.org/10.3390/ma12152436, 2-s2.0-85070598578.
10.3390/ma12152436
Web of Science® Google Scholar
15 Kohandehghan A. R. and Serajzadeh S., Experimental investigation into the effects of weld sequence and fixture on residual stresses in Arc welding process, Journal of Materials Engineering and Performance. (2012) 21, no. 6, 892–899, https://doi.org/10.1007/s11665-011-9969-1, 2-s2.0-84862236904.
10.1007/s11665-011-9969-1
CAS Web of Science® Google Scholar
16 Aalami-aleagha M. E. and Eslampanah A. H., Mechanical constraint effect on residual stress and distortion in T-fillet welds by three-dimensional finite element analysis, Proceedings of the Institution of Mechanical Engineers - Part B: Journal of Engineering Manufacture. (2013) 227, no. 2, 315–323, https://doi.org/10.1177/0954405412466781, 2-s2.0-84875888350.
10.1177/0954405412466781
CAS Web of Science® Google Scholar
17 Deng D., Liu X. Z., He J., and Liang W., Investigating the influence of external restraint on welding distortion in thin-plate bead-on joint by means of numerical simulation and experiment, International Journal of Advanced Manufacturing Technology. (2016) 82, no. 5-8, 1049–1062, https://doi.org/10.1007/s00170-015-7413-7, 2-s2.0-84955170358.
10.1007/s00170-015-7413-7
Web of Science® Google Scholar
18 Venkatkumar D. and Ravindran D., Effect of boundary conditions on residual stresses and distortion in 316 stainless steel butt welded plate, High Temperature Materials and Processes. (2019) 38, 827–836, https://doi.org/10.1515/htmp-2019-0048.
10.1515/htmp-2019-0048
CAS Web of Science® Google Scholar
19 Liu C. and Zhang J. X., Investigation of external restraining force effects on welding residual stresses using three-dimensional thermal elastic-plastic multi-body coupling finite element model, Proceedings of the Institution of Mechanical Engineers - Part B: Journal of Engineering Manufacture. (2009) 223, no. 12, 1591–1600, https://doi.org/10.1243/09544054jem1548, 2-s2.0-72449120821.
10.1243/09544054JEM1548
Web of Science® Google Scholar
20 Heinze C., Schwenk C., and Rethmeier M., Numerical calculation of residual stress development of multi-pass gas metal arc welding under high restraint conditions, Materials & Design. (2012) 35, 201–209, https://doi.org/10.1016/j.matdes.2011.09.021, 2-s2.0-80155186959.
10.1016/j.matdes.2011.09.021
CAS Web of Science® Google Scholar
21 Wang J. C. and Yi B., Effective thermal elastic plastic finite element computation for welding distortion investigation of pozidriv-type welded structure with rectangular pipes and its mitigation, Proceedings of the Institution of Mechanical Engineers - Part B: Journal of Engineering Manufacture. (2020) 234, no. 14, 1729–1741, https://doi.org/10.1177/0954405420933092.
10.1177/0954405420933092
Web of Science® Google Scholar
22 Tomków J., Sobota K., and Krajewski S., Influence of tack welds distribution and welding sequence on the angular distortion of tig welded joint, Facta Universitatis – Series: Mechanical Engineering. (2020) 18, no. 4, 611–621, https://doi.org/10.22190/fume200520044t.
10.22190/FUME200520044T
Web of Science® Google Scholar
23 Giri A., Mahapatra M. M., Sharma K., and Singh P. K., A study on the effect of weld groove designs on residual stresses in SS 304LN thick multipass pipe welds, International Journal of Steel Structures. (2017) 17, no. 1, 65–75, https://doi.org/10.1007/s13296-016-0118-4, 2-s2.0-85016053887.
10.1007/s13296-016-0118-4
Web of Science® Google Scholar
24 Goldak J., Chakravarti A., and Bibby M., A new finite element model for welding heat sources, Metallurgical Transactions A B. (1984) 15, no. 2, 299–305, https://doi.org/10.1007/bf02667333, 2-s2.0-0021444557.
10.1007/BF02667333
Web of Science® Google Scholar
25 Attarha M. J. and Sattari-Far I., Study on welding temperature distribution in thin welded plates through experimental measurements and finite element simulation, Journal of Materials Processing Technology. (2011) 211, no. 4, 688–694, https://doi.org/10.1016/j.jmatprotec.2010.12.003, 2-s2.0-79251627626.
10.1016/j.jmatprotec.2010.12.003
CAS Web of Science® Google Scholar
26 Deng D., FEM prediction of welding residual stress and distortion in carbon steel considering phase transformation effects, Materials & Design. (2009) 30, no. 2, 359–366, https://doi.org/10.1016/j.matdes.2008.04.052, 2-s2.0-51249094514.
10.1016/j.matdes.2008.04.052
CAS Web of Science® Google Scholar
27 Deng D. and Murakawa H., Prediction of welding distortion and residual stress in a thin plate butt-welded joint, Computational Materials Science. (2008) 43, no. 2, 353–365, https://doi.org/10.1016/j.commatsci.2007.12.006, 2-s2.0-46749113889.
10.1016/j.commatsci.2007.12.006
Web of Science® Google Scholar
28 Biswas P., Kumar D. A., Mandal N. R., and Mahapatra M. M., A study on the effect of welding sequence in fabrication of large stiffened plate panels, Journal of Marine Science and Application. (2011) 10, no. 4, 429–436, https://doi.org/10.1007/s11804-011-1088-8, 2-s2.0-81255150639.
10.1007/s11804-011-1088-8
Google Scholar
29 Mondal A. K., Biswas P., and Bag S., Experimental and FE analysis of submerged arc weld induced residual stress and angular deformation of single and double sided fillet welded joint, International Journal of Steel Structures. (2017) 17, no. 1, 9–18, https://doi.org/10.1007/s13296-016-0093-9, 2-s2.0-85016031102.
10.1007/s13296-016-0093-9
Web of Science® Google Scholar
30 Yi M. S. and Park J. S., Study of heat source model and residual stress caused by welding in GMAW of Al alloy, Metals. (2022) 12, no. 6, https://doi.org/10.3390/met12060891.
10.3390/met12060891
Web of Science® Google Scholar
31 Qu L. J., Li H. Q., Wang Y. Q., and Zhang H., Strain-temperature-stress material model of Q345 (16Mn) steel under elevated temperature and constant loading, Tu Mu Gong Cheng Xue Bao. (2008) 41, no. 7, 41–47.
Google Scholar
32 Wang H. L., Qin S. F., Wang B., and Zhou S., Welding-induced residual stresses in U-Ribs of a steel bridge Deck, Periodica Polytechnica: Civil Engineering. (2021) 65, no. 4, 1239–1246, https://doi.org/10.3311/ppci.18112.
10.3311/ppci.18112
Web of Science® Google Scholar
33 Lu Y. H., Wu X. W., Zeng J., and Wu P. B., Study on FEM numerical simulation method for the welding distortion, Materials Science Forum. (2012) 704-705, 1316–1321, https://doi.org/10.4028/www.scientific.net/msf.704-705.1316, 2-s2.0-84862971354.
10.4028/www.scientific.net/MSF.704-705.1316
Google Scholar
34 Gu Y., Li Y. D., Zhou Z. H., Ren S., and Kong C., Numerical simulation and measurement of welding residual stresses in orthotropic steel decks stiffened with U-shaped ribs, International Journal of Steel Structures. (2020) 20, no. 3, 856–869, https://doi.org/10.1007/s13296-020-00327-3.
10.1007/s13296-020-00327-3
Web of Science® Google Scholar
35 Tomków J., Fydrych D., and Rogalski G., Role of bead sequence in underwater welding, Materials. (2019) 12, no. 20, https://doi.org/10.3390/ma12203372.
10.3390/ma12203372
Web of Science® Google Scholar
36 Li S., Hu L., Dai P. Y., Bi T., and Deng D., Influence of the groove shape on welding residual stresses in P92/SUS304 dissimilar metal butt-welded joints, Journal of Manufacturing Processes. (2021) 66, 376–386, https://doi.org/10.1016/j.jmapro.2021.04.030.
10.1016/j.jmapro.2021.04.030
Web of Science® Google Scholar

Citing Literature

All articles

Effect of Welding Sequence and Constraint on the Residual Stress and Deformation of Thick Welded Butt Joint Made of Q345qD Steel

Abstract

1. Introduction