1. Introduction

The nonlinear system JM equation has been analyzed in past years by several researchers through different methods like homotopy perturbation transform method [7], optimal homotopy asymptotic method and Hermite wavelets [8], invariant subspace technique [9], and others [10–12].

Systems of nonlinear partial differential equation [13–17] appear in a variety of scientific physical models. The classical Jaulent-Miodek equations have been the subject of extensive investigation in recent years. Several techniques such as suitable algebraic technique [18], Adomian decomposition technique [19], tanh-sech technique [20], homotopy perturbation technique [21], Exp-function technique [22], and homotopy analysis technique [23] had been applied for solving of the system of Jaulent-Miodek equations. But the complete evaluation of the nonlinear fractional-order combined with the Jaulent-Miodek equation is only an initiation by the available information.

Abdeljawad and Jarad [24] recently developed the Laplace transform of the fractional-order Caputo derivatives. We proposed a new iterative technique based on the ρ-Laplace transformation to study fractional-order ordinary and partial differential equations with fractional-order Caputo derivatives. This novel proposed method is used to solve numerous fractional-order differential equations, including linear and nonlinear diffusion equations, fractional-order Fokker-Planck equations, and Zakharov-Kuznetsov equations [25–27]. Adomian, an American mathematician, introduced the Adomian decomposition method. It concentrates on obtaining series-like solutions and decomposing the nonlinear operator into a sequence, with the terms currently obtained using Adomian polynomials [28–31]. The ρ-Laplace transform is used to modify this procedure, resulting in the ρ-Laplace decomposition method. This method is applied to the nonhomogeneous fractional differential equations [32–34]. He [35, 36] was the first to introduce the variational iteration method (VIM), which was successfully applied to autonomous ordinary differential equations in [37], nonlinear polycrystal line solids in [38], and other fields. The variational iteration method is modified with the help of ρ-Laplace transform, known as ρ-Laplace variational iteration method. Different types of ODEs and PDEs have been analyzed with the aid of the variational iteration method. For instance, this method is investigated for solving fractional differential equations in [37]. In [38], this method is used to solve nonlinear oscillator equations. Compared to the Adomians decomposition method, variational iteration transforms approach solving without the need to compute Adomian’s polynomials. The [39] mesh point procedures provide an analytical solution, whereas this scheme provides a fast response to the equation [40–42]. This technique can also be used to approximate accurate results.

This article has applied the ρ-Laplace decomposition method and ρ-Laplace variational iteration method to solve the fractional coupled Jaulent-Miodek equation with the Caputo fractional derivative operator. The analytical results attained via the ρ-Laplace decomposition method were compared with exact results and those derived by using the ρ-Laplace variational iteration method in case of fractional order.

2. Basic Preliminaries

3. The Methodology of ρ-Laplace Decomposition Method

where is $$ the Caputo fractional derivative of order ϑ, $$, $$, and $$, $$ are linear and nonlinear functions, respectively, and $$ and $$ are source operators.

4. The Producer of ρ-LVITM

5. Implementation of Techniques

5.1. Problem

Consider the fractional-order non-linear Jaulent-Miodek equation is given as

$$ (31)

$$ (32)

With initial conditions

$$ (33)

$$ (34)

Taking ρ-Laplace transform of (31),

$$ (35)

$$ (36)

Using inverse ρ-Laplace transformation, we get

$$ (37)

$$ (38)

Applying Adomian procedure, we have

$$ (39)

$$ (40)

$$ (41)

$$ (42)

The nonlinear terms find with the help of Adomain polynomials

For κ = 1

$$ (43)

for κ = 2

$$ (44)

for κ = 2

$$ (45)

$$ (46)

The ρ-LDM solution of Example 1 is

$$ (47)

$$ (48)

$$ (49)

The approximate solution by ρ-LVIM.

Apply the iteration technique, we have

$$ (50)

$$ (51)

where

$$ (52)

For κ = 0, 1, 2, ⋯

$$ (53)

$$ (54)

$$ (55)

$$ (56)

$$ (57)

$$ (58)

$$ (59)

$$ (60)

$$ (61)

$$ (62)

$$ (63)

$$ (64)

$$ (65)

$$ (66)

The exact solution of equation (8) at ϑ = 1,

$$ (67)

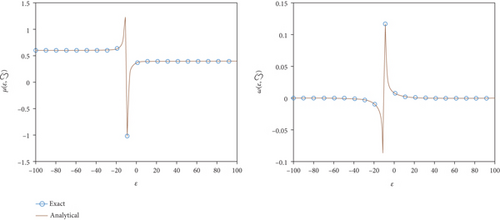
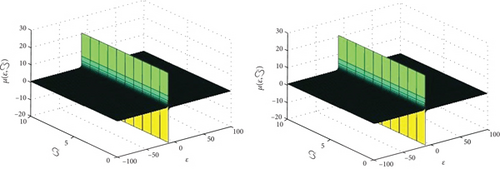
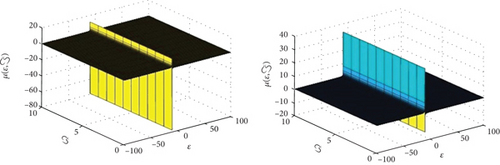
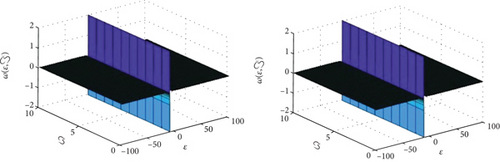
In Figure 1, the first figure shows the ρ-Laplace decomposition method and ρ-Laplace variational transform method and exact solutions graphs of the given problem at $$ and $$. From the given graphs, it can be observed that both the exact, ρ-Laplace decomposition method, and ρ-Laplace variational transform method solution are in strong agreement with each other. In Figure 2, the exact and approximate solution of $$ at ϑ = 1. Figure 3, different fractional-order of ϑ = 0.8 and 0.6 of the model. Similarly, in Figure 4, the exact and approximate solution of $$ at ϑ = 1. Figure 5, different fractional-order of ϑ = 0.8 and 0.6 of the model. It is investigated that results of fractional-order problem are convergent to an integer-order result as fractional-order analysis to integer-order. The same phenomenon of convergence of fractional-order solutions towards integral-order solutions is observed.

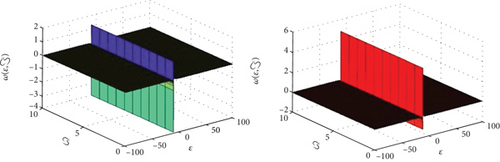
6. Conclusion

In this paper, two analytical methods are applied to solve fractional-order nonlinear Jaulent-Miodek equation. The analytical results of the equations are calculated to show the reliability and validity of the suggested techniques. Figures of the results are plotted to show the closed contact between the achieved and exact solutions. Moreover, the proposed methods provide easily computable components for the series-form solutions. It has been discovered that the results obtained in series form have a better rate of convergence to the exact solutions. Finally, the proposed strategies are found to be a sophisticated strategy for solving various fractional-order nonlinear partial differential equations.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this article.

Authors’ Contributions

Ahmad Haji Zadeh and Nehad Ali Shah contributed equally to this work and are the co-first authors.