Nowadays, all scientists are in the race to find a cure for COVID-19. This is a viral disease that is due to severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). Different antiviral drugs are under investigation. Dexamethasone is being used for the treatment of COVID-19. In this article, the chemical structure of dexamethasone is explored using computational techniques such as topological indices. Proofs of a few closed formulas that describe the degree-dependent topological indices calculated from the M-polynomial of the graphs are also given in this article.

1. Introduction

Epidemics such as flu, cholera, and plague disturb the life of the people of the world for centuries. COVID-19 began in China on December 19 and has since claimed many lives and is responsible for the largest global recession. This is due to the virus named severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) [1, 2]. The spread of this virus can be reduced by using personal protective equipment and physical distance. The search for a cure to prevent COVID-19 is an important need of today.

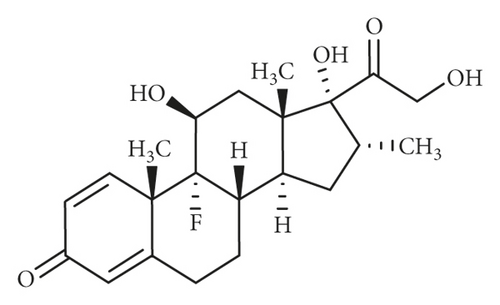
Different techniques such as antiviral drugs, vaccines, and plasma therapy are under progress to control this viral disease [3]. So far, no effective medicine has been developed to treat patients with COVID-19. Several clinical trials have been conducted to study the effect of different drugs on patients [4]. The results of the dexamethasone on patients with COVID-19 are encouraging [5, 6]. Dexamethasone is a corticosteroid that is used for its immunosuppressant and anti-inflammatory properties. The chemical formula of dexamethasone is C₂₂H₂₉FO₅ and also known as 9α-fluoro-11β, 17α, 21-trihydroxy-16α-methylpregna-1,4-diene-3,20-dione. Dexamethasone is white to off-white crystalline powder. It has a slightly bitter taste and is odorless. 3D and 2D structures of dexamethasone are shown in Figure 1.

Details are in the caption following the image — Open in figure viewer PowerPoint

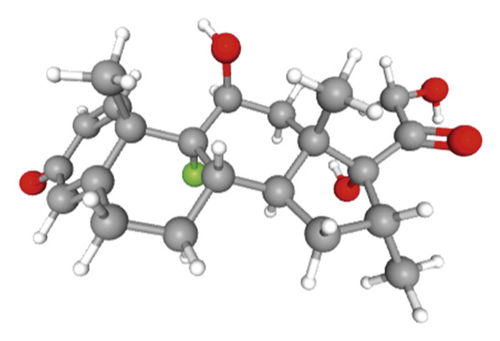
A graph is represented with G(V_G, E_G) where V_G and E_G have represented the vertex set and edge set, respectively. The number of edges that meet at a vertex x is called the degree of a vertex (d_x). The graphical form of the structure of the chemical compound is known as a chemical graph. In a chemical graph, atoms behave as vertex and bonds as edges. This graph is a valuable source of the physical and chemical properties of the substance. Computational analysis of the chemical graph has been studied in chemical graph theory. C-H bond does not have a serious effect on the characteristics of the chemical species. So, during the computational analysis, we ignore it.

During computational analysis, a chemical graph is converted into a real number called topological index that can reflect the different physical, chemical, and biological features of the chemical compounds [7]. The study of the topological index is started by the formulation of the Wiener index [8]. Different topological applications have been found in [9–14]. For a graph G, a degree-dependent topological index is defined as

(1)

By counting edges that have the same end-degrees in the chemical graph, then we can rewrite equation (1) as

(2)

where the relation {d_x, d_y} = {j, k} satisfied and m_jk is the total count of edges xy of the graph G. In 2015, Gutman et al. [15] formulated a reduced reciprocal Randic’ index, which can be defined as

(3)

In 2016, Shegehalli and Kanabur presented the first arithmetic-geometric index [16] and defined as

(4)

Shigehalli and Kanabur also introduced the three new indices [17] defined as

(5)

Miličcević et al. presented a first Zagreb index in terms of edge degree [18] defined as

(6)

Du et al. [19] formulated the general sum-connectivity index which can be described as

(7)

Ranjini et al. [20] redefined the Zagreb indices as

(8)

These topological indices are either calculated directly by their formula or by using the graph polynomials such as M-polynomial. Deutsch and Klawzar [21] define the M-polynomial as

(9)

Here, ψ = min{d_x|x ∈ V_G}, Ψ = max{d_x|x ∈ V_G} Numerous graphs have been studied in the past through M-polynomial and topological indices [22–24]. Some operators, which are used further, are defined as

(10)

Shin et al. [25] presented the closed form of topological indices via M-polynomial, but they are not provided the relationship between them. In the following section, we provide this relationship.

2. Main Results

Theorem 1. Let M_G(u, v) be the M-polynomial for the graph G, then the reduced reciprocal index is calculated as .

Proof. By taking

(11)

Hence, .

Theorem 2. If M_G(u, v) is the M-polynomial of the graph G, then the first arithmetic-geometric index is given by .

Proof. By taking

(12)

Hence, .

Theorem 3. If M_G(u, v) is represented the M-polynomial of the graph G, then .

Proof. By taking

(13)

Hence, .

Theorem 4. If M_G(u, v) is the M-polynomial of the graph G, then .

Proof. By taking

(14)

Hence, .

Theorem 5. If M_G(u, v) is the M-polynomial of the graph G, then .

Proof. By taking

(15)

Hence, .

Theorem 6. Let M_G(u, v) be the M-polynomial for the graph G, then .

Proof. By taking

(16)

Hence, .

Theorem 7. Let M_G(u, v) be the M-polynomial for the graph G, then the sum-connectivity index is given by .

Proof. By taking

(17)

Hence, .

Theorem 8. IF M_G(u, v) is the M-polynomial of the graph G, then the general sum-connectivity index is given by .

Proof. By taking

(18)

Hence, .

Theorem 9. If M_G(u, v) is the M-polynomial of the graph G, then the redefined third Zagreb index is also calculated as .

Proof. By taking

(19)

Hence, .

3. M-Polynomial of Dexamethasone

The chemical graph of dexamethasone (D_M) is shown in Figure 2, in which green, red, pink, and brown dots represent the vertices of degrees 1, 2, 3, and 4, respectively; cyan, orange, yellow, purple, blue, black, gray, violet, and magenta edges represent the edges having the degree of end-vertices (1,2), (1,3), (1,4), (2,2), (2,3), (2,4), (3,3), (3,4), and (4,4), respectively. In this present work, we extract some topological indices via M-polynomial of (D_M).

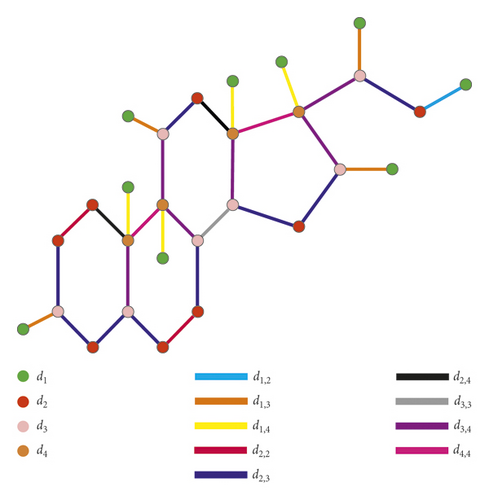
Theorem 10. Let D_M be dexamethasone, then M-polynomial of D_M is .

Proof. Let D_M represent the dexamethasone, then by using Figures 1 and 2 and Table 1, we have that there are four partitions of the vertex set with respect to the vertex degree defined as where n = 1,2,3,4.

Figures 1 and 2 and Table 2 show that there are nine partitions of the edge set with respect to the degree of end-vertices of the edge. These partitions are represented with E_n, where where n = 1,2,3, …, 9 and a, b = 1,2,3,4 with a ≤ b. We have the following result by using the definition of M-polynomial:

(20)

The plot of the M-polynomial of D_M is shown in Figure 3.

1. Vertex partition of D_M.

d_x	1	2	3	4
Number of vertices	9	8	7	4

2. Edge partition of D_M.

(d_x, d_y)	(1,2)	(1,3)	(1,4)	(2,2)	(2,3)	(2,4)	(3,3)	(3,4)	(4,4)
Number of edges	1	4	4	2	9	2	1	6	2

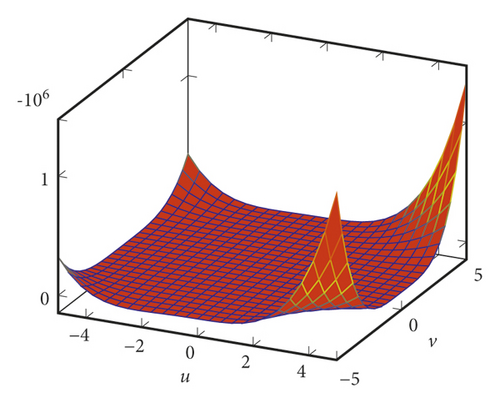
4. Topological Indices of Dexamethasone

Theorem 11. Let D_M represent the dexamethasone and

(21)

Then,

(1)
(2)
(3)
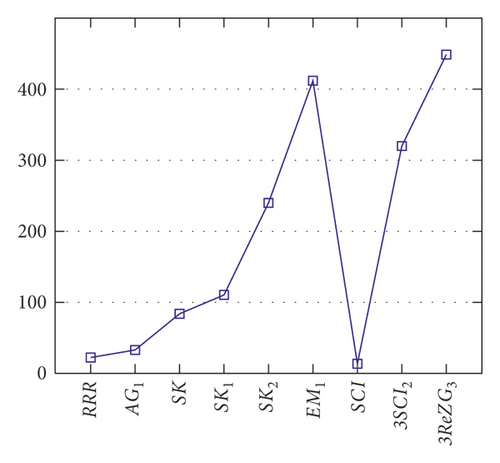
SK[D_M] = 84
(4)
SK₁[D_M] = (221/2)
(5)
SK₂[D_M] = 240
(6)
EM₁[D_M] = 412
(7)
(8)
SCI_λ[D_M] = 3^λ + 6 · 4^λ + 13 · 5^λ + 3 · 6^λ + 6 · 7^λ + 2 · 8^λ
(9)
ReZG₃[D_M] = 1346

Proof.

(22)

The results of topological indices are plotted in Figure 4.

5. Conclusion

We have presented the proofs of the formulas of some topological indices, which are derived from M-polynomial. The structure of the molecule can explore the chemical and biological behavior of the chemical compound. In the present work, we gave the computational analysis of the dexamethasone used during the treatment of COVID-19 by finding the topological indices. These topological indices are calculated from the M-polynomial of dexamethasone.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Open Research

Data Availability

No data were used in this research.

References

1 Fernandez-Garcia L., Pacios O., Gonzlez-Bardanca M., Blasco L., Bleriot I., Ambroa A., Lpez M., Bou G., and Toms M., Viral related tools against SARS-CoV-2, Viruses. (2020) 12, no. 10, https://doi.org/10.3390/v12101172.
10.3390/v12101172
PubMed Google Scholar
2 Gorbalenya A., Baker S., Baric R., Drosten C., Gulyaeva A., and Haagmans B., The species Severe acute respiratory syndrome-related coronavirus: classifying 2019-nCoV and naming it SARS-CoV-2, Nature Microbiology. (2020) 5, no. 4, 536–544.
10.1038/s41564-020-0695-z
PubMed Web of Science® Google Scholar
3 Ianevski A., Yao R., Fenstad M. H., Biza S., Zusinaite E., Reisberg T., Lysvand H., Løseth K., Landsem V. M., Malmring J. F., Oksenych V., Erlandsen S. E., Aas P. A., Hagen L., Pettersen C. H., Tenson T., Afset J. E., Nordbø S. A., Bjørås M., and Kainov D. E., Potential antiviral options against SARS-CoV-2 infection, Viruses. (2020) 12, no. 6, https://doi.org/10.3390/v12060642.
10.3390/v12060642
Google Scholar
4 Morse J. S., Lalonde T., Xu S., and Liu W. R., Learning from the past: possible urgent prevention and treatment options for severe acute respiratory infections caused by 2019-nCoV, ChemBioChem. (2020) 21, no. 5, 730–738, https://doi.org/10.1002/cbic.202000047.
10.1002/cbic.202000047
CAS PubMed Web of Science® Google Scholar
5 Hosseinzadeh M. H., Shamshirian A., and Ebrahimzadeh M. A., Dexamethasone vs. COVID-19: an experimental study in line with the preliminary findings of a large trial, International Journal of Clinical Practice. (2020) 75, no. 6, 1–5, https://doi.org/10.1111/ijcp.13943.
10.1111/ijcp.13943
Web of Science® Google Scholar
6 Matthay M. A. and Thompson B. T., Dexamethasone in hospitalised patients with COVID-19: addressing uncertainties, The Lancet Respiratory Medicine. (2020) 8, no. 12, 1170–1172, https://doi.org/10.1016/s2213-2600(20)30503-8.
10.1016/S2213-2600(20)30503-8
CAS PubMed Web of Science® Google Scholar
7 Trinajstić N., Chemical Graph Theory, 1992, Routledge, New York, NY, USA.
Google Scholar
8 Wiener H., Structural determination of paraffin boiling points, Journal of the American Chemical Society. (1947) 69, no. 1, 17–20, https://doi.org/10.1021/ja01193a005, 2-s2.0-8544254107.
10.1021/ja01193a005
CAS PubMed Web of Science® Google Scholar
9 Rouvray D. H., The prediction of biological activity using molecular connectivity indices, Acta Pharmaceutica Jugoslavica. (1986) 36, 239–252.
CAS Web of Science® Google Scholar
10 Hosamani S., Perigidad D., Jamagoud S., Maled Y., and Gavade S., QSPR analysis of certain degree based topological indices, Journal of Statistics Applications & Probability. (2017) 6, no. 2, 361–371, https://doi.org/10.18576/jsap/060211.
10.18576/jsap/060211
Google Scholar
11 Ramakrishnan S., Senbagamalar J., and Babujee J. B., Topological indices of molecular graphs under specific chemical reactions, International Journal of Computing Algorithm. (2013) 2, no. 1, 68–74, https://doi.org/10.20894/ijcoa.101.002.001.019.
10.20894/IJCOA.101.002.001.019
Google Scholar
12 Haris Mateen M., Khalid Mahmmod M., Mahmmod M. K., Kattan D. A., and Ali S., A novel approach to find partitions of with equal sum subsets via complete graphs, AIMS Mathematics. (2021) 6, no. 9, 9998–10024, https://doi.org/10.3934/math.2021581.
10.3934/math.2021581
Web of Science® Google Scholar
13 Mateen M. H., Mahmmod M. K., Mahmmod M. K., Alghazzawi D., and Liu J.-B., Structures of power digraphs over the congruence equation ≡ y (mod m) and enumerations, AIMS Mathematics. (2021) 6, no. 5, 4581–4596, https://doi.org/10.3934/math.2021270.
10.3934/math.2021270
Web of Science® Google Scholar
14 Mateen M. H., Mahmood M. K., and Ali S., Importance of power digraph in computer science, Proceedings of the 2019 International Conference on Innovative Computing (ICIC), November 2019, Lahore, Pakistan, 1–6.
Google Scholar
15 Gutman I., Furtula B., and Elphick C., Three new/old vertex-degree-based topological indices, Communications in Mathematical and in Computer Chemistry. (2014) 72, no. 3, 617–632.
Web of Science® Google Scholar
16 Shigehalli V. and Kanabur R., Arithmetic-geometric indices of path graph, A Journal of Computer and Mathematical Sciences. (2015) 6, no. 1, 19–24.
Google Scholar
17 Shigehalli V. and Kanabur R., Computing degree based topological indices of polyhex nanotube, Journal of Mathematical Nanoscience. (2016) 6, no. 1, 47–55.
Google Scholar
18 Miličcević A., Nikolić S., and Trinajstić N., On reformulated Zagreb indices, Molecular Diversity. (2004) 8, no. 1, 393–399.
10.1023/B:MODI.0000047504.14261.2a
PubMed Web of Science® Google Scholar
19 Du Z., Zhou B., and Trinajstić N., On the general sum-connectivity index of trees, Applied Mathematics Letters. (2011) 24, no. 3, 402–405, https://doi.org/10.1016/j.aml.2010.10.038, 2-s2.0-78649972069.
10.1016/j.aml.2010.10.038
Web of Science® Google Scholar
20 Ranjini P., Lokesha V., and Usha A., Relation between phenylene and hexagonal squeeze using harmonic index, International Journal of Graph Theory. (2013) 1, no. 4, 116–121.
Google Scholar
21 Deutsch E. and Klawzar S., M-polynomial and degree-based topological indices, Iranian Journal of Mathematical Chemistry. (2015) 6, no. 2, 93–102.
Web of Science® Google Scholar
22 Afzal F., Hussain S., Afzal D., and Hameed S., M-polynomial and topological indices of zigzag edge coronoid fused by starphene, Open Chemistry. (2020) 18, no. 1, 1362–1369, https://doi.org/10.1515/chem-2020-0161.
10.1515/chem-2020-0161
CAS Web of Science® Google Scholar
23 Afzal F., Hussain S., Afzal D., and Razaq S., Some new degree based topological indices via M-polynomial, Journal of Information and Optimization Sciences. (2020) 41, no. 4, 1061–1076, https://doi.org/10.1080/02522667.2020.1744307.
10.1080/02522667.2020.1744307
Web of Science® Google Scholar
24 Hussain S., Afzal F., Afzal D., Cancan M., Ediz S., and Farahani M. R., Analyzing the boron triangular nanotube through topological indices via M-polynomial, Journal of Discrete Mathematical Sciences and Cryptography. (2021) 24, no. 2, 415–426, https://doi.org/10.1080/09720529.2021.1882158.
10.1080/09720529.2021.1882158
Web of Science® Google Scholar
25 Shin D. Y., Hussain S., Afzal F., Park C., Afzal D., and Farahani M. R., Closed formulas for some new degree based topological descriptors using M-polynomial and boron triangular nanotube, Frontiers of Chemistry. (2021) 8, 613873, https://doi.org/10.3389/fchem.2020.613873.
10.3389/fchem.2020.613873
PubMed Web of Science® Google Scholar

Citing Literature

All articles

[Retracted] The Study about Relationship of Direct Form of Topological Indices via M-Polynomial and Computational Analysis of Dexamethasone

Retraction(s) for this article

Retracted: The Study about Relationship of Direct Form of Topological Indices via M-Polynomial and Computational Analysis of Dexamethasone

Abstract

1. Introduction

2. Main Results

3. M-Polynomial of Dexamethasone

4. Topological Indices of Dexamethasone

5. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

[Retracted] The Study about Relationship of Direct Form of Topological Indices via M-Polynomial and Computational Analysis of Dexamethasone

Retraction(s) for this article

Retracted: The Study about Relationship of Direct Form of Topological Indices via M-Polynomial and Computational Analysis of Dexamethasone

Abstract

1. Introduction

2. Main Results

3. M-Polynomial of Dexamethasone

4. Topological Indices of Dexamethasone

5. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information