Volume 2022, Issue 1 4398388

Research Article

Open Access

Nonlinear Buckling Analysis and Optimization Design of the Y-Type Composite Insulator String

Hua Bao,

Hua Bao

China Energy Engineering Group Anhui Electric Power Design Institute Co., Ltd.,, 369 Fanhua Avenue, Hefei 230601, China

Search for more papers by this author

Lingzhi Xia,

Lingzhi Xia

Electric Power Research Institute of State Grid Anhui Electric Power Co., Ltd.,, 299 Ziyun Road, Hefei 230001, China

Search for more papers by this author

Shengcong Chai,

Shengcong Chai

China Energy Engineering Group Anhui Electric Power Design Institute Co., Ltd.,, 369 Fanhua Avenue, Hefei 230601, China

Search for more papers by this author

Yang Cheng,

Yang Cheng

Electric Power Research Institute of State Grid Anhui Electric Power Co., Ltd.,, 299 Ziyun Road, Hefei 230001, China

Search for more papers by this author

Songyuan Cao,

Songyuan Cao

State Grid Anhui Electric Power Co., Ltd.,, 9 Huangshan Road, Hefei 230061, China

Search for more papers by this author

Zhiwen Lan,

Corresponding Author

Zhiwen Lan

[email protected]

orcid.org/0000-0001-8944-5011

Institute of Engineering Mechanics, Nanchang University, 999 Xuefu Avenue, Nanchang 330031, China ncu.edu.cn

Search for more papers by this author

Hua Bao,

Hua Bao

China Energy Engineering Group Anhui Electric Power Design Institute Co., Ltd.,, 369 Fanhua Avenue, Hefei 230601, China

Search for more papers by this author

Lingzhi Xia,

Lingzhi Xia

Electric Power Research Institute of State Grid Anhui Electric Power Co., Ltd.,, 299 Ziyun Road, Hefei 230001, China

Search for more papers by this author

Shengcong Chai,

Shengcong Chai

China Energy Engineering Group Anhui Electric Power Design Institute Co., Ltd.,, 369 Fanhua Avenue, Hefei 230601, China

Search for more papers by this author

Yang Cheng,

Yang Cheng

Electric Power Research Institute of State Grid Anhui Electric Power Co., Ltd.,, 299 Ziyun Road, Hefei 230001, China

Search for more papers by this author

Songyuan Cao,

Songyuan Cao

State Grid Anhui Electric Power Co., Ltd.,, 9 Huangshan Road, Hefei 230061, China

Search for more papers by this author

Zhiwen Lan,

Corresponding Author

Zhiwen Lan

[email protected]

orcid.org/0000-0001-8944-5011

Institute of Engineering Mechanics, Nanchang University, 999 Xuefu Avenue, Nanchang 330031, China ncu.edu.cn

Search for more papers by this author

First published: 30 December 2022

https://doi.org/10.1155/2022/4398388

Citations: 1

Academic Editor: Krishanu Roy

Share a link

Email
Wechat
Bluesky

Abstract

Under the action of extreme wind load, the overhead transmission line will lead to the fracture of the traditional V-type insulator string, which greatly affects the safety of the power system. Compared with the V-type insulator string, the Y-type insulator string has better stability under the wind load. Therefore, the overhead lines in the mountainous areas of Anhui Province are taken as the research object, considering the combined effect of wind load and conductor dead weight, and through theoretical derivation, the calculation formula of insulator string wind deflection angle is obtained. Using numerical simulation software, the nonlinear mechanical analysis of Y-type insulator strings is conducted, and under the action of different wind speeds, the windage yaw angle and unloading angle of the Y-type insulator string are obtained. Compared with the calculation results of the V-type insulator string, the stability of the Y-type insulator string in the structure is better than that of the V-type insulator string, and the Y-type insulator string can make full use of the distance between layers and the gap margin of the tower head, reduce the length of the cross arm, and reduce the weight of the tower, which has obvious advantages. Combined with the results of theoretical analysis and numerical simulation, the optimal design method of the Y-type insulator string is given. Under the condition of ensuring the safety and stability of insulators, the distance of the cross arm is shortened as much as possible and the weight of the transmission line tower is reduced. The research results will provide a theoretical reference for engineering design and improvement.

1. Introduction

In recent years, with the steady improvement of China’s economic level, the demand for power in industrial production and construction is increasing day by day. A sufficient and sustained energy supply is an important condition for the development of the national economy. However, due to the uneven distribution of power resources, it is necessary to build a reasonable power network to reasonably allocate power resources [1–3]. When the transmission line system is subjected to the transverse wind load perpendicular to the conductor, the conductor swings under the wind load, which reduces the electrical gap between it and the tower structure. When the electrical gap is less than the safe distance allowed by the transmission line specifications, breakdown and discharge may occur, which may lead to tripping accidents. This phenomenon is called wind bias discharge tripping [4]. Wind bias discharge tripping is one of the main causes of transmission line faults, which has a great impact on the safety of the power system and has brought huge economic losses to people’s production and lives [5–9]. The insulator string of the transmission tower is composed of two or more insulator units. The insulator string is a protective device required for fixation and operation, which can insulate the conductor from the transmission tower. Due to differences in transmission tower structure, the conductor model, number of subconductors per phase, and voltage grade, the assembly type of insulator string is also different, which can be divided into two categories: suspension insulator string and tension insulator string. The number of insulator units in the insulator string is related to the voltage level, e.g., in China, the minimum number of insulator units under different voltage levels is 7 units for 110 kV, 13 units for 220 kV, 17 units for 330 kV, 25 units for 500 kV, and 32 units for 750 kV, which can be determined according to the actual situation in the actual project. With the development and application of UHV transmission line system, the design and optimization of insulator string’s antiwindage yaw need to be revised urgently. In most existing transmission line systems, insulator strings are mostly I-type or V-type. Only a few transmission line projects use Y-type insulator strings, and the research on Y-type insulator strings is relatively lacking [10–12]. Therefore, it is of great engineering significance to analyze the mechanical characteristics and windage yaw angle of the Y-type insulator string under wind load.

The safe distance between the transmission conductor and the tower structure is affected by the tower structure, insulator string form, wind load, vertical load, and surrounding environment. An et al. [13] propose a systematic method to analyze windage yaw flashovers of transmission lines. El-Refaie et al. [14] studied the effect of pollution layer thickness and conductivity on the electric field distribution. Scholars at home and abroad have studied the windage yaw characteristics of various types of insulator strings under wind load, mainly focusing on the research of I-type and V-type insulator strings, while the research of Y-type insulator strings is relatively less. Feng et al. [15] combined with the calculation results of the fine numerical simulation of multispan transmission lines, fitted the calculation formula of the swing angle of I-type insulator strings, and found that the swing angle decreased with the increase in ice thickness. Yan et al. [16] corrected the normative calculation formula of the windage yaw angle of I-type insulator string by introducing the dynamic wind load coefficient, and combined with the calculation results of numerical simulation, gave the corresponding coefficients in different cases. Li et al. [17] studied the influence of complex wind farms on the windage yaw characteristics of insulator strings and compared the theoretical calculation with the simulation results. Yan et al. [18] proposed the dynamic wind load coefficient in the formula for determining the swing angle of I-type insulator string through numerical simulation. Jia et al. [19] studied the windage yaw characteristics of I-type insulator strings through numerical simulation and found that the span has a certain impact on the windage yaw angle and wind load adjustment coefficient of suspension insulator strings and provided the corresponding wind load adjustment coefficient for different spans. Wang et al. [20] established a finite element coupling model of V-type insulator strings of transmission lines and calculated the stress distribution of insulator strings under fluctuating wind excitation. Li et al. [21] considered the composite material parameters of the insulator string and analyzed the buckling characteristics of the composite insulator string and the deformation characteristics of the V-type composite insulator string based on the finite element method. Xie et al. [22] analyzed the failure mechanism of V-type insulator strings from the aspects of manufacturing process, structural characteristics, experimental research, and numerical simulation. Fu and Gong [23] studied the dynamic tensile and compressive loads of V-type insulator strings under dynamic operating conditions through numerical simulation and obtained the amplification ratio of the dynamic peak load to the corresponding static load. A large number of studies have shown that both I-type and V-type insulator strings have their own application advantages, and Y-type insulator strings combine the advantages of both I-type and V-type insulator strings and have better mechanical, windage yaw, and pollution flashover characteristics [24]. However, the research on Y-type insulator strings is relatively scarce, and the stress characteristics are complex, so it is difficult to establish accurate calculation methods.

A large number of studies have shown that when the wind speed is large, the included angle of the V-type insulator string is large, which will lead to the corresponding increase in the length of the insulator and cross arm and the interlayer spacing, which is not controlled by the gap. The Y-type insulator string combines the advantages of I-type and V-type insulator string structures, can fully reduce the length of the insulator string and cross arm, reduce the length of line corridor to a certain extent, and have good economic benefits. At home and abroad, the research on I-type and V-type insulator strings is relatively complete. As a new type of structure, Y-type insulator string has a good prospect in engineering application. However, the research on the mechanical properties of Y-type insulator strings at home and abroad is not perfect, and the research on Y-type insulator strings is relatively lacking. Therefore, through theoretical analysis and numerical simulation, this article calculates the displacement of V-type and Y-type insulator strings under wind load, gives the optimization design method of Y-type insulator strings, and compares the nonlinear buckling performance of V-type and Y-type insulator strings. The research results will provide a theoretical reference for the optimization design of Y-type insulator strings and their promotion and application in transmission lines.

2. The Windage Yaw Theory of the Composite Insulator String

The windage yaw angle is the included angle formed by the deviation of the conductor insulator string from the vertical position under the action of wind load, which can be determined according to the vertical load and wind load as shown in Figure 1. Generally, if the wind deflection angle is too large, the air gap between the electrified body at the lower end of the insulator string and the iron tower will be reduced, and the line is prone to wind deflection tripping accident and discharge. Therefore, we first calculate the wind load of the conductor in this section. Under the action of the wind load, we obtain the theoretical calculation expression of the wind deflection angle of the new Y-shaped insulator string through theoretical analysis.

Details are in the caption following the image — Open in figure viewer PowerPoint

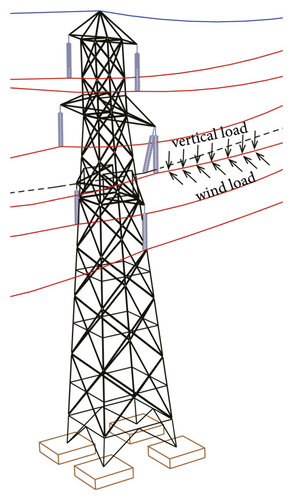
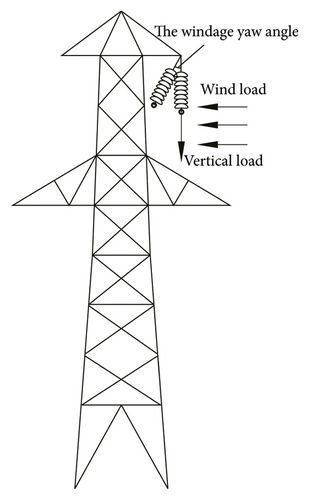
2.1. The Calculation of Wind Load

2.1.1. The Wind Load Calculation of the Composite Insulator String

The wind load of the single insulator of the suspension insulator string is [25–30]

(1)

where P_j is the load on the single insulator, V is the average wind speed within ten minutes adopted in the design, and A is the wind receiving area of single insulator, when the diameter of single disc of insulator is less than 254 mm, the area is taken as 0.02 m², and the area of large disc diameter and double diameter is taken as 0.03 m².

2.1.2. The Calculation of Wind Load on the Conductor

The wind load on the conductor with horizontal span L_h is [25–30]

(2)

where W_x is the wind load on the conductor, α is the uneven coefficient of wind pressure, as shown in Table 1, μ_sc is the shape coefficient of the conductor, as shown in Table 2, d is the diameter of the conductor, L_h is the horizontal span of the conductor, and θ is the windage yaw angle of the conductor.

1. The value of α under different wind speeds.

Wind speed v (m/s)	v < 20	20 ≤ v < 30	30 ≤ v < 35	v ≥ 30
The uneven coefficient of wind pressure α	1.0	0.85	0.75	0.70

2. The shape coefficient values of conductors with different diameters.

Surface condition of the conductor	No ice		Ice
The conductor diameter d (mm)	d < 17	d ≥ 17	—
The conductor shape coefficient μ_sc	1.2	1.1	1.2

2.1.3. The Calculation of the Conductor Vertical Load

The theoretical calculation expression of the vertical load of the conductor is

(3)

where W_g is the vertical load of the conductor, L_v is the vertical span of the conductor, q is the gravity per unit length of the conductor, and n is the number of bundled conductors.

2.2. The Theoretical Derivation of the Composite Insulator String

The windage yaw angle of the composite insulator string is mainly affected by the horizontal wind load. Through mechanical analysis, when ϕ < θ/2, both limbs of the V-type insulator string are under tension. When ϕ = θ/2, the windward side is under tension and the leeward side is not under stress. When ϕ > θ/2, the windward side is under tension and the leeward side is under compression, as shown in Figure 2. When the wind speed is large enough, the structure is unstable, and unloading angle will occur α (i.e., the difference between the maximum windage yaw angle and half of the included angle between the two limbs). According to relevant data, the unloading angle should not exceed 10^°. In 1989, Guangdong Electric Power Design Institute carried out relevant experiments on V-type composite insulator strings. The results showed that the unloading angle of composite insulator strings should not exceed 15^°. That is, reasonable control of the unloading angle can ensure the safety of the line. Since the gravity of the insulator string is different from the dead weight of the conductor by an order of magnitude, the load of the insulator string itself is ignored.

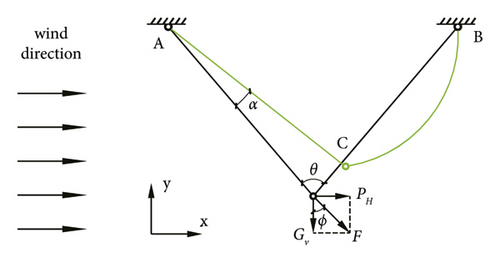
In Figure 2, G_v is the conductor gravity, P_H is the horizontal wind load, F is the resultant force, ϕ is the windage yaw angle, θ is the angle between two limbs, and α is the unloading angle.

Assuming the coordinate origin is point A and the length of the insulator string is L, the motion trajectory of point C is

(4)

By geometric relationship

(5)

The mechanical analysis of tension limb point C is shown in Figure 3(a), by analysis

(6)

Assuming the axial deformation of the compression limb is ∆L, then

(7)

Simultaneous (5) and (7)

(8)

where P_H1 is the horizontal wind load component of the windward limb, F₁ is the tension on the windward limb, and F₂ is the force from the windward limb to the leeward limb.

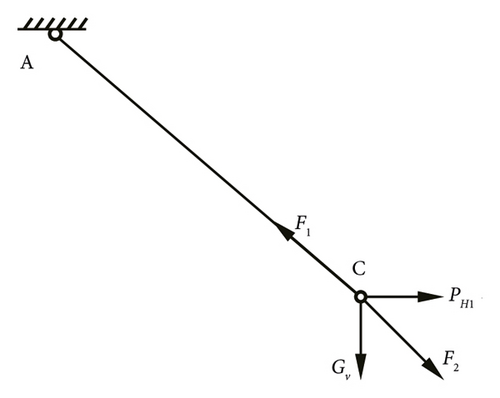
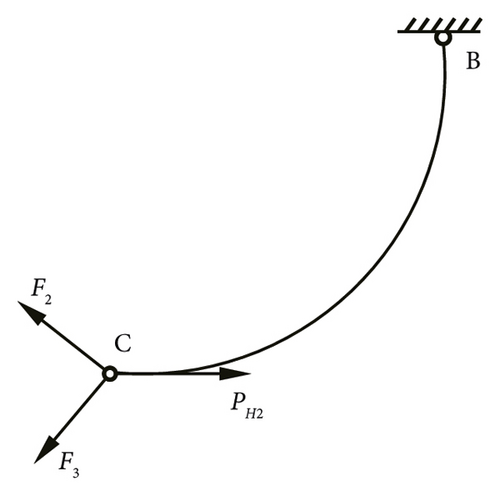
The mechanical analysis of compression limb point C is shown in Figure 3(b).

By geometric similarity

(9)

Then,

(10)

where P_H2 is the horizontal wind load component of the leeward limb and F₃ is the pressure on the leeward limb.

For the I-type section of the lower half of the Y-type insulator string, the displacement is mainly considered to ensure sufficient safety clearance. Its analysis method is similar to that of the I-type insulator string. The rigid straight rod method [31] and the chord polygon method [32] can be used. In order to ensure sufficient accuracy, the chord polygon method is selected to reflect the true deformation state of the insulator string.

As shown in Figure 4, we assume the length of each rigid body part in the insulator string is λ₁, λ₂, ⋯, λ_n, each vertical load is g_V1, g_V2, ⋯, g_Vn, and each transverse wind load is g_h1, g_h2, ⋯, g_hn. These forces act on the center of the component. According to the balance condition after windage yaw, the horizontal displacement λ_h and vertical displacement λ_v of the I-type section are

(11)

(12)

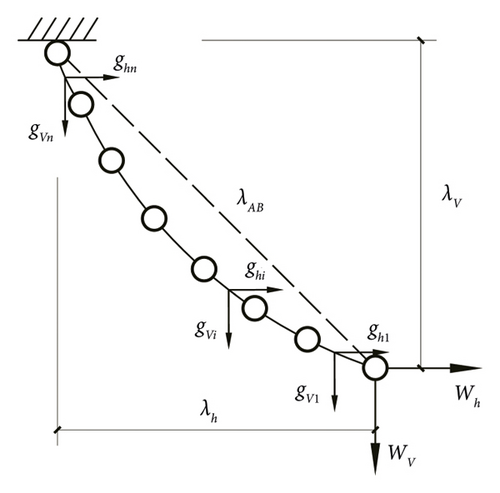
By equations (11) and (12), combined with the mechanical analysis of the leeward limb and the displacement of the lower half, the insulator string type can be optimized to obtain the most appropriate string type. The design length of the cross arm can be shortened under the condition of ensuring safety, which provides the foundation for finite element numerical simulation.

3. The Buckling Analysis of the Insulator String

When the wind speed is large enough, due to structural and other factors, the insulators on the leeward side will be subjected to different degrees of pressure, and the composite insulator string will buckle under the pressure. The insulator string still has a certain bearing capacity after buckling [33–35]. Therefore, it is necessary to conduct buckling analysis on the rod core. Composite mandrels are shown in Figure 5. Table 3 shows the material parameters of mandrels.

3. The parameters of the FXPW-1000/300 composite insulator.

Elastic modulus E(MPa)	Poisson’s ratio μ	Monolithic quality (kg)	Monolithic height (m)	Monolithic windward area (m²)
40000	0.3	13	0.195	0.03

3.1. The Eigenvalue Buckling Analysis of the Insulator String

According to the connection mode of the composite insulator, one end is hinged and the other end is sliding, as shown in Figure 6.

The length L of the insulator string is 10 m, and the section diameter d is 0.04 m. According to the theoretical analysis [36, 37], the critical force P_cr of the composite core rod buckling in compression is

(13)

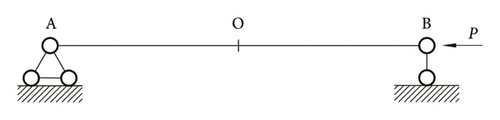
We use ANSYS finite element software to conduct eigenvalue buckling analysis. Before eigenvalue buckling analysis, we conduct a static calculation and turn on the prestress effect switch. The static solution EMAT and ESAV files obtained will be used for eigenvalue buckling analysis. We use the 189 beam element for numerical simulation and assume that both ends are hinged. Through buckling analysis, the first-order buckling load is 496.91 N, which is basically consistent with the theoretical calculation results. The first-order mode is shown in Figure 7.

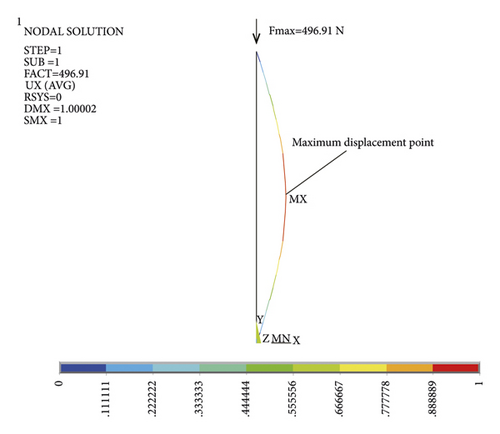
3.2. The Nonlinear Buckling Analysis of the Insulator String

On the basis of eigenvalue buckling analysis, the nonlinear buckling analysis of composite mandrel is carried out to study the stress and deformation after buckling. The nonlinear buckling analysis adopts the arc length method [28, 38–42], which is controlled by the ARCLEN and ARCTRM commands. The large deformation options are turned on, and the analysis substep is set to 20 steps. At the same time, the nonlinear buckling analysis needs to introduce initial defects. We use the UPGEOM command to update the model, and on applying 800 N force at point B for analysis and solution, we obtain the displacement-load curve of the mandrel as shown in Figure 8.

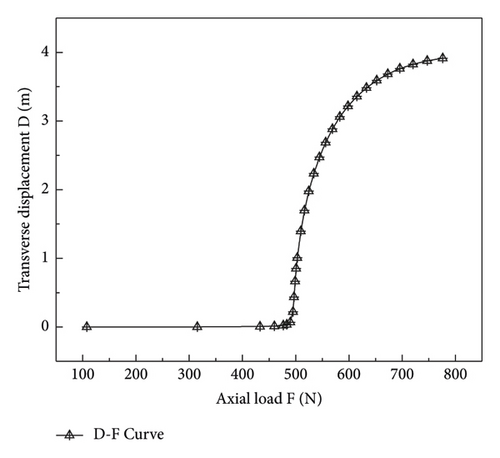
According to the displacement-load curve shown in Figure 8, the maximum critical force of the composite core rod is 496.91 N, and the displacement-load curve maintains a linear relationship before the component is unstable. As the load increases beyond the critical load, the core rod will buckle and become unstable, and there will still be a certain bearing capacity after buckling and instability.

The overall analysis of the insulator string can be controlled and compared according to the displacement of the insulator on the leeward side, providing a basis for the optimal design of the composite insulator string.

4. The Numerical Simulation Analysis of the Composite Insulator String

4.1. The Comparison and Analysis of V-type and Y-type Insulator String Structures

The finite element numerical models of V-type and Y-type insulator strings are established, and the wind-induced deflection characteristics of different structural strings are compared through mechanical analysis. The model of conductor is JL/GIA-630/45, the span of the conductor is 400 m, and the basic parameters of materials are shown in Table 4. The Fxpw-1000/300 composite insulator is selected as the insulator, and the basic parameters are shown in Table 3. The numerical model of the Y-type insulator string is established by using ANSYS. According to the characteristics of the insulator string, the Beam 189 element is used for simulation. Hinged joints are used at the connection between two legs of the insulator string and tower structure. In the numerical model, articulated joints are used at the connection between section I and V, and vertical load and horizontal wind load are applied to the bottom node of the Y-type insulator string.

4. The conductor parameters of JL/GIA-630/45.

Conductor diameter d(mm)	Sectional area A(mm²)	Elastic modulus E(MPa)	Unit mass M(kg/m)	Rated breaking force F(kN)
33.8	674	63000	2.079	150.45

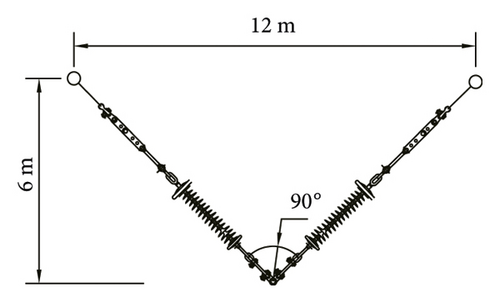
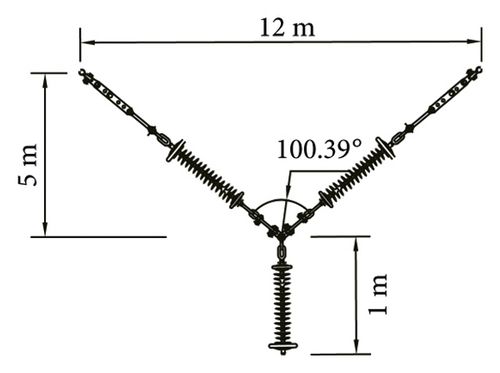
We select V-type and Y-type insulator strings for numerical analysis. The length of I-type section of the Y-type insulator string is 1 m. The vertical height of the two insulator string types is 6 m. The vertical load of the conductor remains unchanged. The included angle of the insulator string and the length of the cross arm are changed. Comparative analysis is carried out through numerical simulation. The structural parameters are shown in Table 5, and the insulator string model is shown in Figure 9.

5. The conductor parameters of JL/GIA-630/45.

Group no	Type of insulator string	Angle between two limbs (°)	Length of cross arm (m)	Total height (m)
1	V-type	90.00	12.00	6.00
1	Y-type	90.00	10.00	6.00

2	V-type	90.00	12.00	6.00
2	Y-type	100.39	12.00	6.00

3	V-type	100.00	14.30	6.00
3	Y-type	100.00	11.92	6.00

4	V-type	100.00	14.30	6.00
4	Y-type	110.07	14.30	6.00

5	V-type	120.00	20.78	6.00
5	Y-type	120.00	17.32	6.00

6	V-type	120.00	20.78	6.00
6	Y-type	128.60	20.78	6.00

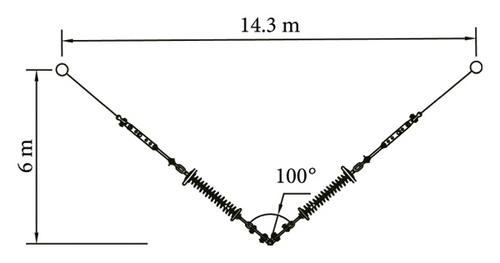
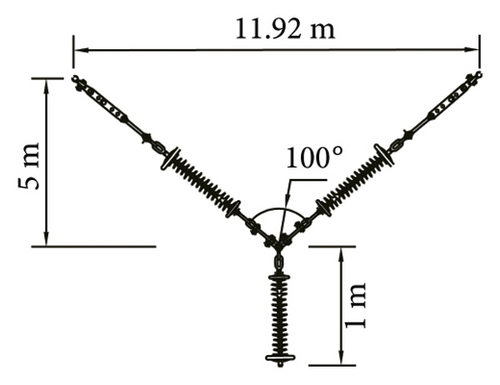
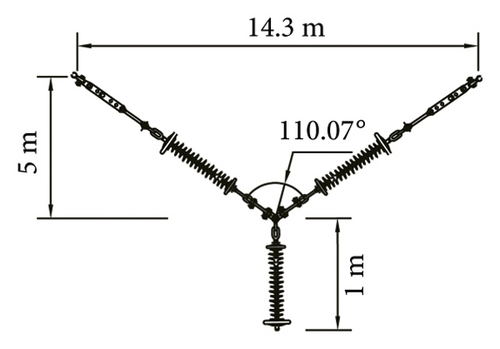
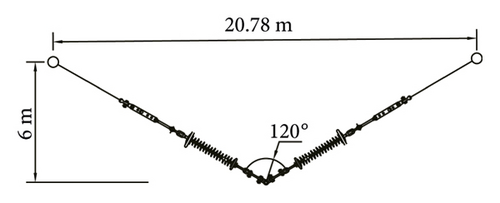
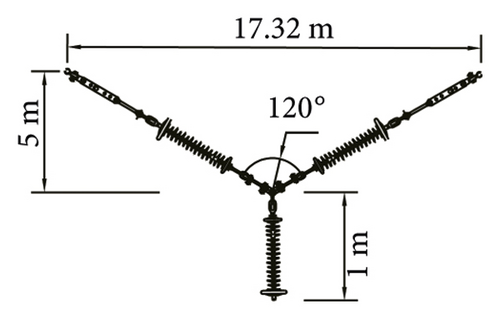
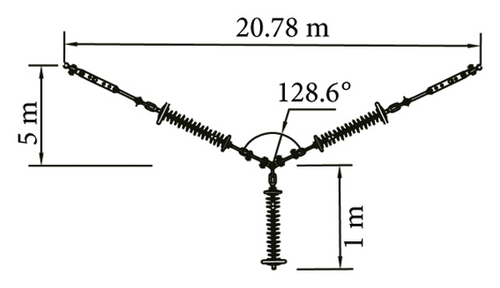
Considering the influence of insulator string gravity, the V-type section of the insulator strings forms catenary shape, as shown in Figure 10.

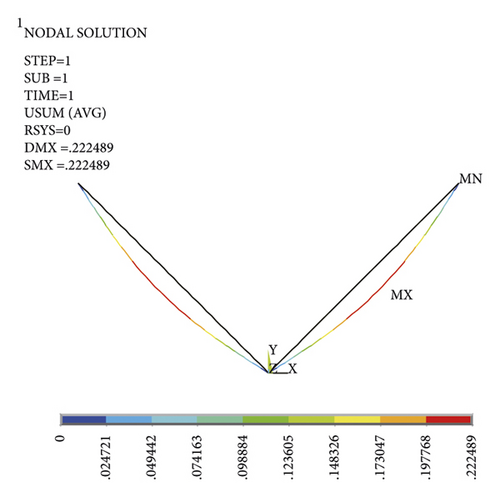
In the state of gravity shape finding, fixed constraints are imposed on the top of the V-type section of the insulator strings. The gravity load of the conductor is 33264 N. The horizontal load mainly considers the role of wind load. In the design, the included angle of the two limbs of the Y-type insulator string structure can be optimized. The larger the included angle of the two limbs, the stronger the wind resistance of the Y-type insulator string. Hence, when the included angle of the two limbs is large, the low wind speed has little impact on it, and the structure is in a stable state, so its calculation is meaningless. When the angle between the two limbs is large, the larger wind speed is selected to make the unloading angle or displacement of the Y-type insulator string occur, so the wind speed ranges from 20 m/s to 45 m/s. They are converted into horizontal wind loads and applied to the string-conductor connection of the insulator string structure. When the wind speed is small, the structure is relatively stable with small deformation, as shown in Figure 11.

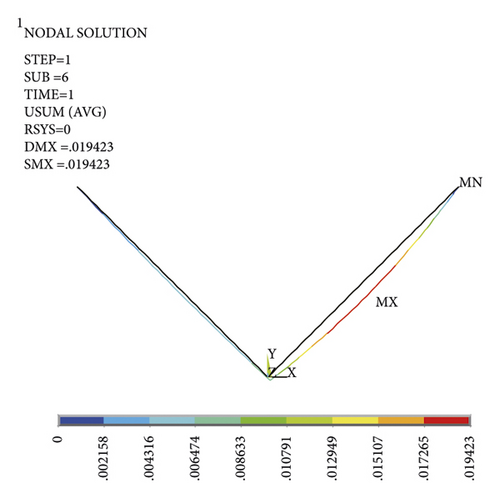
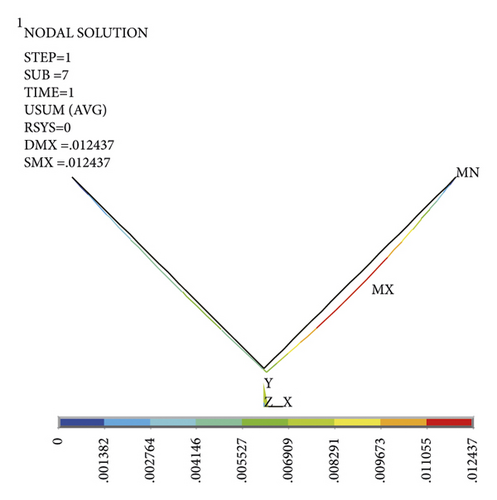
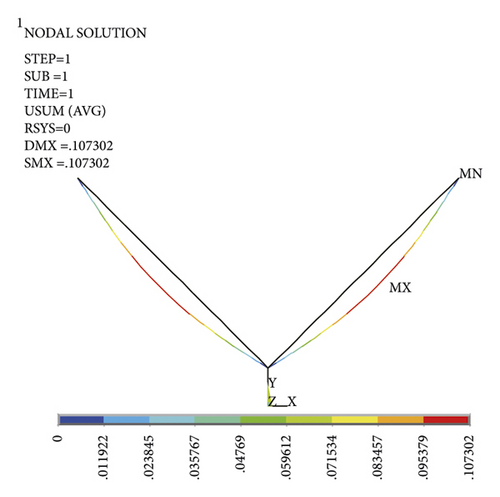
When the wind speed is 45 m/s, the leeward limb is compressed and deformed by buckling, and the overall structure is greatly deformed, as shown in Figure 12.

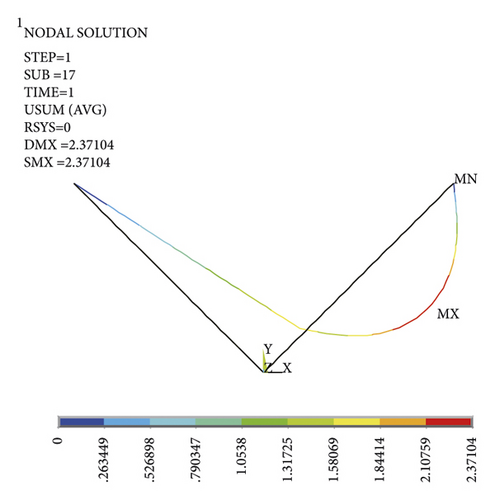
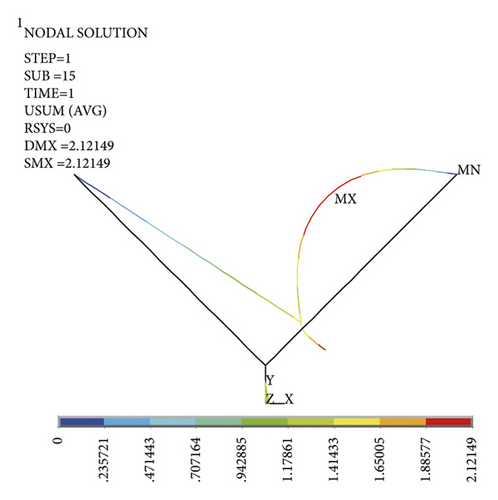
Through finite element numerical analysis, the unloading angle is compared with the maximum displacement of the leeward leg, and the analysis results are shown in Tables 6–8.

6. The comparison of analysis results between the no. 1 and no. 2 insulator strings.

Wind speed (m/s)	Unloading angle (°)			Maximum displacement (m)
Wind speed (m/s)	V-type	Y-type	Y-type	V-type	Y-type	Y-type
20	0	0	0	0	0	0
25	0.17	0.13	0	0.22	0.117	0
30	6.35	6.03	0	1.467	1.172	0.137
35	12.75	12.29	7.47	2.632	1.986	1.63

7. The comparison of analysis results between the no. 3 and no. 4 insulator strings.

Wind speed (m/s)	Unloading angle (°)			Maximum displacement (m)
Wind speed (m/s)	V-type	Y-type	Y-type	V-type	Y-type	Y-type
25	0	0	0	0	0.03	0
30	0.2	0.14	0	0.278	0.157	0
35	7.93	7.71	2.93	1.996	1.643	1.12
40	14.49	14.02	9.66	2.471	2.048	1.824

8. The comparison of analysis results between the no. 5 and no. 6 insulator strings.

Wind speed (m/s)	Unloading angle (°)			Maximum displacement (m)
Wind speed (m/s)	V-type	Y-type	Y-type	V-type	Y-type	Y-type
30	0	0	0	0	0	0
35	0.08	0	0	0.152	0	0
40	4.64	4.40	0.52	1.72	1.42	0.597
45	9.75	9.19	5.03	2.162	1.785	1.542

Through numerical simulation analysis, when the wind speed is small, there is little difference between the stability of V-type and Y-type insulator string structures, and there is no unloading angle and displacement. Under the same wind speed, the unloading angle of V-type and Y-type insulator strings with the same included angle has little difference. The Y-type insulator string is about 5% smaller than the V-type insulator string, but the displacement control of the leeward leg of the Y-type insulator string is 20% smaller than the V-type insulator string. For V-type and Y-type insulator strings with the same cross arm, Y-type insulator strings have greater included angle advantages, the unloading angle can be reduced by 30%–60%, and the maximum displacement of the leeward leg can be reduced by 30%–60%. The analysis results show that Y-type insulator strings are obviously better in structure than V-type insulator strings.

4.2. The Structural Optimization Analysis of the Y-type Insulator String

The optimization plan is mainly to optimize the structural size of the Y-type insulator string, check the structural strength after structural optimization, and shorten the distance of the cross arm hanging point on the premise of ensuring the structural strength and electrical clearance displacement. Under different working conditions, the theoretical optimal point can be obtained by using this optimization scheme, which will be further determined according to the actual situation in the project. The optimization design process of the Y-type insulator string is shown in Figure 13.

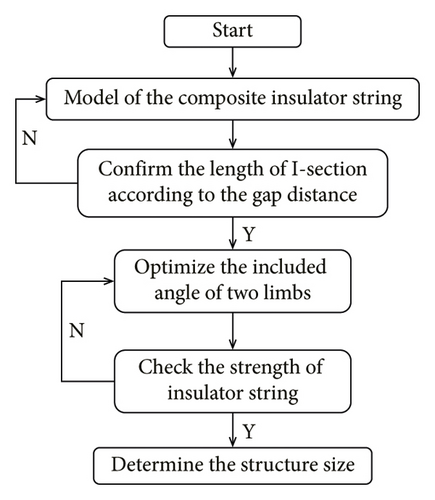
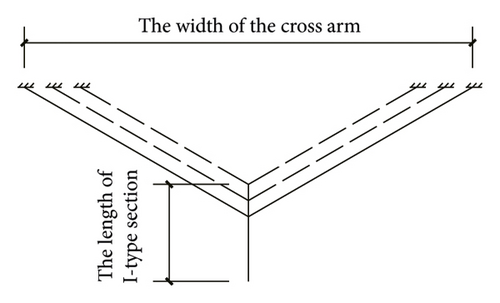
In order to reduce the cross arm length of the insulator string, the current project needs to carry out structural optimization design [43–45]. Combined with the comparative analysis in Section 4.1, structural optimization design is carried out for the Y-type insulator string. Under the condition of ensuring the safety clearance and structural stability, the cross arm length is reduced to achieve the optimal design scheme of the cross arm structure. Under the condition that the total height of the insulator string remains unchanged, the length of the cross arm of the transmission tower can be reduced by changing the length of the I-type section and reducing the angle between the two legs. Under the condition of ensuring the safety clearance distance, we control the length of I-type section, optimize the angle between the two legs under the condition of ensuring the stability of the unloading angle and leeward leg compression, conduct the finite element numerical simulation, and obtain a set of practical structural optimization design scheme, as shown in Figure 14. The dotted line represents the optimization design mode.

4.3. Examples of Optimization Design of the Y-type Insulator String

The size of the calculation example model is shown in Figure 15. The material is composite, and the conductor is the JL/GIA-630/45 quad bundled conductor. The span is 400 m, the height difference is 7 m, the conductor gap is not more than 2 m, and the windage yaw angle generated under the action of wind load is 45^°.

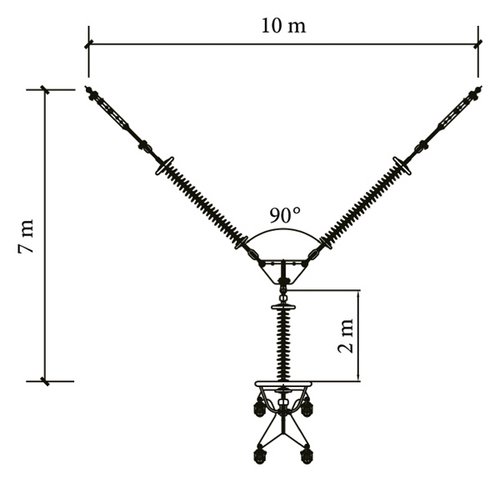
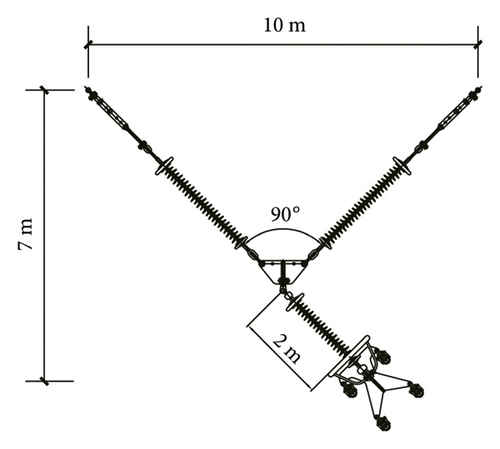
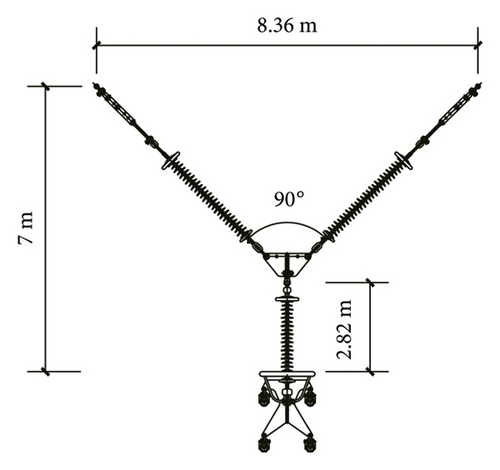
Optimization scheme 1: the horizontal displacement value of I-type section is not more than 2 m. According to Section 2.2, the optimal length of I-type section is 2.82 m, and the hanging point distance of the cross arm is shortened to 8.36 m, with a reduction of 16.4%, as shown in Figure 16. Through mechanical analysis, the leeward leg of the Y-type insulator string is not stressed, and the tension is borne by the windward leg, so the structure is safe.

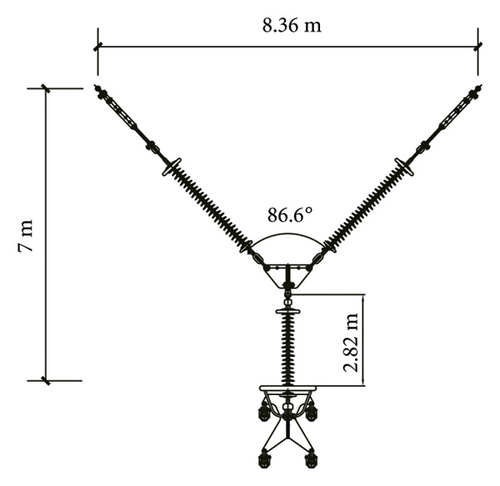
Optimization scheme 2: according to the results of optimization scheme 1, through theoretical calculation, we obtain the critical force P_cr = 1420 N for the buckling and instability of the leeward limb of the insulator string. According to Section 2.2, the included angle between the two legs is reduced to 43.3° through calculation, and the hanging point distance of the cross arm is shortened to 7.878 m by 5.76%, as shown in Figure 17. At this time, the unloading angle is 1.7°, and the pressure borne by the leeward leg is 1400 N, which is less than the calculated buckling critical force, and the structure is safe.

Through two times of optimization design, for example, the total length of the cross arm is shortened from 10 m to 7.878 m by 21.22%, as shown in Table 9, and the safety and stability meet the safety requirements.

9. Optimization results of the insulator string.

Optimization no	Angle between two limbs (°)	Cross arm hanging point distance (m)	Length of I-section(m)	Unloading angle (°)
Before optimization	90.0	10.00	2.00	0.0
Optimization 1	90.0	8.360	2.82	0.0
Optimization 2	86.6	7.878	2.82	1.7

4.4. Discussion

Through theoretical analysis and numerical simulation, we found that the wind deflection characteristics of Y-type insulator strings are obviously better than those of V-type and I-type insulator strings. According to the results of theoretical analysis and numerical simulation, the optimization scheme of Y-type insulator strings was formulated. The feasibility of the optimization scheme of the Y-type insulator string is verified by an optimization example. After optimization design, the length of the cross arm can be greatly shortened, and the economic benefits of project construction can be improved on the premise of meeting the requirements of structure and power safety.

5. Conclusion

In this article, through theoretical analysis and finite element numerical simulation under the action of wind load, the mechanical characteristics of V-type and Y-type insulator strings were studied. Through comparative analysis, the advantages of Y-type insulator strings in the application of transmission tower structures were explained. Combined with the research results, the optimal design scheme of Y-type insulator strings was proposed.

(1)
Through nonlinear buckling analysis, the nonlinear ultimate bearing capacity of the composite insulator string can be obtained. Combined with the maximum deformation of the insulator string, the optimization design limit of the insulator string can be obtained, which provides a theoretical basis for the optimization design of the Y-type insulator string.
(2)
Under the same load, the Y-type insulator string is obviously better than the V-type insulator string in unloading angle and maximum displacement control of the leeward leg, which is mainly determined by the included angle of two legs. The larger the included angle is, the more stable the structure will be, and the length of the cross arms will increase. The included angle of the two legs can be determined through calculation, which can guide the structural optimization design of V-type and Y-type insulator strings.
(3)
Combining the results of theoretical calculation and numerical simulation analysis, the structure of the Y-type insulator string was optimized through two examples, which can greatly reduce the length of short cross arms and ensure the safety and stability of the structure.

In this article, the structural optimization design scheme of the Y-type insulator string is proposed, which provides theoretical and numerical simulation reference for the promotion and application of the Y-type insulator string, and it has certain engineering application value. However, this article only analyzed the individual insulator string, and the string-line coupling model can be established for the overall coupling analysis, which will improve the authenticity of the simulation calculation. In addition, the insulator string model was simplified during theoretical and numerical simulation calculation in this article. Subsequent research can improve the model and add hardware fittings, coupling plates, and other components so as to obtain more real mechanical properties.

6. Scope for Future Work

Under the action of wind load, the windage yaw angle of the transmission conductor insulator string will directly affect the safety of the transmission line system. As a new type of string, there are still many deficiencies in the research of Y-type insulator strings at home and abroad. The in-depth research of Y-type insulator strings will promote its popularization and application in the project.

(1)
This article studied the Y-type insulator string. However, the role of Y-type insulator strings in the whole transmission line system is very important. Therefore, it is very necessary to carry out the coupling analysis of Y-type insulator strings and the transmission line system in the next step.
(2)
In this article, the mechanical properties of Y-type insulator strings are studied from the aspects of theoretical analysis and numerical simulation, and the advantages of Y-type insulator strings are found. Next, through the experimental study of Y-type insulator strings, we will find its shortcomings in practical engineering applications and further correct the theoretical and numerical simulation results.

Consent

Not applicable.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Authors’ Contributions

Z. L. was responsible for conceptualization, project administration, and resources; H. S. and Z. J. were responsible for software; L. Z. and H. Y. were responsible for formal analysis; H. S. was involved in investigation; T. Z. and Z. J. were involved in data curation; Z. L. and T. Z. were involved in writing—original draft preparation; T. Z. and Z. L. were involved in writing—review and editing. All authors read and agreed to the published version of the manuscript.

Acknowledgments

This research was funded by the Jiangxi Province Education Science “14th Five-Year Plan” Project (Award no. 22QN007) and the National Natural Science Foundation of China (Award no. 51568046).

Open Research

Data Availability

The data of this study are available from the corresponding author upon request.

References

1 Ugleva E. M., Zmieva K. A., and Kuznetsova E. V., Intelligent power consumption management systems, IERI Procedia. (2014) 9, 117–122.
10.1016/j.ieri.2014.09.050
Google Scholar
2 He Y., Chen Y., Yang Z., He H., and Liu L., A review on the influence of intelligent power consumption technologies on the utilization rate of distribution network equipment, Protection and Control of Modern Power Systems. (2018) 3, no. 1, 1–11.
10.1186/s41601-018-0092-2
Google Scholar
3 Wang D., Zhang S., Wang Y., and Mao J., Impact of spatial misallocation of electric power resources on economic efficiency and carbon emissions in China, Environmental Science and Pollution Research. (2022) 29, no. 36, 55250–55277, https://doi.org/10.1007/s11356-022-19100-6.
10.1007/s11356-022-19100-6
PubMed Web of Science® Google Scholar
4 Wang J., Study on Meteorological Disaster Risk Analysis and Early Warning Method of Transmission Lines, 2016, Chongqing University, Chongqing, China.
Google Scholar
5 Battista R. C., Rodrigues R. S., and Pfeil M. S., Dynamic behavior and stability of transmission line towers under wind forces, Journal of Wind Engineering and Industrial Aerodynamics. (2003) 91, no. 8, 1051–1067, https://doi.org/10.1016/s0167-6105(03)00052-7, 2-s2.0-0042031202.
10.1016/S0167-6105(03)00052-7
Web of Science® Google Scholar
6 Fei Q., Zhou H., Han X., and Wang J., Structural health monitoring oriented stability and dynamic analysis of a long-span transmission tower-line system, Engineering Failure Analysis. (2012) 20, 80–87, https://doi.org/10.1016/j.engfailanal.2011.11.001, 2-s2.0-83555176266.
10.1016/j.engfailanal.2011.11.001
Web of Science® Google Scholar
7 He B., Zhao M., Feng W., Xiu Y., Wang Y., Feng L., Qin Y., and Wang C., A method for analyzing stability of tower-line system under strong winds, Advances in Engineering Software. (2019) 127, 1–7, https://doi.org/10.1016/j.advengsoft.2018.10.004, 2-s2.0-85055739623.
10.1016/j.advengsoft.2018.10.004
Web of Science® Google Scholar
8 Qin X., Jia B., Lei J., Zhang J., Li H., Li B., and Li Z., A novel flying–walking power line inspection robot and stability analysis hanging on the line under wind loads, Mechanical Sciences. (2022) 13, no. 1, 257–273, https://doi.org/10.5194/ms-13-257-2022.
10.5194/ms-13-257-2022
Web of Science® Google Scholar
9 Shi T., Lin X., Yang J., and Hu D., Modeling of dynamic behavior for suspension insulator string under wind and rain loadings, 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), IEEE. (2020) 1111–1116.
Google Scholar
10 Liu X., Huang R., Jiang C., Xu Y., Li C., and Wu C., Numerical investigation on the dynamic response and fatigue analysis of the tension insulator string under stochastic wind, IEEE Transactions on Power Delivery. (2022) 37, no. 6, 4657–4667, https://doi.org/10.1109/tpwrd.2022.3153315.
10.1109/TPWRD.2022.3153315
Web of Science® Google Scholar
11 Zhao S., Yue J., Savory E., Yan Z., Chen J., Zhang B., and Peng L., Dynamic windage yaw angle and dynamic wind load factor of a suspension insulator string, Shock and Vibration. (2022) 2022, 12, 6822689, https://doi.org/10.1155/2022/6822689.
10.1155/2022/6822689
Web of Science® Google Scholar
12 Guo K., Jiang B., Liu B., Kong K., Wu Y., Tian S., Gao Z., Zong L., Yao S., Zhao M., and Mi C., Research status of the external insulation pollution flashover of high voltage transmission line, IOP Conference Series: earth and Environmental Science, IOP Conference Series: Earth and Environmental Science. (2021) 651, no. 2, 022082, https://doi.org/10.1088/1755-1315/651/2/022082.
10.1088/1755-1315/651/2/022082
Google Scholar
13 An L., Guan Y., Zhu Z., and Zhang R., Research on windage yaw flashovers of transmission lines under wind and rain conditions, Energies. (2019) 12, no. 19, https://doi.org/10.3390/en12193728, 2-s2.0-85072776799.
10.3390/en12193728
Web of Science® Google Scholar
14 El-Refaie E. S. M., Abd Elrahman M. K., and Mohamed M. K., Electric field distribution of optimized composite insulator profiles under different pollution conditions, Ain Shams Engineering Journal. (2018) 9, no. 4, 1349–1356, https://doi.org/10.1016/j.asej.2016.08.012, 2-s2.0-85000399496.
10.1016/j.asej.2016.08.012
Web of Science® Google Scholar
15 Feng Z., Li T., Zheng L., and Li J., Numerical simulation of wind-induced swing angle of 1000kV transmission line suspension insulator strings considering dynamic response, Journal of Physics: Conference Series. IOP Publishing.(2022) 2237, no. 1, 012001, https://doi.org/10.1088/1742-6596/2237/1/012001.
10.1088/1742-6596/2237/1/012001
Google Scholar
16 Yan B., Lin X., Luo W., Liu Z., and Chen Z., Research on dynamic wind load factors for windage yaw angle of suspension insulator strings, Engineering Mechanics. (2010) 27, no. 1, 221–227.
Google Scholar
17 Li J., Mao D., Zhu Q., and Gao Q., Research on windage yaw characteristics of high-voltage insulators in complex wind field, IOP Conference Series: materials Science and Engineering, IOP Conference Series: Materials Science and Engineering. (2020) 892, no. 1, 012113, https://doi.org/10.1088/1757-899x/892/1/012113.
10.1088/1757-899X/892/1/012113
Google Scholar
18 Yan B., Lin X., Luo W., Chen Z., and Liu Z., Numerical study on dynamic swing of suspension insulator string in overhead transmission line under wind load, IEEE Transactions on Power Delivery. (2009) 25, no. 1, 248–259.
10.1109/TPWRD.2009.2035391
Web of Science® Google Scholar
19 Jia Y., Xiao M., and You B., The windage yaw numerical simulation of 500KV overhead transmission lines, Proceedings of the 2010 International Conference on Power System Technology, October 2010, Zhejiang, China, IEEE, 1–5.
Google Scholar
20 Wang J. C., Zhu S. W., Peng B., Duan S. B., and Li P., Static and dynamic mechanical characteristic comparison research of v-type insulator string under gale condition, IOP Conference Series: earth and Environmental Science, IOP Conference Series: Earth and Environmental Science. (2017) 61, no. 1, 012094, https://doi.org/10.1088/1755-1315/61/1/012094, 2-s2.0-85019672678.
10.1088/1755-1315/61/1/012094
Google Scholar
21 Li L., Lin C., and Wu X., Research on windage yaw of V-type composite insulators in ultra-high voltage, Proceedings of the Second International Conference on Mechanics, Materials and Structural Engineering (ICMMSE 2017), April 2017, Beijing, China, Atlantis Press, 1–7.
Google Scholar
22 Xie Z. S., Zheng Y., Shi W. D., Ni H. J., Zhang Y. Q., Cao Y. P., Chen Y., Tian Q., and Wang A. N., Investigation on the failure analysis of crimped composite insulators used in “V” type string, Engineering Failure Analysis. (2018) 94, 274–284, https://doi.org/10.1016/j.engfailanal.2018.08.010, 2-s2.0-85051775448.
10.1016/j.engfailanal.2018.08.010
Web of Science® Google Scholar
23 Fu G. and Gong Y., Application of long tonnage composite insulators on UHVDC V-type strings, 2015 5th international conference on electric utility deregulation and restructuring and power technologies (DRPT), Proceedings of the 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), November 2015, Changsha, China, IEEE, 1822–1826.
Google Scholar
24 Chen J., Qiu W., Tao J., Guo Y., and Chen J., Design of UHVDC Transmission Lines, Ultra-high Voltage AC/DC Power Transmission, 2017, Springer, Heidelberg, Germany, 1429–1475.
10.1007/978-3-662-54575-1_28
Google Scholar
25 Diansheng Z., Design Manual of High Voltage Transmission Lines in Power Engineering, 2003, China Electric Power Press, Beijing China, 24–29.
Google Scholar
26 Farr H. H., Transmission Line Design Manual, 1980, US Department of the Interior, Water and Power Resources Service, Denver CO, USA.
Google Scholar
27 Fu X. and Li H. N., Uncertainty analysis of the strength capacity and failure path for a transmission tower under a wind load, Journal of Wind Engineering and Industrial Aerodynamics. (2018) 173, 147–155, https://doi.org/10.1016/j.jweia.2017.12.009, 2-s2.0-85037972441.
10.1016/j.jweia.2017.12.009
Web of Science® Google Scholar
28 Ananthi G. B. G., Deepak M. S., Roy K., and Lim J. B., Influence of intermediate stiffeners on the axial capacity of cold-formed steel back-to-back built-up unequal angle sections, Structures. (2021) 32, no. 5, Elsevier, 827–848.
10.1016/j.istruc.2021.03.059
Web of Science® Google Scholar
29 Zhang J. and Xie Q., Failure analysis of transmission tower subjected to strong wind load, Journal of Constructional Steel Research. (2019) 160, 271–279, https://doi.org/10.1016/j.jcsr.2019.05.041, 2-s2.0-85067030417.
10.1016/j.jcsr.2019.05.041
Web of Science® Google Scholar
30 Tian L., Zhang X., and Fu X., Fragility analysis of a long-span transmission tower–line system under wind loads, Advances in Structural Engineering. (2020) 23, no. 10, 2110–2120, https://doi.org/10.1177/1369433220903983.
10.1177/1369433220903983
Web of Science® Google Scholar
31 Wang J., Tang Y., Shao J., and Long M., A real-time alarm and early warning model for windage yaw of cat-head type tower, IEEJ Transactions on Electrical and Electronic Engineering. (2018) 13, no. 3, 448–454, https://doi.org/10.1002/tee.22587, 2-s2.0-85041407770.
10.1002/tee.22587
Web of Science® Google Scholar
32 Huxley M. N. and Plunkett S. M., Integer chords and configurations of lattice points, Indagationes Mathematicae. (2016) 27, no. 2, 534–545, https://doi.org/10.1016/j.indag.2015.12.004, 2-s2.0-84961233959.
10.1016/j.indag.2015.12.004
Web of Science® Google Scholar
33 Kalaga S. and Yenumula P., Design of Electrical Transmission Lines: Structures and Foundations, 2016, CRC Press, Boca Raton, FL, USA.
10.1201/9781315755687
Google Scholar
34 Chen J., Xian Q., and Zhang P., Buckling analysis of transmission tower considering ice load, IOP Conference Series: materials Science and Engineering, IOP Conference Series: Materials Science and Engineering. (2019) 473, no. 1, 012036, https://doi.org/10.1088/1757-899x/473/1/012036, 2-s2.0-85062861984.
10.1088/1757-899X/473/1/012036
Google Scholar
35 Liu B., Liu C., Zhu K., and Liu S., A study on swing and buckling of Y-type insulator strings under strong wind action for± 800kV UHDV transmission lines, Proceedings of the 2013 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), December 2013, Hong Kong, China, IEEE, 1–4.
Google Scholar
36 Zhao T., Li A., Yan H., Zhang L., Lan Z., Huang M., and Wu H., Comparison of the influence of double-limbdouble-plate joint on the stability bearing capacity of triangular and quadrilateral transmission tower structures, Buildings. (2022) 12, no. 6, https://doi.org/10.3390/buildings12060784.
10.3390/buildings12060784
Web of Science® Google Scholar
37 Zhao T., Yan H., He P., Zhang L., Lan Z., and Huang M., Influence of double-limbdouble-plate connection on stable bearing capacity of quadrilateral transmission tower, Applied Sciences. (2021) 11, no. 24, 12024, https://doi.org/10.3390/app112412024.
10.3390/app112412024
CAS Google Scholar
38 Fang Z., Roy K., Chi Y., Chen B., and Lim J. B., Finite element analysis and proposed design rules for cold-formed stainless steel channels with web holes under end-one-flange loading, Structures. (2021) 34, 2876–2899, https://doi.org/10.1016/j.istruc.2021.09.017.
10.1016/j.istruc.2021.09.017
Web of Science® Google Scholar
39 Fang Z., Roy K., Uzzaman A., and Lim J. B., Numerical simulation and proposed design rules of cold-formed stainless steel channels with web holes under interior-one-flange loading, Engineering Structures. (2022) 252, 113566, https://doi.org/10.1016/j.engstruct.2021.113566.
10.1016/j.engstruct.2021.113566
Web of Science® Google Scholar
40 Mathieson C., Roy K., Clifton G. C., Ahmadi A., and Lim J. B., Failure mechanism and bearing capacity of cold-formed steel trusses with HRC connectors, Engineering Structures. (2019) 201, 109741.
10.1016/j.engstruct.2019.109741
Web of Science® Google Scholar
41 Ananthi G. B. G., Roy K., and Lim J. B. P., Experimental and numerical study of an innovative 4-channelscold-formed steel built-up column under axial compression, Steel and Composite Structures. (2022) 42, no. 4, 513–538.
Web of Science® Google Scholar
42 Ananthi G. B. G., Roy K., and Lim J. B. P., Behaviour and strength of back-to-back built-upcold-formed steel unequal angle sections with intermediate stiffeners under axial compression, Steel and Composite Structures. (2022) 42, no. 1, 1–22.
Web of Science® Google Scholar
43 Raghavendra T., Computer aided analysis and structural optimization of transmission line tower, International Journal of Advances in Engineering & Technology. (2012) 3, no. 3, 44–50.
Google Scholar
44 Couceiro I., París J., Martínez S., Colominas I., Navarrina F., and Casteleiro M., Structural optimization of lattice steel transmission towers, Engineering Structures. (2016) 117, 274–286, https://doi.org/10.1016/j.engstruct.2016.03.005, 2-s2.0-84962582279.
10.1016/j.engstruct.2016.03.005
Web of Science® Google Scholar
45 Khodzhaiev M. and Reuter U., Structural optimization of transmission towers using a novel Genetic Algorithm approach with a variable length genome, Engineering Structures. (2021) 240, 112306, https://doi.org/10.1016/j.engstruct.2021.112306.
10.1016/j.engstruct.2021.112306
Web of Science® Google Scholar

Citing Literature

All articles

Nonlinear Buckling Analysis and Optimization Design of the Y-Type Composite Insulator String

Abstract

1. Introduction

2. The Windage Yaw Theory of the Composite Insulator String

2.1. The Calculation of Wind Load

2.1.1. The Wind Load Calculation of the Composite Insulator String

2.1.2. The Calculation of Wind Load on the Conductor

2.1.3. The Calculation of the Conductor Vertical Load

2.2. The Theoretical Derivation of the Composite Insulator String

3. The Buckling Analysis of the Insulator String

3.1. The Eigenvalue Buckling Analysis of the Insulator String

3.2. The Nonlinear Buckling Analysis of the Insulator String

4. The Numerical Simulation Analysis of the Composite Insulator String

4.1. The Comparison and Analysis of V-type and Y-type Insulator String Structures

4.2. The Structural Optimization Analysis of the Y-type Insulator String

4.3. Examples of Optimization Design of the Y-type Insulator String

4.4. Discussion

5. Conclusion

6. Scope for Future Work

Consent

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Nonlinear Buckling Analysis and Optimization Design of the Y-Type Composite Insulator String

Abstract

1. Introduction

2. The Windage Yaw Theory of the Composite Insulator String

2.1. The Calculation of Wind Load

2.1.1. The Wind Load Calculation of the Composite Insulator String

2.1.2. The Calculation of Wind Load on the Conductor

2.1.3. The Calculation of the Conductor Vertical Load

2.2. The Theoretical Derivation of the Composite Insulator String

3. The Buckling Analysis of the Insulator String

3.1. The Eigenvalue Buckling Analysis of the Insulator String

3.2. The Nonlinear Buckling Analysis of the Insulator String

4. The Numerical Simulation Analysis of the Composite Insulator String

4.1. The Comparison and Analysis of V-type and Y-type Insulator String Structures

4.2. The Structural Optimization Analysis of the Y-type Insulator String

4.3. Examples of Optimization Design of the Y-type Insulator String

4.4. Discussion

5. Conclusion

6. Scope for Future Work

Consent

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information