This paper studies the dynamics of an opinion formation model with a leader associated with a system of fractional differential equations. We applied the concept of α-exponential stability and the uniqueness of equilibrium to show the consensus of the followers with the leader. A sufficient condition for the consensus is obtained for both fractional formation models with and without time-dependent external inputs. Moreover, numerical results are provided to illustrate the dynamical behavior.

1. Introduction

Humans and some animals are social animals. Living together as a society requires mutual assistance and generosity, which will lead to happiness. Whether it is a small or a large society, social animals, for instance, a flock of birds, bees, insects, and fish, have a complex thought structure and they tend to have a leader to lead their lives to peacefulness. Some research focuses on the behavior of these social animals, including an all-leader agent-based model for turning and flocking birds [1], the migration of honeybees to a new nest site [2], leadership in fish shoals [3], and the effective leadership and decision-making in animal groups on the move [4]. In these systems, individuals are mutually dependent and communicate some information to their peers in a certain region around them. Many researchers have studied and developed a group of opinion formation models, which have been developed into many approaches. Examples of these approaches are opinion formation models on a gradient [5], opinion formation models based on game theory [6], Boltzmann and Fokker–Planck equations for opinion formation models associated with strong leaders [7], opinion formation models based on kinetic equations [8], agent-based models for opinion formation [9], consensus and clustering in opinion formation on networks [10], and Boltzmann-type control of consensus of the opinion with leaders [11].

In recent years, fractional differential and integral operators have been utilized in various real-world problems and areas of study, such as physical and biological sciences [12], environmental science, signal and image processing, and engineering [13–19]. New generalizations and definitions of the fractional derivative are also of interest by choosing different kernels [20]. In particular, it motivates a generalization of the opinion formation model to involve fractional calculus.

Consider the fractional opinion formation model

()

with the initial condition x_i(0) = ξ_i ∈ ℝ for i = 0,1, …, N. The coefficient a_ij reflects the weight for which agents influence each other. The fractional derivative of order α is used to describe the memory effects of the interaction.

It is natural to introduce a leader to the above system in order to drive a consensus among all agents x_i. The leader is regarded as a virtual agent whose opinion x₀ is independent of all the remaining agents’ opinions. The fractional opinion formation model associated with a leader is described by

()

subject to the initial condition x_i(0) = ξ_i ∈ ℝ for i = 0,1, …, N. The coefficient c_i describes the influence of the leader on another agent. In particular, c_i > 0, when the leader has an impact on the i^th agent’s opinion.

During the last few years, the opinion formation model with leadership based on the fractional differential system has attracted tremendous attention and has been extensively studied by many researchers. For example, Almeida et al. [21] discussed an optimal control strategy for two types of fractional opinion formation models with leadership to reach a consensus. The result was given by a numerical scheme to approximate the Caputo fractional derivative based on the Grunwald–Letnikov approximation. Next, in 2019, Almeida et al. [22] used Mittag-Leffler stability to discuss sufficient conditions of (2) to guarantee that all agents have a consensus opinion approaching the leader’s opinion. They also studied the opinion formation model with external inputs h_i(t) described by

()

with the initial data x_i(0) = ξ_i ∈ ℝ for i = 0,1, …, N. In the above system, optimal control strategies were designed for the leader to obtain a consensus opinion.

Motivated by [21, 22], this paper aims to study the dynamics of a nonautonomous nonlinear fractional leader-follow opinion formation model

()

with x_i(0) = ξ_i ∈ ℝ for i = 0,1, …, N as well as the model with time-dependent external inputs

()

subject to x_i(0) = ξ_i ∈ ℝ for i = 0,1, …, N. Here, we include the time-dependence in the source term f_i(t, x_j(t)).

Rather than focusing on the design of an optimal control, we mainly focus on the exponential stability of the solutions and establish some sufficient conditions for the consensus opinion of all agents with the leader x₀.

The rest of this paper is organized as follows. In Section 2, we provide some definitions and preliminary results in integral and differential fractional calculus and exponential stability of systems of fractional differential equations. The existence of a unique consensus equilibrium point of fractional opinion formation models associated with a leader will be investigated in Section 3 and Section 4 for the systems described by (4) and (5), respectively. In Section 5, we provide examples and numerical simulations to demonstrate our analytical results.

2. Fractional Calculus Framework

In this section, we briefly outline some notions from fractional calculus that will be used throughout the paper.

Definition 1 (see [23].)For α > 0, the left Caputo fractional derivative of order α is given by

()

where n is a natural number such that α ∈ (n − 1, n) and D = d/dτ.

Definition 2 (see [23].)The Riemann–Liouville fractional integral of order α > 0 is given by

()

provided the right-side integral exists point wisely, on (0, ∞).

Lemma 1 (see [23].)Let α > 0 be a real number. The general solution of the fractional Caputo type differential equation

()

is a function satisfying

()

for some constants k_i, i = 0,1, …, n − 1 where n = [α] + 1 if α ∉ ℕ,and

()

for some constant k, if α ∈ ℕ.

Lemma 2 (see [23].)For a positive constant α > 0 and y ∈ Cⁿ[0, T], we have

()

for some constants k_i, i = 0,1, …, n − 1 where n = [α] + 1 Here, D^α = d^α/dt^α(⋅) is the Caputo fractional derivative.

Consider the differential equation with the Caputo fractional derivative defined by

()

for some initial data y₀ ∈ ℝ^m, where

, 0 < α < 1, and the nonhomogeneous term f : [0, ∞) × ℝ^m⟶ℝ^m satisfies the continuity in t and locally Lipschitz continuity in y.

Definition 3 (see [24].)We say the y^∗ ∈ ℝ^m is an equilibrium of system (12) whenever f(t, y^∗) = 0 for all t ∈ [0, ∞).

Definition 4 (see [24].)System (12) is α-exponentially stable if there exist two positive constants M > 0 and λ > 0 such that for any solutions x(t) and y(t) of system (6) subject to the initial conditions x₀ and y₀, respectively, we have

()

for t ≥ 0 where ‖.‖ denotes the Euclidean norm.

It should be noted that the notion of α-exponential stability concerns the closeness of solutions x(t) and y(t) subject to different initial conditions x₀ and y₀, respectively, while the definition of the Mittag-Leffler stability in [12] concerns the convergence of a solution x(t) to an equilibrium point.

Lemma 3 (see [17].)If d^αx/dt^α ≤ d^αy/dt^α with α ∈ (0,1) and x(0) = y(0), then x(t) ≤ y(t).

Lemma 4 (see [17].)Let W ∈ C[0, ∞) be a function such that d^αy/dt^α ≤ δW(t), where α ∈ (0,1) and δ is an arbitrary constant. Then, we have

()

We define the signum function as

()

3. Stability and Consensus of Fractional Leader-Follower Opinion Formation Model

In this section, we present a sufficient condition for the consensus opinion in a leader-follower opinion formation model (4) based on the exponential stability concept and the uniqueness of the equilibrium. We first outline the following assumptions for the problem (4)

(H1) The functions f_i, i = 1,2, …, N are Lipschitz continuous with respect to the second variable on ℝ with Lipschitz constants L_i > 0, that is,
()
for all x, y ∈ ℝ uniformly with respect to t,
And another prerequisite for proving results.
(H2) The constants c_i is positive for i = 1,2, …, N and satisfies
()

Under the Lipschitz condition of the source term (H1), we obtain the existence and uniqueness of the solution to the Cauchy problem (4) from the standard result [25].

Motivated by [24], we prove the following result.

Theorem 1. Under the assumptions (H1) and (H2), system (4) is exponentially stable.

Proof. Let and be the solutions of system (4) subject to the different initial conditions x_i(0) = ξ_i and y_i(0) = ζ_i, i = 1,2, …, N.

Let for i = 1,2, …, N, then . By (4) we get

()

If is positive, then

()

if is negative, then

()

hence,

()

next, we construct a function W by

()

we compute the Caputo fractional derivative of W(t) using the assumptions (H1) and (H2) to obtain

()

where k = min_1≤i≤Nk_i. Lemma 4 implies that

()

it follows that system (4) is exponentially stable.

Next, we assume that the leader’s opinion is kept constant as ξ₀ for all time, that is, u(t) = 0 in (4). Let be an equilibrium of (4). Hence, it satisfies the following system

()

Theorem 2. Assume that (H1) and (H2) hold. Then, system (4) has a unique equilibrium.

Proof. Let c_iy_i = p_i for i = 1,2, …, N. We get from (25) that

()

consider the map defined by , where and

()

by the Lipschitz condition (H1), for any p, q ∈ ℝ^N, we have

()

We have from (H1) that for i = 1,2, …, N. Hence,

()

Thus, the map is a contraction. Therefore, has a unique fixed point, showing that system (4) has a unique equilibrium.

The next result shows that all the agents’ opinions are in consensus with the leader.

Theorem 3. Assume that (H1) and (H2) hold. Suppose that f_i(t, ξ₀) = 0 for t ∈ [0, ∞) and for all i = 1,2, …, N. Then, all agents’ opinions x_i(t) of (4) converge to the consensus opinion ξ₀.

Proof. The proof follows the same argument as in [22, Theorem 2] where the system is autonomous. We outline the proof when the nonautonomous source term is considered here. Let (x₀(t), x₁(t), …, x_N(t)) be a solution of (4). Since we assume that u(t) = 0, we have that x₀(t) = ξ₀ is a constant function. Let y_i = x_i − ξ₀ and define g_i(t, y_i) : = f_i(t, y_i + ξ₀), for i = 1, …, N. Then, system (4) can be written as

()

we see that for any ,

()

for i = 1,2, …, N. It follows from Theorem 2 that system (30) has a unique equilibrium y^∗ = (y₁, y₂, …y_N). Furthermore, the exponential stability in Theorem 1 implies that every solution y of (30) converges to the equilibrium, that is, lim _t⟶∞‖y(t) − y^∗‖ = 0. Since g_i(t, 0) = f_i(t, ξ₀) = 0 for i = 1,2, …, N, we see that y^∗ = (0, …,0)^T. Consequently, we have lim _t⟶∞x_i(t) = ξ₀ for every i = 1, …, N showing the consensus of opinion.

4. Stability and Consensus of Leader-Follower Opinion Formation Model with Time-dependent External Inputs

In this section, we extend the study to consider a leader-follower opinion formation model with time-dependent external inputs.

Consider the leader-follower opinion formation model with time-dependent external inputs h_i(t), i = 1,2, …, N in (5).

We assume the following conditions for the external inputs.

(H3) The functions h_i, i = 1,2, …, N are bounded that is, there exists O_i > 0 such that

()

for each i = 1,2, …, N.

Theorem 4. Assume that (H1), (H2), and (H3) hold. Then, system (5) is exponentially stable. Moreover, for any solution x(t), there exists T ≥ 0 such that

()

where

()

and ε > 0 is arbitrary small.

Proof. Let and be the solutions of system (5) subject to the different initial conditions x_i(0) = ξ_i and y_i(0) = ζ_i, i = 1,2, …, N. By setting w^∗(t) = y(t) − x(t) and using a similar argument as in the proof of Theorem 1, there exists M > 0 such that

()

showing the exponential stability of (5). Next, we construct a function W by

()

Using assumptions (H1) and (H2), we compute the Caputo fractional derivative of W(t) as

()

where k = min_1≤i≤nk_i.

Consider the fractional-order system

()

It is easily seen that (38) is exponentially stable, so that any solution converges to the unique equilibrium V^∗ = w/k, that is

()

Hence, for any arbitrary ε > 0, there exists T > 0 such that

()

By Lemma 3, we have W(t) ≤ V(t) with W(0) = V(0). Thus, there exists T ≥ 0 such that for any solution x(t),

()

We next state the consensus result for an opinion model with time-dependent external inputs.

Theorem 5. Assume that (H1), (H2), and (H3) hold. Suppose that f_i(t, ξ₀) = 0 for t ∈ [0, ∞) and lim_t⟶∞h_i(t) = 0 for all i = 1,2, …, N. Then, all agents’ opinions x_i(t) of (5) converge to the consensus opinion ξ₀.

Proof. Let (x₀(t), x₁(t), …, x_N(t)) be a solution of (5). Since we assume that u(t) = 0, the leader’s opinion is a constant function x₀(t) = ξ₀. Let y_i = x_i − ξ₀ and define g_i(t, y_i) : = f_i(t, y_i + ξ₀), for i = 1, …, N. Then, system (5) can be written as

()

it can be seen that g_i satisfies Lipschitz continuity condition as

()

for any

and i = 1,2, …, N. Hence, by applying Theorem 4 for (42), that is, considering g_i instead of f_i and taking ξ₀ = 0 in (5), and using the assumption g_i(t, 0) = f_i(t, ξ₀) = 0 for t ∈ [0, ∞), we see that the solution y(t) = (y₁(t), y₂(t), …, y_N(t)) of (42) satisfies

()

for some T > 0 where

()

since lim_t⟶∞h_i(t) = 0 for i = 1,2, …, N, we have |h_i(t)| ≤ ε whenever t is sufficiently large for all i = 1,2, …, N. Hence, if we consider (37) for some sufficiently large time , then the bound of h_i in (H3) can be chosen as an arbitrary small ε. Consequently, we obtain

()

As ε > 0 was arbitrary, we have y_i(t)⟶0 as t⟶∞. Consequently, we obtain the consensus opinion lim_t⟶∞x_i(t) = ξ₀ for every i = 1, …, N.

5. Numerical Examples

In this section, we give examples of the fractional opinion formation model of order 0 < α < 1 to illustrate the dynamics of the system. In particular, we demonstrate through numerical examples that consensus opinion can be achieved when the assumptions of our results are satisfied.

Example 1. Consider the following system of opinion formation model with leader

()

subject to the initial condition x₀(0) = 0, x₁(0) = 25, x₂(0) = 10, x₃(0) = 30, x₄(0) = 1.5, x₅(0) = −10, x₆(0) = −4.5.

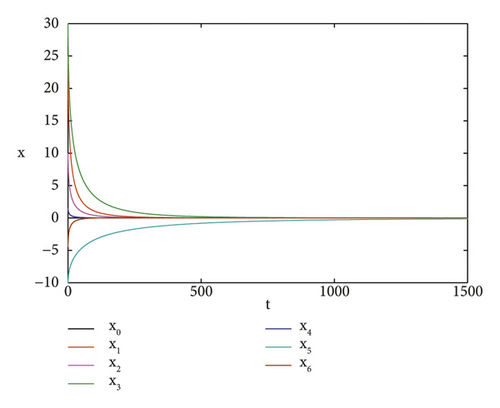
In this system of opinion formation model (47) with leader x₀(t) = ξ₀ = 0, we set a₁₁ = 0.06, a₁₂ = −0.01, a₁₆ = −0.02, a₂₁ = 0.03, a₂₂ = −0.02, a₂₄ = −0.02, a₃₃ = −0.01, a₃₄ = 0.01, a₄₄ = 0.03, a₄₅ = −0.02, a₄₆ = 0.02, a₅₂ = 0.05, a₅₃ = −0.09, a₅₆ = 0.08, a₆₁ = 0.03, a₆₂ = 0.05, a₆₃ = 0.09, a₆₆ = 0.02, c₁ = 0.3, c₂ = 0.3, c₃ = 0.2, c₄ = 0.4, c₅ = 0.1, and c₆ = 0.4, respectively. We see that f_i(t, ξ₀) = 0, lim_t⟶∞h_i(t) = 0 and L_i = 1 for i = 1,2, …, 6 so that all the assumptions of Theorem 5 are satisfied. Hence, the leader-follower for opinion formation model (47) is exponentially stable. The states of x₀, x₁, x₂, x₃, x₄, x₅ and x₆ of system (47) converges to a consensus state (0,0,0,0,0,0,0) as shown in Figure 1 for α = 0.5.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The states of the system of opinion formation model (47) with α = 0.5.

Example 2. Consider the leader-follower opinion formation model

()

where f(t, x) = (x − 2/x² + e^t) subject to the initial condition x₀(0) = 2, x₁(0) = 1.5, x₂(0) = −5, x₃(0) = 3.

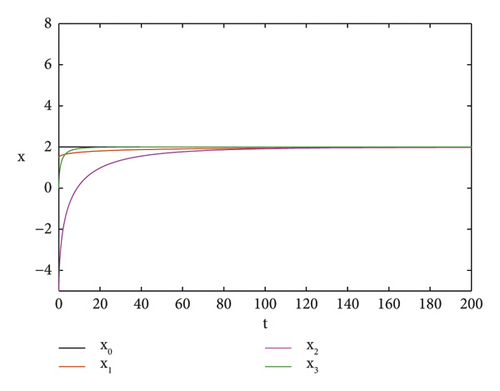
In this system of opinion formation model (48) with leader x₀(t) = ξ₀ = 2, we set a₁₁ = −0.06, a₁₂ = 0.01, a₁₃ = −0.04, a₂₁ = 0.01, a₂₂ = 0.01, a₂₃ = −0.02, a₃₁ = 0.06, a₃₂ = −0.2, a₃₃ = 0.01, c₁ = 0.2, c₂ = 0.4, c₃ = 1, respectively. We see that f(t, ξ₀) = 0, lim_t⟶∞h_i(t) = 0 and L_i = 1 for i = 1,2,3 so that all assumptions of Theorem 5 are satisfied. Hence, the leader-follower for opinion formation model (48) is exponentially stable. The states of x₀, x₁, x₂, and x₃ of system (48) converges to a consensus state (2,2,2,2) as shown in Figure 2 for α = 0.8.

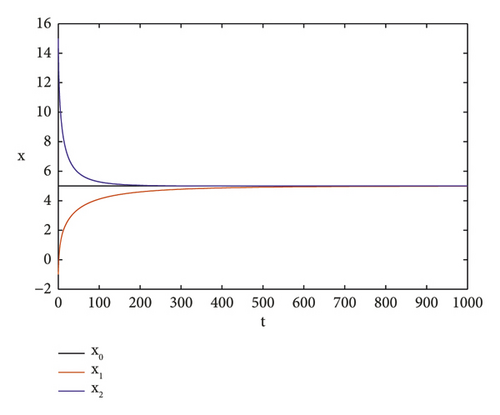
Example 3. Consider leader-follower for the opinion formation model

()

Subject to the initial condition x₀(0) = 5, x₁(0) = −1, x₂(0) = 15. In this system of opinion formation model (49) with leader x₀(t) = ξ₀ = 5, we set a₁₁ = −0.06, a₁₂ = 0.01, a₂₁ = −0.03, a₂₂ = −0.02, c₁ = 0.2, c₂ = 0.3, respectively. We see that f_i(t, ξ₀) = 0, lim_t⟶∞h_i(t) = 0 and L_i = 1 for i = 1,2 so that all assumptions of Theorem 5 are satisfied. Hence, the leader-follower for opinion formation model (49) is exponentially stable. The states of x₀, x₁, and x₂ of system (49) converges to a consensus state (5,5,5) as shown in Figure 3 for. α = 0.5

6. Discussion and Conclusion

We study the exponential stability of a leader-follower opinion formation model given by the system of nonlinear fractional differential equations. We mainly focus on the sufficient conditions for a consensus opinion of the system when time-dependent inputs are involved. In particular, under the Lipschitz continuity of the source terms, the boundedness condition on the interaction of agents, and the boundedness of external inputs, we apply the concept of α− exponential stability to prove the consensus of the followers with the leader. Our main theoretical result is illustrated by a numerical model to verify that consensus opinion can be achieved. The result is complementary to the optimal control problem for the leader-follower opinion formation model where external control is added to drive all agents’ opinions to consensus, for example, in [21, 22]. A general framework for α-exponential stability can also be considered for fractional-order neural networks as in [24]. In many real-world phenomena, a group of agents can be described by a network where the information exchange between agents is represented by some weight. The results of this paper could be applied to obtain sufficient conditions for the system that ensures consensus with the leader.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The first author was supported by the Kanchanaburi Rajabhat University. The second author was supported by the King Mongkut’s University of Technology Thonburi.

Open Research

Data Availability

No data were used to support this study.

References

1 Cristiani E., Menci M., Papi M., and Brafman L., An all-leader agent-based model for turning and flocking birds, Journal of Mathematical Biology. (2021) 83, no. 4, https://doi.org/10.1007/s00285-021-01675-2.
10.1007/s00285-021-01675-2
PubMed Google Scholar
2 Fetecau R. C. and Guo A., A mathematical model for flight guidance in honeybee swarms, Bulletin of Mathematical Biology. (2012) 74, no. 11, 2600–2621, https://doi.org/10.1007/s11538-012-9769-2, 2-s2.0-84867992865.
10.1007/s11538-012-9769-2
CAS PubMed Web of Science® Google Scholar
3 Krause J., Hoare D., Hemelrijk C. K., and Rubenstein D. I., Leadership in fish shoals, The State University of New Jersey. (2000) 1, 82–89.
Google Scholar
4 Couzin I. D., Krause J., Franks N. R., and Levin S. A., Effective leadership and decision-making in animal groups on the move, Nature. (2005) 433, no. 7025, 513–516, https://doi.org/10.1038/nature03236, 2-s2.0-13444292210.
10.1038/nature03236
CAS PubMed Web of Science® Google Scholar
5 Gastner MT., Markou N., Pruessner G., and Draief M., Opinion formation models on a gradient, PLoS One. (2014) 9, no. 12, 1140888–e114113, https://doi.org/10.1371/journal.pone.0114088, 2-s2.0-84915748052.
10.1371/journal.pone.0114088
Google Scholar
6 Di Mare A. and Latora V., Opinion formation models based on game theory, International Journal of Modern Physics C. (2007) 18, no. 09, 1377–1395, https://doi.org/10.1142/s012918310701139x, 2-s2.0-35448968952.
10.1142/S012918310701139X
Google Scholar
7 Düring B., Markowich P., Pietschmann JF., and Wolfram MT., Boltzmann and Fokker-Planck equations modelling opinion formation in the presence of strong leaders, Proceedings of The Royal Society A Mathematical Physical and Engineering Sciences. (2009) 465, no. 2112, 3687–3708, https://doi.org/10.1098/rspa.2009.0239, 2-s2.0-73149092039.
10.1098/rspa.2009.0239
Web of Science® Google Scholar
8 Boudin L. and Salvarani F., Modelling opinion formation by means of kinetic equations, Mathematical Modeling of Collective Behavior in Socio-Economic and Life Sciences, Modeling and Simulation in Science, 2010, Engineering and Technology, G. Naldi, L. Pareschi, G. Toscani, Birkhäuser, Boston, MA, USA, 245–270.
10.1007/978-0-8176-4946-3_10
Google Scholar
9 Mastroeni L., Vellucci P., and Naldi M., Agent-based models for opinion formation: a bibliographic survey, IEEE Access. (2019) 7, 58836–58848, https://doi.org/10.1109/access.2019.2913787, 2-s2.0-85065894169.
10.1109/ACCESS.2019.2913787
Google Scholar
10 Bujalski J., Dwyer G., Kapitula T., Le QN., Malvai H., Rosenthal-Kay J., and Ruiter J., Consensus and clustering in opinion formation on networks, Philosophical Transactions of the Royal Society A: Mathematical, Physical & Engineering Sciences. (2018) 376, no. 2117, 20170186–20170221, https://doi.org/10.1098/rsta.2017.0186, 2-s2.0-85045509195.
10.1098/rsta.2017.0186
PubMed Web of Science® Google Scholar
11 Albi G., Pareschi L., and Zanella M., Boltzmann-type control of opinion consensus through leaders, Philosophical Transactions of the Royal Society A: Mathematical, Physical & Engineering Sciences. (2014) 372, no. 2028, 20140138–20140218, https://doi.org/10.1098/rsta.2014.0138, 2-s2.0-84907882516.
10.1098/rsta.2014.0138
PubMed Web of Science® Google Scholar
12 Khalid H., On the stability and numerical scheme of fractional differential equations with application to biology, Computation. (2022) 10, 1–12.
Google Scholar
13 Tarasov VE., Review of some promising fractional physical models, International Journal of Modern Physics B. (2013) 27, no. 09, 1330005–1330032, https://doi.org/10.1142/s0217979213300053, 2-s2.0-84875294094.
10.1142/S0217979213300053
Web of Science® Google Scholar
14 He JH., A tutorial review on fractal spacetime and fractional calculus, International Journal of Theoretical Physics. (2014) 53, no. 11, 3698–3718, https://doi.org/10.1007/s10773-014-2123-8, 2-s2.0-84939890949.
10.1007/s10773-014-2123-8
Web of Science® Google Scholar
15 Ionescu C., Lopes A., Copot D., Machado J. A. T., and Bates J. H. T., The role of fractional calculus in modeling biological phenomena: a review, Communications in Nonlinear Science and Numerical Simulation. (2017) 51, 141–159, https://doi.org/10.1016/j.cnsns.2017.04.001, 2-s2.0-85017591809.
10.1016/j.cnsns.2017.04.001
Web of Science® Google Scholar
16 Rihan FA., Numerical modeling of fractional-order biological systems, Abstract and Applied Analysis. (2013) 2013, 816803.
10.1155/2013/816803
Google Scholar
17 Assaleh K. and Ahmad WM., Modeling of Speech signals using fractional calculus in Proceedings of signal processing and its Applications, Proceedings of the 9th International Symposium on Signal Processing and its Applications, March 2007, Sharjah, United Arab Emirates, IEEE, 1–4.
Google Scholar
18 Kumar S., A new fractional modeling arising in engineering sciences and its analytical approximate solution, Alexandria Engineering Journal. (2013) 52, no. 4, 813–819, https://doi.org/10.1016/j.aej.2013.09.005, 2-s2.0-84889659604.
10.1016/j.aej.2013.09.005
Google Scholar
19 Yang Q., Chen D., Zhao T., and Chen YQ., Fractional calculus in image processing: a review, Fractional Calculus and Applied Analysis. (2016) 19, no. 5, 1222–1249, https://doi.org/10.1515/fca-2016-0063, 2-s2.0-84995579334.
10.1515/fca-2016-0063
Web of Science® Google Scholar
20 Khalid H., A new generalized definition of fractional derivative with non-singular kernel, Computation. (2020) 8, 1–9.
Google Scholar
21 Almeida R., Malinowska A. B., and Odzijewicz T., Fractional opinion formation models. With leadership, Proceedings of the the 23rd International Conference on Methods & Models in Automation & Robotics (MMAR), August 2018, Miedzyzdroje, Poland, IEEE, 259–264.
Google Scholar
22 Almeida R., Malinowska A. B., and Odzijewicz T., Optimal leader–follower control for the fractional opinion Formation Model, Journal of Optimization Theory and Applications. (2019) 182, no. 3, 1171–1185, https://doi.org/10.1007/s10957-018-1363-9, 2-s2.0-85051850653.
10.1007/s10957-018-1363-9
Web of Science® Google Scholar
23 Bragdi A., Frioui A., and Guezane Lakoud A., Existence of solutions for nonlinear fractional integro-differential equations, Advances in Difference Equations. (2020) 2020, 418–419, https://doi.org/10.1186/s13662-020-02874-9.
10.1186/s13662-020-02874-9
Google Scholar
24 Xu C. and Li P., α-Stability of fractional-order Hopfield neural networks, International Journal of Dynamical Systems and Differential Equations. (2018) 8, 270–279.
10.1504/IJDSDE.2018.096207
Google Scholar
25 Kilbas AA., Srivastava HM., and Trujillo JJ., Theory and Applications of Fractional Differential Equations, 2006, Elsevier, London.
10.1016/S0304-0208(06)80001-0
Google Scholar

Citing Literature

All articles

Exponential Stability for an Opinion Formation Model with a Leader Associated with Fractional Differential Equations

Abstract

1. Introduction

2. Fractional Calculus Framework

3. Stability and Consensus of Fractional Leader-Follower Opinion Formation Model

4. Stability and Consensus of Leader-Follower Opinion Formation Model with Time-dependent External Inputs

5. Numerical Examples

6. Discussion and Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Exponential Stability for an Opinion Formation Model with a Leader Associated with Fractional Differential Equations

Abstract

1. Introduction

2. Fractional Calculus Framework

3. Stability and Consensus of Fractional Leader-Follower Opinion Formation Model

4. Stability and Consensus of Leader-Follower Opinion Formation Model with Time-dependent External Inputs

5. Numerical Examples

6. Discussion and Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information