If the degrees of any two consecutive vertices differ by exactly one, the graph is called a stepwise irregular graph. The study of choosing specific vertices in an ordered subset of the vertex set such that no two vertices have the same representations with regard to the chosen subset is known as resolving parameters. This concept has been expanded for edges as well as a combined version of both. We examine a unique unicyclic stepwise irregular graph and an extended structure of stepwise irregular graph in terms of resolvability parameters to connect the stepwise irregular graph and resolving parameter concepts.

1. Introduction

Let λ be a simple, connected, undirected graph with V as the vertex set and E as the edge set. The degree of a vertex x ∈ V, which is the count of edges related to a, is denoted by χ(x). If every vertex in V has the same χ(x), the graph belongs to a regular class of graphs; otherwise, it is irregular. Regular graphs have a history that may be traced back to either theoretical or practical applications.

In 1988, a question was aroused by Chartrand et al. [1] that “what if the graph vertices do not have the same degree? In which class of graphs it will be considered?” Although in 1987 the idea of highly irregular graphs was posed in [2], this idea begins with the new thoughts of studying graphs. To answer the question that “how irregular a graph is?”, the Albertson index [3] was introduced, which is defined as follows:

(1)

where imb(a₁a₂) = |χ(a₁) − χ(a₂)| is the imbalance of an edge a₁a₂. The updated version of this index is the Mostar index [4]. Motivated by the Albertson index, Gutman in 2018 proposed a new idea which is known as a stepwise irregular graph and is defined as imb(ab) = |χ(a₁) − χ(a₂)| = 1 for each a₁a₂ ∈ E [5]. To count the number of cycles in a graph, the cyclomatic number of a graph λ is γ = |E(λ)| − |V(λ)| + 1 [5].

Researchers of [6] proposed the concept of metric dimension, which was based on the idea of identifying the location of invaders in networks first and foremost and called the metric generators as locating sets. The idea of metric dimension for trees is defined in [6] and for any graph in [7]. The resolving sets are also known as metric generators, using a similar technique. Radar or loran terminals were classified as components of the metric base set. If a single station fails to work, then the entire set ℵ resulted in failures to serve as a station hub. To overcome this problem, in 2008, the authors of [8] proposed an idea of a fault-tolerant resolving set. The idea of the adjacency generator was established in [9]; it was introduced to explain the metric dimension of composition of two networks.

Putting natural thinking on the pattern of recognizing the vertices of a graph by a subset (resolving set) of the vertex set, the edge metric dimension defined in [10], and later analogous to this definition, the authors of [11] proposed a mixed metric dimension in which both concepts (recognising vertices and edges) are combined, with the additional condition that no two elements (vertices and edges) have the same distances with respect to a chosen subset.

For η₁, η₂ ∈ V, the distance (also called as geodesics) d(η₁, η₂) between vertices η₁ and η₂ is the count of edges between η₁ and η₂. Let η ∈ V be a vertex for distinguished two vertices η₁ and η₂, if d(η, η₁) ≠ d(η, η₂). A set ℵ ⊂ V is called a resolving set for λ, if any pair of distinct vertices of λ is uniquely determined by some vertices of ℵ. The minimum cardinality of ℵ is named as a resolving set, and its cardinality is the metric dimension of λ, denoted by dim(λ) . If for each u ∈ ℵ_f, ℵ_f\u remains a resolving set for λ, then ℵ_f is named as a fault-tolerant resolving set and the minimum count of elements of ℵ_f is called as a fault-tolerant metric dimension. For a vertex η and an edge e = η₁η₂, the distance between η and e is measured as d(e, η) = min{d(η₁, η), d(η₂, η)}. A vertex η ∈ V identifies two edges e₁, e₂ ∈ E, if d(η, e₁) ≠ d(η, e₂). A subset ℵ_e having minimum vertices from a graph λ is an edge resolving set for λ, if each pair of two distinct edges of λ are distinguished by some vertex of ℵ_e. The minimum cardinality of an edge resolving set for a graph λ is called the edge metric dimension and is denoted by dim_e(λ). A vertex η of a graph λ distinguishes two elements (vertices or edges) η₁, η₂ of λ, if d(η₁, η) ≠ d(η₂, η). A subset ℵ_m is a mixed resolving set, if any vertex and edge of λ are distinguished by some vertex of ℵ_m. The smallest cardinality of a mixed resolving set for λ is called the mixed metric dimension and is denoted by dim_m(λ). Moreover, the mixed metric dimension is a blended version of metric and edge metric dimension.

Computational complexity and NP hardness of the metric dimension problem was discussed in [12, 13]. The metric dimension has a range of useful uses in our everyday lives, which motivates scholars to study it. The metric dimension is extensively used in the varied fields such as combinatorial optimization [14], pharmaceutical chemistry [15], robot navigation [16], sonar and coastguard loran, facility location problems, image processing [6] weighing problems [17], and computer networks [18]; for more practical applications, see the literature [19, 20].

The concept of metric dimension has a wide range of applications due to its versatility and also its generalizations which are edge, fault-tolerant, and mixed metric dimension are widely used to solve many difficult problems. The study of metric dimension on some cycle-based graphs are discussed in [21]. The preprint on the application of metric dimension and its algorithm is available at [22]. The metric dimension of chemical structures are discussed in [23]. The upper bounds for some chemical networks, one can find at [24]. The metric dimension and its related parameters are discussed in [25]. Generalized classes of some basic graphs are discussed in [26]. For the recent work on the computer 3D network ,we refer to [27]. For a detailed study on these parameters of metric dimensions, see [28]. The fault-tolerance of chemical topologies are discussed in [29]. The generalized resolving set for the circulant graph is available at [30, 31]. The famous convex structure’s resolving set can be seen at [32, 33]. The fault-tolerant of some computer networks are available at [34]. Some rotationally symmetric, extremal structures, and generalized Peterson graph are discussed in [35–37]. For the edge metric of polytopes structure, we refer to [38]. Th seminal works on edge and mixed metric are available at [10, 11]. All the resolvability parameters of graph theory on the polycyclic aromatic hydrocarbons are discussed in [39]. For the recent study of stepwise irregular graph, we refer to [40–43] and some important applications of irregular graphs and their measures [44–46]. For some topological work on this topic, one can find it in [47, 48].

Following are some important results which are very helpful to prove our main work.

Theorem 1. Reference [11]: Let dim(λ) and dim_f(λ) be the metric and fault-tolerant metric dimension of graph λ, respectively. Then,

(2)

Theorem 2. Reference [11]: If λ is a simple connected graph; then, dim_m(λ) ≥ max{dim(λ), dim_e(λ)}.

Theorem 3. Reference [15]: If λ is a simple, undirected connected graph; then, (1) dim(λ) = 1 if λ = P_n.

Theorem 4. Reference [10]: For integers n, r, t ≥ 2, dim_e(P_n) = 1, dim_e(C_n) = 2, and dim_e(K_n) = n − 1. Moreover, dim_e(λ) = 1 if λ is a path P_n.

Theorem 5. Reference [11]: If λ is a graph with order |λ|; then, dim_m(λ) = 2 if λ is a path.

Figure 1 is the stepwise irregular unicyclic graphs having a minimum number of vertices and the maximum degree of a vertex is Δ = 3 and due to equal order and size, its cyclomatic number is γ = 1. It is the only graph having γ = 1 with even order and size. It is a unique graph in terms of even order of a stepwise irregular unicyclic graph [5]. To check the resolvability of the stepwise irregular graph, we consider this the minimum order and a special graph. The following lemmas start the discussion of the resolvability of the stepwise irregular graph.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Stepwise irregular unicyclic graph.

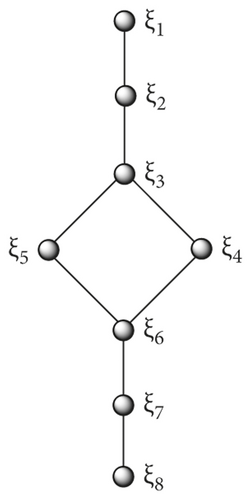
Lemma 1. If G₁ is a unicyclic stepwise irregular graph with order 8, then

(3)

Proof. To prove that dim(G₁) = 2, we will use the double inequality method. Let dim(G₁) ≤ 2 and the resolving set ℵ = {ξ₁, ξ₄}. In Table 1, we provide with regard to ℵ, the representations of whole vertex set are given as follows:

Since the representations in the above table are distinct and there are no two vertices with same representations, we can say that dim(G₁) ≤ 2.

On the contrary, let dim(G₁) = 1. By Theorem.3, it is not possible, which concludes that the stepwise irregular graph in Figure 1 with

(4)

Table 1. Representations of all vertices w.r.t.ℵ.

r(ξ_i\|ℵ)	r(ξ_i\|ξ₁)	r(ξ_i\|ξ₄)
r(ξ₁\|ℵ)	0	3
r(ξ₂\|ℵ)	1	2
r(ξ₃\|ℵ)	2	1
r(ξ₄\|ℵ)	3	0
r(ξ₅\|ℵ)	4	1
r(ξ₆\|ℵ)	3	2
r(ξ₇\|ℵ)	5	2
r(ξ₈\|ℵ)	6	3

Lemma 2. Let G₁ be a unicyclic stepwise irregular graph with order 8. Then,

(5)

Proof. On the contrary to prove that dim_f(G₁) = 3, first we will show that dim_f(G₁) ≤ 3 and the fault-tolerant resolving set ℵ_f = {ξ₂} ∪ ℵ. In Table 2, we provide with regard to ℵ_f, the representations of whole vertex set are given as follows:

Since, the representations in the above table are distinct and there are two vertices with same representations, we can say that dim_f(G₁) ≤ 3.

On contrary to prove that dim_f(G₁) ≥ 3 we resulted to dim_f(G₁) = 2 which is not possible by Theorem 1. It proves that the stepwise irregular graph that is defined in Figure 1 has

(6)

Table 2. Representations of all vertices w.r.t.ℵ_f.

r(ξ_i\|ℵ_f)	r(ξ_i\|ξ₁)	r(ξ_i\|ξ₂)	r(ξ_i\|ξ₄)
r(ξ₁\|ℵ_f)	0	1	3
r(ξ₂\|ℵ_f)	1	0	2
r(ξ₃\|ℵ_f)	2	1	1
r(ξ₄\|ℵ_f)	3	2	0
r(ξ₅\|ℵ_f)	4	3	1
r(ξ₆\|ℵ_f)	3	2	2
r(ξ₇\|ℵ_f)	5	4	2
r(ξ₈\|ℵ_f)	6	5	3

Lemma 3. Let G₁ be a unicyclic stepwise irregular graph with order 8. Then,

(7)

Proof. On the contrary to prove that dim_e(G₁) = 2, let dim_e(G₁) ≤ 2, and the edge resolving set ℵ_e = ℵ. In Table 3, we provide with regard to ℵ_e, the representations of whole edge set are given as follows:

Since, the representations in the above table are distinct and we cannot see any two edges with same representations, we can say that dim_e(G₁) ≤ 2.

Now, to prove the reverse inequality, dim_e(G₁) ≥ 2 on contrary dim_e(G₁) = 1 and it is not possible by Theorem 1. It is concluded that the stepwise irregular graph in Figure 1 with

(8)

Table 3. Representations of all edges w.r.t.ℵ_e.

r(ξ_iξ_j\|ℵ_e)	r(ξ_iξ_j\|ξ₁)	r(ξ_iξ_j\|ξ₄)
r(ξ₁ξ₂\|ℵ_e)	0	2
r(ξ₂ξ₃\|ℵ_e)	1	1
r(ξ₃ξ₄\|ℵ_e)	2	0
r(ξ₃ξ₆\|ℵ_e)	2	1
r(ξ₄ξ₅\|ℵ_e)	3	0
r(ξ₅ξ₆\|ℵ_e)	3	1
r(ξ₅ξ₇\|ℵ_e)	4	1
r(ξ₇ξ₈\|ℵ_e)	5	2

Lemma 4. Let G₁ be a unicyclic stepwise irregular graph with order 8. Then

(9)

Proof. On the contrary to prove that dim_m(G₁) = 3, let dim_m(G₁) ≤ 3, and the mixed metric resolving set ℵ_m = {ξ₈} ∪ ℵ. In Table 4, we provide with regard to ℵ_m, the representations of whole edge and vertex sets are given as follows:

Since, the representations in Table 4 are distinct and we cannot see any two components of the graph with same representations, we can say that dim_m(G₁) ≤ 3.

Now, to prove reverse inequality dim_m(G₁) ≥ 3, on contrary dim_m(G₁) = 2 which is not possible by Theorem 5.

It is concluded that the stepwise irregular graph in Figure 1 with

(10)

Table 4. Representations of all vertices and edges w.r.t.ℵ_m.

r(ξ_i\|ℵ_m)	r(ξ_i\|ξ₁)	r(ξ_i\|ξ₄)	r(ξ_i\|ξ₈)
r(ξ₁\|ℵ_m)	0	3	6
r(ξ₂\|ℵ_m)	1	2	5
r(ξ₃\|ℵ_m)	2	1	4
r(ξ₄\|ℵ_m)	3	0	3
r(ξ₅\|ℵ_m)	4	1	2
r(ξ₆\|ℵ_m)	3	2	3
r(ξ₇\|ℵ_m)	5	2	1
r(ξ₈\|ℵ_m)	6	3	0
r(ξ_iξ_j\|ℵ_m)	r(ξ_iξ_j\|ξ₁)	r(ξ_iξ_j\|ξ₄)	r(ξ_iξ_j\|ξ₈)
r(ξ₁ξ₂\|ℵ_m)	0	2	5
r(ξ₂ξ₃\|ℵ_m)	1	1	4
r(ξ₃ξ₄\|ℵ_m)	2	0	3
r(ξ₃ξ₆\|ℵ_m)	2	1	3
r(ξ₄ξ₅\|ℵ_m)	3	0	2
r(ξ₅ξ₆\|ℵ_m)	3	1	2
r(ξ₅ξ₇\|ℵ_m)	4	1	1
r(ξ₇ξ₈\|ℵ_m)	5	2	0

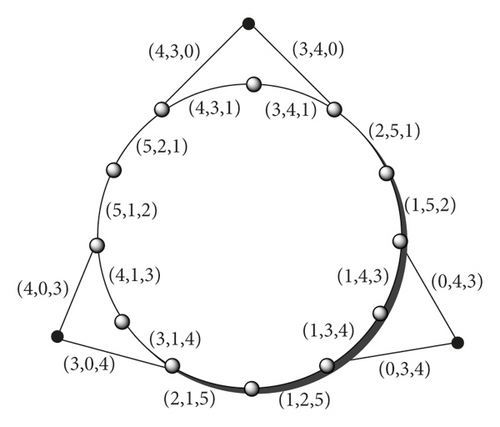
The graph shown in Figure 2 is the stepwise irregular graph with order 5β and size 6β. Its cyclomatic number is γ = 6β − 5β + 1 = β + 1. As shown in Figure 3, if we use β = 3, it create three cycles with order 4 and one cycle with order 4β and it adds up to 3 + 1 = 4-cycles in a graph. In the following sections, we discuss different resolvability parameters of the stepwise irregular graph such as resolving of vertices (metric dimension) or edges (edge metric dimension) and also resolving of vertices along edges (mixed metric dimension). Moreover, the updated version of the resolving set, which is a fault-tolerant resolving set, is also discussed.

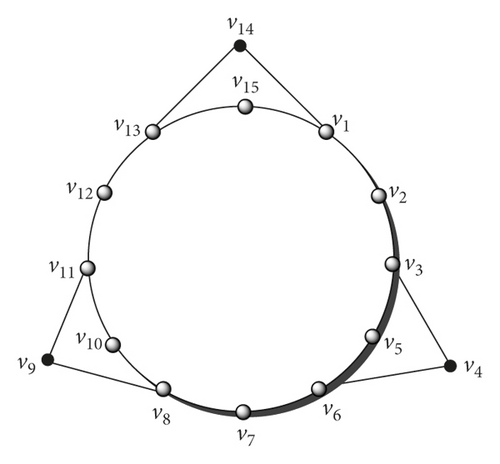
2. Metric Dimension of a Stepwise Irregular Graph

This section refers to the resolving of vertices and computation of metric dimension of stepwise irregular graph .

Theorem 6. Let be a stepwise irregular graph with β = 3. Then,

(11)

Proof 5. To prove that when β = 3, we assume a resolving set ℵ = {v₄, v₉, v₁₄}. On the vertex set of , we build the following examples:

(12)

From this representation, we obtain , that shows all the vertices of have unique representations with respect to resolving set ℵ.

For reverse inequality which is , by contradiction, it becomes . Following are some discussion for this claim.

Case 1. Consider the resolving set with ϕ = {v₁, v_i} where i = 2,3, …, 15, then the same representations are either in r(v₄|ϕ) = r(v₅|ϕ) or r(v₉|ϕ) = r(v₁₀|ϕ).

Case 2. Consider the resolving set ϕ = {v_i, v_j} where i = 2,3, j = 2,3, …, 15 and i ≠ j, then the same representations are either in r(v₄|ϕ) = r(v₅|ϕ) or r(v₉|ϕ) = r(v₁₀|ϕ).

Case 3. By assuming the resolving set ϕ = {v_i, v_j} where i, j = 4,5, …, 15 and i ≠ j, then the same representations are either in r(v₄|ϕ) = r(v₅|ϕ) or r(v₉|ϕ) = r(v₁₀|ϕ) or r(v₁₄|ϕ) = r(v₁₅|ϕ).

All discussion resulting in same representations of vertices. Hence, for β = 3,

(13)

Theorem 7. Let be a stepwise irregular graph with β ≥ 3. Then,

(14)

Proof. Assume that the resolving set ℵ = {v_i+4 : i ≡ 0(mod5)}, |ℵ| = β. To show that , the induction will be applied to β the number of copies of the C₄ graph. Assume that the assumption is valid for β = α and that the base case is β = 3, as demonstrated in Theorem 6.

(15)

We will prove that it is true for β = α + 1. We assume the following:

(16)

Then, by using (13) and (15) in (16), we will obtain the following:

(17)

Hence, it is true for all positive values of β ≥ 3

3. Fault-Tolerant Metric Dimension of

This section refers to the resolving of vertices with possibility of choosing one vertex extra for the replacement of faulty vertex in resolving set and also the computation of fault-tolerant metric dimension of stepwise irregular graph .

Theorem 7. Let be a stepwise irregular graph with β = 3. Then,

(18)

Proof. To prove that when β = 3, we assume a fault-tolerant resolving set ℵ_f = {v₁, v₄, v₉, v₁₄}. We construct the following cases on vertex set of

(19)

As a result of the preceding reasoning in the form of representations that , all the vertices of have unique representations with respect to fault-tolerant resolving set ℵ_f.

For , our claim becomes contradictory as a result of the conflict which is not possible by Theorem 1. Hence, for β = 3,

(20)

Theorem 8. Let be a stepwise irregular graph with β ≥ 3. Then,

(21)

Proof. The fault-tolerant resolving set ℵ_f = {v₁} ∪ ℵ. Now to show that , the induction will be applied to β the number of copies of the C₄ graph. We assume that the assumption is valid for β = α and that the base case is β = 3, as demonstrated in Theorem 7.

(22)

We will show that it is true for β = α + 1. Suppose

(23)

Using (19) and (22) in (23), we obtain the following:

(24)

Hence, it is true for all positive values of β ≥ 3

4. Edge Metric Dimension of

This section refers to the resolving of edges of stepwise irregular graph ; it also for the computation of edge metric dimension of that graph.

Theorem 9. If be a stepwise irregular graph of order 5β, then

(25)

for β = 3.

Proof. To prove that when β = 3, we assume an edge resolving set ℵ_e = {v₄, v₉, v₁₄}. We can see edge representations in Figure 2 and it has a distinct representation with respect to edge metric resolving set ℵ_e.

Hence, it follows that because all the edges of have unique representations with respect to edge resolving set ℵ_e.

For , our claim becomes contradictory as a result of the conflict . Following are some cases for this claim.

Case 4. Consider the edge resolving set with 2-cardinality where i = 2,3, …, 15, then the same representations are either in or .

Case 5. Consider the edge resolving set again with 2-cardinality where i, j = 2,3, …, 15 and i ≠ j, then the same representations are either in or . All the cases resulted in contradiction, so this concludes that when β = 3,

(26)

Theorem 10. If is a stepwise irregular graph of order 5β, then

(27)

for β ≥ 3.

Proof. The vertex and edge resolving set have similar vertices and same cardinality so that ℵ_e = ℵ. To show that , the induction will be applied to β the number of copies of the C₄ graph. Assuming that the assumption is valid for β = α and that the base case is β = 3, as demonstrated in Theorem 9,

(28)

We will show that it is true for β = α + 1. Suppose

(29)

Then, by using (26) and (28) in (29), we obtain the following:

(30)

Hence, it is true for all positive values of β ≥ 3.

5. Mixed Metric Dimension of

The mixed version of vertex and edge resolving is the mixed metric resolvability parameter. This section deals with resolving vertices as well as edges at a time.

Theorem 11. Let be a stepwise irregular graph with β = 3. Then,

(31)

Proof. To prove that when β = 3, we assume a mixed metric resolving set ℵ_m = {v₄, v₉, v₁₄}. We can see vertex representations from Theorem 6 and edge representations from Figure 3 which are showing that every vertex and edge has a distinct representation with respect to mixed metric resolving set ℵ_m.

Hence, it follows that , because all the vertices and edges of have unique representations with respect to mixed metric resolving set ℵ_m.

For , our claim becomes contradictory as a result of the conflict which is not possible by Theorem 2. So, all discussion concludes that when β = 3,

(32)

Theorem 12. Let be a stepwise irregular graph with β ≥ 3. Then,

(33)

Proof. The mixed metric resolving set is same as the vertex resolving set and edge resolving set with same cardinality so that ℵ_m = ℵ. To show that , the induction will be applied to β the number of copies of the C₄ graph. We assume that the assumption is valid for β = α and that the base case is β = 3, as demonstrated in Theorem 11.

(34)

We will show that it is true for β = α + 1. Suppose

(35)

Using (32) and (34) in (35), we obtain

(36)

Hence, it is true for all positive values of β ≥ 3.

Figure 2 is the stepwise irregular graph with β = 3, the labeling of vertices can be extended similarly to define in the figure and β can be any natural number greater than 2. Moreover, the dark black vertices show the vertex, edge, and mixed metric resolving set when β = 3 and the position of resolving set vertices remains the same while increasing the number of copies of β’s.

6. Conclusion

Recently, the generalized class of graphs known as stepwise irregular graphs was introduced. In this research, we initiate to discuss the resolvability parameters of this new type of graphs. One of the generalized stepwise irregular graphs is as shown in Figure 3. Each resolving parameter of is not constant, the cardinality of each resolving parameter (ℵ, ℵ_f, ℵ_e, ℵ_m) increases with increasing graph’s cyclomatic number which is γ = β + 1. As we have seen that the resolving parameters are also dependent on the degree of vertices of a graph and the stepwise irregular class of graphs is purely dependent on the degree of vertices, so the discussion of resolvability parameters of stepwise irregular graphs is interesting and opens the way of thinking on either stepwise irregular graphs or resolvability parameters of graphs. To extend this idea, we provide the following open problems at the end of this work. [50, 51].

Open problem 1. Do all the stepwise irregular graphs have varying resolving parameters (ℵ, ℵ_f, ℵ_e, ℵ_m) ?

Open problem 2. Is there any class of stepwise irregular graph with constant resolving parameters( (ℵ, ℵ_f, ℵ_e, ℵ_m) ?

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

There are no data associated with this paper.

References

1 Chartrand G., Erdös P., and Oellermann O. R., How to define an irregular graph, The College Mathematics Journal. (1988) 19, no. 1, 36–42, https://doi.org/10.1080/07468342.1988.11973088.
10.1080/07468342.1988.11973088
Google Scholar
2 Alavi Y., Chartrand G., Chung F. R. K., Erdös P., Graham R. L., and Oellermann O. R., Highly irregular graphs, Journal of Graph Theory. (1987) 11, no. 2, 235–249, https://doi.org/10.1002/jgt.3190110214, 2-s2.0-84986516373.
10.1002/jgt.3190110214
Web of Science® Google Scholar
3 Albertson M. O., The Irregularity of a Graph, Ars Combinatoria. (1997) 46, 219–225.
Web of Science® Google Scholar
4 Došlić T., Martinjak I., Škrekovski R., Spužević S. T., and Zubac I., Mostar index, Journal of Mathematical Chemistry. (2018) 56, 2995–3013, https://doi.org/10.1007/s10910-018-0928-z, 2-s2.0-85049079597.
10.1007/s10910-018-0928-z
CAS Web of Science® Google Scholar
5 Gutman I., Stepwise irregular graphs, Applied Mathematics and Computations. (2018) 325, 234–238, https://doi.org/10.1016/j.amc.2017.12.045, 2-s2.0-85040132710.
10.1016/j.amc.2017.12.045
Web of Science® Google Scholar
6 Slater P. J., Leaves of trees, 14, Proceedings of the 6th Southeastern Conference on Combinatorics, Graph Theory, and Computing, February 1975, Boca Raton, Florida, 549–559.
Google Scholar
7 Harary F. and Melter R. A., On the Metric Dimension of a Graph, Ars Combinatoria. (1976) 2, 191–195.
Google Scholar
8 Cáceres J., Hernando C., Mora M., Pelayo I. M., Puertas M. L., Seara C., and Wood D. R., On the metric dimension of cartesian products of graphs, SIAM Journal on Discrete Mathematics. (2007) 21, no. 2, 423–441, https://doi.org/10.1137/050641867, 2-s2.0-38149005958.
10.1137/050641867
Web of Science® Google Scholar
9 Jannesari M. and Omoomi B., The metric dimension of the lexicographic product of graphs, Discrete Mathematics. (2012) 312, no. 22, 3349–3356, https://doi.org/10.1016/j.disc.2012.07.025, 2-s2.0-84865072850.
10.1016/j.disc.2012.07.025
Web of Science® Google Scholar
10 Kelenc A., Tratnik N., and Yero I. G., Uniquely identifying the edges of a graph: the edge metric dimension, Discrete Applied Mathematics. (2018) 251, 204–220, https://doi.org/10.1016/j.dam.2018.05.052, 2-s2.0-85048930524.
10.1016/j.dam.2018.05.052
Web of Science® Google Scholar
11 Kelenc A., Kuziak D., Taranenko A., and Yero I. G., Mixed metric dimension of graphs, Applied Mathematics and Computation. (2017) 314, 429–438, https://doi.org/10.1016/j.amc.2017.07.027, 2-s2.0-85025658194.
10.1016/j.amc.2017.07.027
Web of Science® Google Scholar
12 Hauptmann M., Schmied R., and Viehmann C., Approximation complexity of metric dimension problem, Journal of Discrete Algorithms. (2012) 14, 214–222, https://doi.org/10.1016/j.jda.2011.12.010, 2-s2.0-84860833747.
10.1016/j.jda.2011.12.010
Google Scholar
13 Lewis H. R., Garey M. R., and Johnson D. S., Michael R. ΠGarey and David S. Johnson. Computers and intractability. A guide to the theory of NP-completeness. W. H. Freeman and Company, San Francisco1979, x + 338 pp, Journal of Symbolic Logic. (1983) 48, no. 2, 498–500, https://doi.org/10.2307/2273574.
10.2307/2273574
Google Scholar
14 Sebö A. and Tannier E., On Metric Generators of Graphs, Mathematics and Operational Research. (2004) 29, 383–393.
10.1287/moor.1030.0070
Web of Science® Google Scholar
15 Chartrand G., Eroh L., Johnson M. A., and Oellermann O. R., Resolvability in graphs and the metric dimension of a graph, Discrete Applied Mathematics. (2000) 105, no. 1-3, 99–113, https://doi.org/10.1016/s0166-218x(00)00198-0, 2-s2.0-0037756351.
10.1016/S0166-218X(00)00198-0
Web of Science® Google Scholar
16 Khuller S., Raghavachari B., and Rosenfeld A., Landmarks in Graphs, Discrete Applied Mathematics. (1996) 70, no. 3, 217–229, https://doi.org/10.1016/0166-218x(95)00106-2, 2-s2.0-0013510156.
10.1016/0166-218X(95)00106-2
Web of Science® Google Scholar
17 Söderberg S. and Shapiro H. S., A combinatory detection problem, The American Mathematical Monthly. (1963) 70, no. 10, 1066–1070, https://doi.org/10.2307/2312835.
10.1080/00029890.1963.11992174
Web of Science® Google Scholar
18 Manuel P., Bharati R., Rajasingh I., and Monica M C., On minimum metric dimension of honeycomb networks, Journal of Discrete Algorithms. (2008) 6, no. 1, 20–27, https://doi.org/10.1016/j.jda.2006.09.002, 2-s2.0-39449091612.
10.1016/j.jda.2006.09.002
Google Scholar
19 Perc M., Gómez-Gardeñes J., Szolnoki A., Floría L. M., and Moreno Y., Evolutionary dynamics of group interactions on structured populations: a review, Journal of The Royal Society Interface. (2013) 10, no. 80, https://doi.org/10.1098/rsif.2012.0997, 2-s2.0-84876137675.
10.1098/rsif.2012.0997
PubMed Web of Science® Google Scholar
20 Szolnoki M. P. A., Coevolutionary Games—A Mini Review, Biosystems. (2010) 99, no. 2, 109–125, https://doi.org/10.1016/j.biosystems.2009.10.003, 2-s2.0-73449112588.
10.1016/j.biosystems.2009.10.003
PubMed Web of Science® Google Scholar
21 Ahmad A., Bača M., and Sultan S., Computing the metric dimension of kayak paddles graph and cycles with chord, Proyecciones (Antofagasta). (2020) 39, no. 2, 287–300, https://doi.org/10.22199/issn.0717-6279-2020-02-0018.
10.22199/issn.0717-6279-2020-02-0018
Google Scholar
22 Badr E. and Aloufi K., A robot's response acceleration using the metric dimension problem, Preprints. (2019) 2019110194, https://doi.org/10.20944/preprints201911.0194.v1.
10.20944/preprints201911.0194.v1
Google Scholar
23 Hussain Z., Munir M., Choudhary M., and Kang S. M., Computing metric dimension and metric basis of 2D lattice of alpha-boron nanotubes, Symmetry. (2018) 10, https://doi.org/10.3390/sym10080300, 2-s2.0-85052517010.
10.3390/sym10080300
PubMed Web of Science® Google Scholar
24 Imran S., Siddiqui M. K., and Hussain M., Computing the upper bounds for the metric dimension of cellulose network, Applied Mathematics E-Notes. (2019) 19, 585–605.
Web of Science® Google Scholar
25 Liu J. B., Zafari A., and Zarei H., Metric dimension, minimal doubly resolving sets, and the strong metric dimension for jellyfish graph and cocktail party graph, Complexity. (2020) 2020, 7, 9407456, https://doi.org/10.1155/2020/9407456.
10.1155/2020/9407456
Web of Science® Google Scholar
26 Liu J. B., Nadeem M. F., Siddiqui H. M. A., and Nazir W., Computing metric dimension of certain families of Toeplitz graphs, IEEE Access. (2019) 7, 126734–126741, https://doi.org/10.1109/ACCESS.2019.2938579.
10.1109/ACCESS.2019.2938579
Web of Science® Google Scholar
27 Nadeem M. F., Azeem M., and Khalil A., The locating number of hexagonal Möbius ladder network, Journal of Applied Mathematics and Computation. (2020) 66, https://doi.org/10.1007/s12190-020-01430-8.
10.1007/s12190-020-01430-8
PubMed Web of Science® Google Scholar
28 Yero I. G., Vertices, edges, distances and metric dimension in graphs, Electronic Notes in Discrete Mathematics. (2016) 55, 191–194, https://doi.org/10.1016/j.endm.2016.10.047, 2-s2.0-84995699201.
10.1016/j.endm.2016.10.047
Google Scholar
29 Somasundari M. and Raj F. S., Fault-Tolerant Resolvability of Oxide Interconnections, International Journal of Innovative Technology and Exploring Engineering. (2019) 8, 2278–3075, https://doi.org/10.35940/ijitee.L3245.1081219, 2-s2.0-85073929557.
10.35940/ijitee.L3245.1081219
Google Scholar
30 Basak M., Saha L., Das G. K., and Tiwary K., Fault-tolerant metric dimension of circulant graphs C(1, 2, 3), Theoretical Computer Science. (2020) 817, 66–79, https://doi.org/10.1016/j.tcs.2019.01.011, 2-s2.0-85060525332.
10.1016/j.tcs.2019.01.011
Web of Science® Google Scholar
31 Seyedi N. and Maimani H. R., Fault-tolerant metric dimension of circulant graphs, Facta Universitatis – Series: Mathematics and Informatics. (2019) 34, 781–788, https://doi.org/10.22190/fumi1904781s.
10.22190/FUMI1904781S
Web of Science® Google Scholar
32 Siddiqui H. M. A., Hayat S., Khan A., Imran M., Razzaq A., and Liu J.-B., Resolvability and fault-tolerant resolvability structures of convex polytopes, Theoretical Computer Science. (2019) 796, 114–128, https://doi.org/10.1016/j.tcs.2019.08.032, 2-s2.0-85071663013.
10.1016/j.tcs.2019.08.032
Web of Science® Google Scholar
33 Raza H., Hayat S., and Pan X.-F., On the fault-tolerant metric dimension of convex polytopes, Applied Mathematics and Computation. (2018) 339, 172–185, https://doi.org/10.1016/j.amc.2018.07.010, 2-s2.0-85050861044.
10.1016/j.amc.2018.07.010
Web of Science® Google Scholar
34 Hayat S., Khan A., Malik M. Y. H., Imran M., and Siddiqui M. K., fault-tolerant metric dimension of interconnection networks, IEEE Access. (2020) 8, 145435–145445, https://doi.org/10.1109/access.2020.3014883.
10.1109/ACCESS.2020.3014883
Web of Science® Google Scholar
35 Raza H., Imran M., Hayat S., and Pan X. F., Fault-tolerant resolvability and extremal structures of graphs, Mathematics. (2019) 7, https://doi.org/10.3390/math7010078, 2-s2.0-85060240189.
10.3390/math7010078
Web of Science® Google Scholar
36 Raza H. and Ji Y., Computing the mixed metric dimension of a generalized petersen graph P(n, 2), Frontiers in Physics. (2020) 8, https://doi.org/10.3389/fphy.2020.00211.
10.3389/fphy.2020.00211
Web of Science® Google Scholar
37 Raza H., Liu J.-B., and Qu S., On mixed metric dimension of rotationally symmetric graphs, IEEE Access. (2020) 8, 11560–11569, https://doi.org/10.1109/access.2019.2961191.
10.1109/ACCESS.2019.2961191
Web of Science® Google Scholar
38 Zhang Y. and Gao S., On the edge metric dimension of convex polytopes and its related graphs, Journal of Combinatorial Optimization. (2020) 39, no. 2, 334–350, https://doi.org/10.1007/s10878-019-00472-4.
10.1007/s10878-019-00472-4
Web of Science® Google Scholar
39 Azeem M. and Nadeem M. F., Metric-based resolvability of polycyclic aromatic hydrocarbons, The European Physical Journal Plus. (2021) 136, no. 4, https://doi.org/10.1140/epjp/s13360-021-01399-8.
10.1140/epjp/s13360-021-01399-8
Web of Science® Google Scholar
40 Abdo H., Dimitrov D., and Gutman I., Graph irregularity and its measures, Applied Mathematics and Computation. (2019) 357, 317–324, https://doi.org/10.1016/j.amc.2019.04.013, 2-s2.0-85064091209.
10.1016/j.amc.2019.04.013
Web of Science® Google Scholar
41 Boaventura-Netto P., de Lima L., and Caporossi G., Exhaustive and metaheuristic exploration of two new structural irregularity measures, MATCH Community of Mathematics and Computational Chemistry. (2019) 82, 561–580.
Web of Science® Google Scholar
42 Deng K. and Li S., On the Extremal values for the mostar index of trees with given degree sequence, Applied Mathematics and Computations. (2020) 390, 125598, https://doi.org/10.1016/j.amc.2020.125598.
10.1016/j.amc.2020.125598
Web of Science® Google Scholar
43 Ghalavand A. and Sohail T., On Some Variations of the Irregularity, Discrete Mathematics Letter. (2020) 3, 25–30.
Google Scholar
44 Abdo H., Cohen N., and Dimitrov D., Graphs with maximal irregularity, Filomat. (2014) 28, no. 7, 1315–1322, https://doi.org/10.2298/fil1407315a, 2-s2.0-84899681068.
10.2298/FIL1407315A
Web of Science® Google Scholar
45 Réti T., Sharafdini R., Drégelyi-Kiss A., and Haghbin H., Graph irregularity indices used as molecular descriptors in qspr studies, MATCH Community Mathematics and Computational Chemistry. (2018) 79, 509–524.
Web of Science® Google Scholar
46 Tepeh A., Extremal bicyclic graphs with respect to mostar index, Applied Mathematics and Computation. (2019) 355, 319–324, https://doi.org/10.1016/j.amc.2019.03.014, 2-s2.0-85062858158.
10.1016/j.amc.2019.03.014
Web of Science® Google Scholar
47 Horoldagva B., Buyantogtokh L., Dorjsembe S., and Gutman I., Maximum size of maximally irregular graphs, MATCH Community of Mathematics and Computational Chemistry. (2016) 76, 81–98.
Web of Science® Google Scholar
48 Horoldagva B., Das K. C., and Selenge T.-A., On ve-degree and ev-degree of graphs, Discrete Optimization. (2019) 31, 1–7, https://doi.org/10.1016/j.disopt.2018.07.002, 2-s2.0-85050570924.
10.1016/j.disopt.2018.07.002
Web of Science® Google Scholar
49 Chaudhry M. A., Javaid I., and Salman M., Fault-tolerant metric and partition dimension of graphs, Utilitas Mathematica. (2010) 83, 187–199.
Web of Science® Google Scholar
50 Buyantogtokh L., Azjargal E., Horoldagva B., Dorjsembe S., and Adiyanyam D., On the maximum size of stepwise irregular graphs, Applied Mathematics and Computations. (2020) 392, 125683, https://doi.org/10.1016/j.amc.2020.125683.
10.1016/j.amc.2020.125683
Web of Science® Google Scholar
51 Huang S., Li S., and Zhang M., On the extremal mostar indices of hexagonal chains, MATCH Community of Mathematics and Computational Chemistry. (2020) 84, 249–271.
Web of Science® Google Scholar

All articles

r(ξ_i\|ℵ)	r(ξ_i\|ξ₁)	r(ξ_i\|ξ₄)
r(ξ₁\|ℵ)	0	3
r(ξ₂\|ℵ)	1	2
r(ξ₃\|ℵ)	2	1
r(ξ₄\|ℵ)	3	0
r(ξ₅\|ℵ)	4	1
r(ξ₆\|ℵ)	3	2
r(ξ₇\|ℵ)	5	2
r(ξ₈\|ℵ)	6	3

r(ξ_i\|ℵ_f)	r(ξ_i\|ξ₁)	r(ξ_i\|ξ₂)	r(ξ_i\|ξ₄)
r(ξ₁\|ℵ_f)	0	1	3
r(ξ₂\|ℵ_f)	1	0	2
r(ξ₃\|ℵ_f)	2	1	1
r(ξ₄\|ℵ_f)	3	2	0
r(ξ₅\|ℵ_f)	4	3	1
r(ξ₆\|ℵ_f)	3	2	2
r(ξ₇\|ℵ_f)	5	4	2
r(ξ₈\|ℵ_f)	6	5	3

r(ξ_iξ_j\|ℵ_e)	r(ξ_iξ_j\|ξ₁)	r(ξ_iξ_j\|ξ₄)
r(ξ₁ξ₂\|ℵ_e)	0	2
r(ξ₂ξ₃\|ℵ_e)	1	1
r(ξ₃ξ₄\|ℵ_e)	2	0
r(ξ₃ξ₆\|ℵ_e)	2	1
r(ξ₄ξ₅\|ℵ_e)	3	0
r(ξ₅ξ₆\|ℵ_e)	3	1
r(ξ₅ξ₇\|ℵ_e)	4	1
r(ξ₇ξ₈\|ℵ_e)	5	2

r(ξ_i\|ℵ_m)	r(ξ_i\|ξ₁)	r(ξ_i\|ξ₄)	r(ξ_i\|ξ₈)
r(ξ₁\|ℵ_m)	0	3	6
r(ξ₂\|ℵ_m)	1	2	5
r(ξ₃\|ℵ_m)	2	1	4
r(ξ₄\|ℵ_m)	3	0	3
r(ξ₅\|ℵ_m)	4	1	2
r(ξ₆\|ℵ_m)	3	2	3
r(ξ₇\|ℵ_m)	5	2	1
r(ξ₈\|ℵ_m)	6	3	0
r(ξ_iξ_j\|ℵ_m)	r(ξ_iξ_j\|ξ₁)	r(ξ_iξ_j\|ξ₄)	r(ξ_iξ_j\|ξ₈)
r(ξ₁ξ₂\|ℵ_m)	0	2	5
r(ξ₂ξ₃\|ℵ_m)	1	1	4
r(ξ₃ξ₄\|ℵ_m)	2	0	3
r(ξ₃ξ₆\|ℵ_m)	2	1	3
r(ξ₄ξ₅\|ℵ_m)	3	0	2
r(ξ₅ξ₆\|ℵ_m)	3	1	2
r(ξ₅ξ₇\|ℵ_m)	4	1	1
r(ξ₇ξ₈\|ℵ_m)	5	2	0

Stepwise Irregular Graphs and Their Metric-Based Resolvability Parameters

Abstract

1. Introduction

2. Metric Dimension of a Stepwise Irregular Graph

3. Fault-Tolerant Metric Dimension of

4. Edge Metric Dimension of

5. Mixed Metric Dimension of

6. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Stepwise Irregular Graphs and Their Metric-Based Resolvability Parameters

Abstract

1. Introduction

2. Metric Dimension of a Stepwise Irregular Graph

3. Fault-Tolerant Metric Dimension of

4. Edge Metric Dimension of

5. Mixed Metric Dimension of

6. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Figures

References

Related

Information