Volume 2022, Issue 1 3665713

Research Article

Open Access

Yosida Approximation Iterative Methods for Split Monotone Variational Inclusion Problems

Mohammad Dilshad

orcid.org/0000-0003-3217-8295

Computational & Analytical Mathematics and Their Applications Research Group, Department of Mathematics, Faculty of Science, University of Tabuk, Tabuk, Saudi Arabia ut.edu.sa

Search for more papers by this author

Abdulrahman F. Aljohani,

Abdulrahman F. Aljohani

Computational & Analytical Mathematics and Their Applications Research Group, Department of Mathematics, Faculty of Science, University of Tabuk, Tabuk, Saudi Arabia ut.edu.sa

Search for more papers by this author

Mohammad Akram,

Mohammad Akram

orcid.org/0000-0003-1416-5351

Department of Mathematics, Faculty of Sciences, Islamic University of Madinah, Madinah, Saudi Arabia iu.edu.sa

Search for more papers by this author

Ahmed A. Khidir,

Corresponding Author

Ahmed A. Khidir

[email protected]

orcid.org/0000-0002-2053-6377

Computational & Analytical Mathematics and Their Applications Research Group, Department of Mathematics, Faculty of Science, University of Tabuk, Tabuk, Saudi Arabia ut.edu.sa

Faculty of Technology of Mathematical Sciences and Statistics, Alneelain University, Khartoum, Sudan neelain.edu.sd

Search for more papers by this author

Mohammad Dilshad,

Mohammad Dilshad

orcid.org/0000-0003-3217-8295

Computational & Analytical Mathematics and Their Applications Research Group, Department of Mathematics, Faculty of Science, University of Tabuk, Tabuk, Saudi Arabia ut.edu.sa

Search for more papers by this author

Abdulrahman F. Aljohani,

Abdulrahman F. Aljohani

Computational & Analytical Mathematics and Their Applications Research Group, Department of Mathematics, Faculty of Science, University of Tabuk, Tabuk, Saudi Arabia ut.edu.sa

Search for more papers by this author

Mohammad Akram,

Mohammad Akram

orcid.org/0000-0003-1416-5351

Department of Mathematics, Faculty of Sciences, Islamic University of Madinah, Madinah, Saudi Arabia iu.edu.sa

Search for more papers by this author

Ahmed A. Khidir,

Corresponding Author

Ahmed A. Khidir

[email protected]

orcid.org/0000-0002-2053-6377

Computational & Analytical Mathematics and Their Applications Research Group, Department of Mathematics, Faculty of Science, University of Tabuk, Tabuk, Saudi Arabia ut.edu.sa

Faculty of Technology of Mathematical Sciences and Statistics, Alneelain University, Khartoum, Sudan neelain.edu.sd

Search for more papers by this author

First published: 25 January 2022

https://doi.org/10.1155/2022/3665713

Citations: 3

Academic Editor: Nawab Hussain

Share a link

Email
Wechat
Bluesky

Abstract

In this paper, we present two iterative algorithms involving Yosida approximation operators for split monotone variational inclusion problems (S_pMVIP). We prove the weak and strong convergence of the proposed iterative algorithms to the solution of S_pMVIP in real Hilbert spaces. Our algorithms are based on Yosida approximation operators of monotone mappings such that the step size does not require the precalculation of the operator norm. To show the reliability and accuracy of the proposed algorithms, a numerical example is also constructed.

1. Introduction

Variational inequality which was brought into existence by Hartman and Stampacchia [1] plays an important role as mathematical model in physics, economics, optimization, networking structural analysis, and medical images. In 1994, Censor and Elfving [2] first presented the split feasibility problems (in short, SFP) for modeling in medical image reconstruction. From the last two decades, SFP has been implemented widely in intensity-modulation therapy treatment planning and other branches of applied sciences (see, e.g., [3–5]). Censor et al. [6] combined the VIP and SFP and presented a new type of variational inequality problem called split variational inequality problem (in short, SVIP) as follows:

(1)

where C and Q are closed, convex subsets of Hilbert spaces H₁ and H₂, respectively, A : H₁⟶H₂ is a bounded linear operator, V₁ : H₁⟶H₁ and V₂ : H₂⟶H₂ are two operators, VIP(V₁; C) = {y ∈ C : 〈V₁(y), x − y〉 ≥ 0, ∀x ∈ C} and VIP(V₂; Q) = {z ∈ Q : 〈g(z), x − z〉 ≥ 0, ∀x ∈ Q}.

Moudafi [7] generalized SVIP into split monotone variational inclusion problem (in short, S_pMVIP) as follows:

(2)

where

and

are set-valued mappings on Hilbert spaces H₁ and H₂, respectively, VI(V₁, G₁; H₁) = {y ∈ H₁ : 0 ∈ V₁(y) + G₁(y)} and VI(V₂, G₂; H₂) = {z ∈ H₂ : 0 ∈ V₂(z) + G₂(z)}.

Moudafi [7] formulated the following iterative algorithm to find the solution of S_pMVIP. Let λ > 0, select an arbitrary starting point x₀ ∈ H₁, and compute

(3)

where A^∗ is an adjoint operator of A, γ ∈ (0, 1/L) with L being a spectral radius of operator A^∗A,

and

Let N_C(x) = {z ∈ H₁ : 〈z, y − x〉 ≤ 0, ∀y ∈ C} and N_Q(x) = {w ∈ H₂ : 〈w, y − x〉 ≤ 0, ∀ y ∈ Q} be normal cones to the closed and convex sets C and Q, respectively. If G₁ = N_C and G₂ = N_Q, then S_pMVIP reduces to S_pVIP. If V₁ = V₂ = 0, then S_pMVIP reduces to the split variational inclusion problem (in short, S_pVIP) for set-valued maximal monotone mappings, introduced and studied by Byrne et al. [8]:

(4)

where VI(G₁; H₁) = {y ∈ H₁ : 0 ∈ G₁(y)} and VI(G₂; H₂) = {z ∈ H₂ : 0 ∈ G₂(z)}, G₁, G₂ are the same as in (2). We denote the solution set of S_pVIP by Δ. Moreover, Byrne et al. [8] presented the following iterative algorithm to find the solution of S_pVIP. Let λ > 0, and select a starting point x₀ ∈ H₁. Then, compute

(5)

where A^∗ is the adjoint operator of A, L = ‖A^∗A‖, γ ∈ (0, 2/L) and

are the resolvents of monotone mappings G₁, G₂, respectively. It can be easily seen that x^∗ solves S_pVIP if and only if

. Kazmi and Rizwi [9] proposed the following iterative method for approximating the common solutions of S_pVIP and fixed point problem of a nonexpansive mapping:

(6)

where f is a contraction and S is nonexpansive mapping. Later, Sitthithakerngkiet et al. [10] studied the common solutions of S_pVIP and a fixed point of an infinite family of nonexpansive mappings and introduced the following iterative method:

(7)

where u ∈ H₁ is a given point and W_n is W-mapping which is generated by an infinite family of nonexpansive mappings. Similar results related to S_pVIP can be found in [11–17].

The common figure among the above-explained iterative methods is that they used the resolvent of associated monotone mappings; secondly, the step size depends on the operator norm ‖A^∗A‖. To avoid this obstacle, self-adaptive step size iterative algorithms have been introduced (see, for example, [18–24]). Lopez et al. [20] introduced a relaxed method for solving split feasibility problem with self-adaptive step size. Recently, Dilshad et al. [25] proposed two iterative algorithms to solve S_pVIP in which the precalculation of the operator norm ‖A^∗A‖ is not required. They studied the weak and strong convergence of the proposed methods to approximate the solution of S_pVIP with the step size , which do not depend upon the precalculated operator norm.

The resolvent of a maximal monotone operator G is defined as , where λ is a positive real number. A resolvent operator of maximal monotone operator is single valued and firmly nonexpansive. Due to the fact that the zeros of maximal monotone operator are the fixed point sets of resolvent operator, the resolvent associated with a set-valued maximal monotone operator plays an important role to find the zeros of monotone operators. Following Byrne’s iterative method (5), which is mainly based on the resolvents of monotone mappings, many researchers introduced and studied various iterative methods for S_pVIP (see, for example, [7–9, 18, 25, 26] and references therein).

Yosida approximation operator for a monotone mapping G and parameter λ > 0 is defined as . It is well known that set-valued monotone operator can be regularized into a single-valued monotone operator by the process known as the Yosida approximation. Yosida approximation is a tool to solve a variational inclusion problem using nonexpansive resolvent operator and has been used to solve various variational inclusions and system of variational inclusions in linear and nonlinear spaces (see, for example, [18, 25–30]).

Due to the fact that the zero of Yosida approximation operator associated with monotone operator G is the zero of inclusion problem 0 ∈ G(x) and inspired by the work of Moudafi, Byrne, Kazmi, and Dilshad et al., our motive is to propose two iterative methods to solve S_pMVIP. The rest of the paper is organized as follows.

The next section contains some fundamental results and preliminaries. In Section 3, we describe two iterative algorithms using Yosida approximation of monotone mappings G₁ and G₂. Section 4 is devoted to the study of weak and strong convergence of the proposed iterative methods to the solution of S_pMVIP. In the last section, we give a numerical example in support of our main results and show the convergence of sequence obtained from the proposed algorithm to the solution of S_pMVIP.

2. Preliminaries

Let H be a real Hilbert space endowed with norm ‖·‖ and inner product 〈·, ·〉. The strong and weak convergence of a sequence {x_n} to x is denoted by x_n⟶x and x_n⇀x, respectively. The operator T : H⟶H is said to be a contraction if ∀x, y ∈ H, ‖T(x) − T(y)‖ ≤ κ‖x − y‖, κ ∈ (0, 1); if κ = 1, then T is called nonexpansive and firmly nonexpansive if ∀x, y ∈ H, ‖T(x) − T(y)‖² ≤ 〈x − y, Tx − Ty〉; T is called τ-inverse strongly monotone if there exists τ > 0 such that 〈T(x − T(y), x − y〉 ≥ τ‖T(x) − T(y)‖².

For some x ∈ H₁, there exists a unique nearest point in C denoted by P_Cx such that

(8)

P_Cx is called the projection of x onto C ⊂ H, which satisfies

(9)

Moreover, P_Cx is also characterized by the fact that

(10)

In Hilbert spaces, the following equality and inequality hold for all x, y, z ∈ H, α, β, γ ∈ [0, 1] such that α + β + γ = 1

(11)

(12)

Let G : H⟶2^H be a set-valued operator. The graph of G is defined by {(x, y): y ∈ G(x)}, and inverse of G is denoted by G⁻¹ = {(y, x): y ∈ G(x)}. A set-valued mapping G is said to be monotone if 〈u − v, x − y〉 ≥ 0, for all u ∈ G(x), v ∈ G(y). A monotone operator G is called a maximal monotone if there exists no other monotone operator such that its graph properly contains the graph of G.

Lemma 1 (see [31].)If {a_n} is a sequence of nonnegative real numbers such that

(13)

where {β_n} is a sequence in (0, 1) and {δ_n} is a sequence in ℝ such that

(i)
(ii)
or

then

Lemma 2 (see [32].)Let H be a Hilbert space. A mapping F : H⟶H is τ -inverse strongly monotone if and only if I − τF is firmly nonexpansive, for τ > 0.

Lemma 3 (see [33].)Let H be a Hilbert space and {x_n} be a bounded sequence in H. Assume there exists a nonempty subset C ⊂ H satisfying the properties

(i)
lim_n⟶∞‖x_n − z‖ exists for every z ∈ C
(ii)
ω_w(x_n) ⊂ C

Then, there exists x^∗ ∈ C such that {x_n} converges weakly to x^∗.

Lemma 4 (see [34].)Let Γ_n be a sequence of real numbers that does not decrease at infinity in the sense that there exists a subsequence of Γ_n such that for all k ≥ 0. Also, consider the sequence of integers defined by

(14)

Then, is a nondecreasing sequence verifying lim_n⟶∞σ(n) = ∞ and for all n ≥ n₀,

(15)

3. Yosida Approximation Iterative Methods

Let V₁ : H₁⟶H₁, V₂ : H₂⟶H₂ be single-valued monotone mappings and be set-valued mappings such that and are set-valued maximal monotone mappings; , and , are the resolvents and Yosida approximation operators of V₁ + G₁ and V₂ + G₂, respectively. We propose the following iterative methods to approximate the solution of S_pMVIP.

Algorithm 1. For an arbitrary x₀, compute the n + 1^th iteration as follows:

(16)

where γ_n and μ_n are defined as

(17)

(18)

where λ₁ > 0, λ₂ > 0 and θ = min{2λ₁, 2λ₂} such that τ_n ∈ (0, θ).

Algorithm 2. For an arbitrary x₀, compute the n + 1^th iteration as follows:

(19)

where γ_n and μ_n are defined as

(20)

where α_n, β_n ∈ (0, 1), λ₁ > 0, λ₂ > 0, and θ = min{2λ₁, 2λ₂} such that τ_n ∈ (0, θ).

4. Main Results

We assume that the problem S_pMVIP is consistent and the solution set is denoted by Δ.

First, we prove following lemmas, which are used in the proof of our main results.

Lemma 5. Let V₁ : H₁⟶H₁ be single-valued monotone mappings and be set-valued mappings such that be set-valued maximal monotone mapping. If and are the resolvent and Yosida approximation operators of V₁ + G₁, respectively, then for λ₁ > 0, following are equivalent:

(i)
x^∗ ∈ H₁ is the solution of
(ii)
(iii)

Proof. The proof is trivial which is an immediate consequence of definitions of resolvent and Yosida approximation operator of maximal monotone mapping V₁ + G₁.☐

Theorem 6. Let H₁, H₂ be real Hilbert spaces; V₁ : H₁⟶H₁, V₂ : H₂⟶H₂ be single-valued monotone mappings, , be set-valued maximal monotone mappings such that V₁ + G₁ and V₂ + G₂ are maximal monotone, and A : H₁⟶H₂ be a bounded linear operator. Assume that θ = min{2λ₁, 2λ₂} such that infτ_n(θ − τ_n) > 0. Then, the sequence {x_n} generated by Algorithm 1 converges weakly to a point z ∈ Δ.

Proof. Let z ∈ Δ. Since the Yosida approximation operator is λ₁-inverse strongly monotone, for λ₁ > 0, then by Algorithm 1 and (12), we have

(21)

Now, using (17), we estimate that

(22)

From (21) and (22), we get

(23)

Since is λ₂-inverse strongly monotone and using (12), we estimate

(24)

By (18), it turns out that

(25)

It follows from (24) and (25) that

(26)

Combining (23) and (26), we get

(27)

(28)

which implies that {x_n} is Fejér monotone with respect to Δ and hence bounded, which assures that

exists for all z ∈ Δ. Keeping in mind that θ = min{2λ₁, 2λ₂}, from (27), we have

(29)

Due to the assumption that infτ_n(θ − τ_n) > 0 and the properties of convergent series, we conclude that

(30)

Hence, there exist constants K₁ and K₂ such that

(31)

By Algorithm 1 and (30), we get

(32)

Let{x^⋆} ∈ ω_w(x_n)andbe a subsequence of{x_n}that converges weakly to{x^⋆}, which implies thatandalso converge to{x^⋆}. Recall that is λ₁-inverse strongly monotone and converges to x^⋆, and using (30), we get

(33)

Taking limit k⟶∞, we obtain

Replacing by , by with the same arguments, we get This completes the proof.☐

Theorem 7. Let H₁, H₂ be real Hilbert spaces; V₁ : H₁⟶H₁, V₂ : H₂⟶H₂ be single-valued monotone mappings, , be set-valued maximal monotone mappings such that V₁ + G₁ and V₂ + G₂ are maximal monotone, and A : H₁⟶H₂ be a bounded linear operator. If {α_n}, {β_n} are real sequences in (0, 1) and θ = min{2λ₁, 2λ₂} such that τ_n ∈ (0, θ) and

(34)

then the sequence {x_n} generated by Algorithm 2 converges strongly to z = P_Δ(0).

Proof. Let z = P_Δ(0); then, from (23) and (26) of the proof of Theorem 6, we have

(35)

(36)

Since τ_n ≤ min{2λ₁, 2λ₂}, we get ∥v_n − z∥≤∥u_n − z∥≤∥x_n − z∥. From Algorithm 2, we have

(37)

which implies that the sequence {x_n} is bounded and hence, the sequences {u_n},{v_n},

and

are also bounded. Now,

(38)

Combining (35), (36), and (38), we obtain

(39)

We discuss the two possible cases.

Case 1. If the sequence{‖x_n − z‖} is nonincreasing, then there exists a number k ≥ 0 such that ‖x_n+1 − z‖ ≤ ‖x_n − z‖, for each n ≥ k. Then, exists and hence, . Thus, it follows from (39) that

(40)

From (40), we conclude that and We observe from Algorithm 2 that x_n+1 − u_n = α_n(v_n − u_n) + γ_nu_n⟶0; thus,

(41)

This shows that the sequence {x_n} is asymptotically regular. By Theorem 6, we have that ω_w(x_n) ⊂ Δ. Settingz_n = (1 − α_n)u_n + α_nv_nand rewritingx_n+1 = (1 − β_n)z_n + α_nβ_n(v_n − u_n), we have

(42)

From (42) and Algorithm 2, we get

(43)

(44)

where a_n = ‖x_n − z‖, b_n = 2β_n{α_n〈v_n − u_n, x_n+1 − z〉 + 〈−z, x_n+1 − z〉}.

Since ω_w(x_n) ⊂ Δ and z = P_Δ(0), then using (40), we get

(45)

Thus, by Lemma 1, we obtain x_n⟶z.

Case 2. If the sequence {‖x_n − z‖} is not nonincreasing, we can select a subsequence of {‖x_n − z‖} such that for all k ∈ ℕ. In this case, we define a subsequence of positive integers σ(n)⟶∞ with the properties

(46)

If ‖x_n+1 − z‖ > ‖x_n − z‖ for some n ≥ 0, then it follows from (39) that

(47)

Replacing n by σ(n) and taking limit n⟶∞, we get the following relation for the subsequences {x_σ(n)}, {u_σ(n)}, and {v_σ(n)}:

(48)

Thus, we have ‖x_{σ(n + 1)} − x_σ(n)‖⟶0, as n⟶∞ and ω_w(x_σ(n)) ⊂ Δ. It is remaining to show that x_n⟶z.

Replacing n by σ(n) in (47), using ‖x_σ(n) − z‖ < ‖x_σ(n)+1 − z‖ and boundedness of ‖x_n − z‖, we have

(49)

Since z = P_Δ(0), ω(x_σ(n)) ⊂ Δ with using ‖v_σ(n) − u_σ(n)‖⟶0 and ‖x_σ(n)+1 − x_σ(n)‖⟶0, we have

(50)

From (49) and (52), we conclude that x_σ(n)⟶z and

(51)

that is, x_n⟶z. This complete the proof.☐

For τ_n = 1, we have the following result for the convergence of Algorithm 2.

Corollary 8. Let H₁, H₂, V₁, V₂, G₁, G₂, and A, A^∗ be the same as defined in Theorem 7. If {α_n}, {β_n} are sequences in (0, 1) and assuming that λ₁ > 1/2 and λ₂ > 1/2 satisfying

(52)

then the sequence {x_n} generated by Algorithm 2 (with τ_n = 1) converges strongly to z = P_Δ(0).

For β_n = 0, we have the following corollary for the convergence of Algorithm 2.

Corollary 9. Let H₁, H₂, V₁, V₂, G₁, G₂, and A, A^∗ be the same as defined in Theorem 7. If {α_n} is a sequence in (0, 1) and assuming that θ = min{2λ₁, 2λ₂} such that τ_n ∈ (0, θ) and

(53)

then the sequence {x_n} generated by the iterative method

(54)

where γ_n and μ_n are defined as in Algorithm 2 (with τ_n = 1), converges strongly to z ∈ Δ.

For τ_n = 1 and β_n = 0, we have the following corollary for the convergence of Algorithm 2.

Corollary 10. Let H₁, H₂, V₁, V₂, G₁, G₂, and A, A^∗ be the same as defined in Theorem 7. If {α_n} be a sequence in (0, 1) and assuming that

(55)

then the sequence {x_n} generated by the iterative method

(56)

where γ_n and μ_n are defined in Algorithm 2 (with τ_n = 1), converges strongly to z ∈ Δ.

5. Numerical Example

Let H₁ = H₂ = ℝ and V₁ = V₂ = 0; G₁ : ℝ⟶ℝ, G₂ : ℝ⟶ℝ are defined as G₁(x) = 2x + 3 and G₂(x) = 2(x + 1), respectively. One can easily check that G₁ and G₂ are monotone and the Yosida approximation operator of G₁ and G₂ for λ₁ = λ₂ = 1 is computed as

(57)

Let A : H₁⟶H₂ be defined as A(x) = 2x/3, then, for τ_n = (2 − (e^1/n/2)) ∈ (0, 2), we compute the step size as

(58)

Then, for α_n = (2 − (e^1/n/3)) and two different values of (β_n) (for example, β_n = 1/(n + 5) and β_n = 1/(n + 10)) and for arbitrary x₀ (for example, x₀ = −2 and x₀ = 0), we compute the iterative sequences from Algorithm 2 as follows:

(59)

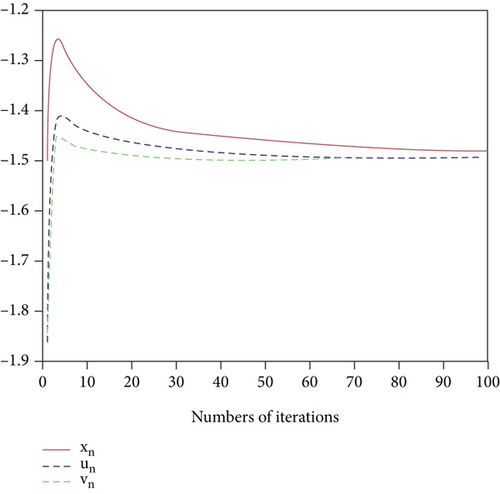
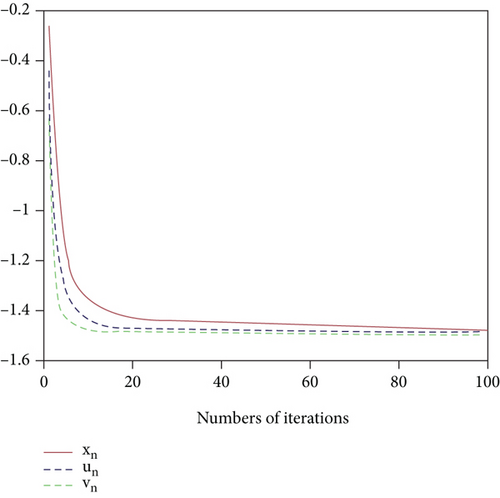
In Figures 1 and 2, we show that the obtained sequences {u_n}, {v_n}, and {x_n} converge to z = −(3/2) for randomly selected arbitrary values of x₀ = −2 and 0.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Convergence of iterative sequences {u_n}, {v_n}, and {x_n} to z = −1.5 for β_n = 1/n + 5 and x₀ = −2.

6. Conclusions

We have proposed two iterative algorithms for S_pMVIP which are mainly based on the Yosida approximation operators. Since the zero of Yosida approximation of monotone mapping V₁ + G₁ is the solution of , we used the Yosida approximations of monotone mappings V₁ + G₁ and V₂ + G₂ to solve S_pMVIP. We proved the weak and strong convergence of the composed iterative algorithms to investigate the solution of S_pMVIP under some suitable assumptions such that the estimation of step size does not require any prior calculation of the operator norm ‖A^∗A‖. To show the accuracy and efficiency of our algorithms, we have present a numerical example and showed the convergence using different parameters.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

We claim that this work is a theoretical result, and there is no available data source.

References

1 Hartman P. and Stampacchia G., On some nonlinear elliptic differential functional equations, Acta Mathematica. (1956) 115, 271–310.
10.1007/BF02392210
Google Scholar
2 Censor Y. and Elfving T., A multiprojection algorithm using Bregman projections in a product space, Numerical Algorithms. (1994) 8, no. 2, 221–239, https://doi.org/10.1007/BF02142692, 2-s2.0-0000424337.
10.1007/BF02142692
Google Scholar
3 Censor Y., Bortfeld T., Martin B., and Trofimov A., A unified approach for inversion problems in intensity-modulated radiation therapy, Physics in Medicine and Biology. (2006) 51, no. 10, 2353–2365, https://doi.org/10.1088/0031-9155/51/10/001, 2-s2.0-33646480792.
10.1088/0031-9155/51/10/001
PubMed Web of Science® Google Scholar
4 Censor Y., Elfving T., Kopf N., and Bortfeld T., The multiple-sets split feasibility problem and its applications for inverse problems, Inverse Problems. (2005) 21, no. 6, 2071–2084, https://doi.org/10.1088/0266-5611/21/6/017, 2-s2.0-28544451131.
10.1088/0266-5611/21/6/017
Web of Science® Google Scholar
5 Censor Y., Motova X. A., and Segal A., Perturbed projections and subgradient projections for the multiple-sets split feasibility problem, Journal of Mathematical Analysis and Applications. (2007) 327, no. 2, 1244–1256, https://doi.org/10.1016/j.jmaa.2006.05.010, 2-s2.0-33751021369.
10.1016/j.jmaa.2006.05.010
Web of Science® Google Scholar
6 Censor Y., Gibali A., and Reich S., The Split Variational Inequality Problem, 2010, The Technion Institute of Technology, Haifa, https://arxiv.org/abs/1009.3780.
Google Scholar
7 Moudafi A., Split monotone variational inclusions, Journal of Optimization Theory and Applications. (2011) 150, 275–283.
10.1007/s10957-011-9814-6
Web of Science® Google Scholar
8 Byrne C., Censor Y., Gibali A., and Reich S., Weak and strong convergence of algorithms for split common null point problem, Journal of Nonlinear and Convex Analysis. (2012) 13, 759–775.
Web of Science® Google Scholar
9 Kazmi K. R. and Rizvi S. H., An iterative method for split variational inclusion problem and fixed point problem for a nonexpansive mapping, Optimization Letters. (2014) 8, no. 3, 1113–1124, https://doi.org/10.1007/s11590-013-0629-2, 2-s2.0-84894615265.
10.1007/s11590-013-0629-2
Web of Science® Google Scholar
10 Sitthithakerngkiet K., Deepho J., Martinez-Moreno J., and Kumam P., Convergence analysis of a general iterative algorithm for finding a common solution of split variational inclusion and optimization problems, Numerical Algorithms. (2018) 79, no. 3, 801–824, https://doi.org/10.1007/s11075-017-0462-2, 2-s2.0-85040001946.
10.1007/s11075-017-0462-2
Web of Science® Google Scholar
11 Abbas H. A., Aremu K. O., Jolaoso L. O., and Mewomo O. T., An inertial forward-backward splitting method for approximating solutions of certain optimization problems, Journal of Nonlinear Functional Analysis. (2020) 2020, article 6.
Google Scholar
12 Bello Cruz J. Y. and Shehu Y., An iterative method for split inclusion problems without prior knowledge of operator norms, Journal of Fixed Point Theory and Applications. (2017) 19, no. 3, 2017–2036, https://doi.org/10.1007/s11784-016-0387-8, 2-s2.0-85000963977.
10.1007/s11784-016-0387-8
Web of Science® Google Scholar
13 Ceng L. C., A subgradient extragradient method for bilevel equlibrium problems with the constraints of variational inclusion systems and fixed point problems, Communications in Optimization Theory. (2021) 2021, article 4.
Google Scholar
14 Liu L., Cho S. Y., and Yao J. C., Convergence analysis of an inertial T-seng’s extragradient algorithm for solving pseudomonotone variational inequalities and applications, Journal of Nonlinear and Variational Analysis. (2021) 5, 627–644.
Web of Science® Google Scholar
15 Suantai S., Shehu Y., and Cholamjiak P., Nonlinear iterative methods for solving the split common null point problem in Banach spaces, Optimization Methods and Software. (2019) 34, no. 4, 853–874, https://doi.org/10.1080/10556788.2018.1472257, 2-s2.0-85047120584.
10.1080/10556788.2018.1472257
Web of Science® Google Scholar
16 Takahashi W., The split common null point problem in Banach spaces, Archiv der Mathematik. (2015) 104, no. 4, 357–365, https://doi.org/10.1007/s00013-015-0738-5, 2-s2.0-84931263167.
10.1007/s00013-015-0738-5
Web of Science® Google Scholar
17 Takahashi S. and Takahashi W., The split common null point problem and the shrinking projection method in Banach spaces, Optimization. (2016) 65, no. 2, 281–287, https://doi.org/10.1080/02331934.2015.1020943, 2-s2.0-84953349716.
10.1080/02331934.2015.1020943
Web of Science® Google Scholar
18 Dilshad M., Siddiqi A. H., Ahmad R., and Khan F. A., P. Manchanda, R. Lozi, and A. Siddiqi, An iterative algorithm for a common solution of a split variational inclusion problem and fixed point problem for non-expansive semigroup mappings, Industrial Mathematics and Complex Systems. Industrial and Applied Mathematics, 2017, Springer, Singapore.
10.1007/978-981-10-3758-0_15
Google Scholar
19 Gibali A., Mai D. T., and Nguyen T. V., A new relaxed CQ algorithm for solving split feasibility problems in Hilbert spaces and its applications, Journal of Industrial & Management Optimization. (2018) 2018, 1–25.
Google Scholar
20 Lopez G., Martin-Marquez V., and Xu H. K., Solving the split feasibility problem without prior knowledge of matrix norms, Inverse Problems. (2012) 28, no. 8, article 085004, https://doi.org/10.1088/0266-5611/28/8/085004, 2-s2.0-84864409043.
10.1088/0266-5611/28/8/085004
Web of Science® Google Scholar
21 Moudafi A. and Gibali A., l₁-l₂ regularization of split feasibility problems, Numerical Algorithms. (2018) 78, no. 3, 739–757, https://doi.org/10.1007/s11075-017-0398-6, 2-s2.0-85027684751.
10.1007/s11075-017-0398-6
Web of Science® Google Scholar
22 Moudafi A. and Thakur B. S., Solving proximal split feasibilty problem without prior knowledge of matrix norms, Optimization Letters. (2014) 8, no. 7, 2099–2110, https://doi.org/10.1007/s11590-013-0708-4, 2-s2.0-84907591580.
10.1007/s11590-013-0708-4
Web of Science® Google Scholar
23 Shehu Y. and Iyiola O. S., Convergence analysis for the proximal split feasibility problem using an inertial extrapolation term method, Journal of Fixed Point Theory and Applications. (2017) 19, no. 4, 2483–2510, https://doi.org/10.1007/s11784-017-0435-z, 2-s2.0-85018415025.
10.1007/s11784-017-0435-z
Web of Science® Google Scholar
24 Tang Y. and Gibali A., New self-adaptive step size algorithms for solving split variational inclusion problems and its applications, Numerical Algorithms. (2020) 83, no. 1, 305–331, https://doi.org/10.1007/s11075-019-00683-0, 2-s2.0-85063350968.
10.1007/s11075-019-00683-0
Web of Science® Google Scholar
25 Dilshad M., Akram M., and Ahmad I., Algorithms for split common null point problem without pre-existing estimation of operator norm, Journal of Mathematical Inequalities. (2020) 14, no. 4, 1151–1163, https://doi.org/10.7163/jmi-2020-14-75.
10.7153/jmi-2020-14-75
Web of Science® Google Scholar
26 Dilshad M., Aljohani A. F., and Akram M., Iterative scheme for split variational inclusion and a fixed-point problem of a finite collection of nonexpansive mappings, Journal of Function Spaces. (2020) 2020, 10, 3567648, https://doi.org/10.1155/2020/3567648.
10.1155/2020/3567648
Web of Science® Google Scholar
27 Ahmad R., Ishtyak M., Rahaman M., and Ahmad I., Graph convergence and generalized Yosida approximation operator with an application, The Mathematical Scientist. (2017) 11, no. 2017, 155–163, https://doi.org/10.1007/s40096-017-0221-5.
10.1007/s40096-017-0221-5
Google Scholar
28 Akram M., Chen J. W., and Dilshad M., Generalized Yosida approximation operator with an application to a system of Yosida inclusions, Journal of Nonlinear Functional Analysis. (2018) 2018, article 17, 1–20.
Google Scholar
29 Alansari M., Dilshad M., and Akram M., Remark on the Yosida approximation iterative technique for split monotone Yosida variational inclusions, Computational and Applied Mathematics. (2020) 39, https://doi.org/10.1007/s40314-020-01231-6.
10.1007/s40314-020-01231-6
Web of Science® Google Scholar
30 Dilshad M., Solving Yosida inclusion problem in Hadamard manifold, Arabian Journal of Mathematics. (2020) 9, no. 2, 357–366, https://doi.org/10.1007/s40065-019-0261-9.
10.1007/s40065-019-0261-9
Web of Science® Google Scholar
31 Xu H. K., Iterative algorithms for nonlinear operators, Journal of the London Mathematical Society. (2002) 66, no. 1, 240–256, https://doi.org/10.1112/S0024610702003332, 2-s2.0-0036692463.
10.1112/S0024610702003332
Web of Science® Google Scholar
32 Bauschke H. H. and Combettes P. L., Convex Analysis and Monotone Operator Theory in Hilbert Space, 2011, Springer, Berlin.
10.1007/978-1-4419-9467-7
Google Scholar
33 Opial Z., Weak covergence of the sequence of successive approximations of nonexpansive mappings, Bulletin of the American Mathematical Society. (1976) 73, 591–597.
10.1090/S0002-9904-1967-11761-0
Google Scholar
34 Mainge P. E., Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization, Set-Valued Analysis. (2008) 16, no. 7-8, 899–912, https://doi.org/10.1007/s11228-008-0102-z, 2-s2.0-58149142982.
10.1007/s11228-008-0102-z
Web of Science® Google Scholar

Citing Literature

All articles

Yosida Approximation Iterative Methods for Split Monotone Variational Inclusion Problems

Abstract

1. Introduction

2. Preliminaries

3. Yosida Approximation Iterative Methods

4. Main Results

5. Numerical Example

6. Conclusions

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Yosida Approximation Iterative Methods for Split Monotone Variational Inclusion Problems

Abstract

1. Introduction

2. Preliminaries

3. Yosida Approximation Iterative Methods

4. Main Results

5. Numerical Example

6. Conclusions

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information