Volume 2022, Issue 1 3340057

Research Article

Open Access

[Retracted] Eccentricity-Based Topological Descriptors of First Type of Hex-Derived Network

Retraction(s) for this article

Usman Babar,

Usman Babar

Department of Mathematics, Government College University, Lahore, Pakistan gcu.edu.pk

Search for more papers by this author

Asim Naseem,

Asim Naseem

Department of Mathematics, Government College University, Lahore, Pakistan gcu.edu.pk

Search for more papers by this author

Hani Shaker,

Hani Shaker

orcid.org/0000-0003-2500-2179

Department of Mathematics, COMSATS University Islamabad, Lahore Campus, Lahore, Pakistan comsats.edu.pk

Search for more papers by this author

Mian Muhammad Zobair,

Corresponding Author

Mian Muhammad Zobair

[email protected]

orcid.org/0000-0002-5749-0608

Department of Mathematics, National University of Sciences and Technology, Islamabad, Pakistan nust.edu.pk

Search for more papers by this author

Haidar Ali,

Haidar Ali

orcid.org/0000-0002-9815-7158

Department of Mathematics, Riphah International University, Faisalabad Campus, Pakistan riphah.edu.pk

Search for more papers by this author

Usman Babar,

Usman Babar

Department of Mathematics, Government College University, Lahore, Pakistan gcu.edu.pk

Search for more papers by this author

Asim Naseem,

Asim Naseem

Department of Mathematics, Government College University, Lahore, Pakistan gcu.edu.pk

Search for more papers by this author

Hani Shaker,

Hani Shaker

orcid.org/0000-0003-2500-2179

Department of Mathematics, COMSATS University Islamabad, Lahore Campus, Lahore, Pakistan comsats.edu.pk

Search for more papers by this author

Mian Muhammad Zobair,

Corresponding Author

Mian Muhammad Zobair

[email protected]

orcid.org/0000-0002-5749-0608

Department of Mathematics, National University of Sciences and Technology, Islamabad, Pakistan nust.edu.pk

Search for more papers by this author

Haidar Ali,

Haidar Ali

orcid.org/0000-0002-9815-7158

Department of Mathematics, Riphah International University, Faisalabad Campus, Pakistan riphah.edu.pk

Search for more papers by this author

First published: 09 May 2022

https://doi.org/10.1155/2022/3340057

Citations: 1

Academic Editor: Andrea Penoni

Share a link

Email
Wechat
Bluesky

Abstract

Graph theory has made significant progress in mathematical chemistry and has gained a lot of traction among scientists due to its numerous applications in mathematical chemistry. The numerical invariants of a molecular structure are known as molecular topological descriptors, and they are highly effective for predicting their bioactivity. A number of such indices are examined and applied in pharmaceutical research, chemistry, medication development, and other fields. The eccentricity-based Zagreb indices, total eccentricity, geometric arithmetic (GA₄), atom-bond connectivity (ABC₅), and average eccentricity indices of a hex-derived network of first type are computed in this article. We also provide analytically closed formulas for these descriptors, which may be used to investigate the underlying topologies.

1. Introduction

Graph theory is a vital organ of scientific tools to study the mechanism of different molecular structures and networks without going into the labor of laboratory work. It provides valid reasons to adopt the techniques of topological indices to cater for the difficult molecular structures which might not be studied by any other technique. It has several applications in social sciences, computer science, neural network, genomics, molecular biology, and chemistry. Chemical graph theory is a hot topic among researchers and allows us to estimate some physicochemical features of chemical substances just by looking at their visual representations [1, 2]. A molecular frame can be described by covalent bonds which connects the atoms. In case of graph theory, atoms are vertices and these covalent bonds are edges between atoms. Information sciences, mathematics, and chemistry are combined in cheminformatics. This is a new research field that attracts the attention of researchers. Chemical graph theory is a branch of chemistry that uses graph theory to represent chemical substances mathematically. There has been a lot of study on this topic during the last few decades. The importance of graph theory in chemistry is demonstrated by few references [3, 4].

Consider a graph G = (V, E), where V and E are nonempty sets of vertices and edges. Chemical graph theory uses graph theory to model molecular phenomena mathematically, which is useful for studying molecular structures. Pharmaceutical researchers study and apply a wide range of TI’s in theoretical chemistry. There are several TI’s for graph in chemical graph theory that are useful in the study of chemical compounds. This approach has had a significant impact on chemical science advancement.

d(i, j) is distance between i and j and can be defined as the length of shortest path in G if i, j ∈ V(G). Eccentricity is distance between vertex i and the farthest vertex in the graph.

In a numerical format,

(1)

Farooq and Malik [5] proposed the total eccentricity index as

(2)

where is the eccentricity of the vertex s.

Average eccentricity of a graph

(3)

Many researchers like Hinz, Ilic, Dankelmann, and Tang have worked on average eccentricity index, demonstrated by few references [6–9].

Ghorbani and Khaki [10] proposed the geometric-arithmetic index based on eccentricity, as

(4)

Additional details on the average eccentricity and eccentricity-based geometric-arithmetic indices can be seen in [11]. Farahani [12] proposed the eccentricity version of the ABC index, expressed as

(5)

Imran et al. computed ABC₅ and GA₄ indices of copper oxide in [13], and Gao et al. [14] shows the results of linear polycene parallelogram benzenoid.

Some modified eccentric versions of Zagreb indices mentioned in [15, 16] are

(6)

Second and third eccentric versions of Zagreb indices are as follows, respectively:

(7)

(8)

2. Applications and Motivation

Because degree-based TI’s are beneficial for analyzing the chemical properties of various molecule structures. As a result of this inspiration, we concentrate on eccentricity-based TI’s. Topological index based on eccentricity is a useful method to predict physicochemical and toxicological properties of a substance [17–19]. Recent activity on hex-derived networks can be studied in [20–22].

Zobair et al. studied TI’s of carbon nanocones as well as TI’s of different families of David-derived networks in [23, 24]. One index, known as the ABC index, has extremely good results for determining the stability and strain energy of hydrocarbons. [25–28]. The GA index has much stronger prediction potential than the Randic connectivity index [29–31]. Within specified approximate formulas, the Zagreb indices used for computation of total Π-electron energy of the molecules [32].

3. Hex-Derived Network

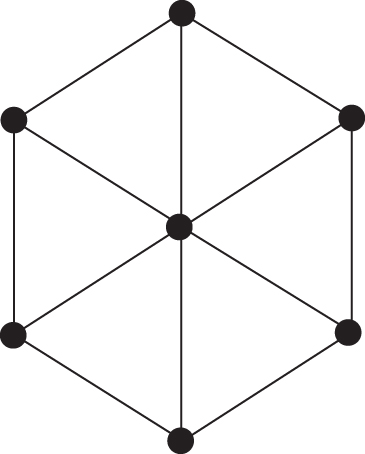
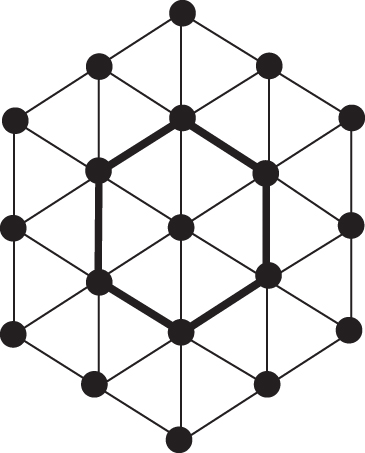
Hexagonal structures had observed a lot of applications in different fields including chemical engineering, transportation, mechanical engineering, architecture, nanofabrication, and recently bioinformatics. The greatest challenge in this research direction is to comprehend the unique characteristics of hex-derived structures, relying on their structures, scales, and the materials used to allow the minimization of the materials to get minimum weight and maximum strength. Hex-derived networks are under consideration in the present research article which are further extracted from hexagonal structures. Figure 1(a)shows a hex-derived network for two dimension, Figure 1(c) demonstrates thatHX(2)has faces, and Figure 2 shows an example of HDN₁(3) [33].

Details are in the caption following the image — Open in figure viewer PowerPoint

We adopt the combinatorial computing approach, the vertex and edge partitioning technique, tools for graphs, analytic methods, degree counting, and the sum of degrees of neighbours techniques to compute our results [34, 35]. Furthermore, for numerical calculations and verifications, we use MATLAB software. We also plot mathematical conclusions using the Maple software.

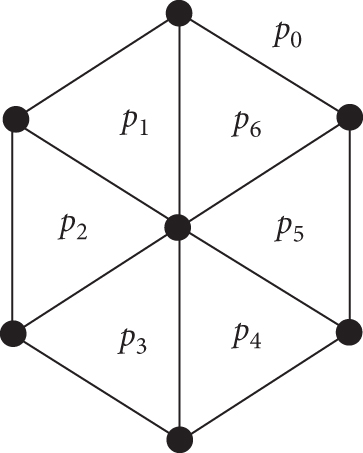
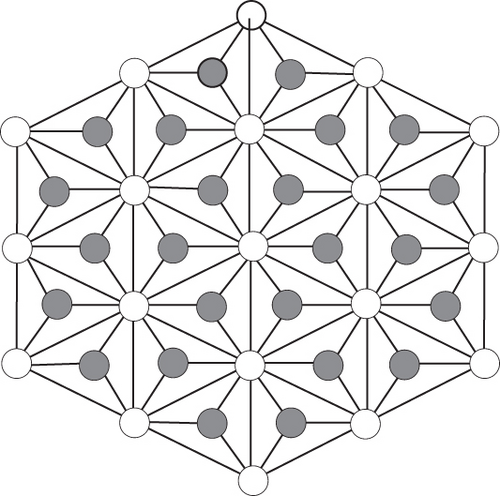
(i)
For major findings, based on eccentricity, we divide the vertices of the HDN₁(n) into two sets. The eccentricity of the set V₁ is , and the number of vertices in the set is 1, β = 1, and n ≥ 2. The set V₂ contains the vertices with the eccentricity , and the number of vertices in the set V₂ is 6(3β − 4), 2 ≤ β ≤ n, n ≥ 2. In addition, the variable β denotes the distance between two vertices, which assists in the creation of this vertex division. Additionally, β denotes the range of the total number of vertices having that eccentricity. Table 1 shows the vertex division of a HDN₁ depending on the eccentricity of each vertex.

(ii)
Now, we divide the edges of the HDN₁(n) based on the eccentricity into two sets of the end vertices. The set E₁ contains edges with eccentricities , 2 ≤ β ≤ n, n ≥ 2, and E₁ set is (30m − 18), 1 ≤ m ≤ n − 1. The set E₂ contains the edges with eccentricities , 2 ≤ β ≤ n, n ≥ 2, and E₂ set is (24m − 6), 1 ≤ m ≤ n − 1. In addition, β denotes the total number of pairing with that eccentricities. Table 2 shows the edge division of a HDN₁(n) Â depending on the eccentricity of end vertices.

1. Vertex partition of HDN1(n) based on range and n.

Sets		Number of vertices	Range of β and n
V₁	n − 1	1	β = 1, n ≥ 2
V₂	n + β − 2	6(3β − 4)	2 ≤ β ≤ n, n ≥ 2

2. Eccentricity-based edge partition of HDN₁(n).

Sets		Edge frequency	β value range	Range of m and n
E₁	(n + β − 3, n + β − 2	30m − 18	2 ≤ β ≤ n	1 ≤ m ≤ n − 1
E₂	n + β − 2, n + β − 2	24m − 6	2 ≤ β ≤ n	1 ≤ m ≤ n − 1

3.1. Main Results for HDN₁(n)

The close approximations of some TI’s for this network were calculated in this section. We have founnd here the closed results for total eccentricity, average eccentricity, eccentricity version of Zagreb, eccentric ABC, and GA indices for hex-derived networks of first type.

Theorem 3.1.1. Consider HDN₁(n), ∀n ∈ N, n ≥ 2, be the graph of first type of hex-derived network, then ζ index of HDN₁(n) is

(9)

Proof. Consider HDN₁(n), ∀n ∈ N, n ≥ 2, be the first type Hex-derived network.

We calculated the total eccentricity index as follows, using the vertices partitioned from Table 1 and Equation (2):

(10)

After calculations, we have

(11)

Theorem 3.1.2. Consider HDN₁(n), ∀n ∈ N, n ≥ 2, be the graph of first type of hex-derived network, then the avec index of HDN₁(n) is

(12)

Proof. Consider HDN₁(n), ∀n ∈ N and n ≥ 2 containing 9n² − 15n + 7 vertices and 27n² − 51n + 24 edges.

We calculated the average eccentricity index as follows, using the vertices partitioned from Table 1 and Equation (3):

(13)

After calculations, we have

(14)

Theorem 3.1.3. Consider HDN₁(n), ∀n ∈ N, n ≥ 2, be the graph of first type of hex-derived network, then of HDN₁(n) is

(15)

Proof. Consider HDN₁(n), ∀n ∈ N and n ≥ 2. We calculated as follows, using Table 2 edge partitioning and Equation (6):

(16)

After calculations, we have

(17)

Theorem 3.1.4. Consider HDN₁(n), ∀n ∈ N, n ≥ 2, be the graph of first type of hex-derived network, then index of HDN₁(n) is

(18)

Proof. Consider HDN₁(n), ∀n ∈ N, n ≥ 2, be the hex-derived network of first type. We calculated the second Zagreb eccentricity index as follows, using the vertices partitioned from Table 1 and Equation (7); the proof is analogue of Theorem 3.1.3.

Theorem 3.1.5. Consider HDN₁(n), ∀n ∈ N, n ≥ 2, be the graph of first type of hex-derived network, then the index of HDN₁(n) is

(19)

Proof. Consider HDN₁(n), ∀n ∈ N, n ≥ 2, be the hex-derived network of first type.

We calculated the third Zagreb eccentricity index as follows, using Table 2 edge partitioning and Equation (8):

(20)

After calculations, we have

(21)

Theorem 3.1.6. Consider HDN₁(n), ∀n ∈ N, n ≥ 2, be the graph of first type of hex-derived network, then the GA₄ index of HDN₁(n) is

(22)

Proof. Consider HDN₁(n), ∀n ∈ N, n ≥ 2, be the hex-derived network of first type.

We calculated the eccentric GA₄ index as follows, using Table 2 edge partitioning and Equation (4):

(23)

After calculations, we have

(24)

Theorem 3.1.7. Consider HDN₁(n), ∀n ∈ N, n ≥ 2, be the graph of first type of hex-derived network, then the ABC₅ index of HDN₁(n) is

(25)

Proof. Consider HDN₁(n), ∀n ∈ N, n ≥ 2, be the hex-derived network of first type.

We calculated the eccentric ABC₅ index as follows, using Table 2 edge partitioning and Equation (5); the proof is analogue of Theorem 3.1.6.

4. Comparison and Discussion

The eccentricity-based TI’s of the HDN₁(n) first type of hex-derived network for specific values of m and β are compared in Figures 3–5. It is obvious from the graphs that the values of indices are increasing for different m and β. So that it provides an indication that the results provided for different indices are true.

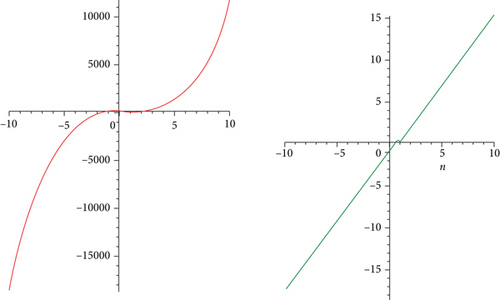
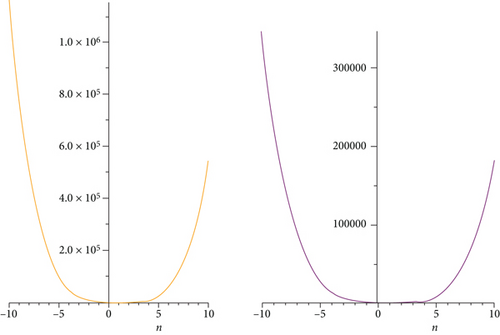
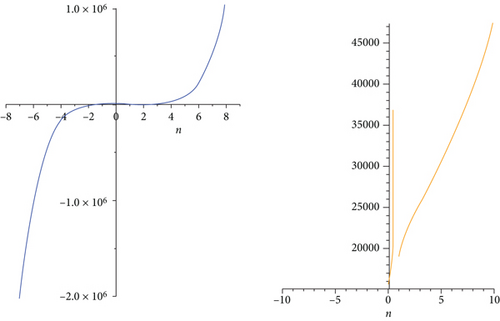
5. Conclusion

In this article, eccentricity-based TI’s, the average eccentricity, eccentric version of Zagreb indices, total eccentricity index, eccentricity version of geometric-artithmatic index, and atom-bond connectivity index based on eccentricity for first type of hex-derived network are contemplated and investigate the basic topologies of these networks. Furthermore, we made a comparison in Figures 3–5 by the use of graph comparison. This analysis will facilitate researchers engaged in network science in recognizing the topology of the abovementioned networks. Furthermore, the results presented in this paper might be helpful in the QSPR/QSAR analysis to predict further structural and physicochemical properties of molecular graphs under discussion.

Conflicts of Interest

There is no conflict of interest among the authors.

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Imran M., Ali M. A., Ahmad S., Siddiqui M. K., and Baig A. Q., Topological characterization of the symmetrical structure of bismuth tri-iodide, Symmetry. (2018) 10, no. 6, https://doi.org/10.3390/sym10060201, 2-s2.0-85048872977.
10.3390/sym10060201
PubMed Web of Science® Google Scholar
2 Hayat S., Malik M. A., and Imran M., Computing topological indices of honeycomb derived networks, Romanian journal of Information science and technology. (2015) 18, 144–165.
Web of Science® Google Scholar
3 Gao W. and Siddiqui M. K., Molecular descriptors of nanotube, oxide, silicate, and triangulene networks, Journal of Chemistry. (2017) 2017, 10, https://doi.org/10.1155/2017/6540754, 2-s2.0-85013339690, 6540754.
10.1155/2017/6540754
Web of Science® Google Scholar
4 Bie R. J., Siddiqui M. K., Razavi R., Taherkhani M., and Najaf M., Possibility of C₃₈ and Si₁₉Ge₁₉ nanocages in anode of metal ion batteries: computational examination, Acta Chimica Slovenica. (2018) 65, 303–311.
10.17344/acsi.2017.3925
CAS PubMed Web of Science® Google Scholar
5 Farooq R. and Malik M. A., On some eccentricity based topological indices of nanostar dendrimers, Optoelectronics and Advanced Materials, Rapid Communications. (2015) 9, no. 5-6, 842–849.
CAS Web of Science® Google Scholar
6 Ilic A., On the extremal properties of the average eccentricity, Computers & Mathematcs with Applications. (2012) 64, no. 9, 2877–2885, https://doi.org/10.1016/j.camwa.2012.04.023, 2-s2.0-84867337646.
10.1016/j.camwa.2012.04.023
Web of Science® Google Scholar
7 Tang Y. and Zhou B., On average eccentricity, Match-Communications in Mathematical and Computer Chemistry. (2012) 67, no. 2, 405–423.
Web of Science® Google Scholar
8 Hinz A. M. and Parisse D., The average eccentricity of Sierpiński graphs, Graphs and Combinatorics. (2012) 28, no. 5, 671–686, https://doi.org/10.1007/s00373-011-1076-4, 2-s2.0-84865811808.
10.1007/s00373-011-1076-4
Web of Science® Google Scholar
9 Dankelmann P., Goddard W., and Swart C. S., The average eccentricity of a graph and its subgraphs, Utilitas Mathematica. (2004) 65, 41–52.
Web of Science® Google Scholar
10 Ghorbani M. and Khaki A., A note on the fourth version of geometric-arithmetic index, Optoelectronics and Advanced Materials, Rapid Communications. (2010) 4, no. 12, 2212–2215.
CAS Web of Science® Google Scholar
11 Zhang X., Baig A. Q., Azhar M. R., Farahani M. R., and Imran M., The average eccentricity and eccentricity based geometric-arithmetic index of tetra sheets, International Journal of Pure and Applied Mathematics. (2017) 117, no. 3, 467–479.
Google Scholar
12 Farahani M. R., Eccentricity version of atom bond connectivity index of benzenoid family ABC₅(Hk), Applied Sciences Journal. (2013) 21, no. 9, 1260–1265.
Google Scholar
13 Imran M., Baig A. Q., Azhar M. R., Farahani M. R., and Zhang X., Eccentricity based geometric-arithmetic and atom-bond connectivity indices of copper oxide CuO, International Journal of Pure and Applied Mathematics. (2017) 117, no. 3, 481–502.
Google Scholar
14 Gao W., Farahani M. R., and Jamil M. K., The eccentricity version of atom-bond connectivity index of linear polycene parallelogram benzoid ABC₅ (P(n,n)), Acta Chimica Slovenica. (2016) 63, no. 2, 376–379.
10.17344/acsi.2016.2378
CAS PubMed Web of Science® Google Scholar
15 Ghorbani M. and Hosseinzadeh M. A., A new version of Zagreb indices, Filomat. (2012) 26, no. 1, 93–100, https://doi.org/10.2298/FIL1201093G, 2-s2.0-80054823570.
10.2298/FIL1201093G
Web of Science® Google Scholar
16 Vukičević D. and Graovac A., Note on the comparison of the first and second normalized Zagreb eccentricity indices, Acta Chimica Slovenica. (2010) 57, 524–528.
CAS PubMed Web of Science® Google Scholar
17 Liu J. B., Shaker H., Nadeem I., and Farahani M. R., Eccentric connectivity index of t-polyacenic nanotubes, Advances in Materials Science and Engineering. (2019) 2019, 9, 9062535.
10.1155/2019/9062535
Web of Science® Google Scholar
18 Gupta S., Singh M., and Madan A. K., Application of graph theory: relationship of eccentric connectivity index and Wiener's index with anti-inflammatory activity, Journal of Mathematical Analysis and Applications. (2002) 266, no. 2, 259–268, https://doi.org/10.1006/jmaa.2000.7243, 2-s2.0-0037084418.
10.1006/jmaa.2000.7243
Web of Science® Google Scholar
19 Zobair M. M., Ali M., Shaker H., and Rehman N., Eccentricity based topological invariants of triangulane dendrimers, Utilitas Mathematica. (2018) 107, 193–206.
Web of Science® Google Scholar
20 Koam A. N. A., Ahmad A., Ahmad Y., Department of Mathematics, College of Science, Jazan University, New Campus, Jazan 2097, Saudi Arabia, and College of Computer Science and Information Technology, Jazan University, Jazan, Saudi Arabia, Computation of reverse degree-based topological indices of hex-derived networks, AIMS Mathematics. (2021) 6, no. 10, 11330–11345, https://doi.org/10.3934/math.2021658.
10.3934/math.2021658
Web of Science® Google Scholar
21 Ahmad M., Javaid M., Bonyah E., and Saeed M., Comparative analysis of subdivided hex-derived networks using structural descriptors, Journal of Chemistry. (2022) 2022, 18, https://doi.org/10.1155/2022/6502473, 8944080.
10.1155/2022/6502473
Web of Science® Google Scholar
22 Ahmad M. and Imran M., Vertex-edge-degree-based topological properties for hex-derived networks, Complexity. (2022) 2022, 13, https://doi.org/10.1155/2022/7025480, 7025480.
10.1155/2022/7025480
Web of Science® Google Scholar
23 Zobair M. M., Ali M., and Shaker H., Eccentricity based topological invariants of tightest non-adjacently configured stable pentagonal structure of carbon nanocones, International Journal of Quantum Chemistry. (2021) 121, no. 24, 1–11, https://doi.org/10.1002/qua.26807.
10.1002/qua.26807
Web of Science® Google Scholar
24 Imran M., Zobair M. M., and Shaker H., Eccentricity-based topological invariants of dominating David-Derived networks, Journal of Chemistry. (2021) 2021, 10, https://doi.org/10.1155/2021/8944080, 8944080.
10.1155/2021/8944080
Web of Science® Google Scholar
25 Siddiqui M. K., Naeem M., Rahman N. A., and Imran M., Computing topological indices of certain networks, Journal of Optoelectronics and Advanced Materials. (2016) 18, 884–892.
Web of Science® Google Scholar
26 Estrada E., Torres L., Rodriguez L., and Gutman I., An atom-bond connectivity inde: Modelling the enthalpy of formation of alkanes, Indian Journal of Chemistry. (1998) 37, 849–855.
Web of Science® Google Scholar
27 Gao W., Siddiqui M. K., Naeem M., and Rehman N. A., Topological characterization of carbon graphite and crystal cubic carbon structures, Molecules. (2017) 22, no. 9, https://doi.org/10.3390/molecules22091496, 2-s2.0-85029627172, 28880212.
10.3390/molecules22091496
PubMed Web of Science® Google Scholar
28 Shao Z., Wu P., Zhang X., Dimitrov D., and Liu J., On the maximum ABC index of graphs with prescribed size and without pendent vertices, IEEE Access. (2018) 6, 27604–27616, https://doi.org/10.1109/ACCESS.2018.2831910, 2-s2.0-85046356847.
10.1109/ACCESS.2018.2831910
Web of Science® Google Scholar
29 Siddiqui M. K., Imran M., and Ahmad A., On Zagreb indices, Zagreb polynomials of some nanostar dendrimers, Applied Mathematics and Computation. (2016) 280, 132–139, https://doi.org/10.1016/j.amc.2016.01.041, 2-s2.0-84957831267.
10.1016/j.amc.2016.01.041
Web of Science® Google Scholar
30 Baig A. Q., Imran M., and Ali H., On topological indices of poly oxide, poly silicate, DOX, and DSL networks, Canadian Journal of Chemistry. (2015) 93, no. 7, 730–739, https://doi.org/10.1139/cjc-2014-0490, 2-s2.0-84932617253.
10.1139/cjc-2014-0490
CAS Web of Science® Google Scholar
31 Shao Z., Wu P., Gao Y., Gutman I., and Zhang X., On the maximum ABC index of graphs without pendent vertices, Applied Mathematics and Computation. (2017) 315, 298–312, https://doi.org/10.1016/j.amc.2017.07.075, 2-s2.0-85044140180.
10.1016/j.amc.2017.07.075
Web of Science® Google Scholar
32 Shao Z., Siddiqui M. K., and Muhammad M. H., Computing Zagreb indices and Zagreb polynomials for symmetrical nanotubes, Symmetry. (2018) 10, no. 7, https://doi.org/10.3390/sym10070244, 2-s2.0-85050315637.
10.3390/sym10070244
PubMed Web of Science® Google Scholar
33 Song P., Ali H., Binyamin M. A., and Ali B., On computation of entropy of hex derived network, Complexity. (2021) 2021, 18, https://doi.org/10.1155/2021/9993504, 9993504.
10.1155/2021/9993504
Web of Science® Google Scholar
34 Chartrand G. and Zhang P., Introduction to Graph Theory, 2007, McGraw-Hill Higher Education, New York, NY, USA.
Google Scholar
35 Harris J. M., Hirst J. L., and Mossinghoff M. J., Combinatorics and Graph Theory, 2008, Springer Science and Business Media, Berlin/Heidelberg, Germany, https://doi.org/10.1007/978-0-387-79711-3.
10.1007/978-0-387-79711-3
Google Scholar

Citing Literature

All articles

[Retracted] Eccentricity-Based Topological Descriptors of First Type of Hex-Derived Network

Retraction(s) for this article

Retracted: Eccentricity-Based Topological Descriptors of First Type of Hex-Derived Network

Abstract

1. Introduction

2. Applications and Motivation

3. Hex-Derived Network

3.1. Main Results for HDN₁(n)

4. Comparison and Discussion

5. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

[Retracted] Eccentricity-Based Topological Descriptors of First Type of Hex-Derived Network

Retraction(s) for this article

Retracted: Eccentricity-Based Topological Descriptors of First Type of Hex-Derived Network

Abstract

1. Introduction

2. Applications and Motivation

3. Hex-Derived Network

3.1. Main Results for HDN1(n)

4. Comparison and Discussion

5. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

3.1. Main Results for HDN₁(n)