Convex polytopes are special types of polytopes having an additional property that they are also convex sets in the n-dimensional Euclidean space. The convex polytope topologies are being used in the antitracking networks due to their stability, resilience, and destroy-resistance. The metric related parameters have been extensively studied in the recent times due to their applications in several areas including robot navigation, network designing, image processing, and chemistry. In this article, the sharp bounds for the fault tolerant partition dimension of certain well-known families of convex polytopes R_n, Qn, Sn, T_n, and D_n have been computed. Furthermore, we have studied the graphs having fault tolerant partition dimension bounded below by 4.

1. Introduction

The ability of a network to maintain its working capacity and functionality if one of its components fails to work is called fault tolerance. This guarantees the lower maintenance cost and longer durability of the network. Antitracking networks are used to protect users’ identities and communication confidentiality. A robust and resilient network topology is always required to ensure the strength and protection of antitracking network. Tian et al. [1], in their recent research, proposed the convex polytope topology in the antitracking network due to the stability, resilience, and destroy-resistance. The convex polytope topology can preserve the network stability, avoid the threat to key nodes and cut vertices, and achieve the self-optimization of network topology. Convex polytopes have been studied to a great extent for metric dimension and partition dimension. Imran et al. [2] computed the metric dimension of convex polytopes, whereas the bounds of fault tolerant metric dimension for some convex polytopes have been discussed in [3, 4]. Furthermore, fractional versions of metric related parameters for certain convex polytopes have been calculated in [5, 6].

Garey and Johnson in [7] concluded that computation of metric basis of a network is an NP-hard problem; it was further implied that computation of partition related metric parameters for general graphs is also NP-hard. This leads the current research trends to focus on the computation of these metric parameters for specific classes of graphs. In this regard, Liu et al. [8] and Chu et al. [9] recently computed sharp bounds of partition dimension for some families of convex polytopes. Following the same spirit, the fault tolerant partition dimension of certain convex polytopes is computed in the current work.

In a connected graph W, the node and edge sets of W are denoted by V(W) and E(W), respectively. The length of the shortest path connecting two nodes p and q is known as the distance between p and q denoted by d(p, q). For any node p of W and a nonempty subset A of V(W), the sets (HTML translation failed) and N(p) = {q ∈ V(G)|pq ∈ E(W)} are called the distance of a node p from subset A and the neighborhood of node p, respectively. Let Ω = {x₁, x₂, …, x_l} be the set of ordered nodes; the representation of a node p with reference to Ω is a vector r(p|Ω) such that r(p|Ω) = (d(p, x₁), d(p, x₂), …, d(p, x_l)). If the vectors r(p|Ω) are different, for every node of the graph, then Ω is termed as a resolving set of W. The minimal cardinality of Ω is termed as the metric dimension of W, represented by dim(W). Let Ψ = {B₁, B₂, …, B_l} be an ordered l−partition of a connected graph W. The representations of nodes with reference to Ψ are vectors r(p|ψ) such that r(p|ψ) = (d(p, B₁), d(p, B₂), …, d(p, B_l)). If vectors r(p|ψ) are different for every node of the graph, then l− partition is termed as a resolving partition of W. The minimal cardinality of a resolving partition Ψ is termed as the partition dimension of W, represented by p d(W). The basic relationship between metric and partition dimension of graphs is given in [10].

Further study on partition dimension can be seen in [11, 12]. In 2015, Moreno et al. [13] presented the concept of κ− metric. If vectors r(p|Ω) are different in at least κ places for every node of the graph, then Ω is termed as a κ− metric generator for W. The κ− metric basis is a generator with least number of nodes. The minimal cardinality of Ω is termed as the κ− metric dimension of W, represented by dim_κ(W). The 2-metric dimension was first presented in [14]. Further study on κ− metric dimension can be seen in [15, 16].

In 2020, Moreno et al. [17] presented the concept of κ− partition dimension of the graph. If vectors r(p|ψ) are different in at least κ places for every node of the graph, then Ψ is termed as a κ− partition generator of W. The κ− partition basis is a generator with least number of sets. The minimal cardinality of Ψ is termed as the κ− partition dimension of W, represented by pd_κ(W). For κ = 2, the κ− partition dimension is known as fault tolerant partition dimension denoted by pd₂(W). pd₂(W) was computed for some important graphs in [18, 19] and further for circulant graphs in [20].

1.1. Main Results

The research conducted in this article leads to the subsequent results.

Theorem 1.

(1)
For a graph W of order m ≥ 5 and having a vertex of degree at least 4, pd₂(W) ≥ 4
(2)
For n ≥ 5, 4 ≤ pd₂(R_n) ≤ 5
(3)
For n ≥ 6,
- (a)
  4 ≤ pd₂(Q_n) ≤ 5
- (b)
  4 ≤ pd₂(S_n) ≤ 5
- (c)
  4 ≤ pd₂(T_n) ≤ 5
- (d)
  3 ≤ pd₂(D_n) ≤ 5

The rest of the article is organised in the following manner. In Section 2, the convex polytopes R_n, Q_n, S_n, T_n, D_n are defined and lower and upper bounds of fault tolerant partition dimension for these infinite families of graphs are also computed. In Section 3, the article is concluded with a conjecture and an open problem.

2. Fault Tolerant Partition Dimension of Convex Polytopes

In this section, the bounds of fault partition dimensions of certain classes of convex polytopes R_n, Q_n, S_n, T_n, D_n have been computed. In the following theorem, the graphs with fault tolerant partition dimension bounded below by 4 has been characterized.

Lemma 1. Let W be a graph of order m ≥ 5. If W has a node of degree at least 4, then pd₂(W) ≥ 4.

Proof. Assume that pd₂(W) = 3 for m ≥ 5. Let Λ = {B₁, B₂, B₃} be a 2− partition basis of V(W). Let v_k be the node of degree 4. Assume that v_k ∈ B₁. Let N(v_k) = {x₁, x₂, x₃, x₄}.

Case 1: When |B₁| = 1, the subcases are as follows:
Case 1.1: If each node of N(v_k) is in either set B₂ or B₃, assuming that N(v_k)⊆B₂, then, for x ∈ N(v_k), r(x_i|Λ) = (1,0, b_i), for 1 ≤ i ≤ 4, which results in a contradiction.
Now if N(v_k)⊆B₃, then, for x ∈ N(v_k), r(x_i|Λ) = (1, a_i, 0), for 1 ≤ i ≤ 4, which again contradicts our assumption.
Case 1.2: Assume that B₂ or B₃ contains three nodes of N(v_k).
Let x_p, x_q, x_r ∈ N(v_k)∩B₂ and x_t ∈ N(v_k)∩B₃; then r(v_k|Λ) = (0,1,1), r(x_q|Λ) = (1,0, b₁), r(x_q|Λ) = (1,0, b₂), and r(x_r|Λ) = (1,0, b₃), which clearly leads to a contradictory situation. Meanwhile three nodes of N(v_k) in B₃ generate a similar case of contradiction.
Case 1.3: Assume that each of B₂ and B₃ contains two nodes from set N(v_k). Let x_p, x_q ∈ N(v_k)∩B₂; then r(x_p|Λ) = (1,0, b₁) and r(x_q|Λ) = (1,0, b₂), which again results in a contradiction.
Case 2: When |B₁| ≥ 2, the subcases are as follows:
Case 2.1: When |N(v_k)∩B₁| = 4, this implies that N(v_k)⊆B₁, and then r(v_k|Λ) = (0, a₀, b₀) and, for x ∈ N(v_k), r(x_i|Λ) = (0, a_i, b_i), for 1 ≤ i ≤ 4. Hence, a₀ − 1 ≤ a₁, a₂, a₃, a₄ ≤ a₀ + 1. Pigeonhole principle implies that at least two of nodes v_k and x_i are equidistant from B₁ and B₂, which results in a contradiction.
Case 2.2: When |N(v_k)∩B₁| = 3.
Let x_p, x_q, x_r ∈ N(v_k)∩B₁ and x_t ∈ N(v_k)∩B₂, and then r(v_k|Λ) = (0,1, b₀), r(x_p|Λ) = (0, a₁, b₁), r(x_q|Λ) = (0, a₂, b₂), and r(x_r|Λ) = (0, a₃, b₃). In this situation, we get 1 ≤ a₁, a₂, a₃ ≤ 2. Again Pigeonhole principle implies that at least two nodes among v_k, x_p, x_q, and x_r are equidistant from B₁ and B₂, which results in a contradiction. Meanwhile x_t ∈ N(v_k)∩B₃ generates a similar case of contradiction.
Case 2.3: When |N(v_k)∩B₁| = 2.
Case 2.3.1: Let x_p, x_q ∈ N(v_k)∩B₁ and x_r, x_t ∈ N(v_k)∩B₂, and then r(v_k|Λ) = (0,1, b₀), r(x_p|Λ) = (0, a₁, b₁), and r(x_q|Λ) = (0, a₂, b₂). In this situation, we get 1 ≤ a₁, a₂ ≤ 2. Now the Pigeonhole principle implies that minimum two nodes among v_k, x_p, and x_q are at the same distances from B₁ and B₂. This results in a contradiction. Meanwhile x_r, x_t ∈ N(v_k)∩B₃ generates a similar case of contradiction.
Case 2.3.2: Let x_p, x_q ∈ N(v_k)∩B₁, x_r ∈ N(v_k)∩B₂, and x_t ∈ N(v_k)∩B₃, and then r(v_k|Λ) = (0,1,1), r(x_p|Λ) = (0, a₁, b₁), and r(x_q|Λ) = (0, a₂, b₂). In this situation, we get 1 ≤ a₁, a₂ ≤ 2. Now the Pigeonhole principle implies that the minimum two nodes among v_k, x_p, and x_q are at the same distances from B₁ and B₂. This results in a contradiction.
Case 2.4: When |N(v_k)∩B₁| = 1.
Case 2.4.1: Let x_p ∈ N(v_k)∩B₁ and x_q, x_r, x_t ∈ N(v_k)∩B₂, and then r(v_k|Λ) = (0,1, b₀), r(x_p|Λ) = (0, a₁, b₁), r(x_q|Λ) = (1,0, b₂), r(x_r|Λ) = (1,0, b₃), and r(x_t|Λ) = (1,0, b₄), which is a clear case of contradiction. Meanwhile x_q, x_r, x_t ∈ N(v_k)∩B₃ generates a similar case of contradiction.
Case 2.4.2: Let x_p ∈ N(v_k)∩B₁, x_q, x_r ∈ N(v_k)∩B₂, and x_t ∈ N(v_k)∩B₃, and then r(v_k|Λ) = (0,1,1), r(x_p|Λ) = (0, a₁, b₁), r(x_q|Λ) = (1,0, b₂), r(x_r|Λ) = (1,0, b₃), and r(x_t|Λ) = (1, a₄, 0), which is again a clear case of contradiction. Meanwhile x_q, x_r ∈ N(v_k)∩B₃ and x_t ∈ N(v_k)∩B₂ generates a similar case of contradiction.
Case 2.5: When |N(v_k)∩B₁| = 0. This case is similar to Case 1.

Hence, pd₂(W) ≥ 4 for m ≥ 5 with (HTML translation failed) containing a node of degree at least 4.

2.1. Fault Tolerant Partition Dimension of R_n

In [21], Baca defined convex polytope R_n for n ≥ 5 with V(R_n) = {u_i, v_i, x_i : 1 ≤ i ≤ n} and E(R_n) = {u_iu_i+1; u_i, v_i; u_i+1v_i; v_iv_i+1; v_ix_i; x_ix_i+1 : 1 ≤ i ≤ n}.

Conventionally, we assume that u_n+1 = u₁, v_n+1 = v₁, and x_n+1 = x₁. The graph of convex polytope R_n is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Convex polytope R_n.

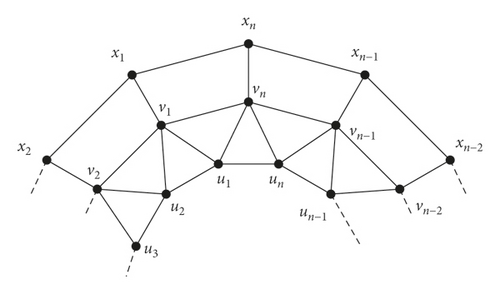
In the subsequent theorem, we compute the bounds of the fault tolerant partition dimension of convex polytope R_n.

Theorem 2. Consider convex polytope R_n with n ≥ 5; then 4 ≤ pd₂(R_n) ≤ 5.

Proof. Let Ψ = {B₁, B₂, B₃, B₄, B₅} be a partition of the node set V(R_n). We divide the proof in four parts and, in each part, it will be shown that Ψ is the fault tolerant partition generator for R_n. Let a = ⌊p/2⌋.

Case 1: For n = 4p.
Let B₁ = {u_i, v_i : 1 ≤ i ≤ n}, B₂ = {x_i : 1 ≤ i ≤ p}, B₃ = {x_i : p + 1 ≤ i ≤ 2p}, B₄ = {x_i : 2p + 1 ≤ i ≤ 3p}, and B₅ = {x_i : 3p + 1 ≤ i ≤ 3n}.
r(q|Ψ) are tabulated in Table 1.
Case 2: For n = 4p + 1.
Let B₁ = {u_i, v_i : 1 ≤ i ≤ n}, B₂ = {x_i : 1 ≤ i ≤ p + 1}, B₃ = {x_i : p + 2 ≤ i ≤ 2p + 1}, B₄ = {x_i : 2p + 2 ≤ i ≤ 3p + 1}, and B₅ = {x_i : 3p + 2 ≤ i ≤ 3n}.
r(q|Ψ) are tabulated in Table 2.
Case 3: For n = 4p + 2.
Let B₁ = {u_i, v_i : 1 ≤ i ≤ n}, B₂ = {x_i : 1 ≤ i ≤ p + 1}, B₃ = {x_i : p + 2 ≤ i ≤ 2p + 2}, B₄ = {x_i : 2p + 3 ≤ i ≤ 3p + 2}, and B₅ = {x_i : 3p + 3 ≤ i ≤ 3n}.
r(q|Ψ) are tabulated in Table 3.
Case 4: For n = 4p + 3.
Let B₁ = {u_i, v_i : 1 ≤ i ≤ n}, B₂ = {x_i : 1 ≤ i ≤ p + 1}, B₃ = {x_i : p + 2 ≤ i ≤ 2p + 2}, B₄ = {x_i : 2p + 3 ≤ i ≤ 3p + 3}, and B₅ = {x_i : 3p + 4 ≤ i ≤ 3n}.
r(q|Ψ) are tabulated in Table 4.

When p is odd, we have t = 2, whereas when p is even, t = 1 in the tables. Tables 1–4 clearly show that Ψ is the 2− resolving generator for R_n when n ≥ 5; therefore, pd₂(R_n) ≤ 5 for n ≥ 5. Lemma 1 implies that pd₂(R_n) ≥ 4 for n ≥ 5. This establishes our claim.

Table 1. r(q|Ψ) for R_n when n = 4p and a = ⌊p/2⌋.

Nodes	d(q, B₁)	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
u_i(1 ≤ i ≤ a + 1)	0	2	p − i + 3	p + i + 1	i + 1
u_i(a + 2 ≤ i ≤ p + 1)	0	2	p − i + 3	2p − i + 3	i + 1
u_i(p + 2 ≤ i ≤ p + a + 1)	0	i − p + 1	2	2p − i + 3	i + 1
u_i(p + a + 2 ≤ i ≤ 2p + 1)	0	i − p + 1	2	2p − i + 3	3p − i + 3
u_i(2p + 2 ≤ i ≤ 2p + a + 1)	0	i − p + 1	i − 2p + 1	2	3p − i + 3
u_i(2p + a + 2 ≤ i ≤ 3p + 1)	0	n − i + 3	i − 2p + 1	2	3p − i + 3
u_i(3p + 2 ≤ i ≤ n − 2t + 1)	0	n − i + 3	i − 2p + 1	i − n + p + 1	2
u_i(n − 2t + 2 ≤ i ≤ n)	0	n − i + 3	5p − i + 3	i − n + p + 1	2
v_i(1 ≤ i ≤ a + t − 1)	0	1	p − i + 2	p + i + 1	i + 1
v_i(a + t ≤ i ≤ p)	0	1	p − i + 2	2p − i + 2	i + 1
v_i(p + 1 ≤ i ≤ p + a + t − 1)	0	i − p + 1	1	2p − i + 2	i + 1
v_i(p + a + t ≤ i ≤ 2p)	0	i − p + 1	1	2p − i + 2	3p − i + 2
v_i(2p + 1 ≤ i ≤ 2p + a + t − 1)	0	i − p + 1	i − 2p + 1	1	3p − i + 2
v_i(2p + a + t ≤ i ≤ 3p)	0	n − i + 2	i − 2p + 1	1	3p − i + 2
v_i(3p + 1 ≤ i ≤ n − a)	0	n − i + 2	i − 2p + 1	i − 3p + 1	1
v_i(n − a + 1 ≤ i ≤ n)	0	n − i + 2	5p − i + 2	i − 3p + 1	1
x_i(1 ≤ i ≤ a + t − 1)	1	0	p − i + 1	i + p	i
x_i(a + t ≤ i ≤ p)	1	0	p − i + 1	2p − i + 1	i
x_i(p + 1 ≤ i ≤ p + a + t − 1)	1	i − p	0	2p − i + 1	i
x_i(p + a + t ≤ i ≤ 2p)	1	i − p	0	2p − i + 1	3p − i + 1
x_i(2p + 1 ≤ i ≤ 2p + a + t − 1)	1	i − p	i − 2p	0	3p − i + 1
x_i(2p + a + t ≤ i ≤ 3p)	1	n − i + 1	i − 2p	0	3p − i + 1
x_i(3p + 1 ≤ i ≤ n − a)	1	n − i + 1	i − 2p	i − 3p	0
x_i(n − a + 1 ≤ i ≤ n)	1	n − i + 1	5p − i + 1	i − 3p	0

Table 2. Representations of nodes for R_n when n = 4p + 1 and a = ⌊p/2⌋.

Nodes	d(q, B₁)	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
u_i(1 ≤ i ≤ a + 1)	0	2	p − i + 4	p + i + 1	i + 1
u_i(a + t + 1 ≤ i ≤ p + 2)	0	2	p − i + 4	2p − i + 4	i + 1
u_i(p + 3 ≤ i ≤ p + a + t)	0	i − p	2	2p − i + 4	i + 1
u_i(p + a + t + 1 ≤ i ≤ 2p + 2)	0	i − p	2	2p − i + 4	3p − i + 4
u_i(2p + 3 ≤ i ≤ 2p + a + 2)	0	i − p	i − 2p	2	3p − i + 4
u_i(2p + a + 3 ≤ i ≤ 3p + 2)	0	n − i + 3	i − 2p	2	3p − i + 4
u_i(3p + 3 ≤ i ≤ n − a + 1)	0	n − i + 3	i − 2p	i − 3p	2
u_i(n − a + 2 ≤ i ≤ n)	0	n − i + 3	5p − i + 5	i − n + p + 1	2
v_i(1 ≤ i ≤ a + 1)	0	1	p − i + 3	p + i + 1	i + 1
v_i(a + 2 ≤ i ≤ 2a + t)	0	1	p − i + 3	2p − i + 3	i + 1
v_i(2a + t + 1 ≤ i ≤ p + a + 1)	0	i − p	1	2p − i + 3	i + 1
v_i(p + a + 2 ≤ i ≤ 2p + 1)	0	i − p	1	2p − i + 3	3p − i + 3
v_i(2p + 2 ≤ i ≤ 2p + a + t)	0	i − p	i − 2p	1	3p − i + 3
v_i(2p + a + t + 1 ≤ i ≤ 3p + 1)	0	n − i + 2	i − 2p	1	3p − i + 3
v_i(3p + 2 ≤ i ≤ n − a − t + 2)	0	n − i + 2	i − 2p	i − 3p	1
v_i(n − a − t + 3 ≤ i ≤ n)	0	n − i + 2	5p − i + 4	i − 3p	1
x_i(1 ≤ i ≤ a + 1)	1	0	p − i + 2	i + p	i
x_i(a + 2 ≤ i ≤ p + 1)	1	0	p − i + 2	2p − i + 2	i
x_i(p + 2 ≤ i ≤ p + a + 1)	1	i − p − 1	0	2p − i + 2	i
x_i(p + a + 2 ≤ i ≤ 2p + 1)	1	i − p − 1	0	2p − i + 2	3p − i + 2
x_i(2p + 2 ≤ i ≤ 2p + a + 1)	1	i − p − 1	i − 2p − 1	0	3p − i + 2
x_i(2p + a + 2 ≤ i ≤ 3p + 1)	1	n − i + 1	i − 2p − 1	0	3p − i + 2
x_i(3p + 2 ≤ i ≤ n − a − t + 2)	1	n − i + 1	i − 2p − 1	i − 3p − 1	0
x_i(n − a − t + 3 ≤ i ≤ n)	1	n − i + 1	5p − i + 3	i − 3p − 1	0

Table 3. Representations of nodes for R_n when n = 4p + 2 and a = ⌊p/2⌋.

Nodes	d(q, B₁)	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
u_i(1 ≤ i ≤ a + 2)	0	2	p − i + 4	p + i + 1	i + 1
u_i(a + 3 ≤ i ≤ p + 2)	0	2	p − i + 4	2p − i + 5	i + 1
u_i(p + 3 ≤ i ≤ p + a + 2)	0	i − p	2	2p − i + 5	i + 1
u_i(p + a + 3 ≤ i ≤ 2p + 3)	0	i − p	2	2p − i + 5	3p − i + 5
u_i(2p + 4 ≤ i ≤ 2p + a + t + 1)	0	i − p	i − 2p − 1	2	3p − i + 5
u_i(2p + a + t + 2 ≤ i ≤ 3p + 3)	0	n − i + 3	i − 2p − 1	2	3p − i + 5
u_i(3p + 4 ≤ i ≤ n − a + 1)	0	n − i + 3	i − 2p − 1	i − n + p + 1	2
u_i(n − a + 2 ≤ i ≤ n)	0	n − i + 3	5p − i + 6	i − n + p + 1	2
v_i(1 ≤ i ≤ a + t)	0	1	p − i + 3	p + i + 1	i + 1
v_i(a + t + 1 ≤ i ≤ p + 1)	0	1	p − i + 3	2p − i + 4	i + 1
v_i(p + 2 ≤ i ≤ p + a + t)	0	i − p	1	2p − i + 4	i + 1
v_i(p + a + t + 1 ≤ i ≤ 2p + 2)	0	i − p	1	2p − i + 4	3p − i + 4
v_i(2p + 3 ≤ i ≤ 2p + a + 2)	0	i − p	i − 2p − 1	1	3p − i + 4
v_i(2p + a + 3 ≤ i ≤ 3p + 2)	0	n − i + 2	i − 2p − 1	1	3p − i + 4
v_i(3p + 3 ≤ i ≤ n − a − t + 2)	0	n − i + 2	i − 2p − 1	i − 3p − 1	1
v_i(n − a − t + 3 ≤ i ≤ n)	0	n − i + 2	5p − i + 5	i − 3p − 1	1
x_i(1 ≤ i ≤ a + t)	1	0	p − i + 2	i + p	i
x_i(a + t + 1 ≤ i ≤ p + 1)	1	0	p − i + 2	2p − i + 3	i
x_i(p + 2 ≤ i ≤ p + a + t)	1	i − p − 1	0	2p − i + 3	i
x_i(p + a + t + 1 ≤ i ≤ 2p + 2)	1	i − p − 1	0	2p − i + 3	3p − i + 3
x_i(2p + 3 ≤ i ≤ 2p + a + 2)	1	i − p − 1	i − 2p − 2	0	3p − i + 3
x_i(2p + a + 3 ≤ i ≤ 3p + 2)	1	4p − i + 3	i − 2p − 2	0	3p − i + 3
x_i(3p + 3 ≤ i ≤ n − a − t + 2)	1	4p − i + 3	i − 2p − 2	i − 3p − 2	0
x_i(n − a − t + 3 ≤ i ≤ n)	1	4p − i + 3	5p − i + 4	i − 3p − 2	0

Table 4. Representations of nodes for R_n when n = 4p + 3 and a = ⌊p/2⌋.

Nodes	d(q, B₁)	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
u_i(1 ≤ i ≤ a + 2)	0	2	p − i + 4	p + i + 1	i + 1
u_i(a + 3 ≤ i ≤ p + 2)	0	2	p − i + 4	2p − i + 5	i + 1
u_i(p + 3 ≤ i ≤ p + a + t + 1)	0	i − p	2	2p − i + 5	i + 1
u_i(p + a + t + 2 ≤ i ≤ 2p + 3)	0	i − p	2	2p − i + 5	3p − i + 6
u_i(2p + 4 ≤ i ≤ 2p + a + 3)	0	i − p	i − 2p − 1	2	3p − i + 6
u_i(2p + a + 4 ≤ i ≤ 3p + 4)	0	n − i + 3	i − 2p − 1	2	3p − i + 6
u_i(3p + 5 ≤ i ≤ n − a − t + 2)	0	n − i + 3	i − 2p − 1	i − 3p − 2	2
u_i(n − a − t + 3 ≤ i ≤ n)	0	n − i + 3	5p − i + 7	i − n + p + 1	2
v_i(1 ≤ i ≤ a + t)	0	1	p − i + 3	p + i + 1	i + 1
v_i(a + t + 1 ≤ i ≤ p + 1)	0	1	p − i + 3	2p − i + 4	i + 1
v_i(p + 2 ≤ i ≤ p + a + 2)	0	i − p	1	2p − i + 4	i + 1
v_i(p + a + 3 ≤ i ≤ 2p + 2)	0	i − p	1	2p − i + 4	3p − i + 5
v_i(2p + 3 ≤ i ≤ 2p + a + t + 1)	0	i − p	i − 2p − 1	1	3p − i + 5
v_i(2p + a + t + 2 ≤ i ≤ 3p + 3)	0	n − i + 2	i − 2p − 1	1	3p − i + 5
v_i(3p + 4 ≤ i ≤ n − a)	0	n − i + 2	i − 2p − 1	i − 3p − 2	1
v_i(n − a + 1 ≤ i ≤ n)	0	n − i + 2	5p − i + 6	i − 3p − 2	1
x_i(1 ≤ i ≤ a + t)	1	0	p − i + 2	i + p	i
x_i(a + t + 1 ≤ i ≤ p + 1)	1	0	p − i + 2	2p − i + 3	i
x_i(p + 2 ≤ i ≤ p + a + 2)	1	i − p − 1	0	2p − i + 3	i
x_i(p + a + 3 ≤ i ≤ 2p + 2)	1	i − p − 1	0	2p − i + 3	3p − i + 4
x_i(2p + 3 ≤ i ≤ 2p + a + t + 1)	1	i − p − 1	i − 2p − 2	0	3p − i + 4
x_i(2p + a + t + 2 ≤ i ≤ 3p + 3)	1	n − i + 1	i − 2p − 2	0	3p − i + 4
x_i(3p + 4 ≤ i ≤ n − a)	1	n − i + 1	i − 2p − 2	i − 3p − 3	0
x_i(n − a + 1 ≤ i ≤ n)	1	n − i + 1	5p − i + 5	i − 3p − 3	0

2.2. Fault Tolerant Partition Dimension of Q_n

In [22], Baca et al. defined convex polytope Q_n for n ≥ 6 consisting of 3-sided, 4-sided, 5-sided, and n-sided faces, respectively. Here V(Q_n) = {u_i, v_i, x_i, y_i : 1 ≤ i ≤ n} and E(Q_n) = {u_iu_i+1; v_iv_i+1; y_iy_i+1; u_iv_i; v_ix_i; v_i+1x_i; x_iy_i : 1 ≤ i ≤ n}. Conventionally, we assume that u_n+1 = u₁, v_n+1 = v₁, x_n+1 = x₁, and y_n+1 = y₁. The graph of convex polytope Q_n is shown in Figure 2.

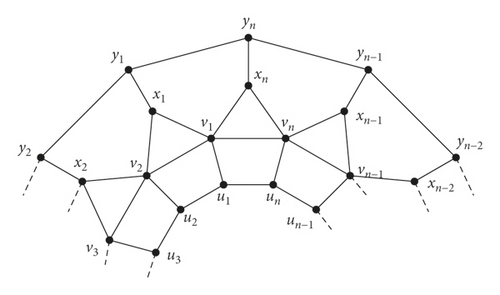
In the subsequent theorem, we compute the bounds of the fault tolerant partition dimension of convex polytope Q_n.

Theorem 3. Consider convex polytope Q_n with n ≥ 6; then 4 ≤ pd₂(Q_n) ≤ 5.

Proof. Let Ψ = {B₁, B₂, B₃, B₄, B₅} be a partition of the node set V(Q_n). We divide the proof in four parts and, in each part, it will be shown that Ψ is the fault tolerant partition generator for Q_n. Let a = ⌊p/2⌋.

Case 1: For n = 4p.
Let B₁ = {u_i, v_i, x_i : 1 ≤ i ≤ n}, B₂ = {y_i : 1 ≤ i ≤ p}, B₃ = {y_i : p + 1 ≤ i ≤ 2p}, B₄ = {y_i : 2p + 1 ≤ i ≤ 3p}, and B₅ = {y_i : 3p + 1 ≤ i ≤ 4n}.
r(q|Ψ) are tabulated in Table 5.
Case 2: For n = 4p + 1.
Let B₁ = {u_i, v_i, x_i : 1 ≤ i ≤ n}, B₂ = {y_i : 1 ≤ i ≤ p + 1}, B₃ = {y_i : p + 2 ≤ i ≤ 2p + 1}, B₄ = {y_i : 2p + 2 ≤ i ≤ 3p + 1}, and B₅ = {y_i : 3p + 2 ≤ i ≤ 4n}.
r(q|Ψ) are tabulated in Table 6.
Case 3: For n = 4p + 2.
Let B₁ = {u_i, v_i, x_i : 1 ≤ i ≤ n}, B₂ = {y_i : 1 ≤ i ≤ p + 1}, B₃ = {y_i : p + 2 ≤ i ≤ 2p + 2}, B₄ = {y_i : 2p + 3 ≤ i ≤ 3p + 2}, and B₅ = {y_i : 3p + 3 ≤ i ≤ 4n}.
r(q|Ψ) are tabulated in Table 7.
Case 4: For n = 4p + 3.
Let B₁ = {u_i, v_i, x_i : 1 ≤ i ≤ n}, B₂ = {y_i : 1 ≤ i ≤ p + 1}, B₃ = {y_i : p + 2 ≤ i ≤ 2p + 2}, B₄ = {y_i : 2p + 3 ≤ i ≤ 3p + 3}, and B₅ = {y_i : 3p + 4 ≤ i ≤ 4n}.
r(q|Ψ) are tabulated in Table 8.

When p is odd, we have t = 2, whereas when p is even, t = 1 in the tables. Tables 5–8 clearly show that Ψ is the 2− resolving generator for Q_n when n ≥ 6; therefore, pd₂(Q_n) ≤ 5 for n ≥ 6. Lemma 1 implies that pd₂(Q_n) ≥ 4 for n ≥ 6. This establishes our claim.

Table 5. r(q|Ψ) for Q_n when n = 4p and a = ⌊p/2⌋.

Nodes	d(q, B₁)	d(q, B₂)
u_i(1 ≤ i ≤ a + 1)	0	3
u_i(a + 2 ≤ i ≤ p + 1)	0	3
u_i(p + 2 ≤ i ≤ p + a + 1)	0	i − p + 2
u_i(p + a + 2 ≤ i ≤ 2p + 1)	0	i − p + 2
u_i(2p + 2 ≤ i ≤ 2p + a + 1)	0	i − p + 2
u_i(2p + a + 2 ≤ i ≤ 3p + 1)	0	5p − i − 3t + 3
u_i(3p + 2 ≤ i ≤ n − 2t + 1)	0	5p − i − 3t + 3
u_i(n − 2t + 2 ≤ i ≤ n)	0	5p − i − 3t + 3
v_i(1 ≤ i ≤ a + 1)	0	2
v_i(a + 2 ≤ i ≤ p + 1)	0	2
v_i(p + 2 ≤ i ≤ p + a + 1)	0	i − p + 1
v_i(p + a + 2 ≤ i ≤ 2p + 1)	0	i − p + 1
v_i(2p + 2 ≤ i ≤ 2p + a + 1)	0	i − p + 1
v_i(2p + a + 2 ≤ i ≤ 3p + 1)	0	5p − i − 3t + 2
v_i(3p + 2 ≤ i ≤ n − 2t + 1)	0	5p − i − 3t + 2
v_i(n − 2t + 2 ≤ i ≤ n)	0	5p − i − 3t + 2
x_i(1 ≤ i ≤ a + t − 1)	0	1
x_i(a + t ≤ i ≤ p)	0	1
x_i(p + 1 ≤ i ≤ p + a + t − 1)	0	i − p + 1
x_i(p + a + t ≤ i ≤ 2p)	0	i − p + 1
x_i(2p + 1 ≤ i ≤ 2p + a + t − 1)	0	i − p + 1
x_i(2p + a + t ≤ i ≤ 3p)	0	5p − i − 3t + 1
x_i(3p + 1 ≤ i ≤ n − t − 1)	0	5p − i − 3t + 1
x_i(n − t ≤ i ≤ n)	0	5p − i − 3t + 1
y_i(1 ≤ i ≤ a + t − 1)	1	0
y_i(a + t ≤ i ≤ p)	1	0
y_i(p + 1 ≤ i ≤ p + a + t − 1)	1	i − p
y_i(p + a + t ≤ i ≤ 2p)	1	i − p
y_i(2p + 1 ≤ i ≤ 2p + a + t − 1)	1	i − p
y_i(2p + a + t ≤ i ≤ 3p)	1	5p − i − 3t
y_i(3p + 1 ≤ i ≤ n − t − 1)	1	5p − i − 3t
y_i(n − t ≤ i ≤ n)	1	5p − i − 3t

Table 6. r(q|Ψ) for Q_n when n = 4p + 1 and a = ⌊p/2⌋.

Nodes	d(q, B₁)	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
u_i(1 ≤ i ≤ a + t)	0	3	p − i + 5	p + i + 2	i + 2
u_i(a + t + 1 ≤ i ≤ p + 2)	0	3	p − i + 5	2p − i + 5	i + 2
u_i(p + 3 ≤ i ≤ p + a + t)	0	i − p + 1	3	2p − i + 5	i + 2
u_i(p + a + t + 1 ≤ i ≤ 2p + 2)	0	i − p + 1	3	2p − i + 5	3p − i + 5
u_i(2p + 3 ≤ i ≤ 2p + a + 2)	0	i − p + 1	i − 2p + 1	3	3p − i + 5
u_i(2p + a + 3 ≤ i ≤ 3p + 2)	0	5p − i − 3t + 4	i − 2p + 1	3	3p − i + 5
u_i(3p + 3 ≤ i ≤ n − t)	0	5p − i − 3t + 4	i − 2p + 1	i − 3p + 1	3
u_i(n − t + 1 ≤ i ≤ n)	0	5p − i − 3t + 4	6p − i − 3t + 5	i − 3p + 1	3
v_i(1 ≤ i ≤ a + t)	0	2	p − i + 4	p + i + 1	i + 1
v_i(a + t + 1 ≤ i ≤ p + 2)	0	2	p − i + 4	2p − i + 4	i + 1
v_i(p + 3 ≤ i ≤ p + a + t)	0	i − p	2	2p − i + 4	i + 1
v_i(p + a + t + 1 ≤ i ≤ 2p + 2)	0	i − p	2	2p − i + 4	3p − i + 4
v_i(2p + 3 ≤ i ≤ 2p + a + 2)	0	i − p	i − 2p	2	3p − i + 4
v_i(2p + a + 3 ≤ i ≤ 3p + 2)	0	5p − i − 3t + 3	i − 2p	2	3p − i + 4
v_i(3p + 3 ≤ i ≤ n − t)	0	5p − i − 3t + 3	i − 2p	i − 3p	2
v_i(n − t + 1 ≤ i ≤ n)	0	5p − i − 3t + 3	6p − i − 3t + 4	i − 3p	2
x_i(1 ≤ i ≤ a + 1)	0	1	p − i + 3	p + i + 1	i + 1
x_i(a + 2 ≤ i ≤ p + 1)	0	1	p − i + 3	2p − i + 3	i + 1
x_i(p + 2 ≤ i ≤ p + a + 1)	0	i − p	1	2p − i + 3	i + 1
x_i(p + a + 2 ≤ i ≤ 2p + 1)	0	i − p	1	2p − i + 3	3p − i + 3
x_i(2p + 2 ≤ i ≤ 2p + a + t)	0	i − p	i − 2p	1	3p − i + 3
x_i(2p + a + t + 1 ≤ i ≤ 3p + 1)	0	5p − i − 3t + 2	i − 2p	1	3p − i + 3
x_i(3p + 2 ≤ i ≤ n − 2t + 1)	0	5p − i − 3t + 2	i − 2p	i − 3p	1
x_i(n − 2t + 2 ≤ i ≤ n)	0	5p − i − 3t + 2	6p − i − 3t + 3	i − 3p	1
y_i(1 ≤ i ≤ a + 1)	1	0	p − i + 2	p + i	i
y_i(a + 2 ≤ i ≤ p + 1)	1	0	p − i + 2	2p − i + 2	i
y_i(p + 2 ≤ i ≤ p + a + 1)	1	i − p − 1	0	2p − i + 2	i
y_i(p + a + 2 ≤ i ≤ 2p + 1)	1	i − p − 1	0	2p − i + 2	3p − i + 2
y_i(2p + 2 ≤ i ≤ 2p + a + t)	1	i − p − 1	i − 2p − 1	0	3p − i + 2
y_i(2p + a + t + 1 ≤ i ≤ 3p + 1)	1	5p − i − 3t + 1	i − 2p − 1	0	3p − i + 2
y_i(3p + 2 ≤ i ≤ n − 2t + 1)	1	5p − i − 3t + 1	i − 2p − 1	i − 3p − 1	0
y_i(n − 2t + 2 ≤ i ≤ n)	1	5p − i − 3t + 1	6p − i − 3t + 2	i − 3p − 1	0

Table 7. r(q|Ψ) for Q_n when n = 4p + 2 and a = ⌊p/2⌋.

Nodes	d(q, B₁)	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
u_i(1 ≤ i ≤ a + 2)	0	3	p − i + 5	p + i + 2	i + 2
u_i(a + 3 ≤ i ≤ p + 2)	0	3	p − i + 5	2p − i + 6	i + 2
u_i(p + 3 ≤ i ≤ p + a + 2)	0	i − p + 1	3	2p − i + 6	i + 2
u_i(p + a + 3 ≤ i ≤ 2p + a + 1)	0	i − p + 1	3	2p − i + 6	3p − i + 6
u_i(2p + a + 2 ≤ i ≤ 3p)	0	i − p + 1	i − 2p	3	3p − i + 6
u_i(3p + 1 ≤ i ≤ n − a − t)	0	5p − i + 2	i − 2p	3	3p − i + 6
u_i(n − a − t + 1 ≤ i ≤ n − 1)	0	5p − i − t + 3	i − 2p	i − 3p	3
u_i(i = n)	0	5p − i − t + 3	6p − i − t + 4	i − 3p	3
v_i(1 ≤ i ≤ a + 2)	0	2	p − i + 4	p + i + 1	i + 1
v_i(a + 3 ≤ i ≤ p + 2)	0	2	p − i + 4	2p − i + 5	i + 1
v_i(p + 3 ≤ i ≤ p + a + 2)	0	i − p	2	2p − i + 5	i + 1
v_i(p + a + 3 ≤ i ≤ 3p − t)	0	i − p	2	2p − i + 5	3p − i + 5
v_i(3p − t + 1 ≤ i ≤ 3p)	0	i − p	i − 2p − 1	2	3p − i + 5
v_i(3p + 1 ≤ i ≤ n − a − t)	0	5p − i − t + 2	i − 2p − 1	2	3p − i + 5
v_i(n − a − t + 1 ≤ i ≤ n − 1)	0	5p − i − t + 2	i − 2p − 1	i − 3p − 1	2
v_i(i = n)	0	5p − i − t + 2	6p − i − t + 3	i − 3p − 1	2
x_i(1 ≤ i ≤ a + t)	0	1	p − i + 3	p + i + 1	i + 1
x_i(a + t + 1 ≤ i ≤ p + 1)	0	1	p − i + 3	2p − i + 4	i + 1
x_i(p + 2 ≤ i ≤ p + a + t)	0	i − p	1	2p − i + 4	i + 1
x_i(p + a + t + 1 ≤ i ≤ 3p − t − 1)	0	i − p	1	2p − i + 4	3p − i + 4
x_i(3p − t ≤ i ≤ 3p − t + 1)	0	i − p	i − 2p − 1	1	3p − i + 4
x_i(3p − t + 2 ≤ i ≤ n − a − t − 1)	0	5p − i − t + 1	i − 2p − 1	1	3p − i + 4
x_i(n − a − t ≤ i ≤ n − t)	0	5p − i − t + 1	i − 2p − 1	i − 3p − 1	1
x_i(n − t + 1 ≤ i ≤ n)	0	5p − i − t + 1	6p − i − t + 2	i − 3p − 1	1
y_i(1 ≤ i ≤ a + t)	1	0	p − i + 2	p + i	i
y_i(a + t + 1 ≤ i ≤ p + 1)	1	0	p − i + 2	2p − i + 3	i
y_i(p + 2 ≤ i ≤ p + a + t)	1	i − p − 1	0	2p − i + 3	i
y_i(p + a + t + 1 ≤ i ≤ 3p − t − 1)	1	i − p − 1	0	2p − i + 3	3p − i + 3
y_i(3p − t ≤ i ≤ 3p − t + 1)	1	i − p − 1	i − 2p − 2	0	3p − i + 3
y_i(3p − t + 2 ≤ i ≤ n − a − t − 1)	1	5p − i − t	i − 2p − 2	0	3p − i + 3
y_i(n − a − t ≤ i ≤ n − t)	1	5p − i − t	i − 2p − 2	i − 3p − 2	0
y_i(n − t + 1 ≤ i ≤ n)	1	5p − i − t	6p − i − t + 1	i − 3p − 2	0

Table 8. r(q|Ψ) for Q_n when n = 4p + 3 and a = ⌊p/2⌋.

Nodes	d(q, B₁)	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
u_i(1 ≤ i ≤ a + 2)	0	3	p − i + 5	p + i + 2	i + 2
u_i(a + 3 ≤ i ≤ p + 2)	0	3	p − i + 5	2p − i + 6	i + 2
u_i(p + 3 ≤ i ≤ p + a + t + 1)	0	i − p + 1	3	2p − i + 6	i + 2
u_i(p + a + t + 2 ≤ i ≤ 2p + a − t + 2)	0	i − p + 1	3	2p − i + 6	3p − i + 7
u_i(2p + a − t + 3 ≤ i ≤ 3p − 2t + 3)	0	i − p + 1	i − 2p	3	3p − i + 7
u_i(3p − 2t + 4 ≤ i ≤ n − 3t)	0	5p − i − 3t + 6	i − 2p	3	3p − i + 7
u_i(n − 3t + 1 ≤ i ≤ n − 2t + 1)	0	5p − i − 3t + 6	i − 2p	i − 3p − 1	3
u_i(n − 2t + 2 ≤ i ≤ n)u_i(n − 2t + 2 ≤ i ≤ n)	0	5p − i − 3t + 6	6p − i − 3t + 7	i − 3p − 1	3
v_i(1 ≤ i ≤ a + 2)	0	2	p − i + 4	p + i + 1	i + 1
v_i(a + 3 ≤ i ≤ p + 2)	0	2	p − i + 4	2p − i + 5	i + 1
v_i(p + 3 ≤ i ≤ p + a + t + 1)	0	i − p	2	2p − i + 5	i + 1
v_i(p + a + t + 2 ≤ i ≤ 2p + 3)	0	i − p	2	2p − i + 5	3p − i + 6
v_i(2p + a + 4 ≤ i ≤ 3p + 4)	0	i − p	i − 2p − 1	2	3p − i + 6
v_i(2p + a + 4 ≤ i ≤ 3p + 4)	0	5p − i − 3t + 5	i − 2p − 1	2	3p − i + 6
v_i(3p + 5 ≤ i ≤ n − 2t + 1)	0	5p − i − 3t + 5	i − 2p − 1	i − 3p − 2	2
v_i(n − 2t + 2 ≤ i ≤ n)	0	5p − i − 3t + 5	6p − i − 3t + 6	i − 3p − 2	2
x_i(1 ≤ i ≤ a + t)	0	1	p − i + 3	p + i + 1	i + 1
x_i(a + t + 1 ≤ i ≤ p + 1)	0	1	p − i + 3	2p − i + 4	i + 1
x_i(p + 2 ≤ i ≤ p + a + 2)	0	i − p	1	2p − i + 4	i + 1
x_i(p + a + 3 ≤ i ≤ 2p + 2)	0	i − p	1	2p − i + 4	3p − i + 5
x_i(2p + 3 ≤ i ≤ 2p + a + t + 1)	0	i − p	i − 2p − 1	1	3p − i + 5
x_i(2p + a + t + 2 ≤ i ≤ 3p + 3)	0	5p − i − 3t + 4	i − 2p − 1	1	3p − i + 5
x_i(3p + 4 ≤ i ≤ n − t − 1)	0	5p − i − 3t + 4	i − 2p − 1	i − 3p − 2	1
x_i(n − t ≤ i ≤ n)	0	5p − i − 3t + 4	6p − i − 3t + 5	i − 3p − 2	1
y_i(1 ≤ i ≤ a + t)	1	0	p − i + 2	p + i	i
y_i(a + t + 1 ≤ i ≤ p + 1)	1	0	p − i + 2	2p − i + 3	i
y_i(p + 2 ≤ i ≤ p + a + 2)	1	i − p − 1	0	2p − i + 3	i
y_i(p + a + 3 ≤ i ≤ 2p + 2)	1	i − p − 1	0	2p − i + 3	3p − i + 4
y_i(2p + 3 ≤ i ≤ 2p + a + t + 1)	1	i − p − 1	i − 2p − 2	0	3p − i + 4
y_i(2p + a + t + 2 ≤ i ≤ 3p + 3)	1	5p − i − 3t + 3	i − 2p − 2	0	3p − i + 4
y_i(3p + 4 ≤ i ≤ n − t − 1)	1	5p − i − 3t + 3	i − 2p − 2	i − 3p − 3	0
y_i(n − t ≤ i ≤ n)	1	5p − i − 3t + 3	6p − i − 3t + 4	i − 3p − 3	0

2.3. Fault Tolerant Partition Dimension of S_n

In [12], Imran et al. defined convex polytope S_n for n ≥ 6 consisting of 2n 3-sided faces, 2n 4-sided faces, and a pair of n-sided faces which can be constructed by combining convex polytope R_n with prism graph. Here V(S_n) = {u_i, v_i, x_i, y_i : 1 ≤ i ≤ n} and E(S_n) = {u_iu_i+1; v_iv_i+1; x_ix_i+1; y_iy_i+1; u_j+1v_i; u_i, v_i; v_i, x_i; x_i, y_i : 1 ≤ i ≤ n}. Conventionally, we assume that u_n+1 = u₁, v_n+1 = v₁, x_n+1 = x₁, and y_n+1 = y₁. The graph of convex polytope S_n is shown in Figure 3.

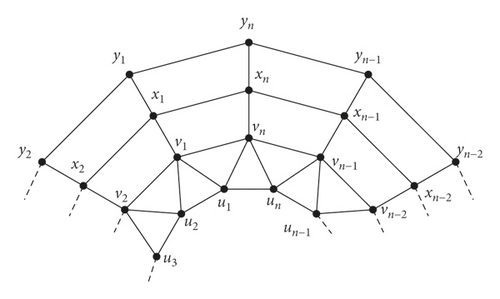
In the subsequent theorem, we compute the bounds of the fault tolerant partition dimension of convex polytope S_n.

Theorem 4. Consider convex polytope S_n with n ≥ 6; then 4 ≤ pd₂(S_n) ≤ 5.

Proof. Let Ψ = {B₁, B₂, B₃, B₄, B₅} be a partition of the node set V(S_n). The partition sets B₁, B₂, B₃, B₄, and B₅ defined for convex polytope Q_n are the same for S_n. Let a = ⌊p/2⌋. The representations of nodes u_i, x_i, and y_i are the same in both Q_n and S_n. The representations of nodes v_i are shown in the tables below. When p is odd, we have t = 2 , whereas when p is even, t = 1 in the tables. Tables 9–12 clearly show that Ψ is the 2− resolving generator for S_n when n ≥ 6; therefore, pd₂(S_n) ≤ 5 for n ≥ 5. Lemma 1 implies that pd₂(S_n) ≥ 4 for n ≥ 6. This establishes our claim.

Table 9. r(q|Ψ) for S_n when n = 4p and a = ⌊p/2⌋.

Nodes	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
v_i(1 ≤ i ≤ a + t − 1)	2	p − i + 3	p + i + 2	i + 2
v_i(a + t ≤ i ≤ p)	2	p − i + 3	2p − i + 3	i + 2
v_i(p + 1 ≤ i ≤ p + a + t − 1)	i − p + 2	2	2p − i + 3	i + 2
v_i(p + a + t ≤ i ≤ 2p)	i − p + 2	2	2p − i + 3	v_i(p + a + t ≤ i ≤ 2p)
v_i(2p + 1 ≤ i ≤ 2p + a + t − 1)	i − p + 2	i − 2p + 2	2	3p − i + 3
v_i(2p + a + t ≤ i ≤ 3p)	5p − i − 3t + 2	i − 2p + 2	2	3p − i + 3
v_i(3p + 1 ≤ i ≤ n − t − 1)	5p − i − 3t + 2	i − 2p + 2	i − 3p + 2	2
v_i(n − t ≤ i ≤ n)	5p − i − 3t + 2	6p − i − 3t + 2	i − 3p + 2	2

Table 10. r(q|Ψ) for S_n when n = 4p + 1 and a = ⌊p/2⌋.

Nodes	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
v_i(1 ≤ i ≤ a + 1)	2	p − i + 4	p + i + 2	i + 2
v_i(a + 2 ≤ i ≤ p + 1)	2	p − i + 4	2p − i + 4	i + 2
v_i(p + 2 ≤ i ≤ p + a + 1)	i − p + 1	2	2p − i + 4	i + 2
v_i(p + a + 2 ≤ i ≤ 2p + 1)	i − p + 1	2	2p − i + 4	3p − i + 4
v_i(2p + 2 ≤ i ≤ 2p + a + t)	i − p + 1	i − 2p + 1	2	3p − i + 4
v_i(2p + a + t + 1 ≤ i ≤ 3p + 1)	5p − i − 3t + 3	i − 2p + 1	2	3p − i + 4
v_i(3p + 2 ≤ i ≤ n − 2t + 1)	5p − i − 3t + 3	i − 2p + 1	i − 3p + 1	2
v_i(n − 2t + 2 ≤ i ≤ n)	5p − i − 3t + 3	6p − i − 3t + 4	i − 3p + 1	2

Table 11. r(q|Ψ) for S_n when n = 4p + 2 and a = ⌊p/2⌋.

Nodes	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
v_i(1 ≤ i ≤ a + t)	2	p − i + 4	p + i + 2	i + 2
v_i(a + t + 1 ≤ i ≤ p + 1)	2	p − i + 4	2p − i + 5	i + 2
v_i(p + 2 ≤ i ≤ p + a + t)	i − p + 1	2	2p − i + 5	i + 2
v_i(p + a + t + 1 ≤ i ≤ 2p + 2)	i − p + 1	2	2p − i + 5	3p − i + 5
v_i(2p + 3 ≤ i ≤ 3p − 2t + 2)	i − p + 1	i − 2p	2	3p − i + 5
v_i(3p − 2t + 3 ≤ i ≤ n − a − 2t)	5p − i − 3t + 4	i − 2p	2	3p − i + 5
v_i(n − a − 2t + 1 ≤ i ≤ n − 2t + 1)	5p − i − 3t + 4	i − 2p	i − 3p	2
v_i(n − 2t + 2 ≤ i ≤ n)	5p − i − 3t + 4	6p − i − 3t + 5	i − 3p	2

Table 12. r(q|Ψ) for S_n when n = 4p + 3 and a = ⌊p/2⌋.

Nodes	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
v_i(1 ≤ i ≤ a + t)	2	p − i + 4	p + i + 2	i + 2
v_i(a + t + 1 ≤ i ≤ p + 1)	2	p − i + 4	2p − i + 5	i + 2
v_i(p + 2 ≤ i ≤ p + a + 2)	i − p + 1	2	2p − i + 5	i + 2
v_i(p + a + 3 ≤ i ≤ 2p + 2)	i − p + 1	2	2p − i + 5	3p − i + 6
v_i(2p + 3 ≤ i ≤ 3p − t + 1)	i − p + 1	i − 2p	2	3p − i + 6
v_i(3p − t + 2 ≤ i ≤ n − a − 2t)	5p − i − 3t + 5	i − 2p	2	3p − i + 6
v_i(n − a − 2t + 1 ≤ i ≤ n − t − 1)	5p − i − 3t + 5	i − 2p	i − 3p − 1	2
v_i(n − t ≤ i ≤ n)	5p − i − 3t + 5	6p − i − 3t + 5	i − 3p − 1	2

2.4. Fault Tolerant Partition Dimension of T_n

In [12], Imran et al. defined convex polytope T_n for n ≥ 6 consisting of 4n 3-sided faces, n 4-sided faces, and a pair of n-sided faces which can be constructed by combining convex polytope R_n with antiprism graph. Here V(T_n) = {u_i, v_i, x_i, y_i, 1 ≤ i ≤ n} and E(T_n) = {u_iu_i+1; u_iv_i; u_i+1v_i; v_iv_i+1; v_i, x_i; x_i, x_i+1; x_iy_i; x_i+1y_i; y_iy_i+1 : 1 ≤ i ≤ n}. Conventionally, we assume that u_n+1 = u₁, v_n+1 = v₁, x_n+1 = x₁, and y_n+1 = y₁. The graph of convex polytope T_n is shown in Figure 4.

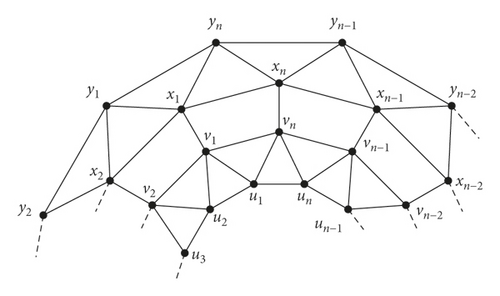
In the subsequent theorem, we compute the bounds of the fault tolerant partition dimension of convex polytope T_n.

Theorem 5. Consider convex polytope T_n with n ≥ 6; then 4 ≤ pd₂(T_n) ≤ 5.

Proof. Let Ψ = {B₁, B₂, B₃, B₄, B₅} be a partition of the node set V(T_n). The partition sets B₁, B₂, B₃, B₄, and B₅ defined for convex polytope Q_n are the same for T_n. Let a = ⌊p/2⌋. The representations of nodes v_i and y_i are the same in both Q_n and T_n. The representations of nodes u_i and x_i are shown in the tables below. When p is odd, we have t = 2, whereas when p is even, t = 1 in the tables. Tables 13–16 clearly show that Ψ is the 2− resolving generator for T_n when n ≥ 6; therefore, pd₂(T_n) ≤ 5 for n ≥ 6. Lemma 1 implies that pd₂(T_n) ≥ 4 for n ≥ 6. This establishes our claim.

Table 13. r(q|Ψ) for T_n when n = 4p and a = ⌊p/2⌋.

Nodes	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
u_i(i = 1)	3	p − i + 4	p + i + 1	i + 2
u_i(2 ≤ i ≤ p − t)	3	p − i + 4	p + i + 1	i + 1
u_i(p − t + 1 ≤ i ≤ p + 1)	3	p − i + 4	2p − i + 4	i + 1
u_i(p + 2 ≤ i ≤ 2p − t)	i − p + 1	3	2p − i + 4	i + 1
u_i(2p − t + 1 ≤ i ≤ 2p + 1)	i − p + 1	3	2p − i + 4	3p − i + 4
u_i(2p + 2 ≤ i ≤ 3p − t)	i − p + 1	i − 2p + 1	3	3p − i + 4
u_i(3p − t + 1 ≤ i ≤ n − 3t)	5p − i − 3t + 3	i − 2p + 1	3	3p − i + 4
u_i(n − 3t + 1 ≤ i ≤ n − t)	5p − i − 3t + 3	i − 2p + 1	i − 3p + 1	3
u_i(n − t + 1 ≤ i ≤ n)	5p − i − 3t + 3	6p − i − 3t + 3	i − 3p + 1	3
x_i(1 ≤ i ≤ a + 1)	1	p − i + 2	p + i	i
x_i(a + 2 ≤ i ≤ p + 1)	1	p − i + 2	2p − i + 2	i
x_i(p + 2 ≤ i ≤ p + t + 2)	i − p	1	2p − i + 2	i
x_i(p + t + 3 ≤ i ≤ 2p + 1)	i − p	1	2p − i + 2	3p − i + 2
x_i(2p + 2 ≤ i ≤ 3p − 2t + 1)	i − p	i − 2p	1	3p − i + 2
x_i(3p − 2t + 2 ≤ i ≤ 3p + 1)	5p − i − 3t + 1	i − 2p	1	3p − i + 2
x_i(3p + 2 ≤ i ≤ n − 2t + 1)	5p − i − 3t + 1	i − 2p	i − 3p	1
x_i(n − 2t + 2 ≤ i ≤ n)	5p − i − 3t + 1	6p − i − 3t + 1	i − 3p	1

Table 14. r(q|Ψ) for T_n when n = 4p + 1 and a = ⌊p/2⌋.

Nodes	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
u_i(i = 1)	3	p − i + 5	p + i + 1	i + 2
u_i(2 ≤ i ≤ p − 2t + 2)	3	p − i + 5	p + i + 1	i + 1
u_i(p − 2t + 3 ≤ i ≤ p + 2)	3	p − i + 5	2p − i + 5	i + 1
u_i(p + 3 ≤ i ≤ 2p − 2t + 2)	i − p	3	2p − i + 5	i + 1
u_i(2p − 2t + 3 ≤ i ≤ 2p + 2)	i − p	3	2p − i + 5	3p − i + 5
u_i(2p + 3 ≤ i ≤ 3p − t + 1)	i − p	i − 2p	3	3p − i + 5
u_i(3p − t + 2 ≤ i ≤ n − 3t)	5p − i − 3t + 4	i − 2p	3	3p − i + 5
u_i(n − 3t + 1 ≤ i ≤ n − 2t + 1)	5p − i − 3t + 4	i − 2p	i − 3p	3
u_i(n − 2t + 2 ≤ i ≤ n)	5p − i − 3t + 4	6p − i − 3t + 5	i − 3p	3
x_i(1 ≤ i ≤ a + t)	1	p − i + 3	p + i	i
x_i(a + t + 1 ≤ i ≤ p + 2)	1	p − i + 3	2p − i + 3	i
x_i(p + 3 ≤ i ≤ p + 2t + 1)	i − p − 1	1	2p − i + 3	i
x_i(p + 2t + 2 ≤ i ≤ 2p + 2)	i − p − 1	1	2p − i + 3	3p − i + 3
x_i(2p + 3 ≤ i ≤ 3p − 2t + 2)	i − p − 1	i − 2p − 1	1	3p − i + 3
x_i(3p − 2t + 3 ≤ i ≤ 3p + 2)	5p − i − 3t + 2	i − 2p − 1	1	3p − i + 3
x_i(3p + 3 ≤ i ≤ n − t)	5p − i − 3t + 2	i − 2p − 1	i − 3p − 1	1
x_i(n − t + 1 ≤ i ≤ n)	5p − i − 3t + 2	6p − i − 3t + 3	i − 3p − 1	1

Table 15. r(q|Ψ) for T_n when n = 4p + 2 and a = ⌊p/2⌋.

Nodes	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
u_i(i = 1)	3	p − i + 5	p + i + 1	i + 2
u_i(2 ≤ i ≤ p − t + 1)	3	p − i + 5	p + i + 1	i + 1
u_i(p − t + 2 ≤ i ≤ p + 2)	3	p − i + 5	2p − i + 6	i + 1
u_i(p + 3 ≤ i ≤ 2p − t + 1)	i − p	3	2p − i + 6	i + 1
u_i(2p − t + 2 ≤ i ≤ 2p + 3)	i − p	3	2p − i + 6	3p − i + 6
u_i(2p + 4 ≤ i ≤ 3p − 2t + 3)	i − p	i − 2p − 1	3	3p − i + 6
u_i(3p − 2t + 4 ≤ i ≤ n − 3t)	5p − i − 3t + 5	i − 2p − 1	3	3p − i + 6
u_i(n − 3t + 1 ≤ i ≤ n − t)	5p − i − 3t + 5	i − 2p − 1	i − 3p − 1	3
u_i(n − t + 1 ≤ i ≤ n)	5p − i − 3t + 5	6p − i − 3t + 6	i − 3p − 1	3
x_i(1 ≤ i ≤ a + 2)	1	p − i + 3	p + i	i
x_i(a + 3 ≤ i ≤ p + 2)	1	p − i + 3	2p − i + 4	i
x_i(p + 3 ≤ i ≤ p + t + 3)	i − p − 1	1	2p − i + 4	i
x_i(p + t + 4 ≤ i ≤ 2p + 3)	i − p − 1	1	2p − i + 4	3p − i + 4
x_i(2p + 4 ≤ i ≤ 3p − t + 1)	i − p − 1	i − 2p − 2	1	3p − i + 4
x_i(3p − t + 2 ≤ i ≤ 3p + 3)	5p − i − 3t + 3	i − 2p − 2	1	3p − i + 4
x_i(3p + 4 ≤ i ≤ n − t)	5p − i − 3t + 3	i − 2p − 2	i − 3p − 2	1
x_i(n − t + 1 ≤ i ≤ n)	5p − i − 3t + 3	6p − i − 3t + 4	i − 3p − 2	1

Table 16. r(q|Ψ) for T_n when n = 4p + 3 and a = ⌊p/2⌋.

Nodes	d(q, B₂)	d(q, B₃)	d(q, B₄)	d(q, B₅)
u_i(i = 1)	3	p − i + 5	p + i + 1	i + 2
u_i(2 ≤ i ≤ p − t + 1)	3	p − i + 5	p + i + 1	i + 1
u_i(p − t + 2 ≤ i ≤ p + 2)	3	p − i + 5	2p − i + 6	i + 1
u_i(p + 3 ≤ i ≤ 2p − 2t + 3)	i − p	3	2p − i + 6	i + 1
u_i(2p − 2t + 4 ≤ i ≤ 2p + 3)	i − p	3	2p − i + 6	3p − i + 7
u_i(2p + 4 ≤ i ≤ 3p − t + 2)	i − p	i − 2p − 1	3	3p − i + 7
u_i(3p − t + 3 ≤ i ≤ n − 3t)	5p − i − 3t + 6	i − 2p − 1	3	3p − i + 7
u_i(n − 3t + 1 ≤ i ≤ n − t)	5p − i − 3t + 6	i − 2p − 1	i − 3p − 2	3
u_i(n − t + 1 ≤ i ≤ n)	5p − i − 3t + 6	6p − i − 3t + 7	i − 3p − 2	3
x_i(1 ≤ i ≤ a + 2)	1	p − i + 3	p + i	i
x_i(a + 3 ≤ i ≤ p + 2)	1	p − i + 3	2p − i + 4	i
x_i(p + 3 ≤ i ≤ p + t + 2)	i − p − 1	1	2p − i + 4	i
x_i(p + 2t + 3 ≤ i ≤ 2p + 3)	i − p − 1	1	2p − i + 4	3p − i + 5
x_i(2p + 4 ≤ i ≤ 3p − 2t + 3)	i − p − 1	i − 2p − 2	1	3p − i + 5
x_i(3p − 2t + 4 ≤ i ≤ 3p + 4)	5p − i − 3t + 4	i − 2p − 2	1	3p − i + 5
x_i(3p + 5 ≤ i ≤ n − 2t + 1)	5p − i − 3t + 4	i − 2p − 2	i − 3p − 2	1
x_i(n − 2t + 2 ≤ i ≤ n)	5p − i − 3t + 4	6p − i − 3t + 5	i − 3p − 2	1

2.5. Fault Tolerant Partition Dimension of D_n

In [4], Baca et al. defined convex polytope D_n for n ≥ 4 consisting of 2n5-sided faces. Here V(D_n) = {u_i, v_i, x_i, y_i : 1 ≤ i ≤ n} and E(D_n) = {u_iu_i+1; y_iy_i+1; u_iv_i; v_ix_i; v_i+1x_i; x_iy_i : 1 ≤ i ≤ n}. Conventionally, we assume that u_n+1 = u₁, x_n+1 = v₁, x_n+1 = x₁, and y_n+1 = y₁. The graph of convex polytope D_n is shown in Figure 5.

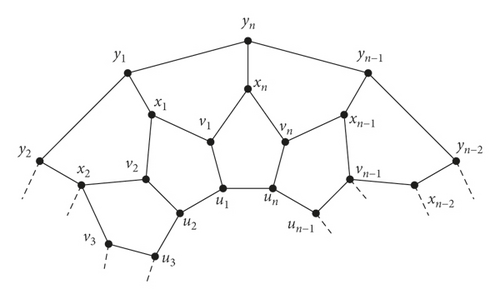
The following results in [6, 8] are important for us.

Proposition 1. Let G be a connected graph of order n; then

(1)
p d(G) = 2 if and only if G = P_n, where P_n is a path of order n ≥ 2;
(2)
p d(G) ≤ pd₂(G).

In the subsequent theorem, we compute the bounds of the fault tolerant partition dimension of convex polytope D_n.

Theorem 6. Consider convex polytope D_n with n ≥ 6; then 3 ≤ pd₂(D_n) ≤ 5.

Proof. Let ψ = {B₁, B₂, B₃, B₄, B₅} be a partition of the node set V(D_n). The partition sets B₁, B₂, B₃, B₄, B₅ defined for convex polytope Q_n are the same for D_n. The representations of all the nodes are the same in both Q_n and D_n. Hence, in view of Theorem 3 and Proposition 1, we have 3 ≤ pd₂(D_n) ≤ 5 for n ≥ 6.

3. Conclusion

In this research article, we conclude that the fault tolerant partition dimension of the convex polytopes R_n, Q_n, S_n, T_n, D_n is bounded above by 5. We also proved that the lower bound of fault tolerant partition dimension of all the families of graphs with order greater than or equal to 5 and having a node of degree at least 4 is 4 which includes first four of these convex polytopes. We conclude the article with a conjecture and an open problem.

Conjecture 1. The fault tolerant partition dimension of convex polytopes R_n, Q_n, S_n, T_n, D_n is 5.

Open Problem 1. Compute the exact value of fault tolerant partition dimension of the convex polytopes R_n, Q_n, S_n, T_n, D_n.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

All data are included within this article. However, the reader may contact the corresponding author for more details of the data.

References

1 Tian C., Zhang Y., and Yin T., Modeling of Anti-tracking Network Based on Convex-Polytope Topology, 2020, Springer link, New Yark,NY, USA, https://doi.org/10.1007/978-3-030-50417-5-32.
10.1007/978-3-030-50417-5_32
Google Scholar
2 Imran M., Ul Haq Bokhary S. A., and Baig A. Q., On families of convex polytopes with constant metric dimension, Computers & Mathematics with Applications. (2010) 60, no. 9, 2629–2638, https://doi.org/10.1016/j.camwa.2010.08.090, 2-s2.0-77957884772.
10.1016/j.camwa.2010.08.090
Web of Science® Google Scholar
3 Raza H., Hayat S., and Pan X.-F., On the fault-tolerant metric dimension of convex polytopes, Applied Mathematics and Computation. (2018) 339, 172–185, https://doi.org/10.1016/j.amc.2018.07.010, 2-s2.0-85050861044.
10.1016/j.amc.2018.07.010
Web of Science® Google Scholar
4 Siddiqui H. M. A., Hayat S., Khan A., Imran M., Razzaq A., and Liu J.-B., Resolvability and fault-tolerant resolvability structures of convex polytopes, Theoretical Computer Science. (2019) 796, 114–128, https://doi.org/10.1016/j.tcs.2019.08.032, 2-s2.0-85071663013.
10.1016/j.tcs.2019.08.032
Web of Science® Google Scholar
5 Aslam M. K., Javaid M., Zhu Q., and Raheem A., On the fractional metric dimension of convex polytopes, Mathematical Problems in Engineering. (2021) 2021, 13, 3925925, https://doi.org/10.1155/2021/3925925.
10.1155/2021/3925925
Web of Science® Google Scholar
6 Jamil F., Kashif A., Zafar S., Bassfar Z., and Alanazi A. M., Local fractional strong metric dimension of certain rotationally symmetric planer networks, IEEE Access. (2021) 9, 159326–159333, https://doi.org/10.1109/access.2021.3131311.
10.1109/ACCESS.2021.3131311
Web of Science® Google Scholar
7 Garey M. R. and Johnson D. S., Computers and Intractability: A Guide to the Theory of NP-Completeness, 1979, Freeman, New York.
Google Scholar
8 Liu J. B., Nadeem M. F., and Azeem M., Bounds on the partition dimension of convex polytopes, Combinatorial Chemistry & High Throughput Screening. (2020) 23, 1–13.
Google Scholar
9 Chu Y.-M., Nadeem M. F., Azeem M., and Siddiqui M. K., On sharp bounds on partition dimension of convex polytopes, IEEE Access. (2020) 8, 224781–224790, https://doi.org/10.1109/access.2020.3044498.
10.1109/ACCESS.2020.3044498
Web of Science® Google Scholar
10 Chartrand G., Salehi E., and Zhang P., The partition dimension of a graph, Aequationes Mathematicae. (2000) 59, no. 1, 45–54, https://doi.org/10.1007/pl00000127, 2-s2.0-17844400423.
10.1007/PL00000127
Google Scholar
11 Koam A. N. A., Ahmad A., Alatawi M. S., Nadeem M. F., and Azeem M., Computation of metric-based resolvability of quartz without pendant nodes, IEEE Access. (2021) 9, 151834–151840, https://doi.org/10.1109/access.2021.3126455.
10.1109/ACCESS.2021.3126455
Web of Science® Google Scholar
12 Wei C., Nadeem M. F., Siddiqui H. M. A., Azeem M., Liu J. B., and Khalil A., On partition dimension of some cycle-related graphs, Mathematical Problems in Engineering. (2021) 2021, 8, 4046909, https://doi.org/10.1155/2021/4046909.
10.1155/2021/4046909
Web of Science® Google Scholar
13 Estrado-Moreno A., Rodriguez-Velaquez J. A., and Yero I. G., The k-metric dimension of a graph, Appl. Math. Inf. Sci.(2015) 9, no. 6, 2829–2840.
Google Scholar
14 Hernando C., Mora M., Slater P. J., and Wood D. R., Fault-tolerant metric dimension of graphs, Proceedings of the international conference on convexity in Discrete Structures, April 2008, India, Ramanujan Mathematical Society: Tiruchirappalli, 81–85.
Google Scholar
15 Somasundari M. and Raj F. S., Fault-tolerant resolvability of oxide interconnections, IJITEE. (2019) 8, no. 12.
Google Scholar
16 Yero I. G., Estrada-Moreno A., and Rodríguez-Velázquez J. A., Computing the k -metric dimension of graphs, Applied Mathematics and Computation. (2017) 300, 60–69, https://doi.org/10.1016/j.amc.2016.12.005, 2-s2.0-85007400311.
10.1016/j.amc.2016.12.005
Web of Science® Google Scholar
17 Estrado-Moreno A., On the k-partition dimension of graphs, Theoretical Computer Science. (2020) 806, 42–52.
10.1016/j.tcs.2018.09.022
Web of Science® Google Scholar
18 Azhar K., Zafar S., Kashif A., and Zahid Z., On fault-tolerant partition dimension of graphs, Journal of Intelligent and Fuzzy Systems. (2021) 40, no. 1, 1129–1135, https://doi.org/10.3233/jifs-201390.
10.3233/JIFS-201390
Web of Science® Google Scholar
19 Chaudhry M. A., Salman M., and Javaid I., Fault-tolerant metric and partition dimension of graphs, Utilitas Mathematica. (2010) 83, 187–199.
Web of Science® Google Scholar
20 Nadeem A., Kashif A., Zafar S., and Zahid Z., On 2-partition dimension of the circulant graphs, Journal of Intelligent and Fuzzy Systems. (2021) 40, no. 5, 9493–9503, https://doi.org/10.3233/jifs-201982.
10.3233/JIFS-201982
Web of Science® Google Scholar
21 Baca M., On magic labeling of convex polytopes, Annals Discrete Math. (1992) 51, 13–16.
10.1016/S0167-5060(08)70599-5
Google Scholar
22 Baca M., Labelling of two classes of convex polytopes, Utilitas Mathematica. (1988) 34, 24–31.
Web of Science® Google Scholar

Citing Literature

All articles

Fault Tolerant Partition Resolvability in Convex Polytopes

Abstract

1. Introduction

1.1. Main Results

2. Fault Tolerant Partition Dimension of Convex Polytopes

2.1. Fault Tolerant Partition Dimension of R_n

2.2. Fault Tolerant Partition Dimension of Q_n

2.3. Fault Tolerant Partition Dimension of S_n

2.4. Fault Tolerant Partition Dimension of T_n

2.5. Fault Tolerant Partition Dimension of D_n

3. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Fault Tolerant Partition Resolvability in Convex Polytopes

Abstract

1. Introduction

1.1. Main Results

2. Fault Tolerant Partition Dimension of Convex Polytopes

2.1. Fault Tolerant Partition Dimension of Rn

2.2. Fault Tolerant Partition Dimension of Qn

2.3. Fault Tolerant Partition Dimension of Sn

2.4. Fault Tolerant Partition Dimension of Tn

2.5. Fault Tolerant Partition Dimension of Dn

3. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

2.1. Fault Tolerant Partition Dimension of R_n

2.2. Fault Tolerant Partition Dimension of Q_n

2.3. Fault Tolerant Partition Dimension of S_n

2.4. Fault Tolerant Partition Dimension of T_n

2.5. Fault Tolerant Partition Dimension of D_n