1. Introduction

For a long time, designers have effectively inherited the regional agricultural production culture when planning and designing the rural landscape, so that the regionality, originality, and uniqueness are well reflected. It can be seen that rural landscape is an important heritage of regional culture, which needs to be protected and effectively inherited. Moreover, even in the context of rapid urban development, it is necessary to provide sufficient space for the survival and development of rural culture. At the same time, in the planning and design, it is necessary to effectively integrate the elements of actual rural life, so that urban people can come into contact with more representative rural facilities, actively participate in rural activities, feel pleasure and happiness in the process of referring to landscape architecture, and cultivate their own sentiments. For example, when designing landscape gardens, we can design fruit and vegetable picking gardens, plan planting areas, and organize people to carry out picking activities, so that people can experience the joy of harvest while enjoying the beauty of the garden.

There are also great differences in rural landscapes from region to region. Therefore, when planning and designing landscape gardens, we should pay attention to grasp the integrity and conduct in-depth investigations, so that the planning and design can conform to the specific conditions of the garden and can be well coordinated with the surrounding environment. In particular, it is necessary to focus on the analysis of factors such as water flow and topography and reasonably choose the rural landscape, so that the two can be naturally integrated and the overall coordination can be well guaranteed [1].

Designers also need to pay attention to the coordination of benefits and costs. Under the premise of conditions permitting, they can transform rural consumption patterns and set up style restaurants, entertainment facilities, and so on. By combining these elements, commercial development requirements, market development needs, and modern people’s needs can be met. The entertainment and construction needs are well met, ensuring the visibility of the planning and design, which is more conducive to the increase of local farmers’ economic income [2]. Construction of farming landscape to create “practical integration” of landscape architectures has been studied. In the process of landscape architecture planning and design, the relevant personnel should be based on the rural landscape and effectively integrate into the regional culture. In detail, when planning and designing, it is necessary to fully respect and pay attention to local culture, history, and customs, while fully protecting economic crops, start the construction of landscapes with regional characteristics. At the same time, designers can appropriately introduce local economic actions when starting the planning and design of gardens and promote the development of landscape gardens to “practical integration” through appropriate crop planting [3]. It is also necessary to focus on integrating into the unique local rural landscape, continuously improve the level of regional consumption, and make foreign and local tourists have more expectations for entering the landscape garden, which will also play a certain role in driving the development of the local economy. Through reasonable planning and design, after entering the garden, foreign and local tourists can carry out a variety of outdoor activities, appreciate the unique customs, and enrich their spiritual world [4]. In addition, when planning and designing landscape architecture, relevant personnel should also innovatively integrate into the rural landscape, combine the characteristics of the times, make the planning and design more creative, and carry out reasonable innovation based on the local cultural foundation and the actual situation of landscape architecture, so as to better display the landscape architecture. Cultural connotation and promoting the sustainable development of landscape architecture are very important [5].

The colorful garden landscape is inseparable from the combination of design concepts and various technologies. In recent years, with the help of powerful modern horticultural technology, garden landscape design has made great progress in both quality and quantity of works [6]. For example, in the process of landscape design, computer software, 3DMAX, and other auxiliary technologies can be used to optimize the real effects such as landscape color matching in advance, thereby making the layout of the real scene more reasonable and richer in connotation. In the process of garden plant maintenance, the reasonable use of small-scale irrigation technology suitable for horticultural cultivation can not only make large-scale garden green vegetation fully absorb water, improve water resource utilization efficiency, play a role in energy conservation and environmental protection but also reduce maintenance costs. Cost and the investment of excessive human resources should be considered [7]. It can be seen that the continuous development of modern horticultural technology provides a better platform for garden landscape design, avoids the direct copying of previous construction models in the design process of garden landscape, and helps designers fully open their minds, give full play to their imagination, and burst into inspiration, to design an innovative landscape with both aesthetics and practicality [8].

There are many influencing factors in the actual design process of garden landscape. When designing for a specific location, the local conditions should be considered, and appropriate technical means should be used for design and construction [9]. The design process should be eclectic. For example, the use of axisymmetric structural patterns in buildings may not meet the aesthetic needs of garden landscape design, while minor repairs based on the original ecological environment can also make people’s eyes shine may be even better in terms of economy and compatibility. In addition, special attention should be paid to the layout and planning of gardens. Reasonable regional spatial distribution and design can drive the flow of local tourists and improve the aesthetics of tourists [10].

Garden landscape design and modern horticultural technology are interdependent. Garden landscape reflects the level of regional economic and technological development to a certain extent and is an important indicator to measure the satisfaction of local people. With the progress of a new round of scientific and technological revolution and industrial transformation, the introduction of modern horticultural technology in the process of garden landscape design can not only enrich the layout and modeling methods of gardens but also put forward higher requirements for horticultural technology itself, thereby promoting modern horticultural technology as constantly evolving, bringing forth new ideas. Landscape design and modern horticultural technology are interdependent and mutually reinforcing, and it is impossible to design satisfactory garden and garden works by ignoring either party [11].

In traditional Chinese architecture, there are many works of ingenious craftsmanship, and garden architecture is an important part of these works. Garden works can not only reflect the level of architecture but also reflect the level of social civilization. The level of architecture is not only affected by the level of science and technology of the times but also by the culture of the times. People put forward higher requirements for building quality and style, which promotes the improvement of building level [12]. The architectural level is of positive significance for the construction and protection of rural landscape gardens, and more excellent rural landscape gardens can be built through the improvement of the architectural level [13]. In the construction of rural landscape gardens, it is necessary to fully integrate the culture of the times, which is the deep excavation of the construction of rural landscape gardens. In the construction of rural landscapes, different architectural principles should be followed, different construction methods should be adopted in different areas, and local characteristics should be combined into the construction of rural landscape gardens. In its construction, it is necessary to ensure the development mode of combining landscape and use and combine garden construction with local economic development, which can not only promote the development of garden construction but also promote the improvement of the local economic level [14]. In the garden landscape, it is necessary to deeply integrate the local characteristics of economic development crops to make their development more modern. In the construction of rural garden landscapes, regional issues should be fully considered, and landscape construction should be carried out within the rural gardens [15]. When constructing rural gardens, it is necessary to fully consider landscape construction, choose natural landscapes that are more in line with reality, use as few artificial construction methods as possible, and directly select natural products to integrate them into gardens to make the gardens more attractive and attractive. Competitiveness is the most important factor in many cases [16]. The above construction requirements are a test of architectural level and architectural art. Only superb architectural level and art can build superb gardens. It is necessary to continuously strengthen research awareness and concepts to truly achieve sustainable development [17].

This paper combines the virtual simulation technology to carry out the rural garden landscape design and evaluates its design effect, so as to improve the rural garden landscape design effect.

2. Virtual Imaging Technology

2.1. Principle of One-Dimensional Linear Projection Optical Tomography

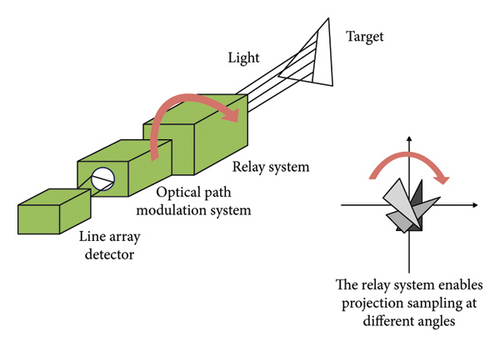
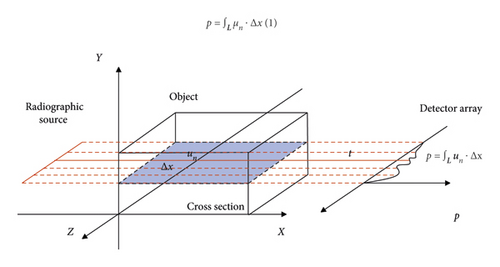
As shown in Figure 1, the image relay system realizes the surrounding of the target section by the detectors and pixel points in a similar virtual light, and the optical modulation system realizes the modulation of the signal after the image transfer into the projection of the target object. In the past research, the light intensity distribution of the target object on the camera target surface was collected by the area array camera as the original information of the two-dimensional distribution function of the target object, and then the integral projection function was obtained through calculation processing.

In the virtual light of garden landscape design, the line integral of the attenuation coefficient of the object along the specific path of the pixels collected by the detector is used as a measurement result. As shown in Equation (1), p is the projected measurement value and μ_n is the attenuation coefficient on a specific path L.

$$ (1)

The pixel point source and detector translate the acquired data along paths parallel and equally spaced to each other to form a set of projection measurements and then repeat the projection measurements around the target object at a fixed angle with a rotation center. It continues the whole process until the cumulative rotation angle reaches more than 180°, and the reconstructed virtual ray image is obtained by calibrating the collected data and calculating and reconstructing it, as shown in Figure 2. The mathematical modeling of this projection acquisition process is the Radon transform. In the Radon transform, formula (1) can be replaced by

$$ (2)

Among them, f(x, y) represents the target object, the straight line L can be represented as xcosθ + ysinθ = d, d represents the distance from the straight line to the coordinate origin or the center of rotation, and θ is the direction of the straight line. Equation (2) can be transformed into a function of angle θ and distance d and expanded by using the function δ, and then we have

$$ (3)

The radon transform is shown in Figure 3. In the normal image capturing process, the light reflected by the object passes through the lens group and falls on the camera target surface as a real image of the lens imaging law. After that, the area array detector obtains the distribution of the light intensity of the object, and the process of doing a line integral of the light intensity distribution along a specific direction is a set of projection measurements in the virtual light. The combined Radon transform is shown in formula (4), p(d, θ) is the line integral projection representation of the two-dimensional light intensity function of the target object, and l is the light intensity.

$$ (4)

After obtaining the projection function p(d, θ) of the target object, taking x = d when θ is 0 as an example, the Fourier transform of the projection function about x is obtained:

$$ (5)

Then, this paper performs a two-dimensional Fourier transform on the target object function f(x, y) and then sets v = 0 to obtain

$$ (6)

$$ (7)

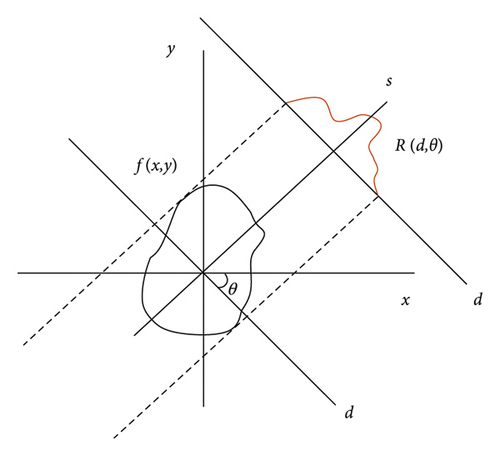
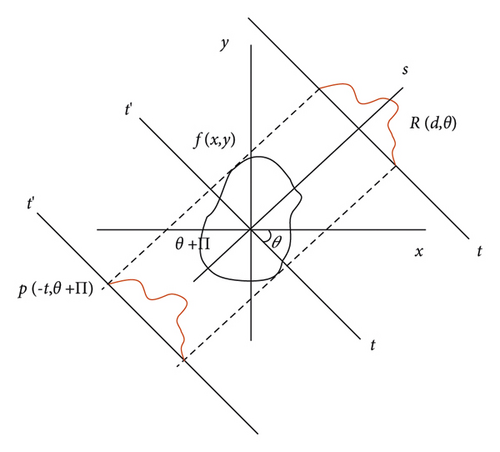
From formula (7), it can be concluded that the Fourier transform of the projection function of the target object function when the angle is $$ is equivalent to the straight line along the same direction angle in the two-dimensional Fourier transform of the target object function. Combined with the rotating coordinate system of formula (3), the projection of any angle can be generalized, as shown in Figure 4.

The coordinate system of f(x, y) is transformed into f^′(t, s), t = xcosθ + ysinθ, s = −xsinθ + ycosθ, and the projection function of the transformed target original function is subjected to Fourier transform with respect to the variable t:

$$ (8)

In addition, coordinate transformation is carried out with the Jacobian determinant and then substituted into formula (8) to get

$$ (9)

At the same time, this paper performs two-dimensional Fourier transform on the target object f(x, y) to obtain

$$ (10)

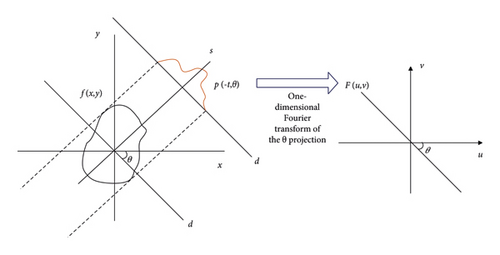
It can be observed that when u = ωcosθ and v = ωsinθ, formulas (9) and (10) are equal, and the line defined by the two conditions u = ωcosθ and v = ωsinθ coincides with the projection direction, resulting in the general form of the previous conclusion, namely, the Fourier slice theorem: the object f(x, y) obtains the Fourier parallel projection function at the angle θ to generate a 256∗256 pixels Shepp-Logan image using MATLAB. The one-dimensional Fourier transform of the $$ projection data is performed on the left as shown in Figure 5, and then the two-dimensional Fourier transform is performed on the Shepp-Logan head and body membrane and the corresponding Fourier space map is selected as shown on the right as shown in Figure 5. The second simulation argument is the same.

After completing the one-dimensional Fourier transform of a series of projections at different angles, the reconstructed image can be calculated by directly performing the inverse Fourier transform on the frequency domain space according to the following formula:

$$ (11)

Transforming (10) into polar coordinates, we get

$$ (12)

Substituting P(ω, θ) for F(ωcosθ, ωsinθ) according to the projected slice in the Fourier slice theorem, then (11) gets

$$ (13)

Extending this formula and according to the symmetry principle of the parallel beam sampling model, the projection data separated by 180^° are opposite to each other and equal to each other:

$$ (14)

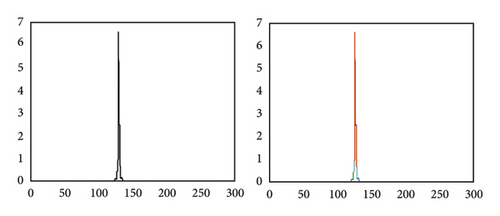
Figure 6 shows a schematic diagram of the symmetry of parallel beam sampling.

Correspondingly, in the frequency domain space, their respective Fourier transform expressions about the variable t also satisfy the symmetry. That is, P(ω, θ + π) = P(−ω, θ), and the integral domain of the angle is reduced from (0,2π) to (0, π) Therefore, formula (13) can be simplified to get

$$ (15)

The target object function f(x, y) can be obtained by the inverse Fourier transform of P(ω, θ)|ω| about ω, and t is the corresponding value of ω in the Fourier frequency space. The |ω| function is an inverted right triangle and extends infinitely. Therefore, P(ω, θ)|ω| can be understood as the filtering of the projection function in the frequency domain space through the |ω| function.

The filter function |ω| is an ideal “ramp” filter, and its two ends extend infinitely, so that the impulse response corresponding to the filter function is infinite. In the computer implementation, it is necessary to consider the finiteness and discreteness of the data, so the reconstruction calculation range is reduced from the frequency range (−∞, ∞) in formula (15) to setting the effective range (−Γ, Γ) and determining the number of frequency samples. According to the Nyquist sampling theorem, the sampling frequency range is at least twice the reciprocal of the sampling space interval d.

$$ (16)

The windowing function q(ω) is used to limit the sampling range to adapt the sampling number of the projection data, as shown in Figure 7.

The window function q(ω) is

$$ (17)

The filter function after windowing is

$$ (18)

The spatial domain form of the inverse Fourier transform corresponding to H(ω) is an impulse function:

$$ (19)

Based on the property that the product of the Fourier transform in the frequency domain is equal to the spatial convolution, the post integral in (14) can be converted into the convolution integral of the corresponding spatial domain function:

$$ (20)

From formula (20), it can be found that the original target image can be reconstructed by taking the angle integral of the directly sampled projection data and the corresponding airspace value of the impulse function. In the computer discretization process, the impulse function h(t) after the variable t is discretized as follows:

$$ (21)

The inner integral part in formula (20) is converted to spatial domain convolution as follows:

$$ (22)

where N is the number of samples for a single projection, and the value of k in p(k, θ) ranges from 0 to N − 1.

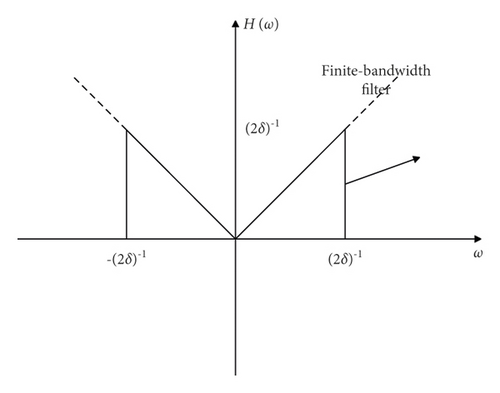
Since the signal strength of the sampling projection function is 0 outside [−N + 1, N − 1], it is only necessary to calculate the impulse response in the range of [−N + 1, N − 1]. In fact, in order to speed up the operation, the fast Fourier transform is generally used in the computer, so it is necessary to convert the h(t) function into a discrete frequency domain function H^′(ω) for calculation. For the wrapping effect and the artifacts at the edge of the image caused by the aperiodic convolution operation, it is also necessary to pad the projection data with zeros in the spatial domain before the operation.

Usually, using a certain window function can greatly improve the noise performance of tomography. In this study, we added a sinc window function to the filter function and set the upper and lower frequency limits to control the cutoff frequency to correct the image. The sinc window function is

$$ (23)

Compared with the matrix window function, the sinc window function focuses on compressing the high-frequency part, and the image noise is generally a high-frequency signal, so it can significantly reduce the image noise. However, it will lead to a slight decrease in spatial resolution, which can be optimized by adjusting the cutoff frequency.

2.2. One-Dimensional Optical Modulation System

Pechan prism is composed of a half pentagonal prism and a Schmidt prism in parallel with inclined planes, and the air gap between the two prisms generally has a thickness of 0.1 mm.

As shown in Figure 8, the angle between the incident light and the optical axis is a, which enters the prism from face 1 and exits from face 6 at an exit angle of −a after five reflections. To establish a rectangular calibration coordinate system (x′, y′, z′), the object-image conjugate relationship of the Pechan prism can be represented by the imaging matrix T, and the optical characteristics of the Pechan prism can be obtained:

$$ (24)

When the Pechan prism is rotated around the optical axis by an angle θ, the corresponding conjugate image vector is

$$ (25)

where $$ is the rotation matrix representing the rotation of the prism around the optical axis.

$$ (26)

Because of $$, by plugging it into formula (23), we get

$$ (27)

This shows that when the prism rotates θ and the image plane rotates 2θ with the optical axis as the center of rotation, the angle between the component $$ of the image vector conjugate A′ perpendicular to the optical axis and the component $$ of the rotated image in the same plane is

$$ (28)

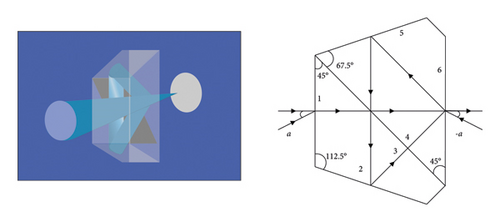
That is to say, the image rotation law of the Bielhan prism is that the rotation speed of the image is twice the rotation speed of the Bihan prism.

When the two segmented prisms in the Pechan prism are deflected relative to each other at the cemented surface, the outgoing optical axis is no longer collinear with the incident optical axis. When one of the segmented prisms rotates ω around the z-axis, the direction vector of the edge between the A-plane and the C-plane in the rotated Schmidt prism is $$. According to the action matrix and coordinate transformation matrix of the Schmidt prism, the relationship between the outgoing vector and the incoming vector can be obtained. After calculation according to formula (25), it can be obtained that when the ω angle is not large,

$$ (29)

From this, it can be obtained that when the main section of the two-point prism has a slight deflection angle, the outgoing light will be deflected to the main section deflection direction by 0.7 times the main section deflection error angle. The tower aberration is corrected by placing a wedge in the rotating prism assembly that produces opposite and equal deflection angles.

The second is the three-axis offset error. The plane where the incident ray and the outgoing ray are collinear is called the prism axis section. First, it is assumed that the prism axis coincides with the mechanical axis, and only the influence of the prism axis and the incident beam axis on the image point is considered. The offset between the incident optical axis $$ and the prism optical axis OO′ is Δi, A^′′ is the image point after the offset, and its translation on the plane perpendicular to the prism axis will only cause the offset of the image point on this plane.

When the incident light is perpendicular to the incident surface of the prism, the angle of rotation of the prism is θ. According to the translation error formula,

$$ (30)

Because of normal incidence, α = 0 and Δ_o1 = 2Δ_i1 can be obtained.

When the incident light axis and the prism axis have an inclination angle γ_i1 on the perpendicular plane of the prism axis plane at the incident plane, the corresponding image point A′ will also be shifted accordingly, and the outgoing light will also have a certain inclination angle relative to the prism axis. According to the law of angle deviation of Pechan prism, the angle of incidence γ_o1 = 2γ_i1 can be obtained, and the offset of the image point at the distance L from the main section can be obtained according to the similarity of triangles:

$$ (31)

On the premise that the prism axis coincides with the mechanical axis, after synthesizing the translational deviation and angular deviation between the incident optical axis and the prism axis, the comprehensive deviation can be obtained as follows:

$$ (32)

The moving position of the image point can be expressed by the following formula:

$$ (33)

$$ (34)

In the formula, β is the prism rotation angle.

When there is no deviation between the prism axis and the optical axis of the system, there are also translation errors and declination errors in the assembly between the mechanical rotation axis RR^′ and the prism axis OO^′. Unlike the optical axis deviation, which does not depend on the prism rotation angle in the translation deviation, the mechanical axis deviation can be obtained when the prism rotates a certain angle to obtain the offset components of the image point in two directions:

$$ (35)

$$ (36)

The two-component image point offset at the distance from the center point L of the main section can be expressed as follows:

$$ (37)

$$ (38)

By synthesizing the translational deviation and angular deviation of the mechanical axis, the corresponding image point trajectory expression of the rotating prism can be obtained:

$$ (39)

$$ (40)

3. Evaluation of the Application Effect of Virtual Simulation Technology in Rural Garden Landscape Design

The virtual simulation technology is applied to the rural garden landscape design, and the shot script is designed according to the nearby environment and the planning of the rural garden landscape. In the overall design, we must follow the principle of smoothness, and the connection between them must also conform to the law. In this process, we also need to display the rural garden landscape under different scenes, such as panoramic, medium, close-up, and close-up (Figure 9).

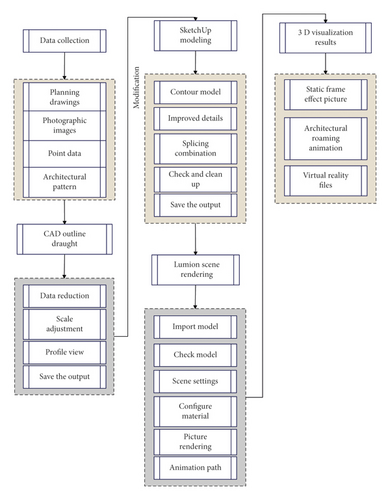
Figure 10 shows the effect of garden landscape design based on virtual reality technology.

This paper quantitatively evaluates the effect of the garden landscape design system based on virtual reality technology and counts the design effect, as shown in Table 1.

It can be seen from the above research that the garden landscape design system based on virtual reality technology proposed in this paper has a good effect and is of great significance to the effect of rural garden landscape design.

4. Conclusion

In the planning and design of landscape gardens, the relevant elements in the rural landscape should be harmoniously and effectively integrated to make the planning and design innovative. Specifically, when planning and designing landscape gardens, designers should appropriately reserve some cultivated land and rural buildings on both sides of the road based on the actual situation of the rural landscape. They can open farmhouses and homestays in the play area to effectively integrate the rural landscape. Moreover, they can set up rural activity areas, focusing on highlighting the idyllic scenery with the continuous advancement of the current urbanization construction. The use of rural landscapes in landscape architecture planning and design requires relevant personnel to reasonably design specific areas and be able to make reasonable use of farmland areas, wells, farm houses, and pastoral landscapes. This paper combines the virtual simulation technology to design the rural garden landscape and evaluates its design effect. The research shows that the garden landscape design based on virtual reality technology proposed in this paper has a good effect and is of great significance to the effect of rural garden landscape design.

Conflicts of Interest

The authors declare that there are no conflicts of interest.