Fixed Point Results of Jaggi-Type Hybrid Contraction in Generalized Metric Space
Abstract
In this manuscript, a new family of contractions called Jaggi-type hybrid (G − ϕ)-contraction is introduced and some fixed point results in generalized metric space that are not deducible from their akin in metric space are obtained. The preeminence of this class of contractions is that its contractive inequality can be extended in a variety of manners, depending on the given parameters. Consequently, several corollaries that reduce our result to other well-known results in the literature are highlighted and analyzed. Substantial examples are constructed to validate the assumptions of our obtained theorems and to show their distinction from corresponding results. Additionally, one of our obtained corollaries is applied to set up unprecedented existence conditions for the solution of a family of integral equations.
1. Introduction
The prominent Banach contraction in metric space has laid a solid foundation for fixed point theory in metric space. The applications of fixed point range across inequalities, approximation theory, optimization, and so on. Researchers in this area have introduced several new concepts in metric space and obtained a great deal of fixed point results for linear and nonlinear contractions. Recently, Karapınar and Fulga [1] introduced a new notion of hybrid contraction which is a unification of some existing linear and nonlinear contractions in metric space.
On the other hand, Mustafa [2] pioneered an extension of a metric space by the name, generalized metric space (or more precisely, G-metric space), and proved some fixed point results for Banach-type contraction mappings. This new generalization was brought to spotlight by Mustafa and Sims [3]. Subsequently, Mustafa et al. [4] obtained some engrossing fixed point results for Lipschitzian-type mappings on G-metric space. However, Jleli and Samet [5] as well as Samet et al. [6] noted that most of the fixed point results in G-metric space are direct consequences of existence results in corresponding metric space. Jleli and Samet [5] further observed that if a G-metric is consolidated into a quasimetric, then the resultant fixed point results become the known fixed point results in the setting of quasimetric space. Motivated by the latter observation, many investigators (see for instance, [7, 8]) have established techniques of obtaining fixed point results in G-metric space that are not deducible from their ditto ones in metric space or quasimetric space.
Following the existing literature, we realize that hybrid fixed point results in G-metric space are not adequately investigated. Hence, motivated by the ideas in [1, 7, 8], we introduce a new concept of Jaggi-type hybrid (G − ϕ)-contraction in G-metric space and prove some related fixed point theorems. An example is constructed to demonstrate that our result is valid, an improvement of existing results and the main ideas obtained herein do not reduce to any existence result in metric space. Some corollaries are presented to show that the concept proposed herein is a generalization and improvement of well-known fixed point results in G-metric space. Finally, one of our obtained corollaries is applied to establish novel existence conditions for solution of a class of integral equations.
2. Preliminaries
In this section, we will present some fundamental notations and results that will be deployed subsequently.
Throughout, every set Φ is considered nonempty, ℕ is the set of natural numbers, and ℝ represents the set of real numbers and ℝ+ the set of nonnegative real numbers.
Definition 1 (see [3].)Let Φ be a nonempty set and let G : Φ × Φ × Φ⟶ℝ+ be a function satisfying
(G1) G(r, s, t) = 0 if r = s = t
(G2) 0 < G(r, r, s) for all r, s ∈ Φ with r ≠ s
(G3) G(r, r, s) ≤ G(r, s, t), for all r, s, t ∈ Φ with t ≠ s
(G4) G(r, s, t) = G(r, t, s) = G(s, r, t) = ⋯ (symmetry in all variables)
(G5) G(r, s, t) ≤ G(r, u, u) + G(u, s, t), for all r, s, t, u ∈ Φ (rectangle inequality)
Then, the function G is called a generalized metric or, more precisely, a G-metric on Φ, and the pair (Φ, G) is called a G-metric space.
Example 2 (see [4].)Let (Φ, d) be a usual metric space; then, (Φ, Gk) and (Φ, Gm) are G-metric spaces, where
Definition 3 (see [4].)Let (Φ, G) be a G-metric space and let {rn} be a sequence of points of Φ. Then, {rn} is said to be G-convergent to r if limn,m⟶∞G(r, rn, rm) = 0; that is, for any ε > 0, there exists n0 ∈ ℕ such that G(r, rn, rm) < ε, ∀n, m ≥ n0. We refer to r as the limit of the sequence {rn}.
Proposition 4 (see [4].)Let (Φ, G) be a G-metric space. Then, the following are equivalent:
- (i)
{rn} is G-convergent to r
- (ii)
G(r, rn, rm)⟶0, as n⟶∞
- (iii)
G(rn, r, r)⟶0, as n⟶∞
- (iv)
G(rn, rn, r)⟶0, as n⟶∞
Definition 5 (see [4].)Let (Φ, G) be a G-metric space. A sequence {rn} is called G-Cauchy if for any ε > 0, we can find n0 ∈ ℕ such that G(rn, rm, rl) < ε, ∀n, m, l ≥ n0, that is, G(rn, rm, rl)⟶0, as n, m, l⟶∞.
Proposition 6 (see [4].)If (Φ, G) is a G-metric space, the following statements are equivalent:
- (i)
The sequence {rn} is G-Cauchy
- (ii)
For every ε > 0, there exists n0 ∈ ℕ such that G(rn, rm, rm) < ε, ∀n, m ≥ n0
Definition 7 (see [4].)Let (Φ, G) and (Φ′, G′) be G-metric spaces and f : (Φ, G)⟶(Φ′, G′) be a function. Then, f is G-continuous at a point u ∈ Φ if and only if for any ε > 0, there exists δ > 0 such that r, s ∈ Φ; and G(u, r, s) < δ implies G′(f(u), f(r), f(s)) < ε. A function f is G-continuous on Φ if and only if it is G-continuous at all u ∈ Φ.
Proposition 8 (see [4].)Let (Φ, G) and (Φ′, G′) be G-metric spaces. Then, a function f : (Φ, G)⟶(Φ′, G′) is said to be G-continuous at a point r ∈ Φ if and only if it is G-sequentially continuous at r; that is, whenever {rn} is G-convergent to r, {frn} is G-convergent to fr.
Definition 9 (see [4].)A G-metric space (Φ, G) is called symmetric G-metric space if
Proposition 10 (see [4].)Let (Φ, G) be a G-metric space. Then, the function G(r, s, t) is jointly continuous in all variables.
Proposition 11 (see [4].)Every G-metric space (Φ, G) defines a metric space (Φ, dG) by
Note that for a symmetric G-metric space (Φ, G),
On the other hand, if (Φ, G) is not symmetric, then by the G-metric properties,
and that in general, these inequalities are sharp.
Definition 12 (see [4].)A G-metric space (Φ, G) is referred to as G-complete (or complete G-metric) if every G-Cauchy sequence in (Φ, G) is G-convergent in (Φ, G).
Proposition 13 (see [4].)A G-metric space (Φ, G) is G-complete if and only if (Φ, dG) is a complete metric space.
Mustafa [2] proved the following result in the framework of G-metric space.
Theorem 14 (see [2].)Let (Φ, G) be a complete G-metric space, and let Γ : Φ⟶Φ be a mapping satisfying the following condition:
for all r, s, t ∈ Φ where 0 ≤ k < 1; then, Γ has a unique fixed point (say u, i.e., Γu = u), and Γ is G-continuous at u.
Definition 15 (see [9].)Let Ψ be the set of all functions ϕ : ℝ+⟶ℝ+ satisfying
- (i)
ϕ is monotone increasing, that is, t1 ≤ t2 implies ϕ(t1) ≤ ϕ(t2)
- (ii)
the series is convergent for all t > 0
Then, ϕ is called a (c)-comparison function.
Remark 16. If ϕ ∈ Ψ, then ϕ(t) < t for any t > 0, ϕ(0) = 0, and ϕ is continuous at 0.
Karapınar and Fulga [1] gave the following definition of Jaggi-type hybrid contraction in metric space.
Definition 17 (see [1].)Let (Φ, d) be a complete metric space. A self-mapping Γ : Φ⟶Φ is called a Jaggi-type hybrid contraction; if there exists ϕ ∈ Φ such that
λ1, λ2 ≥ 0 with λ1 + λ2 = 1 and Fix(Γ) = {r ∈ Φ : Γr = r}.
3. Main Results
We begin this section by defining the notion of Jaggi-type hybrid (G − ϕ)-contraction in G-metric space.
Definition 18. Let (Φ, G) be a G-metric space. A self-mapping Γ : Φ⟶Φ is called a Jaggi-type hybrid (G − ϕ)-contraction, if there exists ϕ ∈ Φ such that
λ1, λ2 ≥ 0 with λ1 + λ2 = 1 and Fix(Γ) = {r ∈ Φ : Γr = r}.
We now present the following results.
Theorem 19. Let (Φ, G) be a complete G-metric space and let Γ : Φ⟶Φ be a continuous Jaggi-type hybrid (G − ϕ)-contraction on (Φ, G). Then, Γ has a fixed point in Φ (say c), and for any c0 ∈ Φ, the sequence converges to c.
Proof. Let r0 ∈ Φ be an arbitrary point and define a sequence in Φ by rn = Γnr0. If there exists some n ∈ ℕ such that Γrn = rn+1 = rn, then rn is a fixed point of Γ, and so the proof is complete. Assume now that rn ≠ rn−1 for any n ∈ ℕ. Since Γ is a Jaggi-type hybrid (G − ϕ)-contraction, then we have from (9) that
We then consider the given cases of (10).
Case 1. For q > 0, we have
so we get Γc = c, that is, c is a fixed point of Γ.
Case 2. For q = 0, we have
By similar argument as the case of q > 0, we can show that there exists a G-Cauchy sequence {rn} in (Φ, G) and a point c in Φ such that limn⟶∞rn = c. Similarly, under the assumption that Γ is continuous and by the uniqueness of limit, we have that Γc = c, that is, c is a fixed point of Γ.
In the next result, we examine the existence of unique fixed point of Γ under the restriction of continuity of some iterates of Γ.
Theorem 20. Let (Φ, G) be a complete G-metric space and let Γ : Φ⟶Φ be a Jaggi-type hybrid (G − ϕ)-contraction. If for some integer i > 2, we have that Γi is continuous, then Γ has a unique fixed point in Φ.
Proof. In Theorem 19, we have established that there exists a G-Cauchy sequence in (Φ, G) with rn = Γrn−1 such that rn⟶c for some c in Φ. Let be a subsequence of where nl = l · i for all l ∈ ℕ, i > 2 fixed. Notice that Γ0 is an identity self-mapping on Φ so that . Hence, by the continuity of Γi, we have
that is, c is a fixed point of Γi.
which is a contradiction. Hence, Γc = c.
By similar argument as in Case 1, we obtain a contradiction. Hence, Γc = c.
Example 21. Let Φ = [−1, 1] and let Γ : Φ⟶Φ be a self-mapping on Φ defined by
for all r ∈ Φ. Define G : Φ × Φ × Φ⟶ℝ+ by
Then, (Φ, G) is a complete G-metric space and Γ is continuous for all r ∈ Φ. Define ϕ ∈ Ψ by ϕ(x) = x/2 for all x ≥ 0.
To see that Γ is a Jaggi-type hybrid (G − ϕ)-contraction, notice that G(Γr, Γs, Γ2s) = 0 for all r, s ∈ (−1, 1). Hence, inequality (9) holds for all r, s ∈ (−1, 1).
Hence, inequality (9) is satisfied for all r, s ∈ Φ. Therefore, Γ is a Jaggi-type hybrid (G − ϕ)-contraction. Consequently, all the assumptions of Theorem 19 are satisfied, and r = 1/5 is the fixed point of Γ.
Also, Karapınar and Fulga [1] declared in Definition (17) that r and s are distinct, since M(r, s) is undefined for Case 1 if r = s. However, our result is valid for all r, s ∈ Φ\Fix(Γ).
The above comparison is illustrated graphically for all r, s ∈ {−1, 1}, using the following Figures 1 and 2.
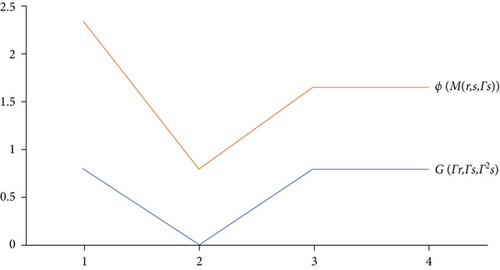
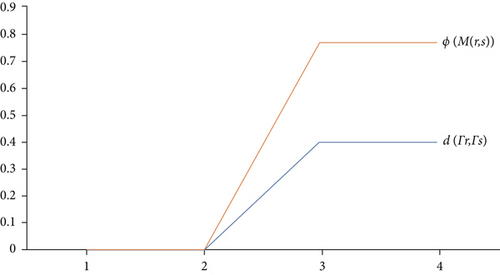
Therefore, Jaggi-type hybrid (G − ϕ)-contraction is not Jaggi-type hybrid contraction defined by Karapınar and Fulga [1], and so Theorem 1 due to Karapınar and Fulga [1] is not applicable to this example.
Corollary 22 (see Theorem 14.)Let (Φ, G) be a complete G-metric space, and let Γ : Φ⟶Φ be a mapping satisfying the following condition:
for all r, s, t ∈ Φ where 0 ≤ k < 1; then, Γ has a unique fixed point (say u) and Γ is G-continuous at u.
Proof. Consider Definition (18) and let Γs = t, λ1 = 0, λ2 = 1, q > 0, and ϕ(p) = kp for all p ≥ 0 and k ∈ [0, 1). Clearly, ϕ ∈ Ψ and Γ is a Jaggi-type hybrid (G − ϕ)-contraction. Hence, (9) coincides with (6) of Theorem 14 due to Mustafa [2]. Therefore, it is easy to see that we can find a unique point u in Φ such that Γu = u and Γ is G-continuous at u.
Corollary 23 (see [10], Theorem 3.1.)Let (Φ, G) be a complete G-metric space. Suppose the mapping Γ : Φ⟶Φ satisfies
for all r, s, t ∈ Φ. Then, Γ has a unique fixed point (say u) and Γ is G-continuous at u.
Proof. Consider Definition 18 and let Γs = t, λ1 = 0, λ2 = 1 and q > 0. Then,
for all r, s, t ∈ Φ. Hence, inequality (9) becomes
for all r, s, t ∈ Φ and ϕ ∈ Ψ. This coincides with Theorem 3.1 due to Shatanawi [10] and so the proof follows in a similar manner.
By specializing the parameters λi(i = 1, 2) and q, as well as letting ϕ(p) = μp for all p ≥ 0 and for μ ∈ (0, 1), the following result is also a direct consequence of Theorem 19.
Corollary 24. Let (Φ, G) be a complete G-metric space. If there exists μ ∈ (0, 1) such that for all r, s ∈ Φ, the mapping Γ : Φ⟶Φ satisfies
then Γ has a fixed point in Φ.
4. Applications to Solution of Integral Equation
In this section, Corollary 24 is applied to examine the existence criteria for a solution to a class of integral equations. Ideas in this section are motivated by [7, 11, 12].
Then, (Φ, G) is a complete G-metric space.
Then, a point u∗ is said to be a fixed point of Γ if and only if u∗ is a solution to (52).
Now, we study existence conditions of the integral equation (52) under the following hypotheses.
Theorem 25. Assume that the following conditions are satisfied:
(C1) and f : [a, b] × ℝ⟶ℝ are continuous
(C2) For all r, s ∈ Φ, x ∈ [a, b], we have |f(x, r(x)) − f(x, s(x))| ≤ |r(x) − s(x)|
(C3) for some μ < 1
Then, the integral equation (52) has a solution u∗ in Φ.
Proof. Observe that for any r, s ∈ Φ, using (55) and the above hypotheses, we obtain
Hence, all the required hypotheses of Corollary 24 are satisfied, implying that there exists a solution u∗ in Φ of the integral equation (52).
Conversely, if u∗ is a solution of (52), then u∗ is also a solution of (55) so that Γu∗ = u∗, that is, u∗ is a fixed point of Γ.
Remark 26.
- (i)
We can deduce a number of corollaries by particularizing some of the parameters in Definition 18
- (ii)
None of the results presented in this work can be expressed in the form G(r, s, s) or G(r, r, s). Hence, they cannot be obtained from their corresponding versions in metric space
5. Conclusion
A generalization of metric space was introduced by Mustafa and Sims [3], namely, G-metric space and several fixed point results were studied in that space. However, Jleli and Samet [5] as well as Samet et al. [6] established that most fixed point theorems obtained in G-metric space are direct consequences of their analogues in metric space. Contrary to the above observation, a new family of contractions called Jaggi-type hybrid (G − ϕ)-contraction is introduced in this manuscript and some fixed point theorems that cannot be deduced from their corresponding ones in metric space are proved. The main distinction of this class of contractions is that its contractive inequality is expressible in a number of ways with respect to multiple parameters. Consequently, some corollaries including recently announced results in the literature are highlighted and analyzed. Nontrivial comparative examples are constructed to validate the assumptions of our obtained theorems. Furthermore, one of our obtained corollaries is applied to set up novel existence conditions for solution of a class of integral equations.
Conflicts of Interest
The authors declare that they have no competing interests.
Authors’ Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Acknowledgments
This work was funded by the University of Jeddah, Saudi Arabia, under grant no. UJ-21-DR-92. The authors, therefore, acknowledge with thanks the university technical and financial support.
Open Research
Data Availability
No data were used to support this study.




