Volume 2022, Issue 1 1899130

Research Article

Open Access

Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform

Pongsakorn Sunthrayuth

orcid.org/0000-0001-5210-8505

Department of Mathematics and Computer Science, Faculty of Science and Technology, Rajamangala University of Technology Thanyaburi (RMUTT), Thanyaburi, Pathumthani, Thailand rmutt.ac.th

Search for more papers by this author

Haifa A. Alyousef,

Haifa A. Alyousef

Department of Physics, College of Science, Princess Nourah Bint Abdulrahman University, P.O. Box 84428, Riyadh 11671, Saudi Arabia pnu.edu.sa

Search for more papers by this author

S. A. El-Tantawy,

S. A. El-Tantawy

orcid.org/0000-0002-6724-7361

Department of Physics, Faculty of Science, Port Said University, Port Said 42521, Egypt psu.edu.eg

Research Center for Physics (RCP), Department of Physics, Faculty of Science and Arts, Al-Mikhwah, Al-Baha University, Al Bahah 1988, Saudi Arabia bu.edu.sa

Search for more papers by this author

Adnan Khan,

Adnan Khan

Department of Mathematics, Abdul Wali Khan University Mardan, Mardan 23200, Pakistan awkum.edu.pk

Search for more papers by this author

Noorolhuda Wyal,

Corresponding Author

Noorolhuda Wyal

[email protected]

orcid.org/0000-0002-8425-6446

Department of Mathematics, Polytechnical University of Kabul, Kabul, Afghanistan

Search for more papers by this author

Pongsakorn Sunthrayuth,

Pongsakorn Sunthrayuth

orcid.org/0000-0001-5210-8505

Department of Mathematics and Computer Science, Faculty of Science and Technology, Rajamangala University of Technology Thanyaburi (RMUTT), Thanyaburi, Pathumthani, Thailand rmutt.ac.th

Search for more papers by this author

Haifa A. Alyousef,

Haifa A. Alyousef

Department of Physics, College of Science, Princess Nourah Bint Abdulrahman University, P.O. Box 84428, Riyadh 11671, Saudi Arabia pnu.edu.sa

Search for more papers by this author

S. A. El-Tantawy,

S. A. El-Tantawy

orcid.org/0000-0002-6724-7361

Department of Physics, Faculty of Science, Port Said University, Port Said 42521, Egypt psu.edu.eg

Research Center for Physics (RCP), Department of Physics, Faculty of Science and Arts, Al-Mikhwah, Al-Baha University, Al Bahah 1988, Saudi Arabia bu.edu.sa

Search for more papers by this author

Adnan Khan,

Adnan Khan

Department of Mathematics, Abdul Wali Khan University Mardan, Mardan 23200, Pakistan awkum.edu.pk

Search for more papers by this author

Noorolhuda Wyal,

Corresponding Author

Noorolhuda Wyal

[email protected]

orcid.org/0000-0002-8425-6446

Department of Mathematics, Polytechnical University of Kabul, Kabul, Afghanistan

Search for more papers by this author

First published: 21 May 2022

https://doi.org/10.1155/2022/1899130

Citations: 12

Academic Editor: Hemen Dutta

Share a link

Email
Wechat
Bluesky

Abstract

Motivated by the importance of diffusion equations in many physical situations in general and in plasma physics in particular, therefore, in this study, we try to find some novel solutions to fractional-order diffusion equations to explain many of the ambiguities about the phenomena in plasma physics and many other fields. In this article, we implement two well-known analytical methods for the solution of diffusion equations. We suggest the modified form of homotopy perturbation method and Adomian decomposition methods using Jafari-Yang transform. Furthermore, illustrative examples are introduced to show the accuracy of the proposed methods. It is observed that the proposed method solution has the desire rate of convergence toward the exact solution. The suggested method’s main advantage is less number of calculations. The proposed methods give series form solution which converges quickly towards the exact solution. To show the reliability of the proposed method, we present some graphical representations of the exact and analytical results, which are in strong agreement with each other. The results we showed through graphs and tables for different fractional-order confirm that the results converge towards exact solution as the fractional-order tends towards integer-order. Moreover, it can solve physical problems having fractional order in different areas of applied sciences. Also, the proposed method helps many plasma physicists in modeling several nonlinear structures such as solitons, shocks, and rogue waves in different plasma systems.

1. Introduction

The integer-order differentiation operators are used to study local phenomena, whereas fractional-order operators are used to studying nonlocal phenomena [1]. The mathematical groundwork for fractional-order derivatives was laid by the collective struggles of various mathematicians, such as Riemann, Liouville, Caputo, Podlubny, Miller, and Ross. Afterward, numerous mathematicians dedicated their efforts to this area. Fractional calculus (FC) can be described as very successful in many phenomena in applied sciences, fluid mechanics, physics of plasmas [2, 3], and other biology utilising mathematical tools of FC. [4, 5]. Other numerous applications of FC in the field of science and technology are related to solid mechanics [6, 7], anomalous transport [8], continuum and statistical mechanics [9], economics [10], relaxation electrochemistry [11], diffusion procedures [12], complex networks [13, 14], and optimal control problems [15, 16].

Fractional differential equations (FDEs) have gotten a lot of attention from researchers in the last decade due to their ability to improve real-world challenges in different areas of engineering and physics. Mathematicians used various methods described based on the above applications to solve different important fractional-order differential equations (FDEs), mainly partial differential equations of fractional-orders (FPDEs). FPDEs are fundamental mathematical approaches that can be utilized to model different physical models more accurately than integer-order models. Nonlinear FPDEs define various phenomena in engineering, plasma physics, and applied sciences. Especially, nonlinear FPDEs are the preeminent tools to be used in various areas, for example, electrochemistry [17], mathematical social dynamics [18, 19], signal processing [20], informatics [21], traffic model [22], theory of solitons in plasma physics [23], biology [24], and much more [25–28]. Moreover, many authors reduced the fluid plasma equations to FDEs for studying the impact of derivative time-frational on the profile of nonlinear structures in a plasma [2, 3]. For instance, El-Wakil et al. [2] reduced the basic equations of a collisionaless unmagnetized nonthermal plasma having cold inertial electrons and inertialess nonthermal electrons as well as stationary positive ions to a normal KdV equation. After that, the authors use a suitable transformation to convert the normal KdV equation to a time-fractional KdV equation in order to investigate the time-fractional on the profile of electron-acoustic (EA) solitons. Furthermore, the basic equations of an ultrarelativistic plasma were reduced to the normal cylindrical Kadomtsev–Petviashvili (CKP) and cylindrical modified KP (CmKP) equations using a reductive perturbation techniques [3]. Posteriorly, the mentioned equations were converted into space-time fractional CKP and CmKP equations using one of the proper transformations in order to study the influence of space-time fractional domain of the characteristics of the ion-acoustic waves (IAWs) in the ultrarelativistic plasma. The authors made a comparison between the integer- and fractional-order models and found that the fractional-order model gives description to the IAWs in the ultrarelativistic plasmas better than the integer-order model [3]. In literature, different methods are implemented for solving FDEs, such as Iterative Laplace Transform method (ILTM) [29, 30], Approximate-analytical method (AAM) [31], Homotopy Analysis method (HAM) [32], Variational Iteration method (VIM) [33], Elzaki Transform Decomposition method (ETDM) [34], the Differential Transformation method (DTM) [35], and the homotopy perturbation method (HPM) [36, 37].

In literature, there is lot of transformations [38–40], but in this article, we implement the Homotopy Perturbation Jafari-Yang Transform Method (HPYTM) and Jafari-Yang transform decomposition method (YTDM) for the analysis of fractional-order diffusion equations. Xiao-Jun Jafari-Yang introduce the Jafari-Yang transformation and applied for the analysis of different differential problems with constant coefficients, while the Adomian decomposition method [41, 42], on the other hand, is a renowned method to solve linear and nonlinear and nonhomogeneous and homogeneous differential, integro, ordinary, and partial differential equations. It gives analysis in the form of series that converges towards the exact solutions quickly. In 1998, He introduced the homotopy perturbation technique [43, 44]. Later, the nonlinear nonhomogeneous partial differential equations are solved using the HPM (homotopy perturbation method), a semianalytical technique [45–48]. The solution is assumed to be the sum of an infinite sequence that converges rapidly to the exact results. This approach was investigated to analyze both linear and nonlinear problems. In the current work, we proposed a novel approximate analytical method known as (HPYTM). The newly developed technique is the combination of Jafari-Yang transform and HPM. It is investigated that the present methods are very effective in finding fractional diffusion equations analytical solution. The fractional problem results using the proposed methods are also devoted to the fractional view analysis of the problems. It is confirmed that the current techniques can be modified to solve other fractional partial differential equations.

A type of PDE that expresses the phenomenon of atoms or molecule’s movement from a region of higher concentration to an area of lower concentration is known as diffusion equations. Adolf Fick, a physiologist, was the first to present Fick’s law of diffusion. Fick’s law was then transformed into the diffusion equation. Scholar modified diffusion equations such as slow diffusion and the hybrid classical wave equation by generalizing the classical diffusion law [49]. Several implementations of diffusion equation are phase transition, electromagnetism, filtration, biochemistry, geochemistry, dynamics of biological groups, cosmology, plasma physics, and acoustics [50]. There are many investigations related to the Diffusion-type equation and its applications in plasma physics and fluids [51–53]. Motivated by these investigation, in this article, we implement YTDM and HPYTM for solving diffusion equations of the form.

(1)
Fractional-order diffusion equation in one dimension as
(1)
having initial values
(2)
(2)
Fractional-order diffusion equation in two dimension as
(3)
having initial values
(4)
(3)
Fractional-order diffusion equation in three dimension as
(5)
having initial values
(6)

2. Preliminaries

We covered several fundamental fractional calculus definitions as well as Laplace transform theory properties in this section.

Definition 1. In Caputo manner, the fractional derivative is given as [54].

(7)

Definition 2. Yang and Jafari introduced the Jafari-Yang Laplace transform in 2018. Y(.) determines the Jafari-Yang transform for a function ξ(τ) and is given as [55].

(8)

The inverse transform is given as

(9)

Definition 3. For derivative of order n, the Jafari-Yang transform is determined as [55].

(10)

Definition 4. For fractional-order derivatives, the Jafari-Yang transform is given as [55].

(11)

Definition 5. The Mittag-Leffler function, a generalisation of the exponential function, is as [54].

(12)

Equation (12) further generalization is of the form

(13)

3. Homotopy Perturbation Jafari-Yang Transform Method

To explain the basic ideas of this approach the following equation is considered:

(14)

with some initial sources

(15)

where Caputo‘s derivative, and L[ψ] and N[ψ] are the linear and nonlinear operators respectively.

Implement Jafari-Yang transform to (14), we have

(16)

(17)

Equation (17) implies that

(18)

We now have by using the inverse Jafari-Yang transform

(19)

Now, perturbation technique having parameter ε is given as

(20)

where perturbation parameter is ε and ε ∈ [0, 1].

The decomposition of nonlinear terms is defined as

(21)

where H_n are of the form ν₀, ν₁, ν₂, ⋯, ν_n, and can be determined as

(22)

where

Using (21) and (22) in (19) and making the homotopy, we get

(23)

When the coefficient of ε on both sides is compared, we get

(24)

As a result, we can quickly determine component ν_k(ψ, τ), which leads us to the convergent series. We get by taking ε⟶1,

(25)

The result is in the form of a series that rapidly converges to the exact solution of the problem.

4. Idea of YTDM

Consider the fractional order partial differential equation

(26)

with some initial sources

(27)

where

denotes the derivative having fractional-order σ in Caputo manner, and

and

denote linear and nonlinear functions.

On taking Jafari-Yang transformation of (26), we get

(28)

By using Jafari-Yang transform property of differentiation, we have

(29)

Equation (29) implies that

(30)

We now have by using the inverse Jafari-Yang transform

(31)

The infinite series of ν(ψ, τ)

(32)

The nonlinear term decomposition of

by Adomian polynomials is expressed as

(33)

All nonlinear terms can be denoted by means of Adomian polynomials as

(34)

putting Equations (32) and (34) into (31), gives

(35)

The following terms are described as

(36)

The general for k ≥ 1 is determined as

(37)

5. Applications

The solutions to various fractional order diffusion equations are obtained by implementing HPYTM and YTDM in this section.

Example 1. Consider one-dimension fractional-order diffusion equation [54]

(38)

with initial source

(39)

On taking Jafari-Yang transformation of Equation (38), we get

(40)

We get by using the Jafari-Yang transform’s differential property

(41)

(42)

By applying inverse Jafari-Yang transform to Equation (42)

(43)

Now, applying the abovementioned homotopy perturbation technique as in (23), we obtain

(44)

where H_k(ν) are He’s polynomial that represents the nonlinear terms. He’s polynomials first few components are given by

(45)

Comparing the same power coefficient of ε, we obtain

(46)

By taking ε⟶1, we obtain the convergence series type result is given as

(47)

When σ = 1, the HPYTM solution is

(48)

The analytical results by YTDM.

On taking Jafari-Yang transformation of Equation (38), we obtain

(49)

Using the Jafari-Yang transform the differential property, we get

(50)

(51)

By inverse Jafari-Yang transform of Equation (51)

(52)

Assuming the unknown ν(ψ, τ) function has the following infinite series form solution:

(53)

The Adomian polynomials and , as well as the nonlinear term, have been described. Applying specific function, Equation (52) may be determined as

(54)

According to Equation (34), the nonlinear function can be find with the help of Adomian polynomials is given as

(55)

Thus, on comparing both sides of Equation (54)

(56)

For k = 0

(57)

For k = 1

(58)

For k = 2

(59)

The remaining YTDM solution elements ρ_k for (k ≥ 2) are similarly simple to get. As a result, the solution in series form is as

(60)

When σ = 1, the solution by YTDM is

(61)

In closed form, the exact solution is

(62)

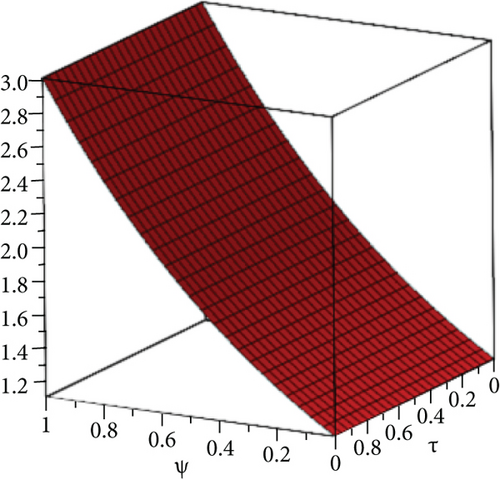
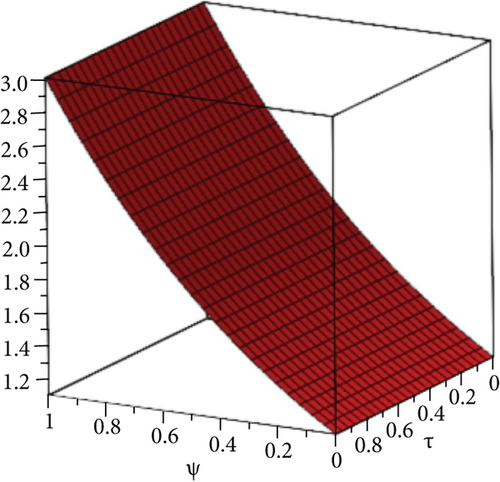
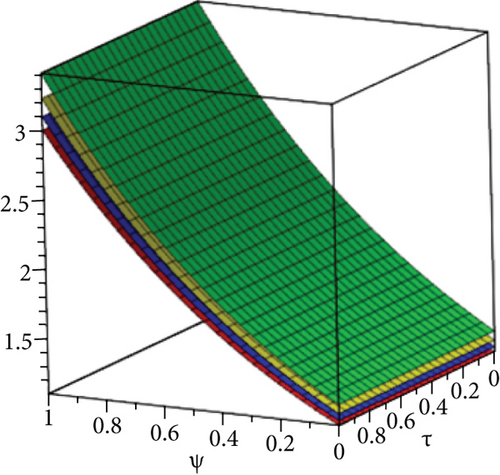
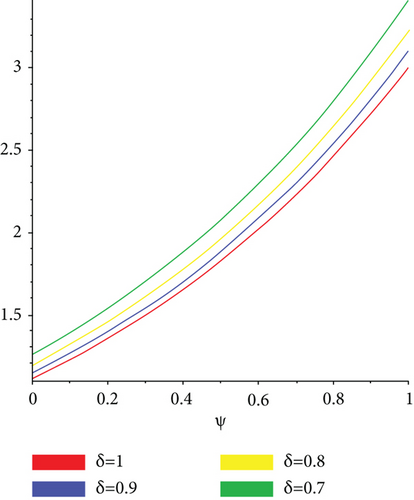
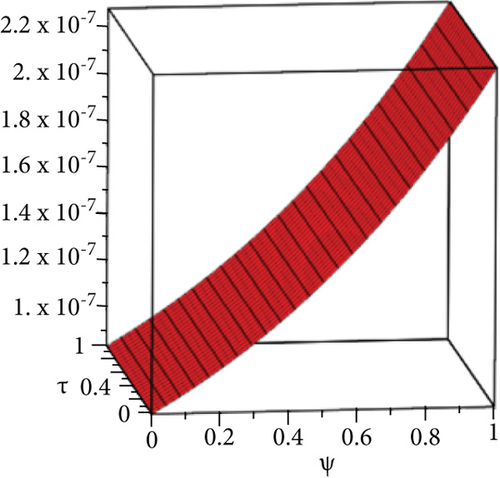
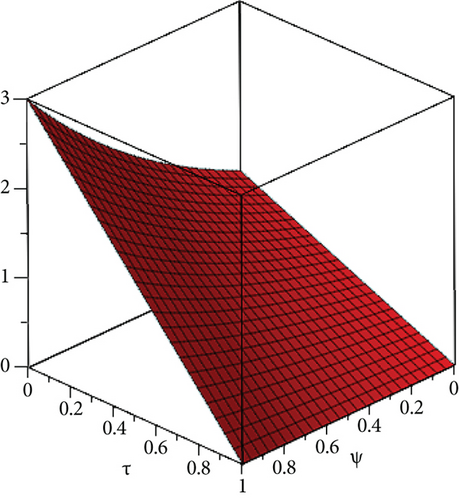
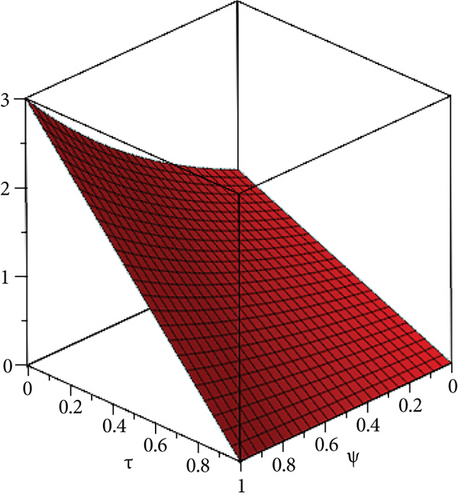
The exact solution shown in Figures 1(a) and 1(b) shows HPYTM and YTDM solution at σ = 1 and 0 ≤ ψ ≥ 1. Figure 2(a) shows the solution graph for different values of σ = 1,0.9,0.8,0.7 and 0 ≤ ψ ≥ 1 of Example 1 and Figure 2(b), respectively, at τ ∈ [0, 1] and 0 ≤ ψ ≥ 1 while Figure 2(c) shows the error graph. Also, Table 1 shows the comparison of the exact solution and our methods solution with the aid of absolute error at various fractional order. From the figures and table, it is clear that HPYTM and YTDM solution shows strong contact with the exact solutions of the problem.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Example 1 solution graph. (a) Exact solution and (b) analytical solution at σ = 1.

Table 1. ν(ψ, τ) comparison of exact solution, our methods’ solution, and Absolute Error (AE) of Example 1.

τ = 0.01	Absolute error	Absolute error	Exact solution	Our methods’ solution	Absolute error
ψ	σ = 0.8	σ = 0.9	σ = 1	σ = 1	σ = 1
0	5.2118400000E-04	5.0962000000E-05	1.0100501670000	1.0100501670000	0.00000000E+00
0.1	5.7599800000E-04	5.6322000000E-05	1.1162780700000	1.1162780700000	0.00000000E+00
0.2	6.3657500000E-04	6.2245000000E-05	1.2336780600000	1.2336780600000	0.00000000E+00
0.3	7.0352500000E-04	6.8792000000E-05	1.3634251140000	1.3634251140000	0.00000000E+00
0.4	7.7751600000E-04	7.6027000000E-05	1.5068177850000	1.5068177850000	0.00000000E+00
0.5	8.5928700000E-04	8.4022000000E-05	1.6652911950000	1.6652911950000	0.00000000E+00
0.6	9.4965800000E-04	9.2858000000E-05	1.8404313990000	1.8404313980000	1.00000000E-09
0.7	1.0495350000E-03	1.0262400000E-04	2.0339912590000	2.0339912580000	1.00000000E-09
0.8	1.1599150000E-03	1.1341700000E-04	2.2479079870000	2.2479079860000	1.00000000E-09
0.9	1.2819060000E-03	1.2534600000E-04	2.4843225330000	2.4843225330000	0.00000000E+00
1.0	1.4167240000E-03	1.3852800000E-04	2.7456010150000	2.7456010140000	1.00000000E-09

Example 2. Consider one-dimension fractional-order gas dynamic equation [56]

(63)

with initial source

(64)

On taking Jafari-Yang transformation of Equation (63), we get

(65)

We get by using the Jafari-Yang transform’s differential property

(66)

(67)

By applying inverse Jafari-Yang transform to Equation (67)

(68)

Now, applying the abovementioned homotopy perturbation technique as in (23), we obtain

(69)

where H_k(ν) are He’s polynomial that represents the nonlinear terms. He’s polynomials first few components are given by

(70)

Comparing the same power coefficient of ε, we obtain

(71)

By taking ε⟶1, we obtain the convergence series type result is given as

(72)

When σ = 1, the HPYTM solution is

(73)

The analytical results by YTDM

On taking Jafari-Yang transformation of Equation (63), we obtain

(74)

using the Jafari-Yang transform the differential property, we get

(75)

(76)

By inverse Jafari-Yang transform of Equation (76)

(77)

Assuming the unknown ν(ψ, τ) function has the following infinite series form solution:

(78)

The Adomian polynomials and , as well as the non-linear term, have been described. Applying specific function, Equation (77) may be determined as

(79)

According to Equation (34), the nonlinear function can be found with the help of Adomian polynomials is given as

(80)

Thus, on comparing both sides of Equation (79)

(81)

For k = 0

(82)

For k = 1

(83)

For k = 2

(84)

The remaining YTDM solution elements ρ_k for (k ≥ 3) are similarly simple to get. As a result, the solution in series form is as

(85)

When σ = 1, the solution by YTDM is

(86)

In closed form, the exact solution is

(87)

Figure 3(a) shows the solution graph for different values of σ = 1, 0.9, 0.8, 0.7 and 0 ≤ ψ, ϕ ≥ 1 of Example 2 and Figure 3(b), respectively, at ϕ = 0.5, τ ∈ [0, 1] and 0 ≤ ψ ≥ 1 while Figure 3(c) shows the error graph. It is verified from the figures that HPYTM and YTDM solution is closely related with the exact solution.

Example. 3. Consider two-dimension fractional-order diffusion equation [54]

(88)

with initial source

(89)

Taking Jafari-Yang transformation to Equation (88), we get

(90)

We get by using the Jafari-Yang transform’s differential property

(91)

By applying inverse Jafari-Yang transform to Equation (91)

(92)

Now, using the abovementioned homotopy perturbation technique as in (23), we get

(93)

Comparing the same power coefficient of ε, we obtain

(94)

By taking ε⟶1, we obtain convergence series type result is

(95)

When σ = 1, the HPYTM solution is

(96)

The analytical results by YTDM

Taking Jafari-Yang transformation of Equation (88), we obtain

(97)

We get by using the Jafari-Yang transform’s differential property

(98)

(99)

By inverse Jafari-Yang transform of Equation (99)

(100)

Assuming the unknown ν(ψ, ϕ, τ) function has the following infinite series form solution:

(101)

Thus, on comparing both sides of Equation (101)

(102)

For k = 0

(103)

For k = 1

(104)

For k = 2

(105)

For k = 3

(106)

The remaining YTDM solution elements ρ_k for (k ≥ 3) are similarly simple to get. As a result, the solution in series form is as

(107)

When σ = 1, the solution by YTDM is

(108)

In closed form, the exact solution is:

(109)

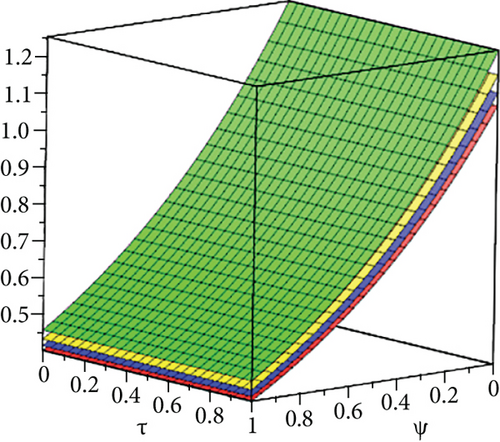
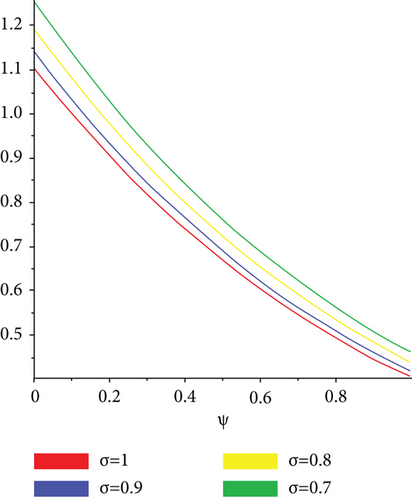
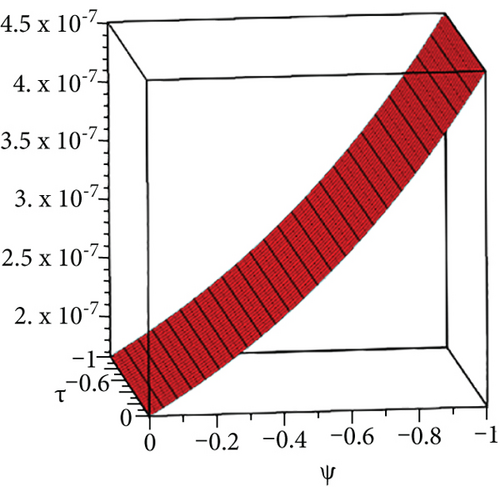
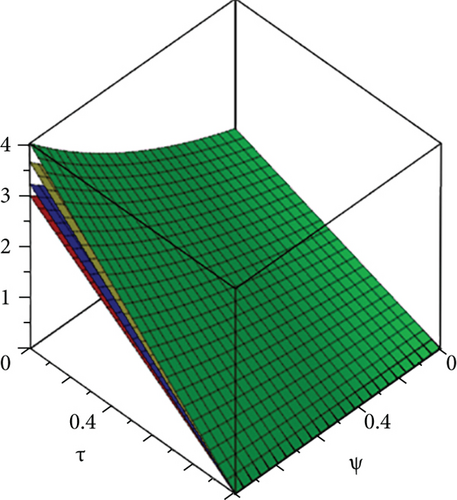
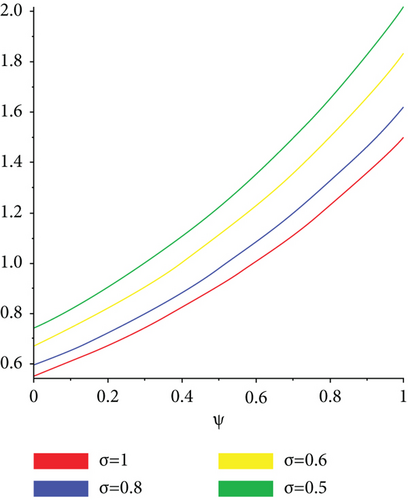
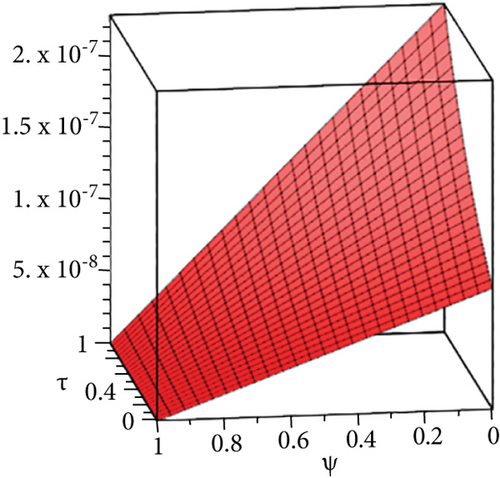
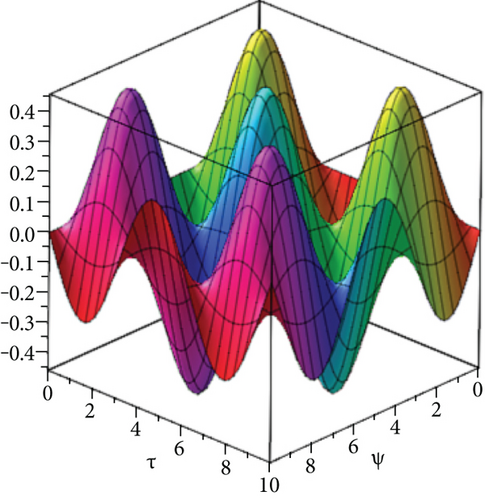
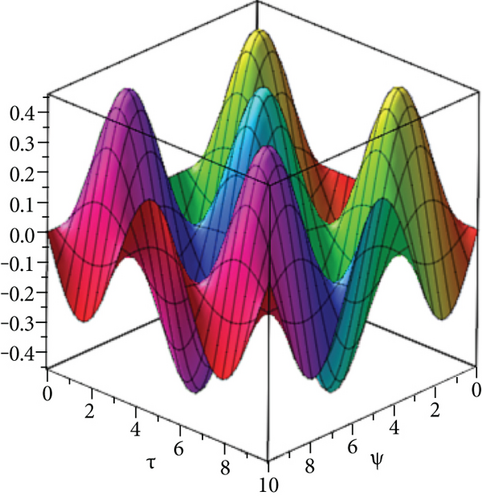
The exact solution shown in Figures 4(a) and 4(b) shows HPYTM and YTDM solutions at σ = 1 and 0 ≤ ψ, ϕ ≥ 1. Figure 5(a) shows the error graph for different values of σ = 1,0.8,0.6,0.5 and 0 ≤ ψ, ϕ ≥ 1 of Example 3 and Figure 5(d) respectively, at ϕ = 0.5, τ ∈ [0, 1] and 0 ≤ ψ ≥ 1 while Figure 5(e) shows the error graph. From the figures and Table 2, it is clear that HPYTM and YTDM solution shows strong agreement with the exact solutions of the problem.

Example 4. Consider three-dimension fractional-order diffusion equation [54]

(110)

with initial source

(111)

Taking Jafari-Yang transformation of Equation (110), we get

(112)

We get by using the Jafari-Yang transform’s differential property

(113)

(114)

By applying inverse Jafari-Yang transform to Equation (113)

(115)

Now, using the abovementioned homotopy perturbation technique as in (23), we obtain

(116)

Comparing the same power coefficient of ε, we get

(117)

By taking ε⟶1, we obtain the convergence series type result is given as

(118)

When σ = 1, then the HPYTM solution in a closed form:

(119)

The analytical results by YTDM

Taking Jafari-Yang transformation of Equation (110), we obtain

(120)

We get by using the Jafari-Yang transform’s differential property

(121)

(122)

by inverse Jafari-Yang transform of Equation (121)

(123)

Assuming the unknown ν(ψ, ϕ, φ, τ) function has the following infinite series form solution:

(124)

(125)

Thus, on comparing both sides of Equation (124)

(126)

For k = 0

(127)

For k = 1

(128)

For k = 2

(129)

For k = 3

(130)

The remaining YTDM solution elements ρ_k for (k ≥ 3) are similarly simple to get. As a result, the solution in series form is as

(131)

When σ = 1, then the closed form solution by YTDM

(132)

In closed form, the exact solution is

(133)

Table 2. ν(ψ, ϕ, τ) comparison of exact solution, our methods’ solution, and Absolute Error (AE) of Example 3.

τ = 0.01	Exact solution	Our methods’ solution	AE of our methods	AE of our methods	AE of our methods
ψ	σ = 1	σ = 1	σ = 1	σ = 0.9	σ = 0.8
0	0.505025083500000	0.505025083500000	0.0000000000E+00	2.5480900000E-05	2.6059160000E-04
0.1	0.558139035000000	0.558139035100000	1.0000000000E-10	2.8160900000E-05	2.8799840000E-04
0.2	0.616839030000000	0.616839029800000	2.0000000000E-10	3.1122300000E-05	3.1828710000E-04
0.3	0.681712557000000	0.681712557200000	2.0000000000E-10	3.4395800000E-05	3.5176210000E-04
0.4	0.753408892500000	0.753408892700000	2.0000000000E-10	3.8013200000E-05	3.8875720000E-04
0.5	0.832645597500000	0.832645597600000	1.0000000000E-10	4.2011000000E-05	4.2964300000E-04
0.6	0.920215699500000	0.920215699100000	4.0000000000E-10	4.6428800000E-05	4.7482850000E-04
0.7	1.016995630000000	1.016995629000000	1.0000000000E-09	5.1311000000E-05	5.2476600000E-04
0.8	1.123953994000000	1.123953993000000	1.0000000000E-09	5.6708000000E-05	5.7995600000E-04
0.9	1.242161266000000	1.242161267000000	1.0000000000E-09	6.2673000000E-05	6.4095200000E-04
1.0	1.372800508000000	1.372800507000000	1.0000000000E-09	6.9263000000E-05	7.0836100000E-04

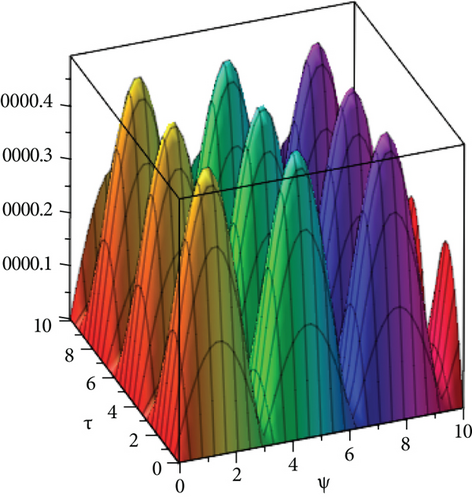
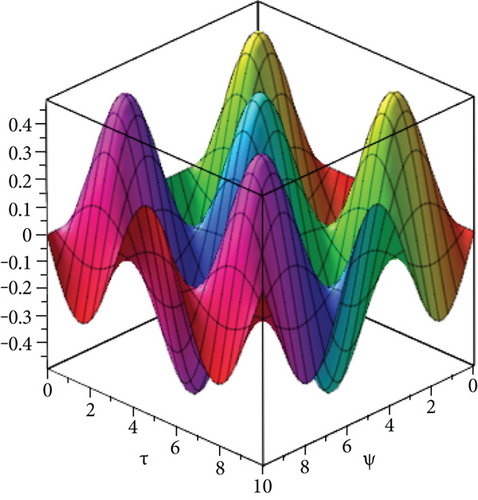
In Figures 6(a) and 6(b), we consider fixed order σ = 1 for piecewise approximation values of ψ, ϕ in the domain 0 ≤ ψ, ϕ ≥ 10 and = 1 . Figure 7(a) shows error graph and Figure 7(b) represents HPYTM and YTDM solution at σ = 0.6 of Example 4. It is verified from the Figures 6(a) and 6(b) and Table 3 that HPYTM and YTDM solution is closely related with the exact solution.

Table 3. ν(ψ, ϕ, φ, τ) comparison of exact solution, our methods’ solution, and Absolute Error (AE) of Example 4.

τ = 0.01	Exact solution	Our methods’ solution	AE of our methods	AE of our methods	AE of our methods
ψ	σ = 1	σ = 1	σ = 1	σ = 0.9	σ = 0.8
0	0.00000000000000	0.00000000000000	0.000000000E+00	0.000000000E+00	0.000000000E+00
0.1	0.039084756460000	0.039084756470000	8.4147098480E-12	5.8916348320E-06	6.0179783350E-05
0.2	0.077778990960000	0.077778990980000	1.6829419700E-11	1.1724408770E-05	1.1975827680E-04
0.3	0.115696083500000	0.115696083500000	0.0000000000E+00	1.7440075190E-05	1.7814016480E-04
0.4	0.152457179000000	0.152457179000000	0.0000000000E+00	2.2981414070E-05	2.3474221550E-04
0.5	0.187694972800000	0.187694972800000	8.4147098480E-11	2.8293115510E-05	2.8899866580E-04
0.6	0.221057380400000	0.221057380400000	0.0000000000E+00	3.3322251000E-05	3.4036760840E-04
0.7	0.252211055800000	0.252211055900000	8.4147098480E-11	3.8018332270E-05	3.8833574600E-04
0.8	0.280844721700000	0.280844721700000	8.4147098480E-11	4.2334573540E-05	4.3242369270E-04
0.9	0.306672279900000	0.306672280000000	8.4147098480E-11	4.6227807340E-05	4.7219102240E-04
1.0	0.329435670100000	0.329435670200000	8.4147098480E-11	4.9659157730E-05	5.0724039260E-04

6. Conclusion

In the present article, different analytical techniques are used to show the fractional view analysis of diffusion equations. In Caputo, manner fractional derivative is considered. The suggested techniques are tested to solve fractional-order diffusion equations. It is observed that the suggested techniques are the best tool for investigating fractional partial differential equations. The close relation between the exact and analytical results is confirmed by the plotted graphs. The given methods give series form solution which have higher convergence rate towards the exact results. It is also shown that both methods give same solution for the proposed problems. Finally, both proposed methods are very methodical and efficient and may be used to investigate nonlinear physical problems related to physics of plasmas such as modeling nonlinear unmodulated and modulated structures. Moreover, the obtained results/solutions can be useful in investigating the diffusion characteristics of some plasmas and fluids.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this article.

Acknowledgments

The authors express their gratitude to Princess Nourah Bint Abdulrahman University Researchers Supporting Project (Grant No. PNURSP2022R17), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.

Open Research

Data Availability

The numerical data used to support the findings of this study are included within the article.

References

1 He J. H., Nonlinear oscillation with fractional derivative and its applications, International conference on vibrating engineering, 1998, Dalian, China, 288–291.
Google Scholar
2 El-Wakil S. A., Abulwafa E. M., El-Shewy E. K., and Mahmoud A. A., Time-fractional KdV equation for plasma of two different temperature electrons and stationary ion, Physics of Plasmas. (2011) 18, no. 9, article 092116, https://doi.org/10.1063/1.3640533, 2-s2.0-80053537615.
10.1063/1.3640533
Web of Science® Google Scholar
3 Liu Q. and Chen L., Time-space fractional model for complex cylindrical ion-acoustic waves in Ultrarelativistic plasmas, Complexity. (2020) 2020, 16, 9075823, https://doi.org/10.1155/2020/9075823.
10.1155/2020/9075823
Web of Science® Google Scholar
4 Atangana A. and Gmez-Aguilar J. F., Decolonisation of fractional calculus rules: breaking commutativity and associativity to capture more natural phenomena, The European Physical Journal Plus. (2018) 133, no. 4, https://doi.org/10.1140/epjp/i2018-12021-3, 2-s2.0-85046029896.
10.1140/epjp/i2018-12021-3
Web of Science® Google Scholar
5 Almeida R., Bastos N. R., and Monteiro M. T. T., Modeling some real phenomena by fractional differential equations, Mathematical Methods in the Applied Sciences. (2016) 39, no. 16, 4846–4855, https://doi.org/10.1002/mma.3818, 2-s2.0-84951728518.
10.1002/mma.3818
Web of Science® Google Scholar
6 Rossikhin Y. A. and Shitikova M. V., Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results, Applied Mechanics Reviews. (2010) 63, no. 1, https://doi.org/10.1115/1.4000563, 2-s2.0-85065556461.
10.1115/1.4000563
Web of Science® Google Scholar
7 Rossikhin Y. A., Reflections on two parallel ways in the progress of fractional calculus in mechanics of solids, Applied Mechanics Reviews. (2010) 63, no. 1, https://doi.org/10.1115/1.4000246.
10.1115/1.4000246
Web of Science® Google Scholar
8 R. Klages, G. Radons, and I. M. Sokolov, Anomalous Transport: Foundations and Applications, 2008, John Wiley and Sons, https://doi.org/10.1002/9783527622979, 2-s2.0-84889426838.
10.1002/9783527622979
Google Scholar
9 A. Carpinteri and F. Mainardi, Fractals and Fractional Calculus in Continuum Mechanics, 2014, 378, Springer.
Google Scholar
10 Tarasov V. E., On history of mathematical economics: application of fractional calculus, Mathematics. (2019) 7, no. 6, https://doi.org/10.3390/math7060509, 2-s2.0-85066821676.
10.3390/math7060509
Web of Science® Google Scholar
11 Martynyuk V. and Ortigueira M., Fractional model of an electrochemical capacitor, Signal Processing. (2015) 107, 355–360, https://doi.org/10.1016/j.sigpro.2014.02.021, 2-s2.0-85027943946.
10.1016/j.sigpro.2014.02.021
Web of Science® Google Scholar
12 Zhang Y., Sun H., Stowell H. H., Zayernouri M., and Hansen S. E., A review of applications of fractional calculus in earth system dynamics, Chaos, Solitons and Fractals. (2017) 102, https://doi.org/10.1016/j.chaos.2017.03.051, 2-s2.0-85017185071.
10.1016/j.chaos.2017.03.051
Web of Science® Google Scholar
13 Turalska M. and West B. J., Fractional dynamics of individuals in complex networks, Frontiers in Physics. (2018) 6, https://doi.org/10.3389/fphy.2018.00110, 2-s2.0-85055132782.
10.3389/fphy.2018.00110
Web of Science® Google Scholar
14 Li H. L., Cao J., Jiang H., and Alsaedi A., Finite-time synchronization and parameter identification of uncertain fractional-order complex networks, Physica A: Statistical Mechanics and its Applications. (2019) 533, article 122027, https://doi.org/10.1016/j.physa.2019.122027, 2-s2.0-85068847735.
10.1016/j.physa.2019.122027
Web of Science® Google Scholar
15 Mohammadi F., Moradi L., Baleanu D., and Jajarmi A., A hybrid functions numerical scheme for fractional optimal control problems: application to nonanalytic dynamic systems, Journal of Vibration and Control. (2017) 24, no. 21, 107754631774176–107754631775043, https://doi.org/10.1177/1077546317741769, 2-s2.0-85045293850.
10.1177/1077546317741769
Web of Science® Google Scholar
16 Jajarmi A. and Baleanu D., On the fractional optimal control problems with a general derivative operator, Asian Journal of Control. (2021) 23, no. 2, 1062–1071, https://doi.org/10.1002/asjc.2282.
10.1002/asjc.2282
Web of Science® Google Scholar
17 Oldham K. B., Fractional differential equations in electrochemistry, Advances in Engineering Software. (2010) 41, no. 1, 9–12, https://doi.org/10.1016/j.advengsoft.2008.12.012, 2-s2.0-70350567183.
10.1016/j.advengsoft.2008.12.012
Web of Science® Google Scholar
18 Vitanov N. K., Dimitrova Z. I., and Ausloos M., Verhulst-Lotka-Volterra (VLV) model of ideological struggle, Physica A. (2010) 389, no. 21, 4970–4980, https://doi.org/10.1016/j.physa.2010.06.032, 2-s2.0-77956174396.
10.1016/j.physa.2010.06.032
Web of Science® Google Scholar
19 Vitanov N. K. and Panchev S., Generalization of the model of conflict between two armed groups, Comptes Rendus de l'Académie Bulgare des Sciences. (2008) 61, 1121–1126.
Google Scholar
20 Povstenko Y., Signaling problem for time-fractional diffusion-wave equation in a half-space in the case of angular symmetry, Nonlinear Dynamics. (2010) 59, no. 4, 593–605, https://doi.org/10.1007/s11071-009-9566-0, 2-s2.0-77949274545.
10.1007/s11071-009-9566-0
Web of Science® Google Scholar
21 Mandelbrot B., Some noises withI/fspectrum, a bridge between direct current and white noise, IEEE Transactions on Information Theory. (1967) 13, no. 2, 289–298, https://doi.org/10.1109/TIT.1967.1053992, 2-s2.0-84926570205.
10.1109/TIT.1967.1053992
Web of Science® Google Scholar
22 He J. H., Some applications of nonlinear fractional differential equations and their approximations, Bulletin of Science and Technology. (1999) 15, no. 2, 86–90.
Google Scholar
23 Ablowitz M. and Clarkson P. A., Solitons, Nonlinear Evolution Equations and Inverse Scattering, 2010, Cambridge University Press, Cambridge, England.
Google Scholar
24 Scott A. C., Neuroscience: A Mathematical Primer, 2002, Springer, New York, NY, USA.
Google Scholar
25 Singh H. and Wazwaz A. M., Computational method for reaction diffusion-model arising in a spherical catalyst, International Journal of Applied and Computational Mathematics. (2021) 7, no. 3, 1–11, https://doi.org/10.1007/s40819-021-00993-9.
10.1007/s40819-021-00993-9
CAS Google Scholar
26 Agarwal R. P., Mofarreh F., Shah R., Luangboon W., and Nonlaopon K., An analytical technique, based on natural transform to solve fractional-order parabolic equations, Entropy. (2021) 23, no. 8, https://doi.org/10.3390/e23081086.
10.3390/e23081086
Web of Science® Google Scholar
27 Singh H., Srivastava H. M., and Kumar D., A reliable numerical algorithm for the fractional vibration equation, Chaos, Solitons & Fractals. (2017) 103, 131–138, https://doi.org/10.1016/j.chaos.2017.05.042, 2-s2.0-85020285442.
10.1016/j.chaos.2017.05.042
Web of Science® Google Scholar
28 Aljahdaly N. H., Agarwal R. P., Shah R., and Botmart T., Analysis of the time fractional-order coupled burgers equations with non-singular kernel operators, Mathematics. (2021) 9, no. 18, https://doi.org/10.3390/math9182326.
10.3390/math9182326
Google Scholar
29 Khan H., Khan A., Al-Qurashi M., Shah R., and Baleanu D., Modified modelling for heat like equations within Caputo operator, Energies. (2020) 13, no. 8, https://doi.org/10.3390/en13082002.
10.3390/en13082002
Web of Science® Google Scholar
30 Jafari H., Nazari M., Baleanu D., and Khalique C. M., A new approach for solving a system of fractional partial differential equations, Computers & Mathematics with Applications. (2013) 66, no. 5, 838–843, https://doi.org/10.1016/j.camwa.2012.11.014, 2-s2.0-84881474367.
10.1016/j.camwa.2012.11.014
Web of Science® Google Scholar
31 Mirmoradia S. H., Hosseinpoura I., Ghanbarpour S., and Barari A., Application of an approximate analytical method to nonlinear Troeschs problem, Applied Mathematical Sciences. (2009) 3, no. 32, 1579–1585.
Google Scholar
32 Liao S., On the homotopy analysis method for nonlinear problems, Applied Mathematics and Computation. (2004) 147, no. 2, 499–513, https://doi.org/10.1016/S0096-3003(02)00790-7, 2-s2.0-0141961626.
10.1016/S0096-3003(02)00790-7
Web of Science® Google Scholar
33 Lu J., An analytical approach to the Fornberg-Whitham type equations by using the variational iteration method, Computers & Mathematcs with Applications. (2011) 61, no. 8, 2010–2013, https://doi.org/10.1016/j.camwa.2010.08.052, 2-s2.0-79953736761.
10.1016/j.camwa.2010.08.052
Web of Science® Google Scholar
34 Khan H., Khan A., Kumam P., Baleanu D., and Arif M., An approximate analytical solution of the Navier–Stokes equations within Caputo operator and Elzaki transform decomposition method, Adv. Difference Equ.(2020) 2020, no. 1, https://doi.org/10.1186/s13662-020-03058-1.
10.1186/s13662-020-03058-1
PubMed Web of Science® Google Scholar
35 Shou D. H. and He J. H., Beyond Adomian method: the variational iteration method for solving heat-like and wave-like equations with variable coefficients, Physics Letters A. (2008) 372, no. 3, 233–237, https://doi.org/10.1016/j.physleta.2007.07.011, 2-s2.0-37449033064.
10.1016/j.physleta.2007.07.011
CAS Web of Science® Google Scholar
36 Qin Y., Khan A., Ali I., Al Qurashi M., Khan H., Shah R., and Baleanu D., An efficient analytical approach for the solution of certain fractional-order dynamical systems, Energies. (2020) 13, no. 11, https://doi.org/10.3390/en13112725.
10.3390/en13112725
Web of Science® Google Scholar
37 Iqbal N., Akgül A., Shah R., Bariq A., Mossa Al-Sawalha M., and Ali A., On solutions of fractional-order gas dynamics equation by effective techniques, Journal of Function Spaces. (2022) 2022, https://doi.org/10.1155/2022/3341754.
10.1155/2022/3341754
Web of Science® Google Scholar
38 Jafari H., A new general integral transform for solving integral equations, Journal of Advanced Research. (2021) 32, 133–138, https://doi.org/10.1016/j.jare.2020.08.016, 34484832.
10.1016/j.jare.2020.08.016
PubMed Web of Science® Google Scholar
39 Meddahi M., Jafari H., and Yang X. J., Towards new general double integral transform and its applications to differential equations, Mathematical Methods in the Applied Sciences. (2022) 45, no. 4, 1916–1933, https://doi.org/10.1002/mma.7898.
10.1002/mma.7898
Web of Science® Google Scholar
40 Meddahi M., Jafari H., and Ncube M. N., New general integral transform via Atangana-Baleanu derivatives, Adv. Difference Equ.(2021) 2021, no. 1, https://doi.org/10.1186/s13662-021-03540-4.
10.1186/s13662-021-03540-4
Web of Science® Google Scholar
41 Adomian G., Solution of physical problems by decomposition, Computers and Mathematics with Applications. (1994) 27, no. 9-10, 145–154, https://doi.org/10.1016/0898-1221(94)90132-5, 2-s2.0-0000244996.
10.1016/0898-1221(94)90132-5
Web of Science® Google Scholar
42 Adomian G., A review of the decomposition method in applied mathematics, Journal of Mathematical Analysis and Applications. (1988) 135, article 501544.
Web of Science® Google Scholar
43 He J. H., Homotopy perturbation technique, Computer Methods in Applied Mechanics and Engineering. (1999) 178, no. 3-4, 257–262, https://doi.org/10.1016/S0045-7825(99)00018-3, 2-s2.0-0032672778.
10.1016/S0045-7825(99)00018-3
Web of Science® Google Scholar
44 He J. H., A coupling method of a homotopy technique and a perturbation technique for non-linear problems, International Journal of Non-Linear Mechanics. (2000) 35, no. 1, 37–43, https://doi.org/10.1016/S0020-7462(98)00085-7, 2-s2.0-0033702384.
10.1016/S0020-7462(98)00085-7
Web of Science® Google Scholar
45 He J. H., Application of homotopy perturbation method to nonlinear wave equations, Chaos, Solitons & Fractals. (2005) 26, no. 3, 695–700, https://doi.org/10.1016/j.chaos.2005.03.006, 2-s2.0-18844426016.
10.1016/j.chaos.2005.03.006
Web of Science® Google Scholar
46 He J. H., Limit cycle and bifurcation of nonlinear problems, Chaos, Solitons & Fractals. (2005) 26, no. 3, 827–833, https://doi.org/10.1016/j.chaos.2005.03.007, 2-s2.0-18844391045.
10.1016/j.chaos.2005.03.007
Web of Science® Google Scholar
47 He J. H., Homotopy perturbation method for solving boundary value problems, Physics Letters A. (2006) 350, no. 1-2, 87–88, https://doi.org/10.1016/j.physleta.2005.10.005, 2-s2.0-30644460357.
10.1016/j.physleta.2005.10.005
CAS Web of Science® Google Scholar
48 He J. H., Non-perturbative Methods for Strongly Nonlinear Problems, [Ph.D. thesis], 2006, de-Verlag im Internet GmbH.
Google Scholar
49 Jafari H., Iterative Methods for Solving System of Fractional Differential Equations, [Ph.D. thesis], 2006, Pune University, Pune City, India.
Google Scholar
50 Shah K., Khalil H., and Khan R. A., Analytical solutions of fractional order diffusion equations by natural transform method, Iranian Journal of Science and Technology, Transactions A: Science. (2018) 42, no. 3, 1479–1490, https://doi.org/10.1007/s40995-016-0136-2, 2-s2.0-85051222556.
10.1007/s40995-016-0136-2
Web of Science® Google Scholar
51 El-Tantawy S. A., Salas A. H., and Albalawi Wedad, New localized and periodic solutions to a Korteweg-de Vries equation with power law nonlinearity: applications to some plasma models, Symmetry. (2020) 14, no. 2, https://doi.org/10.3390/sym14020197.
10.3390/sym14020197
Web of Science® Google Scholar
52 El-Tantawy S. A., Alharbey R. A., and Salas A. H., Novel approximate analytical and numerical cylindrical rogue wave and breathers solutions: An application to electronegative plasma, Chaos, Solitons & Fractals. (2022) 155, https://doi.org/10.1016/j.chaos.2021.111776.
10.1016/j.chaos.2021.111776
Web of Science® Google Scholar
53 Shah N. A., Alyousef H. A., El-Tantawy S. A., Shah R., and Chung J. D., Analytical investigation of fractional-order Korteweg-De-Vries-Type equations under Atangana-Baleanu-Caputo operator: modeling nonlinear waves in a plasma and fluid, Symmetry. (2022) 14, no. 4, https://doi.org/10.3390/sym14040739.
10.3390/sym14040739
Google Scholar
54 Liu H., Khan H., Mustafa S., Mou L., and Baleanu D., Fractional-order investigation of diffusion equations via analytical Approach, Physics. (2021) 8, https://doi.org/10.3389/fphy.2020.568554.
10.3389/fphy.2020.568554
Google Scholar
55 Dattu M. K. U., New integral transform: fundamental properties, investigations and applications, Journal for Advanced Research in Applied Sciences. (2018) 5, no. 4, 534–539.
Google Scholar
56 Singh B. K. and Kumar P., Numerical Computation for Time-Fractional Gas Dynamics Equations by Fractional Reduced Differential, Journal of Mathematics and System Science. (2016) 6, no. 6, 248–259.
Google Scholar

Citing Literature

All articles

Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform

Abstract

1. Introduction

2. Preliminaries

3. Homotopy Perturbation Jafari-Yang Transform Method

4. Idea of YTDM

5. Applications

6. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform

Abstract

1. Introduction

2. Preliminaries

3. Homotopy Perturbation Jafari-Yang Transform Method

4. Idea of YTDM

5. Applications

6. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information