In this paper, the trajectory tracking problem of industrial manipulator with fixed periodic external force on human-robot cooperative assembly line is studied. An advanced fuzzy adaptive supertwisting sliding mode control (FASTSMC) algorithm is proposed to realize the rapid convergence and continuous control of nonlinear control system. In order to enhance the robustness of the system, an arctangent terminal sliding mode surface is designed to deal with the concentrated uncertain disturbance. The supertwisting method is used to overcome the chattering problem in the control law. The fuzzy adaptive technique is used to compensate the centralized disturbance with unknown upper bound. A stiffness identification model is designed to estimate the deviation of the manipulator under external force. Finally, the feasibility of the proposed control scheme is verified by a simulation example of a 4-DOF manipulator.

1. Introduction

The development of Industry 4.0 has led to great changes in manufacturing specifications and aims to reduce human participation by replacing industrial robots to perform the most repetitive tasks [1]. Human-robot cooperation is a representative technology, which has become the key technology of the future factory. For example, this technology has been used in assembly lines in the automotive industry such as the Volkswagen factory in Wolfsburg, Germany. It combines the advantages of human workers and assistant robots and allows different degrees of automation in the workplace to meet the increasing flexibility needs of manufacturing systems. In the hybrid team of human and robot, the organization needs intelligent planning and control algorithms. The system must be reconfigured quickly to meet the needs of high production of different products, but human participation is inevitable [2]. Human-robot cooperative system is a nonlinear time-varying dynamic system with uncertain interference, in which the uncertainty and external interference greatly improve the complexity of the system. Many researchers have designed corresponding controllers for this technical problem, such as variable impedance control method [3], adaptive admittance controller [4], underactuated redundant low impedance method [5], and efficiency weighting strategy [6]. However, the existing methods lack ideal solutions to three main challenges: (1) the control system cannot guarantee the convergence of stable equilibrium. (2) The robustness of human-robot cooperative system is endangered by uncertainty and external interference. (3) The nature and characteristics of external interference are difficult to identify and compensate.

Although many advanced control methods, such as adaptive control [7], neural network control [8], and variable structure control [9], can be applied to human-robot cooperation manipulator control system, they all have some limitations. Deng [10] developed a novel finite-time command filter backstepping method, which allows the traditional command filter backstepping control and ensures the finite-time convergence. Figueredo et al. [11] proposed a robust dual-quaternion-based H-infinity task-space kinematic controller for robot manipulators, and this controller provides higher precision and faster response than the conventional H-infinity control. Although the above schemes have achieved some positive conclusions, the design of these controllers is complex, and the steps of adjusting parameters in practical engineering application are cumbersome, which is not conducive to wide popularization. Therefore, this paper attempts to improve the more easily realized sliding mode control and apply it to the end trajectory tracking control of human-robot cooperation manipulator.

The conventional sliding mode control principle is to use the symbolic function to make a decision on the input signal and then process the feedback, respectively, so that the control system can obtain strong robustness. The conventional linear sliding mode control can only achieve the asymptotic convergence of the state. Generally, increasing the gain to make the actuator saturate quickly is a common method to accelerate the convergence speed of tracking error [12]. In order to make the sliding mode control more in line with the needs of practical application, many improved schemes of sliding mode control have been proposed one after another. In reference [13], a terminal sliding mode control of PID type is proposed to strengthen the nonlinear relationship between state variables and control inputs. In reference [14], combining the sliding mode control method and the fast exponential convergence method, the sliding mode surface can be obtained faster, and the tracking error converges in the form of fast exponential convergence. In addition, terminal sliding mode control has the characteristics of reduced control gain, strong anti-interference ability, and finite-time convergence. It is also often used in the control of manipulator. For example, based on the terminal sliding mode control scheme proposed in reference [15], the low gain control of the manipulator system is realized. For the stabilization of underactuated robotic systems, reference [16] designed a fast terminal sliding mode control technology based on disturbance observer, estimated the external disturbance of the system by using the finite-time disturbance observer, and established the finite-time control law. In order to eliminate the singularity in the control process, a nonsingular continuous terminal sliding mode control system is designed by using the power reaching law in reference [17]. Tracking control of manipulator system can be realized by establishing reference signal and synchronizing it. Reference [18] uses neural network technology and sliding mode control method to design controller. In reference [19], the combination of sliding mode control method and fault-tolerant control is adopted. In the design of the manipulator controller, the supertwisting method is used to eliminate the control chattering and realize the finite-time tracking control. An adaptive finite-time sliding mode control is applied to chameleon chaotic systems with uncertainties and disturbances [20]. Alattas et al. [21] applied the optimal integral terminal sliding mode control based on the control Lyapunov method to the asymmetric nonholonomic robot system with external disturbances and obtained positive conclusions. In reference [22], the finite-time tracking control is realized by formulating the boundary layer. The sliding mode control method realizes quasi-sliding mode control by adjusting symbolic function and exponential function. However, this method has the disadvantage of reducing the dynamic accuracy of the system.

There are many research achievements in the end trajectory tracking control of manipulator based on sliding mode control scheme and the solution of human-robot cooperation. In reference [23], an impedance control structure for monitoring the contact force between the end effector and the environment is proposed, and the model-free fuzzy sliding mode control strategy is used to design the position controller and force controller. A fuzzy controller is proposed in reference [24]. A nonlinear model is used to track the trajectory of the micro robot in the human vascular system. In addition, the application of sliding mode control in the field of external force control of manipulator not only improves the robustness of the controller but also improves the estimation of force through sliding disturbance observer, so as to avoid the use of expensive force sensors in connecting rods and joints, such as reference [25]. The estimation of force is closely related to the stiffness identification of manipulator link and joint. Some studies identify the change of manipulator stiffness matrix and then calculate the change of external force, but it requires high accuracy of sensor for stiffness measurement [26, 27]. In the above research, in addition to the research on the manipulator control system in the fixed application field, the impact of stiffness change on the end trajectory tracking control effect is rarely considered in the related research using the general manipulator dynamic model. The main difficulty is that special sensors need to be added to measure the change of stiffness, and the installation position of the sensor is difficult to determine because the trigger point of the change of manipulator link or joint stiffness is not fixed in different application environments. On the premise of considering the elastic deformation law under the influence of external force, the elastic deformation law model is introduced into the general manipulator model, and the compensation mechanism is introduced. The most common case of periodic variation of elastic deformation is the scene where the manipulator works repeatedly on the assembly line.

During the observation of the production process, it is found that in the common scene of human-robot cooperation in industrial production, the external force generated by man on the manipulator often has a periodic law, which often occurs in the assembly line. Because the operation of the workpiece in the assembly line is cyclic and unified, the physical contact rate between man and the manipulator will appear in a specific action. Therefore, this paper believes that the stiffness change caused by this external force can be summarized into the corresponding model. The main innovation of this paper is to solve the elastic deformation law of manipulator joints and links, combined with the stiffness identification model, and combined with the general dynamic model of manipulator. The trajectory deviation caused by external force contact is no longer regarded as uncertain disturbance, which improves the performance of the controller. In addition, the fuzzy adaptive supertwisting sliding mode controller proposed in this paper uses the arctangent function to replace the symbolic function, which improves the performance of the controller. In addition, 2-DOF and 4-DOF manipulators are used to verify the effectiveness of the proposed algorithm and control scheme. From the perspective of practical application, the scheme proposed in this paper does not need to add additional sensors on the manipulator and will not increase the economic cost of industrial production.

2. Model Derivation and Control Objectives

Based on the general dynamic equation of the manipulator, the dynamic equation of the n-DOF manipulator under external disturbance can be obtained as follows [28].

(1)

where

are the vectors of joint positions, velocities, and accelerations, respectively. M(q) ∈ R^n×n is the positive definite inertia matrix of the manipulator;

is the Coriolis force and centrifugal force matrix of the manipulator; G(q) ∈ Rⁿ is the gravity matrix of the manipulator;

is the friction matrix; τ ∈ Rⁿ is the control torque of the manipulator joint; τ_d ∈ Rⁿ is the uncertain external disturbances. In practical industrial applications, the values of these physical parameters cannot be accurately obtained due to modelling errors, payload changes, external interference, other inherent factors, and human factors. Therefore, the uncertainty caused by the system parameter error can be expressed as

(2)

where the subscript has the symbol of 0, such as M₀, which means the nominal matrix of manipulator parameters, and the symbol with Δ in front means the uncertain part of the robot arm control system, such as ΔM.Combined with formulas (1) and (2), a new dynamic equation of manipulator can be obtained.

(3)

Then, through the above analysis, it can be concluded that in the presence of uncertainty and interference, the dynamic equation (3) can be expressed as

(4)

In order to facilitate representation and calculation, a simplified dynamic model can be obtained according to equation (4), which is written as

(5)

where D(t) is the uncertainty and disturbance in the manipulator control system and

represents a nonlinear function with known boundary.

As can be seen from (1), the parameters in the manipulator control system are highly coupled and are also affected by dynamic time-varying parameters, which will affect the stability of the system. In practical engineering, it is very difficult to accurately obtain the mathematical model, such as unknown parameters, unmodeled nonlinear functions, and payload changes. However, some prior knowledge of the model can be obtained by analyzing the dynamic time-varying characteristics. Therefore, in the design of model-based manipulator controller, we should not give up considering the influence of unknown disturbances but summarize the corresponding approximate mathematical model through the existing data. Based on the above classical model, this paper considers the cooperative work of the manipulator in the task, and this cooperation is different from the parallel manipulator in most cases. It may be human-robot cooperation or the cooperative work of multiple independent mechanical systems, so it is inevitable to have direct or indirect mutual contact and collision. In this paper, the resulting external force and influence are expressed by the following equation.

(6)

where F_e is the external generalized force exerted by the manipulator on the environment and Κ ∈ R^n×n is the stiffness matrix. While

is the end effector tracking error with x_r being the reference trajectory, it is worth noting that there is a difference in meaning between the end trajectory error here and the end position error later. The trajectory error here refers to the trajectory error generated during the execution of the task, and the end position error later refers to the signal error between the controller and the sensor.

For the end control of the manipulator, the goal is to design a robust sliding mode control to ensure high-precision tracking of the desired known trajectory of the manipulator in the presence of uncertainty and external interference.

(7)

where q_d ∈ Rⁿ is a desired trajectory, e = q − q_d is trajectory tracking error, and t_f is finite time. Then, the controller is designed according to the control objectives mentioned in the paper. In order to ensure the rationality of the designed controller, the stability is analyzed through the following basic assumptions and lemmas.

The assumptions are as follows:

(i)
Joint position and speed status are data that can be measured by manipulator sensors
(ii)
The total uncertainty ψD(t) satisfies the following conditions, |ψD(t)| ≤ ω₀ and , where ψ is a constant diagonal matrix, which is formulated in advance. Constants ω₀ and ω₁ are unknown and positive

Through the above assumptions and according to the relevant lemmas, the stability of the following invariant system can be proved.

(8)

Suppose there is a continuous function V(z) in the system shown in equation (7), which satisfies the following conditions, i.e., it is a positive definite function on D⊆Rⁿ and satisfies constraint condition:

(9)

where k > 0 and λ ∈ (0, 1), it can be concluded that the system based on equation (7) is locally finite time stable. If D = Rⁿ is satisfied, the system is globally finite time stable.

3. FASTSMC of Manipulator with External Force Prediction

3.1. Design of Sliding Surface

The nonlinear sliding surface describing the manipulator control system in equation (5) can be defined as

(10)

(11)

where e(t) = q − q_d is the joint space tracking position error with q_d ∈ Rⁿ as the known desired position trajectory. From these, we can get the result that

represents the tracking speed error of the joint,

means the desired speed trajectory given by the control system, ψ is a constant diagonal matrix, and λ and β are the positive coefficients. Then, the derivative of equation (10) with respect to t can be obtained.

(12)

Combining equation (5), equation (12) can be rewritten as

(13)

The above formula can be further simplified to obtain

(14)

3.2. Sliding Mode Controller

Firstly, the conventional supertwisting algorithm formula is rewritten as

(15)

(16)

where

, and

are diagonal positive matrices and η(t) is the unknown bounded uncertainties, same as ψD(t) stated in the above assumptions. Moreover, it is necessary to keep

for a finite time [29].

When the uncertainty boundary ω₀ of the error is known, the parameters l₁ and l₂ can be taken according to the method of reference [17], i.e., and . It should be added that in the above case, l₁ and l₂ are constants, and the gain l₂ must be greater than the boundary ω₀ in order to switch the term l₂sgn(σ(t)). The uncertainty term η(t) can be controlled. It is worth noting that in many cases, the control gain may be overestimated, resulting in increased chattering. Later, we will design a fuzzy adaptive compensation method to reduce chattering.

According to the conclusion in reference [18], equivalent control on the sliding surface means average control. Once the control system reaches the sliding surface, equivalent control will occur. In order to keep the system moving on the sliding surface, the sliding mode gain should not be less than the upper limit of uncertainty. Obviously, due to the switching characteristics of sliding mode control, the motion of the system on the sliding model surface is discontinuous, but the system controller needs to be continuous and equivalent approximate. Therefore, it is necessary to use a low-pass filter to obtain equivalent control.

(17)

where 0 < μ < 1/β₀ < 1 and ϵ > 0 A is a positive scalar and cannot be too large and u_eq(t) = η(t) = l₂sgn(σ(t)) is equivalent control on the sliding surface. The proposed adaptive control law K(t) is defined as

(18)

(19)

(20)

(21)

where k₀, r₀, and γ are positive constants and ϱ(t) is a time-varying scalar.

In (15) and (16), discontinuous symbolic functions exacerbate the chattering of sliding mode control. For sliding mode control, the effective method to suppress chattering is to select the appropriate switching function to improve its continuity and smoothness. The common method is to replace the traditional symbolic function with the saturation function, so that the boundary layer can be a continuous state linear feedback control, but there is a problem of uneven transition stage, resulting in drastic changes in slope. In order to improve the smoothness of boundary layer transition stage, some recent studies use hyperbolic tangent function as switching function. As shown in the figure, the transition of hyperbolic tangent function is smooth in the boundary layer, and the curve slope in the transition stage of hyperbolic tangent function changes little near the boundary layer. In addition, it is a continuous state feedback control in the boundary layer to improve the smoothness.

Different from the existing sliding mode control, this paper uses the arctangent function as the switching function. It can be seen from Figure 1 that the characteristics of the arctangent function and the hyperbolic tangent function are similar when they are used as the switching function. However, there is an exponential function in the hyperbolic tangent function. In the operation process, especially when calculating the derivative, the amount of operation is large, and the occupation of operation resources is more obvious when calculating the high-dimensional model. Therefore, considering the above reasons, equation (19) in system (17) is rewritten as

(22)

Details are in the caption following the image — Open in figure viewer PowerPoint

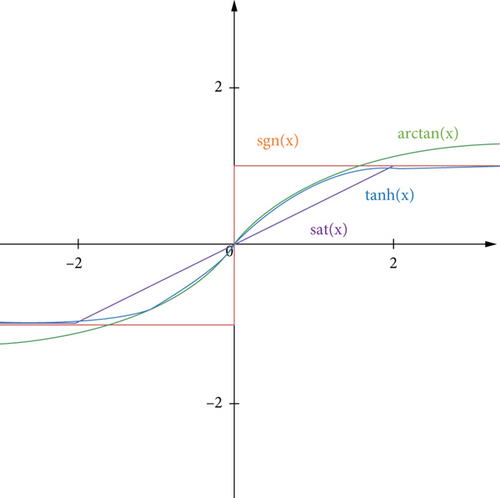
Considering that the robotic manipulator system (1) satisfies the above assumptions and proposes the control equation as equation (17), it can guarantee the finite-time convergence of the error e(t) to zero point, and it can track even in the presence of uncertainty and external disturbances asymptotically expected known trajectory q_d.

We can get the convergence of systems (15) and (16) in a finite time. Especially σ(t) = 0, then from equation (10), we can get the following result:

(23)

Then, (23) can be regarded as the solution of the following first-order differential equation:

(24)

Since β > 0, θ(t) will converge gradually to zero; therefore, it can be inferred that when t⟶∞, θ(t)⟶0, and this will cause e(t)⟶0 and q⟶q_d. This just verifies the closed-loop stability of the controller in the manipulator system.

3.3. Fuzzy Adaptive Sliding Mode Controller

Sliding mode control is an effective control technology to solve the zero dynamic problem of nonminimum phase nonlinear systems. However, in these designs, the concern about chattering has not been completely solved without reducing the robustness of the closed-loop system. High-order sliding mode control and integral sliding mode control are alternative control methods to effectively solve the chattering problem and further enhance the robustness of the closed-loop system. However, the design of these controllers still requires a priori knowledge of the uncertainty boundary. This paper adopts the construction of fuzzy rules as the formulation standard of uncertainty boundary in controller design, and these rules and membership functions often rely on empirical knowledge.

Aiming at the problem of manipulator control with unknown model uncertainty and external interference, this paper uses fuzzy logic inference algorithm to compensate for the unknown uncertainty of the system. Among them, the fuzzy function contains the adaptive parameters of sliding mode control to realize the adaptive sliding mode control.

The sliding surface θ(t) and

are selected as the inputs of the fuzzy system. Input and output fuzzy sets are defined as

, where NL represents negative large, NM represents negative medium, ZO represents zero, PM represents positive medium, and PL represents positive large. The Gaussian membership function of fuzzy system can be expressed as

(25)

where Ω_i is the input and output of the fuzzy system, the subscript z of the membership function represents the fuzzy rule set, α and ρ represent the center and width of the fuzzy rule set z, respectively.

When the state trajectory deviates from the sliding mode surface or the approaching speed is small, the output should be increased appropriately to make it reach the sliding mode surface quickly. When the state trajectory approaches the sliding surface or the approaching speed is large, the output should be appropriately reduced to suppress chattering. According to the above analysis, the determination of fuzzy rules is shown in Table 1.

1. Fuzzy control rules.

s
s	NB	NM	ZO	PM	PL
NL	PL	PL	PL	PM	ZO
NM	PL	PM	PM	ZO	NM
ZO	PM	PM	ZO	NM	NM
PM	PM	ZO	NM	NM	NM
PL	ZO	NM	NL	NL	NL

In the rule base, the central average defuzzification and product reasoning methods are adopted, and the output of the fuzzy system can be expressed as

(26)

where

and

This paper defined Γ_i shown as

(27)

Therefore, the fuzzy function can be obtained.

(28)

where Γ^T is a membership function and Ψ is an adaptive fuzzy parameter. The adaptive fuzzy parameters are formulated as follows:

(29)

where δ > 0 is a scalar design parameter.

3.4. Simulation

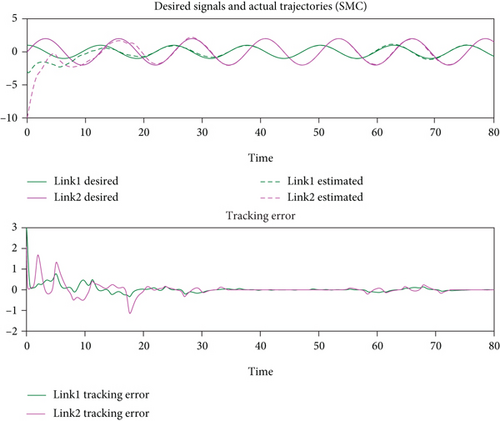
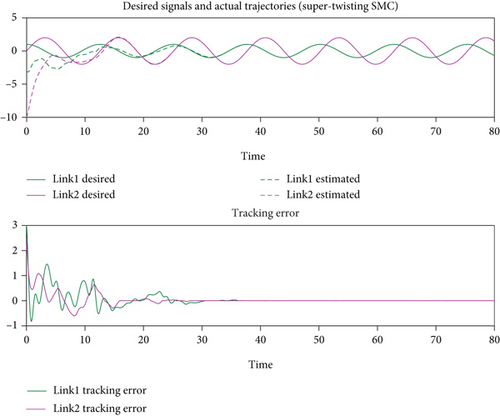
This part will take a 2-link manipulator as an example to complete a simple trajectory, observe the effectiveness of the proposed FASTSMC in the basic example, and compare it with the classical sliding mode control [30] and the conventional supertwisting sliding mode control [31] to reflect the application performance of the proposed method. The desired trajectory given by this simulation is .

It can be seen from Figure 2 that the tracking effect of classical sliding mode control is poor, the convergence speed is slow, and it is not stable enough in the tracking process. After stabilization, some errors will still occur sometimes. Supertwisting sliding mode control is a high-order sliding mode control method. It has the advantage of realizing the finite-time convergence of sliding mode variables and their derivatives, can avoid the singularity problem existing in other sliding mode control methods, and can make the chattering in the output control signal more subtle. As shown in Figure 3, the track tracking effect of supertwisting sliding mode control is very excellent, but the convergence speed is not satisfactory, which is difficult to apply in the case of uncertainty in the system. The FASTSMC proposed in this paper can quickly and accurately maintain trajectory tracking. Compared with the above two traditional methods, as shown in Figure 4, the method proposed in this paper has better performance in convergence speed and stability.

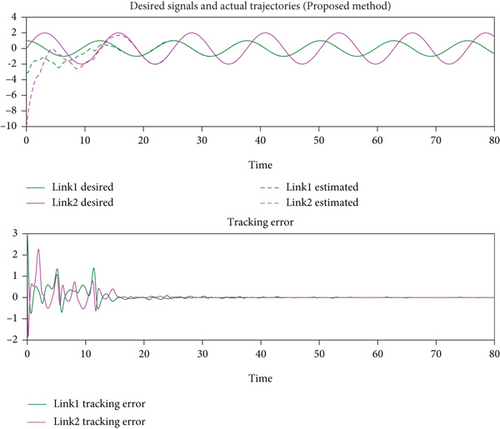
Then, the complexity of the algorithm proposed in this paper is shown in Table 2. The computational complexity of the algorithm proposed in this paper is expressed by the time required for operation in MATLAB. The simulation is run using MATLAB 2020a on a personal computer with Intel Core, CPU i7-7700 @ 3.60 GHz, and 8 GB RAM. It is not only compared with the above sliding mode control and supertwisting sliding mode control but also with the computational complexity of quantum interference artificial neural network proposed in [8]. In order to make the test results more accurate, each scheme was tested ten times, and the calculation time was taken as their average.

2. Comparison of processing time of control schemes.

Control scheme	Processing time (s)
Sliding mode control	2.230
Supertwisting sliding mode control	2.520
Quantum-interference artificial neural network	132.565
FASTSMC (proposed in this paper)	7.372

It can be seen from Table 2 that the processing time of the control scheme proposed in this paper is longer than that of some conventional sliding mode control schemes, which is mainly caused by MATLAB calling fuzzy logic module. Compared with other novel schemes, the method proposed in this paper has advantages in complexity.

3.5. Predict Joint Stiffness Model

In the manipulator control system with n rotating joints, the driving system of the joint can be regarded as a cantilever system, and its stiffness can be expressed by the spring constant k_θ. On this basis, the joint stiffness of the manipulator system can be expressed as the following diagonal matrix:

(30)

In the use of industrial manipulator, because the end effector of the manipulator is affected by external contact force, each joint will deform, resulting in the change of the direction of the end effector. By analyzing the mechanical characteristics of the industrial manipulator, it can be found that there is the following relationship between the elastic deformation at the joint of the manipulator and the torque applied at the joint:

(31)

where e_k(t) is the vector representing the deformation of joint angle under the influence of joint stiffness change.

Firstly, the stiffness of each joint of the manipulator is assumed to be known, and the model between each joint is established by Jacobian matrix, and the mapping relationship with the elastic deformation of the end joint is obtained. After that, through the kinematic model of the manipulator, the law between the end deformation of the manipulator and the deformation of other joints can be obtained as follows:

(32)

where ΔX is a vector used to describe the relationship between the joint deformation of the manipulator and the position deviation of the end actuator of the manipulator and J is the Jacobian matrix calculated by the vector product method according to the kinematic model of the manipulator.

The influence of joint friction and gravity has been considered above, and these factors are ignored in this part. Therefore, the relationship between the joint torque caused by compensation deformation and the applied generalized force can be obtained:

(33)

Substituting (31) and (32) into (33), respectively, we can get

(34)

Assuming that the Jacobian matrix and the terminal generalized force vector are known, we can obtain the joint deformation mapping of the manipulator in the workspace and calculate the joint torque caused by the change of joint stiffness caused by external force. Therefore, we define a model predictive control, which links the deformation law of the rigid body with the sliding mode control above. The system assumption of the stiffness part has no uncertainty, and the dynamics is given by a simple integrator chain and controlled by v.

(35)

If there is no activation constraint, the nominal solution can be obtained from the model predictive control conclusion v by minimizing the square norm of the prediction derivative of the sliding vector evaluated using the nominal dynamics. Otherwise, a compromise will be reached to meet the constraints. The prediction derivative can be easily calculated from the state prediction without uncertainty [32].

(36)

The predicted values referenced by the model are direct because they are designed by the user. For external forces without high-order information, it is obvious that the longer the delay time, the less effective the assumption is, resulting in performance degradation during contact transients. The predicted slip vector can be easily calculated by (36). The same method applies to each joint.

4. Simulation Results

In this part, the manipulator model is established by using MATLAB 2021a, and the designed controller is simulated. The simulated manipulator adopts the practical 4-DOF manipulator. In the simulation of this paper, fixed kinematic parameters are assumed, but we introduce serious 15% uncertainty in other parameters, that is, connecting link mass, connecting link inertia, and connecting link centroid position, and periodically introduce 20% torque error to simulate periodic collision caused by human-robot cooperation. The structure diagram of the controller is shown in Figure 5.

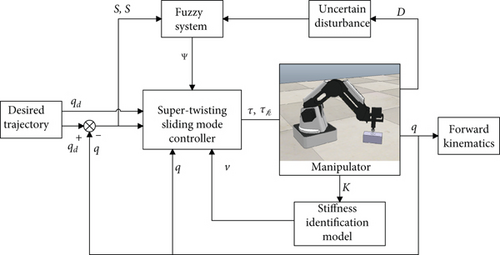
In the simulation part, we compare the proposed scheme with sliding mode control [30], supertwisting sliding mode control [31], and model predictive control [33], which are common methods used in manipulator trajectory tracking control. And we design two case examples to illustrate the application effect of the algorithm under different conditions. In the simulation, the controller parameters and manipulator mechanical parameters of the scheme proposed in this paper are shown in Table 3

Case 1. In this case, we designed a large-area cutting scheme of the manipulator. There are no sharp turns in the whole track. In order to respond to the interference of human-robot cooperation, a periodic external force is added at the second joint, and the trajectory tracking results are shown in Figure 6.

3. Parameters used in controller simulation.

Type	Parameter	Value
Controller parameters	λ (in equation (11))	5
	β₀, k₀, r₀, γ (in equations (17)-(21))	1.99, 3, 3, and 5
	ω₀ (in equations (15) and (16))	4
	α, ρ (in equation (25))	3, 1.4

Manipulator weight (kg)	Link 1 and Dynamixel MX106	0.45
	Link 2 and Dynamixel MX64	0.30
	Link 3, Dynamixel MX64, and actuator	0.50

Manipulator length (m)	Link 1	0.25
	Link 2	0.15
	Link 3	0.15
	Link 4	0.05

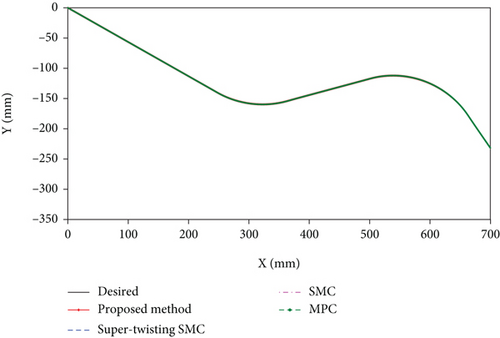
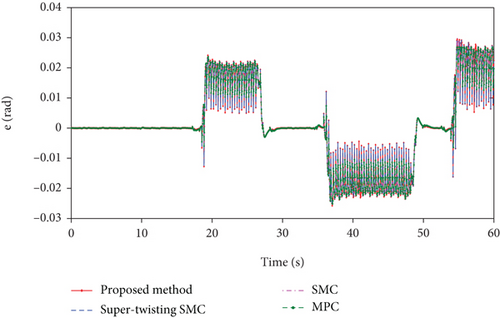
From the track tracking effect shown in Figure 6 and the tracking error shown in Figure 7, it can be seen that the adopted method does not cause obvious error under the influence of periodic external force, which shows that these classical algorithms have strong robustness, and the selected comparison scheme is suitable for manipulator control.

Case 2. In this case, we designed the cutting work of the small area sharp turning process of the manipulator. There are many turning points in the trajectory, but no external force interference is added. The track tracking results are shown in Figure 8.

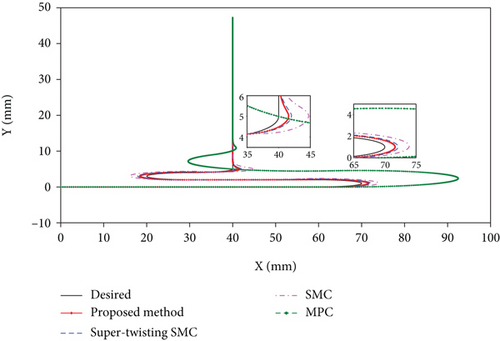
As can be seen from Figure 8, the method proposed in this paper can track the desired trajectory faster than other methods after the turning of the trajectory. This shows that the proposed method still has performance advantages in trajectory tracking control even without direct external force. As shown in Figure 9, the method proposed in this paper has an advantage in convergence speed, and the trajectory can track the desired trajectory quickly after errors arise from uncertain disturbances and acute trajectories.

Case 3. In this case, the trajectory of the manipulator is the same as that in Case 2. At the same time, the same periodic external force as in Case 1 is added. The track tracking results are shown in Figure 10.

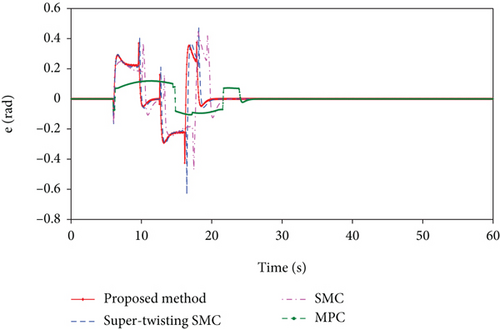
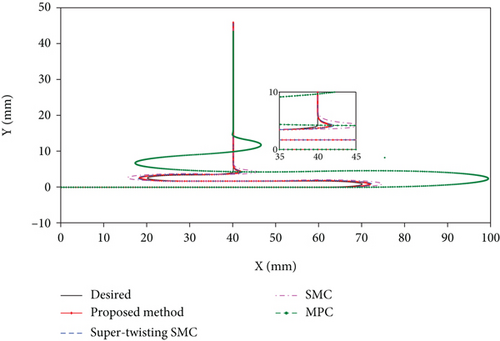
From the tracking effect of model predictive control in Figure 10, it can be seen that the error with the desired trajectory is larger than that in Figure 8, which shows that the influence of the applied external force on trajectory tracking is obvious. For other sliding mode control methods, due to the model prediction of stiffness matrix, it can actively compensate the influence caused by the external force. Therefore, it can be seen in Figure 11. In terms of error and convergence time, there is little difference between several sliding mode controls and Figure 9, which reflects the effectiveness of the joint stiffness model prediction proposed in this paper.

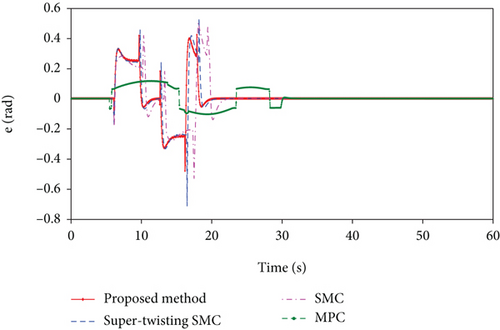
It should be noted that since the tracking effect of the model predictive control has a large error, in order to describe the convergence process of the control method simultaneously with other methods, in Figures 9 and 11, the error of the model prediction is based on the deviation between the interpolation projection points of the nearest sampling point and the next sampling point.

In order to illustrate the performance of the scheme proposed in this paper in practical application in manipulator as much as possible, a 4-DOF manipulator model is established by using MATLAB/Simscape, and the external force is added at the joint to verify the performance of the scheme in the human-robot cooperation application of the assembly line. Because Simscape involves many variables and the coupling between parameters is strong, the simulation needs a lot of calculation. With the permission of computer performance and time, we will increase the number of simulation iterations as much as possible. The following figure shows the simulation results of the 10th iteration.

Firstly, the coordinate data of the desired trajectory of the manipulator in the motion space are read, and the constraints of the motion process are fitted according to the physical model established based on the mechanical characteristics of the manipulator. Secondly, the stiffness identification model is used to process the trajectory deviation caused by external force, which is converted into servo motor control signal and provided to the joint controller. Finally, the motion process obtained after Simscape simulation is visualized in MATLAB, and the proposed stiffness matrix compensation method will be used to correct the error before entering the next iteration. The specific process described above is shown in Figure 12.

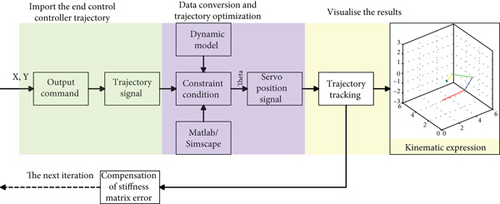
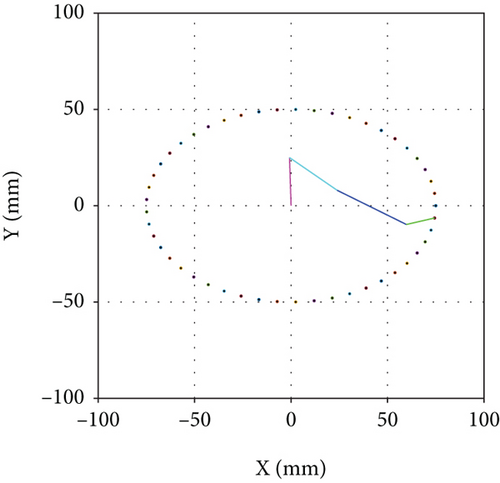
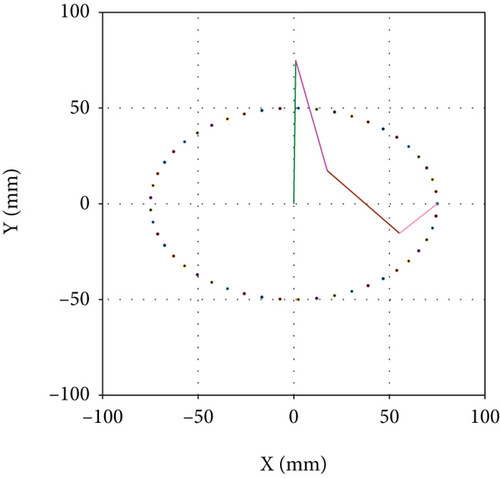
The experiment of two closed curves is designed according to the process in Figure 12. In the application process of industrial manipulator, the requirements of closed pattern are high. It needs to overlap the starting point and terminal point, and this standard should still be maintained after repeated operations; otherwise, waste workpieces or unqualified products will be produced. The experiments of the two closed curves shown in Figure 13 take the effect after the 10th iteration, and the applied periodic external force is 20 ± 2 N. The difference between the two groups of experiments is that the length of the connecting rod of the manipulator is different, but as shown in Figures 13(a) and 13(b), the starting point and end point can be kept coincident, which shows that the specification of the manipulator has little impact on the application effect of the scheme proposed in this paper.

5. Conclusion

In this paper, the arctangent terminal sliding mode surface and sliding mode controller are designed for the manipulator with fixed periodic external force on the assembly line applied to human-robot cooperation, so as to track the reference trajectory quickly and accurately. In order to suppress the influence of uncertain disturbance on the controller, the fuzzy logic adaptive parameters are constructed, combined with sliding mode control to enhance the robustness in the control process. Then, the supertwisting and fuzzy adaptive theory are used to reduce the chattering and compensate the concentrated disturbance of the manipulator under the action of external force. Then, because the sensor has some limitations in stiffness measurement, this paper designs a stiffness identification model to estimate the disturbance caused by the applied external force, which saves the hardware cost of the sensor and improves the control effect. The feasibility of the proposed FASTSMC is verified by the simulation of 4-DOF manipulator system.

In the future, we will study the trajectory tracking control of the manipulator under the influence of external forces with more complex characteristics, so as to reduce the torque amplitude and disturbance on the premise of ensuring the convergence speed. In addition, the stiffness identification method proposed in this paper is only limited to the case that the manipulator receives the influence of strong periodic external force, which has certain limitations in practical applications. In the follow-up research, we will study a reasonable data-driven method and combine the end trajectory offset caused by deformation law with stiffness identification to improve the robustness of the controller.

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Acknowledgments

This work is supported by the National Natural Science Foundation of China under Grant 52077027 and Liaoning Province Science and Technology Major Project No. 2020JH1/10100020.

Open Research

Data Availability

No data were used to support this study.

References

1 Inkulu A. K., Bahubalendruni M. V. A. R., Dara A., and SankaranarayanaSamy K., Challenges and opportunities in human robot collaboration context of Industry 4.0-a state of the art review, Industrial Robot: the International Journal of Robotics Research and Application. (2021) 49, https://doi.org/10.1108/IR-04-2021-0077.
10.1108/IR-04-2021-0077
Web of Science® Google Scholar
2 Kolbeinsson A., Lagerstedt E., and Lindblom J., Foundation for a classification of collaboration levels for human-robot cooperation in manufacturing, Production & Manufacturing Research. (2019) 7, no. 1, 448–471, https://doi.org/10.1080/21693277.2019.1645628, 2-s2.0-85069762392.
10.1080/21693277.2019.1645628
Google Scholar
3 Kizir S. and Elşavi A., Position-based fractional-order impedance control of a 2 DOF serial manipulator, Robotica. (2021) 39, no. 9, 1560–1574, https://doi.org/10.1017/S0263574720001356.
10.1017/S0263574720001356
Web of Science® Google Scholar
4 Reyes-Uquillas D. and Hsiao T., Safe and intuitive manual guidance of a robot manipulator using adaptive admittance control towards robot agility, Robotics and Computer-Integrated Manufacturing. (2021) 70, https://doi.org/10.1016/j.rcim.2021.102127.
10.1016/j.rcim.2021.102127
PubMed Web of Science® Google Scholar
5 Boucher G., Laliberté T., and Gosselin C., A parallel low-impedance sensing approach for highly responsive physical human-robot interaction, 2019, International Conference on Robotics and Automation, May 2019, Montreal, QC, Canada.
Google Scholar
6 Li J., Zhang W., and Zhu Q., Weighted multiple-model neural network adaptive control for robotic manipulators with jumping parameters, Complexity. (2020) 2020, 12, https://doi.org/10.1155/2020/3172431.
10.1155/2020/3172431
Web of Science® Google Scholar
7 Reina A. R., Nguyen K.-D., and Dankowicz H., Experimental validation of an adaptive controller for manipulators on a dynamic platform, Robotica. (2021) 39, no. 4, 582–605, https://doi.org/10.1017/S0263574720000600.
10.1017/S0263574720000600
Web of Science® Google Scholar
8 She Y., Li S., and Xin M., Quantum-interference artificial neural network with application to space manipulator control, IEEE Transactions on Aerospace and Electronic Systems. (2021) 57, no. 4, 2167–2182, https://doi.org/10.1109/TAES.2021.3053124.
10.1109/TAES.2021.3053124
Web of Science® Google Scholar
9 Wei D., Gao T., Mo X., Xi R., and Zhou C., Flexible bio-tensegrity manipulator with multi-degree of freedom and variable structure, Chinese Journal of Mechanical Engineering. (2020) 33, no. 1, 1–11, https://doi.org/10.1186/s10033-019-0426-7.
10.1186/s10033-019-0426-7
Web of Science® Google Scholar
10 Deng Y., Adaptive finite-time fuzzy command filtered controller design for uncertain robotic manipulators, International Journal of Advanced Robotic Systems. (2019) 16, no. 1, https://doi.org/10.1177/1729881419828148, 2-s2.0-85061637267.
10.1177/1729881419828148
Web of Science® Google Scholar
11 Figueredo C. and Felipe L., Robust H∞ kinematic control of manipulator robots using dual quaternion algebra, Automatica. (2021) 132, https://doi.org/10.1016/j.automatica.2021.109817.
10.1016/j.automatica.2021.109817
Web of Science® Google Scholar
12 Yi S. and Zhai J., Adaptive second-order fast nonsingular terminal sliding mode control for robotic manipulators, ISA Transactions. (2019) 90, 41–51, https://doi.org/10.1016/j.isatra.2018.12.046, 2-s2.0-85061606497, 30777314.
10.1016/j.isatra.2018.12.046
PubMed Web of Science® Google Scholar
13 Nasiri M., Mobayen S., and Arzani A., PID-type terminal sliding mode control for permanent magnet synchronous generator based enhanced wind energy conversion systems, CSEE Journal of Power and Energy Systems. (2021) https://doi.org/10.17775/CSEEJPES.2020.06590.
10.17775/CSEEJPES.2020.06590
Web of Science® Google Scholar
14 Zhang X. and Shi R., Research on adaptive non-singular fast terminal sliding mode control based on variable exponential power reaching law in manipulators, Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering. (2022) 236, no. 3, 567–578, https://doi.org/10.1177/09596518211040288.
10.1177/09596518211040288
Web of Science® Google Scholar
15 Truong T. N., Vo A. T., and Kang H.-J., A backstepping global fast terminal sliding mode control for trajectory tracking control of industrial robotic manipulators, IEEE Access. (2021) 9, 31921–31931, https://doi.org/10.1109/ACCESS.2021.3060115.
10.1109/ACCESS.2021.3060115
Web of Science® Google Scholar
16 Rojsiraphisal T., Mobayen S., Asad J. H., Chang A., and Puangmala J., Fast terminal sliding control of underactuated robotic systems based on disturbance observer with experimental validation, Mathematics. (2021) 9, https://doi.org/10.3390/math9161935.
10.3390/math9161935
Web of Science® Google Scholar
17 Zhai J. and Gui X., A novel non-singular terminal sliding mode trajectory tracking control for robotic manipulators, IEEE Transactions on Circuits and Systems II: Express Briefs. (2021) 68, no. 1, 391–395, https://doi.org/10.1109/TCSII.2020.29999377.
10.1109/TCSII.2020.29999377
Web of Science® Google Scholar
18 Tran D.-T., Truong H.-V.-A., and Ahn K. K., Adaptive nonsingular fast terminal sliding mode control of robotic manipulator based neural network approach, International Journal of Precision Engineering and Manufacturing. (2021) 22, no. 3, 417–429, https://doi.org/10.1007/s12541-020-00427-4.
10.1007/s12541-020-00427-4
Web of Science® Google Scholar
19 Mazare M., Taghizadeh M., and Ghaf-Ghanbari P., Fault-tolerant control based on adaptive super-twisting nonsingular integral-type terminal sliding mode for a delta parallel robot, Journal of the Brazilian Society of Mechanical Sciences and Engineering. (2020) 42, no. 8, 1–15, https://doi.org/10.1007/s40430-020-02510-3.
10.1007/s40430-020-02510-3
Web of Science® Google Scholar
20 Mobayen S., Fekih A., Vaidyanathan S., and Sambas A., Chameleon chaotic systems with quadratic nonlinearities: an adaptive finite-time sliding mode control approach and circuit simulation, IEEE Access. (2021) 9, 64558–64573, https://doi.org/10.1109/ACCESS.2021.3074518.
10.1109/ACCESS.2021.3074518
Web of Science® Google Scholar
21 Alattas K. A., Mobayen S., Assawinchaichote W., Asad J. H., Awrejcewicz J., Aly A. A., and Alghtani A. H., A Lyapunov-based optimal integral finite-time tracking control approach for asymmetric nonholonomic robotic systems, Symmetry. (2021) 13, no. 12, https://doi.org/10.3390/sym13122367.
10.3390/sym13122367
Web of Science® Google Scholar
22 Boukattaya M., Mezghani N., and Damak T., Adaptive nonsingular fast terminal sliding-mode control for the tracking problem of uncertain dynamical systems, ISA Transactions. (2018) 77, 1–19, https://doi.org/10.1016/j.isatra.2018.04.007, 2-s2.0-85046159315, 29699696.
10.1016/j.isatra.2018.04.007
PubMed Web of Science® Google Scholar
23 Huang S.-J., Liu Y.-C., and Hsiang S.-H., Robotic end-effector impedance control without expensive torque/force sensor, International Journal of Mechanical and Mechatronics Engineering. (2013) 7, no. 7, 1446–1453, https://doi.org/10.5281/zenodo.1087175.
10.5281/zenodo.1087175
Google Scholar
24 Mitra A. and Behera L., Development of a fuzzy sliding mode controller with adaptive tuning technique for a mri guided robot in the human vasculature, IEEE 13th International Conference on Industrial Informatics, July 2015, Cambridge, UK.
Google Scholar
25 Han L., Tang G., Zhou Z., Huang H., and Xie D., Adaptive wave neural network nonsingular terminal sliding mode control for an underwater manipulator with force estimation, Transactions of the Canadian Society for Mechanical Engineering. (2021) 45, no. 2, 183–198, https://doi.org/10.1139/tcsme-2020-0010.
10.1139/tcsme-2020-0010
Web of Science® Google Scholar
26 Ma Z. and Dong G., Variable stiffness and damping impedance control with disturbance observer, 7th International Conference on Control, Mechatronics and Automation, November 2019, Delft, Netherlands.
Google Scholar
27 Fayazi A., Pariz N., Karimpour A., and Hosseinnia S. H., Robust position-based impedance control of lightweight single-link flexible robots interacting with the unknown environment via a fractional-order sliding mode controller, Robotica. (2018) 36, no. 12, 1920–1942, https://doi.org/10.1017/S0263574718000802, 2-s2.0-85053147768.
10.1017/S0263574718000802
Web of Science® Google Scholar
28 Chen C., Zhang C., Hu T., Ni H., and Chen Q., Finite-time tracking control for uncertain robotic manipulators using backstepping method and novel extended state observer, International Journal of Advanced Robotic Systems. (2019) 16, no. 3, article 1729881419844655, https://doi.org/10.1177/1729881419844655, 2-s2.0-85065386554.
10.1177/1729881419844655
Web of Science® Google Scholar
29 Ma Y. J., Zhao H., and Li T., Robust adaptive dual layer sliding mode controller: methodology and application of uncertain robot manipulator, Transactions of the Institute of Measurement and Control. (2022) 44.
10.1177/01423312211025330
Web of Science® Google Scholar
30 Ge W., Ye D., Jiang W., and Sun X., Sliding mode control for trajectory tracking on mobile manipulators., APCCAS 2008-2008 IEEE Asia Pacific Conference on Circuits and Systems, December 2008, Macao.
Google Scholar
31 Jeong C.-S., Kim J.-S., and Han S.-I., Tracking error constrained super-twisting sliding mode control for robotic systems, International Journal of Control, Automation and Systems. (2018) 16, no. 2, 804–814, https://doi.org/10.1007/s12555-017-0134-y, 2-s2.0-85042604674.
10.1007/s12555-017-0134-y
Web of Science® Google Scholar
32 Fan S. and Fan S., Approximate stiffness modelling and stiffness defect identification for a heavy-load parallel manipulator, Robotica. (2019) 37, no. 6, 1120–1142, https://doi.org/10.1017/S0263574718001492, 2-s2.0-85061756933.
10.1017/S0263574718001492
Web of Science® Google Scholar
33 Belda K. and Tchaikovsky M., Predictive and anisotropic control design for robot motion under stochastic disturbances, 18th European control conference (ECC)., June 2019, Naples, Italy.
Google Scholar

Citing Literature

All articles

A Novel Trajectory Tracking Control with Modified Supertwisting Sliding Mode for Human-Robot Cooperation Manipulator in Assembly Line

Abstract

1. Introduction

2. Model Derivation and Control Objectives