The calibration of response spectra is an important issue that needs further research in engineering earthquake resistance. This paper proposes an improved calibration method for site-related response spectra. The seismic acceleration response spectra are statistically analyzed in the random period bands in the form of regression analysis, and the fitting indices in each frequency band under 11 different functions are given. Accordingly, the best fitting function for each period band is determined. Combined with a genetic algorithm, the control parameters of the seismic acceleration response spectrum are calibrated according to the determined new design spectral shape. After comparing the calibration results with the proposed piecewise results, a new calibration model of the three-section curve expression is proposed by improving the piecewise standard until the calibration results are identical to the proposed period point. The accuracy of the proposed calibration method is validated against the other four available methods using Qian’a earthquake records and actual engineering examples. The research results show that the site-related response spectrum calibration method given in this paper objectively reflects the spectrum characteristics of the site-related response spectrum. The proposed method may have a certain reference value for the calibration of the site-related response spectrum.

1. Introduction

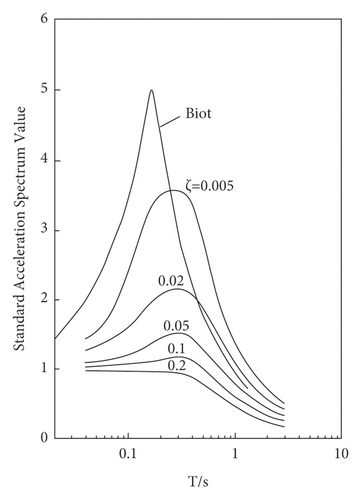
The calibration of the design response spectrum is a key issue in the seismic design of the building structure of the engineering site. The calibration results of the site-related design response spectrum should appropriately reflect the ground motion characteristics of the engineering site. For the calibration of the site-related seismic response spectrum, the critical issues are the expression of the design response spectrum and the selection of calibration methods. Any calibration of the site-related seismic response spectrum is based on the design response spectrum calibration model, i.e., the design response spectrum shape. The earliest seismic design spectrum calculated from ground motion records for engineering design was proposed by Housner. Eight horizontal component records of ground motion from four earthquakes (El Centro in 1934, Olympia in 1940, Washington in 1949, and Taft in 1952) were adopted, normalized by 0.2 g, and then averaged. The design spectrum is expressed in the form of a curve [1]. Later, Newmark described the design response spectrum in the form of a straight line and proposed a three-parameter calibration method [2]. Figure 1 shows a comparison between the Biot standard spectrum and the Housner design spectrum. At present, most calibration methods for the site-related response spectrum in China adopt the three-section expression given in the Code for Seismic Design of Buildings (GB50011-2010), and the mid-frequency band uses a horizontal line to reflect the spectral characteristics of the site-related response spectrum in this frequency band [3, 4]. It is not difficult to find that the shape of the actual site-related response spectrum is irregular. The spectrum variation characteristics of each frequency band vary with changes in the soil layer conditions, seismic wave propagation path, and seismic environment [5–15]. The expression of the design response spectrum given in the Code for Seismic Design of Buildings is based on a statistical analysis of a large number of seismic response spectra, which is an average result [16–19]. However, the average spectrum is smooth [20, 21], and the peak value is flattened at the same time [22–24]. Although the mid-frequency band satisfies the engineering seismic design requirements to a certain extent, it conceals the characteristics of the maximum amplification factor β_max, and it is difficult to reflect the real ground motion response characteristics of the engineering site [25, 26]. Therefore, this paper abandons the linear form design response spectrum expression to calibrate the site-related response spectrum. Instead, it performs statistical analysis on the shape of the actual site-related response spectrum and then performs segmental fitting using regression analysis to give a curve expression that can truly reflect the spectrum characteristics of each frequency band. Based on the new design response spectrum expression form, a new site-related response spectrum calibration method is proposed with the help of the genetic algorithm.

Details are in the caption following the image — Open in figure viewer PowerPoint

2. Determination of the Target Spectrum Shape

The site-related response spectra calculated from different strong earthquake records are different. Considering the influence of the uncertainty of site-related seismic response spectrum curves on the estimated design response spectrum curve form, this article is not limited to the use of traditional engineering seismic design. Instead, a new design response spectrum expression form that combines genetic algorithms is proposed. The design response spectrum curve is expressed by a dynamic amplification factor. The main process of the new site-related response spectrum calibration method is as follows:

(a)
Segment points for the site-related response spectrum are assumed, given segment control period points T_1i and T_2i parameter values (where i is the number of calculation cycles, i = 1∼n);
(b)
Regression analysis is performed on the segmented site-related response spectrum curve, and the fitting index R² is used to determine the expression form of each segmented function. R² is the fitting index given by the regression analysis, which is used to judge the fitness of the function. The closer the R² value is to 1, the better the fitting effect;
(c)
The curve shape determined by regression analysis is used as the target spectrum; then, the genetic algorithm is introduced to calibrate the target spectrum.

3. Genetic Algorithm-Aided Calibration of Inflection Point Periods

3.1. Genetic Algorithm

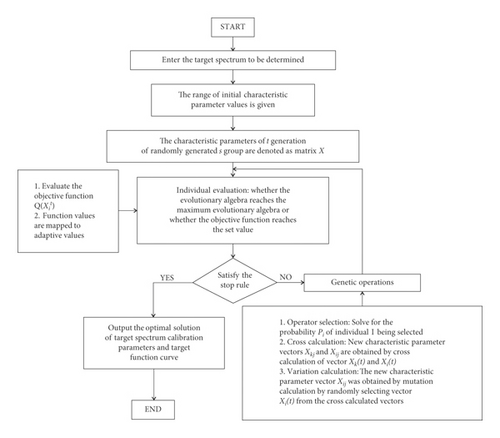
The genetic algorithm was first proposed in 1975 by Holland in the monograph “Adaptability of Nature and Artificial Systems” [27, 28]. This is a self-adaptive global optimization probabilistic search algorithm that draws on the laws of natural genetics and natural selection in the biological world [29, 30]. In seismic design, the calibration of the response spectrum is essentially a global optimization problem of the multiparameter fitting. The global optimization problem is an important field in the application of the genetic algorithm.

The specific calculation process of the genetic algorithm is as follows:

Suppose the group wants to fit n individuals x₁, x₂, x₃, …, x_n;

3.1.1. Initialization

Design cycle counter t = 0; Design maximum cycle upper limit number T; Write n individuals in array form X = [x₁,x₂,x₃,…, x_n]. Specify the maximum and minimum values for n individuals: X_max = [x_1max,x_2max, x_3max,…, x_nmax]，X_min = [x_1min,x_2min, x_3min,…, x_nmin]; Generate initial random values: According to the formula, s groups of “t-th generation” populations are randomly generated, and the initial value of t is 0.

3.1.2. Individual Evaluation

The fitness function is a criterion used to distinguish between good and bad individuals in a group. Set the population size as S and calculate the fitness function of each individual in the s group and the selection probability of each individual is proportional to its fitness. This fitness function is actually a criterion for calculating the error between the fitted value and the original record β, such as the variance.

3.1.3. Crossover Operation

Two individuals are randomly selected from the population, and two new individuals are obtained by exchanging partial genes of two chromosomes. The crossover operation adopts the real number crossover method and the crossover operation of the k-th chromosome X_k and l-th chromosome X_l at the j position is as follows:

(1)

Among them, b is a random number in the interval [0, 1].

3.1.4. Mutation Operation

The purpose of mutation operation is to maintain the diversity of the population. Mutation calculation randomly selects an individual from the population and selects a point in the individual to mutate. The operation method for mutation of the j-th gene X_ij of the i-th individual is as follows:

(2)

Among them, X_max is the upper bound of gene X_ij, and X_min is the lower bound of X_ij; is a random number, t is the current iteration number, T_max is the maximum evolution number, and r is a random number in the [0,1] interval [31].

3.1.5. Determine the Termination Calculation Conditions

If t (number of iteration cycles) <T_max (maximum cycle algebra), go to Step 2. If t>T_max (or objective function Q < 10⁻⁵), the optimal solution is the individual with the maximum fitness in the evolutionary iteration process, and the calculation ends at this point.

3.2. Genetic Algorithm Calibration Target Response Spectrum and Characteristic Parameters

The seismic response spectrum can be obtained by calculating strong earthquake records. The process of normalizing the spectrum into simple rules is called the calibration of the response spectrum. The response spectrum used in the earthquake resistance of construction projects is called the design response spectrum (the target response spectrum calibrated in this paper is the design response spectrum). There are differences in the expression of the standardized design response spectrum, and the design spectrum curve in this paper is represented by the dynamic amplification coefficient spectrum. According to the regression analysis, the initial target spectrum is expressed as follows:

(3)

where β(T) is the dynamic amplification coefficient spectrum; T₀ is the first inflection point period; T_g is the characteristic period (the second inflection point period); T_m is the cut-off period; γ is the decay index.

Considering the continuity of the designed response spectrum curve, the calibration parameters a₀ and a₇ are simply replaced at the subperiod points T₀ and Tg, and then there are 9 parameters to be calibrated in formula (3): a₁, a₂, a₃, a₄, a₅, a₆, T₀, T_g, γ. The calibration calculation of the response spectrum is actually to find the calibration parameters by selecting the appropriate mathematical method of the optimal value, which minimizes the error of the objective function valuefd4.

(4)

In the formula, β_i(T) is the calibrated seismic response spectrum.

In this paper, the genetic algorithm is used to find the optimal values of a₁, a₂, a₃, a₄, a₅, a₆, T₀, T_g, γ and determine the target spectrum shape so that the value of the function formula (4) is the smallest.

The specific process of genetic algorithm calibration target response spectrum calibration and inflection point period is as follows:

3.2.1. Initial Value

According to the algorithm, the 9 parameters a₁, a₂, a₃, a₄, a₅, a₆, T₀, T_g, γ that need to be fitted to the target spectrum are taken as individuals, and the individual maximum and minimum values of each parameter are given. Use formula (3) to randomly generate s group t generation population, the initial value of t is 0, and its expression form is as follows:

(5)

3.2.2. Individual Evaluation

When the maximum evolutionary generation reaches T or the objective function (variance) satisfies < 10⁻⁵, the calculation is terminated; otherwise, the calculation is continued.

3.2.3. Operator Selection

In the process of calibrating the target response spectrum by the genetic algorithm, the objective function is fitted with the minimum error of the whole frequency band, and the problem of the minimum value of the objective function is solved. For solving the maximum value problem, the genetic algorithm can directly convert the objective function into a fitness function for optimization calculation. Therefore, in the process of calibrating the response spectrum of the genetic algorithm, the objective function needs to be processed to form a mapping relationship when the value of the objective function is larger, and the value of the fitness function is smaller, and then the calculation can be performed. After completing the mapping conversion, the probability of individual i being selected is .

3.2.4. Crossover Operation

Perform the point j cross calculation on the target vector individuals X_k(t) and X_l(t) in the group according to the cross calculation principle formula (1), and obtain two vectors after cross evolution as follows:

(6)

3.2.5. Mutation Operation

Select an individual X_i(t) from the population that has completed the crossover operation and select a point in the individual to perform mutation operation according to formula (2) to obtain the mutation vector as follows:

(7)

3.2.6. Judging Termination Conditions

Evaluate the fitness function of the optimal individual; if the fitness function calculated by the vector is less than the given threshold, the algorithm terminates; if not, turn to step (2) to repeat the calculation until the termination calculation conditions are met. Or preset the number of iterations, output the best fitting solution a_1x, a_2x, a_3x, a_4x, a_5x, a_6x, T_0x, T_gx, γ_x.

The flow chart of genetic algorithm calibration target spectrum and characteristic parameters:

4. Determination of the Design Response Spectrum Shape and the Control Parameters

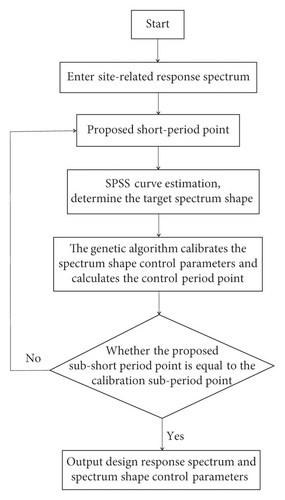
First, comparing the assumed control period points (T_1i, T_2i) with the characteristic period value calibrated by the genetic algorithm, if the periods are not equal, the control period points are set as the mean value of the genetic algorithm and the assumed control period points (T_1i, T_2i). The design response spectrum curve expression is determined until assuming that the piecewise control period value is consistent with the calibration period point value (T_1i = T₀; T_2i = T_g; i = 1∼n). Then, the curve expression determined by regression analysis is the expression form of the final designed response spectrum, and the parameters calibrated by the genetic algorithm are the characteristic parameters. Figure 3 shows the calibration process of site-related design response spectra.

5. Applications

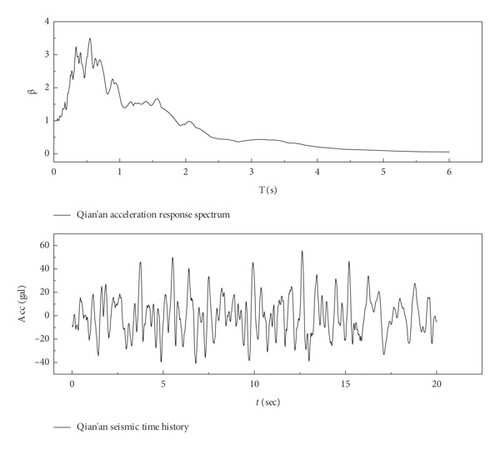
This paper takes the Qian’a earthquake time history obtained from the Tangshan earthquake as an example to carry out practical application research on the method proposed in this paper. Table 1 shows the Qian’a wave information table, and Figure 4 shows the response spectrum and acceleration time history of the Qian’a wave with a damping ratio of 5%.

1. Strong earthquake record information table.

Earthquake name	Record name	Site conditions	Earthquake magnitude (M)	Epicenter distance (km)	Peak acceleration (gal)
Tangshan earthquake	Qian’a wave	II site	7.8	154	55.49

5.1. Determination of the Shape of the Target Spectrum

According to the spectral shape characteristics of the seismic response spectrum, the values of T₁₁ = 0.10 s and T₂₁ = 1 s are assumed first. Based on the SPSS regression analysis, the piecewise seismic acceleration response spectrum curve is fitted, the mathematical expression of the calibration model of each piecewise is estimated, and the relevant determination coefficient R² is obtained. Figure 5 shows the fitting diagrams of each segment of the Qian’a earthquake acceleration response spectrum under 11 different functions.

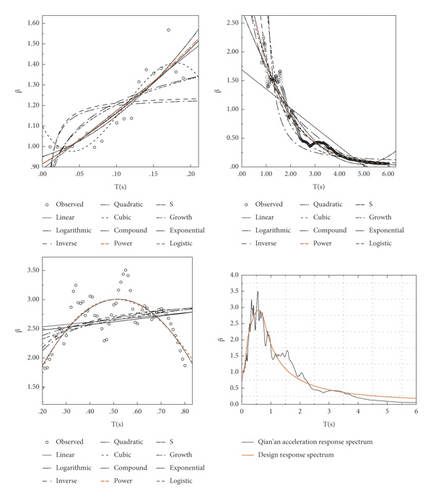
According to the seismic response spectrum curve in Figure 5, the actual seismic response spectrum curve has complex spectrum changes and irregular peak changes in the frequency band where the peak period occurs. The original design response spectrum curve expression cannot objectively describe the response of the mid-frequency site characteristics of the spectrum. Therefore, when determining the reasonable expression form of the calibration model, the regression analysis of each piecewise of the seismic acceleration response spectrum is adopted. According to the calculation results of the regression analysis, it is concluded that the R² values of the quadratic function and the cubic function are the highest. In the T_g ∼ T_m piecewise, the R² value of the cubic function and the power function is the largest. Thus, the target spectrum used in this paper is expressed as equation (3).

5.2. Genetic Algorithm Calibration Target Spectrum and Inflection Point Period(T₀, T_g)

A genetic algorithm is introduced for calibration. 9 individual parameters need to be fitted in the target spectrum, namely: T₀, T_g and γ, and a₁, a₂, a₃, a₄, a₅ and a₆. According to the abovementioned genetic algorithm calibration process, the 9 individual parameters are counted into the algorithm in turn. According to the target spectrum expression, the standard deviation of the genetic algorithm when calibrating the spectrum parameters can be expressed as equation (4).

5.3. Shape of the Design Response Spectrum and Determination of its Control Parameters

The periods T₀ and T_g calculated by the genetic algorithm are 0.20 s and 0.79 s, respectively, which are different from the initially assumed periods (T₁₁ = 0.10 s, T₂₁ = 1 s). The average value (mean value: T₁₂ = 0.15 s and T₂₂ = 0.90 s) of the initial and calibrated periods is taken as the piecewise period of the next fitting and then iteratively calibrated until the average period is equal to the piecewise period calibrated by the genetic algorithm. Therefore, the calibration curve of the site-related response spectrum determined by this calibration model combined with the genetic algorithm is the optimal design response spectrum curve expression of the field response spectrum.

Table 2 shows the expression form of the objective spectrum function when the proposed piecewise period is equal to the period point calibrated by the genetic algorithm. For high-frequency band fitting, the quadratic function and cubic function R² values are the largest. The principle behind the determination of the design response spectrum curve is as follows: For the response spectrum calibration of the entire frequency band, too many unknown parameters will increase the dispersion and fluctuation of the calibration parameters. Considering the efficiency of the algorithm, the quadratic function expression form is therefore selected for calibration in the high-frequency band. The middle frequency band (T₀∼T_g section) and the low-frequency band (T_g ∼ T_m section) have the best fitting results with cubic and power functions, respectively. Table 3 shows the design spectrum calibration parameters, and the design response spectrum curve is shown in Figure 5.

2. The target spectral function expression form and R² value are determined when the proposed period point is equal to the calculated period point.

Model R² value	Linear	Logarithmic	Inverse	Quadratic	Cubic	Composite	Power	S	Growth	Exponential	Logistic
High-frequency band	0.814	0.604	0.280	0.884	0.884	0.840	0.635	0.301	0.817	0.817	0.817
Mid-frequency band	0.029	0.091	0.180	0.595	0.996	0.038	0.109	0.210	0.038	0.038	0.038
Low-frequency band	0.791	0.924	0.937	0.950	0.954	0.930	0.963	0.760	0.930	0.930	0.930

3. Design spectrum calibration parameters calibrated by the new method.

Calibration parameters	T₀	T_g	γ	a₁	a₂	a₃	a₄	a₅	a₆
Record name: Qian’a wave	0.20	0.79	−1.29	18.38	2.70	−4.43	−0.09	4.55	1.17

From the final calibration results, it is not difficult to find that the final piecewise period and the calibration inflection point period are the same as the value of the inflection point period in the initial genetic algorithm calibration. The design response spectrum shape is determined by repeatedly comparing the assumed piecewise period and the inflection point period obtained by the genetic algorithm calibration. Through a large number of statistical analyses of the seismic response spectrum, it is found that the regression analysis of each piecewise of the seismic response spectrum is performed at the artificially assumed segmented period point. The calibration model of each segment is estimated, and the calibration model expression form of the design response spectrum always satisfies formula (3). Then, combined with the genetic algorithm calibration, two inflection point periods will not change or vary in a narrow range. It is the process of the proposed piecewise period continuously moving closer to the inflection point period calibrated by the genetic algorithm. According to the spectral shape change characteristics of different frequency bands, regression analysis is carried out to estimate that the calibration models for the high-, medium- and low-frequency bands conform to the expression form of the formula (3), which proves that the selection error of the proposed piecewise point does not influence the response spectrum calibration model, and the expression form of the designed response spectrum curve is stable.

5.4. Comparison of Calibration Results

The efficiency of the proposed method is validated against the three-parameter calibration method, two-parameter calibration method, least-square calibration method, and differential evolution algorithm [32, 33]. For the Qian’a earthquake records, the comparison results are presented in Figure 6 and Tables 4 and 5.

4. List of characteristic parameters of the traditional response spectrum.

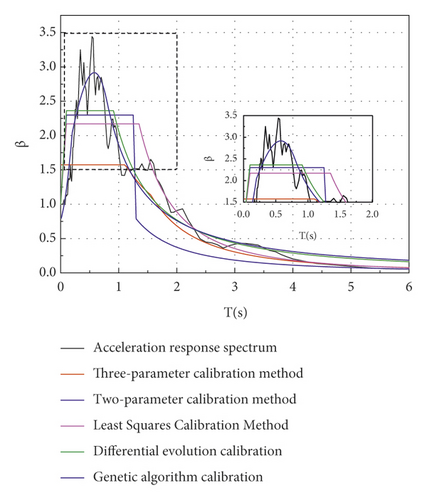
Characteristic parameters	T₀/s	T_g/s	β_max	γ
Calibration method	T₀/s	T_g/s	β_max	γ
Three-parameter calibration method	1.12	1.55	1.57	—
Two-parameter calibration method	0.10	0.90	2.30	1.73
Least-squares algorithm	0.10	1.35	2.17	2.27
Differential evolution algorithm	0.10	0.91	2.36	1.42

5. Standard deviation list of the five calibration methods.

Calibration method	Three-parameter calibration method	Two-parameter calibration method	Least-squares algorithm	Least-squares algorithm	Differential evolution algorithm
Qian’a earthquake record	0.62	0.67	0.61	0.28	0.14

The error between the design response spectrum curve given by the improved design response spectrum calibration model combined with the genetic algorithm and the seismic acceleration response spectrum is the smallest. The curve expression of the design response spectrum curve given in this paper in the middle frequency band truly and reasonably reflects the spectral variation characteristics and peak characteristics of the seismic response spectrum and reduces the discreteness caused by the platformization of the design response spectrum calibration. To verify the feasibility of this method in the seismic safety evaluation of engineering sites, the next part selects an engineering example in an earthquake safety evaluation report for calculation and compares the values of the characteristic parameters.

5.5. An Engineering Example

A hospital building is planned to be built in Tangshan city, the project is located in the VI fortified area of China, and the site category is a Class I site. The bedrock acceleration peaks and response spectra under the 50-year, 2%, 10%, and 63% probability of exceedance given in the seismic hazard analysis report are taken as the objective functions to artificially synthesize the bedrock ground motion time history and input separately to carry out the site seismic response analysis. The calculated horizontal acceleration response spectra are used for calibration by the two-parameter method, the least-square method, the differential evolution algorithm, and the improved genetic algorithm [32, 33]. The fitting results are shown in Tables 6–11 and Figure 7.

6. [34] The characteristic parameters in the safety evaluation report of a project site.

Exceeding probability	β_m	T₁/s	T_g/s	γ
50a-2%	2.50	0.10	0.50	0.90
50a-10%	2.50	0.10	0.35	0.90
50a-63%	2.50	0.10	0.25	0.90

7. Two-parameter calibration method to calibrate the design spectral characteristic parameters.

Exceeding probability	β_m	T₁/s	T_g/s	γ
50a-2%	2.11	0.10	0.44	1.18
50a-10%	2.79	0.10	0.42	1.15
50a-63%	2.79	0.10	0.25	1.35

8. Calibration of design spectral characteristic parameters by the least-squares piecewise fitting method.

Exceeding probability	β_m	T₁/s	T_g/s	γ
50a-2%	2.08	0.10	0.46	1.14
50a-10%	2.79	0.10	0.40	1.05
50a-63%	2.90	0.10	0.21	1.28

9. Design spectrum characteristic parameters calibrated by the differential evolution algorithm.

Exceeding probability	β_m	T₁/s	T_g/s	γ
50a-2%	2.32	0.13	0.36	0.89
50a-10%	2.49	0.08	0.34	1.18
50a-63%	3.15	0.12	0.23	1.18

10. Spectrum calibration parameter list of genetic algorithm calibration design.

Characteristic parameters	T₀	T_g	γ	a₁	a₂	a₃	a₄	a₅	a₆
Exceeding probability	T₀	T_g	γ	a₁	a₂	a₃	a₄	a₅	a₆
50a-2%	0.15	1.09	−1.16	23.45	12.22	−20.12	−15.44	3.29	3.20
50a-10%	0.14	0.95	−1.18	19.13	15.46	4.31	−5.27	−0.95	3.26
50a-63%	0.14	0.18	−1.15	23.45	11.83	2.78	−4.25	−0.29	2.85

11. Error analysis table of four calibration methods.

Calibration method	Genetic algorithm		Two-parameter calibration method		Least-squares calibration		Differential evolution algorithm
Exceeding probability	Standard deviation
50a-2%	0.15	1.09	−1.16	23.45	12.22	−20.12	−15.44	3.29
50a-10%	0.14	0.95	−1.18	19.13	15.46	4.31	−5.27	−0.95
50a-63%	0.14	0.18	−1.15	23.45	11.83	2.78	−4.25	−0.29

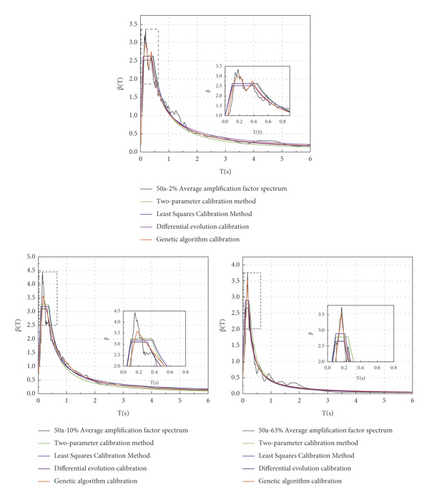
Figure 7 shows that the spectrum shape obtained by the improved genetic algorithm is close to the average amplification factor at each probability level. The platform value β_max given in the seismic safety evaluation report of the engineering site is taken as 2.5, which lacks rationality. The calibration parameters given in this paper are not constant values of β_max. The shape of the design response spectrum is controlled by 9 different characteristic parameters given by the calibration, and a clear mathematical expression of each piecewise of the design response spectrum can be given according to the calibration parameters. Second, comparing the given site ground motion parameters, the site characteristic period and attenuation index given in this paper are larger than those in the engineering site safety evaluation report. The calibration method takes into account the variability of the first inflection point period and the expression of the design spectrum. It reasonably reflects the peak characteristics of the power amplification coefficient spectrum.

In summary, the expression form and calibration method of the design response spectrum given in this article have the following three advantages:

(1)
The expression of the design response spectrum is not limited to the traditional three-section platform expression but is given based on the shape characteristics of the actual seismic acceleration response spectrum.
(2)
The design response spectrum changes from the original four calibration parameters to 9 calibration parameters. The increase in the parameters improves the calibration accuracy of the design spectrum shape to a certain extent.
(3)
The curve expression of the design spectral response spectrum objectively and reasonably reflects the influence of local site conditions and the seismic, geological environment on the spectral characteristics of the site-related response spectrum.

6. Conclusions

The calibration of the design response spectrum should not only meet the requirements of seismic engineering design but also fully consider the influence of the geological conditions and the seismic environment in the project site area to obtain the ground motion parameters more in line with the project site. In this paper, the site-related response spectrum calibration method is proposed, which improves the influence of the expression of the original design response spectrum platform section peak clipping on the design response spectrum calibration. The design response spectrum expression and characteristic parameters objectively reflect the site condition to a certain extent. The spectral characteristics of the relevant response spectrum and the influence of the site-specific soil geological conditions on the ground motion parameters provide a reference for future research on the calibration of the site-related response spectrum. However, the calibration method given in this article is currently mainly aimed at the calibration of the relevant response spectrum of major engineering sites and a single seismic acceleration response spectrum. For a large number of industrial and civilian buildings in China that do not need to be evaluated for the seismic safety of engineering sites, the seismic fortification of such buildings is mostly calculated according to the design response spectrum expression given in the “Code for Seismic Design of Buildings” (GB50011-2010). For the seismic fortification of such buildings, proposing a new design response spectrum expression that is in line with the code site classification and seismic design requirements and providing a new reference basis for seismic design are problems that still need further research and discussion.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This study was supported by Earthquake Science and Technology Project of Gansu Earthquake Agency(KY2021M3), https://doi.org/10.13039/501100001809National Natural Science Foundation of China (51508096) and (51808118), and Key Talent Project of Gansu Province: Research on Key Technologies for Rapid Assessment of Building Earthquake Damage with Radar Data in Northwest China.

Open Research

Data Availability

All the data are from the strong earthquake records obtained from the actual observation of previous earthquakes.

References

1 Housner G. W., Behavior of structures during earthquakes, Journal of the Engineering Mechanics Division. (1959) 85, no. 4, 109–129, https://doi.org/10.1061/jmcea3.0000102.
10.1061/JMCEA3.0000102
Google Scholar
2 Hall W. J., Mohraz B., and Newmark N. M., Statistical studies of vertical and horizontal earthquake spectra, Nathan M. Newmark Consulting Engineering Services. (1975) Urbana, Illinois, IL, USA.
Google Scholar
3 China Construction Industry Press, Ministry of construction of the people’s Republic of China, general administration of quality supervision, inspection and quarantine of the people’s Republic of China, Code for Seismic Design of Building Structures (GB50011-2010). (2010) China Construction Industry Press, Beijing, China, in Chinese.
Google Scholar
4 Hu Y. X., Earthquake engineering in China, Earthquake Engineering and Engineering Vibration. (2002) 1, no. 1, 1–9, in Chinese.
10.1007/s11803-002-0001-5
Google Scholar
5 Mohraz B., A study of earthquake response spectra for different geological conditions, Bull. Seismol. Soc.(1976) 66, no. 3, 915–935.
Web of Science® Google Scholar
6 Idriss I. M. and Seed H. B., Seismic response of horizontal soil layers, ASCE Soil Mechanics and Foundation Division Journal. (1968) 94, no. 4, 1003–1031.
10.1061/JSFEAQ.0001163
Google Scholar
7 Seed H. B. and Idriss I. M., Influence of soil conditions ground motions during earthquake, ASCE Soil Mechanics and Foundation Division Journal. (1969) 95, no. 1, 99–137.
10.1061/JSFEAQ.0001260
Google Scholar
8 Kuribayashi E., Iwasaki T., and Iida Y., Effects of seismic and subsoil conditions on earthquake response spectra, Proceedings of the international Conference on Microzonation, 1972, Seattle, WA, USA.
Google Scholar
9 Seed H. B., Ugas C., and Lysmer J., Site-dependent spectra for earthquake-resistant design, Bulletin of the Seismological Society of America. (1976) 66, no. 1, 221–243, https://doi.org/10.1785/bssa0660010221.
10.1785/BSSA0660010221
Web of Science® Google Scholar
10 Mohraz B., Recent studies of earthquake ground motion and amplification, Proceedings of the 10th World Conference on Earthquake Engineering, 1992, Madrid, Spain.
Google Scholar
11 Mohraz B., A study of earthquake response spectra for different geological conditions, Bulletin of the Seismological Society of America. (1976) 66, no. 3, 915–935.
Web of Science® Google Scholar
12 Mohraz B., Influences of the magnitude of the earthquake and the duration of strong motion on earthquake response spectra, Proceedings of the Central American Conference on Earthquake Engineering, 1978, San Salvadore, El Salvador.
Google Scholar
13 Ucar T. and Merter O., Effect of design spectral shape on inelastic response of RC frames subjectd to spectrum matched ground motions [J], Structural Engineering & Mechanics. (2019) 69, no. 3, 293–306.
Google Scholar
14 Yazdani A. and Takada T., Probabilistic study of the influence of ground motion variables on response spectra, Structural Engineering & Mechanics. (2011) 39, no. 6, 877–893, https://doi.org/10.12989/sem.2011.39.6.877, 2-s2.0-80052633998.
10.12989/sem.2011.39.6.877
Google Scholar
15 Yang S., Han X., Lei Q., Yu S., and Liu C., Study on the seismic effect of the interbedded soil layer in the yinchuan alluvial plain, Advances in Civil Engineering. (2021) 2021, 12, 1519750, https://doi.org/10.1155/2021/1519750.
10.1155/2021/1519750
Google Scholar
16 Liao Z., Seismic Zoning—Theory and Practice, 1989, Earthquake Press, Beijing, China, in Chinese.
Google Scholar
17 Hayashi S. H., Tsuchida H., Kurata H., and Kurata E., Average response spectra for various subsoil conditions, Proceedings of the Third Joint Meeting of US Japan Panel on Wind and Seismic Effects, 1971, Tokyo, Japan.
Google Scholar
18 Newmark N. M., Hall W. J., and Mohraz B., A study of vertical and horizontal earthquake spectra, 1973, US Atomic Energy Commission: Report WASH-1255 Directorate of Licensing.
Google Scholar
19 Mohraz B. and Sadek F., Earthquake ground motion and response spectra The Seismic Design Handbook, 2001, Springer, Berlin, Germany.
10.1007/978-1-4615-1693-4_2
Google Scholar
20 Freeman S. A., Response spectra as a useful design and analysis tool for practicing structural engineers, ISET Journal of Earthquake Technology. (2007) 44, no. 1, 25–37.
Google Scholar
21 Baker J. W., Conditional mean spectrum: tool for ground-motion selection, Journal of Structural Engineering. (2011) 137, no. 3, 322–331, https://doi.org/10.1061/(asce)st.1943-541x.0000215, 2-s2.0-79953253088.
10.1061/(ASCE)ST.1943-541X.0000215
Web of Science® Google Scholar
22 Malhotra P. K., Smooth spectra of horizontal and vertical ground motions, Bulletin of the Seismological Society of America. (2006) 96, no. 2, 506–518, https://doi.org/10.1785/0120050062, 2-s2.0-33645795447.
10.1785/0120050062
Web of Science® Google Scholar
23 Newmark N. M. and Hall W. J., Earthquake Spectra and Design, 1982, Earthquake Engineering Research Institute, Berkeley, Cl, USA.
Google Scholar
24 Nau J. M., Asce A. M., and Hall W. J., Scaling methods for earthquake response spectra, Journal of Structural Engineering. (1984) 110, no. 7, 1533–1548, https://doi.org/10.1061/(asce)0733-9445(1984)110:7(1533), 2-s2.0-0021642585.
10.1061/(ASCE)0733-9445(1984)110:7(1533)
Web of Science® Google Scholar
25 Han X., Improvement of Major Engineering Design Response Spectrum Shape and Calibration Method, 2020, Institute of Disaster Prevention, in Chinese.
Google Scholar
26 Han X., Discussion on the design of response spectrum platform value and its calibration method, Journal of Institute of Disaster Prevention. (2019) 21, no. 3, 7–15, in Chinese.
Google Scholar
27 Liu H., Calibration method of designed ground motion response spectrum based on niche genetic algorithm, Chinese Journal of Geotechnical Engineering. (2009) 31, no. 6, 975–979, in Chinese.
Google Scholar
28 Jiang X. and Chen Q., Calibration method of design response spectrum based on genetic algorithm, Quarterly Journal of Mechanics. (2006) 27, no. 2, 317–322, in Chinese.
Google Scholar
29 Naeim F., Alimoradi A., and Pezeshk S., Selection and scaling of ground motion time histories for structural design using genetic algorithms, Earthquake Spectra. (2004) 20, no. 2, 413–426, https://doi.org/10.1193/1.1719028, 2-s2.0-2942685520.
10.1193/1.1719028
Web of Science® Google Scholar
30 Coley D. A., An Introduction to Genetic Algorithms for Scientists and Engineers, 2001, World Scientific, Singapore.
Google Scholar
31 Lei Y., Shi F., and Wang H., Analysis of 30 Cases of MATLAB Intelligent Algorithms, 2015, Beihang University Press, Beijing, China, 178–187, in Chinese.
Google Scholar
32 Guo X., Bo J., and Ba W., Response spectrum method for segmental fitting of least squares fitting, World Earthquake Engineering. (2012) 28, no. 3, 29–33, in Chinese.
Google Scholar
33 Zhao P., Research on Design Response Spectrum Fitting Method and Characteristic Parameter Statistics, 2017, Institute of Engineering Mechanics, Earthquake Administration, China, in Chinese.
Google Scholar
34 Lv G., Earthquake Safety Evaluation Report of the Project Site of Zhihuiyuan Community in Tangshan City, Hebei Province, 2007, Research Institute of Earthquake Engineering in Hebei, Hebei, China, in Chinese.
Google Scholar

Citing Literature

All articles

A New Method for the Calibration of Site-Related Response Spectra

Abstract

1. Introduction

2. Determination of the Target Spectrum Shape