An Efficient Revocable Identity-Based Encryption with Equality Test Scheme for the Wireless Body Area Network
Abstract
With the rapid development and popularization of cloud computing, people are willing to upload their own data to the cloud to enjoy the services. However, some personal and private data are not suitable for uploading directly to the cloud. Therefore, these data must be encrypted before uploading to the cloud to ensure the confidentiality. To achieve the confidentiality of data and enjoy cloud services, a notion of identity-based encryption with equality test (IBEET) was proposed. Using IBEET, two ciphertexts encrypted under different public keys can be tested to confirm whether they contain the same plaintext. The equality test can be applied to the wireless body area network system in which the cloud can utilize ciphertexts from patients and medical institutions to perform equality tests to determine whether which patient’s status is abnormal. Indeed, revoking illegal or expired users on any cryptosystem is an important issue. To the best of our knowledge, there is little research on the design mechanism of user revocation in the IBEET. In this paper, we propose a novel notion of revocable identity-based encryption with an equality test, called RIBEET. Based on the notion, we present the first RIBEET scheme. Meanwhile, the proposed scheme will be proven to be secure under the bilinear Diffie-Hellman (BDH) assumption.
1. Introduction
With the rapid development and popularization of cloud computing, people are willing to upload their own data to the cloud to enjoy the services. However, some personal and private data are not suitable for uploading directly to the cloud. To ensure the confidentiality of data, several encryption mechanisms [1–4] have been applied to cloud computing. Identity-based encryption (IBE) [5] is one of the encryption mechanisms of public key systems. The system of an IBE contains two roles: the private key generator (PKG) and users (including senders and receivers). Each user utilizes his own identity (e.g., e-mail address, name, or social security number) to register with the PKG to obtain a private key. Senders can regard the identity of the receiver as a public key to encrypt private data. After receiving the encrypted message (ciphertext), the receiver can decrypt it with her/his own private key.
To achieve the confidentiality of data and enjoy cloud services, the first identity-based encryption with equality test (IBEET) was proposed by Ma [6]. Using IBEET, two ciphertexts encrypted under different public keys can be tested to confirm whether they contain the same plaintext. Ma [6] also gave an application of IBEET used to classify encrypted e-mails. Each encrypted e-mail can be attached with a tag for classification, while the tag can be encrypted under different public keys in the IBEET system. An e-mail server in the cloud can test the equality of any two encrypted tags to classify encrypted e-mails. Subsequently, many studies on IBEET have been published in the literature [7–11].
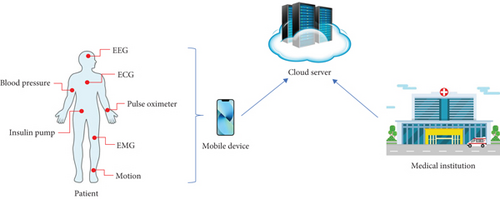
The equality test can be applied to the wireless body area network (WBAN) system [12–17] in which the cloud can utilize ciphertexts from patients and medical institutions to perform equality tests to determine whether the patient’s status is abnormal. Figure 1 shows the architecture of WBANs. A patient is equipped with wearable sensors to collect her/his health record data from sensors of electroencephalogram (EEG), electrocardiogram (ECG), blood pressure, pulse oximeter, insulin pump, electromyogram (EMG), and motion. These health record data are encrypted through the mobile device and uploaded to the cloud server. On the other hand, the medical institution also uploads the patient’s encrypted health data to the cloud server. The ciphertexts can be tested for equality without knowing the health data of the patient by the cloud server. If the patient’s health data are different from the medical institution’s health data, it means that the patient’s health data are abnormal.
Indeed, revoking illegal or expired users on any cryptosystem is an important issue. In the traditional public key cryptosystem (PKC), public key infrastructures (PKI) must be established to manage each user’s certificate which links the user’s identity and public key. In addition, the certificate revocation list [18] is also included in the PKI to revoke illegal or expired users. In identity-based public key cryptosystems (ID-PKC), the first IBE was presented by Boneh and Franklin [5] in which a user can be revoked by the PKG, who sends new private keys for all nonrevoked users at each period, if the user did not receive the new private key. So far, many literatures related to revocable IBE [19–26] have been published. To the best of our knowledge, there is little research on design mechanism of user revocation in the IBEET. In this paper, we propose a novel notion of revocable identity-based encryption with equality test, called RIBEET. Based on the notion, we present the first RIBEET scheme. Meanwhile, the scheme will be proven to be secure under the bilinear Diffie-Hellman (BDH) assumption.
1.1. Related Work
In the era of advanced network communication, cloud computing is an indispensable part. The terminal devices on the user side usually do not have high-performance computing power. However, users can entrust large computing tasks to the cloud. Then, the cloud will return the corresponding results to users after finishing the tasks. Indeed, the cloud can assist each user in performing tasks that require a lot of computation, but it also means that the cloud can know each user’s data if the data is not encrypted. Typically, users will encrypt data to the cloud if the data is sensitive or private. In addition, encrypted data also needs to be quickly retrieved from the cloud. To achieve this function, several schemes [3, 4, 27, 28] related to public key encryption with a keyword search were proposed. Although these schemes can retrieve encrypted data, only data encrypted under the same public key can be retrieved.
To support searchable encrypted data under different public keys, Yang et al. [29] proposed a comparison mechanism of two ciphertexts encrypted under different public keys in the traditional public key cryptosystem, called public key encryption with equality test (PKEET). However, the traditional public key cryptosystem must rely on the public key infrastructure to manage each user’s certificate which links the user’s identity and her/his public key. To avoid the use of public key infrastructure and certificates, Shamir [30] introduced a new concept of ID-PKC in which a user’s public key is her/his identity such as name, e-mail, or telephone number. In this way, certificates will no longer be needed in the ID-PKC since the public key is meaningful and can represent the user’s identity. Combining the concepts of PKEET and ID-PKC, Ma [6] proposed the first identity-based encryption with equality test, called IBEET. To consider more types of authorizations, Li et al. [31] proposed the IBEET scheme with four types of authorizations. Unfortunately, the proposed scheme of Li et al. [31] is not suitable for the IoT environment because the performance of the scheme is not good. Immediately, Elhabob et al. [10] proposed another IBEET scheme with four types of authorizations which has higher performance.
For the issue of user revocation in the ID-PKC, Boneh and Franklin [5] suggested that the new private keys should be resent to users who have not been revoked at different periods. As a result, secure channels will be established to send these private keys, and the PKG’s workload will also increase. To reduce the PKG’s workload, Boldyreva et al. [19] hired a binary tree to propose an IBE scheme with user revocation, named revocable IBE (RIBE). However, Boldyreva et al.’s scheme [19] only satisfied the selective-ID security. Later, Libert and Vergnaud [20] proposed another RIBE scheme which meets the adaptive-ID security. A mechanism for revoking users through public channels was proposed by Tseng and Tsai [21], in which each user’s full private key is divided into two parts: a fixed key and a time updated key. The fixed key is delivered to the user through secure channels only once, while the time updated key is delivered to the user through public channels at different periods. Users can be revoked if they do not receive the new time updated keys. For the security of decryption key exposure, Seo and Emura [22] proposed a new RIBE scheme to enhance the security. To reduce the length of public parameters and meet the security of decryption key exposure resistance, Watanabe et al. [23] presented another RIBE scheme. In addition, several lattice-based RIBE schemes [24–26] were proposed to resist quantum attacks.
1.2. Motivation
As mentioned earlier, revoking illegal or expired users on any cryptosystem is still an important issue. In the traditional PKC, the PKEET [29] can hire the certificate revocation list [18] to revoke illegal or expired users. However, the IBE [5] cannot effectively revoke illegal or expired users in the ID-PKC, so the RIBE [21] was proposed. To the best of our knowledge, there is little research on the design mechanism of user revocation in the IBEET [6]. Table 1 shows the comparisons between the PKEET [29], the IBE [5], the RIBE [21], the IBEET [6], and our RIBEET in terms of public key setting, avoiding the use of certificates, supporting the equality test of ciphertexts, and providing user revocation. Hence, we attempt to propose the first revocable identity-based encryption with equality test, called RIBEET.
1.3. Contribution and Organization
- (i)
Based on the existing syntax and security notions of IBEET, we consider the property of user revocation to define a new syntax and security notions of RIBEET
- (ii)
Following the syntax of RIBEET, a concrete RIBEET scheme is proposed
- (iii)
In the security notions of RIBEET, the proposed scheme is proven to be secure under the bilinear Diffie-Hellman (BDH) assumption
- (iv)
We compare the proposed scheme with the previous RIBE scheme and IBEET scheme. We demonstrate that the proposed scheme not only provides user revocation but also supports the equality test for ciphertexts
The rest of the article includes six sections. Preliminaries are given in Section 2. Section 3 presents the syntax and security notions of RIBEET. A concrete RIBEET scheme is proposed in Section 4. The security analysis of the RIBEET scheme is shown in Section 5. We compare the RIBEET scheme with other existing schemes in Section 6. The last section gives the conclusion.
2. Preliminaries
In this section, we introduce two definitions related to a mathematical tool and security assumption. We hire the bilinear pairings [5] as a mathematical tool to construct our RIBEET scheme. To prove the security of the proposed scheme, we consider the bilinear Diffie-Hellman (BDH) problem and then give a BDH assumption [6]. The definition of the bilinear pairings is given as follows.
Definition 1. Let G1, G2, and GT be three multiplicative cyclic groups of a prime order q. Assume that a mapping is an asymmetric bilinear map. Then, the map satisfies the following properties.
- (1)
Bilinearity: for g1 ∈ G1, g2 ∈ G2, and
- (2)
Nondegeneracy: for some g1 ∈ G1 and g2 ∈ G2
- (3)
Computability: can be efficiently computed for g1 ∈ G1, g2 ∈ G2
For the asymmetric bilinear map, the BDH problem is to compute by given a tuple . We define the BDH assumption as follows.
Definition 2. On inputting a tuple , we say that the BDH problem holds if no algorithm has nonnegligible advantage in computing . The advantage can be denoted as .
3. Syntax and Security Notions
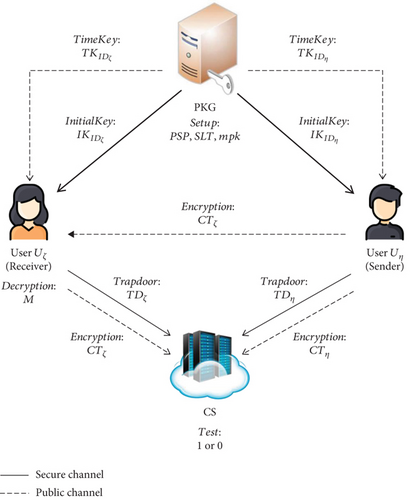
3.1. Syntax of RIBEET
- (i)
Setup: this algorithm is performed by the PKG who takes a security parameter k and a time period t as input to produce the public system parameters PSP, the system life time SLT, and the master private key mpk
- (ii)
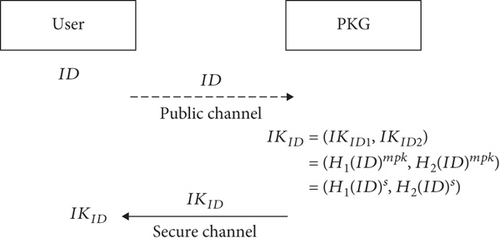
InitialKey: this algorithm is performed by the PKG who takes the public system parameter PSP, the master private key mpk, and a user’s identity ID ∈ {0, 1}∗ as input to produce user initial key IKID
- (iii)
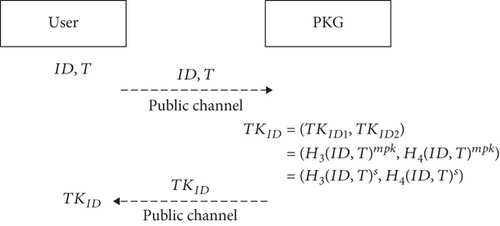
TimeKey: this algorithm is performed by the PKG who takes the public system parameter PSP, the master private key mpk, a user’s identity ID ∈ {0, 1}∗, and a period T ∈ SLT as input to produce user time key TKID
- (iv)
Encryption: this algorithm is performed by a user (sender) who takes the public system parameter PSP, a user’s identity ID ∈ {0, 1}∗, a period T ∈ SLT, and a message M ∈ {0, 1}λ as input to produce a ciphertext CT
- (v)
Decryption: this algorithm is performed by a user (receiver) who takes the public system parameter PSP, the receiver’s initial key IKID, the receiver’s time key TKID, and the ciphertext CT as input to produce the message M
- (vi)
Trapdoor: this algorithm is performed by a user who takes her/his initial key IKID and time key TKID as input to produce the trapdoor TDID
- (vii)
Test: this algorithm is performed by the CS who takes the public system parameters PSP and two ciphertext-trapdoor pairs (CTζ, TDζ) and (CTη, TDη) from any two users Uζ and Uη as input to produce 1 or 0

| Notations | Meaning |
|---|---|
| PSP | The public system parameters |
| SLT | The system life time |
| mpk | The master private key |
| ID | The user’s identity |
| IKID | The user initial key |
| TKID | The user time key |
| M | The message |
| CT | The ciphertext |
| TDID | The trapdoor |
| (CTζ, TDζ) | The ciphertext-trapdoor pair of the user Uζ |
| (CTη, TDη) | The ciphertext-trapdoor pair of the user Uη |
3.2. Security Notions of RIBEET
- (1)
Type I adversary: such an adversary can obtain all information (including time key TKID) transmitted through public channels. The adversary can be regarded as an outside attacker
- (2)
Type II adversary: such an adversary owns her/his initial key IKID, but he does not have the current time key TKID. The adversary can be regarded as a revoked user
- (3)
Type III adversary: this adversary is identical to the type I adversary, except that she/he possesses the trapdoor TD
- (4)
Type IV adversary: this adversary is identical to the type II adversary, except that she/he possesses the trapdoor TD
Following the security notions of IBEET [6], we consider revoked users to define the new security notions of RIBEET. Definitions 3 and 4, respectively, are given to state IND-ID-CCA and OW-ID-CCA security of an RIBEET scheme.
Definition 3 (IND-ID-CCA). Let be a type I or type II adversary for an RIBEET scheme and be a challenger in the following game. The scheme is IND-ID-CCA secure if the advantage that wins the game is negligible.
- (1)
Setup. The challenger takes a security parameter k and a time period t as input to produce the public system parameters PSP, the system life time SLT, and the master private key mpk. The public system parameters PSP and the system life time SLT are sent to the adversary
- (2)
Phase 1. Several queries below can be issued by the adversary
- (a)
InitialKey query(ID): given an identity ID, the challenger generates an initial key IKID as the response by running the InitialKey algorithm of the RIBEET scheme
- (b)
TimeKey query(ID, T): given an identity ID and a period T, the challenger generates a time key TKID as the response by running the TimeKey algorithm of the RIBEET scheme
- (c)
Decryption query(ID, T, CT): given an identity ID, a period T, and a ciphertext CT, the challenger generates the resulting message M as the response by running the Decryption of the RIBEET scheme
- (d)
Trapdoor query(ID, T): given an identity ID and a period T, the challenger generates a trapdoor TDID as the response by running the Trapdoor of the RIBEET scheme
- (3)
Challenge. Two messages , , an identity ID∗, and a period T∗ are submitted by the adversary . The challenger chooses from these two messages, where is a random coin. The challenger then generates a ciphertext CT∗ as the challenge one by running the Encryption of the RIBEET scheme with . Here, the following restrictions must be satisfied
- (i)
The adversary cannot issue the Trapdoor query with ID∗
- (ii)
The adversary cannot issue the InitialKey query with ID∗ if it is the type I adversary
- (iii)
The adversary cannot issue the TimeKey query with (ID∗, T∗) if it is the type II adversary
- (i)
- (4)
Phase 2. Under the above restrictions, can execute the same tasks as in phase 1
- (5)
Guess. The adversary outputs a guess and wins the game if . The advantage that wins the game can be denoted as
Definition 4 (OW-ID-CCA). Let be a type III or type IV adversary for an RIBEET scheme and be a challenger in the following game. The scheme is OW-ID-CCA secure if the advantage that wins the game is negligible.
- (1)
Setup. The challenger takes a security parameter k and a time period t as input to produce the public system parameters PSP, the system life time SLT, and the master private key mpk. The public system parameters PSP and the system life time SLT are sent to the adversary
- (2)
Phase 1. Several queries below can be issued by the adversary
- (a)
InitialKey query(ID): given an identity ID, the challenger generates an initial key IKID as the response by running the InitialKey algorithm of the RIBEET scheme
- (b)
TimeKey query(ID, T): given an identity ID and a period T, the challenger generates a time key TKID as the response by running the TimeKey algorithm of the RIBEET scheme
- (c)
Decryption query(ID, T, CT): given an identity ID, a period T, and a ciphertext CT, the challenger generates the resulting message M as the response by running the Decryption of the RIBEET scheme
- (d)
Trapdoor query(ID, T): given an identity ID and a period T, the challenger generates a trapdoor TDID as the response by running the Trapdoor of the RIBEET scheme
- (3)
Challenge. An identity ID∗ and a period T∗ are submitted by the adversary . The challenger randomly chooses M∗ and then generates a ciphertext CT∗ as the challenge one by running the Encryption of the RIBEET scheme with (ID∗, T∗, M∗). Here, the following restrictions must be satisfied
- (a)
The adversary cannot issue the InitialKey query with ID∗ if it is the type III adversary
- (b)
The adversary cannot issue the TimeKey query with (ID∗, T∗) if it is the type IV adversary
- (4)
Phase 2. Under the above restrictions, can execute the same tasks as in phase 1
- (5)
Guess. The adversary outputs a guess M′ and wins the game if M∗ = M′. The advantage that wins the game can be denoted as .
4. Concrete RIBEET Scheme
- (1)
Setup: this algorithm is performed by the PKG who takes a security parameter k and a time period t as input to produce an asymmetric bilinear map and a system life time SLT = {T0, T1, ⋯, Tt}, where G1, G2, and GT are multiplicative cyclic groups of prime order q. The PKG first chooses two arbitrary generators g1 ∈ G1 and g2 ∈ G2 and picks eight cryptographic one-way hash functions H1 : {0, 1}∗⟶G2, H2 : {0, 1}∗⟶G2, H3 : {0, 1}∗⟶G2, H4 : {0, 1}∗⟶G2, H5 : GT × G1 × G1⟶{0, 1}λ+l, H6 : {0, 1}λ⟶G2, , and H8 : GT⟶G2, where λ and l are fixed lengths. Then, a random value is chosen, and is computed. The public system parameters are , the system life time is SLT = {T0, T1, ⋯, Tt}, and the master private key is mpk = s
- (2)
InitialKey: this algorithm is performed by the PKG who takes the public system parameter PSP, the master private key mpk, and a user’s identity ID ∈ {0, 1}∗ as input to produce user initial key
(1)
- (3)
TimeKey: this algorithm is performed by the PKG who takes the public system parameter PSP, the master private key mpk, a user’s identity ID ∈ {0, 1}∗, and a period T ∈ SLT as input to produce user time key
(2)
- (4)
Encryption: this algorithm is performed by a sender who takes the public system parameter PSP, a user’s identity ID ∈ {0, 1}∗, a period T ∈ SLT, and a message M ∈ {0, 1}λ as input to produce ciphertexts CT = (CT1, CT2, CT3, CT4) which are shown as follows
- (a)
- (b)
- (c)
- (d)
- (5)
Decryption: this algorithm is performed by a receiver who takes the public system parameter PSP, the receiver’s initial key IKID = (IKID1, IKID2), the receiver’s time key TKID = (TKID1, TKID2), and the ciphertext CT = (CT1, CT2, CT3, CT4) as input to produce the message M. The detailed process is shown as follows:
- (a)
Compute to obtain M′||V′
- (b)
Compute r′ = H7(M′, V′)
- (c)
Produce the message M′ as M if and both hold
- (6)
Trapdoor: this algorithm is performed by a user who takes her/his initial key IKID = (IKID1, IKID2) and time key TKID = (TKID1, TKID2) as input to produce the trapdoor TDID = IKID2 · TKID2 = H2(ID)s · H4(ID, T)s
- (7)
Test: this algorithm is performed by the CS who takes the public system parameters PSP and two ciphertext-trapdoor pairs (CTζ, TDζ) and (CTη, TDη), where CTζ = (CTζ1, CTζ2, CTζ3, CTζ4) and CTη = (CTη1, CTη2, CTη3, CTη4), from any two users Uζ and Uη as input to produce 1 or 0 according to the following steps
- (a)
Compute Rζ and Rη as follows:
- (i)
- (ii)
- (b)
Compute and
- (i)
- (ii)
- (c)
Return 1 if . Otherwise, return 0
- (i)
- (ii)
5. Security Analysis
In this section, we give four theorems to show that the proposed scheme has the IND-ID-CCA security for type I and II adversaries and the OW-ID-CCA security for type III and IV adversaries.
Theorem 5. If the BDH assumption holds, the proposed RIBEET scheme satisfies the IND-ID-CCA security in the security game. More precisely, suppose that is a PPT type 1 adversary who has at least ε advantage to break the RIBEET scheme. Then, there exists an algorithm to solve the BDH problem with the advantage
Proof. An algorithm is constructed to solve the BDH problem. The algorithm is given a BDH tuple which is defined in Section 2. The algorithm can be seen as a challenger to find the answer of the BDH problem. The answer A = can be found by interacting with the PPT type I adversary in the following security game.
- (1)
Setup: the challenger utilizes the BDH tuple to set and then generates the public system parameters , where Hi is a random oracle for i = 1, 2, ⋯, 8. In addition, the system life time SLT = {T0, T1, ⋯, Tt} can be generated by the challenger . Then, gives the public system parameters PSP and system life time SLT. Here, the adversary can issue queries to each random oracle as follows
- (a)
H1query(ID): can utilize ID to obtain a response to the random oracle H1 from the challenger . To obtain the response, maintains a list, called ListH1 which is composed of tuples, and the format of the tuple is 〈ID, UID, u, rb〉. The response is acquired from the ListH1 which is initially empty and can be updated by the following steps
- (i)
returns UID as the response if ID exists in a tuple 〈ID, UID, u, rb〉 from the ListH1
- (i)
- (a)
- (ii)
Otherwise, picks a random value and a random bit rb ∈ {0, 1} to compute
- (b)
H2query(ID): can utilize ID to obtain a response to the random oracle H2 from the challenger . To obtain the response, maintains a list, called ListH2 which is composed of tuples, and the format of the tuple is 〈ID, VID, v, rb〉. The response is acquired from the ListH2 which is initially empty and can be updated by the following steps:
- (a)
returns VID as the response if ID exists in a tuple 〈ID, VID, v, rb〉 from the ListH2
- (b)
Otherwise, picks a random value and utilizes ID to find rb in the ListH2. Then, computes
- (c)
H3query(ID, T): can utilize (ID, T) to obtain a response to the random oracle H3 from the challenger . To obtain the response, maintains a list, called ListH3 which is composed of tuples, and the format of the tuple is 〈ID, T, UIDT, η〉. The response is acquired from the ListH3 which is initially empty and can be updated by the following steps
- (i)
returns UIDT as the response if (ID, T) exists in a tuple 〈ID, T, UIDT, η〉 from the ListH3
- (ii)
Otherwise, picks a random value to compute . Then, adds the tuple 〈ID, T, UIDT, η〉 to the ListH3 and returns UIDT to
- (d)
H4query(ID, T): can utilize (ID, T) to obtain a response to the random oracle H4 from the challenger . To obtain the response, maintains a list, called ListH4 which is composed of tuples, and the format of the tuple is 〈ID, T, VIDT, ζ〉. The response is acquired from the ListH4 which is initially empty and can be updated by the following steps
- (i)
returns VIDT as the response if (ID, T) exists in a tuple 〈ID, T, VIDT, ζ〉 from the ListH4
- (ii)
Otherwise, picks a random value to compute . Then, adds the tuple 〈ID, T, VIDT, ζ〉 to the ListH4 and returns VIDT to
- (e)
H5query(W, CT1, CT2): can utilize (W, CT1, CT2) to obtain a response to the random oracle H5 from the challenger . To obtain the response, maintains a list, called ListH5 which is composed of tuples, and the format of the tuple is 〈W, CT1, CT2, ω〉. The response is acquired from the ListH5 which is initially empty and can be updated by the following steps
- (i)
returns ω as the response if (W, CT1, CT2) exists in a tuple 〈W, CT1, CT2, ω〉 from the ListH5
- (ii)
Otherwise, picks a random value ω ∈ {0, 1}λ+l and adds the tuple 〈W, CT1, CT2, ω〉 to the ListH5. Then, returns ω to
- (f)
H6query(M): can utilize M to obtain a response to the random oracle H6 from the challenger . To obtain the response, maintains a list, called ListH6 which is composed of tuples, and the format of the tuple is 〈M, Q〉. The response is acquired from the ListH6 which is initially empty and can be updated by the following steps
- (i)
returns Q as the response if M exists in a tuple 〈M, Q〉 from the ListH6
- (ii)
Otherwise, picks a random point Q ∈ G2 and adds the tuple 〈M, Q〉 to the ListH6. Then, returns Q to
- (g)
H7query(M, V): can utilize (M, V) to obtain a response to the random oracle H7 from the challenger . To obtain the response, maintains a list, called ListH7 which is composed of tuples, and the format of the tuple is 〈M, V, γ〉. The response is acquired from the ListH7 which is initially empty and can be updated by the following steps
- (i)
returns γ as the response if (M, V) exists in a tuple 〈M, V, γ〉 from the ListH7
- (ii)
Otherwise, picks a random value and adds the tuple 〈M, V, γ〉 to the ListH7. Then, returns γ to
- (h)
H8query(N): can utilize N to obtain a response to the random oracle H8 from the challenger . To obtain the response, maintains a list, called ListH8 which is composed of tuples, and the format of the tuple is 〈N, S〉. The response is acquired from the ListH8 which is initially empty and can be updated by the following steps
- (i)
returns S as the response if N exists in a tuple 〈N, S〉 from the ListH8
- (ii)
Otherwise, picks a random point S ∈ G2 and adds the tuple 〈N, S〉 to the ListH8. Then, returns S to
- (2)
Phase 1: the adversary can, respectively, utilize ID, (ID, T), (ID, T, CT) and (ID, T) to issue the InitialKey query, Timekey query, Decryption query, and Trapdoor query. The response to each query can be obtained as follows
- (a)
InitialKey query(ID): utilizes ID to issue the query, while , respectively, finds the corresponding tuples 〈ID, UID, u, rb〉 and 〈ID, VID, v, rb〉 from the ListH1 and the ListH2 according to ID. If rb = 1, interrupts this game. If rb = 0, use u and v to define . Then returns IKID as the user initial key to
- (b)
Timekey query(ID, T): utilizes (ID, T) to issue the query, while , respectively, finds the corresponding tuples 〈ID, T, UIDT, η〉 and 〈ID, T, VIDT, ζ〉 from the ListH3 and the ListH4 according to (ID, T). use η and ζ to define . Then, returns TKID as the user time key to
- (c)
Decryption query(ID, T, CT): utilizes (ID, T, CT) to issue the query, while , respectively, finds the corresponding tuples 〈ID, UID, u, rb〉, 〈ID, VID, v, rb〉, 〈ID, T, UIDT, η〉, and 〈ID, T, VIDT, ζ〉 from the ListH1, ListH2, ListH3, and the ListH4 according to ID and T. The response of this query is acquired from these lists by performing the following tasks
- (i)
If rb = 0, , respectively, uses ID and (ID, T) to run InitialKeyquery and Timekey query to obtain IKID and TKID. Then, utilizes IKID, TKID, and CT to run the Decryption algorithm to produce the message M which is sent to
- (ii)
If rb = 1, utilizes CT1 and CT2, which are from CT = (CT1, CT2, CT3, CT4), to find the corresponding tuple 〈W, CT1, CT2, ω〉 from the ListH5. Then, M′||V′ = CT3 ⊕ ω can be computed by using CT3 and ω. Further, utilizes M′ and V′ to find the corresponding tuples 〈M, V, γ〉 from the ListH7 and 〈M, Q〉 from the ListH6. Obviously, γ and Q can be obtained. If S can be found in the corresponding tuple 〈N, S〉 from the ListH8 such that CT4 = Qγ · S holds, will confirm whether holds. If , the message M′ is sent to
- (d)
Trapdoor query(ID, T): utilizes (ID, T) to issue the query, while , respectively, uses ID and (ID, T) to run InitialKey query and Timekey query to obtain IKID = (IKID1, IKID2) and TKID = (TKID1, TKID2). Then, utilizes IKID2 and TKID2 to produce the trapdoor TDID = IKID2 · TKID2 which is sent to
- (3)
Challenge: when the phase 1 is over, outputs a tuple as the target of the challenge. utilizes ID∗ to find the corresponding tuples 〈ID, UID, u, rb〉 from the ListH1. If rb = 0, interrupts this game. If rb = 1, randomly selects and V ∈ {0, 1}l to run H7 query with and V. Then, γ can be obtained. utilizes γ to set . In addition, sets , while a random value CT3 ∈ {0, 1}λ+l and a random point are chosen. Finally, the challenge ciphertext is sent to
- (4)
Phase 2: can issue the same query as phase 1, but it must be under the condition of ID ≠ ID∗ and CT ≠ CT∗
- (5)
Guess: responds to with a guess . If , responds with failure and terminates. Otherwise, wins the game. Then, randomly selects a tuple from the ListH5 and calculates , where . Hence, can output the BDH solution due to
Analysis. Let us start with two cases, namely, the simulation of Hi query for i = 1, 2, ⋯, 8 and the simulation of decryption query. For the H1, H2, H3, H4, H6, and H7 queries, it is obvious that the simulations are perfect because there exists no relationship between the constructions of these queries and the solution of the BDH problem. For the H5 and H8 queries, we consider two events and which, respectively, issues the H5 query with and the H8 query with . We say that the simulations of H5 and H8 queries are perfect if and do not happen. For the decryption query, we consider an event EDecErr where the challenger cannot decrypt the ciphertext. Assume that qD is the number of decryption query. Then, we obtain Pr[EDecErr] ≤ qD/q
Theorem 6. If the BDH assumption holds, the proposed RIBEET scheme satisfies the IND-ID-CCA security in the security game. More precisely, suppose that is a PPT type 2 adversary who has at least ε advantage to break the RIBEET scheme. Then, there exists an algorithm to solve the BDH problem with the advantage
Proof. An algorithm is constructed to solve the BDH problem. The algorithm is given a BDH tuple which is defined in Section 2. The algorithm can be seen as a challenger to find the answer of the BDH problem. The answer can be found by interacting with the PPT type II adversary in the following security game.
- (1)
Setup: the challenger utilizes the BDH tuple to set and then generates the public system parameters , where Hi is a random oracle for i = 1, 2, ⋯, 8. In addition, the system life time SLT = {T0, T1, ⋯, Tt} can be generated by the challenger . Then, gives the public system parameters PSP and system life time SLT. Here, the adversary can issue queries to each random oracle as follows
- (a)
H1query(ID): can utilize ID to obtain a response to the random oracle H1 from the challenger . To obtain the response, maintains a list, called ListH1 which is composed of tuples, and the format of the tuple is 〈ID, UID, u〉. The response is acquired from the ListH1 which is initially empty and can be updated by the following steps
- (i)
returns UID as the response if ID exists in a tuple 〈ID, UID, u〉 from the ListH1
- (ii)
Otherwise, picks a random value to compute . Then, adds the tuple 〈ID, UID, u〉 to the ListH1 and returns UID to
- (b)
H2query(ID): can utilize ID to obtain a response to the random oracle H2 from the challenger . To obtain the response, maintains a list, called ListH2 which is composed of tuples, and the format of the tuple is 〈ID, VID, v〉. The response is acquired from the ListH2 which is initially empty and can be updated by the following steps
- (i)
returns VID as the response if ID exists in a tuple 〈ID, VID, v〉 from the ListH2
- (ii)
Otherwise, picks a random value to compute . Then, adds the tuple 〈ID, VID, v〉 to the ListH2 and returns VID to
- (c)
H3query(ID, T): can utilize (ID, T) to obtain a response to the random oracle H3 from the challenger . To obtain the response, maintains a list, called ListH3 which is composed of tuples, and the format of the tuple is 〈ID, T, UIDT, η, rb〉. The response is acquired from the ListH3 which is initially empty and can be updated by the following steps
- (i)
returns UIDT as the response if (ID, T) exists in a tuple 〈ID, T, UIDT, η, rb〉 from the ListH3
- (ii)
Otherwise, picks a random value and a random bit rb ∈ {0, 1} to compute
(13)
- (d)
H4query(ID, T): can utilize (ID, T) to obtain a response to the random oracle H4 from the challenger . To obtain the response, maintains a list, called ListH4 which is composed of tuples, and the format of the tuple is 〈ID, T, VIDT, ζ, rb〉. The response is acquired from the ListH4 which is initially empty and can be updated by the following steps
- (i)
returns VIDT as the response if (ID, T) exists in a tuple 〈ID, T, VIDT, ζ, rb〉 from the ListH4
- (ii)
Otherwise, picks a random value and utilizes (ID, T) to find rb in the ListH4. Then, computes
(14)
- (e)
H5query(W, CT1, CT2): can utilize (W, CT1, CT2) to obtain a response to the random oracle H5 from the challenger . To obtain the response, maintains a list, called ListH5 which is composed of tuples, and the format of the tuple is 〈W, CT1, CT2, ω〉. The response is acquired from the ListH5 which is initially empty and can be updated by the following steps
- (i)
returns ω as the response if (W, CT1, CT2) exists in a tuple 〈W, CT1, CT2, ω〉 from the ListH5
- (ii)
Otherwise, picks a random value ω ∈ {0, 1}λ+l and adds the tuple 〈W, CT1, CT2, ω〉 to the ListH5. Then, returns ω to
- (f)
H6query(M): can utilize M to obtain a response to the random oracle H6 from the challenger . To obtain the response, maintains a list, called ListH6 which is composed of tuples, and the format of the tuple is 〈M, Q〉. The response is acquired from the ListH6 which is initially empty and can be updated by the following steps
- (i)
returns Q as the response if M exists in a tuple 〈M, Q〉 from the ListH6
- (ii)
Otherwise, picks a random point Q ∈ G2 and adds the tuple 〈M, Q〉 to the ListH6. Then, returns Q to
- (g)
H7query(M, V): can utilize (M, V) to obtain a response to the random oracle H7 from the challenger . To obtain the response, maintains a list, called ListH7 which is composed of tuples, and the format of the tuple is 〈M, V, γ〉. The response is acquired from the ListH7 which is initially empty and can be updated by the following steps
- (i)
returns γ as the response if (M, V) exists in a tuple 〈M, V, γ〉 from the ListH7
- (ii)
Otherwise, picks a random value and adds the tuple 〈M, V, γ〉 to the ListH7. Then, returns γ to
- (h)
H8query(N): can utilize N to obtain a response to the random oracle H8 from the challenger . To obtain the response, maintains a list, called ListH8 which is composed of tuples, and the format of the tuple is 〈N, S〉. The response is acquired from the ListH8 which is initially empty and can be updated by the following steps
- (i)
returns S as the response if N exists in a tuple 〈N, S〉 from the ListH8
- (ii)
Otherwise, picks a random point S ∈ G2 and adds the tuple 〈N, S〉 to the ListH8. Then, returns S to
- (2)
Phase 1: the adversary can, respectively, utilize ID, (ID, T), (ID, T, CT), and (ID, T) to issue the InitialKey query, Timekey query, Decryption query, and Trapdoor query. The response to each query can be obtained as follows
- (a)
InitialKey query(ID): utilizes ID to issue the query, while , respectively, finds the corresponding tuples 〈ID, UID, u〉 and 〈ID, VID, v〉 from the ListH1 and the ListH2 according to ID. use u and v to define . Then, returns IKID as the user initial key to
- (b)
Timekey query(ID, T): utilizes (ID, T) to issue the query, while , respectively, finds the corresponding tuples 〈ID, T, UIDT, η, rb〉 and 〈ID, T, VIDT, ζ, rb〉 from the ListH3 and the ListH4 according to (ID, T). If rb = 1, interrupts this game. If rb = 0, use η and ζ to define . Then, returns TKID as the user time key to
- (c)
Decryption query(ID, T, CT): utilizes (ID, T, CT) to issue the query, while , respectively, finds the corresponding tuples 〈ID, UID, u〉, 〈ID, VID, v〉, 〈ID, T, UIDT, η, rb〉, and 〈ID, T, VIDT, ζ, rb〉 from the ListH1, ListH2, ListH3, and ListH4 according to ID and T. The response of this query is acquired from these lists by performing the following tasks
- (i)
If rb = 0, , respectively, uses ID and (ID, T) to run InitialKeyquery and Timekey query to obtain IKID and TKID. Then, utilizes IKID, TKID, and CT to run the Decryption algorithm to produce the message M which is sent to
- (ii)
If rb = 1, utilizes CT1 and CT2, which are from CT = (CT1, CT2, CT3, CT4), to find the corresponding tuple 〈W, CT1, CT2, ω〉 from the ListH5. Then, M′||V′ = CT3 ⊕ ω can be computed by using CT3 and ω. Further, utilizes M′ and V′ to find the corresponding tuples 〈M, V, γ〉 from the ListH7 and 〈M, Q〉 from the ListH6. Obviously, γ and Q can be obtained. If S can be found in the corresponding tuple 〈N, S〉 from the ListH8 such that CT4 = Qγ · S holds, will confirm whether holds. If , the message M′ is sent to
- (1)
Trapdoor query(ID, T): utilizes (ID, T) to issue the query, while , respectively, uses ID and (ID, T) to run InitialKey query and Timekey query to obtain IKID = (IKID1, IKID2) and TKID = (TKID1, TKID2). Then, utilizes IKID2 and TKID2 to produce the trapdoor TDID = IKID2 · TKID2 which is sent to
- (3)
Challenge: when phase 1 is over, outputs a tuple as the target of the challenge. utilizes (ID∗, T∗) to find the corresponding tuples 〈ID, T, UIDT, η, rb〉 from the ListH3. If rb = 0, interrupts this game. If rb = 1, randomly selects and V ∈ {0, 1}l to run H7 query with and V. Then, γ can be obtained. utilizes γ to set . In addition, sets , while a random value CT3 ∈ {0, 1}λ+l and a random point are chosen. Finally, the challenge ciphertext is sent to
- (2)
Phase 2: can issue the same query as phase 1, but it must be under the condition of ID ≠ ID∗ and CT ≠ CT∗
- (3)
Guess: responds to with a guess . If , responds with failure and terminates. Otherwise, wins the game. Then, randomly selects a tuple from the ListH5 and outputs the BDH solution due to
The security analysis is similar to Theorem 5. We obtain that ’s advantage to solve the BDH problem is
Theorem 7. If the BDH assumption holds, the proposed RIBEET scheme satisfies the OW-ID-CCA security in the security game. More precisely, suppose that is a PPT type 3 adversary who has at least ε advantage to break the RIBEET scheme. Then, there exists an algorithm to solve the BDH problem with the advantage
Proof. An algorithm is constructed to solve the BDH problem. The algorithm is given a BDH tuple which is defined in Section 2. The algorithm can be seen as a challenger to find the answer of the BDH problem. The answer can be found by interacting with the PPT type III adversary in the following security game.
- (i)
Setup: The challenger utilizes the BDH tuple to set , and then generates the public system parameters , where Hi is a random oracle for i = 1, 2, ⋯, 8. In addition, the system life time SLT = {T0, T1, ⋯, Tt} can be generated by the challenger . Then gives the public system parameters PSP and system life time SLT. Here, the adversary can issue queries to each random oracle as below
- (a)
H1query(ID): answers in the same form as the proof of Theorem 5
- (b)
H2query(ID): can utilize ID to obtain a response to the random oracle H2 from the challenger . To obtain the response, maintains a list, called ListH2 which is composed of tuples, and the format of the tuple is 〈ID, VID, v, rb〉. The response is acquired from the ListH2 which is initially empty and can be updated by the following steps
- (i)
returns VID as the response if ID exists in a tuple 〈ID, VID, v, rb〉 from the ListH2
- (ii)
Otherwise, picks a random value and utilizes ID to find rb in the ListH2. Then computes and adds the tuple 〈ID, VID, v, rb〉 to ListH2. returns VID to
- (c)
H3 − H8 queries: answers in the same form as the proof of Theorem 5
- (ii)
Phase 1: The adversary can, respectively, utilize ID, (ID, T), (ID, T, CT) and (ID, T) to issue the InitialKey query, Timekey query, Decryption query and Trapdoor query. The response to each query can be obtained as follows
- (1)
InitialKey query (ID): answers in the same form as the proof of Theorem 5
- (2)
Timekey query (ID, T): answers in the same form as the proof of Theorem 5
- (3)
Decryption query (ID, T, CT): utilizes (ID, T, CT) to issue the query, while , respectively, finds the corresponding tuples 〈ID, UID, u, rb〉, 〈ID, VID, v, rb〉, 〈ID, T, UIDT, η〉 and 〈ID, T, VIDT, ζ〉 from the ListH1, ListH2, ListH3 and the ListH4 according to ID and T. The response of this query is acquired from these lists by performing the following tasks
- (i)
If rb = 0, , respectively, uses ID and (ID, T) to run InitialKeyquery and Timekey query to obtain IKID and TKID. Then utilizes IKID, TKID and CT to run Decryption algorithm to produce the message M which is sent to
- (ii)
If rb = 1, utilizes CT1 and CT2, which are from CT = (CT1, CT2, CT3, CT4), to find the corresponding tuple 〈W, CT1, CT2, ω〉 from the ListH5. Then M′||V′ = CT3 ⊕ ω can be computed by using CT3 and ω. Further, utilizes M′ and V′ to find the corresponding tuples 〈M, V, γ〉 from the ListH7 and 〈M, Q〉 from the ListH6. Obviously, γ and Q can be obtained. After that, utilizes ID and (ID, T) to run InitialKey query and Timekey query to obtain IKID2 and TKID2 and computes . If S can be found in the corresponding tuple from the ListH8 such that CT4 = Qγ · S holds, will confirm whether holds. If , the message M′ is sent to
- (d)
Trapdoor query (ID, T): utilizes (ID, T) to issue the query, while , respectively, uses ID and (ID, T) to run InitialKey query and Timekey query to obtain IKID = (IKID1, IKID2) and TKID = (TKID1, TKID2). Then utilizes IKID2 and TKID2 to produce the trapdoor TDID = IKID2 · TKID2 which is sent to
- (e)
Challenge: When the phase 1 is over, outputs a tuple 〈ID∗, T∗, M∗〉 as the target of the challenge. utilizes ID∗ to find the corresponding tuples 〈ID, UID, u, rb〉 from the ListH1 If rb = 0, interrupts this game. If rb = 1, randomly selects V ∈ {0, 1}l to run H7 query with M∗ and V. Then γ can be obtained. utilizes γ to set and find and to get Q and S such that . In addition, sets , while a random value CT3 ∈ {0, 1}λ+l is chosen. Finally, the challenge ciphertext is sent to
- (f)
Phase 2: can issue the same query as the phase 1, but it must be under the condition of ID ≠ ID∗ and CT ≠ CT∗
- (g)
Guess: responds to with a guess M′ ∈ {0, 1}λ. If M′ ≠ M, responds with failure and terminates. Otherwise, wins the game. Then randomly selects a tuple from the ListH5, and outputs the BDH solution A = due to
The security analysis is similar to Theorem 5. We obtain that ’s advantage to solve the BDH problem is .
Theorem 8. If the BDH assumption holds, the proposed RIBEET scheme satisfies the OW-ID-CCA security in the security game. More precisely, suppose that is a PPT type 4 adversary who has at least ε advantage to break the RIBEET scheme. Then, there exists an algorithm to solve the BDH problem with the advantage.
Proof. An algorithm is constructed to solve the BDH problem. The algorithm is given a BDH tuple which is defined in Section 2. The algorithm can be seen as a challenger to find the answer of the BDH problem. The answer can be found by interacting with the PPT type IV adversary in the following security game.
- (i)
Setup: The challenger utilizes the BDH tuple to set , and then generates the public system parameters , where Hi is a random oracle for i = 1, 2, ⋯, 8. In addition, the system life time SLT = {T0, T1, ⋯, Tt} can be generated by the challenger . Then gives the public system parameters PSP and system life time SLT. Here, the adversary can issue queries to each random oracle as below
- (a)
H1 − H3 queries: answers in the same form as the proof of Theorem 6
- (b)
H4 − H8 queries: answers in the same form as the proof of Theorem 5
- (ii)
Phase 1: The adversary can, respectively, utilize ID, (ID, T), (ID, T, CT) and (ID, T) to issue the InitialKey query, Timekey query, Decryption query and Trapdoor query. The response to each query can be obtained as follows
- (a)
InitialKey query (ID): answers in the same form as the proof of Theorem 6
- (b)
Timekey query (ID, T): answers in the same form as the proof of Theorem 6
- (c)
Decryption query (ID, T, CT): answers in the same form as the proof of Theorem 7
- (d)
Trapdoor query (ID, T): answers in the same form as the proof of Theorem 7
- (1)
Challenge: When the phase 1 is over, outputs a tuple 〈ID∗, T∗, M∗〉 as the target of the challenge. utilizes (ID∗, T∗) to find the corresponding tuples 〈ID, T, UIDT, η, rb〉 from the ListH3 If rb = 0, interrupts this game. If rb = 1, randomly selects V ∈ {0, 1}l to run H7 query with M∗ and V. Then γ can be obtained. utilizes γ to set and find and to get Q and S such that . In addition, sets , while a random value CT3 ∈ {0, 1}λ+l is chosen. Finally, the challenge ciphertext is sent to
- (2)
Phase 2: can issue the same query as the phase 1, but it must be under the condition of ID ≠ ID∗ and CT ≠ CT∗
- (3)
Guess: responds to with a guess M′ ∈ {0, 1}λ. If M′ ≠ M, responds with failure and terminates. Otherwise, wins the game. Then randomly selects a tuple from the ListH5, and outputs the BDH solution A = due to
The security analysis is similar to Theorem 5. We obtain that ’s advantage to solve the BDH problem is .
Theorem 9. The proposed RIBEET scheme is secure for brute force attacks if the discrete logarithm problem is hard.
Proof. As mentioned in the concrete RIBEET scheme, the public system parameters are PSP = {q, G1, G2, GT, , g1, g2, Ppub, H1, H2, H3, H4, H5, H6, H7, H8}, the system life time is SLT = {T0, T1,⋯, Tt} and the master private key is mpk = s. Based on the discrete logarithm problem, we ensure that the adversary cannot recover the master private key mpk = s form Ppub = . In addition, the security of the user initial key IKID and user time key TKID is also based on the discrete logarithm problem due to IKID = (IKID1, IKID2) = (H1(ID)mpk, H2(ID)mpk) = (H1(ID)s, H2(ID)s) and TKID = (TKID1, TKID2) = (H3(ID, T)mpk, H4(ID, T)mpk) = (H3(ID, T)s, H4(ID, T)s). Hence, the proposed RIBEET scheme can resist brute force attacks.
6. Comparison
- (1)
Pair: time to perform a bilinear pairing
- (2)
Exp: time to perform an exponentiation in G1, G2 or GT
We gain Pair = 7.8351 ms and Exp = 0.4746 ms from the literature [32]. These two execution times are obtained under the hardware device with Intel Core i7-8550U 1.80 GHz processor. Meanwhile, the prime number q selected in the cryptosystem setting phase is 256-bit. In addition, three multiplicative cyclic groups G1, G2, and GT of the prime order q are chosen in the simulation.
In Table 3, we list the comparisons of our proposed RIBEET scheme with the RIBE scheme [21] and several IBEET schemes [6, 10, 11] in terms of the cost of performing encryption, decryption and equality test, and two properties related to user revocation and equality test of ciphertexts. For the cost of performing encryption and decryption, Tseng and Tsai’s RIBE scheme [21] has better performance than the other two schemes. However, Tseng and Tsai’s RIBE scheme does not support equality test of ciphertexts. Although the existing IBEET schemes [6, 10, 11] and our proposed RIBEET scheme support equality test of ciphertexts, the IBEET schemes does not have a mechanism to revoke users. Conversely, our proposed RIBEET scheme not only provides user revocation, but also retains the cost of encryption, decryption and equality test with the existing IBEET schemes. Additionally, Table 4 compares our RIBEET scheme with the RIBE scheme [21] and several IBEET schemes [6, 10, 11] in terms of |PK|, |CT|, and |TD| which are, respectively, denoted as the bit length of user public key, ciphertext and trapdoor. We observed that the communication cost of our RIBEET scheme is similar to that of other schemes.
| Schemes | The cost of performing encryption | The cost of performing decryption | The cost of performing equality test | Supporting equality test of ciphertexts | Providing user revocation |
|---|---|---|---|---|---|
| RIBE [21] | 1 · Pair + 2 · Exp | 1 · Pair | — | No | Yes |
| (8.7843 ms) | (7.8351 ms) | ||||
| IBEET [6] | 2 · Pair + 6 · Exp | 2 · Pair + 2 · Exp | 4 · Pair | Yes | No |
| (18.5178 ms) | (16.6194 ms) | (31.3404 ms) | |||
| IBEET [10] | 2 · Pair + 4 · Exp | 2 · Pair + 1 · Exp | 2 · Pair + 2 · Exp | Yes | No |
| (17.5686 ms) | (16.1448 ms) | (16.6194 ms) | |||
| IBEET [11] | 2 · Pair + 9 · Exp | 2 · Pair + 2 · Exp | 2 · Pair + 2 · Exp | Yes | No |
| (19.9416 ms) | (16.6194 ms) | (16.6194 ms) | |||
| Our RIBEET | 2 · Pair + 5 · Exp | 2 · Pair + 2 · Exp | 4 · Pair | Yes | Yes |
| (18.0432 ms) | (16.6194 ms) | (31.3404 ms) |
As mentioned in Section 1, the data collected from sensors on the patients is finally encrypted by the mobile device and then transmitted to the cloud. For the analysis of energy cost, we employ the “ampere” app to measure the voltage and current on the mobile device. After running this app, we obtain 14.28 V and 2856 mA on the mobile device. Table 5 lists the energy cost of performing encryption on the mobile device by using the formula W = U · I · t, where W, U, I, and t, respectively, are watt, voltage, current, and time.
7. Conclusions
We considered the existing syntax of IBEET and the property of user revocation to present the new syntax of RIBEET. Under the new syntax, we proposed a concrete RIBEET scheme. Meanwhile, we demonstrated that the proposed scheme has the IND-ID-CCA security for type I and II adversaries and the OW-ID-CCA security for type III and IV adversaries. We compared the proposed scheme with the previous RIBE scheme and IBEET scheme. We showed that the proposed scheme not only supports equality test for ciphertexts but also provides user revocation.
Conflicts of Interest
The authors declare no conflicts of interest.
Acknowledgments
This research was partially supported by the Ministry of Science and Technology, Taiwan, under contract nos. MOST 110-2222-E-019-001-MY2 and MOST 110-2221-E-019-041-MY3.
Open Research
Data Availability
The data used to support the findings of this study are included within the article.




