Since the low cost and high flexibility, wireless automatic meter reading network (WAMRN) is widely used by utility companies to realize automatic collection and transmission of remote energy consumption information. Considering that WAMRN is composed of several wireless communication nodes, the lifetime of the network will be affected by factors such as the changeable deployment environment and the limited energy of nodes. Thus, a novel niche quantum ant colony-based WAMRN clustering optimization method is proposed in this paper to address the problem of how to make full use of the limited energy to extend network lifetime and improve data transmission efficiency. In the proposed approach, a clustering model of WAMRN is defined; moreover, an improved Niche Quantum Ant Colony Optimization (NQACO) is proposed to optimize the model therefore to obtain an optimal clustering scheme, which can help WAMRN reduce unnecessary energy loss to achieve the purpose of extending the lifetime of the entire network. To verify the performance of the proposed method, NQACO is compared with some popular clustering methods, i.e., GA and SA, under different scenarios. The results show that under the premise of ensuring network communication, NQACO is superior to the other two methods in reducing the total energy consumption and prolonging the network lifetime.

1. Introduction

In the age of production automation, the realization of automatic meter reading (AMR) for water, electricity, and gas supplies has become an urgent problem for energy companies, for a reason that accurate and timely replication of water and electricity data will directly affect business decisions and economic benefits [1, 2]. By leveraging electronic, communication, computer, and network technologies to identify, read, process, and transmit meter data automatically, it enables the problems of single function, low accuracy, and undesirable real-time performance of traditional meter reading to be solved. Especially, the adoption of automatic meter reading technology not only improves the economic efficiency of enterprises but also enhances the degree of informatization [3]. Hence, there appears an inevitable trend of the application of automatic meter reading technology for water, electricity, and gas data reading.

At present, the technology of automatic meter reading consists of wired automatic meter reading and wireless automatic meter reading according to the mode of data transmission. Specifically, the former mainly makes use of power line networks, telephone line networks, RS-485 bus networks, etc. One disadvantage of the existing wired meter reading method lies in that it cannot be applied in a large scale and reliable way in the home meter reading system. It is because of its high cost, complex wiring, difficulty in commissioning and maintenance, susceptibility to the power grid, poor security, and poor scalability [4]. With the appearance of wireless automatic meter reading, it makes up for the deficiency of the wired automatic meter reading. The technologies used for wireless meter reading include GSM/GPRS, Bluetooth technology, and short-range wireless radio frequency transmission technology. Compared with traditional meter reading methods as well as wired methods, wireless meter reading can save labor costs, reduce wiring costs, and simplify the management to find problems and take corresponding measures promptly. To this end, WAMR has become a leading research direction of AMR.

In WAMRN, each energy meter node is powered by a battery with limited energy. In this way, to prolong the network lifetime as much as possible with energy limitation, researchers have conducted a lot of research on ways which can effectively enhance the energy utilization. Finding that the design of network topology and the selection of routing have a significant impact on the energy dissipation of nodes [5–7], researchers improve the energy utilization in WAMRN by designing a reasonable clustering model and using efficient optimization algorithm [8, 9]. Therefore, the focus of this paper is on the optimization of network clustering to effectively extend the lifetime of WAMRN.

In this paper, the most desirable nodes in the WAMRN are selected as cluster head nodes for clustering, such that the whole network is divided into several connected regions. In addition, the noncluster head nodes in each region are named member nodes, and the cluster head nodes manage the surrounding member nodes. In [10], the authors have shown that the optimal cluster head selection problem is an NP-hard problem. Therefore, we propose a Niche Quantum Ant Colony Optimization (NQACO) which combines the optimization mechanism of quantum evolutionary algorithms with the ant colony optimization. By using this approach, it can significantly enhance the search traversal and convergence speed when the problem size is large, while NQACO uses the niche technique to ensure the species diversity of the whole large ant colony. The existence of stable individual differences in the colony aids NQACO in overcoming the premature problem exhibited by other algorithms and allows for more desirable local search capabilities. In a nutshell, the proposed clustering approach can efficiently search for optimal routing clusters from the solution space, thus effectively decreasing the energy loss in WAMRN and thus extending the network lifecycle.

The structure of this thesis is just as below. In Section 2, the research work related to the clustering of sensor networks is introduced. Section 3 describes the entire network structure of WAMRN. Meanwhile, the corresponding mathematical model is designed and established. Section 4 proposes a new optimization algorithm to optimize the problem of clustering of WAMRN in Section 3. Section 5 shows the optimization performance of NQACO on the cluster routing model by comparing it with GA and SA. Finally, the whole work of this paper is summarized in Section 6.

2. Related Work

At present, there exist many kinds of AMR communication technologies. For instance, paper [11] applying radio frequency technology to AMR systems, which can help energy companies effectively reduce data collection costs and quickly collect key information to provide insights for decision-makers. Paper [12] realizes a wireless power monitoring system based on ZigBee technology monitoring power quality and remotely control power services. In addition, paper [13] uses the single-chip microcomputer STM32 to manage energy data and uses ZigBee for communicating between the electric energy meter and the data center. Afterwards, paper [14] designed a GPRS-based remote automatic meter reading wireless communication system hardware, which supports UDP communication protocol and can carry out remote data transmission through message transmission and network communication.

A lot of research results show that WSN is considered to be the key technology for building a new generation of smart grid AMR systems in the future [15–18]. However, since the energy supply of sensor nodes in WSN is battery-powered, the energy of the nodes has a certain limitation, and the energy of wireless sensor network nodes cannot be replenished at work. Therefore, considering extending the lifetime of the entire network as much as possible, it is an important design principle to improve the energy utilization rate and reduce the energy loss of the wireless sensor node in the construction of WSN. In paper [19], the researchers use the water meter as a node to form a wireless sensor network. That research focuses on making the energy consumption as small as possible by avoiding packets whose lengths exceed the length limit. The paper [20] points out that sensor nodes in WSN send their data to the central cluster head, which forwards the data to the desired receiver. Moreover, clustering can realize bandwidth reuse, thereby increasing system capacity.

To make up for the sustainability of QoS and bridge the gap between suboptimal solutions, the paper [21] proposed a quality-of-service routing algorithm based on genetic algorithm. That work solves the imbalance characteristic schematic diagram of QoS optimization in the ad hoc network and the previous convergence problem. However, the genetic algorithm used in this study has a specific dependence on selecting the initial population. In addition, the algorithm is prone to premature problems when solving large-scale computing problems.

In paper [22], the author proposed a lightweight dynamic TRUST model and bee mating algorithm for clustering. More specifically, to prevent malicious nodes from becoming cluster head nodes, they proposed a gradually reasonable priority scheme in the trust measurement. Nevertheless, since the amount of crossover operation information is small and the similarity of the bee colony is high in the process of optimizing the problem with the bee mating algorithm, it is prone to fall into the local optimum and seriously affect the performance of the algorithm.

Paper [23] proposes a modified clustering method based on LEACH (Low Energy Adaptive Clustering Hierarchy), which uses the Particle Swarm Optimization (PSO) algorithm to optimize the network clustering and determines cluster heads by considering factors such as energy, communication overhead, and load balance. Although the particle swarm algorithm used in the research has the characteristics of simple structure and fast search speed compared with other algorithms, it has some inescapable disadvantages such as low accuracy, easy divergence, and easy falling into local optimum. These shortcomings are in the process of clustering optimization, making the clustering undesirable.

In other perspectives, paper [24] proposes a clustering routing algorithm on the basis of chaotic binary ant colony optimization (CBACO) for wireless sensor networks. The algorithm calculates the energy consumption of the cluster head based on the remaining energy, the number of neighbors, and the distance to the base station (BS). In that paper, the routing process is divided into two steps, where the first step is to process the data transmission from the cluster head to the cluster head and the second one is to apply the biologically inspired optimization technology ant colony algorithm (ACO) to optimize the path finding process from the cluster head to the BS. Although the information interaction of ant colony algorithm is realized by pheromone, the convergence to the optimal solution is the process of information positive feedback. Positive feedback is designed to enhance the quality of the solution and achieve better performance. However, this algorithm will have the problem of evolutionary stagnation.

3. System Model

3.1. WAMRN Network Model

The structure of the WAMRN network model is shown in Figure 1. After the terminal collection node obtains the meter data, it transmits the data to the remote BS through the wireless communication node in WAMRN. To save energy, each wireless communication device can select an optimal path according to the actual situation and then transmit the data to the cluster head node through the optimal path for data integration. Without considering other factors, all wireless communication nodes have the same initial energy. Since each wireless communication device has the same data communication capability, the energy loss in the process of data transmission, fusion, and transmission is also the same. In WAMRN, the energy of the BS is not limited, and the BS is always in a normal working state. However, the wireless communication equipment in the network is restricted by its energy. If the energy is exhausted, the node will no longer work.

Details are in the caption following the image — Open in figure viewer PowerPoint

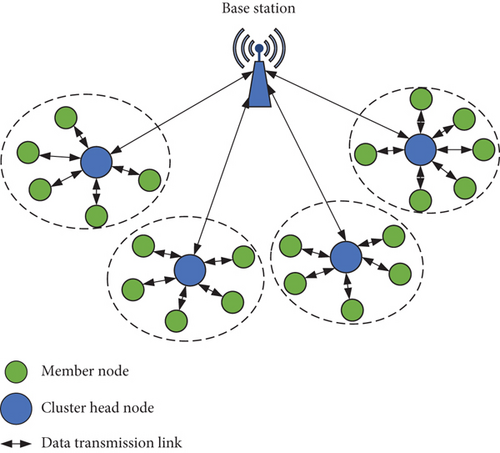
In common cases, the installation location of data collection and transmission wireless equipment depends on the actual situation. Therefore, the distribution of various meters is irregular. This situation can be understood as that each sensor device in WAMRN is randomly distributed.

3.2. Energy Loss Model of Wireless Communication Nodes

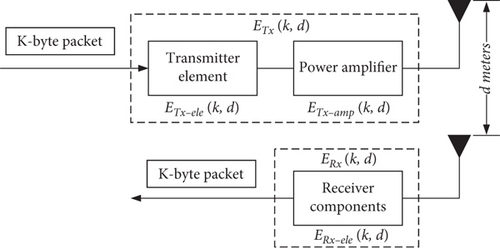
The wireless meter reading device in WAMRN belongs to one kind of the wireless communication device, so the energy consumption of the WAMRN can be calculated by using the energy consumption model of the wireless communication device. In fact, there is a lot of research work on the energy consumption of wireless terminals. Papers [25–27] put forward the theoretical explanation of content radio transmission and microcontroller processing. And in paper [28], the author proposes a first-order radio model, which models that the energy consumption of wireless terminals can widely describe the energy consumption in wireless terminals; it is used to calculate the energy consumption in many related research works. Therefore, this energy model is adopted in our research work.

The energy consumption of wireless communication nodes in WAMRN mainly includes three parts: sensing energy consumption, data communication energy consumption, and microprocessor energy consumption. Many current research results show that the energy consumption of wireless communication nodes in data communication accounts for more than 50% of the total energy consumption of WAMRN. Besides, the sensing energy consumption and microprocessor energy consumption are comparative fixed, so it is hard to reduce them through optimization. Therefore, this paper primarily analyzes the energy loss of each wireless communication node in WAMRN and studies a reasonable clustering method for achieving low energy consumption in the network.

As shown in Figure 2, if the sensor node transmits k bit packets to adjacent nodes with a distance of d meters, the energy consumption generated by the transmitting node is E_tx(k, d), which mainly contains E_TX−elec(k) and E_TX−amp(k, d), where E_TX−elec(k) represents the energy loss generated when the signal transmitting circuit unit transmits data information. And E_TX−amp(k, d) denotes the energy consumption generated when the signal power amplifier circuit unit amplifies the transmission power. Equations (1), (2), and (3) are the calculation of the above three types of energy consumption, respectively.

(1)

(2)

(3)

In formula (3), the E_Tx−amp(k, d) adopts two different calculation methods according to the value of the communication distance d between nodes. If d < d₀, it can be assumed that the signal is in the ideal state of no attenuation, no blocking, and no multipath mode during the propagation process, so that the parameter used for signal power amplification is ε_fs, and then, the calculation method of a is E_Tx−amp(k, d) = k · ε_fs · d². If d > d₀, the signal attenuation caused by the increase in communication distance needs to be considered. At this time, the signal power amplification parameter is ε_mp, and E_Tx−amp(k, d) = k · ε_mp · d⁴. The d₀ is the distance threshold calculated as follows:

(4)

When receiving k bit packets, the energy consumption of nodes is calculated by as follows:

(5)

Additionally, to decrease the amount of communication data and decrease the sending of redundant data, the cluster head will perform data fusion on the data from each member node, and there will be a small amount of energy consumption in this process. In this article, E_Fs is used to represent the energy consumption during data fusion, assuming that the fusion of 1 bit data requires energy consumption E_Df; then, the energy consumption of k-bit data fusion can be defined by as follows:

(6)

4. NQACO for Clustering Optimization in WAMRN

The proposed NQACO, based on quantum evolution and niche technology, is an improvement and upgrade of the traditional ant colony algorithm. It introduces the concept and theory of quantum computing, uses qubit coding to store information, and completes the update of quantum coding through quantum rotation gate. Meanwhile, the quantum evolution ensures that the performance of the algorithm will not be affected, and it can even significantly improve the convergence speed of the algorithm. Besides, to find an optimal solution in the whole solution space, NQACO use the niche mechanism to divide the ant colony into several niches. Due to the relative isolation between multiple niches, there is less gene exchange between different species, so there are some differences in species genes between these niches, which provides the species diversity of the whole ant colony. On the level of swarm intelligence optimization algorithm, stable individual differences facilitate NQACO to overcome the premature problem shown by other algorithms and can enhance the ability of local search.

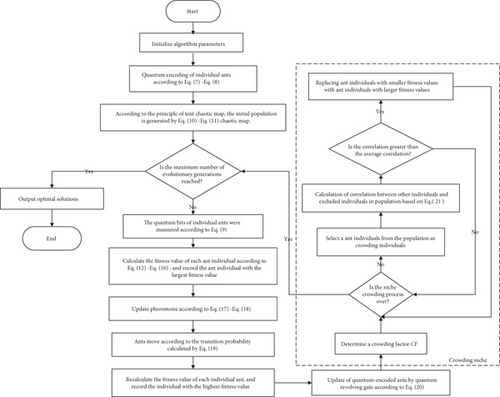
The detailed procedures of using NQACO to solve the clustering optimization problem in WAMRN are as follows.

Step 1. Initialize NQACO with various parameters, including population size, the maximum number of iterations, pheromone trajectory strength, visibility parameters, pheromone volatility factor, number of wireless communication nodes in the network, and crowding factor.

Step 2. Quantum coding for ant colony according to Equation (7) and Equation (8) and initialization by chaotic mapping according to Equation (10) and Equation (11).

Step 3. Measure the qubit state according to Equation (9).

Step 4. Calculate the fitness value of each ant individual according to Equation (12)–Equation (16), and record the ant individual with the largest fitness value.

Step 5. Update pheromones according to pheromone strength and visibility using Equation (17) and Equation (18), and then, move the ants according to the transition probability calculated by formula Equation (19).

Step 6. Recalculate the fitness value of each individual ant, and record the individual with most significant fitness value.

Step 7. Use the optimal solution to update the direction of the quantum revolving gate, and then, update the quantum encoding ant through the quantum revolving gate by Equation (20).

Step 8. Randomly select ant individuals from the current population as crowded individuals. Then, calculate the correlation between other individuals in the ant colony according to Equation (21) and the excluded individual. Suppose the correlation between the excluded individual and another ant individual is greater than the average correlation between all individuals. Based on the exclusion mechanism, the individual with the lower fitness value of the two ants will be replaced by the individual with the higher fitness value.

Step 9. Judge whether the termination condition is reached, and output the optimal individual if it is reached, and use the binary code corresponding to this individual as the optimal clustering scheme for WAMRN. Otherwise, the algorithm will continue from Step 3 to the next iteration.

Figure 3 is the flow chart of NQACO.

4.1. Quantum Coding and State Measurement

In NQACO, the algorithm introduces quantum coding and state measurement to solve the WAMRN clustering problem. Typically, information is stored in the form of binary bits, and the state of the binary bits can only be 0 or 1. But in quantum computing, information is stored in the form of qubits, which are a one-dimensional complex vector space. However, in quantum computing, information units are stored in qubits. A linear combination of two superposition components |0〉 and |1〉 can be used to represent any state of a qubit. In this paper, |ψ〉 is used to represent the state of the qubit, and its calculation method is as follows:

(7)

where α and β represent the probability magnitudes of the two superposition vectors |0〉 and |1〉, respectively, while |α|² and |β|² denote the probability of the quantum bits being at 0 and 1, respectively, and |α|² + |β|² = 1.

In NQACO, the information carried by the ants in the ant colony is represented by a group of qubits. In the clustering optimization problem, the code composed of this group of qubits is actually a clustering scheme. Assume that there are n wireless communication nodes in the WAMRN, where c wireless communication nodes are selected as cluster heads and the remaining n − c wireless communication nodes are member nodes. Thus, the length of the encoding carried by a single ant in the encoding process is n. The following mathematical expression (8) can represent the encoding of the information carried by an individual ant.

(8)

Each column in p_i is the probability of the appearance of two superimposed vectors constituting the state of the corresponding qubit. However, this coding method cannot obtain the clustering scheme directly, so converting quantum coding to binary coding is necessary. Thus, this paper uses the method of measuring the qubit’s state to realize the conversion process. In the measurement process, the n wireless communication nodes in the network are numbered from 1 to n; then, the state of the corresponding quantum bit count can be used to determine whether the wireless communication node is a cluster head or not. In this paper, the state of the i^th qubit is calculated by Equation (9). If the state measurement value of the i^th qubit in a code is 0, the wireless communication node numbered i is a member node. Otherwise, the wireless communication node numbered i is a cluster head.

(9)

4.2. Initialization of Ant Population

Individuals of NQACO carry a feasible clustering scheme. Before the first generation of population evolution, the population with size popSize needs to be initialized. In this article, NQACO uses a tent map to generate the initial information code carried by each ant in the ant colony. Compared with the commonly used logistic mapping, the chaotic sequence generated by the tent mapping in the interval [0,1] is more evenly distributed and faster iteration speed. The calculation method of the tent mapping function is as follows:

(10)

In the formula, x is a random number with a value range of [0,1]. The formula can also be expressed in the following form.

(11)

In the process of population initialization, a random number x₀ with a value range of [0,1] is given first. On this basis, tent mapping is used to generate n chaotic variables. Let the individual ants encode α_n = sin(2πx_n) and β_n = cos(2πx_n) in p_i, so that the probability amplitude of each qubit in the information encoding carried by the initial ant will be evenly distributed in the solution space. By repeating the above operation popSize times, an initial population P = {p₁, p₂, p₃, ⋯, p_popSize} with a population size of popSize can be obtained.

4.3. Construction of the Fitness Function

In this paper, the overall goal of optimizing the entire WAMRN is to minimize the entire network’s energy dissipation during data transmission to extend the network’s life as much as possible. Therefore, in the optimization process, the wireless communication nodes with higher residual energy, smaller communication distance within the cluster, and closer to the BS are more suitable to be selected as cluster heads.

In the process of heuristic optimization algorithm to find the optimal cluster head selection scheme, the fitness function plays a very important role, because the fitness function can be used to measure the efficiency of the algorithm when searching for the optimal cluster head selection scheme. Suppose the expected number of cluster heads in WAMR is c, n_j represents the quantity of member nodes in j^th network cluster, D(CH_j, BS) and D(MEM_i, CH_j), respectively, represent the distance from j^th cluster head to the BS and the distance from i^thmember node to j^th cluster head node. Thus, the fitness function in NQACO is defined as follows:

(12)

where

, f_CH is the energy consumption of the j^th cluster head in the process of one information transmission, and it can be calculated with the help of the following:

(13)

(14)

In formula (12),

, it represents the energy consumption of member nodes. The calculation process of

is as follows:

(15)

(16)

4.4. Mobile Strategy and Positivity Update

To solve the clustering problem of WAMRN, before adjusting the position of individual ants in NQACO, the pheromone on the path needs to be updated. The corresponding update formulas are as follows:

(17)

(18)

where ρ is the pheromone volatilization coefficient, and its value range is [0, 1], where Δτ = 1/fitness(x_best) , fitness(x_best) represents the network energy consumption corresponding to the optimal clustering scheme for each generation.

After the pheromone update is completed, it is necessary to adjust the movement of the ant by calculating the transition probability P_ij of the ant. The calculation method of transition probability P_ij is as follows:

(19)

where τ_ij and η_ij, respectively, represent the pheromone track intensity and visibility parameters. Variable t represents the iteration times of the algorithm, i represents the quantity of steps the ant has taken, and j ∈ {0, 1} represents the two positions that an individual ant may choose during the i^th step.

4.5. Variation of Quantum Bits

The quantum bits act as a guide for the individuals in NQACO to move in a globally optimal direction. After each individual in the ant colony change its positions, all the qubit on an ant is required to be updated base on the optimization scheme in the previous iteration. The update process is indicated as follows:

(20)

where

and

are the probability amplitudes of qubit’s corresponding state after the update. α_l and β_l are the probability amplitudes before the update. The size and direction of the rotation angle θ_l = S(α_lβ_l)Δθ_l are obtained from Table 1.

1. Rotation angle strategy.

z_l			Δθ_l	S(α_lβ_l)
z_l			Δθ_l	α_lβ_l > 0	α_lβ_l < 0	β_l = 0	α_l = 0
1	0	F	0.001π	-1	+1	0	±1
0	0	F	0	0	0	0	0
1	0	T	0.025π	+1	-1	±1	0
0	0	T	0	0	0	0	0
1	1	F	0.005π	+1	-1	±1	0
0	1	F	0.05π	+1	-1	±1	0
1	1	T	0.025π	+1	-1	±1	0
0	1	T	0.005π	-1	+1	0	±1

In Table 1, represents the optimal cluster routing scheme generated by the previous generation, and T and F represent true and false in Boolean algebra, respectively.

4.6. Niche Based on Exclusion Mechanism

This paper mainly uses niche technology based on the crowding mechanism to classify the individuals in the ant colony for obtaining a desirable scheme of clustering. The basic idea stems from the fact that in a limited living environment, in order to survive, various creatures must compete with each other for various limited living resources. Specifically, it is first necessary to determine a crowding factor CF and then randomly select 1/CF ant individuals from the ant colony as crowding individuals and then calculate the correlation between other unselected ant individuals and the crowding individuals. Since the code carried by an individual ant is a quantum code, it can be regarded as a matrix. Therefore, the correlation between two individuals in an ant population can be obtained by calculating the correlation between the encoding matrices representing the two individuals. The calculation method of interindividual correlation is shown as follows:

(21)

where A is the crowding individuals, B is other individuals, C (A, B) is the covariance of A and B, and V(A) and V(B) are the variances of A and B, respectively.

Assuming that the correlation between two individuals is higher than the average value of the correlation between individuals in the colony, based on the exclusion mechanism, the individual with the lower fitness value of the two ants will be replaced by the individual with the higher fitness value.

4.7. Termination Condition

If NQACO runs to the set maximum number of iterations, the clustering scheme carried by the individual with the best fitness value will be output. Otherwise, the iterative optimization is continued.

5. Simulation

To verify the optimization effectiveness of NQACO for the clustered routing problem in WAMRN, this paper compares NQACO with GA; SA under different conditions and through MATLAB simulations, total energy consumption generated during data transmission in the network is used as the evaluation metric. The WAMRN scenario simulated in this paper is static, and the concrete environmental parameters are shown in Table 2.

2. Network environment parameters.

Parameter	Value
k	1000 bits
E_elec	50 nJ/bit
ε_amp	100 pJ/bit/m²

ε_fs	0.0013 pJ/(bit×m⁴)
E_Df	5 nJ/bit

In the following simulation, the maximum number of iterations MAXGEN of the four algorithms for comparison is set to 100 rounds. Noting that different algorithms have different initial parameters, to ensure that these four algorithms can be in their respective optimal optimization states, the specific initial parameter settings of each algorithm are shown in Tables 3–5.

3. Initial parameters of NQACO.

Parameter	Value
Number of individuals	80
Pheromone track intensity	2
Visibility parameter	2
Pheromone volatilization coefficient	0.9

4. Initial parameters of GA.

Parameter	Value
Number of individuals	80
Crossover probability	0.7
Mutation probability	0.05
Computing era	0.9

5. Initial parameters of SA.

Parameter	Value
Starting temperature	300
Cooling factor	0.95
Maximum number of iterations	100

In the simulation experiment of Figure 4, each algorithmic optimization process was repeated 50 times. The corresponding value in the line chart was the average value of 50 simulations.

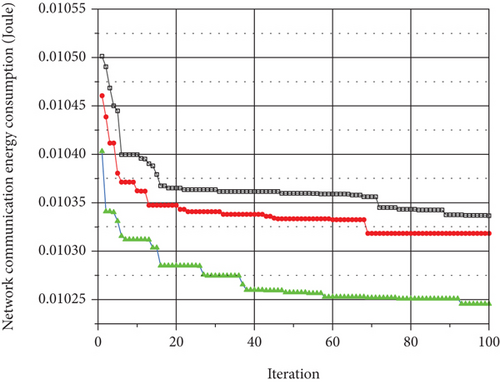
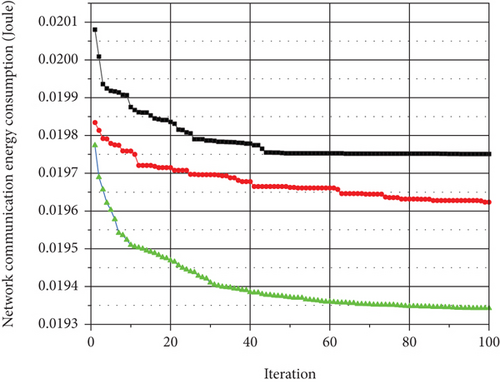
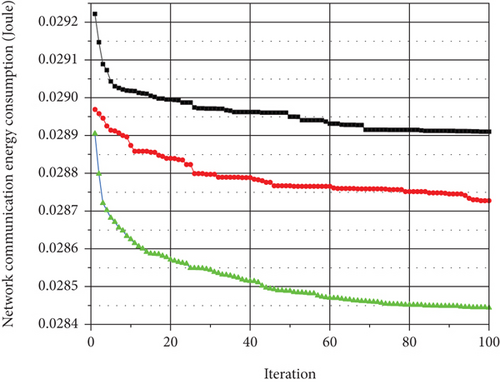
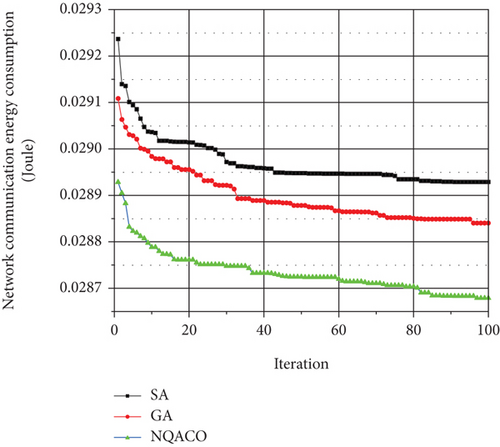
Figure 4 shows the optimization effect of these four algorithms on the total energy consumed of WAMRN when the network contains 100, 200, 300, and 400 wireless communication nodes, and the proportion of cluster heads in each final clustering scheme is 10%. From the trend of the curves in Figures 4(a)–4(d), although the total energy consumption of the three algorithms varies significantly during the first 60 iterations, the network optimized by NQACO is always lower than the GA and SA in terms of total energy consumption. In addition, the advantage of NQACO over the other two algorithms becomes more and more evident as the number of iterations increases.

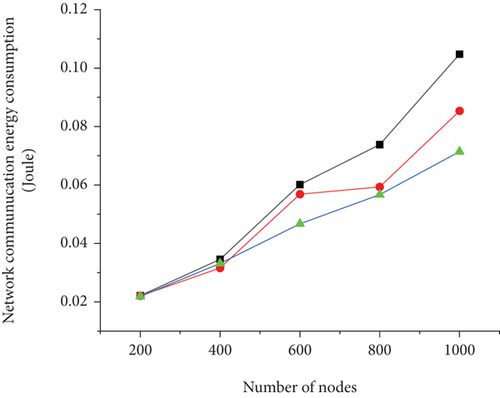
Figure 5 shows the comparison between NQACO and the other two algorithms regarding the optimization of the network energy consumption for four cases of 5%, 10%, 15%, and 20% of the quantity of cluster heads in WAMRN with various wireless sensor sizes. In the simulations, each algorithm was run 100 times, and all calculation results were averaged over 50 Monte Carlo runs. From figure (a), it is clear that the total network energy consumption of the WAMRN optimized by NQACO is always less than that of SA and GA for different sizes of wireless sensor numbers. Meanwhile, when the number of wireless communication nodes in WAMRN increases, the overall network energy consumption also increases. The same conclusion can be easily drawn from figures (b), (c), and (d).

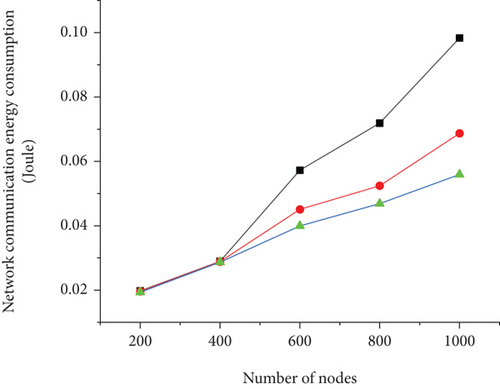
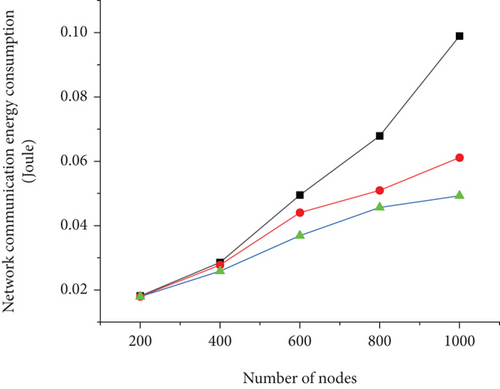
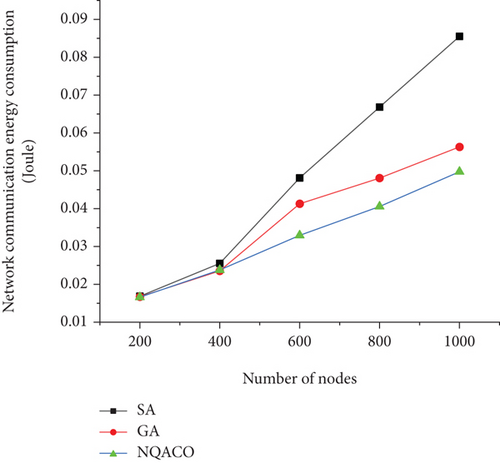
Figures 6 and 7 illustrate the relationship between surviving nodes’ quantity and round. During the experiment, the WAMRN contains 100 wireless communication nodes, and the initial energy of each wireless communication node is set to 0.5 J, and then, we record the number of surviving nodes in each round of data transmission and the remaining energy of each node. When a node runs out of energy, we remove it from the network so that the node cannot send or receive messages. Network lifetime is a key indicator of how well balanced the network’s energy consumption is. The longer the network lifecycle, the more balanced the network energy consumption, and the better the performance of the routing protocol is proven. Otherwise, the network energy consumption is unbalanced. From Figures 6 and 7, it can be seen that the WAMRN after SA and GA optimization starts to have wireless communication nodes die at rounds 484 and 929, respectively; however, NQACO effectively delays the death of the first node of the network until round 978. Moreover, after round 2388, it can be seen that after NQACO optimization, the number of surviving wireless communication nodes in WAMRN is always more than the other two algorithms. When all 100 nodes die due to energy exhaustion, the network after NQACO optimization has more data transmission rounds than GA and SA with more than 6.3% and 6.7%, respectively.

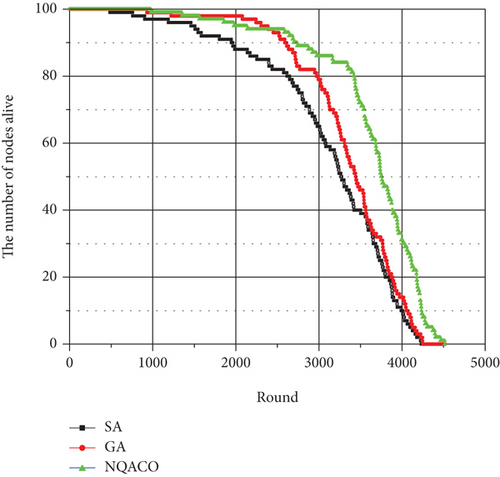
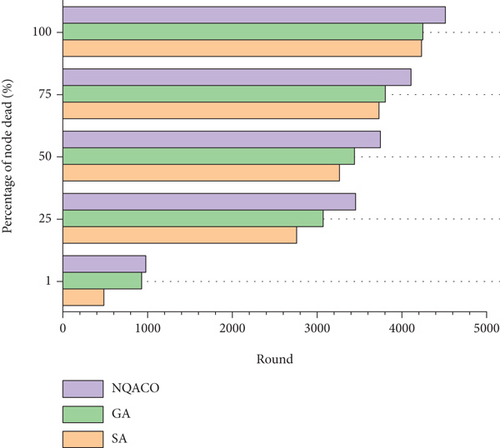
Through the comparative analysis of the above simulation experiments, it can be seen that NQACO introduces the chaos operator, which makes use of the randomness and convenience of chaotic variables so that the individuals in the ant colony can be evenly distributed in the solution space, which significantly enhances the algorithm’s optimality finding ability and prevents NQACO from falling into local optimum prematurely like GA and SA. Meanwhile, the ants in NQACO adopt quantum bit-based coding, which introduces the quantum state vector into the coding of the ant colony algorithm to avoid the phenomenon of premature convergence. Overall, the NQACO proposed in this paper always has better performance in reducing the network’s total energy consumption than GA and SA for the different number of wireless communication nodes.

6. Conclusions

In this paper, a clustering model is proposed to reduce energy consumption and prolong the network lifetime in WAMRN by selecting optimal cluster heads for efficient use of energy. The optimization problem of this model has been shown to be NP-hard, so we propose a new NQACO algorithm to optimize it. Through simulation experiments, the effectiveness and efficiency of the NQACO algorithm in optimizing and reducing the total network energy consumption are verified. The simulation results indicate that our proposed NQACO scheme has lower communication energy consumption than the traditional GA and SA schemes and has more advantages in extending the lifetime of WAMRN.

Additional Points

Additional Information. Correspondence and requests for materials should be addressed to Y.Z.

Conflicts of Interest

The authors declare no competing interests.

Authors’ Contributions

J.L. and Y.Z. conceived and designed the study. J.L. and H.Q. performed the experiments. J.L. and H.Q. wrote the paper. J.L., Y.L., and J.Z. reviewed and edited the manuscript. All authors read and approved the manuscript.

Acknowledgments

This paper was funded by the Major Science and Technology Project of the Eighth Division in Xinjiang (2021ZD002): Study on Key Technologies of Integrated Energy Collaboration Planning and Integrated Operation of PV& Storage Demonstration under the Condition of Independent Power Grid, the Corps Innovative Talents Plan (grant number 2020CB001), the project of Youth and Middle-aged Scientific and Technological Innovation Leading Talents Program of the Corps (grant number 2018CB006), the China Postdoctoral Science Foundation (grant number 220531), the Funding Project for High Level Talents Research in Shihezi University (grant number RCZK2018C38), and the Project of Shihezi University (grant number ZZZC201915B), Postgraduate education innovation program of the Autonomous Region.

Open Research

Data Availability

The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.

References

1 Liu Y., Liu J., and Ke Y., A detection and recognition system of pointer meters in substations based on computer vision, Measurement. (2020) 152, article 107333, https://doi.org/10.1016/j.measurement.2019.107333.
10.1016/j.measurement.2019.107333
Web of Science® Google Scholar
2 Kochneva E. and Sukalo A., Comparison of estimates calculated on the energy flow problem basis and using testing equations method, MATEC Web of Conferences. (2018) 208.
10.1051/matecconf/201820803002
Google Scholar
3 Wu X., Shi X., Jiang Y., and Gong J., A high-precision automatic pointer meter reading system in low-light environment, Sensors. (2021) 21, no. 14.
Web of Science® Google Scholar
4 Kawoosa A. I. and Prashar D., A review of cyber securities in smart grid technology, 2021 2nd International Conference on Computation, Automation and Knowledge Management (ICCAKM), 2021, Dubai, United Arab Emirates, 151–156, https://doi.org/10.1109/ICCAKM50778.2021.9357698.
10.1109/ICCAKM50778.2021.9357698
Google Scholar
5 Yu Y., Xue B., Chen Z., and Qian Z., Cluster tree topology construction method based on PSO algorithm to prolong the lifetime of ZigBee wireless sensor networks, EURASIP Journal on Wireless Communications and Networking. (2019) 1.
Google Scholar
6 Sales F., Marante Y., Vieira A., and Silva E., Energy consumption evaluation of a routing protocol for low-power and lossy networks in mesh scenarios for precision agriculture, Sensors. (2020) 20, no. 14, https://doi.org/10.3390/s20143814, 32650500.
10.3390/s20143814
PubMed Web of Science® Google Scholar
7 Alharbi M. A., Kolberg M., and Zeeshan M., Towards improved clustering and routing protocol for wireless sensor networks, EURASIP Journal on Wireless Communications and Networking. (2021) 1.
Google Scholar
8 Lipare A., Edla D. R., and Dharavath R., Energy efficient fuzzy clustering and routing using BAT algorithm, Wireless Networks. (2021) 27, no. 4, 2813–2828, https://doi.org/10.1007/s11276-021-02615-0.
10.1007/s11276-021-02615-0
Web of Science® Google Scholar
9 Karaboga D., Okdem S., and Ozturk C., Cluster based wireless sensor network routing using artificial bee colony algorithm, Wireless Networks. (2012) 18, no. 7, 847–860, https://doi.org/10.1007/s11276-012-0438-z, 2-s2.0-84869864314.
10.1007/s11276-012-0438-z
Web of Science® Google Scholar
10 Augustine S. and Ananth J. P., Taylor kernel fuzzy C-means clustering algorithm for trust and energy-aware cluster head selection in wireless sensor networks, Wireless Networks. (2020) 26, no. 7, 5113–5132, https://doi.org/10.1007/s11276-020-02352-w.
10.1007/s11276-020-02352-w
Web of Science® Google Scholar
11 van de Kaa G., Fens T., Rezaei J., Kaynak D., Hatun Z., and Tsilimeni-Archangelidi A., Realizing smart meter connectivity: analyzing the competing technologies power line communication, mobile telephony, and radio frequency using the best worst method, Renewable and Sustainable Energy Reviews. (2019) 103, 320–327, https://doi.org/10.1016/j.rser.2018.12.035, 2-s2.0-85059568768.
10.1016/j.rser.2018.12.035
Web of Science® Google Scholar
12 Chen H. and Chang L., Design and implementation of a ZigBee-based wireless automatic meter reading system, Przegląd Elektrotechniczny (Electrical Review). (2012) 88, no. 1B, 64–68.
Web of Science® Google Scholar
13 Zhao L., Qu S., and Zhang W., Design of multi-channel data collector for highway tunnel lighting based on STM32 and Modbus protocol, Optik. (2020) 213, article 164388, https://doi.org/10.1016/j.ijleo.2020.164388.
10.1016/j.ijleo.2020.164388
Web of Science® Google Scholar
14 Sun J., Wu Q., Han F., Liang Y., Sun B., and Wang Y., Design and implementation of remote intelligent meter reading system, 2017 Chinese Automation Congress (CAC), 2017, Jinan, China, 3511–3516, https://doi.org/10.1109/CAC.2017.8243389, 2-s2.0-85050344046.
10.1109/CAC.2017.8243389
Google Scholar
15 Viswanathan A., Sai Shibu N. B., Rao S. N., and Ramesh M. V., Security challenges in the integration of IoT with WSN for smart grid applications, 2017 IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), 2017, Coimbatore, India, 1–4, https://doi.org/10.1109/ICCIC.2017.8524233, 2-s2.0-85057973928.
10.1109/ICCIC.2017.8524233
Google Scholar
16 Hou L. and Qu H., Automatic recognition system of pointer meters based on lightweight CNN and WSNs with on-sensor image processing, Measurement. (2021) 183, article 109819, https://doi.org/10.1016/j.measurement.2021.109819.
10.1016/j.measurement.2021.109819
Web of Science® Google Scholar
17 Nhan N.-Q., Vo M.-T., Nguyen T.-D., and Huynh H.-T., Improving the performance of mobile data collecting systems for electricity meter reading using wireless sensor network, The 2012 International Conference on Advanced Technologies for Communications, 2012, Hanoi, 241–246, https://doi.org/10.1109/ATC.2012.6404268, 2-s2.0-84873551854.
10.1109/ATC.2012.6404268
Google Scholar
18 Liu J., Zhao Z., Ji J., and Hu M., Research and application of wireless sensor network technology in power transmission and distribution system, Intelligent and Converged Networks. (2020) 1, no. 2, 199–220, https://doi.org/10.23919/ICN.2020.0016.
10.23919/ICN.2020.0016
Google Scholar
19 Lineykin S., Sitbon M., and Kuperman A., Design and optimization of low-temperature gradient thermoelectric harvester for wireless sensor network node on water pipelines, Applied Energy. (2021) 283, article 116240, https://doi.org/10.1016/j.apenergy.2020.116240.
10.1016/j.apenergy.2020.116240
Web of Science® Google Scholar
20 Singh H. and Singh D., Hierarchical clustering and routing protocol to ensure scalability and reliability in large-scale wireless sensor networks, The Journal of Supercomputing. (2021) 77, no. 9, 10165–10183, https://doi.org/10.1007/s11227-021-03671-1.
10.1007/s11227-021-03671-1
Web of Science® Google Scholar
21 Radhika M. and Sivakumar P., Energy optimized micro genetic algorithm based LEACH protocol for WSN, Wireless Networks. (2021) 27, no. 1, 27–40, https://doi.org/10.1007/s11276-020-02435-8.
10.1007/s11276-020-02435-8
Web of Science® Google Scholar
22 Sahoo R. R., Sardar A. R., Singh M., Ray S., and Sarkar S. K., A bio inspired and trust based approach for clustering in WSN, Natural Computing. (2016) 15, no. 3, 423–434, https://doi.org/10.1007/s11047-015-9491-8, 2-s2.0-84923834480.
10.1007/s11047-015-9491-8
CAS Web of Science® Google Scholar
23 Kiran W., Smys S., and Bindhu V., Clustering of WSN based on PSO with fault tolerance and efficient multidirectional routing, Wireless Personal Communications. (2021) 121, no. 1, 31–47, https://doi.org/10.1007/s11277-021-08622-w.
10.1007/s11277-021-08622-w
Web of Science® Google Scholar
24 Rajasekaran A. and Nagarajan V., Cluster-based wireless sensor networks using ant colony optimization, International Conference on Intelligent Data Communication Technologies and Internet of Things (ICICI), 2018, Cham, 42–55, https://doi.org/10.1007/978-3-030-03146-6_5.
10.1007/978-3-030-03146-6_5
Google Scholar
25 Halgamuge M. N., Zukerman M., Ramamohanarao K., and Vu H. L., An estimation of sensor energy consumption, Progress in Electromagnetics Research B. (2009) 12, 259–295, https://doi.org/10.2528/PIERB08122303, 2-s2.0-61849153003.
10.2528/PIERB08122303
Google Scholar
26 Batra P. K. and Kant K., LEACH-MAC: a new cluster head selection algorithm for wireless sensor networks, Wireless Networks. (2016) 22, no. 1, 49–60, https://doi.org/10.1007/s11276-015-0951-y, 2-s2.0-84953836642.
10.1007/s11276-015-0951-y
Web of Science® Google Scholar
27 Li C., Liu Y., Xiao J., and Zhou J., MCEAACO-QSRP: a novel QoS secure routing protocol for Industrial Internet of Things, IEEE Internet of Things Journal. (2022) https://doi.org/10.1109/JIOT.2022.3162106.
10.1109/JIOT.2022.3162106
PubMed Web of Science® Google Scholar
28 Heinzelman W. R., Chandrakasan A., and Balakrishnan H., Energy-efficient communication protocol for wireless microsensor networks, Proceedings of the 33rd Hawaii International Conference on System Sciences, 2000, Maui, HI, USA, https://doi.org/10.1109/HICSS.2000.926982.
10.1109/HICSS.2000.926982
Google Scholar

All articles

A Novel Niche Quantum Ant Colony-Based Clustering Optimization Approach for Wireless Auto Meter Reading Network

Abstract

1. Introduction

2. Related Work

3. System Model

3.1. WAMRN Network Model

3.2. Energy Loss Model of Wireless Communication Nodes

4. NQACO for Clustering Optimization in WAMRN

4.1. Quantum Coding and State Measurement

4.2. Initialization of Ant Population

4.3. Construction of the Fitness Function

4.4. Mobile Strategy and Positivity Update

4.5. Variation of Quantum Bits

4.6. Niche Based on Exclusion Mechanism

4.7. Termination Condition

5. Simulation

6. Conclusions

Additional Points

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley