[Retracted] Feudal Multiagent Reinforcement Learning for Interdomain Collaborative Routing Optimization
Abstract
In view of the inability of traditional interdomain routing schemes to meet the sudden network changes and adapt the routing policy accordingly, many optimization schemes such as modifying Border Gateway Protocol (BGP) parameters and using software-defined network (SDN) to optimize interdomain routing decisions have been proposed. However, with the change and increase of the demand for network data transmission, the high latency and flexibility of these mechanisms have become increasingly prominent. Recent researches have addressed these challenges through multiagent reinforcement learning (MARL), which can be capable of dynamically meeting interdomain requirements, and the multiagent Markov Decision Process (MDP) is introduced to construct this routing optimization problem. Thus, in this paper, an interdomain collaborative routing scheme is proposed in interdomain collaborative architecture. The proposed Feudal Multiagent Actor-Critic (FMAAC) algorithm is designed based on multiagent actor-critic and feudal reinforcement learning to solve this competition-cooperative problem. Our multiagent learns about the optimal interdomain routing decisions, focused on different optimization objectives such as end-to-end delay, throughput, and average delivery rate. Experiments were carried out in the interdomain testbed to verify the convergence and effectiveness of the FMAAC algorithm. Experimental results show that our approach can significantly improve various Quality of Service (QoS) indicators, containing reduced end-to-end delay, increased throughput, and guaranteed over 90% average delivery rate.
1. Introduction
With the explosive growth of Internet traffic, network resources have been stressed due to the differentiated network requirements and sudden requirements, which has also led to an increase in the demand for interdomain transmission, network operation, and maintenance and management [1]. There are further requirements for the role of the network, requiring its QoS to be stable and controllable. To support more new applications on limited distributed resources, an efficient collaboration mechanism between Autonomous Systems (ASs) has become the key to solving the traffic surge in interdomain. BGP is an interdomain routing protocol for AS, used to exchange routing information between different AS during interdomain transmission [2]. To ensure good scalability and flexibility, BGP hides the internal information of the AS, including routing strategy, internal topology, and link bandwidth. However, BGP’s opaque characters hinder the collaboration of the AS, which makes it challenging to guarantee end-to-end communication QoS [3]. With the emergence of centralized SDN technology, it is no longer necessary to exchange information through BGP but to exchange routing information through the SDN controller, which is deployed in each AS, and make interdomain routing decisions based on the collected topology information of the entire network [4]. There are still issues that contain interconnection, high latency, flexibility, and flexibility issues, whether the improvement mechanism is based on standard BGP or an interdomain routing approach employing SDN technology.
- (1)
This paper studied the problem of interdomain routing and proposed an interdomain collaborative architecture, and the MARL framework for collaborative routing is installed in the interdomain routing environment
- (2)
After proposing a collaborative routing model based on multiagent MDP, we introduce the multiagent actor-critic architecture and feudal reinforcement learning and construct a corresponding hybrid algorithm to solve the mapping collaborative routing optimization problem
- (3)
We evaluate the performance of the proposed approach compared to other baselines, and experimental results show that the proposed approach can decrease the complexity compared to the conventional MARL methods and achieve better performance than previous routing schemes
The remainder of this paper is organized as follows. In Section 2, we analyse the related works on interdomain routing and MARL. In Section 3, we detail the proposed interdomain collaborative architecture and the collaborative routing optimization model. In Section 4, we describe the FMAAC algorithm for collaborative routing based on multiagent actor-critic and the feudal reinforcement learning. Experiment results validate the performance of the FMAAC algorithm in Section 5. Finally, we conclude the paper and discuss the future works in Section 6.
2. Related Works
2.1. Interdomain Routing
On the Internet divided by AS, the routing problem can be divided into routing within a single AS and routing between ASs, that is, intradomain routing and interdomain routing. As shown in Figure 1, each AS can run any routing protocol on the Internet containing a collection of interconnected AS. Interdomain routing is used to solve the reachability of routing information, which works and needs to know about other routers within and between their AS [8]. BGP is a distance vector routing protocol that provides reachable routes and no loops between AS, which uses the path length between ASs as the main factor in most optimal path calculations. Due to the emergence of lightweight independent networks, the length of AS path in BGP has increased improperly, resulting in a decrease in real-time network traffic routing efficiency [9].
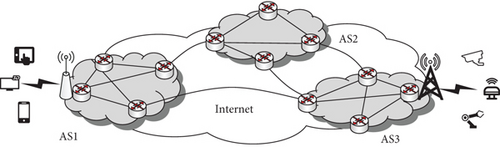
Interdomain routing optimization has been studied for a long time, and plenty of optimization schemes have been proposed. Aiming at the BGP’s convergence delay, Alabdulkreem et al. [10] calculate the optimal value of the advertisement interval to minimize the convergence time without increasing the number of advertising messages. There can be competing factors to consider, such as completion time and resource utilization, which can conflict with each other, and it is hard to draw a balance. In fact, this problem is general NP-hard. Xiang et al. [11] systematically formulate the software-defined internetworking model and develop a Bayesian optimization algorithm to solve the NP-hard routing problem, which can find a near-optimal policy-compliant end-to-end route by sampling. To achieve better Internet real-time experience, Arins [12] proposed to store the bilateral latency measurements in a decentralized blockchain network, and the SDN controller can route according to the shared data in the block. Zhong et al. [13] propose a novel multidomain routing paradigm that transforms the routing problem from heuristic-algorithm-based computation to artificial-intelligence-based data analytics.
2.2. Multiagent Reinforcement Learning
Reinforcement learning is very suitable for solving decision-making problems and has apparent advantages in routing optimization. Sun et al. [14] propose an intelligent network control architecture based on deep reinforcement learning that can dynamically optimize centralized routing strategies. Distributed optimization, game theory, and MARL have been proposed to solve the problems of inaccurate information prediction, high complexity, high cost, and poor scalability faced by centralized methods. Independent Q-Learning (IQL) is a MARL algorithm extended by the DQN, which executes a Q-learning algorithm on each agent, while the environment of each agent is dynamic and unstable, and this algorithm cannot converge [15]. The Centralized Training with Decentralized Execution (CTDE) framework has become the industry standard to reduce unnecessary costs imposed by agent communication [16]. Value Decomposition Networks (VDN) adopt the integration of the value function of each agent to obtain a value function of the joint action [17]. Although the CTDE framework is implemented, its joint action-value function cannot express some complex environments well.
Multiagent Deep Deterministic Policy Gradient (MADDPG) is an actor-critic-based CTDE algorithm, using DDPG as the underlying reinforcement learning algorithm for each agent [16]. Each agent is configured with a separate actor responsible for the generation of actions, and an independent critic is responsible for judging the actions made by the actor to assist in the training of the model. Multiagent-Attention-Critic (MAAC) uses a centralized critic and attention mechanism to integrate information from all agents for more efficient training [18]. Counterfactual multiagent policy gradients (COMA) distinguish the actual value of actions made by each agent through the counterfactual baseline, and credit assignment is realized by determining the contribution of each agent in collaboration [19]. The above-mentioned MARL algorithms provide a good idea for solving interdomain routing optimization problem, while directly applying the MARL algorithms to the interdomain routing optimization problem is likely to generate issues such as high training difficulty, low training efficiency, and robustness, and further optimization is required to make it adapt to the interdomain routing environment.
3. System Model and Problem Formulation
In this section, we introduce the system model and formulation of the collaborative routing optimization problem with networked agents.
3.1. Interdomain Collaborative Architecture
We propose an interdomain collaborative architecture, as shown in Figure 2; the MARL framework for collaborative routing is installed in the interdomain routing environment. In the interdomain network scenario, an agent is installed in each AS, in which the policy network and the value network make and assess routing actions based on their observations of the AS’s environment, respectively. By sending routing actions to the relevant network controller for forwarding, calculating the overall reward and the individual reward of each agent according to the transmission result, and adjusting the next round of routing actions by maximizing the overall reward, the collaborative routing obtains the global optimal interdomain routing. In each time-step, agents make decisions jointly with other agents through information interaction and learn how to generate routing information based on their own local observations during the training process or to determine whether the communication is needed and which agents to communicate with [20]. At the same time, it must learn and find the maximum reward given by the environment to obtain the best strategy. In the process of running after training, it is necessary to explicitly make routing decisions based on the information transmitted by other agents.
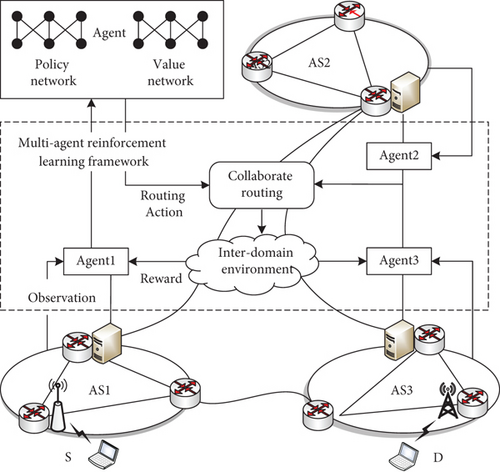
Take a simple service as an example in Figure 2, when the source user located in the AS1 needs to transmit data to the destination user in AS3, its network transmission requirements are recognized by the agent in AS1, and the agent in AS1 generates a service identifier according to the characteristics of the requested service, which triggers pathway AS to coordinate the software and hardware resources in their respective network domains to meet users’ service requirements. Specifically, the agent in AS1 updates the forwarding table by issuing forwarding messages. Then, it is necessary to coordinate the network resources of the AS that need to pass through to meet interdomain transmission requirements, update network status information, and feed resource usage. Finally, the agent in AS3 obtains users’ service requirements and coordinates the network resources to meet them. In general, the above combinatorial optimization problem can be reduced to a classic discrete optimization problem, and it can be solved in polynomial time by linear programming, genetic algorithm, reinforcement learning, and other methods.
3.2. Multiagent MDP
Considering a system of many agents operating in the interdomain routing environment, we assume that the interdomain state and routing actions can be observed by all agents, and only the rewards are unique to each agent [21]. Since single-agent reinforcement learning can be formalised in terms of MDP, we then model the optimization problems of interdomain routing as multiagent MDP. The main notations used in this work are summarized in Table 1. The interdomain collaborative architecture with the MARL framework can be represented by an undirected graph G(μ, ν), where i ∈ μ represents each agent and (i, j) ∈ v represents each interdomain link.
| Notation | Meaning |
|---|---|
| G | Graph |
| i, j | Agent |
| t | Time period |
| μ | Agent collection |
| ν | Link collection |
| N | Number of agents |
| S | Interdomain global state |
| A | Action space |
| O | Observation function |
| R | Reward function |
| T | Transition function |
| π | Policy |
| γ | Discount factor |
- (1)
State definition: each agent can observe the flow state of its own AS, and we define the observations of each agents as Oi. The more comprehensive the information observed, the better the decisions made. To extend the observable range, more state information can be obtained from neighbor ASs or even all, but this also adds additional communication. Here, we only consider that the state is affected by the one-hop neighborhood, and the state is composed of its own observed state and the routing actions with its neighboring agents that are one hop away from it
- (2)
Action definition: for flows with different destinations, the set of candidate next hops advertised by their routes may be different, so we define the set of next hops of all forwarded flows in the next round as the action space. Let {Ai} = ∏Ai represent the action space of all agents and Ai = (a1, a2, a3, ⋯aN) represent the specific actions of all agents at each step. The policy πi of each agent i is determined by the policy network and value network, and the state transition probability T : S × A⟶[0, 1] is designed to transfer all agents to a new state after performing actions in the current state. Each agent i follows a decentralized policy πi : Si × Ai⟶[0, 1] to choose its own action Ai,t ~ πi(⋅∣Si,t) at time t
- (3)
Reward definition: according to the current state S and the actions Ai made by each agent i, the agent can receive corresponding rewards Ri : Si × Ai⟶ℝ from the environment. The objective of multiagent MDP is to find an optimal policy for each agent, and we can maximize the sum of its future expected rewards:
(1)where T is the cumulative number of expected rewards in the future and γ is the discount factor, which is usually set to a number slightly less than 1
3.3. Collaborative Routing Optimization
However, the above global function requires the rewards of all agents to be unbiasedly estimated, so we need to design a MARL algorithm based on consistency constraints. The algorithm can spread local information between agents, thereby promoting the establishment of cooperative relations between agents.
4. Feudal Multiagent Reinforcement Learning
This section builds the corresponding algorithm based on the feudal reinforcement learning framework and multiagent actor-critic to solve the formulated optimization problem.
4.1. Feudal Reinforcement Learning
Due to the enormous state space combination, huge action space combination, and sparse reward in multiagent MDP, a good model cannot be obtained directly through training. Concerning the experience of solving other complex problems, the optimization problem can be decomposed into several easy-to-solve suboptimization problems, which is hierarchical reinforcement learning, which can be divided into two types according to hierarchical methods [22]. One is based on goals, and the primary method is to select a specific goal so that the agent trains toward these goals. It can be foreseen that the difficulty of this method is how to select a suitable goal. The other is multilevel control, whose practice abstracts different control layers and controls the lower layer via the upper layer [23]. Feudal reinforcement learning is a typical multilevel control, and its control level is divided into three levels. The current level is manager, the upper level is supermanager, and the next level is submanager [24]. When the feudal mechanism is adopted, each element in the defined initially multiagent MDP needs to be redefined from both managers and workers in feudal reinforcement learning [25].
The state space of the managers directly uses the state space of the original multiagent MDP, and the state of the multiagent MDP and the goal generated by the managers are used as the state space of the workers. Regarding the action space of the managers, the option-critic framework solution in the MAAC framework is that the action space is used to select different workers to perform operations. For example, the managers first select the first worker to execute and then execute the second worker. To fit the interdomain collaborative routing environment, the managers set a global collaborative optimization goal and then allow the workers to execute it while the workers’ action space remains unchanged. The managers’ reward can directly use the original multiagent MDP’s reward. The long-term credit assignment makes the managers’ goals cruder on the time scale so that the original sparse reward is not so sparse in the managers’ view. However, the workers’ reward cannot directly use the reward of the original problem but can use the more intensive reward evolved from the goal generated by the managers. In addition, the workers’ transition model and discount rate remain unchanged, while the transition function of the managers will change. The managers pay more attention to long-term rewards to have a more significant discount rate than the workers by transforming into a transition policy gradient.
4.2. Multiagent Actor-Critic
4.3. Feudal Multiagent Actor-Critic
Combine the feudal reinforcement learning into the MAAC framework, which can integrate the centralized data of critic more hierarchically and reasonably and has more advantages when the number of agents rises. We proposed Feudal Multiagent Actor-Critic (FMAAC), which is an extension of MAAC with feudal hierarchy for collaborative routing optimization, and the procedures of the proposed approach are shown in Algorithm 1. At each time-step, the manager selects an action from its current policy and exploration, and the worker selects and executes an action. After executing a round of routing actions, the interdomain routing environment gives the manager and the worker corresponding reward RM and RW, respectively. The initial state, managers’ and workers’ actions, rewards, and new state are stored in replay buffer BM and BW, respectively. Then, the policy gradient is used to update managers’ and worker’s actor-critic networks. Finally, the update method of the target network parameters θi is the Soft update method, λ is the target update coefficient, and each parameter is updated to the current policy network in a small amount [30].
-
Algorithm 1: Feudal Multiagent Actor-Critic for collaborative routing.
-
Input: Initialize inter-domain environments with N agents contained managers and workers
-
Output: All managers’ and workers’ routing policies
-
1: for each episode α = 1 to μ do
-
2: Initialize a random process Ν for routing actions exploration, get the initial state S
-
3: for each time-step t = 1 to υ do
-
4: Managers select an action under the current policy πt and exploration
-
5: Workers select and execute an action
-
6: Receive the reward RM, RW and observe the next newly state S′
-
7: Store replay buffer BM⟵{S, AM, RM, S′} and BW⟵{S, AW, RW, S′}
-
8: for each agent j = 1 to N do
-
9: Sample a random minibatch from BM and BW
-
10: Update actor by using policy gradient:
-
11:
-
12: Update critic by minimizing the loss:
-
13:
-
14: end for
-
15: Update target network parameters:
-
16:
-
17: end for
-
18: end for
5. Simulation Experiments
5.1. Experimental Setup
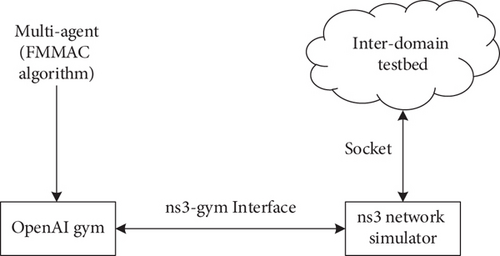
The experimental environment of interdomain collaborative routing was developed based on ns3-gym, which is an open-source project for RL research written in Python [31]. As shown in Figure 3, ns3-gym is a framework that integrates both OpenAI gym and ns-3 network simulator [32, 33]. The interdomain testbed is a multidomain network simulator based on ns-3, and the Interprocess Communication (IPC) between the different machines of the interdomain testbed and the ns-3 network simulator is Socket [34], and we used a network size of 1600 × 1600 m2 in the ns-3 network simulator [35]. In terms of the experimental hardware platform, the CPU is Intel Xeon E5 2630, the GPU is NVIDIA GeForce RTX 2080 Ti, the memory is 64 GB DDR4, the installed operating system is Ubuntu 18.04.5 LTS, and the reinforcement learning framework is PyTorch. We implement the proposed FMAAC algorithm using the Multiagent Particle Environments (MAPE), which is an open-source framework for building a multiagent testbed based on OpenAI gym [16]. On condition that the number of agents and training parameters is designed according to the interdomain collaborative routing environment and the representation of state information, rewards, and ending conditions is designed according to actual needs in MAPE, the framework will automatically generate a function interface for the MARL algorithm. Based on the above experimental parameter settings, we compare the proposed FMAAC algorithm with the following three latest benchmark algorithms: the MARL algorithms with CTEDE framework represented by MADDPG and MAAC [16, 18].
MADDPG is a multiagent policy gradient algorithm in which the agent learns a centralized critic based on the observations and actions of all agents [16]. MAAC algorithm introduces the attention mechanism so that the centralized data used by the critic can be more rationally integrated, which also uses MAPE as the test environment, so this algorithm is selected as the baseline for performance comparison [18]. In the process of model training, FMAAC, MADDPG, and MAAC use the same parameter settings as shown in Table 2 [36]. All use the most commonly used Adam optimizer, which has the advantages of fast convergence speed and easy parameter adjustment, and the learning rate of actor and critic is set to 0.01.
| Parameters | Value |
|---|---|
| Optimizer | Adam |
| Actor learning rate | 0.01 |
| Critic learning rate | 0.01 |
| Minibatch size | 512 |
| Target update coefficient | 0.01 |
| Discount factor | 0.95 |
| Network hidden units | 64 |
| Activation function | ReLU |
| Memory pool size | 106 |
The minibatch size extracted each time during training is 512, the target update coefficient in the Soft update method is set to 0.01, and the discount factor of the expected reward is set to 0.95. Critic and policy networks are represented by the three layers of Multilayer Perceptron (MLP), each layer has 64 hidden units, ReLU is used as the activation function, and the memory pool size is 106.
5.2. Experimental Results
5.2.1. Training Results
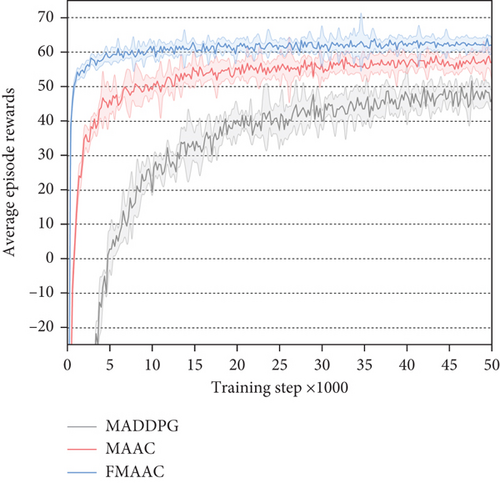
The experiment first verifies the convergence performance of the FMMAC algorithm in the offline training, and we take the average rewards to highlight the convergence performance. As shown in Figure 4, we plot the learning curves with error bars over 50000 training episodes for the proposed FMAAC algorithm and the MADDPG and MAAC algorithms as the baselines, which illustrate the average rewards per training episode. It can be clearly seen that when all algorithms enter the convergence stage, the value of the average episode rewards of the FMAAC algorithm is higher than that of other baseline algorithms. The MADDPG algorithm cannot find a better policy due to its relatively large observation space for all agents, and its performance is at the bottom. MAAC has made a good trade-off in the exploration-exploitation, while each agent’s local observation cannot provide enough information to make an optimal prediction of its expected rewards. Compared with the baseline algorithms, the FMAAC algorithm can infer the decisions of other agents more accurately due to the existence of feudal control, which can achieve more efficient cooperation and achieve better results in an interdomain collaborative routing environment. For the training of the interdomain routing optimization model, the proposed method combines the properties of feudal reinforcement learning to partition tasks spatially rather than temporally, allowing it to be successfully applied to large discrete action spaces in reinforcement learning tasks, which can better meet the requirements of interdomain collaborative routing optimization than the other two baseline algorithms.
5.2.2. Evaluation Results
In verifying the advantages of the multiagent algorithm, the FMAAC is compared with SDN-DDPG and SDN-BGP in the routing optimization performance [37, 38]. SDN-DDPG uses single-agent DDPG to optimize SDN to reduce network operating delay and increase throughput, while the SDN-BGP improves BGP performance through centralized control in SDN. Experiments first pay attention to the performance of FMMAC on end-to-end delay, which is a significant parameter for evaluating the performance of routing schemes. To get closer to the actual network scenario, we use five different data arrival rates in the experiment. For each data arrival rate, a corresponding flow matrix is generated for the training and testing of the FMAAC and SDN-DDPG, and the model after training 50000 steps is used as the comparison object.
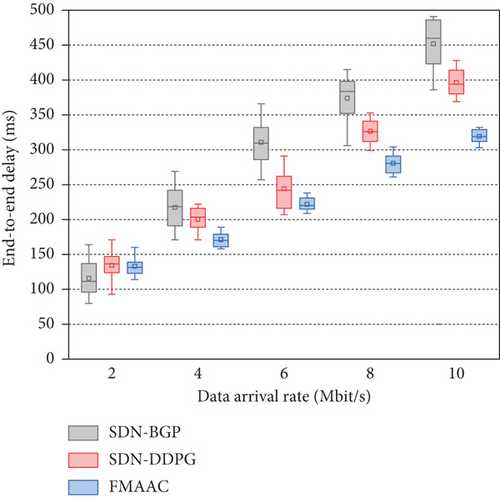
In order to make the observed end-to-end delay more convincing, the three schemes in our experiment sampled the value of the end-to-end delay 10 times. The comparison results of the three schemes are shown in Figure 5 in the form of box plots. The upper and bottom parts of the rectangle in the figure represent the upper quartile and lower quartile of the observed end-to-end delay obtained from the experiment, the horizontal line in the middle of the rectangle represents the median of the experimental observation data, and the upper and lower ends of the straight line extending from the rectangle represent the maximum and minimum values of the observation data in the inner limit range. In addition, invalid data outside the inner limit range is not displayed for brevity. Experimental results show that the end-to-end delay of the route configuration optimized by FMMAC is less than the delay of the SDN-BGP generating route and the delay of SDN-DDPG optimized route generation, which verifies the effectiveness of the FMMAC optimized interdomain routing.
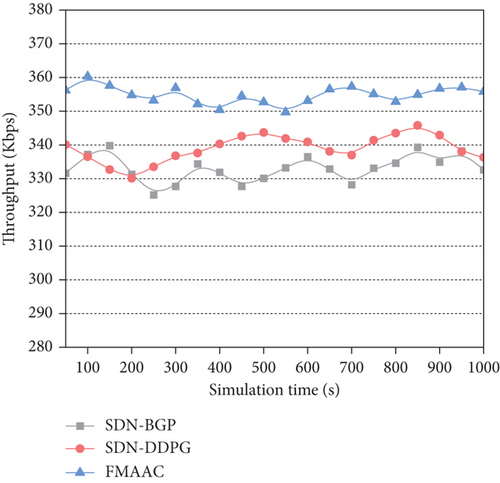
Next, we carried out a simulation experiment on throughput. In this experiment, we use the same data arrival rate and the size of packets and take the real-time throughput in the interdomain routing environment as the optimization goal. SDN-DDPG and FMMAC have been trained 50000 times in the early training stage. The performance of the three mechanisms in throughput is shown in Figure 6. It can be seen obviously that the real-time throughput range of SDN-BGP and SDN-DDPG ranges from 325 Kbps to 345 Kbps while using FMMAC as a routing mechanism increases the throughput range from 350 Kbps to 360 Kbps. This is due to the fact that when extensive routing table information exchanges are considered, the bandwidth consumption cannot be further minimized due to the transmission of large amounts of data, which will contribute to an even lower throughput as it was observed. SDN-BGP and SDN-DDPG need to transmit a large amount of data required for routing optimization, which not only produces a higher end-to-end delay but also increases the transmission burden of the network link and reduces the actual throughput. However, FMAAC uses MARL to make routing decisions, and agents in each AS calculate the best routing path across the entire network through the policy network and value network in each federation agent.
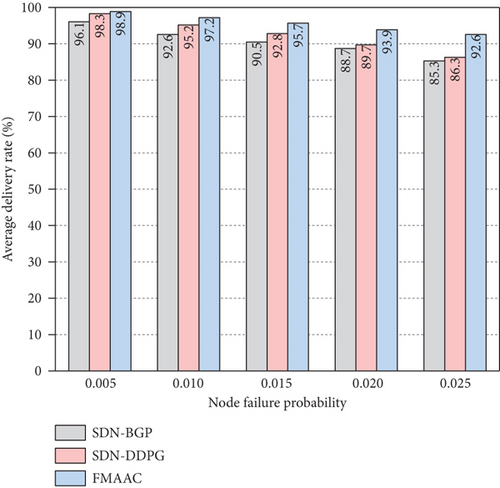
In addition to the end-to-end delay and throughput in the above experiment, another significant metric for evaluating the performance of the routing mechanism is the average delivery rate. We measure the average delivery rate of three schemes using different node failure probabilities in this experiment, which is used to express sudden situations in the interdomain routing testbed, such as destination network unreachable or link failure. Under the condition of keeping the same data arrival rate, SDN-BGP, SDN-DDPG, and FMMAC are, respectively, run as the routing mechanism, and the SDN-DDPG and FMMAC running here have also been trained for 50000 times. In Figure 7, the average delivery rate for each scheme is shown. We observe that the average delivery rate of each scheme decreases when the node failure probability increases. When the value of node failure probability is relatively small, the average delivery rate of the three mechanisms is comparatively similar. When the value of node failure probability continues to increase, the average delivery rate of SDN-BGP and SDN-DDPG has dropped below 90%, while the average delivery rate of FMAAC can still be maintained above 90%. FMAAC has the support of interdomain collaborative architecture so that it can better face problems due to sudden situations. Setting such as end-to-end delay, throughput, and average delivery rate as the FMMAC’s optimization goals can achieve guaranteed end-to-end QoS.
6. Conclusion
In this paper, we have studied the problem of interdomain routing in decentralized multidomain networks. We propose an interdomain collaborative architecture, and the MARL framework for collaborative routing is installed in the interdomain routing environment. We further defined the mapping optimization problem and designed a corresponding algorithm.
FMAAC is based on multiagent actor-critic and feudal reinforcement learning. Experimental evaluation results have demonstrated that the proposed approach can decrease the complexity compared to the conventional MARL methods and achieve better performance on end-to-end delay, throughput, and average delivery rate than previous routing schemes. As future work, our MARL method will be extended to consider different objectives, such as packet loss and resources utilization, and we will compare our MARL method with more interdomain routing optimization methods. We will further study the feasibility of the proposed model in other areas and improve it to make it scalable to similar optimization problems in other multiagent environments.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
This work was supported by the National Key R&D Program of China (Grant No. 2018YFB1800100); the National Natural Science Foundation of China (Grant No. U1909204); the Beijing Natural Science Foundation, China (Grant No. 4202082); and the Open Research Projects of Zhejiang Lab (Grant No. 2021LC0AB03).
Open Research
Data Availability
The data used to support the findings of this study are included within the article.




