Volume 2022, Issue 1 1220208

Research Article

Open Access

[Retracted] On Computation of Degree-Based Entropy of Planar Octahedron Networks

Retraction(s) for this article

Tian-Le Sun,

Tian-Le Sun

orcid.org/0000-0001-8928-6073

College of Economics, Sichuan Agriculture University, Chengdu 610000, China sicau.edu.cn

Search for more papers by this author

Haidar Ali,

Haidar Ali

orcid.org/0000-0002-9815-7158

Department of Mathematics, Riphah International University, Faisalabad Campus, Pakistan riphah.edu.pk

Search for more papers by this author

Bilal Ali,

Corresponding Author

Bilal Ali

[email protected]

orcid.org/0000-0003-4049-9443

Department of Mathematics, Government College University, Faisalabad, Pakistan gcu.edu.pk

Search for more papers by this author

Usman Ali,

Usman Ali

Department of Computer Science, University of Punjab, Lahore, Pakistan pu.edu.pk

Search for more papers by this author

Jia-Bao Liu,

Jia-Bao Liu

orcid.org/0000-0002-9620-7692

School of Mathematics and Physics, Anhui Jianzhu University, Hefei 230601, China ahjzu.edu.cn

Search for more papers by this author

Parvez Ali,

Parvez Ali

orcid.org/0000-0001-7363-4563

Department of Mechanical Engineering, College of Engineering, Qassim University, Unaizah, Saudi Arabia qu.edu.sa

Search for more papers by this author

Tian-Le Sun,

Tian-Le Sun

orcid.org/0000-0001-8928-6073

College of Economics, Sichuan Agriculture University, Chengdu 610000, China sicau.edu.cn

Search for more papers by this author

Haidar Ali,

Haidar Ali

orcid.org/0000-0002-9815-7158

Department of Mathematics, Riphah International University, Faisalabad Campus, Pakistan riphah.edu.pk

Search for more papers by this author

Bilal Ali,

Corresponding Author

Bilal Ali

[email protected]

orcid.org/0000-0003-4049-9443

Department of Mathematics, Government College University, Faisalabad, Pakistan gcu.edu.pk

Search for more papers by this author

Usman Ali,

Usman Ali

Department of Computer Science, University of Punjab, Lahore, Pakistan pu.edu.pk

Search for more papers by this author

Jia-Bao Liu,

Jia-Bao Liu

orcid.org/0000-0002-9620-7692

School of Mathematics and Physics, Anhui Jianzhu University, Hefei 230601, China ahjzu.edu.cn

Search for more papers by this author

Parvez Ali,

Parvez Ali

orcid.org/0000-0001-7363-4563

Department of Mechanical Engineering, College of Engineering, Qassim University, Unaizah, Saudi Arabia qu.edu.sa

Search for more papers by this author

First published: 09 March 2022

https://doi.org/10.1155/2022/1220208

Citations: 1

Academic Editor: Hanan A. Al-Olayan

Share a link

Email
Wechat
Bluesky

Abstract

Chemical graph theory is the combination of mathematical graph theory and chemistry. To analyze the biocompatibility of the compounds, topological indices are used in the research of QSAR/QSPR studies. The degree-based entropy is inspired by Shannon’s entropy. The connectivity pattern such as planar octahedron network is used to predict physiochemical activity. In this article, we present some degree-based entropies of planar octahedron network.

1. Introduction

All the graphs in this article are finite and undirected. A graph is set of points, where each pair of points (also known as vertex) are connected by an edge (also known as link or line). In network, vertices are called nodes, and in chemical graph, vertices are called atoms. In network, edges are called links or lines, while in chemical graph, they are called covalent bonds. The subbranch of chemical graph theory is topological indices. Many articles have been written on the topic of topological index. The representation of molecular graph by a drawing, a polynomial, a sequence of numbers, a matrix, or a derived number is called a topological index. As such, under graph isomorphism, these numeric numbers are unique. Most of the time, molecules and molecular compounds are nicely presented by molecular graph for better understanding.

Topological descriptors assume fundamental job in QSAR/QSPR studies in light of the fact that they convert a compound graph into a numerical number. We compare other physicochemical properties of carbon-based compounds (such as nanotubes, hydrocarbons, nanocones, and fullerenes). Due to these properties, topological descriptors have many applications in organic chemistry, biotechnology, and nanotechnology.

Cheminformatics is a branch of science that participates in mathematics, chemistry, and IT. In chemical graph theory, we consider molecular graph’s solution using the graph theory techniques which is the subdivision of mathematical chemistry. Molecules or atoms are represented by vertices in chemical graph theory, also the bonds between them by edges [1].

The pioneer of topological indices is Wiener [2]. It is defined as

(1)

Randić presented first the vertex-degree-based topological index in 1975 [3], which is written by

(2)

Bollobás and Erdos [4] and Amić et al. [5] compute the “general Randić index” independently in 1998.

(3)

where α = −1/2, 1/2, 1, −1.

ABC index was introduced in 1998, by Estrada et al. [6]. It has the formulae

(4)

Vuki

ević and Furtula were the persons who studied this index for the first time [7]. It is written as GA index and written as

(5)

Entropy is the uncertainty in a random variable or quantity. In other words, it is the information obtained by learning the values of some unknown variables. Entropy has many applications in information theory as information entropy, in chemistry as thermodynamic entropy, and in graph theory as graph entropy [8–16]. In general, entropy is defined as the following: Let x be a discrete random variable and x ∈ X and p be the probability distribution of set X. Then, entropy of x is

(6)

The definition of entropy was given by Shannon in 1948 [17]. In graph theory, the idea of graph entropy was given by Rashevsky in 1955 [18]. It has been used comprehensively to depict the design of graph-based systems in mathematical science [19]. The graph entropy is defined as the following:

For a graph

is finite vertex set. Let

be the density of probability of vertex set and

be the vertex packing polytope of

. Then, entropy of

with respect to

(7)

Octahedron networks have its roots in physical world as natural crystals of diamond are octahedron; also, many metal ions have octahedron configuration. In physics, these networks can be used as circuits. The construction of planar octahedron network POH is based on silicate structure derived by Manuel and Rajasingh [20] and POH was derived by Simonraj and George [21] (for the complete construction of POH, see Figure 1, for triangular prism network TP, see Figure 2, and for hex planar octahedron network, see Figure 3; we refer the reader to read the article [22]).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Planar octahedron network.

Degree-based entropy is defined as

(8)

From Equation (8), edge-based entropy can be deducted as

(9)

From Equation (3) and Equation (9), Randić entropy will be

(10)

From Equation (4) and Equation (9), ABC entropy will be

(11)

From Equation (5) and Equation (9), GA entropy will be

(12)

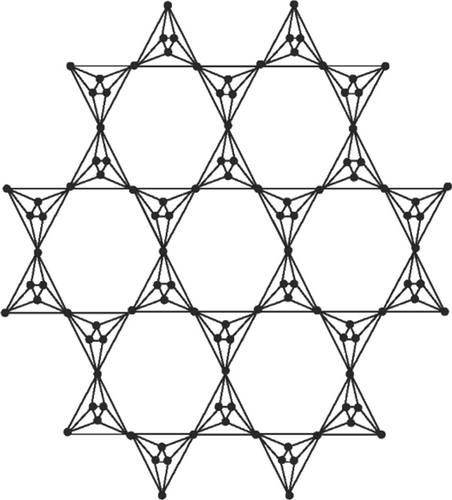
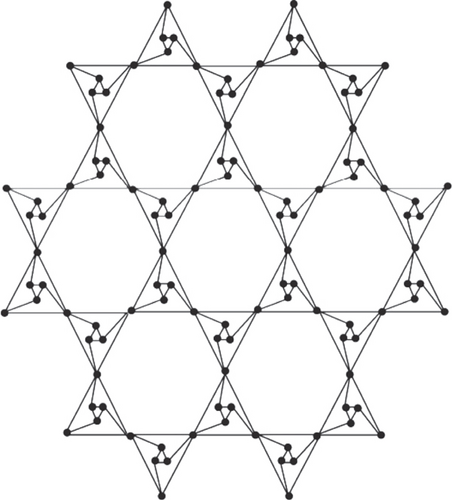
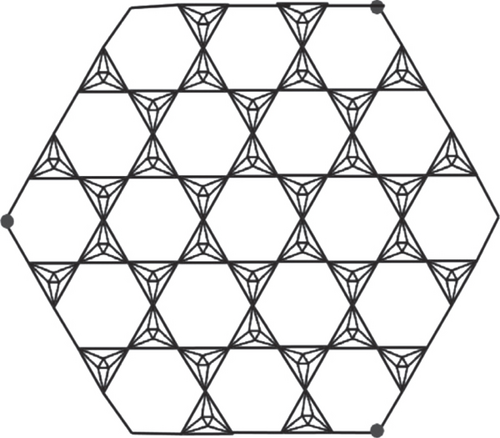
2. Main Results

Planar octahedron network and its derived forms are inorganic structures used in chemistry. Here, we research some degree-based entropies for these networks. These days, there is a broad examination movement on entropies (for further studies, see [23, 24]; for basic definitions and notations, we refer the reader to [25, 26]).

2.1. Results on Planar Octahedron Network

In this section, we will compute Randić, ABC, and GA entropies for planar octahedron network. The edge partition of POH(n) is written in Table 1.

Table 1. Edge partition.

	Number of edges
(4, 4)	18n² + 12n
(4, 8)	36n²
(8, 8)	18n² − 12n

2.1.1. Randić Entropy

, then from Table 1 and Equation (3), we have

(13)

For α = 1,

(14)

For α = −1,

(15)

For α = 1/2,

(16)

For α = −1/2,

(17)

Using Equation (10) and Table 1, we have

(18)

For α = 1,

(19)

For α = −1,

(20)

For α = 1/2,

(21)

For α = −1/2,

(22)

where R_α for α = 1, −1, 1/2, −1/2 is written in (14), (15), (16), and (17), respectively.

2.1.2. ABC Entropy

, then from Table 1 and Equation (4), we have

(23)

Using Equation (11) and Table 1, we have

(24)

where ABC index is written in (24).

2.1.3. GA Entropy

, then from Table 1 and Equation (5), we have

(25)

Using Equation (12) and Table 1, we have

(26)

where GA index is written in (26).

2.2. Results on Triangular Prism Network

In this section, we will compute Randić, ABC, and GA entropies for triangular prism network. The edge partition of TP(n) is written in Table 2.

Table 2. Edge partition.

	Number of edges
(3, 3)	18n² + 6n
(3, 6)	18n² + 6n
(6, 6)	18n² − 12n

2.2.1. Randić Entropy

, then from Table 2 and Equation (3), we have

(27)

For α = 1,

(28)

For α = −1,

(29)

For α = 1/2,

(30)

For α = −1/2,

(31)

Using Equation (10) and Table 2, we have

(32)

For α = 1,

(33)

For α = −1,

(34)

For α = 1/2,

(35)

For α = −1/2,

(36)

where R_α for α = 1, −1, 1/2, −1/2 is written in (28), (29), (30) and (31).

2.2.2. ABC Entropy

, then from Table 2 and Equation (4), we have

(37)

Using Equation (11) and Table 2, we have

(38)

where ABC index is written in (37).

2.2.3. GA Entropy

, then from Table 2 and Equation (5), we have

(39)

Using Equation (12) and Table 2, we have

(40)

where GA index is written in (39).

2.3. Results on Hex Planar Octahedron Network

In this section, we will compute Randić, ABC, and GA entropies for hex planar octahedron network. The edge partition of hex POH(n) is written in Table 3.

Table 3. Edge partition.

	Number of edges
(4, 4)	18n² + 18n − 30
(4, 8)	36n² − 48n + 12
(8, 8)	18n² − 36n + 18

2.3.1. Randić Entropy

hex POH(n), then from Table 3 and Equation (3), we have

(41)

For α = 1,

(42)

For α = −1,

(43)

For α = 1/2,

(44)

For α = −1/2,

(45)

Using Equation (10) and Table 3, we have

(46)

For α = 1,

(47)

For α = −1,

(48)

For α = 1/2,

(49)

For α = −1/2,

(50)

where R_α for α = 1, −1, 1/2, −1/2 is written in (42), (43), (44), and (45), respectively.

2.3.2. ABC Entropy

hex POH(n), then from Table 3 and Equation (4), we have

(51)

Using Equation (11) and Table 3, we have

(52)

where ABC index is written in (51).

2.3.3. GA Entropy

hex POH(n), then from Table 3 and Equation (5), we have

(53)

Using Equation (12) and Table 3, we have

(54)

where GA index is written in (53).

3. Discussion and Conclusion

In this article, we computed some degree-based topological indices of planar octahedron networks. After that, we used the definition of Shannon’s graph entropy to find some exact results of entropies for planar octahedron networks. For the variational change in the values of entropies for the degree-based indices, we construct some tables to enlist the numerical values for these networks. It is clear from Tables 4, 5, and 6 that the increase in the value of n causes a proportional increase or decrease in the values of entropies for Randić, ABC and GA indices. These formulae and their numerical values will help the researchers to predict physio- and biochemical activities of these networks. These numerical values of entropies can also predict the amount of energy that is unavailable for the work done in a chemical system. Furthermore, our future work will based on entropies of some other complex networks.

Table 4. Comparison table of entropies for POH(n).

n					ENT_ABC	ENT_GA
6	−2.525 × 10¹¹³	−22.4506	−6.546 × 10⁵	−1.2835	1.8516	2.3994
7	−2.556 × 10¹¹³	−22.4546	−6.645 × 10⁵	−1.1628	1.9840	2.5333
8	−2.578 × 10¹¹³	−22.4431	−6.717 × 10⁵	−1.0567	2.0988	2.6493
9	−2.596 × 10¹¹³	−22.4225	−6.774 × 10⁵	−0.9622	2.2003	2.7516
10	−2.611 × 10¹¹³	−22.3968	−6.819 × 10⁵	−0.8768	2.2911	2.8431
11	−2.622 × 10¹¹³	−22.3680	−6.856 × 10⁵	−0.7992	2.3733	2.9258
12	−2.632 × 10¹¹³	−22.3376	−6.886 × 10⁵	−0.7278	2.4484	3.0015
13	−2.640 × 10¹¹³	−22.3065	−6.913 × 10⁵	−0.6619	2.5175	3.0709
14	−2.647 × 10¹¹³	−22.2751	−6.935 × 10⁵	−0.6006	2.5815	3.1354
15	−2.653 × 10¹¹³	−22.2437	−6.954 × 10⁵	−0.5434	2.6411	3.1953

Table 5. Comparison table of entropies for TP(n).

n					ENT_ABC	ENT_GA
6	−1.563 × 10⁵⁴	−10.4998	−3228.67	−0.1748	1.8579	2.2787
7	−1.581 × 10⁵⁴	−10.4305	−3275.76	−0.0500	1.9905	2.4127
8	−1.594 × 10⁵⁴	−10.3633	−3310.88	0.0591	2.1055	2.5287
9	−1.604 × 10⁵⁴	−10.2992	−3338.08	0.1561	2.2070	2.6311
10	−1.612 × 10⁵⁴	−10.2384	−3359.77	0.2433	2.2979	2.7226
11	−1.619 × 10⁵⁴	−10.1807	−3377.46	0.3226	2.3802	2.8055
12	−1.625 × 10⁵⁴	−10.1263	−3392.17	0.3952	2.4554	2.8811
13	−1.629 × 10⁵⁴	−10.0746	−3404.58	0.4623	2.5245	2.9506
14	−1.633 × 10⁵⁴	−10.0256	−3415.21	0.5245	2.5886	3.0149
15	−1.637 × 10⁵⁴	−9.9789	−3424.39	0.5826	2.6482	3.0749

Table 6. Comparison table of entropies for hex POH(n).

n					ENT_ABC	ENT_GA
6	−2.425 × 10¹¹³	−21.1812	−617561.93	−1.2328	1.7906	2.3284
7	−2.472 × 10¹¹³	−21.3481	−632989.74	−1.1176	1.9324	2.4732
8	−2.507 × 10¹¹³	−21.4624	−644447.57	−1.0161	2.0541	2.5972
9	−2.533 × 10¹¹³	−21.5419	−653292.98	−0.9252	2.1608	2.7056
10	−2.555 × 10¹¹³	−21.5978	−660327.95	−0.8430	2.2557	2.8019
11	−2.572 × 10¹¹³	−21.6368	−666056.66	−0.7679	2.3413	2.8886
12	−2.586 × 10¹¹³	−21.6636	−670812.03	−0.6988	2.4191	2.9675
13	−2.597 × 10¹¹³	−21.6814	−674822.68	−0.6348	2.4906	3.0397
14	−2.608 × 10¹¹³	−21.6922	−678250.84	−0.5752	2.5565	3.1064
15	−2.617 × 10¹¹³	−21.6978	−681214.82	−0.5194	2.6178	3.1683

Conflicts of Interest

The authors declare no conflict of interest.

Acknowledgments

This work was supported in part by the Natural Science Fund of Education Department of Anhui Province under Grant KJ2020A0478.

Open Research

Data Availability

No data were used to support this study.

References

1 Balaban A. T., Chemical graph theory and the Sherlock Holmes principle, International Journal for Philosophy of Chemistry. (2013) 19, 107–134.
CAS Google Scholar
2 Wiener H., Structural determination of paraffin boiling points, Journal of the American Chemical Society. (1947) 69, no. 1, 17–20, https://doi.org/10.1021/ja01193a005, 2-s2.0-8544254107, 20291038.
10.1021/ja01193a005
CAS PubMed Web of Science® Google Scholar
3 Randic M., Characterization of molecular branching, Journal of the American Chemical Society. (1975) 97, no. 23, 6609–6615, https://doi.org/10.1021/ja00856a001, 2-s2.0-8644280181.
10.1021/ja00856a001
CAS Web of Science® Google Scholar
4 Bollobás B. and Erdos P., Graphs of extremal weights, Ars Combinatoria. (1998) 50, 225–233.
Web of Science® Google Scholar
5 Amić D., Bešlo D., Lucić B., Nikolić S., and Trinajstić N., The vertex-connectivity index revisited, Journal of chemical information and computer sciences. (1998) 38, no. 5, 819–822, https://doi.org/10.1021/ci980039b, 2-s2.0-0000709092.
10.1021/ci980039b
CAS Web of Science® Google Scholar
6 Estrada E., Torres L., Rodriguez L., and Gutman I., An atom-bond connectivity index: modelling the enthalpy of formation of alkanes, Indian Journal of Chemistry. (1998) 37A, no. 10, 849–855.
CAS Google Scholar
7 Vukičević D. and Furtula B., Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges, Journal of mathematical chemistry. (2009) 46, no. 4, 1369–1376, https://doi.org/10.1007/s10910-009-9520-x, 2-s2.0-70350166990.
10.1007/s10910-009-9520-x
CAS Web of Science® Google Scholar
8 Ali G., Afzal M., Asif M., and Shazad A., Attribute reduction approaches under interval-valued q-rung orthopair fuzzy soft framework, Applied intelligence. (2021) 1–26, https://doi.org/10.1007/s10489-021-02853-x.
10.1007/s10489-021-02853-x
Web of Science® Google Scholar
9 Ali G. and Sarwar M., Novel technique for group decision-making under fuzzy parameterized-rung orthopair fuzzy soft expert framework, Mathematical Problems in Engineering. (2021) 2021, 22, 5449403, https://doi.org/10.1155/2021/5449403.
10.1155/2021/5449403
Web of Science® Google Scholar
10 Awais H. M., Javaid M., and Jamal M., Forgotten index of generalized F-sum graphs, Journal of Prime Research in Mathematics. (2019) 15, 115–128.
Google Scholar
11 Javaid M. and Cao J., Computing topological indices of probabilistic neural network, Neural Computing and Applications. (2018) 30, no. 12, 3869–3876, https://doi.org/10.1007/s00521-017-2972-1, 2-s2.0-85018807219.
10.1007/s00521-017-2972-1
Web of Science® Google Scholar
12 Kapur J. N., Maximum-Entropy Models in Science and Engineering, 1989, John Wiley & Sons.
Google Scholar
13 Shanmukha M. C., Basavarajappa N. S., Usha A., and Shilpa K. C., Novel neighbourhood redefined first and second Zagreb indices on carborundum structures, Journal of Applied Mathematics and Computing. (2021) 66, no. 1-2, 263–276, https://doi.org/10.1007/s12190-020-01435-3.
10.1007/s12190-020-01435-3
Web of Science® Google Scholar
14 Shanmukha M. C., Usha A., Basavarajappa N. S., and Shilpa K. C., Graph entropies of porous graphene using topological indices, Computational and Theoretical Chemistry. (2021) 1197, article 113142, https://doi.org/10.1016/j.comptc.2021.113142.
10.1016/j.comptc.2021.113142
Web of Science® Google Scholar
15 Wilson A. G., The use of the concept of entropy in system modelling, Journal of the Operational Research Society. (1970) 21, no. 2, 247–265, https://doi.org/10.1057/jors.1970.48.
10.1057/jors.1970.48
Google Scholar
16 Zuo X., Nadeem M. F., Siddiqui M. K., and Azeem M., Edge weight based entropy of different topologies of carbon nanotubes, IEEE Access. (2021) 9, 102019–102029, https://doi.org/10.1109/ACCESS.2021.3097905.
10.1109/ACCESS.2021.3097905
Web of Science® Google Scholar
17 Shannon C. E., A mathematical theory of communication, The Bell System Technical Journal. (1948) 27, no. 3, 379–423, https://doi.org/10.1002/j.1538-7305.1948.tb01338.x, 2-s2.0-84940644968.
10.1002/j.1538-7305.1948.tb01338.x
Web of Science® Google Scholar
18 Trucco E., A note on the information content of graphs, The Bulletin of Mathematical Biophysics. (1956) 18, no. 2, 129–135, https://doi.org/10.1007/BF02477836, 2-s2.0-51649221175.
10.1007/BF02477836
Google Scholar
19 Bonchev D., Information Theoretic Indices for Characterization of Chemical Structures, 1983, Research Studies Press, Chichester.
Google Scholar
20 Manuel P. D. and Rajasingh I., Minimum metric dimension of silicate networks, Ars Combinatoria. (2011) 98, 501–510.
Web of Science® Google Scholar
21 Raj F. S. and George A., Network embedding on planar octahedron networks, 2015 IEEE international conference on electrical, computer and communication technologies (ICECCT), 2015, March, Coimbatore, India, 1–6, https://doi.org/10.1109/ICECCT.2015.7226174, 2-s2.0-84954136258.
10.1109/ICECCT.2015.7226174
Google Scholar
22 Dustigeer G., Ali H., Khan M. I., and Chu Y. M., On multiplicative degree based topological indices for planar octahedron networks, Main Group Metal Chemistry. (2020) 43, no. 1, 219–228, https://doi.org/10.1515/mgmc-2020-0026.
10.1515/mgmc-2020-0026
CAS Web of Science® Google Scholar
23 Song P., Ali H., Binyamin M. A., Ali B., and Liu J. B., On computation of entropy of hex-derived network, Complexity. (2021) 2021, 18, 9993504, https://doi.org/10.1155/2021/9993504.
10.1155/2021/9993504
Web of Science® Google Scholar
24 Zhao X., Ali H., Ali B., Binyamin M. A., Liu J. B., and Raza A., Statistics and calculation of entropy of dominating David derived networks, Complexity. (2021) 2021, 15, 9952481, https://doi.org/10.1155/2021/9952481.
10.1155/2021/9952481
Web of Science® Google Scholar
25 Dehmer M. and Mowshowitz A., A history of graph entropy measures, Information Sciences. (2011) 181, no. 1, 57–78, https://doi.org/10.1016/j.ins.2010.08.041, 2-s2.0-77958091914.
10.1016/j.ins.2010.08.041
Web of Science® Google Scholar
26 Trinajstic N., Chemical Graph Theory, 1992, Routledge.
Google Scholar

Citing Literature

All articles

[Retracted] On Computation of Degree-Based Entropy of Planar Octahedron Networks

Retraction(s) for this article

Retracted: On Computation of Degree-Based Entropy of Planar Octahedron Networks

Abstract

1. Introduction

2. Main Results

2.1. Results on Planar Octahedron Network

2.1.1. Randić Entropy

2.1.2. ABC Entropy

2.1.3. GA Entropy

2.2. Results on Triangular Prism Network

2.2.1. Randić Entropy

2.2.2. ABC Entropy

2.2.3. GA Entropy

2.3. Results on Hex Planar Octahedron Network

2.3.1. Randić Entropy

2.3.2. ABC Entropy

2.3.3. GA Entropy

3. Discussion and Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

[Retracted] On Computation of Degree-Based Entropy of Planar Octahedron Networks

Retraction(s) for this article

Retracted: On Computation of Degree-Based Entropy of Planar Octahedron Networks

Abstract

1. Introduction

2. Main Results

2.1. Results on Planar Octahedron Network

2.1.1. Randić Entropy

2.1.2. ABC Entropy

2.1.3. GA Entropy

2.2. Results on Triangular Prism Network

2.2.1. Randić Entropy

2.2.2. ABC Entropy

2.2.3. GA Entropy

2.3. Results on Hex Planar Octahedron Network

2.3.1. Randić Entropy

2.3.2. ABC Entropy

2.3.3. GA Entropy

3. Discussion and Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information