Considering the problems of fuzzy repair and low pixel similarity matching in the repair of existing tomb murals, we propose a novel tomb mural repair algorithm based on sequential similarity detection in this paper. First, we determine the gradient value of tomb mural through second-order Gaussian Laplace operator in LOG edge detection and then reduce the noise in the edge of tomb mural to process a smooth edge of tomb mural. Further, we set the mathematical model to obtain the edge features of tomb murals. To calculate the average gray level of foreground and background under a specific threshold, we use the maximum interclass variance method, which considers the influence of small cracks on the edge of tomb murals and separates the cracks through a connected domain labelling algorithm and open and close operations to complete the edge threshold segmentation. In addition, we use the priority calculation function to determine the damaged tomb mural area, calculate the gradient factor of edge information, obtain the information entropy of different angles, determine the priority of tomb mural image repair, detect the similarity of tomb mural repair pixels with the help of sequential similarity, and complete the tomb mural repair. Experimental results show that our model can effectively repair the edges of the tomb murals and can achieve a high pixel similarity matching degree.

1. Introduction

Ancient murals, as one of China’s most important cultural assets, offer a wealth of historical, cultural, and aesthetic information. They serve as an important carrier for China’s 5000-year civilisation [1]. The uncovered murals contain several ailments, such as fractures, fading, armoring, and other maladies because of natural weathering and man-made damage. The employment of digital image restoration technologies to help in the conservation of historical murals can minimize the difficulties of protecting ancient murals and the degradation caused by human causes. Cultural relics protection involves both preventative and rescue measures. The rapid expansion of national economic development is accompanied by a significant number of urban facilities. Because valuable cultural artefacts are frequently found, China’s principal cultural conservation method is “rescue protection” [2]. To prevent further degradation of cultural treasures that do not satisfy the requirements for on-site conservation, excavation and relocation protection are required. Tomb murals are one of the most well-known examples. Due to the effects of tomb collapse, water erosion, and tomb robber damage, uncovering and relocating murals to other locations for preservation is a better protective method. The environment was generally stable before the mural was removed from the tomb, but after the painting was removed, the storage environment altered drastically compared to the curtain chamber, resulting in a series of pathological issues in the mural [3].

Deformity, displacement, deformation, fracture, crack, armor lifting, falling off, empty drum, caustic soda, mildew, and other issues occur in the preservation of the tomb paintings now housed at the Shaanxi History Museum. The number of tomb murals is vast, the demand for restoration is high, the work is complex, and the actual repair is tough, resulting in a long time between the excavation of most murals and meeting with most tourists [4]. As a result, how to improve the restoration impact of tomb murals has become a major study topic in this discipline, with a lot of work done and some promising results.

Based on the paintings of the Yuan Dynasty Tombs at Hansenzhai, Xi’an, Jiang et al. [5] suggested a digital restoration approach. They examined the damage and types of paintings in Yuan Dynasty tombs in Hansenzhai from the perspective of the degree of image information loss and the link between the loss of information and known information. They also proposed a mural digital repair technique that combines human and automated repair, as well as a mural digital automatic repair algorithm that is based on picture blocks and sparse representation models. Finally, a section of sanletu on the west wall of the Hansenzhai corridor is chosen as a digital restoration example. Different scale discriminators have varying receptive fields that guide the generator by creating a global image view with much finer details. The notion of WGAN (Wasserstein GAN) is utilized to mimic the sample data distribution using EM distance to solve gradient disappearance or gradient explosion in GAN training. The algorithm’s network model is trained and evaluated on the CelebA, ImageNet, and place image datasets. The findings demonstrate that, when compared to prior models, the algorithm increases image restoration accuracy, produces more realistic corrected images, and is appropriate for multiple image repair. However, in the process of tomb mural restoration, the algorithm does not evaluate the influence of the actual surroundings on the restored image, which has certain limits.

Tao et al. [6] proposed an image restoration algorithm based on edge features and pixel structure similarity. An adaptive repair template based on information entropy will then fill cracks and bad pixels in the Criminisi algorithm. Finally, the Drosophila optimization algorithm is introduced to reduce the image repair time. The experimental results show that the algorithm in this paper can achieve satisfactory repair effect and repair efficiency for different images, but the algorithm is slightly insufficient in processing pixels, which needs to be further strengthened. The experimental results show that the proposed algorithm can achieve satisfactory repair effect and repair efficiency for different images. However, the algorithm is slightly insufficient in processing pixels, which needs further improvements.

In this paper, we propose a tomb mural restoration algorithm based on sequential similarity detection to cope with the aforementioned problems. By determining the gradient value of the tomb mural through the second-order Gaussian Laplace operator in LOG edge detection, we reduce the noise in the edge of the tomb mural and enhance the smoothness of the edge of the tomb mural. Also, we set up the mathematical model of the features of tomb murals to obtain the edge features of tomb murals. The maximum interclass variance method calculates the average gray level of foreground and background under a specific threshold and considers the influence of small cracks on the edge of tomb murals. The cracks are separated by a connected domain labelling algorithm and open and close operations to complete the edge threshold segmentation of tomb murals. The priority calculation function is used to determine the damaged tomb mural area, calculate the gradient factor of edge information, obtain the information entropy of different angles, determine the priority of tomb mural image repair, detect the similarity of tomb mural repair pixels with the help of sequential similarity, and complete the tomb mural repair. Experimental results verify the effectiveness of our proposed method.

2. Research on Edge Feature Extraction and Prethreshold Segmentation of Tomb Murals

2.1. Extraction of Tomb Mural Edge Features

The primary structure of the painting is outlined by the edge of the tomb mural, and removing the edge helps to show the arrangement of the main picture. Because tomb murals are funeral objects, they have the advantages of a quick build time and a big format. Because most of them travel via the drafting line, the painting area is restricted. The primary picture has a clean shape with a lot of iron lines. Two-dimensional information processing technology’s edge retrieval approach can identify its contour boundary in advance, which is useful for rapidly comprehending the painting level arrangement. The edge of art can depict the entire objective item, allowing the spectator to quickly find the target. The edge protects detailed image data, which is crucial for determining the object’s primary characteristics. Edge retrieval locates the pheromone in the information cluster whose gray value gradient changes abruptly; the gray value varies smoothly along the edge direction and forcefully perpendicular to the edge direction, depending on the features.

In the information cluster, edge retrieval locates the pheromone with a sharp gray value gradient. The gray value varies softly along the edge direction, and the gray value of the pheromone perpendicular to the edge direction changes abruptly until the edge information is located, according to the features. Due to noise and other reasons, the first generated edge information is frequently overconnected or underconnected. There is a requirement for a secondary connection. Different linked domains yield different connection outcomes, and the binary edge information of a single pheromone width may eventually be retrieved. Edge pheromone connectivity consists of two steps: crucial labelling and connection. The pheromones in the linked neighborhood are given a distinct label by labelling [7]. The edge pheromone belongs to the same edge segment when its gray value and direction fulfil the necessary similarity requirements.

To repair the mural image, we can use the gradient operator of the edge pheromone as

\begin{matrix} \nabla I = [\begin{matrix} g_{x} \\ g_{y} \end{matrix}] = [\begin{matrix} \frac{\partial I}{\partial x} \\ \frac{\partial I}{\partial y} \end{matrix}], \\ \{\begin{cases} M (x, y) = \sqrt{g_{x}^{2} + g_{y}^{2}}, \\ N (x, y) = \tan^{- 1} [\begin{cases} g_{x} \\ g_{y} \end{cases}], \end{cases} \end{matrix}

(1)

where M represents the gray scale while N indicates the gray order jump direction. We utilize LOG edge detection to extract the tomb mural’s edge even more precisely. To begin, the second-order Gaussian Laplace operator is employed in LOG edge detection to decrease noise in the tomb mural’s edge and deal with the smoothness of the tomb mural’s edge [8], as follows:

\begin{matrix} G (x, y) = \frac{1}{2 π σ^{2}} \exp (- \frac{1}{2 π σ^{2}} (x^{2} + y^{2})), \end{matrix}

(2)

where parameter σ describes the smoothness of the edge of the tomb chamber. Further, we use the convolution G(x, y) with the tomb mural image I(x, y) to get the smoothness effect of the edge of the final tomb mural image as follows:

\begin{matrix} g (x, y) = I (x, y) \times G (x, y) . \end{matrix}

(3)

Similarly, we can obtain the Laplace calculations for g(x, y) as

\begin{matrix} h (x, y) = \nabla^{2} (I (x, y) \times G (x, y)) . \end{matrix}

(4)

The edge features of tomb murals are extracted by smoothing the edges of tomb murals. The mathematical model for setting the characteristics of tomb murals is as follows:

\begin{matrix} G_{θ} = \frac{\partial G}{\partial θ} = θ \nabla G, \end{matrix}

(5)

where G represents the normal vectors and θ represents the gradient vector.

Maximum features of tomb mural can be calculated as

\begin{matrix} γ (x, y) = \sqrt{E_{X}^{2} + E_{Y}^{2}}, \end{matrix}

(6)

where γ(x, y) represents the edge feature information of the tomb mural at the x and y points and E represents the corner information of the mural in the tomb.

We can minimize the noise in the edge of tomb paintings and achieve the smoothness of the edge of tomb murals by calculating the gradient value of tomb murals and utilizing the second-order Gaussian Laplace operator in LOG edge detection [9] in the edge feature extraction of tomb murals. It also creates a mathematical model of tomb mural features to obtain tomb mural edge features.

2.2. Edge Threshold Segmentation of Tomb Murals

According to the previously mentioned edge features of tomb murals, thresholding and segmenting the edges of tomb murals is required to increase the repair impact of tomb paintings. Because of the filthy muck on the tomb mural’s border, it is impossible to distinguish between the foreground and backdrop. The universal threshold segmentation technique cannot be implemented, despite the fact that histogram equalization improves the crack information. Under a specified threshold, the greatest interclass variance technique determines the average gray level of the foreground and background. When the variance is the greatest, the difference between the foreground and background is regarded to be the greatest.

\begin{matrix} g = w_{0} g_{0} + w_{1} g_{1}, \\ v = w_{0} (g_{0} - g) (g_{0} - g) + w_{1} (g_{1} - g) (g_{1} - g), \end{matrix}

(7)

where g is the total average grayscale of the image, w₀, w₁ represent the proportion of the foreground and background points to the image, respectively, g₀, g₁ represent the average grayscale of the foreground and the background, and v is the variance between the foreground and the background.

Because tomb paintings include stains and numerous small fractures on their edges, these cracks play a major role in tomb mural edge alteration. As a result, before threshold segmentation, it is still important to evaluate the impact of tiny fractures. The tomb mural’s crack information is in the form of numerous discontinuous parts, making it hard to separate from the pit [10]; therefore, it is closed to maintain crack continuity. The fractures are then separated using the linked domain labelling method and open and close procedures as

\begin{matrix} B (i, j) = 1, \\ B (i, j) = A (i, j) o r B (i, j), \end{matrix}

(8)

where A(i, j) is a pixel value and the updated value of B(i, j) is the result of tomb mural cracks.

The greatest interclass variance technique is used to compute the average gray level of foreground and background under a particular threshold in tomb mural edge threshold segmentation. To finish the edge threshold segmentation of tomb paintings, a linked domain labelling algorithm and open and close operations are used to separate the cracks, taking into account the effect of tiny fractures on the edge of the tomb murals [11].

2.3. Priority Calculation of Tomb Mural Image Restoration

After the above edge threshold segmentation of the tomb mural, the image restoration priority needs to reduce the damage to the disordered tomb mural during the restoration process. The tomb mural image is 1, Ω is the broken pixel area, p is a broken block (size 9 × 9), and n_p represents the normal vector of the central pixel p of the damaged block; its vertical direction is the smallest direction of gray value (equal illumination line direction). The priority calculation function is defined as

\begin{matrix} P (p) = C (p) \times D (p), \end{matrix}

(9)

where C(p) is the confidence item while D(p) is the data item.

\begin{matrix} C (p) = \frac{\sum_{q \in p} C (q)}{ϕ_{p}}, \\ D (p) = \frac{|\nabla I (1 / p) \times n_{p}|}{255}, \end{matrix}

(10)

where ∑_q∈pC(q)/φ_p represents the confidence item value of the q pixels in the damaged block φ_p.

Based on this, our model adds the gradient factor G_P reflecting the edge information and the information entropy. H_p measures the complexity of the block to be fixed and G_P represents the gradient information of the image. The final tomb mural image priority can be calculated as

\begin{matrix} G_{P} = \frac{\sum_{q \in p} M_{q}}{|ϕ_{p}|}, \end{matrix}

(11)

where M_q is the gradient modulus of the pixel q and H_p is the derivative of pixel point q in x, y directions.

The damaged area is determined by the priority calculation function in the tomb mural picture repair priority calculation. We may estimate the tomb mural picture restoration priority by calculating the information entropy of different angles using the gradient factor of the edge information.

3. Realizing the Restoration of Tomb Murals Based on Sequential Similarity Detection

The waveform matching continuation technique is a common approach for sequential similarity identification in endpoint effect suppression. The notion behind the method is that the signal’s changing trend is reflected not just at the endpoint but also inside the signal, particularly for signals with strong regularity. The unique surgery procedure is divided into two parts:

(1)
Finding a subwave segment in the signal that is most consistent with the endpoint’s shifting trend.
(2)
For continuation, the best-matched wavelet is translated to the endpoint [12].

Because of its strong endpoint effect suppression performance, the method has been frequently employed, particularly in the endpoint effect processing of signals with robust regularity. The key and core of the method is the search technique for the best matching wavelet. To tackle this problem, this study presents an EMD endpoint effect suppression technique based on adaptive sequential similarity detection. Sequential analysis is a mathematical statistician’s idea. The sequential sampling system and statistical inference with this scheme are its primary study directions.

The main idea is that in the sampling process, the required number of samples is not determined in advance, but rather a small portion is selected first, and whether or not to continue sampling work is determined based on the results of this small part of samples to effectively reduce the number of samples. Because of its benefits of inexpensive processing and high precision, the sequential similarity detection method [13] is frequently employed in picture matching and other domains. The choice of threshold and the technique for adjusting it are the two most important variables determining its success. As a result, the tomb murals are repaired using the sequential similarity detection approach.

First, when the mural is completed, the original pixel is X. The original pixel point picked must have a maximum point and a low point to better depict the shifting trend of the original pixel restoration at the mural conclusion. To sample the original mural pixel point and produce K sampling points, the longitudinal coordinates are stored as M and m:

\begin{matrix} dir (p, q) = \frac{p - q}{p - q} \times N (p), \end{matrix}

(12)

where Y represent the original pixel points of the original tomb mural and form several matching points with the original pixel points of the original tomb mural defined as

\begin{matrix} ζ = \frac{(- u_{y}, u_{x})}{\sqrt{u_{x}^{2} + u_{y}^{2}}} . \end{matrix}

(13)

Similarly, the threshold φ_q of the initial tomb mural image can be calculated as

\begin{matrix} φ_{q} = \arg \min d (φ_{p}, φ_{q}) . \end{matrix}

(14)

The difference between the original point and the counterpart to match is calculated from the first burial chamber mural image pixel point (x_i − y_i)and M − m as

\begin{matrix} {(\frac{(x_{i} - y_{i})}{M - m})}^{2}, i = 1,2, \dots, K . \end{matrix}

(15)

According to the determined pixel matching error of the tomb chamber mural image, the sequential similarity detection algorithm successively selects the pixels on the image to be matched as

\begin{matrix} I (i, j) = \{χ | \min [τ (i, j, m_{k}, n_{k})] > T_{k}\}, \\ K [P (S)] = U (X) \frac{C_{4} (s)}{{[I (i, j)]}^{2}}, \end{matrix}

(16)

where K[P(S)] represents the real value tomb chamber mural image with mean zero, U(X) represents the probability density function, and (C₄(s)/[I(i, j)]²) represents the average zero value of the restored tomb room murals [14].

4. Experimental Results

4.1. Experimental Settings

In order to verify the effectiveness of this repair algorithm, an experimental analysis is carried out. In the experiment, some murals in the polo paintings of Prince Zhang Huai and Li Xianmu were used as research objects. In the experiment, the sample images of the tomb murals were 2 m high and 5 m long. The total number of images of the tomb murals collected by HD equipment was about 10 g, which were cut into several small images. The data volume of each image was more than 1G. One of the obtained sample images was taken as a typical research object to verify the effectiveness of the repair algorithm. The experimental sample image is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Image of the sample tomb room murals.

4.2. Experimental Index Design

To verify the effectiveness of our repair algorithm, we perform experiments with various settings. We undertake tests with various parameters for the validation of the effectiveness of our proposed method. Some of the paintings in the polo paintings of Prince Zhang Huai and Li Xianmu were used as test learning projects. The tomb paintings were 2 m high and 5 m long in the example images. The entire number of photos of the tomb paintings gathered by high-definition equipment was around 10 g, which were then split into many smaller images. Each image has a data capacity of almost 1 GB. One of the generated example photos was used as a specific study object, demonstrating the efficacy of the repair method. Figure 1 depicts an experimental sample picture [15].

Precision, recall, and F1 score are three metrics used to assess the accuracy of the classifier’s predictions. These metrics are defined as follows:

\begin{matrix} precision = \frac{# of true positives}{# of true positives + # of  false positives}, \\ recall = \frac{# of true positives}{# of true positives + # of  false negatives}, \\ F_{1} score = \frac{2}{(1 / recall) + (1 / precision)} . \end{matrix}

(17)

4.3. Analysis of Experimental Results

In order to verify the effectiveness of the proposed algorithm, it is compared with the multiscale generation adversarial network image restoration algorithm and the image restoration algorithm based on edge features, and the pixel structure similarity is used to restore the sample tomb mural image. The presentation effect after the repair is shown in Figure 2.

The performance gap between the results obtained from our proposed restoration of the sample tomb mural images method, the multiscale generation countermeasure network image restoration algorithm, and the image restoration algorithm based on edge features can be seen by examining the repair results in Figure 2. The background of the mural picture of the example tomb has some tiny cracks, and the artwork’s colour has deteriorated significantly. The image’s backdrop effect is smoothed out, and the edge and colour of the tomb mural image may be correctly fixed using this approach. The image restoration algorithms based on edge features and pixel structure similarity, as well as the multiscale generative countermeasure network image restoration method, can eliminate the noise in the tomb mural’s wall. The tomb mural pictures restored by the two restoration algorithms, on the other hand, are absent, as are the human cheeks in Figure 2(c).

This method, as well as the multiscale generative countermeasure network image restoration algorithm and the image restoration algorithm based on edge features and pixel structure similarity, is used to match the pixel similarity in the sample tomb mural image in order to further verify the effectiveness of this restoration algorithm. The representative method’s effect improves as the matching degree increases. Figure 3 depicts the outcomes of the experiment.

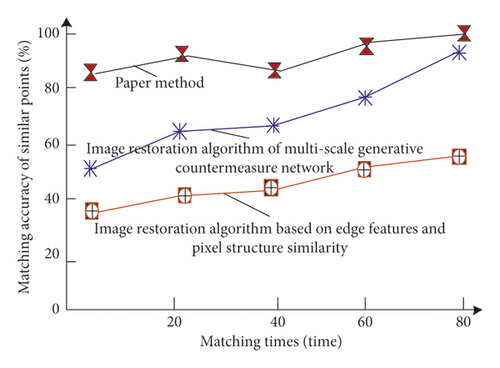
The experimental results in Figure 3 show that there are some differences in the accuracy of matching the pixel similarity in the sample tomb mural image when using the method proposed in this paper, the multiscale generation countermeasure network image restoration algorithm, and the image restoration algorithm based on edge features and pixel structure similarity. The accuracy of matching pixel similarity in the sample tomb mural image by this method is always greater than 80%, with the highest being around 95%, and through multiscale generation to confront the network image restoration algorithm and the image restoration algorithm based on edge features and pixel structure to match the accuracy of the pixel similarity in the sample tomb murals. However, it is always lower than that of the proposed method.

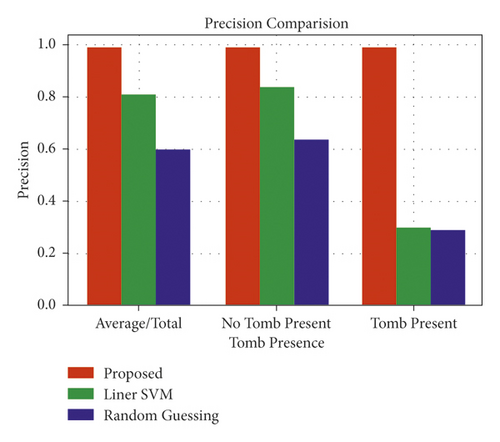
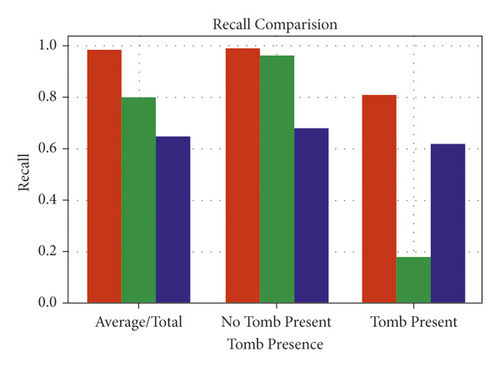
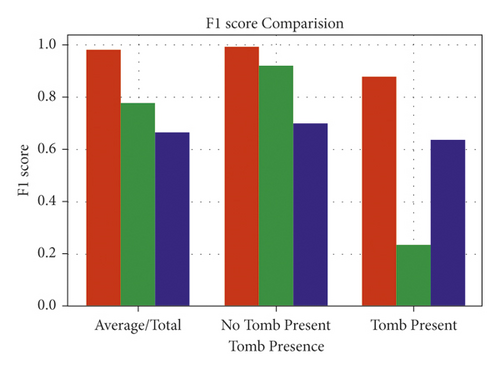
The outcomes of the trained models making predictions on the validation set are summarized in Tables 1 and 2. We can see that the proposed technique works well for both tomb-containing and non-tomb-containing pictures. Interestingly, despite using an enhanced dataset to train SVMs, their performance in recognizing images containing tombs was not comparable to that of the suggested approach. This is unexpected because the tomb forms are mostly basic to the human sight, thus nonlinear classification should function fine. The reason for this is because SVM models are likely to contain a large number of false positives (objects that are not tombs being identified as such). This is because other pictures that are just circular in form are likely to be mistaken for tombs by the SVM models. The number of filters employed in our architecture allows us to notice higher subtlety in the patterns of the training dataset, allowing us to identify a tomb beyond simply the circular form. Figure 4 summarizes both tables and adds an average/total bar with a weighted average for each group. Overall, the findings demonstrate that the proposed model outperforms the competition. Finally, the comparison for recall and F1 score is made in Figures 5 and 6, respectively.

Table 1. Different classification metrics to validate the dataset images without tombs.

Model	Precision	Recall	F₁ score
Random guessing	0.64	0.65	0.65
SVM with linear kernel	0.88	0.91	0.90
SVM with RBF kernel	0.92	0.93	0.91
Proposed	0.98	1	0.99

Table 2. Different classification metrics to validate the dataset images with tombs.

Model	Precision	Recall	F₁ score
Random guessing	0.56	0.55	0.56
SVM with linear kernel	0.25	0.134	0.179
SVM with RBF kernel	0.73	0.64	0.68
Proposed	1	0.84	0.91

5. Conclusion

We present a tomb mural restoration technique based on sequential similarity detection in this study. By using the second-order Gaussian Laplace operator in LOG edge detection to determine the gradient value of the tomb mural, we can minimize noise in the tomb mural’s edge and improve the smoothness of the tomb mural’s edge. Then, to get the edge features of tomb paintings, we created a mathematical model of the features of tomb murals. Under a specified threshold, the greatest interclass variance technique determines the average gray level of foreground and background. The fractures are separated using a linked domain labelling method and open and close operations to complete the edge threshold segmentation of tomb paintings, taking into account the effect of tiny cracks on the edge of tomb murals. To identify the damaged tomb mural area, compute the gradient factor of edge information, acquire the entropy of different angles, and determine the tomb wall painting, the priority calculation function is employed. The proposed approach can restore the tomb mural and increase its efficacy, according to the testing results.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 She W., Digital object restoration using generalized regression neural network deep learning—taking Dunhuang mural restoration as an example, International Journal of Electrical Engineering Education. (2020) 15, no. 2, 2072–2080, https://doi.org/10.1177/0020720920928549.
10.1177/0020720920928549
Google Scholar
2 Tirer T. and Giryes R., Image restoration by iterative denoising and backward projections, IEEE Transactions on Image Processing. (2019) 45, no. 2, 154–152.
Google Scholar
3 Premnath S. P. and Renjit J. A., Image restoration model using Jaya〣at optimization〆nabled noise prediction map, IET Image Processing. (2021) 14, no. 12, 15–21.
Google Scholar
4 Yuan G., Lu J., and Wang Z., The PRP conjugate gradient algorithm with a modified WWP line search and its application in the image restoration problems, Applied Numerical Mathematics. (2020) 152, no. 7, 1–11, https://doi.org/10.1016/j.apnum.2020.01.019.
10.1016/j.apnum.2020.01.019
Web of Science® Google Scholar
5 Jiang C., Tong L. E. I., Lin Y. U., Wang Y.-Y., and Tian-xiang W. U., The digital restoration method for the murals in the yuan dynasty tomb of hansenzhai, Xi’ an, Science Technology and Engineering. (2020) 20, no. 31, 12922–12926.
Google Scholar
6 Tao Z., Zhang J., Wang L., Zhan W., and Wang L., Image inpainting algorithm based on edge feature and pixel structure similarity, Journal of Computer-Aided Design & Computer Graphics. (2019) 31, no. 10, 1768–1776.
Google Scholar
7 Song Q., Xiong R., Fan X., Liu D., Wu F., Huang T., and Gao W., Compressed image restoration via artifacts-free PCA basis learning and adaptive sparse modeling, IEEE Transactions on Image Processing. (2020) 29, no. 99.
10.1109/TIP.2020.3002452
PubMed Web of Science® Google Scholar
8 Meng H., Yan Y., and Cai C., A hybrid algorithm for underwater image restoration based on color correction and image sharpening, Multimedia Systems. (2020) no. 4, 1–11.
Web of Science® Google Scholar
9 Peng Y., Shi H., Wu H., Li R., Kwok N., Liu S. C., Liu S., and Rahnam A., An Optimum Shift-and-Weighted brightness mapping for low-illumination image restoration, The Imaging Science Journal. (2019) 67, no. 3-4, 187–201, https://doi.org/10.1080/13682199.2019.1592891, 2-s2.0-85063150924.
10.1080/13682199.2019.1592891
Web of Science® Google Scholar
10 Koho S., Tortarolo G., Castello M., Deguchi T., Diaspro A., and Vicidomini G., Fourier ring correlation simplifies image restoration in fluorescence microscopy, Nature Communications. (2019) 10, no. 1, 3103, https://doi.org/10.1038/s41467-019-11024-z, 2-s2.0-85069542038.
10.1038/s41467-019-11024-z
PubMed Web of Science® Google Scholar
11 Liu S., Chen J., Ai Y., and Rahardja S., An optimized quantization constraints set for image restoration and its GPU implementation, IEEE Transactions on Image Processing. (2020) 29, no. 99, https://doi.org/10.1109/TIP.2020.2988131.
10.1109/TIP.2020.2988131
Web of Science® Google Scholar
12 Wang G., Sun C., and Sowmya A., Attentive feature refinement network for single rainy image restoration, IEEE Transactions on Image Processing. (2021) 30, no. 1, 3734–3747, https://doi.org/10.1109/tip.2021.3064229.
10.1109/TIP.2021.3064229
PubMed Web of Science® Google Scholar
13 Yuchi S., Simulation of color transfer algorithms between images based on reverse mapping, Computer Simulation. (2021) 38, no. 1, 212–216.
Google Scholar
14 Li K., Zhang W., Mingwen S. H. A. O., and Le L. I., Multi-scale generative adversarial networks image inpainting algorithm, Journal of Frontiers of Computer Science & Technology. (2020) 14, no. 1, 159–170.
Google Scholar
15 Gao Y. and Wu C., On a general smoothly truncated regularization for variational piecewise constant image restoration: construction and convergent algorithms, Inverse Problems. (2020) 36, no. 4, 045007, https://doi.org/10.1088/1361-6420/ab6619.
10.1088/1361-6420/ab6619
Web of Science® Google Scholar

Citing Literature

All articles