This paper deals with numerical treatment of singularly perturbed parabolic differential equations having large time delay. The highest order derivative term in the equation is multiplied by a perturbation parameter ε, taking arbitrary value in the interval (0, 1]. For small values of ε, solution of the problem exhibits an exponential boundary layer on the right side of the spatial domain. The properties and bounds of the solution and its derivatives are discussed. The considered singularly perturbed time delay problem is solved using the Crank-Nicolson method in temporal discretization and exponentially fitted operator finite difference method in spatial discretization. The stability of the scheme is investigated and analysed using comparison principle and solution bound. The uniform convergence of the scheme is discussed and proven. The formulated scheme converges uniformly with linear order of convergence. The theoretical analysis of the scheme is validated by considering numerical test examples for different values of ε.

1. Introduction

A large number of mathematical models appear in different areas of science and engineering such as in control theory, epidemiology, and laser optics that take into account not only the present state of a physical system but also its past history [1]. These models are described by certain classes of functional differential equations often called delay differential equations. Examples of delays include the time taken for a signal to travel to the controlled object, driver reaction time, the time for the body to produce red blood cells, and cell division time in the dynamics of viral exhaustion or persistence. In the life sciences, delays are often introduced to account for hidden variables and processes which, although not well understood, are known to cause a time lag [1]. Time delays are natural components of the dynamic processes of biology, ecology, physiology, economics, epidemiology, and mechanics [2], and to ignore them is to ignore reality [1].

Singularly perturbed delay differential equations are differential equations in which its highest order derivative term is multiplied by small perturbation parameter ε and having at least one delay term. A simplified mathematical model for the control system of a furnace used to process metal sheets is represented by singularly perturbed parabolic delay differential equation of the form [3]

(1)

where u is the temperature distribution in a metal sheet, moving at an instantaneous material strip velocity v and heated by distributed temperature source specified by the function f; both v and f are dynamically adapted by a controlling device monitoring the current temperature distribution. The finite speed of the controller, however, introduces a fixed delay of length τ. When τ = 0, this problem becomes a thermal problem without time delay.

The presence of the singular perturbation parameter ε on the highest order derivative term leads to occurrences of oscillations in the computed solution while using central FDM, Galerkin FEM, and collocation methods on a uniform mesh [4]. While using these methods to avoid the oscillations, an unacceptably large number of mesh points are required when ε is very small. This is not practical due to the limited size of computer memory and rounding off error. Therefore, to overcome this drawback associated with classical numerical methods, authors use the fitted mesh technique which have a fine mesh in the boundary layer region or fitted operator technique. Recently, numerical treatment of singularly perturbed parabolic PDEs has gotten great attention, and different authors in [5–8] have developed uniformly convergent numerical schemes (scheme that converges independent of the influence of the singular perturbation parameter). Currently, authors in [9–13] have developed numerical schemes for solving singularly perturbed parabolic time delay reaction-diffusion equations. In papers [14, 15], the authors considered a singularly perturbed parabolic convection diffusion equation with time delay and degenerate coefficient. They treat the problems using fitted mesh techniques. Different authors in [16–23] developed numerical schemes using fitted mesh techniques for treating singularly perturbed parabolic time delay convection-diffusion equations. In [24], Podila and Kumar used nonstandard FDM for treating singularly perturbed parabolic time delay convection-diffusion equations. Their scheme gives linear order of convergence.

The main motive of this paper is to formulate an accurate and uniformly convergent numerical scheme for the singularly perturbed parabolic time delay convection-diffusion-reaction equation using exponentially fitted operator FDM and to establish the stability and uniform convergence of the scheme. The proposed scheme uses the procedure of Roth (i.e., first discretizing in temporal direction followed by discretization in spatial direction) using the Crank-Nicolson method in temporal direction and exponentially fitted operator FDM on spatial direction. In this method, it is not required to have any restriction on the mesh generation.

Notation 1. Throughout this paper, N and M are denoted for the number of mesh intervals in space and time direction discretization, respectively; C is denoted for positive constant independent of ε, N, and M. The norm ‖.‖ denotes the maximum norm defined as .

2. Continuous Problem

Consider a class of second order singularly perturbed parabolic convection-diffusion-reaction equations having a term with large time delay, on the domain D = Ω_x × Ω_t = (0, 1) × (0, T] and on smooth boundary ∂D = D_l ∪ D_b ∪ D_r is given by

(2)

with the boundary conditions

(3)

and the interval condition

(4)

where ε ∈ (0, 1] is a singular perturbation parameter and τ > 0 is the delay parameter. The terminal time T is assumed to satisfy the condition T = kτ for some positive integer k. The functions a(x), b(x, t), c(x, t), and f(x, t) and ϕ_l(t), ϕ_b(x, t), and ϕ_r(t) are assumed to be sufficiently smooth and bounded and satisfy

(5)

This condition ensures that the solution of the problem in (2)–(4) exhibits a boundary layer of thickness O(ε) on the right side of the spatial domain.

Our objective in this paper is to formulate an accurate and parameter uniformly convergent numerical scheme and to discuss the uniform stability and the parameter uniform convergence of the scheme for the considered problem in (2)–(4).

2.1. Bounds on the Solution and Its Derivatives

The existence and uniqueness of the solution of (2)–(4) can be established by assuming that the data is Holder continuous and imposing appropriate compatibility conditions at the corner points, using the assumptions of sufficiently smoothness ofϕ_l(t), ϕ_b(x, t), andϕ_r(t).

The required compatibility condition at the corner points and the delay term are

(6)

(7)

so that the data matches at the corner points. For a(x), b(x, t), c(x, t), and f(x, t) to be continuous on domain D, then (2)–(4) has the unique solution

. In particular, when the compatibility conditions are not satisfied, a unique classical solution still exists but is not differentiable on all of ∂D.

The reduced problem corresponding to the singularly perturbed parabolic delay PDE (2)–(4) is given as

(8)

with the boundary conditions

(9)

and the interval condition

(10)

It is in the form of hyperbolic delay PDEs. The solution u(x, t) of (2)–(4) becomes very close to the solution u⁰(x, t) of (8)–(10) as ε⟶0.

Lemma 2. The solution u(x, t) of (2)–(4) satisfies the estimate

(11)

where C is a constant independent of ε.

Proof. The result follows from the compatibility condition. See the detailed proof in [16].

Let L be a differential operator that denotes the differential equation in (2)–(4) as L = ∂/∂t − ε(∂²/∂x²) + a(x)(∂/∂x) + b(x, t).

Lemma 3. Suppose the function , which satisfies z(x, t) ≥ 0, (x, t) ∈ ∂D, and Lz(x, t) ≥ 0, (x, t) ∈ D implies that .

Proof. Assume there exists , such that

(12)

It is clear that the point (x^∗, t^∗) ∉ ∂D, which implies that (x^∗, t^∗) ∈ D. Since from extreme values in calculus which implies (∂/∂x)z(x^∗, t^∗) = 0, (∂/∂t)z(x^∗, t^∗) = 0, and (∂²/∂x²)z(x^∗, t^∗) ≥ 0 giving that Lz(x^∗, t^∗) < 0, which is contradiction to the assumption that made Lz(x^∗, t^∗) ≥ 0, ∀(x, t) ∈ D. Therefore, .

Lemma 4. Let u(x, t) be the solution of the continuous problem in (2)–(4). Then, we obtain the bound

(13)

where ζ is the lower bound of b(x, t).

Proof. By defining the barrier functions ϑ^±(x, t) as ϑ^±(x, t) = ζ⁻¹‖f‖ + max{|ϕ_l(t)|, |ϕ_b(x, t)|, |ϕ_r(t)|} ± u(x, t) and applying the maximum principle, we obtain the required bound.

Lemma 5. The bound on the derivative of the solution u(x, t) of the problem in (2)–(4) with respect to x and t is given by

(14)

where α is lower bound of a(x).

Proof. See on [5, 16].

3. Numerical Scheme

In general, for singularly perturbed problems, there are two strategies for designing numerical methods which have a small error in the boundary layer region [25]. The first approach is the class of fitted mesh methods which uses fine mesh in the boundary layer region and coarse mesh in outer layer region. The stability and convergence analyses of this approach are well developed. The second approach is the fitted operator methods in which it uses uniform mesh and an exponentially fitting factor for stabilizing the term containing the singular perturbation parameter. In this approach, the difference schemes reflect the qualitative behaviour of the solution inside the boundary layer region. In this article, we formulate an exponentially fitted operator finite difference scheme to solve the problem in (2)–(4).

3.1. Temporal Semidiscretization

The time domain [0, T] is discretized using a uniform mesh with time step Δt as and where M is the number of mesh points in time direction in the interval [0, T] and m is the number of mesh points in [−τ, 0]. Note that T = kτ for some positive integer k.

For approximating the temporal derivative term of (2)–(4), we use the averaged Crank-Nicolson method, which gives a system of boundary value problems

(15)

with the discretized boundary conditions

(16)

where

(17)

Here, U_j+1(x) is denoted for the approximation of u(x, t_j+1) at the (j + 1)th time level andb(x, t_j+1/2) = (1/2)[b(x, t_j) + b(x, t_j+1)], similarly for c(x, t_j+1/2) and f(x, t_j+1/2).

The semidiscrete difference operator (1 + (Δt/2)L^Δt)U_j+1(x) in (15)–(16) satisfies the maximum principle as follows.

Lemma 6. Semidiscrete maximum principle. Let Z_j+1(x) be a sufficiently smooth function on . If Z_j+1(0) ≥ 0, Z_j+1(1) ≥ 0 and (1 + (Δt/2)L^Δt)Z_j+1(x) ≥ 0, ∀x ∈ Ω_x, then .

Proof. Assume that there exist such that . From the above assumption, it is clear that x^∗ ∉ {0, 1} implies that x^∗ ∈ (0, 1). Since , using the property in calculus, we have (d/dx)Z_j+1(x^∗) = 0 and (d²/dx²)Z_j+1(x^∗) ≥ 0, then we obtain (1 + (Δt/2)L^Δt)Z_j+1(x^∗) < 0 which is in contradiction to (1 + (Δt/2)L^Δt)Z_j+1(x^∗) ≥ 0, ∀x ∈ Ω_x. Therefore, we conclude .

Next, let us analyse the truncation error for the temporal discretization made above.

Let the local error at each time step be denoted by e_j+1(x)≔u(x, t_j+1) − U_j+1(x), j = 0, 1, 2, ⋯, M.

Lemma 7. Suppose that

(18)

The local truncation error in the temporal direction is given by

(19)

Proof. Using Taylor’s series approximation for u(x, t_j) and u(x, t_j+1) centering at t_j+1/2, we obtain

(20)

From the approximation in (20), we obtain

(21)

Using the approximation into (2), we obtain

(22)

where

(23)

Since the error e_j+1(x)≕u(x, t_j+1) − U_j+1(x) satisfies the semidiscrete differential operator

(24)

Hence, by applying the maximum principle, we obtain

(25)

Next, we need to show the bound for the global error of the temporal discretization. Let us denote TE_j+1 as the global error up to the (j + 1)th time step.

Lemma 8. The global error at t_j+1 is given by

(26)

Proof. Using the local error up to the (j + 1)th time step given in the above lemma, we obtain the global error at the (j + 1)th time step as

(27)

where C is a constant independent of ε and Δt. See the detailed proof in [26].

Next, we set a bound for the derivatives of solution of (15)–(16).

Lemma 9. For each j = 0, 1, ⋯, M − 1, the solution U_j+1(x) of the boundary value problems in (15)–(16) satisfies the bound

(28)

Proof. See the proof in [5].

3.2. Spatial Discretization

The spatial domain [0, 1] is discretized into N equal number of subintervals, each of length h. Let 0 = x₀, x_N = 1, and x_i = ih, i = 0, 1, 2, ⋯, N, be the mesh points. For spatial discretization, we apply an exponentially fitted operator finite difference method which helps us to hinder the influence of the singular perturbation parameter.

First, let us find the exponential fitting factor for anonymous BVPs and then apply discretization in the spatial direction.

3.2.1. Computing the Exponential Fitting Factor

To develop the numerical method for (15)–(16), we use the technique designed in the theory of asymptotic method for solving singularly perturbed BVPs. In the considered case, the boundary layer occurs on the right side of the domain. From the theory of singular perturbation in [27], the zero order asymptotic solution of the singularly perturbed boundary value problems of the form

(29)

is given by

(30)

Using Taylor’s series expansion for a(x) and b(x) about x = 1 and restriction to their first terms and simplifying gives

(31)

where u₀ is the solution of the reduced problems (obtained by setting ε = 0) in (29). Considering h is reasonably small and evaluating the result in (31) at x_i gives

(32)

Similarly, we have

(33)

where ρ = h/ε.

Consider a uniform grid

and denote h = x_i+1 − x_i. For any mesh function v_i, define the following difference operators:

(34)

To handle the effect of the perturbation parameter, we multiply artificial viscosity (exponentially fitting factor σ(ρ)) on the diffusive part of the problem. Introducing an exponentially fitting factor σ(ρ) in (29) and applying the central finite difference scheme gives

(35)

Multiplying (35) by h and considering h is small and truncating the term h(f(x_i) − b(x_i)u(x_i)) gives

(36)

From (32), we have

(37)

Substituting (37) and (33) into (36) and simplifying, the exponential fitting factor is obtained as

(38)

3.2.2. The Discrete Scheme

Using the central finite difference method for the spatial discretization of (15)–(16) and applying the exponential fitting factor in (38), for i = 1, 2, ⋯, N − 1, the fully discrete scheme becomes

(39)

where

(40)

In explicit form, the scheme is rewritten as

(41)

where

(42)

(43)

3.3. Stability and Uniform Convergence Analysis

First, we need to prove the discrete comparison principle for the discrete scheme in (39).

Lemma 10. Discrete comparison principle. There exist a comparison function Z_i,j+1 such that (1 + (Δt/2)L^Δt,h)U_i,j+1 ≤ (1 + (Δt/2)L^Δt,h)Z_i,j+1, i = 1, 2, ⋯, N − 1 and if U_0,j+1 ≤ Z_0,j+1 and U_N,j+1 ≤ Z_N,j+1, then U_i,j+1 ≤ Z_i,j+1, i = 0, 1, 2, ⋯, N.

Proof. The matrix associated with operator (1 + (Δt/2)L^Δt,h)U_i,j+1 is of size (N + 1) × (N + 1) with its entries for i = 1, 2, ⋯, N − 1 are

(44)

So, the coefficient matrix satisfies the property of M matrix. So, the inverse matrix exists and it is nonnegative. This guarantees the existence and uniqueness of the discrete solution. See the detailed proof in [28].

Lemma 11. Let Z_i,j+1 = 1 + x_i, for, 0 ≤ i ≤ N. Then, there exist a positive constant C such that (1 + (Δt/2)L^Δt,h)Z_i,j+1 ≥ C, for 1 ≤ i ≤ N − 1.

Proof. The proof is a simple computation, enables one to give a bound, that is uniform in ε for the norm of the inverse of (1 + (Δt/2)L^Δt,h).

(45)

Lemma 12. (uniform stability estimate). The solution U_i,j+1 of the discrete scheme in (39) satisfies the bound

(46)

where b(x_i, t_j+1/2) ≥ ζ > 0.

Proof. Let us construct a barrier function as . We can easily show that. Then,

(47)

Using the discrete comparison principle, we obtain

Lemma 13. If Z_i,j+1 be any mesh function such that Z_0,j+1 = Z_N,j+1 = 0.Then,

(48)

Proof. Consider two barrier functions of the form where P = (1/ζ)max_{1≤k≤N−1}|L^Δt,hZ_k,j+1|. It is easily shown that . Next, we show that .

(49)

Hence, using the discrete comparison principle gives

(50)

Next, we consider the semidiscrete problem in (15)–(16) and the fully discrete scheme in (39) to find the truncation error of the spatial direction discretization.

Theorem 14. Let the coefficient functions a(x) and b(x, t_j+1/2) in (15)–(16) be sufficiently smooth functions so that U_j+1(x) ∈ C⁴[0, 1]. Then, the computed solution U_i,j+1 of the problem in (39) satisfies the bound

(51)

where η ∈ (x₀, x_N) such that

Proof. The local truncation error in space discretization is given as

(52)

where σ(ρ) = a(x_i)(ρ/2)coth(a(1)(ρ/2)) and ρ = h/ε.

Now for ρ > 0, C₁ and C₂ are constants and we have |ρcoth(ρ) − 1| ≤ C₁ρ², for ρ ≤ 1. For ρ⟶∞, since

gives |ρcoth(ρ) − 1| ≤ C₁ρ. In general, for all ρ > 0, we write

(53)

giving that

(54)

Using Taylor series expansion, we obtain the bound for

(55)

where

Using the bounds for the differences of the derivatives in (54) and (55), we obtain

Using the bounds for the derivatives of the solution in Lemma 9 gives

|L^Δt,h(U_j+1(x_i) − U_i,j+1)| ≤ (Ch²/h + ε)(1 + ε⁻²exp(−α(1 − η)/ε)) + Ch²[(ε + ε⁻³exp(−α(1 − η)/ε)) + (1 + ε⁻³exp(−α(1 − η)/ε))]. Since ε⁻³ ≥ ε⁻², we obtain

(56)

which gives the required bound.

Lemma 15. For a fixed number of mesh numbers N, and for ε⟶0, it holds

(57)

where x_i = ih, ∀i = 1, 2, ⋯, N − 1..

Proof. On the discrete domain , for the interior grid points, we have

(58)

Since x₁ = h, 1 − x_N−1 = h. Repeatedly using L’Hospital’s rule gives

(59)

This completes the proof.

Theorem 16. The numerical solution U_i,j+1 of the problem in (39) satisfies the following uniform error bound

(60)

Proof. Using Lemma 15 into (56) gives

(61)

Hence, using the result in Lemma 13, we obtain

(62)

Using the supremum over all ε ∈ (0, 1], we obtain

(63)

Remark 17. For the case ε > h, the developed scheme gives second order convergence. For small values of ε ≪ h, the scheme is first order uniformly convergent in spatial direction.

Theorem 18. Let u and U be the solution of (2)–(4) and (39), respectively. Then, the following uniform error bound holds:

(64)

Proof. The combination of temporal and spatial error bounds gives the required result.

4. Numerical Examples, Results, and Discussions

Here, we illustrate the proposed scheme using model examples. The exact solutions of the considered examples are not known. We investigate the theoretical results by performing experiments using the proposed scheme.

Example 19. Consider singularly perturbed time delay parabolic PDEs:

(65)

with interval condition u(x, t) = 0, on (x, t) ∈ [0, 1] × [−1, 0] and the boundary conditions

(66)

Example 20. Consider singularly perturbed time delay parabolic PDEs:

(67)

with interval condition u(x, t) = 0, on (x, t) ∈ [0, 1] × [−1, 0] and the boundary conditions

(68)

Since the exact solutions of the considered examples are not known, with the help of double mesh techniques, we compute the maximum absolute error

of the scheme. Let

be the computed solution of the problem using N, M mesh points and let

be the computed solution on double number of mesh points 2N, 2M by including the midpoints x_i+1/2 = (x_i+1 + x_i)/2 and t_j+1/2 = (t_j+1 + t_j)/2 into the mesh points. We calculate the maximum absolute error as

(69)

and the ε-uniform (parameter uniform) error estimate by using

(70)

We calculate the rate of convergence of the proposed scheme using

(71)

and the ε-uniform rate of convergence using

(72)

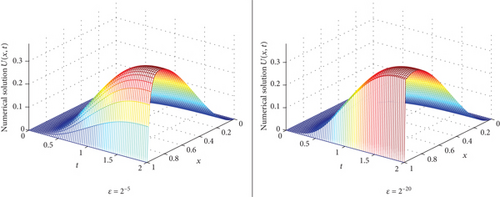
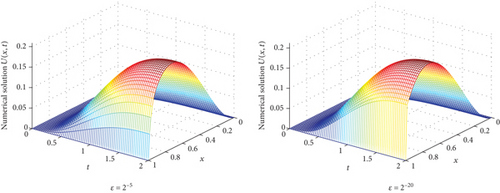
In Figures 1 and 2, the numerical solution of Examples 19 and 20 is given, respectively, for different values of perturbation parameterε. As we observe on these figures, a strong boundary layer is maintained on the right side of the spatial domain as ε goes small starting from ε = 2⁻⁵ to 2⁻²⁰. In these figures, we observe that the proposed scheme approximates the solution without creating oscillations or divergence. Note that time delay does not have an effect on position and size of the boundary layer since the layer occurs on the spatial domain direction. If the delay was on the spatial variable, we may have an interior layer which is created because of the delay parameter. In Tables 1 and 2, the maximum absolute error of Examples 19 and 20 is given, respectively, for different values of perturbation parameter ε and mesh numbers N, M. As we observed the results in these tables for each number of mesh N, M as ε becomes small, the maximum absolute error after showing growth becomes stable and identical. This indicates the stability and uniform convergence of the scheme. In the last two rows of these tables, the ε-uniform error and ε-uniform rate of convergence of the scheme are given. As one observes, the scheme gives first order uniform convergence. The second order convergence of the temporal discretization is depicted in Table 3. In Tables 4 and 5, comparison of the ε-uniform error and ε-uniform rate of convergence of the proposed scheme with results of some recently published papers is given. As we observed, the proposed scheme gives a more accurate result than the results in [16, 18–20] and [24]. The proposed scheme has a limitation for solving nonlinear singularly perturbed problems.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Solution of Example 19, with boundary layer formation.

Table 1. Example 19, maximum absolute errors of the scheme.

ε↓	N = M = 16	32	64	128	256	512
1	1.0742e-04	6.6552e-05	4.4167e-05	2.7392e-05	1.5041e-05	7.8477e-06
2⁻²	3.8959e-04	3.3429e-04	2.5726e-04	1.5142e-04	8.1424e-05	4.2142e-05
2⁻⁴	1.6240e-03	5.6521e-04	4.3969e-04	2.6289e-04	1.4270e-04	7.4226e-05
2⁻⁶	8.3743e-03	2.0823e-03	8.0261e-04	3.8986e-04	1.9220e-04	9.5980e-05
2⁻⁸	1.0404e-02	4.8511e-03	1.9751e-03	7.6437e-04	3.0100e-04	1.2812e-04
2⁻¹⁰	1.0409e-02	4.9874e-03	2.6147e-03	1.3838e-03	5.8980e-04	2.2292e-04
2⁻¹²	1.0409e-02	4.9874e-03	2.6159e-03	1.4219e-03	7.3950e-04	3.6693e-04
2⁻¹⁴	1.0409e-02	4.9874e-03	2.6159e-03	1.4219e-03	7.3985e-04	3.7720e-04
2⁻¹⁶	1.0409e-02	4.9874e-03	2.6159e-03	1.4219e-03	7.3985e-04	3.7720e-04
2⁻¹⁸	1.0409e-02	4.9874e-03	2.6159e-03	1.4219e-03	7.3985e-04	3.7720e-04
2⁻²⁰	1.0409e-02	4.9874e-03	2.6159e-03	1.4219e-03	7.3985e-04	3.7720e-04

E^N,M	1.0409e-02	4.9874e-03	2.6159e-03	1.4219e-03	7.3985e-04	3.7720e-04
r^N,M	1.0615	0.9310	0.8795	0.9425	0.9719	—

Table 2. Example 20, maximum absolute errors of the scheme.

ε↓	N = 16	32	64	128	256	512
ε↓	M = 10	20	40	80	160	320
1	9.0612e-05	7.8840e-05	5.0913e-05	2.8361e-05	1.4905e-05	7.6151e-06
2⁻²	5.0971e-04	3.4843e-04	1.9886e-04	1.0569e-04	5.4425e-05	2.7604e-05
2⁻⁴	1.3108e-03	6.8037e-04	3.4323e-04	1.7164e-04	8.5788e-05	4.2882e-05
2⁻⁶	4.2800e-03	1.6597e-03	6.2601e-04	2.5497e-04	1.1234e-04	5.2343e-05
2⁻⁸	5.4803e-03	3.2949e-03	1.4175e-03	5.1091e-04	1.8211e-04	7.0533e-05
2⁻¹⁰	5.4832e-03	3.3921e-03	1.8283e-03	9.1599e-04	3.8114e-04	1.3511e-04
2⁻¹²	5.4832e-03	3.3921e-03	1.8292e-03	9.4367e-04	4.7807e-04	2.3354e-04
2⁻¹⁴	5.4832e-03	3.3921e-03	1.8292e-03	9.4367e-04	4.7832e-04	2.4067e-04
2⁻¹⁶	5.4832e-03	3.3921e-03	1.8292e-03	9.4367e-04	4.7832e-04	2.4067e-04
2⁻¹⁸	5.4832e-03	3.3921e-03	1.8292e-03	9.4367e-04	4.7832e-04	2.4067e-04
2⁻²⁰	5.4832e-03	3.3921e-03	1.8292e-03	9.4367e-04	4.7832e-04	2.4067e-04

E^N,M	5.4832e-03	3.3921e-03	1.8292e-03	9.4367e-04	4.7832e-04	2.4067e-04
r^N,M	0.6928	0.8910	0.9549	0.9803	0.9909	—

Table 3. Maximum absolute error and rate of convergence of the scheme.

Example 19				Example 20
ε↓	N = 16	64	256	N = 16	64	256
ε↓	M = 16	32	64	M = 10	20	40
2⁻¹⁰	1.0409e-02	2.6147e-03	5.8980e-04	5.4832e-03	1.8283e-03	3.8004e-04
2⁻¹⁰	1.9931	2.1483	—	1.5845	2.0621	—
2⁻¹²	1.0409e-02	2.6159e-03	7.3950e-04	5.4832e-03	1.8292e-03	4.7807e-04
2⁻¹²	1.9925	1.8227	—	1.5838	1.9359	—
2⁻¹⁴	1.0409e-02	2.6159e-03	7.3985e-04	5.4832e-03	1.8292e-03	4.7832e-04
2⁻¹⁴	1.9925	1.8220	—	1.5838	1.9352	—
2⁻¹⁶	1.0409e-02	2.6159e-03	7.3985e-04	5.4832e-03	1.8292e-03	4.7832e-04
2⁻¹⁶	1.9925	1.8220	—	1.5838	1.9352	—
2⁻¹⁸	1.0409e-02	2.6159e-03	7.3985e-04	5.4832e-03	1.8292e-03	4.7832e-04
2⁻¹⁸	1.9925	1.8220	—	1.5838	1.9352	—
2⁻²⁰	1.0409e-02	2.6159e-03	7.3985e-04	5.4832e-03	1.8292e-03	4.7832e-04
2⁻²⁰	1.9925	1.8220	—	1.5838	1.9352	—

Table 4. Comparison of uniform error and uniform rate of convergence of Example 19.

Schemes ↓		N = M = 16	32	64	128	256
Proposed scheme	E^N,M	1.0409e-02	4.9874e-03	2.6159e-03	1.4219e-03	7.3985e-04
Proposed scheme	r^N,M	1.0615	0.9310	0.8795	0.9425	0.9719
Scheme in [19]	E^N,M	3.41e-02	1.84e-02	9.38e-03	4.67e-03	2.31e-03
Scheme in [19]	r^N,M	0.8901	0.9720	1.0062	1.0155	1.0063
Scheme in [16]	E^N,M	4.9485e-02	3.3203e-02	2.1165e-02	1.3320e-02	7.9345e-03
Scheme in [16]	r^N,M	0.5757	0.6496	0.6681	0.7474	0.7908

Table 5. Comparison of uniform error and uniform rate of convergence of Example 20.

Schemes ↓		M = 10	20	40	80	160
Schemes ↓		N = 16	32	64	128	256
Proposed scheme	E^N,M	5.4832e-03	3.3921e-03	1.8292e-03	9.4367e-04	4.7832e-04
Proposed scheme	r^N,M	0.6928	0.8910	0.9549	0.9803	0.9909
Scheme in [20]	E^N,M	1.86e-02	1.00e-02	5.48e-03	2.86e-03	1.46e-03
Scheme in [20]	r^N,M	0.89	0.87	0.94	0.97	1.11
Scheme in [18]	E^N,M	1.6119e-02	9.9504e-03	5.8541e-03	3.3439e-03	1.8650e-03
Scheme in [18]	r^N,M	0.6960	0.7653	0.8079	0.8424	0.8660
Scheme in [24]	E^N,M	7.4252e-03	4.0993e-03	2.1528e-03	1.1033e-03	5.5845e-04
Scheme in [24]	r^N,M	0.8570	0.9291	0.9644	0.9822	—

5. Conclusion

In this paper, singularly perturbed parabolic convection-diffusion-reaction equation with large time delay is considered. The solution of the considered problem exhibits boundary layer of thickness ε on the right side of the spatial domain. The bounds and properties of the analytical solution are discussed. To stabilize the influence of the singular perturbation on the discrete solution, and exponential fitting parameter is developed using the derivation from the asymptotic solution. The numerical scheme is developed using the Crank-Nicolson method in temporal discretization and an exponentially fitted central finite difference method on the spatial discretization. The existence of the discrete solution is discussed using the comparison principle. The stability and uniform convergence of the scheme are investigated well theoretically. Numerical results are depicted using maximum absolute error, ε-uniform error, and ε-uniform rate of convergence in tables which are in good agreement with the theoretical analysis. The developed scheme gives stable and uniformly convergent result with linear order of convergence.

Conflicts of Interest

The authors declare no conflict of interest.

Open Research

Data Availability

No additional data is used in this manuscript.

References

1 Baker C. T., Bocharov G. A., and Rihan F. A., A Report on the Use of Delay Differential Equations in Numerical Modelling in the Biosciences, 1999, Citeseer.
Google Scholar
2 Goodwin D. A., Meares C. F., DeRiemer L. H., Diamanti C. I., Goode R. L., Baumert J. J., Sartoris D. J., Lantieri R. L., and Fawcett H. D., Clinical studies with in-111 BLEDTA, a tumor-imaging conjugate of bleomycin with a bifunctional chelating agent, Journal of nuclear medicine. (1981) 22, no. 9, 787–792, 6168750.
CAS PubMed Web of Science® Google Scholar
3 Wang P. and Keng C., Asymptotic stability of a time-delayed diffusion system, Journal of Applied Mechanics. (1963) 30, no. 4, 500–504.
10.1115/1.3636609
Google Scholar
4 Woldaregay M. M. and Duressa G. F., Higher-order uniformly convergent nu equations with mixed small shifts, International Journal of Differential Equations. (2020) 2020, 15, https://doi.org/10.1155/2020/6661592.
10.1155/2020/6661592
Web of Science® Google Scholar
5 Clavero C., Jorge J. C., and Lisbona F., A uniformly convergent scheme on a non-uniform mesh for convection-diffusion parabolic problems, Journal of Computational and Applied Mathematics. (2003) 154, no. 2, 415–429, https://doi.org/10.1016/S0377-0427(02)00861-0, 2-s2.0-0037849987.
10.1016/S0377-0427(02)00861-0
Web of Science® Google Scholar
6 Gowrisankar S. and Natesan S., Robust numerical scheme for singularly perturbed convection-diffusion parabolic initial-boundary-value problems on equidistributed grids, Computer Physics Communications. (2014) 185, no. 7, 2008–2019, https://doi.org/10.1016/j.cpc.2014.04.004, 2-s2.0-84901641725.
10.1016/j.cpc.2014.04.004
CAS Web of Science® Google Scholar
7 Kadalbajoo M. K., Gupta V., and Awasthi A., A uniformly convergent B-spline collocation method on a nonuniform mesh for singularly perturbed one-dimensional time-dependent linear convection-diffusion problem, Journal of Computational and Applied Mathematics. (2008) 220, no. 1-2, 271–289, https://doi.org/10.1016/j.cam.2007.08.016, 2-s2.0-47849096152.
10.1016/j.cam.2007.08.016
Web of Science® Google Scholar
8 Turuna D. A., Woldaregay M. M., and Duressa G. F., Uniformly convergent numerical method for singularly perturbed convection-diffusion problems, Kyungpook National University. (2020) 60, no. 3, 629–645.
Web of Science® Google Scholar
9 Ansari A. R., Bakr S. A., and Shishkin G. I., A parameter-robust finite difference method for singularly perturbed delay parabolic partial differential equations, Journal of Computational and Applied Mathematics. (2007) 205, no. 1, 552–566, https://doi.org/10.1016/j.cam.2006.05.032, 2-s2.0-34247535463.
10.1016/j.cam.2006.05.032
Web of Science® Google Scholar
10 Bashier E. B. and Patidar K. C., A novel fitted operator finite difference method for a singularly perturbed delay parabolic partial differential equation, Applied Mathematics and Computation. (2011) 217, no. 9, 4728–4739, https://doi.org/10.1016/j.amc.2010.11.028, 2-s2.0-78650177407.
10.1016/j.amc.2010.11.028
Web of Science® Google Scholar
11 Bashier E. B. and Patidar K. C., A second-order fitted operator finite difference method for a singularly perturbed delay parabolic partial differential equation, Journal of Difference Equations and Applications. (2011) 17, no. 5, 779–794, https://doi.org/10.1080/10236190903305450, 2-s2.0-79957441349.
10.1080/10236190903305450
Web of Science® Google Scholar
12 Lolugu G., Mohapatra J., and Das A., A fourth-order numerical scheme for singularly perturbed delay parabolic problem arising in population dynamics, Journal of Applied Mathematics and Computing. (2020) 63, 1–25.
Web of Science® Google Scholar
13 Rao N. R. and Chakravarthy P. P., A fitted Numerov method for singularly perturbed parabolic partial differential equation with a small negative shift arising in control theory, Numerical Mathematics: Theory, Methods and Applications. (2014) 7, no. 1, 23–40.
10.4208/nmtma.2014.1316nm
Web of Science® Google Scholar
14 Kumar S. and Vigo-Aguiar J., A parameter-uniform grid equidistribution method for singularly perturbed degenerate parabolic convection-diffusion problems, Journal of Computational and Applied Mathematics. (2020) no. article 113273, https://doi.org/10.1016/j.cam.2020.113273.
10.1016/j.cam.2020.113273
Web of Science® Google Scholar
15 Rai P. and Swati Y., Robust numerical schemes for singularly perturbed delay parabolic convection-diffusion problems with degenerate coefficient, International Journal of Computer Mathematics. (2020) 98, 195–221.
10.1080/00207160.2020.1737030
Web of Science® Google Scholar
16 Das A. and Natesan S., Uniformly convergent hybrid numerical scheme for singularly perturbed delay parabolic convection-diffusion problems on Shishkin mesh, Applied Mathematics and Computation. (2015) 271, 168–186, https://doi.org/10.1016/j.amc.2015.08.137, 2-s2.0-84942508971.
10.1016/j.amc.2015.08.137
Web of Science® Google Scholar
17 Govindarao L., Mohapatra J., and Sahu S. R., Uniformly convergent numerical method for singularly perturbed two parameter time delay parabolic problem, International Journal of Applied and Computational Mathematics. (2019) 5, no. 3, https://doi.org/10.1007/s40819-019-0672-5.
10.1007/s40819-019-0672-5
PubMed Google Scholar
18 Gowrisankar S. and Natesan S., ε-Uniformly convergent numerical scheme for singularly perturbed delay parabolic partial differential equations, International Journal of Computer Mathematics. (2017) 94, no. 5, 902–921.
10.1080/00207160.2016.1154948
Web of Science® Google Scholar
19 Kumar D. and Kumari P., A parameter-uniform numerical scheme for the parabolic singularly perturbed initial boundary value problems with large time delay, Journal of Applied Mathematics and Computing. (2019) 59, no. 1-2, 179–206, https://doi.org/10.1007/s12190-018-1174-z, 2-s2.0-85041893391.
10.1007/s12190-018-1174-z
Web of Science® Google Scholar
20 Kumar D. and Kumari P., A parameter-uniform scheme for singularly perturbed partial differential equations with a time lag, Numerical Methods for Partial Differential Equations. (2020) 36, no. 4, 868–886, https://doi.org/10.1002/num.22455.
10.1002/num.22455
Web of Science® Google Scholar
21 Lolugu G. and Mohapatra J., Numerical analysis and simulation of delay parabolic partial differential equation involving a small parameter, Engineering Computations. (2019) 37, no. 1, 289–312, https://doi.org/10.1108/EC-03-2019-0115, 2-s2.0-85071654741.
10.1108/EC-03-2019-0115
Web of Science® Google Scholar
22 Lolugu G., Sahu R., and Mohapatra J., Uniformly convergent numerical method for singularly perturbed time delay parabolic problem with two small parameters, Iranian Journal of Science and Technology, Transaction A, Science. (2019) 43, no. 5, 2373–2383.
10.1007/s40995-019-00697-2
Web of Science® Google Scholar
23 Lolugu G. and Mohapatra J., A second order numerical method for singularly perturbed delay parabolic partial differential equation, Engineering Computations. (2019) 36, no. 2, 420–444, https://doi.org/10.1108/EC-08-2018-0337, 2-s2.0-85058347474.
10.1108/EC-08-2018-0337
Web of Science® Google Scholar
24 Podila P. C. and Kumar K., A new stable finite difference scheme and its convergence for time-delayed singularly perturbed parabolic PDEs, Computational & Applied Mathematics. (2020) 39, no. 3, https://doi.org/10.1007/s40314-020-01170-2.
10.1007/s40314-020-01170-2
Web of Science® Google Scholar
25 Miller J. J., O′riordan E., and Shishkin G. I., Fitted Numerical Methods for Singular Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions, 2012, World Scientific.
10.1142/8410
Google Scholar
26 Kadalbajoo M. K. and Awasthi A., Crank-Nicolson finite difference method based on a midpoint upwind scheme on a non-uniform mesh for time-dependent singularly perturbed convection-diffusion equations, International Journal of Computer Mathematics. (2008) 85, no. 5, 771–790, https://doi.org/10.1080/00207160701459672, 2-s2.0-42649121629.
10.1080/00207160701459672
Web of Science® Google Scholar
27 OMalley R. E., Singular perturbation methods for ordinary differential equations, 1991, Springer, https://doi.org/10.1007/978-1-4612-0977-5.
10.1007/978-1-4612-0977-5
Google Scholar
28 Kellogg T. and Tsan A., Analysis of some difference approximations for a singular perturbation problem without turning points, Mathematics of Computation. (1978) 32, no. 144, 1025–1039, https://doi.org/10.1090/S0025-5718-1978-0483484-9, 2-s2.0-84966216257.
10.1090/S0025-5718-1978-0483484-9
Web of Science® Google Scholar

Citing Literature

All articles

Novel Numerical Scheme for Singularly Perturbed Time Delay Convection-Diffusion Equation

Abstract

1. Introduction

2. Continuous Problem

2.1. Bounds on the Solution and Its Derivatives