Novel Concepts of Domination in Vague Graphs with Application in Medicine
Abstract
VG can manage the uncertainty relevant to the inconsistent and indeterminate information of all real-world problems, in which FGs possibly will not succeed in bringing about satisfactory results. The previous definitions’ restrictions in FGs have made us present new definitions in VGs. A wide range of applications have been attributed to the domination in graph theory for several fields such as facility location problem, school bus routing, modeling biological networks, and coding theory. Therefore, in this research, we study several concepts of domination, such as restrained dominating set (RDS), perfect dominating set (PDS), global restrained dominating set (GRDS), total k-dominating set, and equitable dominating set (EDS) in VGs and also introduce their properties by some examples. Finally, we try to represent the application and importance of domination in the field of medical science and discuss the topic in today’s world, namely, the corona vaccine.
1. Introduction
Graph theory began its adventure from the well-known “Konigsberg bridge problem.” This problem is frequently believed to have been the beginning of graph theory. In 1739, Euler finally elucidated this problem using graphs. Even though graph theory is an extraordinarily old concept, its growing utilization in operations research, chemistry, genetics, electrical engineering, geography, sociology, and so forth has reserved it fresh. In recent times, graph principle has been utilized in communication system (mobile, internet, etc.), computer layout, and so forth. In graph theory, it is far considered that the nodes, edges, weights, and so on are definite. To be exact, there may be no question concerning the existence of these objects. However, the real world sits on a plethora of uncertainties, indicating that, in some conditions, it is believed that the nodes, edges, and weights may additionally be or may not be certain. For instance, the vehicle travel time or vehicle capacity on a road network may not be identified or known exactly. To embody such graphs, Rosenfeld [1] brought up the idea of the “fuzzy graph” in 1975. Similar to set theory, the historical past of FG theory is the fuzzy set theory advanced by Zadeh [2] in 1965. Roy and Biswas investigated the importance of interval-valued fuzzy sets on medical diagnosis [3].
The notion of vague set theory, generalization of Zadeh’s fuzzy set theory, was introduced by Gau and Buehrer [4] in 1993. The concepts of rough set, soft set, bipolar soft set, and neutrosophic set were introduced in [5–9]. Kauffman [10] represented FGs based on Zadeh’s fuzzy relation [11]. Mordeson et al. [12–14] described some results in FGs. Akram et al. [15–17] developed several concepts and results on FGs. Samanta et al. [18–21] represented FCGs and some remarks on BFGs. Shao et al. [22–28] investigated new concepts in VGs and fuzzy graphs. VG notion was defined by Ramakrishna in [29]. Borzooei and Rashmanlou [30–34] analyzed new concepts of VGs. Rashmanlou et al. [35–40] investigated new results in VGs. Ghorai and Pal [41] studied regular product vague graphs and product vague line graphs. A VG is referred to as a generalized structure of an FG that delivers more exactness, adaptability, and compatibility to a system when matched with systems running on FGs. Also, a PVG is able to concentrate on determining the uncertainty coupled with the inconsistent and indeterminate information of any real-world problem, where FGs may not lead to adequate results.
Domination in VGs theory is one of the most widely used topics in other sciences, including psychology, computer science, nervous systems, artificial intelligence, decision-making theory, and combinations. Although the dominance of FGs has been stated by some researchers, due to the fact that VGs are wider and are more widely used than FGs, it is observed today that they are used in many branches of engineering and medical sciences. Likewise, they have been used in many applications for the formulation and solution of many problems in various areas of science and technology exemplified by computer networks, combinatorial analyses, physics, and so forth. In 1962, Ore [42] represented “domination” for undirected graphs, and he described the definition of minimum-DSs of nodes in a graph. A. Somasundaram and S. Somasundaram [43] introduced the DS and IDS in FGs. Gani et al. [44, 45] represented the fuzzy-DS and independent-DS notion utilizing strong arcs. The IDN and IR-DN in graphs are defined by Cockayne et al. [46] and Haynes et al. [47]. Parvathi and Thamizhendhi [48] described domination in intuitionistic fuzzy graphs. Jan et al. [49–51] investigated new concepts in interval-valued fuzzy graphs and cubic bipolar fuzzy graphs. Talebi et al. [52–54] introduced some results of domination in VGs, as well as new concepts in interval-valued intuitionistic fuzzy competition graph. So, in this research, we introduce different concepts of domination, such as RDS, PDS, GRDS, EDS, and total k-dominating set in VGS. In the end, an application of domination in medical immunization is introduced.
2. Preliminaries
In this section, some basic concepts of VGs are reviewed to facilitate the next sections.
A graph denotes a pair G∗ = (V, E) satisfying E⊆V × V. The elements of V and E are the nodes and edges of the graph G∗, correspondingly.
An FG has the form of ξ = (γ, ν), where γ : V⟶[0,1] and ν : V × V⟶[0,1] as is defined by ν(ab) ≤ γ(a)∧γ(b), ∀a, b ∈ V, and ν is a symmetric fuzzy relation on γ and ∧ denotes the minimum.
Definition 1. (see [4]). A VS A is a pair (tA, fA) on set V where tA and fA are used as real valued functions which can be defined on V⟶[0,1], so that tA(a) + fA(a) ≤ 1, ∀a ∈ V. The interval [[tA(a), 1 − fA(a)] is considered as the vague value of a in A.
Definition 2. (see [29]). A pair ξ = (A, B) is said to be a VG on a crisp graph G∗, where A = (tA, fA) is a VS on V and B = (tB, fB) is a VS on E⊆V × V such that tB(ab) ≤ min(tA(a), tA(b)) and fB(ab) ≥ max(fA(a), fA(b)), for each edge ab ∈ E.
Definition 3. (see [35]). A VG ξ is called complete VG if tB(ab) = min(tA(a), tA(b)) and fB(ab) = max(fA(a), fA(b)), ∀a, b ∈ V.
Definition 4. (see [35]). The complement of a VG ξ = (A, B) is a VG , where and are defined by the following:
Definition 5. (see [31]). A vague path in a VG ξ = (A, B) is a sequence of distinct nodes b1, b2, …, bn so that either tB(bkbk+1) > 0 or fB(bkbk+1) > 0, ∀ 1 ≤ k ≤ n − 1. It was shown by Pn.
Definition 6. An edge ab of a VG ξ is called an effective edge if tB(ab) = tA(a)∧tA(b) and fB(ab) = fA(a)∨fA(b). Otherwise, it is called a noneffective edge.
Definition 7. (see [31]). An edge ab in a VG ξ is called a strong edge if and .
Definition 8. (see [31]). Let ξ = (A, B) be a VG. Let a, b ∈ V, then a dominates b in ξ, if there exists a strong edge between a and b.
Definition 9. (see [32]). The cartesian product of two VGs ξ1 = (A1, B1) and ξ2 = (A2, B2) of the graphs and , denoted by ξ1 × ξ2 = (A1 × A2, B1 × B2), is defined as follows:
Definition 10. (see [35]). A node a in a VG ξ is said to be an isolated node if tB(ab) = 0 and fB(ab) = 0, for all b ∈ V and a ≠ b. That is, .
Definition 11. (see [31]). S⊆V is called a DS in ξ if, ∀ a ∈ V − S, ∃ b ∈ S, so that a dominates b.
Definition 12. (see [31]). Let ξ = (A, B) be a VG. The vertex cardinality of S⊆V is defined as
Notations are shown in Table 1.
| Notation | Meaning |
|---|---|
| FG | Fuzzy graph |
| VS | Vague set |
| ξ | Vague graph |
| DS | Dominating set |
| RDS | Restrained dominating set |
| IDS | Independent dominating set |
| IDN | Independent dominating number |
| IR-DN | Irredundance dominating number |
| K-DS | K-dominating set |
| PDS | Perfect dominating set |
| PDN | Perfect dominating number |
| K-DN | K-dominating number |
| T-KDN | Total K-dominating number |
| MI-PDS | Minimal perfect dominating set |
| T-KDS | Total K-dominating set |
| RDN | Restrained dominating number |
| GRDN | Global restrained dominating number |
| CVG | Complete vague graph |
| EDS | Equitable dominating set |
| GRDS | Global restrained dominating set |
3. Certain Notions of Domination in Vague Graphs
Definition 13. Let ξ = (A, B) be a VG and let k ≥ 1 be an integer. A subset S⊆V is called a K-DS of ξ if, for each node a ∈ V − S, there exists an a − b vague path which includes at least k effective edges for b ∈ S. The K-DN of ξ, denoted by γk(ξ), is described as the minimum cardinality among all K-DS in ξ.
Definition 14. Let ξ = (A, B) be a VG and let k ≥ 1 be an integer. A subset S⊆V is called a T-KDS of ξ if, for each node a ∈ V, ∃ an a − b vague path that includes at least k effective edges for b ∈ S. The T-KDN of ξ, demonstrated by γtk(ξ), is described as the minimum cardinality between all T-KDS in ξ.
Example 1. Consider an example of a T-2DS of VG ξ shown in Figure 1.
It is clear from Figure 1 that S = {a, f} is a minimal T-2DS of VG ξ. The T-2DN of ξ is γk(ξ) = 0.8.

Definition 15. Let ξ be a VG. A set S⊆V is called an RDS of ξ if each node in V − S dominates a node in S and also a node in V − S. The RDN of ξ, demonstrated by γr(ξ), is described as the minimum cardinality of an RDS in ξ.
Example 2. Consider a VG ξ = (A, B) as shown in Figure 2. It is obvious that S = {c, d} is an RDS of ξ. The RDN of ξ is γr(ξ) = 0.75.

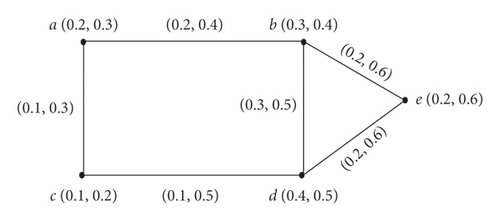
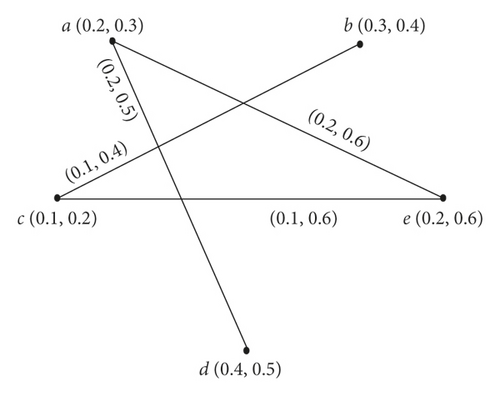
Definition 16. Let ξ be a VG. A set S⊆V is called GRDS of ξ if it is an RDS of both ξ and . The GRDN of ξ, denoted by γgr(ξ), is described as the minimum cardinality of a GRDS in ξ.
Example 3. Consider ξ and as shown in Figures 3 and 4. It is easy to see that S1 = {a, b} and S2 = {c, d} are GRDSs of ξ. The GRDN of ξ is γgr(ξ) = 0.9.
Theorem 1. Suppose that ξ = (A, B) is a CVG; then γr(ξ) = |V|.
Proof. Assume that ξ = (A, B) is a CVG. Then, tB(ab) = min(tA(a), tA(b)) and fB(ab) = max(fA(a), fA(b)). Let S be the MI-RDS of ξ. Then, each node in V − S dominates a node in S and also a node in V − S. Hence, each node dominates all other nodes. So, γr(ξ) = |V|.
Definition 17. Let ξ = (A, B) be a VG. A subset S⊆V is called a PDS of ξ if, for each node b ∈ V − S, there exists exactly one node a ∈ S so that a dominates b.
Definition 18. We say that a PDS S is an MI-PDS if, for every a ∈ S, the set S − {a} is not a PDS in ξ. The minimum cardinality among all MI-PDSs is called the PDN of ξ and it was shown by γpif(ξ) or simply γpif.
Example 4. Consider a VG ξ = (A, B) as shown in Figure 5. It is obvious that S = {a, d} is an MI-PDS. The PDN of ξ is γpif = 0.9.

Theorem 2. Every DS in CVG ξ = (A, B) is a PDS.
Proof. Let S be an MI-DS of a VG ξ. Since ξ is complete, each edge in ξ is one effective edge and each node b ∈ V − S is neighbor to exactly one node a ∈ S. Hence, each DS in ξ is a PDS.
Definition 19. The strong product of two VGs ξ1 = (A1, B1) and ξ2 = (A2, B2) of the graphs and , where V1∩V2 = ∅, denoted by G1 × G2 = (A1 × A2, B1 × B2), is defined as follows:
Theorem 3. Let ξ1 = (A1, B1) and ξ2 = (A2, B2) be two VGs with V1∩V2 = ∅. The strong product ξ = ξ1 × ξ2 remains connected even after removal of all noneffective edges in it.
Proof. Assume that ξ = ξ1 × ξ2 is a strong product of two VGs ξ1 and ξ2. Let e = ((a, a1)(b, b1)) be a noneffective edge in ξ; that is, tB((a, a1)(b, b1)) < min{tA(a, a1), tA(b, b1)}, and fB((a, a1)(b, b1)) > max{fA(a, a1), fA(b, b1)}. Let ξ′ = ξ − e, and suppose that ξ′ is disconnected. The edge e disconnects the graph into more than one component. Hence, there is no path among (a, a1) and (b, b1) except the edge e = ((a, a1), (b, b1)) in ξ′. This implies that tB((a, a1)(b, b1)) = {tA(a, a1), tA(b, b1)} and fB((a, a1)(b, b1)) = {fA(a, a1), fA(b, b1)}, which is a contradiction. So, ξ′ is connected.
Remark 1. The strong product ξ1⊠ξ2 of two connected vague graphs is a connected vague graph.
Theorem 4. If a node a dominates a node b in ξ1 and a node a1 dominates a node b1 in ξ2, then the node ab does not dominate the node a1b1 in ξ1 × ξ2.
Proof. Suppose that a dominates b in ξ1. Then ∃ an effective edge ab in ξ1, i.e., tB(ab) = min{tA(a), tA(b)} and fB(ab) = max{fA(a), fA(b)}. Similarly, assume that a node a1 dominates a node b1 in ξ2, so that tB(a1b1) = min{tA(a1), tA(b1)} and fB(a1b1) = max{fA(a1), fA(b1)}. Now, by definition of Cartesian product, there does not exist any edge among the nodes (a, a1) and (b, b1) in ξ1 × ξ2; i.e., tB((a, a1)(b, b1)) = 0 and fB((a, a1)(b, b1)) = 0. Therefore, (a, a1) does not dominate (b, b1) in ξ1 × ξ2.
Definition 20. The direct product of two VGs ξ1 = (A1, B1) and ξ2 = (A2, B2) of the graphs and , where V1∩V2 = ∅, denoted by ξ1 ⊗ ξ2 = (A1 ⊗ A2, B1 ⊗ B2), is defined as follows:
Note 1. If a node a dominates a node b in ξ1 and a node a1 dominates a node b in ξ2, then the node (a, a1) dominates the node (b, b1) in ξ1 ⊗ ξ2. It is shown in Figure 6.
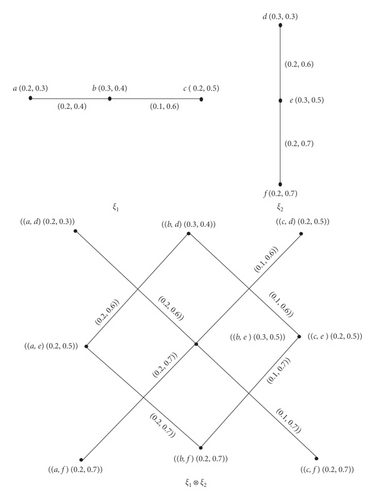
Example 5. Consider a VG as in Figure 6. It is obvious that the node a dominates b in ξ1 and e dominates f in ξ2. Likewise, the node (a, e) dominates the node (b, f) in ξ1 × ξ2.
Definition 21. Let ξ = (A, B) be a VG. A subset S⊆V is called an EDS of ξ if, for each node b ∈ V − S, ∃ a node a ∈ S so that ab ∈ E, |degt(a) − degt(b)| ≤ 1, tB(ab) = min{tA(a), tA(b)}, |degf(a) − degf(b)| ≥ 1, and fB(ab) = max{fA(a), fA(b)}. The EDN of ξ, denoted by γe(ξ), is defined as the minimum cardinality of an EDS S.
Example 6. Consider a VG ξ = (A, B), as shown in Figure 7.
It is obvious that the MI-EDS of a VG ξ is S = {a}. The EDN is γe(ξ) = 0.45. Note that an EDS S is called an MI-EDS of ξ, if, for each node b ∈ S, the set S − {b} is not an EDS.
Theorem 5. Let ξ1 and ξ2 be VGs on nonempty sets V1 and V2, respectively. Then,
Proof. Assume that S1 and S2 are EDSs of minimum cardinality of ξ1 and ξ2, respectively. Then, for each node b ∈ V − S1, ∃ a node a ∈ S1 so that |degt(b) − degt(a)| ≤ 1, tB(ab) = min{tA(a), tA(b)}, |degf(b) − degf(a)| ≥ 1, and fB(ab) = max{fA(a), fA(b)}. Similarly, for each node c ∈ V − S2, ∃ a node d ∈ S2 so that |degt(d) − degt(c)| ≤ 1, tB(c d) = min{tA(c), tA(d)}, |degf(d) − degf(c)| ≥ 1, and fB(c d) = max{fA(c), fA(d)}. That is, a dominates b in ξ1 and d dominates c in ξ2. Therefore, by Note 1, the node (a, d) dominates the node (b, c) in ξ1 ⊗ ξ2. Thus, |degt(a, d) − degt(b, c)| ≤ 1, tB((a, d)(b, c)) = min{tA(a, d), tA(b, c)}, |degf(a, d) − degf(b, c)| ≥ 1, and fB((a, d)(b, c)) = max{fA(a, d), fA(b, c)}. So, γe(ξ1 ⊗ ξ2) ≤ min(|S1 × V1|, |S2 × V2|).
Theorem 6. Let S1 and S2 be K-DSs of connected VGs ξ1 = (A1, B1) and ξ2 = (A2, B2), respectively; then (1) ξ1 × ξ2 is connected. (2) If S1 is a connected K-DS of ξ1, then S1 × V2 is a connected K-DS of ξ1 × ξ2. (3) If S2 is a connected K-DS of ξ2, then V1 × S2 is a connected K-DS of ξ1 × ξ2.
Proof. To prove that ξ1 × ξ2 is connected, consider any two arbitrary distinct nodes (a, d) and (b, c) of V1 × V2. Then, by definition of Cartesian product, ∃ a path between these two nodes in the following cases:
- (1)
If a = b, then, since ξ2 is a connected VG, ∃ a path P : d, d1, d2, …, c so that tB(ef) > 0 and fB(ef) > 0 for any two nodes e, f of vague path P. Hence, and . So, P′:(a, d)(a, d1), (a, d2), …\\, (a, c) is the vague path between (a, d), (b, c) in ξ1 × ξ2.
- (2)
If d = c, then, since ξ1 is a connected VG, ∃ a vague path Q = a, a1, a2, …, b so that and for any two nodes e, f of vague path Q. Hence, , and tB((a, d), …, (b, d)) is the vague path between (a, d), (b, c) in ξ1 × ξ2.
- (3)
If a ≠ b and c ≠ d, then, by case 1, ∃ a vague path between the nodes (a, d) and (a, c) in ξ1 × ξ2. Likewise, by case 2, ∃ a vague path between the nodes (a, d) and (b, d) in ξ1 × ξ2. Hence, the union of these two disjoint vague paths is a vague path between the nodes (a, d) and (b, c) in ξ1 × ξ2. Now, if S1 and S2 are K-DSs of ξ1 and ξ2, respectively, then γk(ξ1 × ξ2) = min{|V1 × S2|, |S1 × V2|}. So, V1 × S2 and S1 × V2 are K-DSs of ξ1 × ξ2 and the connectivity can be proved similarly.
Theorem 7. Let ξ1 and ξ2 be VGs on nonempty sets V1 and V2, respectively. Let S1 and S2 be K-DSs of ξ1 and ξ2; then S1 × V2 is an independent K-DS of ξ1 × ξ2 if and only if S1 is k-independent and and , for a, b ∈ S1 and d ∈ V2; and , for a ∈ S1 and c, d ∈ V2; and and , for c, d ∈ V2.
Proof. To prove that each two distinct nodes (a, d), (b, c) in S1 × V1 are not neighbor, we consider three conditions. If a = b, then
If c = d, the result is obtained by independence of a, b of S1.
If a ≠ b and c ≠ d, then, by definition, we have tB((a, d)(b, c)) = 0 and fB((a, d)(b, c)) = 0. So, (a, d), (b, c) are not neighbors in G1 × G2. Conversely, assume that (iii) is false. That is, ∃ nodes b, c ∈ V2, so that and . Let a ∈ S1; then
Hence, S1 × V2 is not independent. Therefore, condition (iii) is true, i.e., and .
4. Application of Domination in Medical Sciences
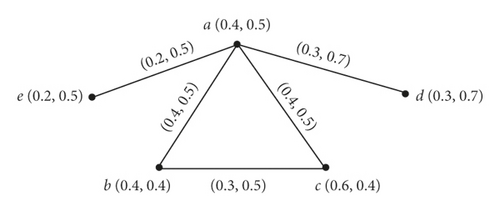
One year has passed since the beginning of the coronary heart disease pandemic in the world. During this year, many people have died in all countries and the lives of all people have been affected. During this period, no definitive cure for this disease has been found and many countries, in attempts to develop a corona vaccine to prevent the disease, are highly contagious. China, Russia, India, and the United States are among these countries, and of course Iran has made efforts in this regard. Most vaccines are in the final stages of production and are about to be sacrificed, and many countries have prepurchased several million doses of these vaccines at this stage. Some vaccines are artificially made from antibodies created following disease; and some other viruses have been killed or weakened. The effectiveness of the study population and less side effects are the most important issues in choosing a vaccine. Relations between countries and political issues between them are also factors affecting the type and amount of vaccines purchased. Although it has been said that the whole world should be safe and these vaccines should be given to all countries, the issues mentioned are definitely on the time required to establish comprehensive security in each country will be effective. Therefore, in this paper, we try to discuss the application and importance of domination in the field of medical sciences and discuss the topic in today’s world, namely, the corona vaccine. For this purpose, we consider five countries: Iran, China, USA, India, and Russia. In fact, we want to buy the most effective vaccine for Iran, given the effectiveness of the vaccine and the political relations that exist between this country and other countries. In this vague graph, the nodes representing the countries and edges indicate the extent of political relations and friendship between the two countries.
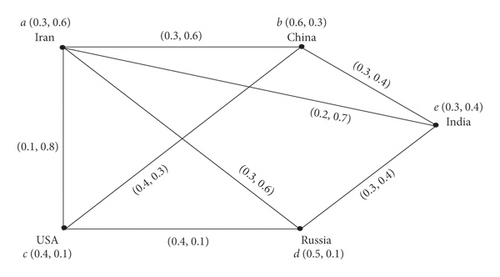
It is clear that S1 has the smallest size among other RDSs, so we conclude that it can be the best choice because, first, China has the most effective vaccine in terms of susceptibility to the virus, and, second, there is a relatively good friendship between Iran and China. Therefore, governments must provide the necessary facilities for the delivery of efficient and useful vaccines to deprived countries in order to prevent the transmission of this deadly virus to the rest of the people as soon as possible.
5. Conclusion
Domination in FGs theory is one of the most widely discussed topics in other sciences including psychology, computer science, nervous systems, artificial intelligence, and combinations. They have also been utilized in summarizing document and in designing secure systems for electrical grids. Hence, in this paper, we introduced several concepts of domination, such as RDS, PDS, GRDS, EDS, and total K-dominating set in VGs and also investigated their properties by some examples. Finally, we described an application of domination in the field of medical sciences and discussed a topic in today’s world, namely, the coronavirus. In our future work, we will introduce vague incidence graphs and study the concepts of connected perfect dominating set, regular perfect dominating set, inverse perfect dominating set, and independent perfect dominating set on vague incidence graph.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
This work was supported by the National Key R&D Program of China (no. 2018YFB1005100).
Open Research
Data Availability
No data were used to support this study.




