On the Optical Stark Effect of Excitons in InGaAs Prolate Ellipsoidal Quantum Dots
Abstract
In this paper, we study the exciton absorption spectra in InGaAs prolate ellipsoidal quantum dots when a strong pump laser resonant with electron quantized levels is active. Our obtained results by renormalized wavefunction theory show that, under suitable conditions, the initial exciton absorption peak is split into two new peaks as the evidence of the existence of the three-level optical Stark effect of excitons. We have suggested an explanation of the origin of the effect as well as investigating the effect of pump field energy, size, and geometric shape of the quantum dots on effect characteristics. The comparison with the results obtained in the spherical quantum dots implies the important role of geometric shape of the quantum structures when we examine this effect.
1. Introduction
One of the low dimensional structures recently attracting much interest from researchers is the semiconductor quantum dots [1–4], which are structures that confine carriers in all three spatial dimensions. Quantum dot structures have many interesting applications, such as producing artificial atoms and molecules [5], single-electron transistors [6], and quantum dot lasers [7]. In recent years, there has seen many studies on optical properties in quantum dots with different shapes, for example, cylindrical, cubic, and spherical quantum dots [8–12]. These studies show that optical properties of quantum dots are highly dependent on external fields and size of quantum dots. It is worth mentioning that the shape of quantum dots also makes a huge difference to the optical properties of quantum dots [13]. Therefore, quantum dots are expected to create even more breakthrough applications in the future.
The optical Stark effect of excitons is one of the unique optical properties of bulk materials in general and low dimensional structures in particular. The optical Stark effect of excitons occurs due to the coupling of the two exciton states under the excitation of near resonant beam [14]. Scientists divided this effect into two types as follows. First, two-level optical Stark effect arises when a pump laser of strong intensity couples exciton ground state and an exciton excited state in the quantum system [14, 15]. Second, three-level optical Stark effect is the result of a couple of two excited states of exciton under the control of a pump laser beam of lower intensity [16, 17]. The latter has received more attention from researchers because they are more likely to occur and have better potential application. In general, optical Stark effect has potential applications in manufacturing ultrafast optical switching of future optical devices [11, 18], optical modulators [19], mesoporous hybrid multifunctional system [20], and optically controlled field-effect transistors [21]. The optical Stark effect of excitons in quantum dots has also been of interest in both experimental and theoretical research [11, 22–24] but mainly for spherical quantum dots. The investigation of this effect in a more complicated and more practical shaped quantum dot structures, such as ellipsoidal quantum dots, has not been carried out in detail.
In this paper, we study theoretically the three-level optical Stark effect of excitons in InGaAs prolate ellipsoidal quantum dots. We applied the renormalized wavefunction method to investigate the dependence of the exciton absorption spectra on the external fields, size, and shape of quantum dot, when there exists the optical Stark effect of excitons. In addition, the effects of the pump laser energy, size, and geometric shape of quantum dots on the behavior of the effect are also clarified. The article includes the following main sections: Section 2 presents model and theory, Section 3 presents the main results and discussion, and conclusions are presented in Section 4.
2. Model and Theory
2.1. Wavefunctions and Energy Levels of Electron and Hole in Prolate Ellipsoidal Quantum Dots
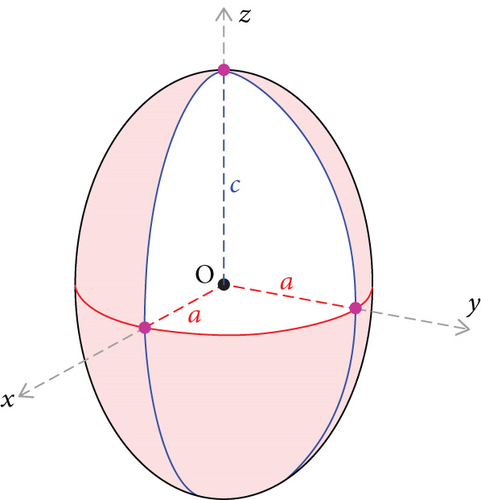
2.2. Intersubband Optical Transition
In this paper, we study the three-level optical Stark effect of excitons in prolate ellipsoidal quantum dots. Thus, we need to examine a three-level system of exciton and thus result in a three-level diagram of electron and hole, which consist of the lowest level corresponding to the first quantized state of the hole in the valence band |0〉, and the other two levels have the energy of and corresponding to two lowest quantized states of the electrons in the conduction band |1〉 and |2〉 as illustrated in Figure 2.
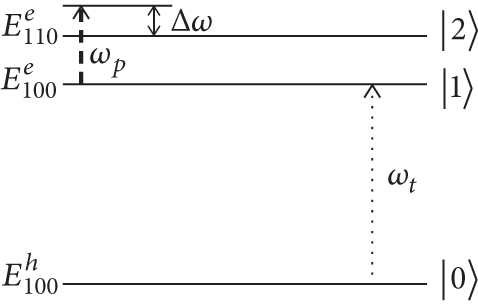
2.3. The Exciton Absorption Spectra
2.3.1. Without the Present of the Pump Laser
and Γ is the phenomenological linewidth of absorption peak.
2.3.2. With the Presence of the Pump Laser
3. Results and Discussion
To clarify the results obtained above, in this section, we perform the calculation for transition rate in In0.53Ga0.47As/In0.52Al0.48As prolate ellipsoidal quantum dots in two cases: without and with the pump laser. The parameters used in the calculation are as follows. The effective mass of electron and hole in the dot material In0.53Ga0.47As are me = 0.042m0 and mh = 0.052m0; the band gap of the dot material is Eg = 750 meV [36]; the pump laser amplitude was chosen to be Ap = 4 × 104 V/cm, and the linewidth was chosen as the Γ = 0.1 meV. In addition, since this paper examines prolate ellipsoidal quantum dot structure. This is a low dimensional structure, so the length of the major axis 2c and minor axis 2a must be selected to be smaller the bulk exciton Bohr radius in the dot material In0.53Ga0.47As. Thus, we have selected the length of the semi-major axis as a = 25 Å to do the calculation in this section, while the length of the semi-minor axis will depend on the selected value of χ (c = χ · a).
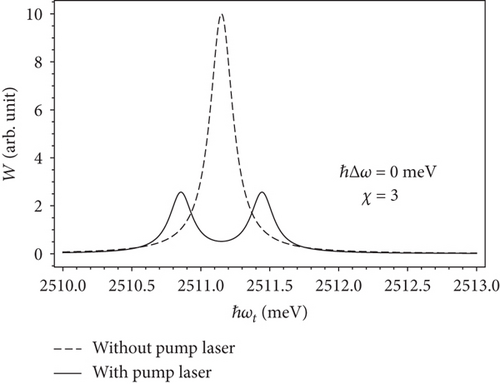
In Figure 3, we depict the dependence of transition rate on the photon energy of the probe laser in a prolate ellipsoidal quantum dot with the value of the ellipsoidal aspect ratio of χ = 3 in two conditions: without the pump laser effect (dashed line) and with the pump laser effect (solid line). From the figure, we can see that, without the pump laser, the absorption spectra of excitons includes only one absorption peak. However, when the system is irradiated by a strong pump laser exactly resonant with the energy distance between the two quantized levels of the electron, the graph appeared two distinct equal peaks in the exciton absorption spectra. These two vertices are bilaterally symmetrical with respect to the original peak when the pump laser does not operate. Moreover, we found that the exciton absorption intensity is drastically reduced in the presence of a laser field. This reduction is the consequence of the conservation of the electronic transition rate as discussed in Ref. [11]. In short, the above results demonstrate the existence of the three-level optical Stark effect of exciton in the prolate ellipsoidal quantum dots. In addition, comparing the results found in the prolate ellipsoidal and spherical quantum dots [11], we find that they are similar. The reason is given to the fact that both prolate ellipsoidal and spherical quantum dots are quasi-zero-dimensional systems.
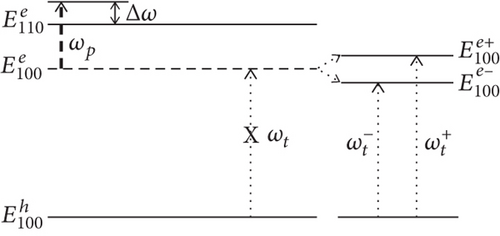
The existence of the two distinct peaks in the absorption spectra of excitons under the effect of a strong pump laser resonating with the energy distance between the two quantized levels of the electron can be explained in Figure 4. From Figure 4, we see that when the pump laser is active, the initial electron levels are split into sub-levels. For example, two new levels and are separated from the initial level , and two sub-levels and are split from the initial level , determined according to Eqs. (43) and (44). Thus, when we use the probe laser, we find two interband transitions from hole level to two sub-levels of electron and , obeying the selection rules of the interband transitions in quantum dots. This means in the absorption spectrum of excitons there appear two new absorption peaks of excitons. These two peaks are located symmetrically on both sides of the original peak according to the energy conservation law.
To better reveal the strong effect of the pump laser detuning on the absorption spectrum of excitons, we investigated the dependence of the transition rate according to the photon energy of probe laser when the ellipsoidal aspect ratio χ = 3 in the absence of the pump laser (dotted line) and in the presence of the pump laser with different detunings ℏΔ ω = 0.1 meV (thin solid line), ℏΔ ω = 0.3 meV (thick solid line), and ℏΔ ω = 0.5 meV (dashed line) as shown in Figure 5. From Figure 5, we can see that in the presence of the pump laser, all absorption spectra of excitons contain two absorption peaks of excitons in the absorption spectra. The heights of two absorption peaks of excitons are different and depend on the pump laser detuning. When the pump laser detuning changes, the height of two exciton absorption peaks will also change, the more the detuning increases, the higher the height of one peak increases while the height of the other peak decreases. As the detuning increases, one absorption peak tends to move towards the original peak (which is the peak in the inactivity of the pump laser); the other is far from the position of the original peak, and this is clearly shown in Figure 6. From Figure 6, we also find that the more the detuning, the more redshifted two peaks. In addition, the detuning of the pump laser also strongly influences the transition rate of two absorption peaks as shown in Figure 7.
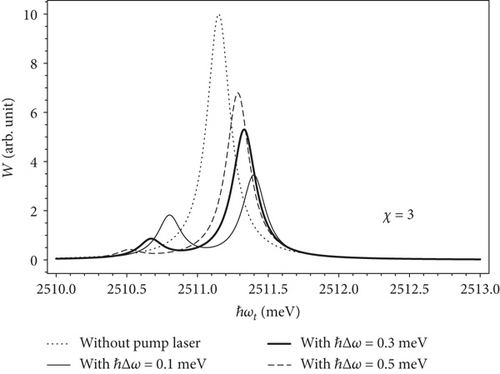
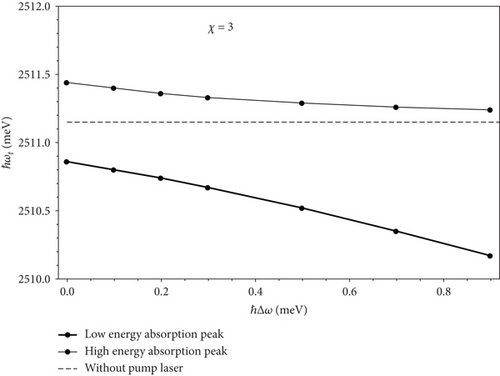
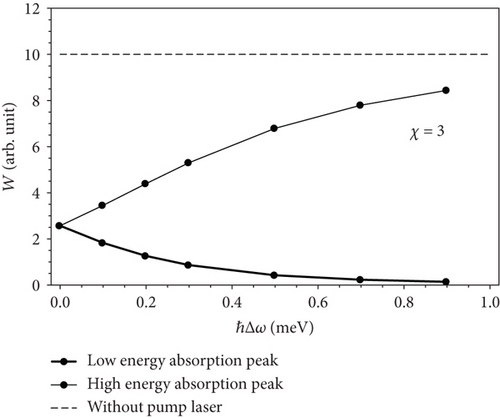
From Figure 7, we see that when the pump laser detuning is increased, the transition rate of the high-energy absorption peak increases and approaches to the transition rate of original peak when the pump laser was not active, while the transition rate of low-energy absorption peak decreases and approaching to zero. At the same time, the transition rate of these two absorption peaks depends monotonously on the pump laser detuning.
Similar to Figure 5, we also examine the dependence of the transition rate according to the photon energy of probe laser when χ = 1.8 as shown in Figure 8. Comparing Figure 5 with Figure 8, we found that the height of the low-energy absorption peak depends very sensitive on the value of χ. With the same ℏΔ ω = 0.3 meV value, when χ = 3, the height of the low-energy absorption peak is still clearly observed, but with χ = 1.8, the height of the low-energy absorption peak is very small. As the value of χ decreases, the low-energy absorption peak will almost disappear, and the high-energy absorption peak will reach the original peak. In addition, the location of these two exciton absorption peaks is also strongly dependent on the amplitude of pump laser as shown in Figure 9. In addition, in the case ℏΔ ω > 0 as presented in Figures 5 and 8, after being split (and decreasing peak intensity), the second peak intensity increases with the detuning and tends to return as in the case of no pump laser. This phenomenon can be explained as follows. When the detuning increases, the pump laser is hard to make an intraband transition between two electron levels (indicated by thick dashed arrow in Figure 4), that means it is hard to connect those two electron levels to become one big degeneracy electron level. Hence, under effect of strong electric field of the pump laser, the symmetry of the initial electron levels (as well as the symmetry of this big degeneracy electron level) is hard to be broken, and hence, the initial electron levels are hard to be split into sub-levels. This is the reason why we see one large splitting peak near the original peak (in the case of no pump laser), while another splitting peak nearly disappears. Therefore, when we probe the exciton spectrum, the second peak intensity increases with the detuning and tends to return as in the case of no pump laser, and if the detuning is large enough, we will see only one peak in the spectrum.
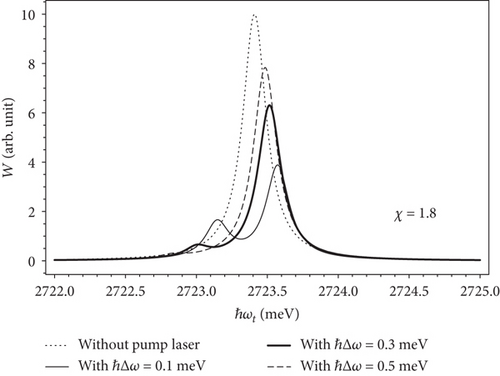
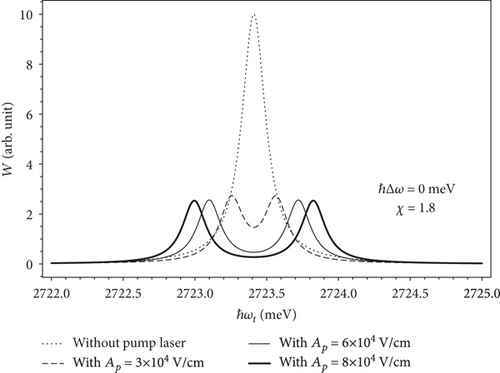
Figure 9 illustrates the absorption spectra of excitons in a prolate ellipsoidal quantum dot in the absence of the pump laser (dotted line) and in the presence of the pump laser with different amplitude of pump laser Ap = 3 × 104 V/cm (dashed line), Ap = 6 × 104 V/cm (solid line), and Ap = 8 × 104 V/cm (thick solid line) when χ = 1.8 and the pump laser detuning ℏΔ ω = 0 meV. From Figure 9, we find that when increasing the amplitude of the pump laser, the distance between the two exciton absorption peaks also increases, but these two peaks are located symmetrically on both sides of the original peak according to energy conservation law. In other words, the optical Stark effect can be controlled using the strong pump laser.
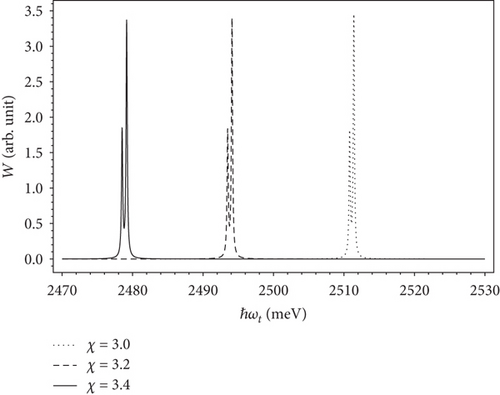
Next, we examine the effect of the χ value on the exciton absorption spectra. Figure 10 describes the dependence of transition rate on the photon energy of probe laser with the different ellipsoidal aspect ratios χ = 3 (dotted line), χ = 3.2 (dashed line), and χ = 3.4 (solid line) in the presence of the pump laser with detuning ℏΔ ω = 0.1 meV. In all three cases, we can see two exciton absorption peaks, which again confirm the existence of the excitonic optical Stark effect in this structure. Besides, when χ was increased, both absorption peaks moved quickly to the lower energy region, corresponding to a red shift in the absorption spectrum. Therefore, changing the optical properties of prolate ellipsoidal quantum dot structures will become easier to control and more flexible by changing only two parameters semi-minor axis and semi-major axis of this quantum dot structure. This is one of the advantages of ellipsoidal quantum dot structures compared to spherical quantum dots.
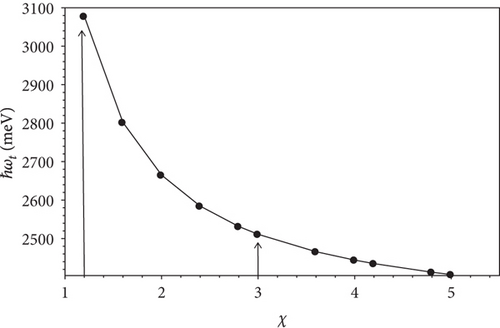
To further investigate the properties of absorption spectra of interband transitions in prolate ellipsoidal quantum dots, we continue examining the shift of the photon energy of probe laser as a function of the ellipsoidal aspect ratio χ in the case of the pump laser is not switched on (Figure 11). As shown in Figure 11, we see a red shift in the absorption spectra when increasing the ellipsoidal aspect ratio χ as mentioned in Figure 10. In particular, the strongest shift occurs in the range of 1.2 < χ < 3, and weaker displacement appears when χ > 3. This clearly shows the characteristic quantum size effect of quantum dot structures in general and of prolate ellipsoidal quantum dots in particular. We think the result will be very useful for experimental studies in choosing the wavelength of probe laser to match the size of the quantum dots to study the existence of the optical Stark effect.
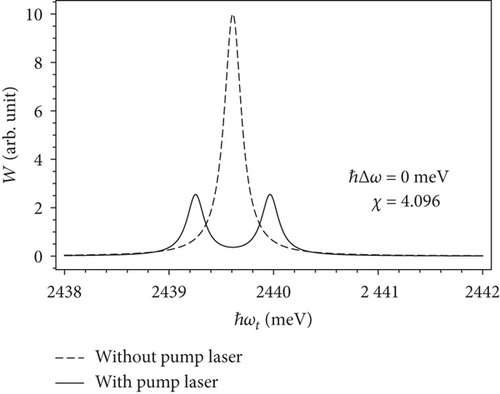
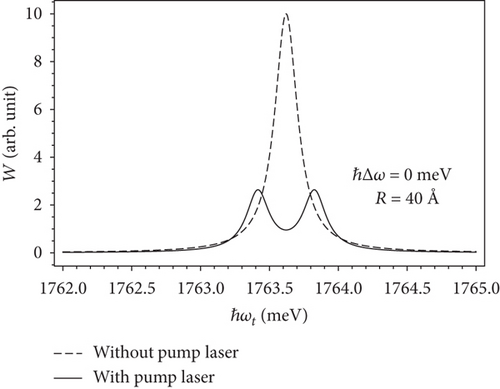
Lastly, we compare the exciton absorption spectra in the prolate ellipsoidal quantum dot (Figure 12(a)) and the spherical quantum dot (Figure 12(b)) [11] with the same volume. Derived from Eq. (15), we consider the prolate ellipsoidal quantum dot in case a = 25 Å and χ = 4.096, which show the same volume as the spherical quantum dot with radius R = 40 Å. From Figure 12, we can see that, although two structures have the same volume, the exciton absorption spectra in two quantum dots of different shapes are completely different. This means that the exciton absorption spectra, or in other words, the optical Stark effect of exciton not only depends on the pump laser detuning and size of quantum dots but also very sensitive on geometric shapes of quantum dots. The reason for the difference between the exciton absorption spectra of two quantum dot structures can be explained as follows. The shape of the quantum dots as well-known strongly affects the wavefunctions and the energy spectra of particles. Hence, the wavefunctions and the energy spectra of particles in quantum dots of different shapes are really distinct from others, though the quantum dots have the same volume. It leads to a change of the electronic transitions in those structures, resulting in a variation in the exciton absorption spectra. Moreover, because the renormalized wavefunction method is a quantum mechanical based approach, so our theory can be easily applied for the other low-dimensional structures as long as we can determine energy levels and wavefunctions of particles. In fact, we have applied our theory to the similar problems in QDs of various shapes as well as in quantum wires and quantum wells [11, 12, 37, 38].
4. Conclusion
To sum up, in this study, we have investigated the characteristics of the exciton absorption spectra in the InGaAs/InAlAs prolate ellipsoidal quantum dot through calculating the transition rate of the interband transition using the renormalized wavefunction theory. The results show that when the two quantized energy levels of electrons are coupled by a polarized pump field, one initial absorption peak of exciton is split into distinct absorption peaks as an evidence of the existence of the three-level optical Stark effect. This is the consequence of the splitting of the electron quantized levels due to the effect of the strong resonant pump laser. We also find analytical expressions for the electron splitting levels and attempt to explain the mechanism of effect generation. Another important result is that the exciton absorption spectra are not only strongly affected by the energy of the pump laser but also depend strongly on geometric shapes of quantum dots. Specifically, with the same volume, the exciton absorption spectra in the spherical quantum dots and the prolate ellipsoidal quantum dots are completely different. Furthermore, when we increase the ellipsoidal aspect ratio of the prolate ellipsoidal quantum dots, a clear red shift in the optical absorption spectra was observed. The existence of two parameters of semi-minor axis and semi-major axis in the prolate ellipsoidal quantum dot structures makes the ability to control optical properties of the ellipsoidal quantum dots easier and more flexible than the spherical quantum dots. This is one of the advantages of the ellipsoidal quantum dot structures compared to the spherical quantum dots. We believe that the interesting features in the optical absorption spectra in the prolate ellipsoidal quantum dots when the optical Stark effect occurs have the great potential application to the development of computing devices and quantum information.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
This research is funded by Vietnamese Ministry of Education and Training (MOET) under grant number B-2020-DHH-06.
Open Research
Data Availability
The material data used to support the findings of this study are included within the article.




