1. Introduction

Greek word “peristaltikos” is the origin of the word “peristalsis” that refers to being clasped and compressed. It is further employed to refer to a progressive contracting wave within a tube which may have a variable cross-sectional area. It is utilized by the bodies in physiology, to push and blend the guts inside a tube such as in uretra and other sorts of glandular vessels. The same principle is used by the roller and finger pumping devices. The theory of peristaltic transport has been deployed by multiple industries on different applications that may include sanitary ducts, blood pumping devices in the lungs. Ever since the most initial research on this topic by Latham [1], few other studies based on numerical models and experiments have also been reported under multiple conditions.

In the recent times, the researchers in the domain of physiology have experienced a peristaltic kind of motion by the intrauterine duct flows. These are caused by myometrial contractions in both symmetric and asymmetric directions. Pozrikidis [2] developed a technique that was based on integral methods to further explore the peristaltic ducts in channels for the Stokes flow conditions to comprehend the process of fluid dynamics. He investigated the patterns and mean flowing rates caused by the amplitude and phase once the walls were deformed. More experiments were done by Eytan et al. [3] to characterize contractions in women who were not pregnant and found those complications as those were of different amplitudes and with a wide range of frequencies with variable wavelengths. There has been an identification that uterine cavity’s cross section breadth tends to increase to the fundus, and it does not occlude while contracting. Similarly, Eytan and Elad [4] managed to develop a model in 2D channels where wave trains tend to move with independence on the upper walls as well as the lower ones. The orientations have been deployed to further perform evaluations in nonpregnant women’s uterus. Calculations have been done to further calculate possible particle movements to better comprehend the process an embryo goes through. Mishra and Ramachandra Rao [5] further investigated the peristaltic transport for Newtonian fluids.

The MHD flows in a channel holds much of importance with linkage to specific concerns related to the mobility of conductive fluids such as blood. This brings a need for research based on theory for the operational MHD compressor. Stud et al. [6] investigated the effects of a changing magnetic field on blood flowing channels. They managed to identify the fact that suitable field can accelerate the speed of the blood in the channel. Srivastava and Agarwal [7] studied other aspects such as after considering blood as conducting channel having a feature to suspend red blood cells in the plasma. Further studies [8–12] have also investigated other aspects related to MHD flows on peristalsis pumping.

These days, nanotechnology is revolutionizing industrial era in the current century. For the same reason, many researchers have directed their work on modeling of such thermal conductivities and have investigated multiple nanofluids having different viscosities. Such fluids have suspended nanoparticles which are generally made of different metals, oxides, or carbon-based nanotubes. Most common ones include water, oil, and toluene. Choi [13] might have been the first researcher to coin the term nanofluid, where he mentioned that heat transfer mechanism is going to be most beneficial applications of the nanofluids. Further in [14], he explained that after adding a very meager number of nanoparticles to basic liquids, thermal conduction can be increased approximately double. Similarly, Masuda et al. [15], Lee et al. [16], Xuan and Li [17], and Xuan and Roetzel [18] showed the same enhancements by more than 20%. Therefore, for heat transfer mechanisms, nanofluids can be taken up as an interesting replacement [17]. In the recent times, studies have been done for nanofluids with peristalsis as the importance of this domain linked with biosciences and chemical and mechanical engineering cannot be undermined. Such mentions are referred as [19–23].

In many industrial applications and engineering processes such as central receivers run on solar energy for creating potential through wind, cooling processes of electrical apparatus have collective forced and free convection in them. Transfer mechanism of heat and masses has effects on each other which also can yield cross-diffusion influences. The delta between the temperatures can generate mass transferring mechanism termed as Soret effect. On the contrary, when there is a heat transfer, and the difference causes an effect on the concentration gradient which is called the Dufour effect. Akram et al. [24] performed analysis in the existence of a tilted magnetic field as there are plenty of applications which are linked with peristaltic flows with double diffusion. Exact results can be acquired for a relatively new domain of nanoparticles, field of temperature, the concentration field, pressure rise, and the pressure gradient while considering the extent restrictions of longwave and a reduced Reynolds number. Authors in [25] have investigated the peristaltic flows that are induced by double diffusive convection naturally. This was to acquire analysis in an asymmetric porous channel. Current available literature studies on peristaltic flows with double diffused convection are available in references [26–29].

The no-slip conditions are used in all of the abovementioned references. In some cases, there is surely a chance that a partial slip may happen between the fluids and the surface in motion. There are recorded instances when the fluids are particulate like there is emulsion or suspension [30]. In all these instances, boundary conditions are well explained by Navier condition [31], in which the proportionality is held between the relative slip and the local stress. Research on the effects on such slips on the peristaltic mobility has been stated in the literature [32–36].

Considering the significance of the available and discussed literature and the applications linked with mixed convection in these peristaltic ducts, researchers have transformed their approaches and attention towards the theory related to double diffusion that have Carreau fluids as a fundamental fluid having slip boundaries. There is a strong chance that this investigation will head in the best manner for using the acquired data most efficiently. All the equations related to momentum, energies, and the concentration were required to be modelled with the suited physical settings such as lower wavenumbers and the Reynolds number. Equations have been solved numerically. All the results are depicted using graphs and further discussed.

2. Mathematical Formulation

For Γ = 0, the Carreau nanofluids are reduced to Newtonian nanofluids.

There are no-slip conditions if η₁, η₂, η₃, η₄ = 0 in the above conditions.

3. Results and Discussion

This section depicts the mathematical and realistic consequences of the present topic under study. The systems of PDE’s (23), (25)–(27), and (28) are coupled and nonlinear in nature. So, finding the exact solution to these equations is extremely difficult. As a result, the built-in command MATHEMATICA is used to calculate the numeric solution (NDSolve). To check the accuracy of the proposed numerical results and to compare our findings to the available literature, a slew of graphs was created.

3.1. Flow Characteristics

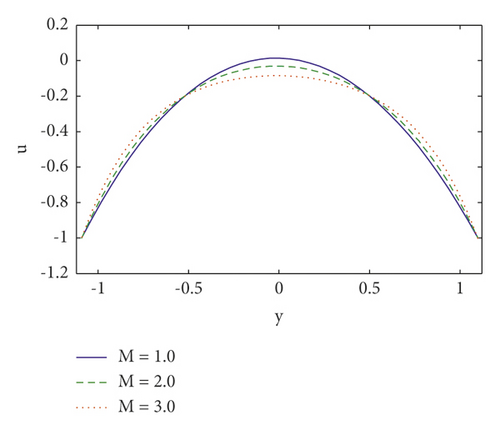
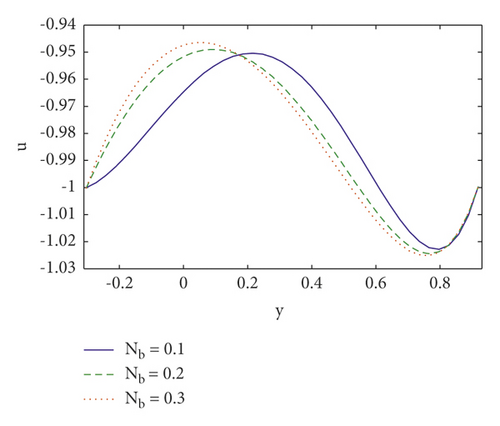
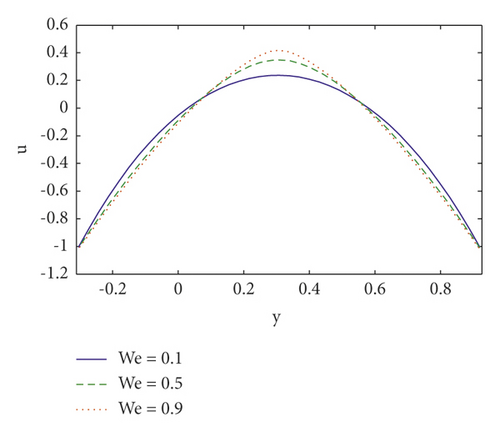
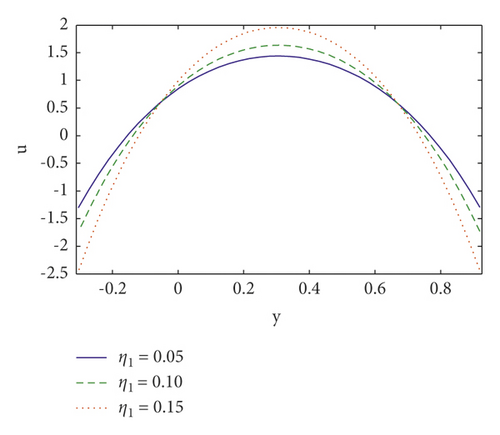
The profile of velocity under the stimulation of Hartmann number M, Brownian motion N_b, Weissenberg number We, and velocity slip parameter η₁ is shown in Figures 1(a)–1(d). The behaviour of velocity field for increasing values of Hartmann number is plotted in Figure 1(a). We can notice that increasing M tends to resist the flow, resulting in a decrease in fluid velocity. This occurs because when a magnetic field is produced, a resistive force (or “Lorentz force”) is created, which operates in the opposite direction of the flow, causing the velocity field to decrease (see Figure 1(a)). It is noted in Figure 1(b)) that the magnitude of velocity distribution decreases at the left side of the channel, whereas it decreases at the right side of the channel by raising the Brownian motion parameter N_b. It is depicted in Figure 1(c) that when Weissenberg number grows, velocity will increase. However, near the channel walls behaviour is opposite. This occurs because We has a direct relationship with the time constant and an inverse relationship with the channel width. The axial velocity increases near the channel’s center as the velocity slip parameter η₁ is raised, as seen in Figure 1(d). Furthermore, opposite behavior is found near the boundaries.

3.2. Pressure Rise and Pressure Gradient

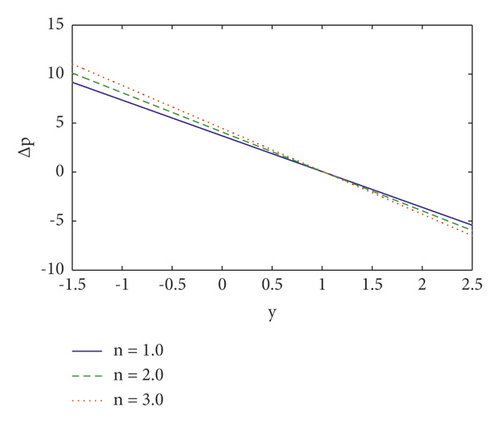
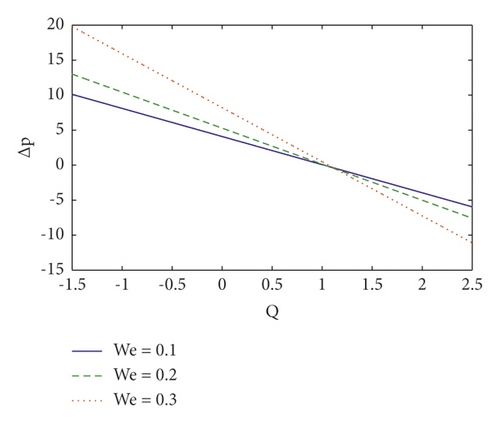
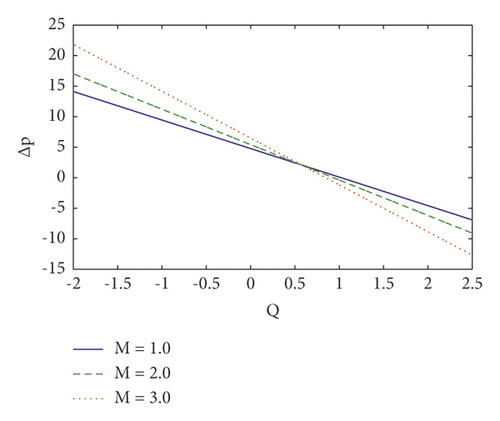
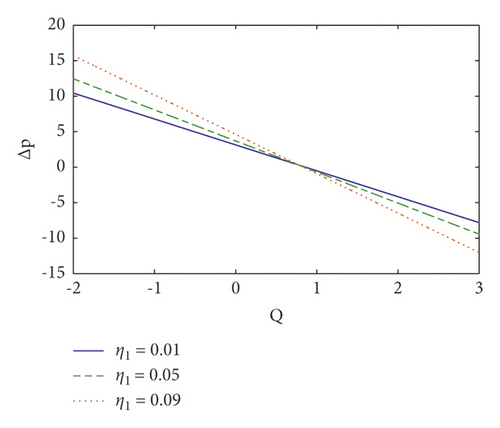
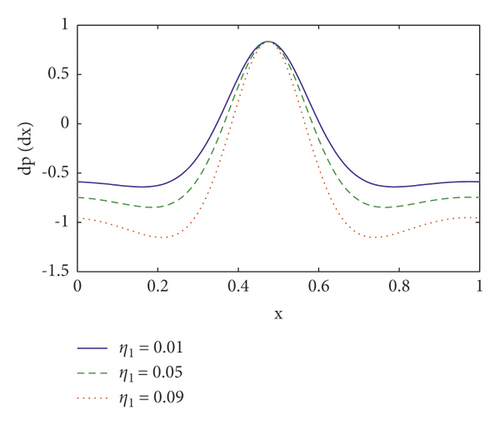
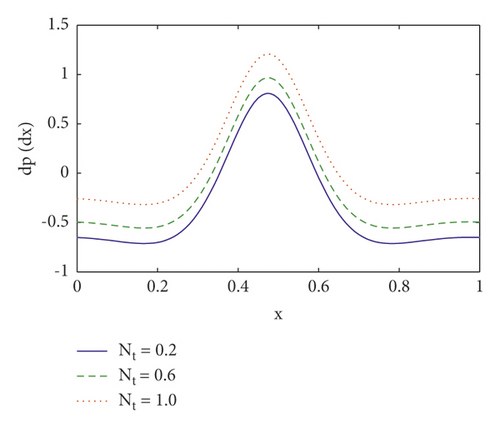
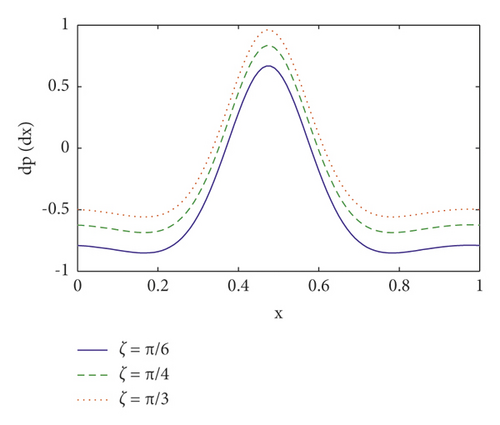
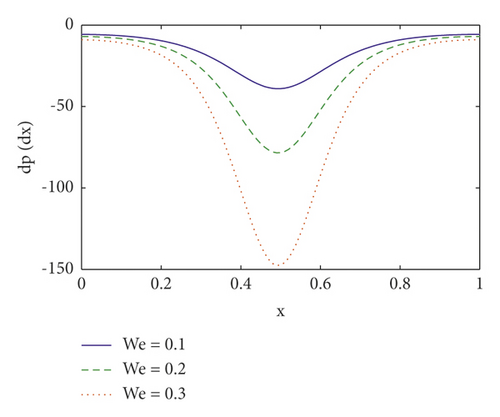
Pumping is a hallmark aspect of peristalsis. The effects of several emergent factors on pressure rise per wavelength and pressure gradient are described in this section. Figures 2(a)–2(d) show the change in pressure rise against flow rate Q for various values of the parameters n (power law index), We (Weissenberg number), M (Hartmann number), and η₁ (velocity slip parameter). From these figures, it is noted that in retrograde (Δp > 0, Q < 0), peristaltic (Δp > 0, Q > 0), and free (Δp = 0) pumping regions, the pressure rise increases due to the increasing values of n, We, M, and η₁ and whereas in copumping (Δp < 0, Q > 0) region pressure rise drops due to the increasing values of n, We, M, and η₁. The fluctuation of axial pressure gradient for different values of the η₁ (velocity slip parameter), N_t (thermophoresis parameter), ζ (inclination angle), and We (Weissenberg number) is shown in Figures 3(a)–3(d). We observe that the pressure gradient is quite modest in the larger region of the channel at x ∈ [0,0.3] and x ∈ [0.5, 1.0], indicating that the flow can readily pass without imposing a high-pressure gradient, where a substantially bigger pressure gradient is necessary to maintain the same flux in a small region of the channel at x ∈ [0.3, 0.5], particularly for the widest region at x = 0.5. This is in line with the current physical situation. We also notice that as the velocity slip parameter η₁ is increased, the axial pressure gradient falls (see Figure 3(a)). When N_t and ζ is increased, the pressure gradient increases (see Figures 3(b) and 3(c)). Furthermore, as seen in Figure 3(d), the magnitude value of axial pressure gradient grows as the Weissenberg number (We) increases.

3.3. Temperature, Concentration, and Nanoparticle Volume Fraction

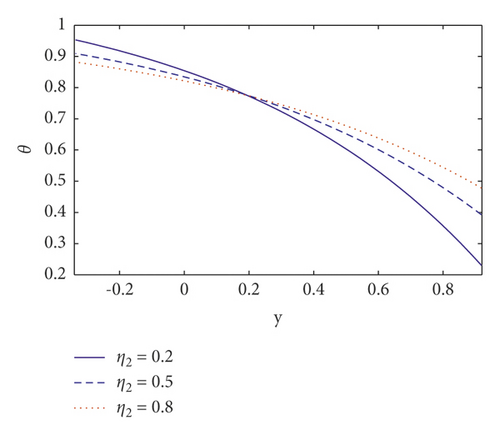
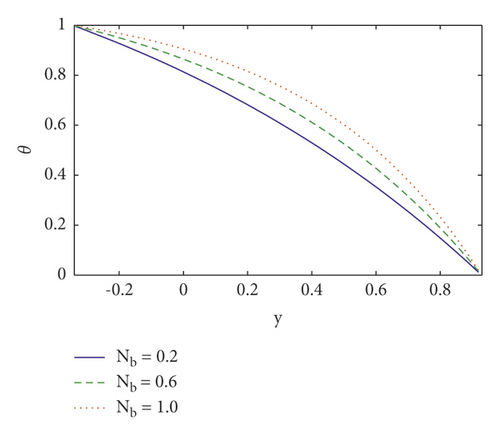
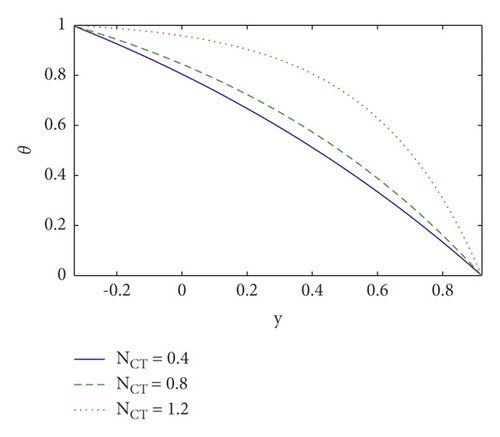
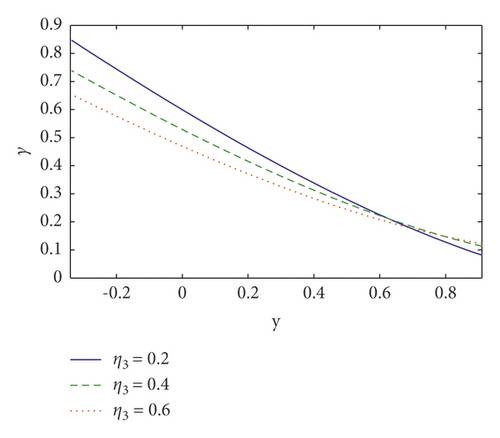
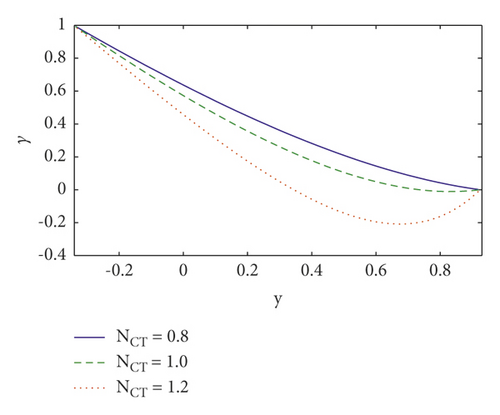
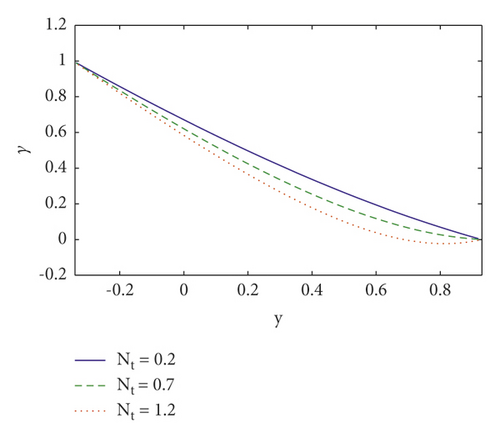
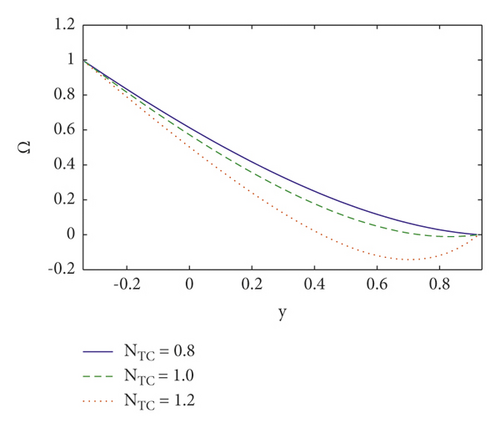
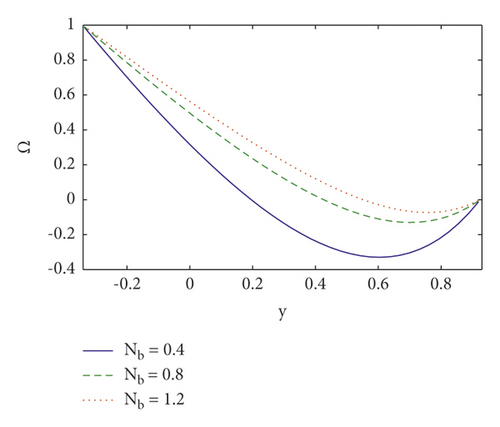
This section analyses the impact of many salient parameters on temperature, concentration, and nanoparticle volume fraction. Figures 4(a)–4(c) shows the temperature profile for various values of thermal slip η₂ parameter, Brownian motion N_b parameter, and Soret parameter N_CT. It is noted in Figure 4(a) that when y ∈ [−0.1, 0.2], the temperature profile drops by increasing thermal slip parameter η₂ whereas when y ∈ [0.2, 1] the temperature profile increases. The temperature increases by increasing Brownian motion parameter and Soret parameter (see Figures 4(b) and 4(c)). It is because Soret parameters have a direct relationship with temperature. Furthermore, nanoparticles travel efficiently from the wall to the fluid via enhancing Brownian motion. As a result of this impact, temperature rises as N_b and N_CT rise. The concentration profile is shown in Figures 5(a)–5(c) for various values of the concentration slip parameter η₃, Soret parameter N_CT, and thermophoresis parameter N_t. It is noted in Figures 5(a) that increasing concentration slip parameter η₃ lowers the concentration profile in the region y ∈ [−0.1, 0.6], while raising it in the region y ∈ [0.6, 1]. The concentration decreases by increasing Soret parameter N_CT and thermophoresis parameter N_t (see Figures 5(b) and 5(c)). It is due to the influence of random motion with micromixing and erratic collision activity of solid nanoparticles, which disperses the solid nanoparticles and so lowers the solute concentration. Figures 6(a)–6(c) show the nanoparticle fraction for various values of the nanoparticle slip parameter η₄, Dufour parameter N_TC, and Brownian motion parameter N_b. It is noticed in Figure 6(a) that increasing nanoparticle slip parameter η₄ lowers the nanoparticle profile in the region where y ∈ [−0.1, 0.6], while raising it in the region where y ∈ [0.6, 1]. When the Dufour parameter N_TC is increased, the nanoparticle fraction falls (see Figure 6(b)). It is observed in Figure 6(c) that the nanoparticle volume fraction profile grows as Brownian motion parameter increases.

3.4. Trapping

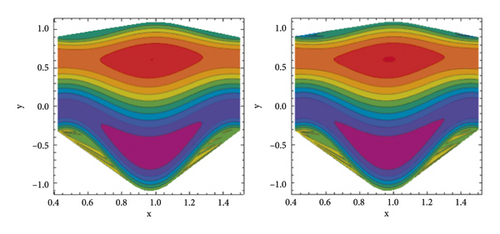
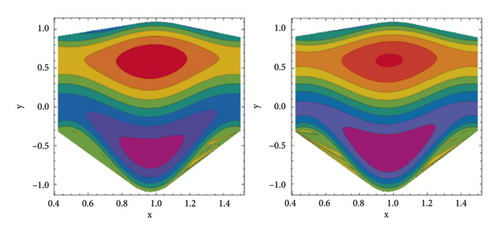
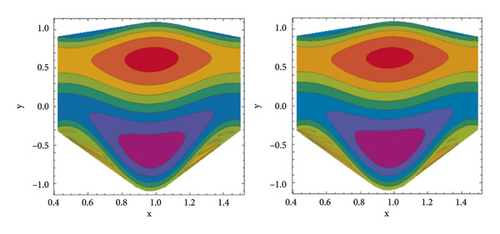
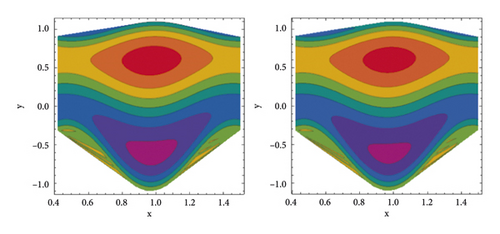
Another remarkable characteristic of peristaltic movement is trapping. It is the phenomenon of closed streamlines generating a bolus of fluid that circulates inside. Streamlines grab the fluid mass bolus and drive it forward with peristaltic waves at high flow rates and substantial occlusions. In Figures 7–10, streamlines are plotted to show the phenomenon of trapping. The behaviour of streamlines for various Weissenberg numbers is depicted in Figure 7. It is observed from these streamlines that, by raising Weissenberg numbers, the number of trapped bolus grows in the upper half of the channel while the size of trapped bolus increases in the lower half. Figure 8 depicts the streamlines when the velocity slip parameter β₁ is increased. As illustrated in Figure 8, the size of trapped bolus reduces in the upper half of the channel, whereas the number and size of trapped bolus decrease in the lower half by increasing β₁ values. As the thermal Grashof number rises, the size of the trapped bolus grows larger (see Figure 9), and as the Hartmann number rises, the size of the trapped bolus shrinks (see Figure 10). The current study’s findings are compared to the existing literature in Table 1.

Table 1. The comparison of velocity profile with existing literature.

y	Present work	Mishra and Rao [5]
0.919093	−1	−1
0.796856	−0.599634	0.530207
0.674618	−0.243748	−0.18806
0.55238	0.0493734	0.0434474
0.430142	0.261644	0.178543
0.307905	0.34998	0.225119
0.185667	0.265135	0.185251
0.063429	0.054073	0.0553249
−0.0588087	−0.239407	−0.174226
−0.181046	−0.596941	−0.519578
−0.303284	−1	−1

4. Conclusions

Conflicts of Interest

The authors declare that they have no conflicts of interest.