Volume 2020, Issue 1 8883655

Research Article

Open Access

ARSS: A Novel Aerial Robot Performs Tree Pruning Tasks

Hao Xu

orcid.org/0000-0002-1658-0068

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China nuaa.edu.cn

School of Mathematics & Physics, Anhui University of Technology, Anhui 243032, Ma’anshan, China ahut.edu.cn

Search for more papers by this author

Zhong Yang,

Corresponding Author

Zhong Yang

[email protected]

orcid.org/0000-0002-0988-3757

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China nuaa.edu.cn

Search for more papers by this author

Le Chang,

Le Chang

orcid.org/0000-0002-6202-9568

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China nuaa.edu.cn

Search for more papers by this author

Kaiwen Lu,

Kaiwen Lu

orcid.org/0000-0003-2618-3733

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China nuaa.edu.cn

Search for more papers by this author

Changliang Xu,

Changliang Xu

orcid.org/0000-0002-8976-6832

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China nuaa.edu.cn

Search for more papers by this author

Qiuyan Zhang,

Qiuyan Zhang

Guizhou Electric Power Research Institute, Guizhou Power Grid Co. Ltd., Guiyang, Guizhou 550000, China

Search for more papers by this author

Hao Xu,

Hao Xu

orcid.org/0000-0002-1658-0068

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China nuaa.edu.cn

School of Mathematics & Physics, Anhui University of Technology, Anhui 243032, Ma’anshan, China ahut.edu.cn

Search for more papers by this author

Zhong Yang,

Corresponding Author

Zhong Yang

[email protected]

orcid.org/0000-0002-0988-3757

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China nuaa.edu.cn

Search for more papers by this author

Le Chang,

Le Chang

orcid.org/0000-0002-6202-9568

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China nuaa.edu.cn

Search for more papers by this author

Kaiwen Lu,

Kaiwen Lu

orcid.org/0000-0003-2618-3733

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China nuaa.edu.cn

Search for more papers by this author

Changliang Xu,

Changliang Xu

orcid.org/0000-0002-8976-6832

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China nuaa.edu.cn

Search for more papers by this author

Qiuyan Zhang,

Qiuyan Zhang

Guizhou Electric Power Research Institute, Guizhou Power Grid Co. Ltd., Guiyang, Guizhou 550000, China

Search for more papers by this author

First published: 14 October 2020

https://doi.org/10.1155/2020/8883655

Citations: 2

Academic Editor: Jia-Bao Liu

Share a link

Email
Wechat
Bluesky

Abstract

In this article, we present a novel aerial robot with a suspended saw (ARSS) for pruning trees that are close to electric power lines. The Robot’s movement process includes free flight and aerial pruning. We first established a dynamic model and designed a controller based on the Active Disturbance Rejection Control (ADRC) on the model. Aiming at the problem of saw swing and residual oscillation during the free flight movement, we adopt the linear state feedback to design a swing angle controller. Finally, we use Matlab/Simulink and CoppeliaSim for simulation, and the simulation results verify the effectiveness and feasibility of the controller.

1. Introduction

As Aerial Robots are increasingly deployed in a broad spectrum of real-world, there is a growing demand to broaden their application scenario [1]. The Robot has the advantages of small size, strong maneuverability, and the ability to hover at a fixed point. It has become an excellent aerial work platform, and it has been used in cargo transportation [2], spraying pesticides [3], etc. Tree barrier pruning is a new application of aerial robots. A tree barrier is a tree that grows near the power line. Its branches will grow between the power lines and may cause a short circuit on the power line. These problems are caused due to contact tree branches with wires of power towers. This contact is one of the significant reasons for interrupting power services. The traditional method is that a person carries a pruning tool to climb the tree to cut the branches that will cause a short circuit of the power line. This method is hazardous and quickly causes personal injury. However, using aerial robots to carry pruning tools and fly to the vicinity of the branches to be cut will improve work efficiency and safety.

Moreover, the installation position of the cutting tool on the aerial Robot will cause differences in modeling and control. To the best of our knowledge, the pruning tool can be installed on the top [4–6], front [7], and bottom of the fuselage [8]. The branches that need to be cut are generally at the crown of the tree. Moving the drone to the top of the tree can improve the pruning efficiency. Therefore, our design is to install the pruning tool under the fuselage through a rope hanging method. This installation method is the mode for a multirotor helicopter with suspended loads [9]. When the robot performs tasks, there are several difficulties to overcome. First, because of the movement of the fuselage and its own inertia, the load will swing in the air. The swing will increase the control difficulty and model uncertainty of the robot. Second, due to the limited space under the fuselage and the problem that the shape of the load does not match the fuselage, there are a lot of restrictions on the choice of load.

To the best of our knowledge, research on the multirotor helicopter with suspended loads has been receiving attention, and many effective control methods have been proposed. In [10], a nonlinear controller based on the backstepping control algorithm is designed so that the drone can still perform a good trajectory tracking when the hanging load swings significantly; Alothman and Gu [11] uses a differential smoothing method to design a four-rotor UAV controller with suspended load, which realizes the trajectory generation and tracking of this system; Faust et al. [12] denotes an iterative linear-quadratic optimal controller, which realizes the trajectory tracking control of the UAV and suppresses the swing of the hanging load. Palunko et al. [13] adopts a reinforcement learning method to train the helicopter flight control system and realize the trajectory planning of hanging load. In [14], the researchers studied the take-off process of a quadcopter drone with a load. Yang et al. [15] solved the problem of the quadrotor achieving safe take-off under the condition that the hanging load is unknown, and the simulation results confirmed the effectiveness of its algorithm. Complex network theory [16, 17] can plan the tasks of aerial robots.

However, the research results of multirotor drones with hanging systems are remarkable, but many methods still have some limitations. The controller designed in [10] can achieve reasonable trajectory tracking control but does not control the position of the hanging load. The control effect of the controller designed in [11, 12] is significant, but the controller is complex and requires high computing resources for the onboard computer. The controller in [13] can only be used under a load of a specific weight. When changing the load, reinforcement learning is required again, and the portability is not good. The authors of [14, 15] focused on the take-off and landing issues, but did not focus on the entire flight process. References [16, 17] only analyze and prove mission planning but do not involve specific controller design.

In this article, we present the ARSS, an Aerial Robot with Suspended Saws. ARSS can use the hanging saw to cut and clean horizontally growing tree barrier. In order to solve the model uncertainty and disturbance in the execution of aerial pruning tasks, we used the Active Disturbance Rejection Control (ADRC) [18] to design the controller. The main components of ADRC include Tracking-Differentiator (TD) [19], Extended State Observer (ESO) [20, 21], and Nonlinear State Error Feedback (NLSEF) [22], all of which we have covered. We summarize the contributions as follows:

(1)
A novel a novel aerial robot can prune trees well.
(2)
As the position and attitude are controlled by the ADRC method without linearizing the system model, this robot system can achieve better control results when it is far from the equilibrium point, and the system has high robustness.
(3)
In addition, the controller has a simple structure and does not require high calculation speed of the onboard microprocessor.

In the rest of the article, we first discuss the dynamic model of ARSS; next, the controller based on ADRC is introduced including attitude control, position control and control allocation. We also verified the entire Robot under Matlab/Simulink and CoppeliaSim. Finally, we give some conclusions and future work.

2. Mathematical Model

2.1. Coordinates and Conventions

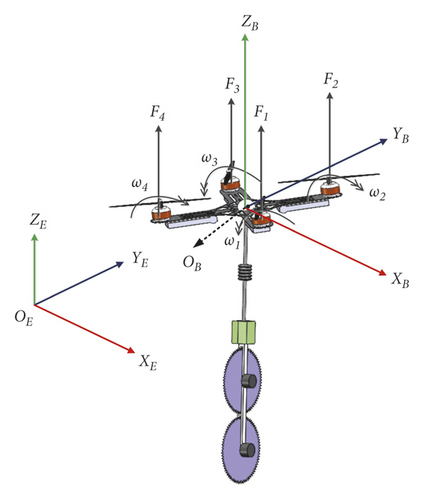
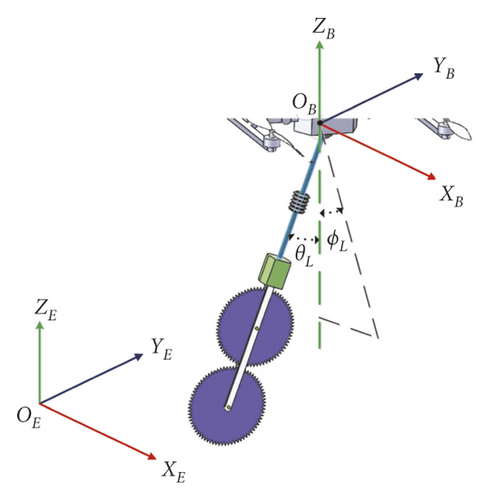
Overall, two coordinate frames were used. The inertial frame E{O_E, X_E, Y_E, Z_E} is fixed on the ground, and its z axis points upward. And the body frame B{O_B, X_B, Y_B, Z_B} is fixed on the COG, the z axis of the frame points upward, as seen in Figure 1. The Suspended Saws system is shown in Figure 2, L is the length of the rope, and l is the distance from the motor axis to the COG. ϕ_L is the angle between the projection of the connecting rod in the O_bX_bZ_b plane and the z_b axis, θ_L is the angle between the connecting rod and the above projection.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The inertial and body frames.

2.2. Assumptions

For the sake of model simplicity and algorithm efficiency, the following assumptions were made:

(1)
The body structure is rigid and symmetric
(2)
The geometric center and CoG of the Robot are the same
(3)
The rope is rigid, non-stretchable, and of no quality
(4)
The load is always under the body

2.3. Notation

Throughout the article, we use right-hand rules for the coordinate system. The attitude angles of the body are [θ, ϕ, ψ]^T ∈ ℝ³ including Pitch angle θ, Roll angle ϕ, and Yaw angle ψ, and [p, q, r]^T ∈ ℝ³ denote the angular velocity in the body frame. [x, y, z]^T ∈ ℝ³ denotes the position in the inertial frame.

The matrix _E^BR stands for the rotation matrix that rotates a vector represented in the inertial frame {E} to the body frame {B}. The rotation matrix is defined as

(1)

where _E^BR ∈ SO(3), SO(3)≜{R|R^TR = I₃, det(R) = 1, R ∈ ℝ^3×3} with s_(⋅) representing the sine and c_(⋅) the cosine.

2.4. Body Dynamic Model

For the modeling of the body dynamics, the Newton–Euler formalism was used. The Equilibrium equation is as follows:

(2)

with M being the mass of the aerial Robot and I_b the moment of inertia. I_b is defined as follows:

(3)

where I₁₂, I₁₃, I₂₃ are smaller than I₁₁, I₂₂, I₃₃, respectively. Define

(4)

The solution to equation (3) is

(5)

According to equation (4), the forces

and torques

act on the COG of the body. Then the relation between angular velocity [p, q, r]^T and attitude angle [θ, ϕ, ψ]^T can expressed as

(6)

Regardless of external disturbances, the aerial Robot is mainly subjected to the gravity in the negative direction of the O_eX_e axis and the lift F_i, i = 1,2,3,4 generated by the four rotors pointed by the positive direction of the O_bZ_b axis. F_i is related to lift coefficient C_T and rotating speed ω_i, which is given by

(7)

Therefore, let F_t be the total lift so that

(8)

According to equation (1),

is obtained as follows:

(9)

Based on assumption (2), the resultant torque is mainly generated by the lift and counter torque at the rotor that does not pass through the center of mass, while gravity does not produce torque. The torque generated by the rotor lift constitutes the moment around the O_bX_b and O_bY_b axis, and the antitorque of the rotor constitutes the moment around the O_bZ_b axis, given by

(10)

where L is the distance between the center point of the rotor and the centroid of the Robot.

On the basis of Equations (8) and (10), one has

(11)

By combining Equations (2), (9), and (11), the body dynamic model is expressed as

(12)

2.5. Suspended Saws Model

For the modeling of the saws dynamics, the Lagrange formalism was used. Its general form is the following:

(13)

where

represents the kinetic energy and u(Θ) expresses potential energy; Θ denotes the generalized coordinate and Q is generalized forces.

As shown in Figure 1, the equation set from Saws position (x_L, y_L, z_L) to the body position (x, y, z) is further obtained as

(14)

where l represents the rod length.

Combining equation (14), kinetic energy

is expressed as

(15)

Then potential energy is

(16)

Among the saws dynamic model, generalized coordinate

and generalized forces

. By combining equations (13)–(17), the ARSS dynamic model is expressed as

(17)

where

(18)

(19)

(20)

3. Controller Design

The general aerial Robot only needs to control the position and attitude, and ARSS not only needs to control the position and attitude, but also needs to control the swing angle of suspended saw. The position change of the Robot will cause the saw swing. If the swing angle is not controlled, the saw may swing violently, affecting the robot stability, so it is necessary to control the swing angle of the suspended saw. ADRC has the advantages of low model dependence and strong anti-disturbance, and it has good applicability to ARSS with complex model and large disturbance.

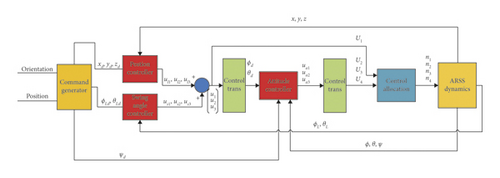
In this section, we present a baseline controller for the ARSS platform. The controller is based on ADRC including attitude and position control, and uses a linear state feedback to design the swing angle controller. The controller is a double-loop structure, the outer loop is position control, and the inner one is attitude control. Control structure shown in Figure 3.

3.1. Attitude Control

The attitude controller controls the attitude angle a, so equation (6) needs to be transformed to obtain the expression of Euler angle. Because the expression contains a large number of non-linear elements and coupling terms, a common solution is the small angle approximation method, which limits the attitude angle change in a small range, so that the Euler angle change is approximately equal to the angular velocity (p, q, r). However, such a processing method can only allow the controller to have a good control effect within a small range of attitude angle changes. If the attitude angle changes too much, the performance of the controller will be greatly reduced. The other method is to add a layer of angular velocity loop on the basis of the small angle approximation method to make the attitude controller into a double-loop structure. Although this method has a certain effect, it will make the structure of the controller very complicated and many parameters, it is difficult to adjust the parameters.

ADRC can solve this problem well. ADRC has low dependence on the mathematical model of the controlled object. It can treat the coupling item as an unmodeled part of the system and compensate the coupling item by Extended State Observer (ESO). Therefore, we adopt ADRC to design ARSS attitude controller.

First, the derivative of equation (6) can be obtained:

(21)

Then, combining equations (3)–(5) with equation (21), one has

(22)

Consequently,

(23)

where R_c is reversible and k is an integer when θ ≠ (2k + 1)π/2 and ϕ ≠ (2k + 1)π/2.

Equation (23) is very complicated and there are non-linear and coupling terms, it is very difficult to design the controller directly for this model. ADRC can simplify the model and treat the nonlinear and coupling terms as unmodeled parts. Consequently, the equation (23) becomes

(24)

where (s₁, s₂, s₃) denote coupling and nonlinear part, (u₁, u₂, u₃) are virtual control and the relationship with input torque is shown in equation (24). From this, the desired control input can be obtained

(25)

Here, the math model required by the attitude controller can be obtained, the decoupling of pitch, roll and yaw is completed, and this multiple input multiple output (MIMO) model is converted into three single-input single-output (SISO) subsystems. From equation (25), these subsystems are second-order linear systems.

Taking the roll angle θ for example, we established the ADRC attitude controller to roll motion, and the structure diagram is shown in Figure 4.

When z₁ = θ,

, equation (24) is rewritten as

(26)

where w_θ represents the disturbance to θ;

represents the sum of internal and external disturbances estimated by the Expanded State Observer (ESO). Equation (26) complies with the second-order form of the ADRC standard and can be designed as a second-order attitude controller. The specific design steps are as follows:

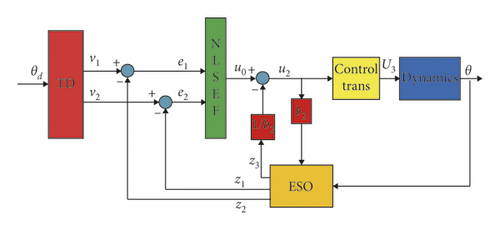
3.1.1. Design TD

TD is shown in equation (27):

(27)

where v(k) is the desired pitch angle θ_d which is given by the position controller, v₁(k) is the tracking signal of θ_d, and v₂(k) is the derivative of v₁(k). T is the sampling period of the discrete signal, fhan(v₁(k) − v(k), v₂(k), r, h) is the nonlinear function, and its expression is as follows:

(28)

where r and h are adjustable gains. r is called the fast factor, and a suitably large one can achieve a faster tracking speed; h is called the filter factor, and the larger the h, the better the filtering effect. But the increase of h will bring about an increase in phase delay, generally h takes 5 ~ 10 T.

3.1.2. Design ESO

The ESO is as shown in equation (29)

(29)

where y(k) denotes the actual pitch angle of θ; z₁ is the estimated value of θ, z₂ is the estimated value of

, z₃ is the estimated value of total disturbance; u represents the virtual control u₂ which mentioned in equation (24), and b = 1.

3.1.3. Design SEF

We use the fastest control synthesis function, which is expressed as

(30)

where r and h are consistent with the description in equation (29), c denotes damping coefficient. When c ∈ (0,1), the system. Underdamped; when c > 1, the system overdamped.

From equation (30), the control output u₀ of SEF can be obtained，then combining equation (31) to compensate for disturbances observed by ESO, we get the total control output u₂ of the rolling channel. Equation (31) is

(31)

where z₃ and b are the same as equation (29)

Using the same method, the control outputs u₁, u₃ of the roll, yaw channel attitude controllers can be obtained, respectively. In this case, according to equation (25), the control input is acquired. The attitude controller is shown in Figure 5.

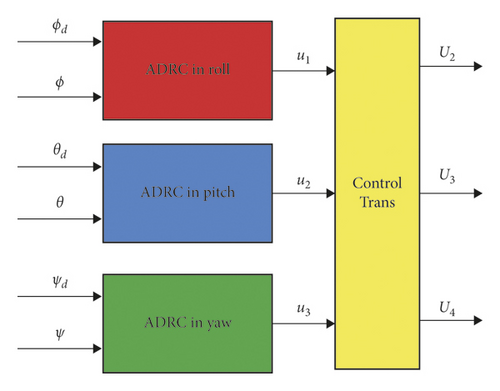
3.2. Position Control

When designing a position controller, we need to control the position of the aerial Robot and suspended saw. The position change will cause the swing of the saw. If the swing angle is not controlled, the saw may swing violently, affecting the stability of the aerial Robot, so it is necessary to control the swing angle of the hanging saw. ADRC has the advantages of low model dependence and strong anti-disturbance, and it has good applicability to ARSS with more complex models and larger disturbances.

Similar to the attitude controller, equation (12) is rewritten as

(32)

where

(33)

T is defined as follows:

(34)

During the flight of the Aerial Robot, the swing angle of the suspended saw is small. According to the Small-Angle Approximation, the approximate solution is given by

(35)

Thus, equations (19) and (20) are simplified as

(36)

The ARSS is decomposed into the aerial robot part of the standard second-order model and the suspended saw part of the linear model. Position control is changed to control the aerial Robot while ensuring the stability of the linear part, so that the saw swing during flight is gradually reduced.

First, design the position controller of the aerial robot part. Similar to the attitude controller, equation (32) is converted into three SISO subsystems, and these subsystems are second-order standard.

Taking x for example. When z₁ = x and

, equation (32) is rewritten as

(37)

where w_x represents the disturbance to x and u₁ denotes virtual control. Similar to the attitude controller, the specific design steps are as follows.

3.2.1. Design TD

TD is defined as

(38)

where v(k) is the desired position x_d which is given by the position controller, v₁(k) is the tracking signal of x_d, and v₂(k) is the derivative of v₁(k). T_s is the sampling period of the discrete signal. r and h are adjustable gains. fhan(v₁(k) − v(k), v₂(k), r, h) is the non-linear function, and its expression is as follows:

(39)

3.2.2. Design ESO

The ESO is shown as

(40)

where y(k) denotes the actual position x; z₁ is the estimated value of x, z₂ is the estimated value of

, and z₃ is the estimated value of total disturbance w_x; u represents the virtual control u₁ and b = 1; β₀₁, β₀₂, β₀₃, α₁ and α₂ are parameters.

fal(∗) is a non-linear function, and its expression is shown as

(41)

where α and δ are parameters, with 0 < α < 1 and δ > 0.

3.2.3. Design State Error Feedback (SEF)

The position control does not have strict requirements for fast response, so a linear SEF with simple structure and easy parameter adjustment can be used. We have

(42)

where β₁ and β₂ are parameters.

From equation (40), we compensate the disturbances observed by ESO, we get the total control output u₂ of the channel x. With the same method, the output and of the other two channels can be obtained, and the required control amount can be obtained according to equation (25). The position controller structure is shown in Figure 6.

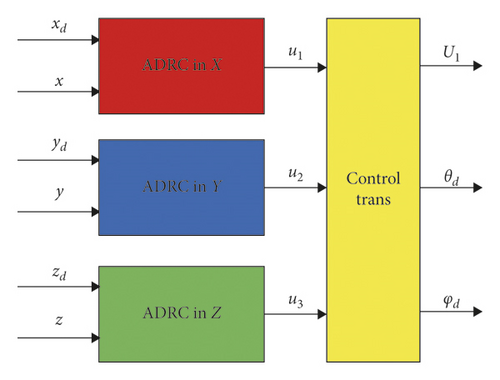
3.3. Suspended Saw Controller

In the Suspended Saw model, ϕ_L and θ_L describe the swing state of the suspended saw. ϕ_L denotes the angle between the projection of the connecting rod in the O_bX_bZ_b plane and the z_b axis, the acceleration of the aerial Robot in the x and z axes will affect ϕ_L. Similarly, the acceleration in the y-axis and z-axis directions will affect θ_L. The height and horizontal position are generally not controlled at the same time, so the influence of the acceleration in the z-axis direction on the swing angle can be ignored. Considering that ARSS performs position control, it also needs to control swing angle, equation (36) is rewritten as

(43)

When designing the position controller, the linear dynamic compensation method of ADRC is used to transform the non-linear model of the aerial Robot into a series model, that is,

(44)

Then, combining equations (43) and (44) with equation (36), the system is described by

(45)

where K_i, i = 1, …, 4 are gains.

For this linear closed-loop system, sufficient and necessary conditions for its asymptotic stability are that all the characteristic roots are in the left half of the complex plane; that is, the real parts of all the characteristic roots are all negative. According to the Routh criterion, its characteristic roots are all in the left half of the complex plane and need to satisfy

(46)

As long as the parameter K_i satisfies, the swing angle of the hanging saw can be gradually stabilized.

4. Evaluation

In this section, we present our experiment. In each experiment, we simulate a complete tree-barrier removal task. Each task is divided into two stages: free flight and aerial pruning. The controller was tested in simulation, which used CoppeliaSim [23] as a physics environment and to model the Robot. The controller is programmed under MATLAB/Simulink. Table 1 summarizes the numerical values used to simulate, and Table 2 shows the controller parameters. The parameters in Table 2 are adjusted by a parameter self-learning algorithm CARLA-ADRC [24].

Table 1. Simulation parameters.

Parameter	Value
M	8.5 kg
l	0.4 m
m	1.0 kg
L	1.0 m
g	9.81 m/s²

Table 2. Controller parameters.

ADRC	ϕ	θ	ψ	x	y	z
TD-r	3000	3000	3000	4	4	4
TD-h	0.01	0.01	0.01	0.01	0.01	0.01
ESO-β₀₁	1000	1000	1000	1000	1000	1000
ESO-β₀₂	19764	19764	19764	19764	19764	19764
ESO-β₀₃	462902	462902	462902	462902	462902	462902
ESO-α₁	0.5	0.5	0.5	0.5	0.5	0.5
ESO-α₂	0.25	0.25	0.25	0.25	0.25	0.25
ESO-δ	0.001	0.001	0.001	0.001	0.001	0.001
ESO-b	1	1	1	1	1	1
SEF-c	0.95	1.05	0.95	—	—	—
SEF-r	108.73	108.73	108.73	—	—	—
SEF-h	0.05	0.05	0.05	—	—	—
SEF-k₁	—	—	—	50	50	400
SEF-k₂	—	—	—	41	41	50

All experiments have considered numerical indicators, including integral of squared of tracking error, integral of squared of control signal. In the next section, we will choose one experiment sample to explain.

4.1. Attitude Control Experiment

First, verify the attitude controller and design the attitude tracking experiment. For example, the desired signals of roll, pitch, and yaw of 10° are given in the first, fourth, and seventh seconds, respectively. The experiment result is shown in Figure 7.

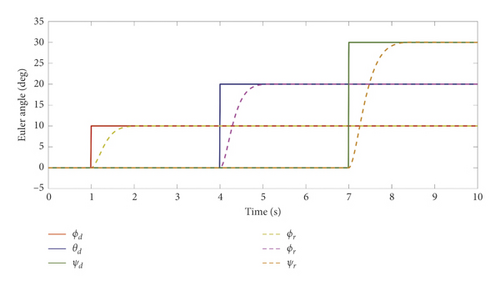
It can be seen from Figure 7 that the attitude controller can quickly track the desired signal, in which the tracking response time of pitch and roll angle is 1 s, the tracking response time of the yaw angle is 1.3 s, and there is no overshoot in each channel of the attitude angle. It proves that the attitude controller has good speed and stability.

4.2. Free-Flight Experiments

When performing the pruning task, we first fly ARSS to a desired position close to the tree. Suppose that in an experiment, the ARSS is controlled to fly to the desired position [2,2,1.5]^T ∈ ℝ³ in the inertial frame. At 0 s, give an 1.5 m step signal in the z axis; at 5 s, give a 2 m step signal in the x-axis; at 10 s, give a 2 m step signal in the y-axis, and then keep hovering. The simulation duration is 25 s in total. The curves of position and swing angle during the simulation are shown in Figure 8.

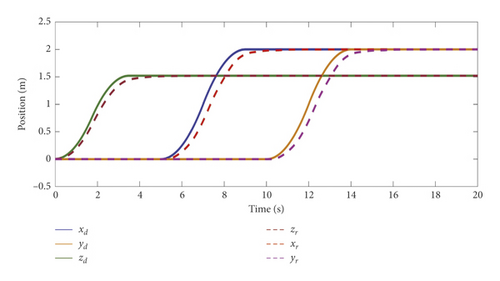
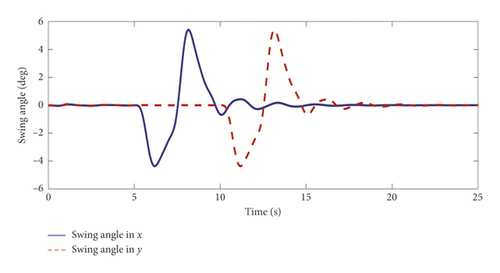
It can be seen from Figure 8(a) that because the swing of the saw cannot be too large, the aerial Robot cannot fly too fast, so the transition process of the TD link arrangement is relatively smooth. The response curve shows that the position error in the x and y axes is always kept within 0.4 m, and there is no overshoot; the error in the x-axis is kept within 0.05 m, and there is no overshoot. It is verified that the position controller has faster tracking speed and accuracy.

Figure 8(b) shows the tracking response curve of the swing angle. It can be seen that the swing angle is always controlled within 6°. The maximum swing angle appeared in 8 s and 13 s, respectively, reached 5.7°. This is because the deceleration occurs when the ARSS is close to the expected position at this time. After 2 s, the swing angle has dropped to within 2°, and when ARSS hovers, it can gradually stabilize to the equilibrium point and remain stable. This shows that the swing angle controller can well reduce the swing amplitude of the saw and can gradually stabilize after reaching the destination.

4.3. Aerial Pruning Experiments

The purpose of ARSS is to perform tree pruning operations. The pruning process is difficult to describe accurately, and the cutting process is not exactly the same for tree bars of different thickness. This experiment will simulate the cutting of a 6 cm diameter tree branch growing laterally to verify the controller. In the early stage, through the actual branch cutting experiment on the ground, the test results were counted and empirical conclusions were drawn: to cut a tree branch with a diameter of 6 cm, a squeezing force of 2 N is required between the saw and the branch, and contact with the tree barrier 2 s, the swing angle reaches −11.5 deg. It can be calculated from this that the body needs to be 20 cm ahead of COG of the saw in the direction of advancement. Considering that the saw diameter used in this article is 14 cm and the branch diameter is 6 cm, so during the cutting process, the flying platform needs to be 0.1 m in front of the tree branch. In this process, the saw will also receive a cutting force of 50 N.

Based on the above analysis, the cutting process can be approximated as follows: the saw is in continuous contact with the branch for 2 s at a swing angle of −11.5 deg and disturbed by a cutting force of 50 N. The experimental process is designed as follows: the initial state of ARSS is hovering, and a tree barrier is placed at a distance of 1 m from the ARSS. On the 0 s, give a step signal of 1.1 m in the x-axis and set the desired swing angle to −11.5 deg. After the aerial Robot reaches the desired position, hover for 2 s and then perform the cutting operation. During this process, a cutting force of 50 N is applied to the saw, and then a step signal of 2 m on the x-axis is given and the desired swing angle is set to 0°, leaving the Working area. The entire simulation process lasts 20 s. This test mainly tests the position of the X direction and the performance of the swing angle controller, so only the curve of the x-axis position and the swing angle during the simulation process is given, as shown in Figures 9 and 10.

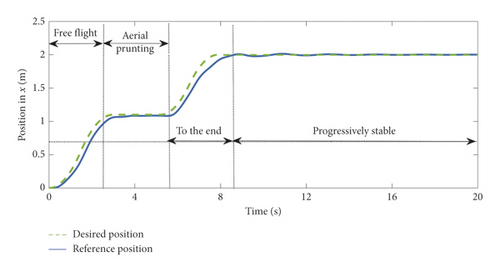
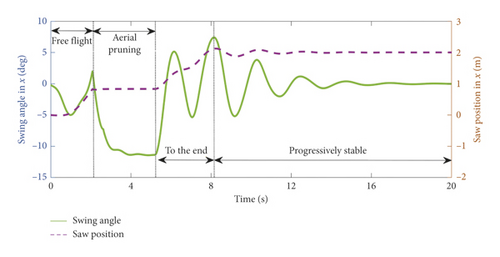
In order to more intuitively explain the simulation results, the simulation process is divided into four stages, as shown in Figure 11.

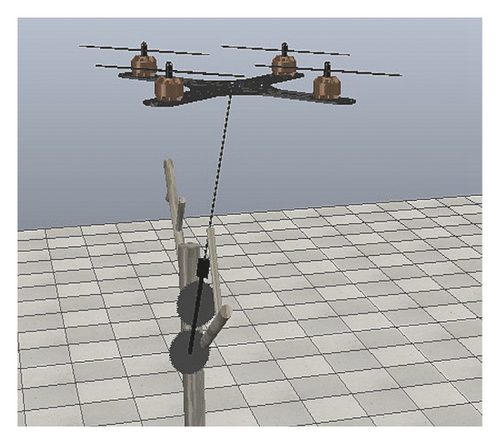
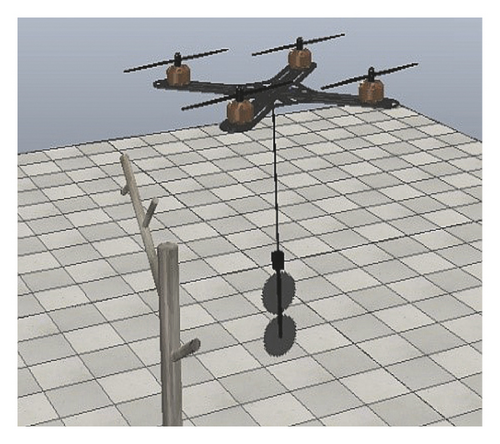
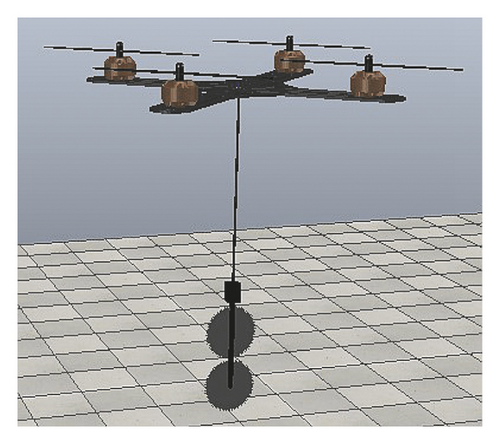
From Figure 11, ARSS made contact with the tree barrier in 2.2 s, and the swing angle before contact was 2 deg (in Figure 11(a)). After the contact, due to the tree barrier blocking the saw, the saw stayed at the position of 1 m, while the flying platform continued to fly, reached 1.1 m in the 3.2 s and hovered, the swing angle gradually increased to −11.5 deg, and keep the angle until 5.2 s (in Figure 11(b)). After the pruning is completed, due to the loss of the barrier to the saw, the saw quickly swings forward. Under the action of the swing angle controller, it reaches a maximum of 7 deg, and stays within 7 deg when going to the destination (in Figure 11(c)), and it can gradually stabilize after reaching the destination (in Figure 11(d)). In terms of position control, the Robot can always quickly track the desired position, and the maximum tracking error is within 0.4 m. After reaching the destination, due to the need to control the swing angle, there is an overshoot of 0.1 m, which can gradually stabilize after a period of time. The experiments demonstrated that the position controller and the swing angle controller can complete the task of aerial pruning well.

5. Discussion and Conclusions

Throughout the development of ARSS, a range of issues were encountered on which we are developing a novel aerial platforms. While building the novel robot for the tree pruning has a range of advantages, it also has the following limitations:

(1)
Physical testing still needs to be carried out in future research.
(2)
The control of the swing angle is linearized by a Small-Angle-Approximation to the dynamic model, and the model uncertainty cannot be completely solved.
(3)
The knife and saw will generate force after contact with the tree. The research does not directly control the force, but indirectly realizes the force control through the control of the position, attitude and swing angle.

However, the article introduces how a novel aerial robot can realize flying motion and aerial pruning and designs a position and attitude controller based on the ADRC method, and a swing angle controller via the linear SEF method. The methodology not only realize the fast, accurate, and stable flight movement to the specified position, but also effectively suppress the swing of the hanging load and the residual oscillation after reaching the specified position. The control effect is remarkable, with good speed and robustness.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This work was supported by the Guizhou Provincial Science and Technology Projects (Grant no. (2020)2Y044), the Science and Technology Projects of China Southern Power Grid Co., Ltd. (Grant no. 066600KK52170074), the Key Laboratory Projects of Aeronautical Science Foundation of China (Grant no. 201928052006), and the National Natural Science Foundation of China (Grant no. 61473144).

Open Research

Data Availability

The figures, tables, and other data used to support this study are included within the article.

References

1 Mahony R., Kumar V., and Corke P., Multirotor aerial vehicles: modeling, estimation, and control of quadrotor, IEEE Robotics & Automation Magazine. (2012) 19, no. 3, 20–32, https://doi.org/10.1109/mra.2012.2206474, 2-s2.0-84866354549.
10.1109/MRA.2012.2206474
Web of Science® Google Scholar
2 Liang X., Fang Y., Sun N., and Lin H., A novel energy-coupling-based hierarchical control approach for unmanned quadrotor transportation systems, IEEE/ASME Transactions on Mechatronics. (2019) 24, no. 1, 248–259, https://doi.org/10.1109/tmech.2019.2891083, 2-s2.0-85062094873.
10.1109/TMECH.2019.2891083
Web of Science® Google Scholar
3 Yallappa D., Veerangouda M., Maski D., Palled V., and Bheemanna M., Development and evaluation of drone mounted sprayer for pesticide applications to crops, Proceedings of the GHTC 2017—IEEE Global Humanitarian Technology Conference, October 2017, San Jose, CA, USA, 1–7, https://doi.org/10.1109/GHTC.2017.8239330, 2-s2.0-85047464505.
10.1109/GHTC.2017.8239330
Google Scholar
4 Molina J. and Hirai S., Pruning tree-branches close to electrical power lines using a skew-gripper and a multirotor helicopter, Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, AIM, July 2017, Munich, Germany, 1123–1128, https://doi.org/10.1109/AIM.2017.8014169, 2-s2.0-85028763370.
10.1109/AIM.2017.8014169
Google Scholar
5 Molina J. and Hirai S., Aerial pruning mechanism, initial real environment test, Robotics and Biomimetics. (2017) 4, https://doi.org/10.1186/s40638-017-0073-3.
10.1186/s40638-017-0073-3
PubMed Google Scholar
6 Molina J. and Hirai S., Kinematic analysis of a novel skew-gripper for aerial pruning tasks, Proceedings of the 3rd International Conference on Mechatronics and Robotics Engineering, February 2017, Paris, France, 134–138, https://doi.org/10.1145/3068796.3068802, 2-s2.0-85021326255.
10.1145/3068796.3068802
Google Scholar
7 Zhang Q., Yang Z., Wang S., and Jiang Y., Attitude controller design for the aerial trees-pruning robot based on nonsingular fast terminal sliding mode, International Journal of Advanced Robotic Systems. (2019) 16, no. 4, 1–14, https://doi.org/10.1177/1729881419871147, 2-s2.0-85071718194.
10.1177/1729881419871147
Google Scholar
8 Azami N., Zarafshan P., Kermani A. M., Khashehchi M., and Kouravand S., Design and analysis of an armed-octorotor to prune trees near the power lines, Proceedings of the International Conference of Iranian Aerospace Society, February 2017, Tehran, Iran.
Google Scholar
9 Klausen K., Fossen T. I., and Johansen T. A., Suspended load motion control using multicopters, Proceedings of the 2014 22nd Mediterranean Conference on Control and Automation, MED 2014, June 2014, Palermo, Italy, 1371–1376, https://doi.org/10.1109/MED.2014.6961567, 2-s2.0-84916919232.
10.1109/MED.2014.6961567
Google Scholar
10 Sreenath K., Michael N., and Kumar V., Trajectory generation and control of a quadrotor with a cable-suspended load—a differentially-flat hybrid system, Proceedings of the IEEE International Conference on Robotics and Automation, May 2013, Karlsruhe, Germany, 4888–4895, https://doi.org/10.1109/ICRA.2013.6631275, 2-s2.0-84887288224.
10.1109/ICRA.2013.6631275
Google Scholar
11 Alothman Y. and Gu D., Quadrotor transporting cable-suspended load using iterative linear quadratic regulator (iLQR) optimal control, Proceedings of the 2016 8th Computer Science and Electronic Engineering Conference, CEEC 2016, September 2016, Colchester, UK, 168–173, https://doi.org/10.1109/CEEC.2016.7835908, 2-s2.0-85015287503.
10.1109/CEEC.2016.7835908
Google Scholar
12 Faust A., Palunko I., Cruz P., Fierro R., and Tapia L., Learning swing-free trajectories for UAVs with a suspended load, Proceedings of the IEEE International Conference on Robotics and Automation, May 2013, Karlsruhe, Germany, 4902–4909, https://doi.org/10.1109/ICRA.2013.6631277, 2-s2.0-84887295086.
10.1109/ICRA.2013.6631277
Google Scholar
13 Palunko I., Fierro R., and Cruz P., Trajectory generation for swing-free maneuvers of a quadrotor with suspended payload: a dynamic programming approach, Proceedings of the IEEE International Conference on Robotics and Automation, May 2012, Saint Paul, MN, USA, 2691–2697, https://doi.org/10.1109/ICRA.2012.6225213, 2-s2.0-84864495616.
10.1109/ICRA.2012.6225213
Google Scholar
14 Yang S. and Xian B., Energy-based nonlinear adaptive control design for the quadrotor UAV system with a suspended payload, IEEE Transactions on Industrial Electronics. (2020) 67, no. 3, 2054–2064, https://doi.org/10.1109/TIE.2019.2902834.
10.1109/TIE.2019.2902834
Web of Science® Google Scholar
15 Yang S., Kunqin L., and Shi J., Design and simulation of the longitudinal autopilot of UAV based on self-adaptive fuzzy PID control, Proceedings of the CIS International Conference on Computational Intelligence and Security, December 2009, Beijing, China, 634–638, https://doi.org/10.1109/CIS.2009.253, 2-s2.0-77949301093.
10.1109/CIS.2009.253
Google Scholar
16 Liu J.-B., Wang S., Wang C., and Hayat S., Further results on computation of topological indices of certain networks, IET Control Theory & Applications. (2017) 11, no. 13, 2065–2071, https://doi.org/10.1049/iet-cta.2016.1237, 2-s2.0-85016957754.
10.1049/iet-cta.2016.1237
Web of Science® Google Scholar
17 Liu J.-B., Cao J., Alofi A., AL-Mazrooei A., and Elaiw A., Applications of Laplacian spectra for n-prism networks, Neurocomputing. (2016) 198, 69–73, https://doi.org/10.1016/j.neucom.2015.06.109, 2-s2.0-84978327315.
10.1016/j.neucom.2015.06.109
Web of Science® Google Scholar
18 Han J., From PID to active disturbance rejection control, IEEE Transactions on Industrial Electronics. (2009) 56, no. 3, 900–906, https://doi.org/10.1109/TIE.2008.2011621, 2-s2.0-63149185343.
10.1109/TIE.2008.2011621
Web of Science® Google Scholar
19 Yang X. and Huang Y., Capabilities of extended state observer for estimating uncertainties, Proceedings of the American Control Conference, June 2009, St. Louis, MO, USA, 3700–3705, https://doi.org/10.1109/ACC.2009.5160642, 2-s2.0-70449625623.
10.1109/ACC.2009.5160642
Google Scholar
20 Zheng Q., Gao L. Q., and Gao Z., On validation of extended state observer through analysis and experimentation, Journal of Dynamic Systems, Measurement, and Control. (2012) 134, no. 2, 1–6, https://doi.org/10.1115/1.4005364, 2-s2.0-84855913911.
10.1115/1.4005364
Web of Science® Google Scholar
21 Guo B.-Z. and Zhao Z.-l., On the convergence of an extended state observer for nonlinear systems with uncertainty, Systems & Control Letters. (2011) 60, no. 6, 420–430, https://doi.org/10.1016/j.sysconle.2011.03.008, 2-s2.0-79955794731.
10.1016/j.sysconle.2011.03.008
Web of Science® Google Scholar
22 Zhou Z. X., Qu Y. Y., Yang J. D., and Liu D. J., Suspension position control of precise planar magnetic bearing, Kongzhi yu Juece/Control and Decision. (2010) 25, no. 3, 437–444.
Google Scholar
23 CoppeliaSim, https://www.coppeliarobotics.com/.
Google Scholar
24 Wu L., Bao H., Du J. L., and Wang C. S., A learning algorithm for parameters of automatic disturbances rejection controller, Zidonghua Xuebao/Acta Automatica Sinica. (2014) 40, no. 3, 556–560, https://doi.org/10.3724/SP.J.1004.2014.00556, 2-s2.0-84897502443.
10.3724/SP.J.1004.2014.00556
Google Scholar

Citing Literature

All articles

ARSS: A Novel Aerial Robot Performs Tree Pruning Tasks

Abstract

1. Introduction

2. Mathematical Model

2.1. Coordinates and Conventions

2.2. Assumptions

2.3. Notation

2.4. Body Dynamic Model

2.5. Suspended Saws Model

3. Controller Design

3.1. Attitude Control

3.1.1. Design TD

3.1.2. Design ESO

3.1.3. Design SEF

3.2. Position Control

3.2.1. Design TD

3.2.2. Design ESO

3.2.3. Design State Error Feedback (SEF)

3.3. Suspended Saw Controller

4. Evaluation

4.1. Attitude Control Experiment

4.2. Free-Flight Experiments

4.3. Aerial Pruning Experiments

5. Discussion and Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

ARSS: A Novel Aerial Robot Performs Tree Pruning Tasks

Abstract

1. Introduction

2. Mathematical Model

2.1. Coordinates and Conventions

2.2. Assumptions

2.3. Notation

2.4. Body Dynamic Model

2.5. Suspended Saws Model

3. Controller Design

3.1. Attitude Control

3.1.1. Design TD

3.1.2. Design ESO

3.1.3. Design SEF

3.2. Position Control

3.2.1. Design TD

3.2.2. Design ESO

3.2.3. Design State Error Feedback (SEF)

3.3. Suspended Saw Controller

4. Evaluation

4.1. Attitude Control Experiment

4.2. Free-Flight Experiments

4.3. Aerial Pruning Experiments

5. Discussion and Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information