Volume 2020, Issue 1 8845160

Research Article

Open Access

The Mean First Passage Time of the Stochastic Resonance Driven by Dual-Sequence-Frequency-Hopping Signal and Noise

Zhaorui Li,

Zhaorui Li

School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China njust.edu.cn

Department of Electronics and Optical Engineering, Army Engineering University, Shijiazhuang 050003, China ust.com.cn

Search for more papers by this author

Xiaobei Wu,

Xiaobei Wu

School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China njust.edu.cn

Search for more papers by this author

Peizhang Cui,

Corresponding Author

Peizhang Cui

[email protected]

orcid.org/0000-0001-8096-4042

Department of Electronics and Optical Engineering, Army Engineering University, Shijiazhuang 050003, China ust.com.cn

Search for more papers by this author

Guangkai Liu,

Guangkai Liu

Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China dl.acm.org

Search for more papers by this author

Zhaorui Li,

Zhaorui Li

School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China njust.edu.cn

Department of Electronics and Optical Engineering, Army Engineering University, Shijiazhuang 050003, China ust.com.cn

Search for more papers by this author

Xiaobei Wu,

Xiaobei Wu

School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China njust.edu.cn

Search for more papers by this author

Peizhang Cui,

Corresponding Author

Peizhang Cui

[email protected]

orcid.org/0000-0001-8096-4042

Department of Electronics and Optical Engineering, Army Engineering University, Shijiazhuang 050003, China ust.com.cn

Search for more papers by this author

Guangkai Liu,

Guangkai Liu

Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China dl.acm.org

Search for more papers by this author

First published: 15 September 2020

https://doi.org/10.1155/2020/8845160

Citations: 1

Academic Editor: Adrian Kliks

Share a link

Email
Wechat
Bluesky

Abstract

The mean first passage time (MFPT) represents the dynamic characteristic of stochastic resonance (SR). The study focuses on how can the Dual-Sequence-Frequency-Hopping (DSFH) signal influence the MFPT and any difficulty in solving the MFPT problem considering the DSFH signal. In this current study, the SR system driven by DSFH signal and Gaussian white noise is described with the parameters of the signal amplitude, the frequency of Intermediate Frequency (IF) of the receptive DSFH signal, the SR system parameter, scale transformation coefficient, the noise intensity, and the sampling multiple, firstly. Secondly, under the assumption that MFPT is small aqueous about the domain of 0, the nonautonomous differential equation with MFPT is transformed to a nonhomogeneous differential equation with one unknown variable coefficient of second order. Finally, the numerical solution of MFPT can be obtained by the method of Runge–Kutta. Theoretical and simulation results are shown as below: (1) the effect of the signal amplitude, the IF frequency, the noise intensity, the SR system parameter, and the scale transformation coefficient, for decrease the MFPT, are positive; however, the effect of the sampling multiple is negative; (2) the MFPT cannot follow the dynamic period of the SR controlled by the IF frequency, when SNR is low; (3) when SNR = −12 dB, the sampling multiple is 200, the IF frequency is 2100, and the duty cycle reaches 25% (available for DSFH signal detection with peek or valley decision Liu et al. (2019)), so we need to decrease the IF frequency or increase the SNR for further availability.

1. Introduction

The Dual-Sequence-Frequency-Hopping (DSFH) communication mode draws lessons from “the medium is the message” [1, 2]. Its typical character is that the message is modulated in the radio frequency, which is the hopping frequency controlled by the PN sequence. When the symbol 1 is transmitted, the hopping frequency controlled by PN 1 is transmitted. And when 0 is transmitted, the hopping frequency controlled by PN 0 is transmitted. The radio frequency of DSFH is combined by hopping frequency controlled by PN 1 and PN 0. The chosen medium is the communication channel; meanwhile, the unchosen one is the dual channel controlled by two PN sequences representing the symbol 0 or 1. Then, the receptive symbol is decided by whether the channel is occupied or not [3–5]. Due to the character of DSFH, the receptive signal of DSFH is a sinusoidal signal that is the typical input signal of stochastic resonance (SR). And the DSFH processed by stochastic resonance (SR) can work under strong color noise as a military emergency communication mode [6, 7]. SR is a nonlinear physical phenomenon that goes against the conventional concept that noise is always harmful for signal detection. Noise can enhance the detection performance of nonlinear SR systems when the signal, noise, and the SR parameters are matched. The SR theory is first proposed in the research of the earth glacier by Benzi et al. [8] and then demonstrated in physics, biology, and electronics [9–12]. And the application of the SR to signal procession is reviewed and discussed [13]. However, SR has a dynamic nature as a nonlinear system. The signal processing needs a steady state of the SR, not a dynamic one. So, when it is applied to signal detection, the researchers must ensure that the output of SR is already steady at the signal decision time during the bit period of DSFH. In other words, the SR system particles are jumping in some well instead of between wells at the decision time.

The mean first passage time (MFPT) is used to describe the dynamic characteristic of SR. The MFPT is defined as the time that a walker or a particle spends before crossing a given position for the first time [14]. As for the MFPT, most researchers mainly focus on the relationship between noise and the SR system. Guardia and San Miguel firstly study the escape time of bistable SR caused by multiple and additive Gaussian noise and obtain the analytic expression of MFPT related with potential function and noise intensity [15], which initiates the research of MFPT. Kang researches the MFPT in underdamped bistable Duffing oscillator [16] and the phenomenological gene transcriptional regulatory model [17] by the method of moments and the period steady solution of Fokker–Planck equation (FPE). Wang studies the MFPT in the Levine model, focusing on the white and color noise in the biological population system [18, 19]. Xu and Jin studies the MFPT in the tristable SR driven by correlated multiplicative and additive white noises [20, 21]. However, most research studies focus on the effect of MFPT caused by the SR system and noise. The adiabatic elimination theory is mostly used to obtain the MFPT with the assumption that the signal amplitude and frequency are small. And there has been no result which can be used to analyze the influence caused by the input signal frequency so far.

When the DSFH signal is considered in the MFPT problem, the nonautonomous item caused by the time-vary signal is introduced in the differential equation related to MFPT, which causes many difficulties in solving the MFPT. Aimed at solving this problem, we assume that MFPT is small aqueous about the domain of 0 based on the experience of communication signals detection and simulation results. And we try to research the relationship between MFPT and the DSFH signal, noise, and SR system. The paper is structured as follows. In Section 2, the SR system driven by DSFH signal and Gaussian white noise is described. In Section 3, the MFPT affected by DSFH signal and Gaussian white noise are analyzed, and the nonhomogeneous differential equation with MFPT of second order is solved with the method of Runge–Kutta. In Section 4, the relationship between MFPT and the DSFH signal, noise, and SR system is discussed in the theoretical and simulation view. Conclusions are given in Section 5.

2. The System Model of the SR Driven by DSFH Signal and Gaussian White Noise

2.1. The Transmitted Signal of the DSFH

The communication and dual carrier controlled by PN sequences are chosen by the transmitted symbol in the DSFH mode and described as Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The transmitted structure of the DSFH.

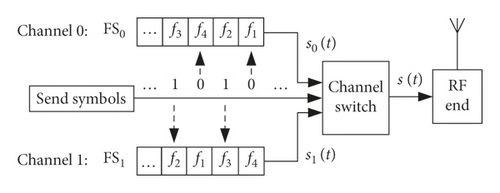
Channel 0 and 1 are, respectively, the carrier f_0,n and f_1,n controlled by PN sequences FS₀ and FS₁. When the send symbol is 0, the carrier f_0,n controlled by PN sequences FS₀ is transmitted. When the send symbol is 1, the carrier f_1,n controlled by PN sequences FS₁ is transmitted. At the time of t, the sine carrier s₀(t) with the frequency of f_0,n is transmitted if the transmitted symbol is 0. Otherwise, the sine carrier s₁(t) represented of symbol 1 is transmitted. Furthermore, the signals s₀(t) and s₁(t) are sinusoidal. The final transmitted signal s(t) of DSFH is the combination of the s₀(t) and the s₁(t), after the channel switch.

Assume that the transmitted data is b = (…, 1,0,1,0, …), for the main analysis, the baseband filter is neglect. Then, the transmitted signal is the sine carrier with a frequency of (…, f₂, f₄, f₃, f₁, …). So, the radio frequency (RF) signal of DSFH can be represented as

(1)

where T_s is the hop duration, ε(t) is the step signal, f_i,n is the radio frequency of the nth hop, and

2.2. The Receptive Signal of the DSFH

The superheterodyne receiver is adopted in the DSFH mode, as depicted in Figure 2.

The signal r(t) is receipted under noise at the RF front end. The noise mostly is white Gaussian noise, the channel fading is neglect, and the receptive signal is ideal sinusoidal signal. Then, it will be mixed with the superheterodyne carriers controlled by two PN sequences. Subsequently, the analogy beat signal as the intermediate frequency (IF) signal be converted to digital one by the A/D convertor. The frequency and waveform of the IF signal obtained by the two receptive branches are the same but not at the same time, which can be descripted as

(2)

where f₀ is the preset frequency of the IF signal.

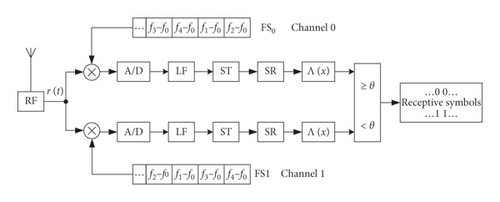
Noting that, in the DSFH system, the signal is just exit in one branch and the other branch is zero at the same time.

Due to the superheterodyne reception and the special modulation of DSFH, the received signal of the DSFH is the simple sinuous signal, which is the typical input signal of SR. With the reason that the f₀ and the sampling rate f_s are set as 1 kHz and 200 kHz, the IF signal can be viewed as low-frequency signal, which can be processed by low-pass filter (LF). In the DSFH communication system, part information of the received signal such as the frequency is known in the reception end. So, we can design the LF based on this. Then, the scale transact unit (ST) completes the parameters of IF signal to fit the demand of SR.

When the receptive signal is deciding, the output of SR must be already steady. So, we need to analyze the dynamic characteristic of SR driven by the receptive signal of DSFH and Gaussian white noise.

2.3. The SR Processing of the Receptive Signal

The IF signal of the two receptive branches is the sine wave as depicted in equation (2). The overdamped bistable SR enforced by sine wave A cos(ω₀t + ϕ) and noise Γ(t) can be depicted as follows:

(3)

where a and b are the SR parameters, Acos(ω₀t + ϕ) is the periodic signal, Γ(t) is the white Gaussian noise satisfied with E[Γ(t)] = 0, E[Γ(t)Γ(t + s)] = 2 Dδ(s), and D is the intensity of the noise.

With the reason that SR unit can only settle the small signal with small frequency and amplitude, so the IF signal with significant frequency and amplitude must be transacted to a small one, which is carried out by the ST unite. Therefore, we introduce the variable substitution [9]

; equation (3) can be transacted to

(4)

So, the frequency scale transacted equation is ω₀/a = 2πf, where the frequency is transacted to the 1/a times of the original. The amplitude scale transacted equation is . When the parameter of a is large enough and b is small enough, the large IF signal can be transacted to small signal after ST. At the same time, the noise intensity becomes .

Therefore, the corresponding FPE of equation (4) can be described as

(5)

where ρ(x, y, t)is the PDF of the particle locating (x, y) at time t.

As for the formal unification, we rewrite equation (5) as

(6)

where

and B(x) = Db/a².

Next, we will analyze the MFPT with time-vary item of equation (6).

3. The MFPT Influenced by DSFH Signal and Gaussian White Noise

3.1. The Nonautonomous Effect of MFPT Caused by a Time-Vary Input Signal

Let w(x, t) represent the probability of the first passage time from the well X₁ to the well X₂ is T and the initial position is x. So, MFPT is the average of T as

(7)

For simplicity, we use T(x) to represent the T(X₁⟶X₂). So, the probability of the first passage time among (t, t + dt) can be described as

(8)

where

is the probability of the particles positing at (a, b) and at time t.

And equation (8) can be simplified as

(9)

Substituting equation (9) to equation (7), we obtain

(10)

So, using the FPE, we can obtain

(11)

Integrating t on both sides of equation (11), it shows

(12)

When the input signal is a sinusoidal wave, the time-vary item can be decomposed into the nontime-vary item A(x) representing the SR system and time-vary item Acos(ωt + ϕ) representing the input signal as

(13)

Then, equation (12) can be expressed as

(14)

Substituting equation (7) to equation (14), we can obtain that

(15)

Next, we emphasize on the nonautonomous item and obtain the solution of T(x).

3.2. The Solution of MFPT with the Transaction from Autonomous Item to Nonautonomous One

The output of SR and the sketch of MFPT are described in Figure 3. We can see that the SR system reaches a steady state quickly in one period. The transaction between wells is so quick, that is, the MFPT is much smaller than the period.

Based on this phenomenon that particles of the SR system jump in a potential well after completing the barrier transition and the electromagnetic particles jump so quickly, a given time of relaxation can represent the drift effect of Acos(ωt + ϕ). And as for the cosine form, the given time is T(x). So, the nonautonomous item can be described as

(16)

Due to T(x) ≪ T_s (T_s is the period of the output signal of the SR system), so ωT(x) ≪ 1. And in consideration of the experience of communication signals detection and simulation results, ωT(x) ≤ 0.1 which can be viewed as small aqueous about the domain of 0. So, we apply the Taylor expansion to the cos(ωT(x) + ϕ) with the whole of ωT(x) as (neglecting the phase effect)

(17)

So, equation (15) can be described as

(18)

Equation (18) is the nonhomogeneous differential equation with one unknown variable coefficient of second order, and there is no analytical solution. So, let

, and equation (18) can be described as

(19)

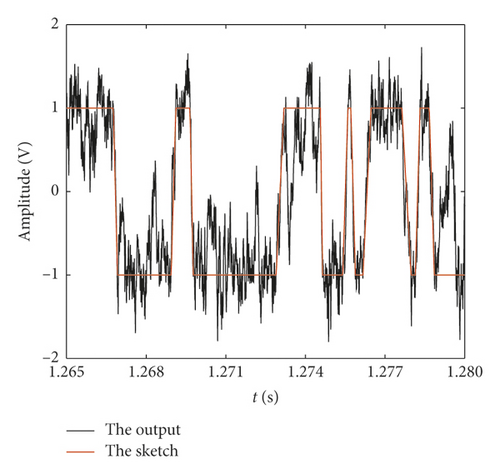
So, we can obtain the numerical solution of T(x)with the method of Runge–Kutta.

As a reminder that when the input signal is a sine wave, the nonautonomous item is

. And the steady well of SR lies in the peak or valley of the sine wave. And the given time of relaxation which can represent the drift effect of Asin(ωt + ϕ) is the T_s/4 − T(x). So, the drift sine wave Asin(ωt + ϕ) can be represented by Asin(ω(T_s/4 − T(x)) + ϕ). And we apply the Taylor expansion to the Asin(ω(T_s/4 − T(x)) + ϕ) with the whole of ω(T_s/4 − T(x)) as

(20)

The form of the differential equation drifted by sine wave is the same with the one drifted by cosine wave. The drift effect caused by the cosine wave is the same as the sine wave demonstrated in the mathematical analytic form.

4. Simulated Analysis

In this section, we set the optimal parameter of SR drawing lessons from the optimal matching SR and statistics for the first passage time of the particles jumping from one well to the other as the simulation results in the Simulink model. And we will analyze the theory and simulation in three aspects. (1) Parameters of a and b of the SR system and the scale transformation coefficient , which represent the intrinsic system nature together. (2) The signal amplitude A and the signal frequency f₀ of the receptive signal of DSFH. (3) The noise intensity D and the multiple sampling R.

4.1. The Relationship between MFPT and Signal Amplitude A

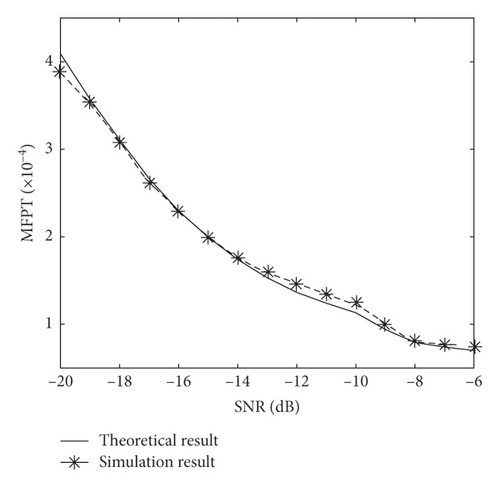
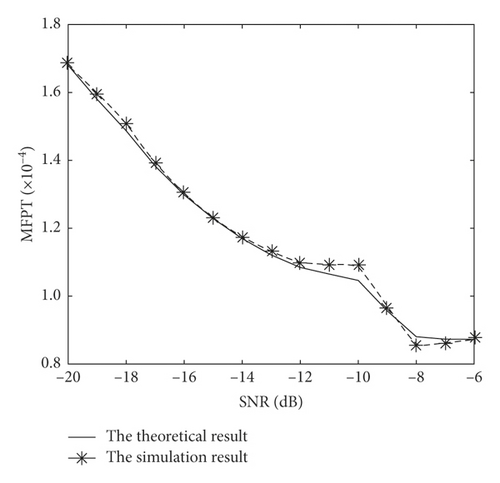
The theoretical and simulation results of the MFPT varying with A are described in Figure 4. We can see that the MFPT decreases as the SNR increases no matter in theoretical or simulation curve. This is because that when the signal frequency f₀, sampling multiple R, and noise power σ² (corresponding to noise variance) are constant, the frequency scale transformation a (one of the parameters of the SR system) and noise intensity D is constant. So, the three factors listed above which can affect the particles to jump vary as follows: the scale transformation coefficient and signal amplitude A increase, while the noise intensity D is constant as the SNR increases. And the scale transformation coefficient representing the system characteristic can promote the particles to jump between wells in the intrinsic nature of the SR system. Furthermore, the signal can pull the particles to jump between wells in external factors. So, it is more conducive to particle transitions that and A are increase, and that is why MFPT decreases as the SNR increases.

4.2. The Relationship between MFPT and Noise Intensity D

The theoretical and simulation results of the MFPT varying with D are described in Figure 5. We can see that the MFPT decreases as the SNR increases no matter in theoretical or simulation curve. Because when the signal frequency f₀, sampling multiple R, and signal amplitude A are constant, the frequency scale transformation a is constant. So, the three factors listed above which can affect the particles to jump vary as follows: the scale transformation coefficient increases and the noise intensity D decreases, while signal amplitude A is constant as the SNR increases. And representing the system characteristic can promote the particles to jump between wells in intrinsic nature of the SR system. Furthermore, the noise can pull the particles to jump between wells in external factors. So, increase has a positive effect on the decrease of MFPT, while D decrease has a negative effect on the dynamic characteristic of SR leading decrease of MFPT. And the overall effect depends on the relative result caused by system and noise. Furthermore, the MFPT decreases when the system parameters and noise intensity are listed in our experiment.

4.3. The Relationship between MFPT and Sampling Multiple R

The theoretical and simulation results of the MFPT varying with R are described in Figure 6. We can see that there are two results. One is that the MFPT increases as the R increases when SNR is constant no matter in the theoretical or simulation curve. Because when SNR, f₀, A and σ² are constant, the parameters a, are constant, and D decreases with the increase of R. So, the positive effect for transaction bring by noise decreases becomes weak as the increase of R, leading the increase of MFPT. The other result is that the MFPT decreases as the SNR increases when R is constant no matter in the theoretical or simulation curve. Because when f₀, R, and σ² are constant, the parameters a and D are constant, while and A increase with increase of SNR. The effect caused by and A are all positive. So, the MFPT decreases. Furthermore, the bigger the R which leads higher quality of A/D converter, the worse the MFPT. However, the SR system vibrate needs a certain R, so for the dynamic system performance, we should decrease R meeting the demand of SR vibration as possible.

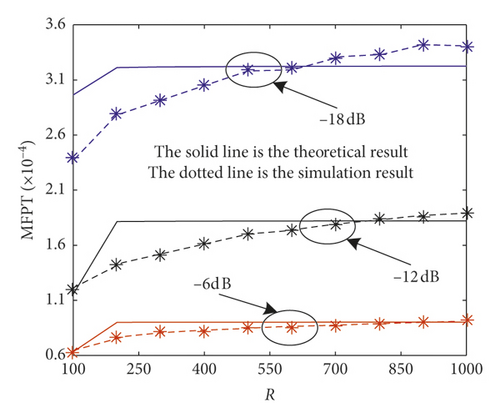
As a reminder, the bigger the T(x), the bigger the error between theoretical and simulation for a constant SNR, which also verify our assumption that the smaller the T(x), the more accuracy of the Taylor expansion to the cos(ωT(x) + ϕ) with the whole of ωT(x). And different SNRs need different system parameters a and b, so the error between theoretical and simulation at different SNRs is mainly due to the system characteristic.

4.4. The Relationship between MFPT or Duty Cycle and the IF Frequency f₀

The theoretical and simulation results of the MFPT varying with f₀ are described in Figure 7(a) and the duty cycle varying with f₀ are described in Figure 7(b).

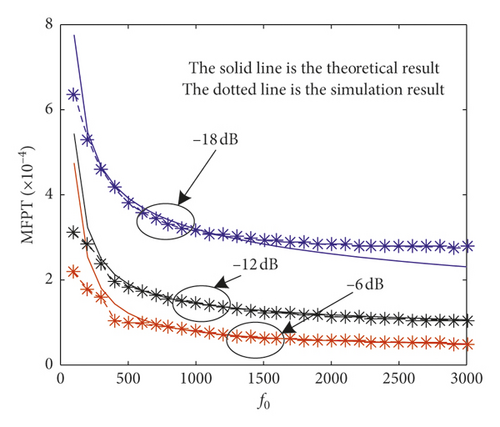
Two results are shown in Figure 7(a). One is that the MFPT decreases as the increases when SNR is constant, no matter in the theoretical or simulation curve. This is because that when SNR, R, A, and σ² are constant, the parameters a and D decrease with the increase of f₀. The overall effect of the positive one for transaction caused by system parameters and a negative one for transaction caused by noise is positive, leading to a decrease of MFPT. The other one is that the MFPT decreases as the SNR increases when f₀ is constant no matter in the theoretical or simulation curve. This is because that when f₀, R, and σ² are constant, the parameters a and D are constant, while and A increase with increase of SNR. The effect of and A are all positive. So, the MFPT decreases.

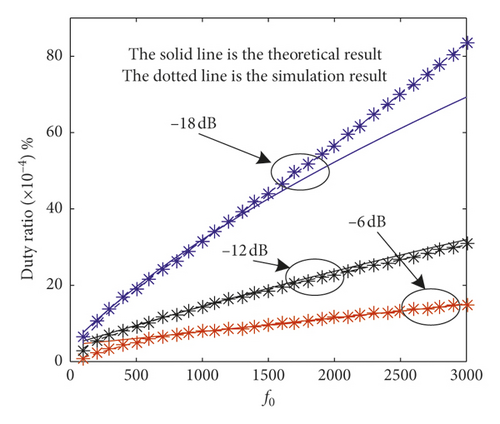
In Figure 7(b), we give the normalization of MFPT as f₀ varies. Because the output of SR has a distinct periodic characteristic that reflects the frequency of the input signal, the normalization is the duty cycle which is T(x)/T₀ and T₀ = 1/f₀. We can also see two results. One is that the duty cycle increases as the f₀ increases when SNR is constant no matter in the theoretical or simulation curve because the period of the SR system at constant SNR mainly depends on the input signal period. And its periodicity can react quickly following with the input signal. However, the MFPT reacts slower than periodicity, which leading the result that the duty cycle increases as the f₀ increases when SNR is constant. And the parameters of SR varies more, following the f₀.

Furthermore, the tracking performance of SR following the f₀, which explains why the SR system is limited to be applied to communication systems with f₀ varying. That is to say when SNR is low, the MFPT cannot follow the dynamic period of SR controlled by the f₀. The other result is that the duty cycle decreases as the SNR increases when f₀is constant in the theoretical or simulation curve. The reason is the same to the one in Figure 7(a), so there is no more detailed description. And related to the sample frequency, the frequency of the received signal locates at the low region of the frequency band, which can be processed by SR.

5. Conclusion

MFPT can represent the dynamic characteristic of SR, and the effect on MFPT caused by the DSFH signal is studied in this paper. Based on the assumption that MFPT is small aqueous about the domain of 0, the nonautonomous differential equation with MFPT is transformed to a nonhomogeneous differential equation with one unknown variable coefficient of second order. The numerical solution of MFPT is obtained by Runge–Kutta. The quantitative relationship between MFPT and DSFH signal, noise, and parameters of SR is obtained. Furthermore, the conclusion that “when SNR = −12 dB, R = 200, and f₀ = 2100, the duty cycle reaches 25% (available for DSFH signal detection), so it is suggested to decrease the IF frequency f₀ of the receptive DSFH or increase the SNR for further availability.” The research method illuminates the way of effect on MFPT caused by input signal. Furthermore, the conclusion provides reference for the dynamic characteristic and signal detection of the SR system driven by the DSFH signal and Gaussian white noise.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Open Research

Data Availability

The data used to support the findings of the study are available from the corresponding author upon request.

References

1 Fitzek F. H. P., The medium is the message, Proceedings of the IEEE International Conference on Communications, August 2006, Istanbul, Turkey, 5016–5021, https://doi.org/10.1109/icc.2006.255461, 2-s2.0-42549152457.
10.1109/icc.2006.255461
Google Scholar
2 Zhou X., Kyritsi P., Eggers P. C. F., and Fitzik F. H. P., “The medium is the message”: secure communication via waveform coding in MIMO systems, Proceedings of the 2007 IEEE 65th Vehicular Technology Conference—VTC2007-Spring, April 2007, Dublin, Ireland, 491–495, https://doi.org/10.1109/vetecs.2007.112, 2-s2.0-34547315189.
10.1109/vetecs.2007.112
Google Scholar
3 Quan H., Zhao H., and Cui P., Anti-jamming frequency hopping system using multiple hopping patterns, Wireless Personal Communications. (2015) 81, no. 3, 1159–1176, https://doi.org/10.1007/s11277-014-2177-1, 2-s2.0-84939959894.
10.1007/s11277-014-2177-1
Web of Science® Google Scholar
4 Zhao H., Quan H. D., and Pei-Zhang C., Follower-jamming resistible multi-sequence frequency hopping wireless communication, Systems Engineering and Electronics. (2015) 3, 671–678.
Google Scholar
5 Du C., Quan H., Cui P., Liang W., Zhou P., and Dou J., Carrier sense random packet CDMA protocol in dual-channel networks, Radioengineering. (2015) 24, no. 2, 507–517, https://doi.org/10.13164/re.2015.0507, 2-s2.0-84932629966.
10.13164/re.2015.0507
Web of Science® Google Scholar
6 Liu G. K., Quan H. D., Sun H. X., Cui P. Z., Chi C., and Yao S. L., Stochastic resonance detection method for the dual-sequence frequency hopping signal under extremely low signal-to-noise radio, Journal of Electronics and Information Technology. (2019) 41, no. 10, 2342–2349.
Web of Science® Google Scholar
7 Liu G., Kang Y., Quan H., Sun H., Cui P., and Guo C., The detection performance of the dual-sequence-frequency-hopping signal via stochastic resonance processing under color noise, Radioengineering. (2019) 27, no. 3, 618–626, https://doi.org/10.13164/re.2019.0618.
10.13164/re.2019.0618
Google Scholar
8 Benzi R., Sutera A., and Vulpiani A., The mechanism of stochastic resonance, Journal of Physics A: Mathematical and General. (1981) 14, no. 11, 453–457, https://doi.org/10.1088/0305-4470/14/11/006, 2-s2.0-20644470598.
10.1088/0305-4470/14/11/006
Web of Science® Google Scholar
9 Liu G. K., Quan H. D., Kang Y. M., Sun H. X., Cui P. Z., and Han Y. M., A quadratic polynomial receiving scheme for sine signals enhanced by stochastic resonance, Acta Physica Sinica. (2019) 68, no. 21, 210501.
10.7498/aps.68.20190952
Web of Science® Google Scholar
10 Gammaitoni L., Hänggi P., Jung P., and Marchesoni F., Stochastic resonance, Reviews of Modern Physics. (1998) 70, no. 1, 223–287, https://doi.org/10.1103/revmodphys.70.223.
10.1103/RevModPhys.70.223
CAS Web of Science® Google Scholar
11 Chapeau-Blondeau F. and Godivier X., Theory of stochastic resonance in signal transmission by static nonlinear systems, Physical Review E. (1997) 55, no. 2, 1478–1495, https://doi.org/10.1103/physreve.55.1478, 2-s2.0-0031078056.
10.1103/PhysRevE.55.1478
CAS Web of Science® Google Scholar
12 Tougaard J., Signal detection theory, detectability and stochastic resonance effects, Biological Cybernetics. (2002) 87, no. 2, 79–90, https://doi.org/10.1007/s00422-002-0327-0, 2-s2.0-0036689876.
10.1007/s00422-002-0327-0
PubMed Web of Science® Google Scholar
13 Qiao Z., Lei Y., and Li N., Applications of stochastic resonance to machinery fault detection: a review and tutorial, Mechanical Systems and Signal Processing. (2019) 122, 502–536, https://doi.org/10.1016/j.ymssp.2018.12.032, 2-s2.0-85059299793.
10.1016/j.ymssp.2018.12.032
ADS Web of Science® Google Scholar
14 Gardiner C. W., Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences, 1985, Springer-Verlag, Berlin, Germany, pp136–142.
10.1007/978-3-662-02452-2
Google Scholar
15 Guardia E. and San Miguel M., Escape time and state dependent fluctuations, Physics Letters A. (1985) 109, no. 1-2, 9–12, https://doi.org/10.1016/0375-9601(85)90380-9, 2-s2.0-0037576056.
10.1016/0375-9601(85)90380-9
Web of Science® Google Scholar
16 Kang Y. M., Xu J. X., and Xie Y., Observing stochastic resonance in an underdamped bistable Duffing oscillator by the method of moments, Physical Review E. (2003) 68, no. 3, 036123, https://doi.org/10.1103/physreve.68.036123, 2-s2.0-85035267681.
10.1103/PhysRevE.68.036123
Web of Science® Google Scholar
17 Kang Y. M., Chen X., Lin X. D. et al., Mean first passage time and stochastic resonance in a transcriptional regulatory system with non-Gaussian noise, Fluctuation and Noise Letters. (2017) 16, no. 1, 201–207, https://doi.org/10.1142/s0219477517500079, 2-s2.0-85011340494.
10.1142/S0219477517500079
Web of Science® Google Scholar
18 Wang K. K., Stochastic Dynamical Characteristics for a Few Class of Biological Population Models, 2014, Nanjing University of Aeronautics and Astronautics College of Aerospace Engineering, Nanjing, China.
Google Scholar
19 Wang K. K., Liu X.-B., and Yang J.-H., The mean extinction time and stability for a metapopulation system driven by colored cross-correlated noises, Acta Physica Sinica. (2013) 63, no. 10, 100502.
10.7498/aps.62.100502
Google Scholar
20 Xu P. and Jin Y., Mean first-passage time in a delayed tristable system driven by correlated multiplicative and additive white noises, Chaos, Solitons & Fractals. (2018) 112, 75–82, https://doi.org/10.1016/j.chaos.2018.04.040, 2-s2.0-85046654416.
10.1016/j.chaos.2018.04.040
Web of Science® Google Scholar
21 Xu P. and Jin Y., Stochastic resonance in an asymmetric tristable system driven by correlated noises, Applied Mathematical Modelling. (2020) 77, 408–425, https://doi.org/10.1016/j.apm.2019.07.053.
10.1016/j.apm.2019.07.053
Web of Science® Google Scholar

Citing Literature

All articles

The Mean First Passage Time of the Stochastic Resonance Driven by Dual-Sequence-Frequency-Hopping Signal and Noise

Abstract

1. Introduction

2. The System Model of the SR Driven by DSFH Signal and Gaussian White Noise

2.1. The Transmitted Signal of the DSFH

2.2. The Receptive Signal of the DSFH

2.3. The SR Processing of the Receptive Signal

3. The MFPT Influenced by DSFH Signal and Gaussian White Noise

3.1. The Nonautonomous Effect of MFPT Caused by a Time-Vary Input Signal

3.2. The Solution of MFPT with the Transaction from Autonomous Item to Nonautonomous One

4. Simulated Analysis

4.1. The Relationship between MFPT and Signal Amplitude A

4.2. The Relationship between MFPT and Noise Intensity D

4.3. The Relationship between MFPT and Sampling Multiple R

4.4. The Relationship between MFPT or Duty Cycle and the IF Frequency f₀

5. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Mean First Passage Time of the Stochastic Resonance Driven by Dual-Sequence-Frequency-Hopping Signal and Noise

Abstract

1. Introduction

2. The System Model of the SR Driven by DSFH Signal and Gaussian White Noise

2.1. The Transmitted Signal of the DSFH

2.2. The Receptive Signal of the DSFH

2.3. The SR Processing of the Receptive Signal

3. The MFPT Influenced by DSFH Signal and Gaussian White Noise

3.1. The Nonautonomous Effect of MFPT Caused by a Time-Vary Input Signal

3.2. The Solution of MFPT with the Transaction from Autonomous Item to Nonautonomous One

4. Simulated Analysis

4.1. The Relationship between MFPT and Signal Amplitude A

4.2. The Relationship between MFPT and Noise Intensity D

4.3. The Relationship between MFPT and Sampling Multiple R

4.4. The Relationship between MFPT or Duty Cycle and the IF Frequency f0

5. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

4.4. The Relationship between MFPT or Duty Cycle and the IF Frequency f₀