Modelling and Simulating the Novel Coronavirus with Implications of Asymptomatic Carriers
Abstract
The World Health Organization declared that the total number of confirmed cases tested positive for SARS-CoV-2, affecting 210 countries, exceeded 3 million on 29 April 2020, with more than 207,973 deaths. In order to end the global COVID-19 pandemic, public authorities have put in place multiple strategies like testing, contact tracing, and social distancing. Predictive mathematical models for epidemics are fundamental to understand the development of the epidemic and to plan effective control strategies. Some hosts may carry SARS-CoV-2 and transmit it to others, yet display no symptoms themselves. We propose applying a model (SELIAHRD) taking in consideration the number of asymptomatic infected people. The SELIAHRD model consists of eight stages: Susceptible, Exposed, Latent, Symptomatic Infected, Asymptomatic Infected, Hospitalized, Recovered, and Dead. The asymptomatic carriers contribute to the spread of disease, but go largely undetected and can therefore undermine efforts to control transmission. The simulation of possible scenarios of the implementation of social distancing shows that if we rigorously follow the social distancing rule then the healthcare system will not be overloaded.
1. Introduction
By the end of 2019, the city of Wuhan, China, and the rest of the world have seen the apparition of a deadly virus, the most recently discovered coronavirus, named “SARS-CoV-2” [1]. Few weeks later, COVID-19 spread widely in China and other countries, making the World Health Organization (WHO) to declare a global pandemic in March 2020 [2]. There have been 3,090,445 confirmed cases and 217,769 confirmed deaths in 212 countries around the globe until 30 April 2020 according to the World Health Organization.
In order to stop the rapid spread of the coronavirus, many countries have introduced widespread physical distancing measures, population-level movement restrictions, and health education knowledge [3, 4]. However, one of the biggest problems is the existence of asymptomatic infection (having very mild symptoms) among the infected people, and unaware of their contagious ability increases the transmission rate [5]. Recently, and to keep up with the biologists, many mathematical models have been developed to enable a more effective response to this hazard. In [6], Peng et al. have numerically studied a SEIR model that includes intrinsic impact of hidden exposed infected population to describe the epidemic of COVID-19. They have estimated the time of the outbreak of this epidemic in several cities in China. However, they did not incorporate the transmission paths and speed of such an epidemic. In [7], M. Peirlinck et al. have introduce the effect of asymptomatic infection on the outbreak of Covid-19 by proposing a SEIIR model and focusing in decomposing the infectious population into a symptomatic and an asymptomatic group and assuming a similar transmission rate β for both groups. They found that the large asymptomatic population is associated with a high risk of Covid-19 spread. On the other hand, the epidemic progresses across countries, and hospital staff are faced with a massive influx of patients and a large number of deaths, causing a huge problem in resource management. Motivated by these reasons, we propose a SELIAHRD model including eight states (Susceptible, Exposed, Latent, Symptomatic, Asymptomatic, Hospitalized, Recovered, and Death) taking into consideration the total population as susceptible, age, and population structure is not considered [7, 8]. This model was developed based on studies of COVID-19 and the H1N1 influenza epidemic model proposed by Lopez et al. [9] however, in this model, they suppose the existence of vaccinated people and used Generalized regression neural network for simulation without taking in consideration the social distancing scenarios.
This article begins with a section that describes the proposed epidemic model and gives an idea about each compartment of the model. The second section presents a discussion of the well-posedness and equilibria of the proposed model. The stability of the disease-free equilibrium, the use of next-generation operator to get the basic reproductive number R0, and the proof of the global stability of the disease-free equilibrium are presented in the third section. The results of the numerical simulation and their discussion are given in the fourth section.
2. Proposed Epidemic Model
As per the recent report from the WHO, a significant number of COVID-19 patients have very mild symptoms. This means the existence of asymptomatic infections, which increase the transmission rate dramatically in some countries.
To take into consideration the effect of undetectable infected persons, we propose the SELIAHRD model including eight compartments shown in Figure 1.
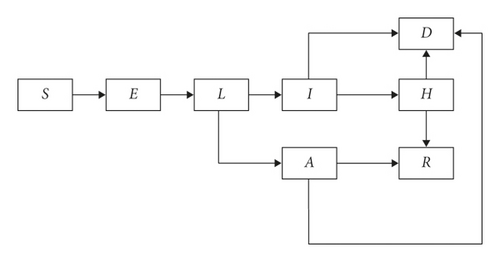
The susceptible state is a person without the disease at time t. The exposed state refers to those near the infected person and has higher risk to get infected. The exposed persons who got infection but not yet infectious are called latent people. From the latent compartment, we can classify the people as symptomatic and asymptomatic people; the symptomatic people will be admitted to the hospital. Asymptomatic and hospitalized people have the probability to go either to the recovered compartment or to the death compartment.
Table 1 shows the definition of symbols in the proposed model.
| Symbol | Definition |
|---|---|
| S | Number of susceptible person |
| E | Number of exposed person |
| L | Number of latent person |
| I | Number of symptomatic person |
| A | Number of asymptomatic person |
| H | Number of hospitalized person |
| R | Number of recovered person |
| D | Number of death person |
| N | Total number of person |
| β | Transmission rate |
| μ | Exposed rate |
| α1 | Symptomatic infection rate |
| α2 | Asymptomatic infection rate |
| σ1 | Symptomatic hospitalized rate |
| σ2 | Asymptomatic recovery rate |
| μ1 | The velocity of latent person becomes symptomatic person |
| μ2 | The velocity of latent person becomes asymptomatic person |
| μ3 | The velocity of symptomatic person becomes hospitalized person |
| μ4 | The velocity of asymptomatic person becomes recovered person |
| μ5 | The velocity of hospitalized person becomes recovered person |
| γ1 | Recovery rate |
| δ | Normal death rate |
3. Well-Posedness and Equilibria
The existence, the positivity, and the boundedness of solutions of the proposed system (1) need to be proved to ensure that the model has a mathematical and biological meaning.
If we put S + E + L + I + A + R + H + D ≤ N, then the following theorems hold.
Theorem 1. The following biological feasible region of system (1) is positively invariant and attracting.
Theorem 2. Let t0 > 0 and the initial conditions satisfy S(t0) > 0, E(t0) > 0, L(t0) > 0, I(t0) > 0, A(t0) > 0, H(t0) > 0, R(t0) > 0, D(t0) > 0, then the solution S(t), E(t), L(t), I(t), A(t), H(t), R(t), D(t) of system (1) are positive for all t ≥ 0.
Proof. From the first equation of system (1), we have
Hence, S(t) is nonnegative for all t ≥ 0. From the other equations of system (1), we set
Therefore, E(t), L(t), I(t), A(t), H(t), and D(t) are all nonnegative for all t ≥ 0.
From the seventh equation of system (1), we can easily deduce the positivity of R(t) for all t ≥ 0.
Hence, the positivity of solution has been proved.
4. Stability of Disease-Free Equilibrium
This section is devoted to studying the stability of the diseases-free equilibrium U0 of system (1).
The equilibrium of the model is obtained by setting dS(t)/dt = dE(t)/dt = dL(t)/dt = dI(t)/dt = dA(t)/dt = dH(t)/dt = dR(t)/dt = dD(t)/dt = 0, and the given system has a disease-free equilibrium given by U0 = (N, 0,0,0,0,0,0,0). In the proposed model, we have multiple types of infected individuals, and then to investigate the stability of the disease-free equilibrium, we will define the basic reproductive number (R0) using the next-generation operator [10], who define R0 as the spectral radius of the next-generation operator.
Theorem 3. If R0 < 1, then DFE (disease-free equilibrium) U0 is locally asymptotically stable (LAS). If R0 > 1, then the DFE is unstable.
4.1. Global Stability Condition for Disease-Free Equilibrium
(H1) for dX/dt = W(X, 0), X∗ is globally asymptotic stable (GAS), (H2) for for (X, Y) ∈ B, where is an Metzler matrix (M-matrix, the off-diagonal elements of Q are nonnegative). If the system satisfies these two conditions, then the following lemma holds.
Lemma 1. The disease-free equilibrium U0 = (X∗, 0) of system (2) is globally asymptotically stable (GAS) provided that R0 < 1 and assumptions (H1) and (H2) are satisfied.
Now, we state the following theorem.
Theorem 4. The disease-free equilibrium of system (1) is globally asymptotically stable if R0 < 1.
Proof. Let X = (S, R) and Y = (E, L, I, A, H, D). We will have
At the point (X, 0), W(X, 0) = (0), X∗ = (N, 0) is globally asymptotically stable for dX/dt = W(X, 0). On the other hand,
In addition, this follows that ,
The off-diagonal elements of Q are nonnegative, i.e., an M-matrix and
Since S ≤ N, 1 − (S/N) ≥ 0, and thus . So, the conditions (H1) and (H2) of Lemma 1 are satisfied, and then this completes the global asymptotic stability of the disease-free equilibrium of the proposed system (1) for R0 < 1.
5. Numerical Results and Discussion
- (a)
The mean incubation period was 5.2 days (95% confidence interval) [9]. Therefore, μ1 = 0.1923.
- (b)
There is a mean 5-day delay from symptom onset to detection/hospitalization of a case. The duration from illness onset to the first medical visit for the 45 patients with illness onset before January 1 was estimated to have a mean of 5.8 days [11]. So, we set μ3 = 0.1724.
- (c)
The recovery rate γ1 = 0.15 is determined by the average duration of recovery D of infection. After this period, they enter the recovery phase.
- (d)
Since there were no data on the proportion of asymptomatic infection of the virus, we simulated μ1 = μ2 and μ4 = 0.08.
- (e)
Symptomatic and asymptomatic infection rates α1and α2 are defined as follows:
-
α1 = (symptomatic infected)/susceptible.
-
α2 = (asymptomatic infected)/susceptible.
-
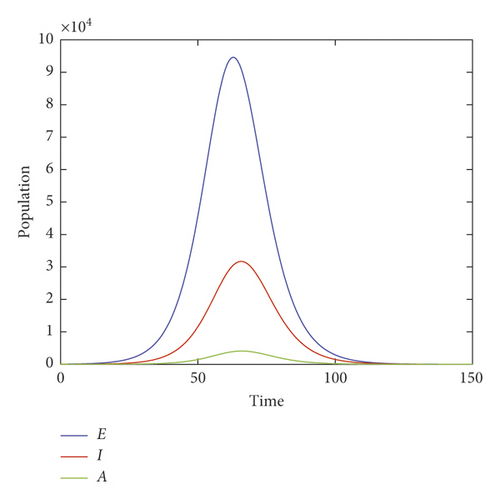
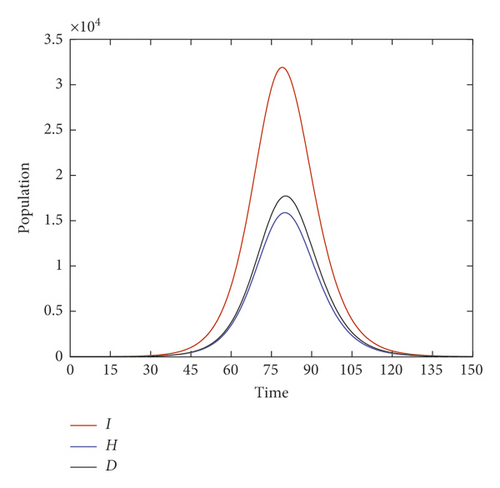
In this first simulation, we assume that there is no social distancing and a total population of 1.5 million. In this scenario, Figures 2 and 3 show that the model predicts in the next 85 days the total symptomatic infected person will reach a peak of 31000 and the healthcare system will be overload (only 15,869 of them get treatment). As a result, the model predicts that the peak of deaths would be 15,665.
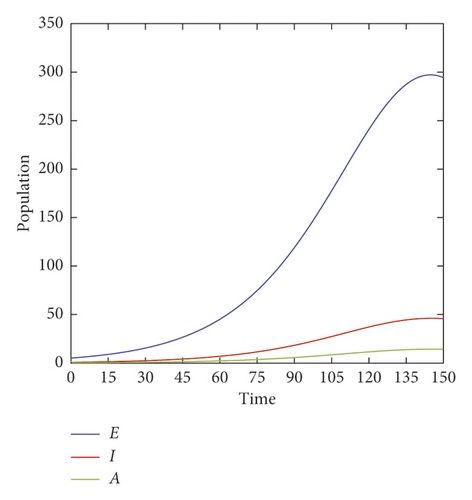
In the second simulation, we assume that 90% of population obey the rule of social distancing.
As can be seen in Figures 4 and 5, the peak of symptomatic infected cases drops significantly to 50 and asymptomatic infected cases to 6, making the healthcare system not overloaded at all and only around 5 deaths.
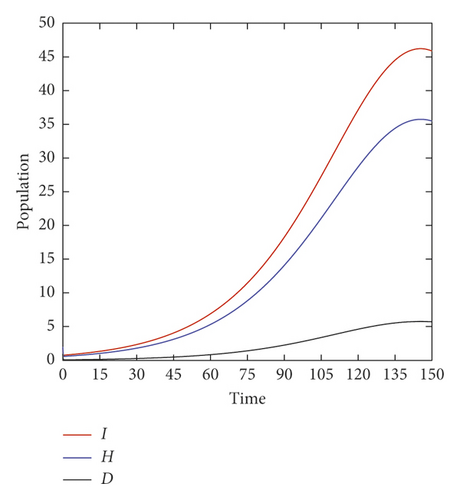
The simulation results show that after 150 days, with the presence of asymptomatic infection the basic reproduction number R0 of coronavirus was 3.25 if there is no social distancing and the healthcare system will be overloaded. On the other hand, if the lockdown is fully operational (90% of population respect of social distancing) even with the presence of asymptomatic infection, the basic reproduction number becomes R0 = 0.68 after 150 days and the healthcare system will not be overloaded. The paper [12] proposed a SEIAR model to simulate the epidemic dynamics of “SARS-COV-2” and demonstrate the efficiency of quarantine and government measure but didn’t take in consideration the velocity of transition between different stages and the effect of lockdown on the healthcare system.
6. Conclusions
The world continues to pay a heavy price as the COVID-19 pandemic spreads. This paper proposes the mathematical model SELIAHRD (Susceptible, Exposed, Latent, Symptomatic, Asymptomatic, Hospitalized, Recovered, and Death), with two kinds of infected people, that is, symptomatic and asymptomatic. We assume that asymptomatic people will not be hospitalized and have the probability to go either recovered or dead. We calculate the basic reproduction number R0 and dynamics of disease-free equilibrium for the “SARS-CoV-2” using the proposed model.
The SELIAHRD model will provide in the presence of asymptomatic infected the number of hospitalized and of deaths for the public authorities to develop the prevention policies (cities lockdown, social distancing, testing, contact tracing, etc.). The simulation shows the importance of the social distancing in making the number of infected and deaths decrease significantly even with the presence of asymptomatic infection and not overloading the healthcare system.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Open Research
Data Availability
The data used to support the findings of this study are available from the corresponding author upon request.




