Smart Contract-Based Cross-Domain Authentication and Key Agreement System for Heterogeneous Wireless Networks
Abstract
Nowadays, it is still a major challenge to design a secure cross-domain authentication protocol for heterogeneous wireless networks with different security parameters. As a new technology, blockchain has attracted people’s attention because of its tamper-proof and decentralized characteristics. In this paper, we propose a cross-domain authentication and key agreement system based on smart contract of blockchains. Public keys of the nodes are managed using the smart contracts, and the system parameters are confirmed by contract query. On this basis, a cross-domain authentication and key agreement protocol is designed. In this protocol, roaming users can select temporary authentication parameters according to the system parameters of the roaming domain to complete authentication and key agreement, and users are anonymous in the process. Security of the protocol is demonstrated under the CK model, and two formal analysis tools are used to further analyze the protocol. Since the protocol does not have complex cryptographic operations and certificate verification, it has lower computational and communication overhead.
1. Introduction
With the development of the Internet and the increase of wireless access devices such as smartphones, laptops, and iPads, people demand more network resources and better network services. Various wireless access technologies have been developed and deployed to meet growing demand, such as CDMA (Code Division Multiple Access), Wi-Fi (Wireless Fidelity), Wi-MAX (Worldwide Interoperability for Microwave Access), and LTE (Long Term Evolution). These technologies have their advantages and disadvantages, and no wireless access technology is perfect to meet the needs of all users. In this context, heterogeneous wireless networks that incorporate multiple access technologies have emerged to take full advantage of the network characteristics of various access technologies. The upcoming 5G [1] and the Internet of Things (IoT) [2] has a typical heterogeneous structure. In 5G, multiple wireless access technologies coexist, and macro stations responsible for wide-area coverage and low-power small stations responsible for hotspot coverage are developed in multilayer.
The purpose of heterogeneous wireless network convergence is to give full play to the advantages of various wireless network resources, so that users can select a suitable access network according to their needs. Users in a heterogeneous network can choose to access or handover to a wireless network that best suits their needs according to current network status and service requirements. Multiple independent and autonomous security domains in heterogeneous wireless networks typically have different security standards, and each domain uses different system parameters. Therefore, a cross-domain authentication key agreement solution that does not restrict domain system parameters is required.
Traditionally, in cross-domain authentication solutions, there are two main frameworks. One is based on the symmetric key scheme such as Mahshid and Eslamipoor [3]. Although the authentication protocol based on symmetric key is low in complexity and easy to implement, the burden of generating, distributing, storing, and managing shared keys is complex and huge. Especially for heterogeneous networks, it will increase the complexity of system management and reduce the scalability. The other is based on the traditional certificate, which has the burden of certificate management and distribution and results in high computation and communication overhead. Millán et al. [4] adopted the Certificate Authority (CA) scheme to establish a bridge CA model that all domains trust. This scheme requires all domains to trust this trusted third party, which is difficult to apply in practice, and there is also the problem of how to obtain certificate status information across domains.
In addition, identity-based cryptography is used to facilitate cross-domain authentication. Peng [5] proposed a multidomain authentication key agreement protocol based on the identity cryptography. The protocol requires all authentication servers to be trusted, and each authentication server uses the same PKG (Private Key Generator) system parameters, which makes the system poor scalability. Papers [6, 7], respectively, gave cross-domain authentication protocols based on identity proxy signatures, which require the agent to establish a security association with the trust domain. But, the signature authorization from the original signer to the proxy signer may bring more security risks, and the introduction of proxy mechanisms increases system complexity. In conclusion, there is a need for a common PKG in most of the current cross-domain authentication key agreement schemes using identity-based cryptography. In 2003, Chen et al. [8] first proposed a user key agreement protocol under different PKGs. In 2004, McCullagh and Barreto [9] proposed a key agreement protocol with key escrow and unmanaged modes in different PKG environments, but then the protocol pointed out that it could not resist key leakage attacks. In recent years, some identity-based key agreement schemes [10, 11] and certificateless authentication key agreement schemes [12] have been proposed one after another, but they cannot meet the requirements of key agreement between different trust domains. However, in the future heterogeneous wireless network application, each trust domain is mostly an independent autonomous domain, where different system parameters are used. Therefore, most of the above solutions are difficult to meet the authentication and key agreement requirements of the heterogeneous wireless network.
Some anonymous cross-domain schemes have been proposed one after another. In 2014, Cheng et al. [13] proposed a distributed anonymous authentication (DAA) protocol, which uses an unlinkable group signature algorithm to provide authentication without sharing keys in advance, which significantly reduced signaling overhead while protecting privacy. In 2017, Fu et al. [14] proposed a scheme based on the (t, n) shared secret key to protect the privacy of users during the handover process and use the unpaired identity encryption method to achieve highly efficient handover. In 2018, a novel group key management protocol [15] for cross-domain dynamic anonymous authentication was proposed to realize cross-domain secure anonymous group communication. However, the above schemes also have the problem of using the same parameters in different domains.
Recently, some other authentication methods were proposed for different network applications. Lu et al. presented an anonymous three-factor key agreement using Elliptic Curve Cryptography (ECC), which is for secure communications to be used in resource-constrained wireless sensor networks [16]. Cheng et al. propose a novel design using an asymmetric bivariate polynomial for user authentication and group key establishment with low communication costs in WSNs [17]. Arezou et al. propose a secure and lightweight authentication and key agreement protocol for IoT based WSNs that concerns the strong replay attacks and perfect forward secrecy [18]. To ensure secure communication over the insecure public network, Qi and Chen propose a privacy-preserving biometrics-based authenticated key agreement scheme using ECC, which has perfect user experience in changing password without interacting with the server [19]. Akram et al. propose an anonymous multiserver authentication which allows for getting services from different servers using only single-time registration [20].
In 2008, Nakamoto designed the Bitcoin system and introduced blockchain technology for the first time in his paper [21]. Blockchain is a distributed ledger technology and a decentralized storage system. In 2014, the blockchain technology began to be applied to distributed applications by introducing smart contract. In 2014, based on the Bitcoin blockchain system, Fromknecht proposed the first distributed PKI authentication system, Certcoin [22, 23]. Certcoin is used instead of CA to provide efficient key query and identity retention. But, it has the problem of user privacy leakage because the binds of user identities and public keys are directly recorded in the public ledger of the blockchain. Axon proposed an improved Certcoin scheme [24], which was a PKI privacy protection authentication system. In 2016, Lewison proposed a certificate-based PKI authentication system using the Ethereum platform [25], which solved the problem of excessive traffic of the traditional PKI certificate management and the use of certificate revocation list (CRL) and online certificate status protocol (OCSP). We refer to these existing schemes to design distributed PKI for wireless networks based on smart contracts. Wang et al. [26] proposed a blockchain-based cross-domain authentication model named BlockCAM to enable users to access shared resources across domains in a secure way. But when the number of nodes is large, its authentication efficiency is low because of the need for traversing the blockchain. Besides, the scheme has not referred to the key agreement. The comparison of these related protocols mentioned above is provided in Table 1. Unfortunately, there is no blockchain-based solution to solve the cross-domain authentication problem of heterogeneous wireless networks so far.
| Protocols in references | Technology | Strengths | Weaknesses |
|---|---|---|---|
| [3] | Symmetric key | Low in complexity and easy to implement | High complexity of system management and low scalability |
| [4] | Bridge CA | Flexible authentication | High computation and communication overhead; requiring trusted third party |
| [5] | Identity-based cryptography | Without public key certification | The same PKG; low scalability |
| [6, 7] | Identity proxy signatures | ||
| [8] | Key agreement | Different PKG; without public key certification | High computation overhead |
| [9] | |||
| [10, 11] | Paring free key agreement | ||
| [12] | Certificateless authentication key agreement | Without public key certification | Complex cryptographic operations |
| [13] | Group signature algorithm | Anonymous cross-domain authentication | Complex cryptographic operations |
| [14] | (t, n) shared secret key | ||
| [15] | Group key management | ||
| [16, 19, 20] | ECC | Anonymous multifactor authentication | Complex cryptographic operations |
| [17] | Asymmetric bivariate polynomial | Low communication cost | |
| [18] | Biohashing function | Multifactor and lightweight authentication | High communication cost |
| [22, 23] | Blockchain | Efficient key management | User privacy leakage |
| [24] | Privacy protection | High computation overhead | |
| [25] | Low communication cost | ||
| [26] | Cross-domain authentication | ||
1.1. Contribution and Motivation
Since the existing schemes are centralized and vulnerable to single point failures and denial of service attacks, they are unsuitable for heterogeneous environments for using different parameters in multidomain. Based on the decentralized and distributed blockchain and the distributed and easy-to-program smart contracts, we propose a smart contract-based cross-domain authentication and key agreement system for heterogeneous wireless networks. The system constructs a blockchain network in which the CA and access point (AP) nodes of each domain are set as blockchain nodes, and the public key of AP nodes and the hash of the public key of registered users are recorded in smart contracts by CA nodes. Cross-domain authentication is realized by mutual query and verification of the public keys stored in the contract instead of the traditional PKI method with mutual issuance of signed certificates and verification of signatures. Our solution implements cross-domain authentication between domains with different parameters and guarantees user anonymity. Evaluation results show that the solution has low communication overhead and computation cost.
1.2. Organization
This paper is organized as follows: Section 2 describes the blockchain system and the CK model. In Section 3, we describe our proposed scheme in detail. In Section 4, we give its security proof under the CK model and other security analysis and results of formal analysis tools. Section 5 shows the real implementation and evaluation results. The paper is concluded in Section 6.
2. Preliminaries
In this section, we will introduce blockchain and CK model in provable security theory briefly, where blockchain improves the security and effectiveness of our system and the CK model helps us to analyze protocol security.
2.1. Blockchain and Smart Contract
Blockchain is a kind of decentralized ledger running on the p2p network that combines data blocks into a specific data structure in the form of chains in the chronological order. The blockchain mainly has three characteristics, namely, distributed multicenter, collective maintenance, and tamper-resistant. The characteristics of the blockchain make it a useful technology for building distributed and transparent storage systems where records cannot be hidden or destroyed by third parties.
Blockchain can be divided into two categories [27]: authorized and unauthorized. The unauthorized blockchain is public blockchain like Bitcoin and Ethereum. It is a blockchain that is open to all and anyone can participate. It usually consumes a lot of energy and time because it involves computational efforts to enhance system security against modification attacks. And, the authorized blockchain is private or consortium blockchain such as Hyperledger Fabric [28]. It limits the consensus peers (only selected trust peers named as committing peers have the right to verify the transaction and generate a new block). It is neither energy-consuming nor time-consuming. Partial decentralization, better permission management, and privacy protection of the consortium blockchain make it better for enterprises and specific scenarios.
Currently, designing programmable currencies and contracts have become a trend to extend blockchain applications beyond the cryptocurrency field. Smart contracts are ways to use blockchains to implement agreements between parties rather than relying on third parties to maintain a trust relationship. Smart contracts are responsible for implementing, compiling, and deploying the business logic of blockchain system in the form of code, triggering the automatic execution of established rules and minimizing manual intervention. Smart contracts allow both parties to participate and can partially or fully execute or enforce certain commitments or agreements, which are a set of commitments in the form of digital [29]. A smart contract is essentially a collection of predefined instructions and data that have been recorded at a specific address in the blockchain. By encapsulating operational logic into bytecode and performing Turing complete computations for distributed miners, smart contracts allow users to transcode more complex business models into new transactions on blockchain networks. Smart contracts can be programmed using the Turing Complete Language. The Turing Complete Language is a programming language that assumes that any computational problem can be solved with sufficient time and space. Typically, smart contracts are compiled into a specific binary format and deployed by the account to a global database of blockchains. Smart contracts provide a promising solution for implementing a more flexible and convenient public key management model on a blockchain network.
2.2. Provable Security Theory
2.2.1. CDH Assumption
Let G be a cyclic addition group and P ∈ G be a generator of order q; given P, aP, bP for random , it is difficult to calculate abP.
2.2.2. CK Security Model
Canetti and Krawczyk [30] extended the model of the paper [31] and proposed the CanettiKrawczyk (CK) model. The CK model defines security with indistinguishability. If the attacker cannot distinguish between the session key generated by the protocol and an independent random value under its allowed attack capability, the key agreement protocol is secure. The CK model defines the session key secure (SK-secure) and presents a modular approach to demonstrating protocol security using SK-secure definitions.
The CK model consists of three parts: an authenticated-link adversarial model (AM), an unauthenticated-link adversarial model (UM), and an authenticator. The authenticator is the link between the AM and the UM. The AM model is an authenticated link adversarial model in an ideal environment. The attacker is passive in AM and cannot forge, tamper with, or replay messages from uncaptured participants. And, it is restricted to faithfully deliver the same message once (although the order of delivery can be delayed or rearranged). In addition, the attacker can also perform the following attacks: party corruption, session-key query, session state reveal, and test-session query.
Definition 1. Test-session query: an attacker can select a test session from those completed, unexpired, and unexposed sessions at any time during the protocol run to obtain a test-session key or a random number. Specifically, let sk be the session key of the test session. When the attacker queries the test session, a coin b is tossed. If b = 0, sk is returned to the attacker; otherwise, a value r randomly chosen from the probability distribution of keys is returned to the attacker. Finally, the attacker outputs b′ as its guess for b.
The UM model is an unauthenticated links adversarial model in a real network environment. In addition to executing all the attacks in AM mentioned above, the attacker can also completely control the network, including inserting, replaying, forging, and tampering with messages. In UM, the attacker can control the scheduling of protocol events and communication links. At the same time, the attacker can also know the secret information of the protocol participant through specific attack means.
Definition 2 (SK-secure). For any adversary in the UM, a protocol is SK-secure if the following properties hold:
- (1)
After two uncorrupted parties complete matching sessions, they both output the same session key.
- (2)
The adversary initiates a test-session query attack and the probability that guesses correctly the bit b is no more than 1/2 plus a negligible fraction in the security parameter.
Theorem 1 (see [30].)Suppose λ is a message transmission (MT) authenticator, that is, λ emulates a simple MT protocol in UM. Suppose Cλ is a compiler constructed based on λ, then Cλ is also an authenticator. The authenticator is a very important mechanism in the modular approach, which ensures that the security protocols in the AM are translated into security protocols in UM.
The proof of Theorem 1 is detailed in the paper [30]. The papers [30–32] detail the basic theory of the CK security model and the basic method of designing a secure key agreement protocol based on the model. For more detailed information about CK model and its application, refer [33–35].
3. Smart Contract-Based Cross-Domain Authentication and Key Agreement System
In order to provide continuous services for mobile users securely, it is necessary to design a secure and efficient cross-domain authentication protocol for wireless networks. Blockchain is one of promising techniques for next-generation wireless networks, which may establish a secure and decentralized resource sharing environment. Once recorded, the data on the blockchain cannot be tampered with. Currently, many blockchain-based schemes as Section 1 have been proposed and leveraged to enhance security. Moreover, a decentralized, trusted, and publicly auditable database could be built based on blockchain in wireless networks, so that decentralized trust can be achieved. Using the decentralized blockchain and the easy-to-program smart contracts, we propose a smart contract-based cross-domain authentication and key agreement system for heterogeneous wireless networks.
3.1. System Model
As we introduce in Section 2.1, the blockchain is a tamper-proof, antiforgery, and distributed storage system and the smart contract is distributed, traceable, and persistently running. Based on these characteristics, a smart contract-based authentication and key agreement system is designed for heterogeneous wireless networks. For the system, based on the needs of the actual network environment, our cross-domain authentication and key agreement system should meet the following basic security requirements [36].
3.1.1. Single Registration
For practice, all nodes in the system can authenticate or communicate with other registered nodes only if they are registered only once.
3.1.2. User Anonymity
The system should ensure that the user ID is not visible to attackers and the AP nodes to protect the anonymity of the user node.
3.1.3. Mutual Authentication
Nodes in the system can believe each other’s identity, ensure that the identity claimed by the other party is itself, and confirm that the message is from the real sender.
3.1.4. Session Key Agreement
To communicate securely between nodes, the system should negotiate a session key with another party during the authentication phase for subsequent communication.
3.1.5. Perfect Forward Secrecy
To prevent the leakage of the session key of the previous communication and protect the previous communication content, any attacker cannot recover the previous session key even if he obtains the private key of both communication parties.
3.1.6. No Online Certificate Authority
To reduce the communication cost, the system should avoid online certificate authorities participating in the authentication and any two nodes can directly authenticate each other without relying on an online certificate authority.
3.1.7. Resilience to Common Attacks
The system should be designed to resist common attacks, such as impersonation attacks, modification attacks, replay attacks, man-in-the-middle attacks, and denial of service attacks or distributed denial of service attacks (DoS/DDoS).
Note: the property of “no certificate authority” is very important for system security. The readers can refer to [33–35] for more information about it.
The system includes a smart contract-based public keys management system (SCPKM) and a cross-domain authentication and key agreement protocol (CAKA). As described in Section 2.1, consortium blockchain, which is partially decentralized, can reach a consensus more quickly and give different privileges to different nodes. In our system, APs have certain computing and storage capacity as general nodes of blockchain for querying and invoking function in contract, and CAs have sufficient computing and storage capacity to complete the consensus task as committing peers of blockchain. A consortium blockchain is built on all AP nodes and CA nodes.
The system consists of APs, CAs, users, blockchain network, and smart contracts, as shown in Figure 1. There are several security domains (two domains in the figure for simplicity), and each security domain consists of one CA, several APs, and many users.

The two protocols SCPKM and CAKA are described in detail below.
3.2. Domain Initialization
There exist some APs and a CA (for simplicity, only one CA is set; in fact, a certain number of CAs should be set according to the size of the domain) in each security domain. Each CA chooses independently different or same (according to security requirement of the domain) system public parameters. We take domain U as an example to illustrate the generation of system public parameters in the domain as follows. A large prime pU is selected, EU is an elliptic curve defined on a finite field , and PU is a generator of EU. HU is a cryptography hash function, where HU : EU⟶{0,1}∗. The basic public parameter basicpareU is <pU, EU, PU, HU>. Define a key generation algorithm GenU : basicpareU⟶(AU, aU), where aU is randomly chosen in and AU = aU · PU. The CA generates public and private key pair (sU, PKU) using GenU. The system public parameter pareU of the domain U is <pU, EU, PU, HU, GenU, PKU>.
The CA and APs in a certain domain join the consortium blockchain as an organization.
3.3. Smart Contract-Based Public Key Management System
| Notations | Description |
|---|---|
| H : (⋅) | A cryptography hash function H : {0,1}∗⟶{0,1}l and l is a fixed constant. |
| sig (sk, m) | A signature algorithm that signs a message m using the private key sk |
| ver(PK, σ, m) | A verification function that verifies whether σ is a valid signature on m under the public key PK |
| A⟶B : m | Node A sends a message m to node B |
| DI∗, ID∗ | A domain identifier and a node identifier |
| Ek(m) | A symmetric encryption algorithm that encrypts m with key k |
| The private key and the public key of a node generated by using GenU of the domain U | |
| CAU | The CA of a node U |
| σ∗ | Signature value |
3.3.1. Contract Deployment
Algorithm 1 is shown in Table 3. The only CA in each domain compiles and deploys the smart contract to manage APs, users, and their public keys of its own domain. At deployment time, the function PK_domain in the contract will be invoked automatically, and information of the domain is written to the contract. Once smart contracts pass the validation process, they will be recorded in the blockchain forever by all the blockchain peers (APs and CAs). Then, all nodes can query the variable CA to get information of the domain.
| Algorithm 1 constructor of smart contract |
|---|
| Structure AP_PK |
| % define the structure of information of AP’s public key. |
| ID; % ID of an AP. |
| PK; % the public key of the AP. |
| T_begin; % the public key effective start time. |
| T_end; % the public key expiration time. |
| sig; % CA’s signature of ID, PK, T_begin, and T_end. |
| Structure CA_Info CA |
| % define the structure of information of CA. And CA, an CA_Info structure variable is public to all node |
| ID_domain; % domain ID |
| Basicpare; % the basic public parameter of the domain. |
| PK; % the public key of CA. |
| sig; % CA’s signature of ID_domain and PK. |
| Map(hash- > bool) user % A map denote if user is registered it returns true. |
| Map(ID- > AP_PK) ap % A map denote if ID is registered it returns the public key information of the node corresponding to ID. |
| Uint len; % the number of nodes. |
| function PK_domain (id, pare, pk, sig) |
| % constructor, it is automatically invoked when this smart contract is deployed; initialize CA and only this function can modify variable CA. |
| owner = sender.addr; % Define CA is the owner of the contract. |
| CA = {id, pare, pk, sig}; |
| len = 0; |
| function get_CA(·) |
| % Invoked to obtain the information of the domain. |
| return CA; |
3.3.2. Node Registration
-
Step 1. AP sends CAU the registration request {IDAP, identification − information} through a secure channel.
-
Step 2. After CAU receives the registration request, and it verifies the identification-information and checks if IDAP has registered. If verification is correct, CAU adds AP into the organization in the blockchain.
-
Step 3. Upon addition into the blockchain, AP invokes the function get_CA() to get the basic public parameter basicpareU and the public key PKU of the domain U, and then it generates its public and private key pair using GenU. Finally, it invokes . AP computes the signature and then it sends CAU the message M1 = {IDAP, σ1}.
-
The signature demonstrates that the AP has the corresponding private key .
-
Step 4. When CAU receives M1, it verifies the signature σ1 by calculating . If the verification is correct, CAU computes the signature and then invokes the function CA _ Confirm(IDAP, tbegin, tend, σ2) to confirm the registration of AP. Otherwise, CAU sends ‘ERROR’ and the error reason to AP.
| Algorithm 2 register |
|---|
| function AP_Register (id, pk) |
| % AP node invokes the function to register to CA. |
| If(AP_node[id] = NULL) % id has not been registered. |
| AP_node[id] = sender.addr; len ++; |
| ap[id] = = { id, pk, NUL, NUL, NUL}; |
| function CA_Confirm(id, t_begin, t_end, sig) |
| % CA invokes the function to confirm the registration of AP by writing the t_begin, t_end and signature sig to the contract. |
| if(sender.pk = = owner) % Guarantee only CA can invoke the function. |
| ap[id]. T_begin = t_begin; |
| ap[id]. T_end = t_end; |
| ap[id].sig = sig; |
| function user_Register (hash) |
| % CA invokes the function to write the hash of user public key to the contract. |
| if(sender.addr = = owner) % Guarantee only CA can invoke the function. |
| User[hash] = true; |
| function getAP(id) |
| % invoked to obtain the public key of an AP. |
| return ap[id]; |
| function user_Verificate (hash) |
| % Invoked by someone to check a certain hash is registered or not. |
| if(user[hash]) |
| return true; |
| else return false; |
-
Step 1. UE sends CAU the registration request {IDUE, identification − information} through a secure channel.
-
Step 2. CAU verifies the identification-information and checks if IDUE has registered. If UE passes further verification, CAU gives UE permission to query the blockchain.
-
Step 3. UE invokes the function get_CA( ) to get the basic public parameter basicpareU and the public key PKU of the domain U, and then it generates its public and private key pair using GenU. UE computes the signature and sends message M2 = {IDUE, PKUE, σ1} to CAU through the secure channel.
-
Step 4. Upon receiving M2, CAU verifies the signature σ1 by calculating ver(PKUE, σ1, m1). If the verification is wrong, CAU sends “ERROR” and the error reason to UE. Otherwise, CAU computes , invokes function user _ Register(h), and maintains the user list . CAU computes and generates the authenticate ticket . Finally, CAU sends to through the secure channel.
3.3.3. Public Key Update
When the user or AP needs to update its public key, it generates a new key pair and sends the new public key to CA through the secure channels. CA invokes user_update or AP_Update function in Table 5 (Algorithm 3) to update public key in the contract and then CA updates the corresponding user list for user update.
| Algorithm 3 update |
|---|
| function AP_Update (id, pk, t_begin, t_end, sig) |
| % CA node invokes the function to update public key. |
| if(sender.addr = = owner) % Guarantee only CA can invoke the function. |
| ap[id].PK = pk; |
| ap[id]. T_begin = t_begin; |
| ap[id]. T_end = t_end; |
| ap[id].sig = sig; |
| function user_update (hash1, hash2) |
| if(sender.addr = = owner) |
| Delete(user[hash1]) |
| user[hash2] = true; |
3.3.4. Public Key Revocation
When an AP or a user detects some node’s suspicious behavior or it detects some node A is broken, it reports the abnormal case to CA. Then the CA checks the report. If it is true, the CA invokes AP_Revoke or user_Revoke in Table 6 (Algorithm 4) to revoke public key of the node A and other nodes will refuse communication with the node A.
| Algorithm 4 revoke |
|---|
| function AP_Revoke (id) |
| % only CA can invoke the function to revoke public key of some node. |
| if(sender.pk = = owner) |
| Delete(ap[id]); |
| function user_Revoke (hash) |
| if(sender.pk = = owner) |
| Delete(user[hash]); |
3.4. Cross-Domain Authentication and Key Agreement Protocol
Based on the above model and public keys management smart contract, we design a cross-domain authentication and key agreement protocol. The CAKA solves the cross-domain problem by querying the public key recorded on SCPKM, and it solves the authentication and key agreement problem by implementing DiffieHellman (DH) authenticated key exchange algorithm. The protocol is shown in Figure 2 (denotes the blockchain). The specific process is as follows.
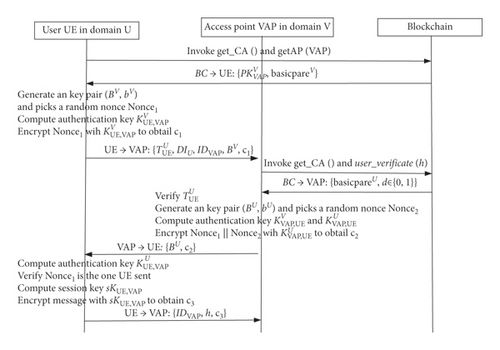
-
Step 1. UE sends a request message to VAP
-
UE invokes get_CA( ) and get AP(VAP) of the smart contract in domain V. Then, the blockchain will return VAP′s public key and system parameters basicpareV of domain V. Then UE generates an authentication public and private key pair (BV, bV) using GenV and picks a random nonce Nonce1. UE computes the authentication key with VAP and encrypts Nonce1 with the key to obtain . At last, it sends message to VAP.
-
Step 2. VAP sends response message {BU, c2} to UE.
-
Upon receiving message from UE, VAP computes ( is in ). Then, VAP invokes get_CA( ) and user _ Verificate(h) of the smart contract in domain U. And, the blockchain will return system parameters basicpareU of domain U and d ∈ {0,1} for user _ Verificate(h). VAP verifies (verify the signature in TU, d = 1 and tbegin ≤ tnow ≤ tend). If the verification is correct, VAP generates an authentication public and private key pair (BU, bU), picks a random nonce Nonce2, and computes authentication keys with UE and . It is obvious that holds by the following equations:
-
VAP decrypts ciphertext c1 with and obtains . Then, VAP checks whether , hold. If all checks pass, VAP computes the session key and encrypts Nonce1‖Nonce2 with the key to obtain . Finally, VAP sends message {BU, c2} to UE.
-
Step 3. UE sends session key confirmation message {IDVAP, h, c3} to VAP.
-
Upon receiving message {BU, c2} from VAP, UE computes another authentication key with VAP. It is obvious that by the following equations:
-
Then, UE decrypts ciphertext c2 with and obtains Nonce1, Nonce2, and . If Nonce1 is the one which UE has sent to VAP, UE authenticates VAP. UE computes the session key and encrypts IDVAP‖h with the key skUE,VAP to obtain . Finally, UE sends message {IDVAP, h, c3} to UE. If Nonce2UE got is the one which VAP has sent, then UE and VAP both get the same session key sk:
-
Step 4. After receiving message {IDVAP, h, c3} from UE, VAP decrypts ciphertext c3 using skVAP,UE. If decryption is successful, it confirms that UE got the right session key and authenticates UE.
UE and VAP belong to different domains using different parameters, but through the above CAKA protocol, they can authenticate each other and negotiate the session key to achieve secure communication.
4. Security Analysis
Security of our proposed cross-domain authentication and key agreement protocol are studied with the following respects.
4.1. Provable Security Analysis
This section proves the security of CAKA based on the CK security model. We first present a SK-secure protocol in AM. Then, we construct MT authenticators. Then, we apply the authenticators to the protocol in AM and get our protocol CAKA after necessary message reorganization and optimization. According to Theorem 1, our protocol is also SK-secure in UM.
4.1.1. Protocol π in AM
-
Step 1. The UE ( is its authentication ticket) obtains the parameter pareV of the domain V and the public key of the VAP through querying contract, then it generates a public-private key pair (BV, bV), randomly picks a nonce Nonce1, and sends the message to the VAP.
-
Step 2. After receiving the message sent by the UE, the VAP firstly computes the hash and then queries the contract to verify h and gets parameter pareU of the domain U. After verifying the validity of , an authentication public and private key pair (BU, bU) is generated and a nonce Nonce2 is randomly picked. Finally, the message {BU, Nonce1, Nonce2} is sent to the UE. The VAP can use BV and to generate its session key skVAS,UE with the UE as follows: , , and .
-
Step 3. After receiving the message {BU, Nonce1, Nonce2}, the UE checks whether Nonce1 is previously sent by itself, and if so, the UE completes the authentication with the VAP. The UE can use and BU to generate its session key skUE,VAS with the VAP as follows: , , and . Then, UE uses skUE,VAP to encrypt IDVAP and h and gets the ciphertext . Then, it sends the message {IDVAP, h, c3} to VAP.

So far, the UE and the VAP complete the authentication and key agreement.
Theorem 2. If the CDH assumption is true and H is a random oracle, the protocol π is session key secure in AM.
Proof. Firstly, it is easy to prove that the protocol π satisfies the first condition of session key secure in Definition 2. Namely, after the protocol is executed, the matching session computes the same session key by equations (2)–(4) and the session key is evenly distributed according to the hash property of H.
Next, it is proved that the protocol also satisfies the second condition of session key secure in Definition 2. In this paper, the algorithm is constructed according to the idea of paper [30]. The algorithm uses the adversary as a subroutine to simulate the execution process of the protocol and answer all the queries and return the output message of the protocol to . The reduction to absurdity is used to prove that the protocol π satisfies condition 2 in the AM.
Suppose there is an adversary . Let ε be a nonnegligible advantage of distinguishing between a session key and a random number of the same length. The session key sk cannot be directly obtained, which can only be acquired by hashing obtained constituent elements. The sk is computed by , where , , BV, BU, Nonce1, and Nonce2 are transmitted in clear text, which is easily obtained by , so the focus of the attack is and , where and . The advantage of solving the CDH problem for adversary is denoted as εCDH. The probability of guessing the test session is at least 1/L (L is number of sessions), and the probability of not guessing the test session is 1 − 1/L. And, suppose in a test-session query, probability of guessing b is 1/2 + ε. So, the probability of guessing b is Pr[b = b′] = (1/2 + ε) × (1/L) + (1/2) × (1/1 − L) = (1/2) + (ε/L). can guess b by the following two cases: (i) completely randomly guess b; the probability is 1/2; (ii) solve the CDH problem. Then, Pr[b = b′] ≤ εC DH + 1/2, so ε/L = Pr[b = b′] − 1/2 ≤ εCDH. If ε is not negligible, εCDH is not negligible and obviously it contradicts the CDH assumption. So, the protocol π can be proved to meet the second condition.
Therefore, protocol π is session key secure in AM.
4.1.2. Construct MT Authenticators
In this protocol, the UE authenticates the VAP and the VAP authenticates the UE, so two MT authenticators λSC,ENC (encryption authenticator based on smart contract) and are required.
MT authenticator λSC,ENC: the UE obtains the parameter pareV of the domain V and the public key of the VAP through inquiring the contract and computes the authentication key using the newly generated private key bV. Then, it randomly picks Nonce1, computes ciphertext , and then sends the message to VAP.
After receiving the message, the VAP computes the authentication key and ( is in ). Since (equation (2) in Section 3.4), the key can be used to decrypt c1 to obtain Nonce1. VAP computes the ciphertext , and sends the message M2 = {BU, c2} to UE.
After receiving the message, the UE computes the authentication key and then decrypts the ciphertext to obtain Nonce1. Finally it checks whether Nonce1 was previously sent to the VAP, and if so, the UE completes the authentication of VAP.
Here, only the MT authenticator λSC,ENC is briefly described. As is similar, we will not elaborate further.
Theorem 3. If HV and H are both random oracles, the CDH assumption is true, and the symmetric encryption algorithm E can resist selection message attacks; λSC,ENC is the MT authenticator.
Proof. Let be the UM adversary who interacts with λSC,ENC. We construct an AM adversary so that the outputs of and are the same except for the negligible probability. initializes the protocol λSC,ENC by selecting the key for a series of entities executing λSC,ENC according to the running conditions of λSC,ENC. In the interaction with entities executing protocol λSC,ENC, adversary runs as a routine. Then, the interaction process runs as per the following rules:
- (i)
As long as the adversary in the UM activates an entity B′ to send a message m to the entity A′, the adversary in the AM activates B to send a message m to A
- (ii)
When the simulated entity A′ outputs that A′ receives a message m from B′, the adversary activates A to output a similar message
- (iii)
As long as the adversary destroys an entity, destroys the corresponding entity in the AM and sends the message to
- (iv)
Finally, outputs the output of
If entity UE is not captured, but the message (UE, VAP, and M1) is not in the undelivered message set, which means that the message is forged by the attacker. We call this event E. We want to prove that the probability of event E occurring is negligible. The adversary forged a message that passed validation. This situation is true unless there are two kinds of events occurring: , the adversary successfully falsifies the ciphertext without knowing the key , that is, breaks the symmetric encryption algorithm; , the attacker computes or to get without knowing private key of VAP or UE, that is, the CDH problem is solved. Since E1 ∪ E2⊇E, Pr(E1) + Pr(E2) ≥ ε. If ε is not negligible, the probability that at least one of E1 and E2 occurs is not negligible. We can use to construct an algorithm F to break through encryption algorithm or CDH problem with a probability of , where n is the number of entities that are activated. This contradicts the assumption that the encryption algorithm E is safe and the CDH assumption is true. So, λSC,ENC is the MT authenticator.
Similarly, is the MT authenticator. So, the protocol CAKA is SK-secure in UM according to Theorem 1.
The provable security analysis shows that the protocol satisfies mutual authentication, key freshness, known key security, antireplay attack, and man-in-the-middle attack security. We also validated these security attributes in Section 3 using formal analysis tools.
4.2. Analysis of Other Security Attributes
4.2.1. User Anonymity and Anonymity Controllability
Identity information of UE that is sent to VAP only include domain identifier and an authentication ticket containing the public key and the signature of CA. VAP is only sure of domain of UE and sure if the public key is registered but not identity by the information.
When the VAP is suspicious of the authentication information of the UE or after the UE roams into the foreign domain, the malicious anonymous access behavior may occur, VAP needs to submit the authentication ticket and related public information to the CA of UE′s domain for anonymous identity tracking. The CA first verifies the validity of the anonymous tracking information, and then, by querying the stored data to provide the identity information (IDUE, PKUE, h) (where h is in the authentication ticket) of UE. After receiving the response information of the CA, the VAP verifies that the equation H(IDUE‖HU(PKUE)) = h is true. If so, the CA provides accurate information and VAP knows the true identity of UE. Otherwise, the information of UE provided is incorrect and VAP requires CA to continue to provide relevant information, that is, CA cannot protect malicious users.
4.2.2. Perfect Forward Secrecy
The random temporary numbers are unpredictable for any party except UE and VAP, because UE and VAP use new authentication private keys in every authentication process. Even if the adversary attacks secret information of UE and VAP or even captures the CA and obtains the long-term private key of UE and VAP, he cannot obtain the past temporary keys and the past encrypted random temporary numbers Nonce1 and Nonce2. And, he cannot get the past session keys certainly. Therefore, the scheme has the property of perfect forward secrecy.
4.2.3. Resilience to DDoS
The distributed architecture of blockchain naturally has point-to-point and multiredundancy characteristics. Even if one node fails, other nodes are not affected, so there is no single-point failure problem. It is much more flexible than a centralized system in terms of denial of service attacks. Once a node fails, users connected to the failed node cannot enter the system.
In addition, based on the analysis of computing overhead for both parties of the protocol, as shown in Table 7, the difference between UE and VAP computing overhead is not significant. And, VAP checks for user identity and avoids replay attacks through receiving only messages with fresh Nonce1. So, the protocol resists DDoS attacks.
| UE | VAP | |
|---|---|---|
| Verification | 0 | 1 |
| Symmetric encryption/decryption | 1/2 | 2/1 |
| DH | 2 | 2 |
| Key pair generation | 1 | 1 |
4.3. Formal Analysis Tools
Compared with other mainstream protocol formal analysis tools, the formal analysis tool Scyther has the advantage that it can give explicit termination for the protocol with infinite session and infinite state set. The Scyther tools are based on the model detection algorithm and have a clear description of the state set trajectory. Scyther based on SPDL description language provides graphical attack output for both finite and infinite sessions. Scyther series tools include Scyther and Scyther-Compromise, among which Scyther-Compromise tools use a variety of adversary enquiry capabilities under the strong security model as tick options, including forward security, weak forward security, perfect forward security, temporary key leakage, state leakage, and other strong security attributes. In the button-based human-computer interaction interface, as long as different combinations of different queries are selected, the protocol is analyzed under different strong security models such as CK or eCK. However, the Scyther tools do not include embedded algebraic operation properties and cannot formally describe algebraic properties, making it difficult to find attacks that involve complex algebraic operations.
AVISPA (automated validation of internet security-sensitive protocols and applications) is an automated validation tool of network security protocol that uses HLPSL formal language to describe target protocols. HLPSL is a modular, role-based formal language that describes the specified control flow patterns and data structures. HLPSL describes attacker models and complex security attributes in AVISPA. The HLPSL2IF algorithm converts the protocol file into a .cpp type file written by an if statement and then calls the four backend analysis tools OFMC, CL-AtSe, SATMC, and TA4SP to verify the security of the protocol. Through these four background analysis operators, AVISPA tools have excellent scope and scalability and can analyze large-scale network security protocols and establish a complex formal model for protocol processes, security targets, and attack trajectories. At the same time, it has high computational efficiency. However, the types of models covered by AVISPA tools are limited, and the supported security models are relatively simple. It is difficult to give complete results for the analysis of security protocols under strong security models.
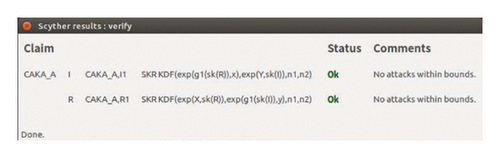
Considering the advantages and disadvantages of Scyther and AVISPA tools, to give a comprehensive and objective formal analysis of the proposed protocol CAKA, this paper uses the combination of Scyther tool and AVISPA tool to analyze the security of the protocol. This can avoid the attack omission which is caused by the algebraic operation property defect of Scyther tool and the security model defect of AVISPA tool. The proposed protocol CAKA is formally described by HLPSL language in Figure 4, in which the role user node is defined as the left algorithm (sigama_Init) of Figure 4, the role AP is defined as the right picture of Figure 4 (sigma_Resp), and the key security and authentication of the protocol are analyzed under the Dolev-Yao security model. The analysis results are shown in Figure 5. The results show that AVISPA’s OFMC engine displays the analysis results as “safe” in 0.02 seconds, and CL-AtSe engine displays the analysis results as “safe” in negligible seconds. As the backend SATMC and TA4SP do not contain the algebraic properties of exponent operation such that these two backends cannot handle the analysis of this scheme. As shown in Figure 6, the SPLA language is used to describe the CAKA protocol, and we use the Scyther-Compromise tool to analyze it under the CK security model by checking the options “Long-Term Key Reveal,” “wPFS,” “Session-Key Reveal,” and “State Reveal” in the analysis options as shown in Figure 7. The Scyther-Compromise tool shows that the protocol is session key secure under the CK model, as shown in Figure 8.




5. Performance Evaluation
Since the nodes register in the form of a blockchain transaction (invoking the smart contract), we do not consider computation overhead and transaction fees of blockchains, and we only briefly analyze the performance of authentication and key agreement protocol.
We analyzed the performance of several typical cross-domain authentication schemes Jeon et al. [37], Huo et al. [38] and ours by analyzing message transmission times and computation cost. Table 8 compares the message transmission times between the nodes (HA is home AP and TA is target AP) in three protocols. As can be seen from the table, our solution has obvious advantages. Our scheme can accomplish two-way authentication only by transmitting messages three times between users and target AP, without the assistance of home server or AP. The other two schemes need to forward messages through home AP, which increases the communication delay, resulting in a total of four messages to be transmitted. So, our scheme has less communication delay.
| Protocol | UE and TA | TA and HA | Total |
|---|---|---|---|
| Jeon | 2 | 2 | 4 |
| Huo | 2 | 2 | 4 |
| Ours | 3 | 0 | 3 |
For computational overhead, we use the OpenSSL library to program calculations using the C program language. Our experimental environment is Ubuntu 18.04 with Intel (R) Core (TM) i7-6700 CPU @ 3.40 GHZ CPU and 4 GB RAM memory. We measure the approximate time cost of cryptography operations through the OpenSSL library, where ECDH, ECDSA, ECIES, and elliptic curve key pair generation are measured on the curve ANSI X9.62 prime192v1. The results are presented in Table 9. It can be seen from Table 9 that public key cryptography (signature, encryption, and key pair generation) takes more time, while symmetric cryptography and hashing take less time. The difference between them is more than 40 times. The times of cryptographic operations of the three protocols are compared in Table 10. As can be seen from the table, our solution requires less public key encryption and less computational latency. Combining Tables 9 and 10, we calculate calculation overheads of the three protocols as 2.31 ms, 2.22 ms, and 0.355 ms, respectively. Clearly, the calculation cost of our solution is very low, less than 1/6 of the other two schemes. So, our scheme has less communication delay. In addition, the computation cost of UE and TA computed from Tables 7 and 10 is 0.1338 ms and 0.2213 ms, respectively.
| Cryptographic operation | Time cost (ms) |
|---|---|
| Signature (ECDSA) | 0.04418 |
| Verification (ECDSA) | 0.08782 |
| Symmetric encryption/decryption (AES) | 0.001207/0.001528 |
| Asymmetric encryption/decryption (ECIES) | 1.05103/0.843882 |
| Hash (SHA256) | 0.000900 |
| ECDH | 0.05408 |
| Key pair generation | 0.017789 |
| Protocol | Signature | Verification | Asymmetric encryption/decryption | DH | Key pair generation | Symmetric encryption/decryption | Hash | Total costs (ms) |
|---|---|---|---|---|---|---|---|---|
| Jeon | 3 | 3 | 1/1 | 0 | 0 | 2/2 | 13 | 2.31 |
| Huo | 2 | 2 | 1/1 | 0 | 3 | 1/1 | 5 | 2.22 |
| Ours | 0 | 1 | 0 | 4 | 2 | 3/3 | 8 | 0.355 |
Our solution communication and computation overhead are relatively small, especially the computation overhead and the performance advantages are obvious. So, our solution not only achieves secure cross-domain authentication but also enables fast real-time authentication.
6. Conclusion
This paper proposes a cross-domain authentication and key agreement system based on smart contract for heterogeneous wireless networks. In the solution, all security domains join into the consortium chain, and the CA in each domain manages the public key through the smart contracts. We implement mutual cross-domain authentication and provide user anonymity in the solution. The protocol CAKA is proved secure under the CK model and two formal analysis tools Scyther tool and AVISPA also report the protocol is safe. Without public key encryption and signature, the protocol improves the efficiency of cross-domain authentication compared with some existed ones. Moreover, the system is based on the design of the consortium chain and it has strong scalability.
The system designed in this paper only tests its computational consumption and does not perform simulation experiments on the whole system to test other performance such as communication. In the future, it is necessary to study the use of network simulation software OPNET or the actual wireless network system for more detailed system evaluation.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Acknowledgments
This work was supported by the Innovative Research Groups of the National Natural Science Foundation of China (61521003) and Youth Program of National Natural Science Foundation of China (61502533).
Open Research
Data Availability
This paper uses the combination of Scyther tool and AVISPA tool to analyze the security of the protocol. The approximate time cost of cryptography operations is measured through the OpenSSL library. The Scyther tool can be downloaded from the website https://people.cispa.io/cas.cremers/scyther/. The AVISPA tool can be downloaded from the website http://www.avispa-project.org/. The OpenSSL library can be downloaded from the website https://www.openssl.org/.




