Numerical Analysis of Vibration Responses in High-Speed Railways considering Mud Pumping Defect
Abstract
As a newly appeared defect under slab tracks in high-speed railways, mud pumping weakens the support ability of the subgrade to slab track, bringing about deviations on the vibration responses of the vehicle, slab track, and subgrade. Therefore, this paper proposes a vehicle-slab track-subgrade coupled model based on the multibody simulation principle and the finite element theory to highlight the influences of mud pumping defect. As an external excitation to this model, random track irregularity is considered. In order to simulate the mud pumping defect, the contact between the concrete base and subgrade is described as a spring-damper system. This model is validated by field test results and other simulation results, and a very good agreement is found. The vibration responses of the vehicle, slab track, and subgrade under different mud pumping lengths and train speeds are studied firstly. The deviations of vibration responses in high-speed railways induced by mud pumping are then obtained, and the limited mud pumping length is put forward finally to provide a recommendation for maintenance works of high-speed railways in practice.
1. Introduction
Slab tracks are widely used in high-speed railways because they have many advantages such as high stability, low deformation, and easy maintenance [1, 2]. In China, the operating mileage of high-speed railway networks reached 29,000 km by the end of 2018, and more than 70% of railway lines are using slab tracks [3]. However, slab tracks also exhibit obvious disadvantages compared with ballasted tracks [4, 5]. When the subgrade has defects like mud pumping, the slab tracks are not easy to adjust their deformation, leading to safety and comfort problems for high-speed trains.
Mud pumping has occurred in several spots in Chinese high-speed railways in recent years [6–8]. Several scholars have studied the main parameters that induced the defect of mud pumping under slab tracks [9–11]. Their studies show that when the sealing material of slab tracks has some cracks, the rainwater could penetrate into the subgrade surface easily. The dynamic train load could arouse excess pore water pressure at the subgrade surface when the train runs upon the railway substructures. Then, the fine particles of subgrade can be taken out by the rainwater under dynamic load, leading to mud pumping defect in high-speed railways. Pham et al. and Bian et al. studied the influence of water content and fine particles amount on the dynamic performance of subgrade. The water infiltration could cause significant performance degradation of subgrade [9, 12]. Huang et al. carried out a model test to analyze the long-term dynamic responses of slab track-subgrade system under mud pumping defect. The mud pumping will significantly reduce the support ability of subgrade [13]. Zhang et al. and Liu et al. carried out a field test to study the vibration responses of slab tracks, and the results show that mud pumping will increase the vibration responses obviously [6, 7]. Therefore, previous studies have mainly focused on the occurrence of mud pumping and vibration responses of slab track under certain mud pumping lengths. However, the length of mud pumping will be different at different spots, and the dynamic responses of the entire dynamic system, which includes vehicle, slab track, and subgrade, will be different as well. It is crucial to study the vibration responses of the whole dynamic system in high-speed railways where there is mud pumping defect.
At present, numerical simulation has become an efficient solution to study the dynamic effects of railways with the development of computer science [14, 15]. Many studies have been conducted with the vehicle-slab track coupled model including the comparison of two- and three-dimensional models [16], the comparison of two-layered and three-layered slab tracks [17], the comparison of linear and nonlinear Hertzian contact theory [18], and the dynamic effects under different irregularities [19–21]. Furthermore, many efficient algorithms have been put forward to solve the nonlinear vehicle-track interaction problem [22–25]. These studies provide a basis for studying the vibration responses under defects. For example, Liu et al. developed a train-slab track-saturated subgrade coupled model to study the dynamic responses of the railway under saturated subgrade [26]. Ren et al. built a finite element model to study the dynamic performance of railways due to the contact loss beneath the concrete base [3]. Cai et al. analyzed the mud pumping mechanism and built a finite element model to study the contact force between subgrade and slab track under mud pumping defect [27]. However, mud pumping will affect not only the contact force but the dynamic responses of the vehicle, slab track, and subgrade.
Thus, in this paper, a vehicle-slab track-subgrade coupled model is developed based on the multibody simulation principle and the finite element theory. The contact between slab track and subgrade is described as a spring-damper system in order to simulate the mud pumping defect. This model is validated by comparing the results from other literature. The vibration responses of the vehicle, slab track, and subgrade are analyzed under different mud pumping lengths and train speeds. Finally, the mud pumping of the railway is assessed on the basis of the calculated vibration responses.
2. Development of the Numerical Model
In order to investigate the vibration responses of the vehicle, slab track, and subgrade induced by mud pumping, a vehicle-slab track-subgrade coupled model has been developed, as shown in Figure 1. The vehicle model is built based on the multibody simulation principle, and the slab track and subgrade are developed based on the finite element theory. The mud pumping is simulated by the spring-damper system. The details of the model are described in the following sections.
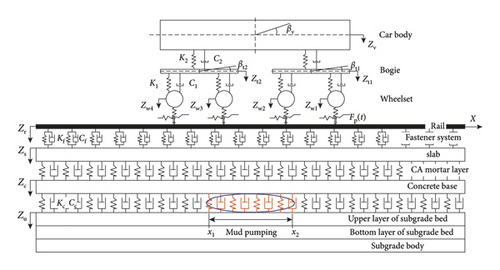
2.1. Characteristics of the Model
In this model, the vehicle is modeled as a four-axle mass-spring-damper system, which contains one car body, two bogies, four wheelsets, and two stage suspensions. The multibody system has 10 degrees-of-freedom, which are vertical and pitch motion of car body (Zv, βv), vertical and pitch motion of bogies (Zti, βti, i = 1,2), and vertical motion of wheelset (Zwj, j = 1, …, 4). The vehicle and slab track can be linked by the contact force between the wheel and rail. The slab track, which is commonly used in high-speed railways in China, is developed in this model, and it consists of rail, fastener system, slab, cement asphalt (CA) mortar layer, and concrete base. The rail is modeled as the Euler beam element, and the length of rail is 500 m in case of the boundary effect. The slab and concrete base are described as the elastic medium, which is similar to the studies from [19, 26]. Meanwhile, the fastener system and CA mortar layer are assumed to act as the spring-damper system. The subgrade, which contains the upper layer of the subgrade bed, the bottom layer of subgrade bed, and the subgrade body, is also modeled as the elastic medium. In order to simulate the mud pumping effect, the contact between the concrete base and subgrade is modeled as a spring-damper system. The mud pumping will cause contact loss between the concrete base and the upper layer of subgrade bed; therefore, the stiffness and damping of contact are different in the mud pumping area when compared with the normal area.
2.2. Equations of Motion
2.3. Numerical Solution
The total mass matrix, damping matrix, and stiffness matrix can be assembled in equation (1) by a conventional technique. The Newmark–Beta integral algorithm and the cross iterative scheme were used to solve the motion equations. The details of the iterative scheme can be found in [22]. Furthermore, the computer simulation program Matlab was used to calculate the dynamic responses of the vehicle, slab track, and subgrade under the mud pumping state.
3. Verification
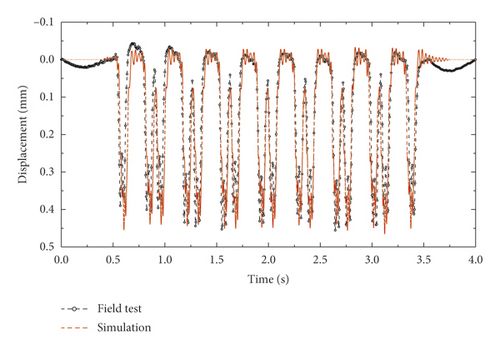
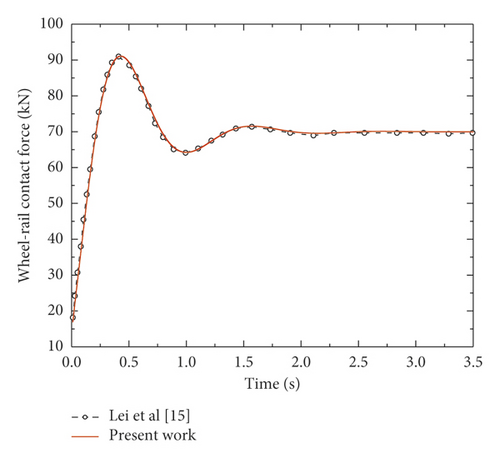
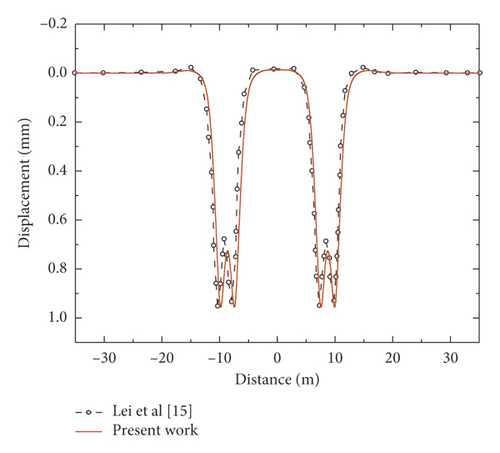
The time-history curves of vertical displacement of the slab were measured in the Shanghai–Nanjing high-speed railway. The sensors layout and results of the field test can be found in [6]. The displacement of the slab calculated in this model is compared with the field test results under mud pumping defect in order to validate the calculation results from this simulation model. Meanwhile, the dynamic force between wheel and rail and vertical displacement of rail is compared with the results from [15].
3.1. Dynamic Properties
The vehicle is the CRH2C train in the Shanghai–Nanjing high-speed railway, and it has 6 motor cars and 2 trailer cars. The slab track is the China Railway Track System (CRTS) I. The dynamic properties of the vehicle, track, and subgrade in Shanghai–Nanjing high-speed railway are shown in Table 1.
| Items | Values |
|---|---|
| Vehicle system | |
| Car body mass (kg) | 41600 |
| Bogie mass (kg) | 3200 |
| Wheelset mass (kg) | 2000 |
| Primary suspension stiffness (N/m) | 1.176 × 106 |
| Primary suspension damping (N·s/m) | 1.96 × 104 |
| Secondary suspension stiffness (N/m) | 6 × 105 |
| Secondary suspension damping (N·s/m) | 9.8 × 103 |
| Track system | |
| Young’s modulus of the rail (N/m2) | 2.059 × 1011 |
| Area moment of inertia of the rail (m4) | 3.217 × 10−5 |
| Mass per unit length of the rail (kg/m) | 60.64 |
| Stiffness of rail pad (N/m) | 5.0 × 107 |
| Damping of rail pad (N·s/m) | 7.0 × 104 |
| Density of the slab (kg/m3) | 2500 |
| Young’s modulus of the slab (N/m2) | 3.6 × 1010 |
| Poisson’s ratio of the slab | 0.2 |
| Stiffness of the CA mortar (N/m) | 3 × 105 |
| Damping of the CA mortar (N·s/m2) | 3.46 × 104 |
| Density of the concrete base (kg/m3) | 2500 |
| Young’s modulus of the concrete base (N/m2) | 3.25 × 1010 |
| Poisson’s ratio of the concrete base | 0.2 |
| Subgrade system | |
| Density of the upper layer of subgrade bed (kg/m3) | 2140 |
| Young’s modulus of the upper layer of subgrade bed (N/m2) | 2 × 108 |
| Poisson’s ratio of the upper layer of subgrade bed | 0.3 |
| Density of the bottom layer of subgrade bed (kg/m3) | 1900 |
| Young’s modulus of the bottom layer of subgrade bed (N/m2) | 1.5 × 108 |
| Poisson’s ratio of the bottom layer of subgrade bed | 0.3 |
| Density of the subgrade body (kg/m3) | 1900 |
| Young’s modulus of the subgrade body (N/m2) | 1 × 108 |
| Poisson’s ratio of the subgrade body | 0.35 |
3.2. Validation Results
The length of mud pumping is set to 3.15 m (5 spans of the fastener system and each span is 0.63 m) in the simulation model because the length of mud pumping in the Shanghai–Nanjing high-speed railway is about 3 m to 4 m, and the precise length was not measured due to certain limitations. Figure 3 shows that the vertical displacement of the slab presents a good agreement with the results tested in the Shanghai–Nanjing high-speed railway. Furthermore, the wheel-rail contact force and vertical displacement of rail from this simulation model are quite similar to the results in [15], as shown in Figure 4. Therefore, the model in this paper could predict the vibration responses of the vehicle, track, and subgrade under both mud pumping state and normal state.
4. Results
In order to study the influences of mud pumping lengths and train speeds on the dynamic responses of vehicle, track, and subgrade, the length of mud pumping is changed from 0 m (normal state without mud pumping) to 6.3 m (10 spans of the fastener system), and the train speed is changed from 200 km/h to 350 km/h.
4.1. Dynamic Responses
4.1.1. Vehicle
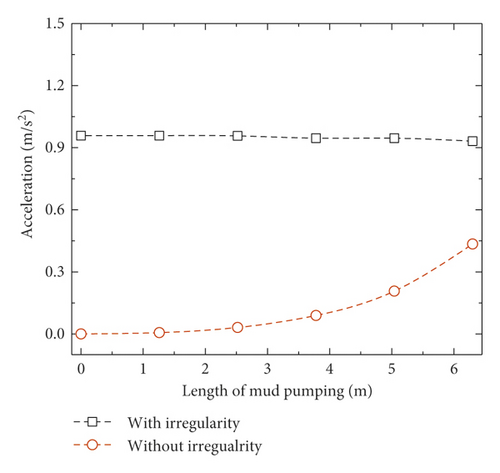
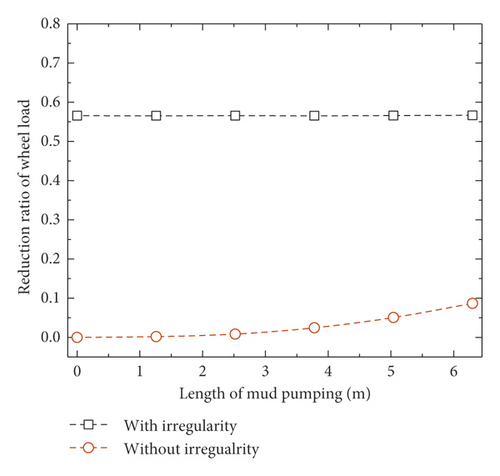
When the train speed is 250 km/h, the vertical acceleration of the car body, the reduction ratio of wheel load, and the wheel-rail contact force are shown in Figure 5. Note that only when the length of mud pumping equals to 0 m, the railway is under the normal state without mud pumping defect. When the system is excited by track irregularity, the dynamic responses do not change much with the mud pumping length. The vertical accelerations of the car body are stable at around 0.95 m/s2. The reduction ratios of wheel load are around 0.56, and the wheel-rail contact forces are around 107 kN. When there is no track irregularity, the vertical acceleration of car body, the reduction ratio of wheel load, and wheel-rail contact force increase when the mud pumping length is increased, but the maximum values are still lower than those with irregularity. Therefore, the dynamic response of the vehicle is dominated by the random track irregularity other than mud pumping.

4.1.2. Slab Track
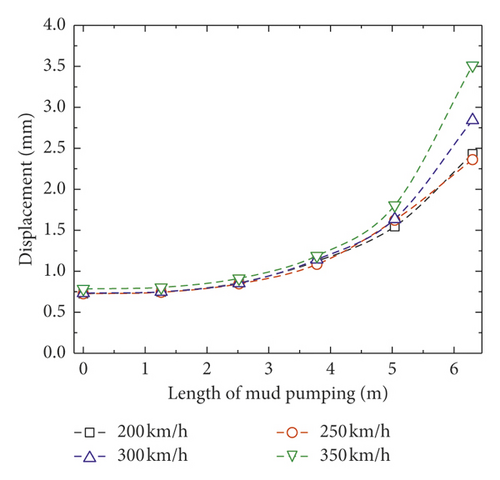
The vertical displacement of rail, slab, and concrete base is shown in Figure 6. Unlike the dynamic responses of the vehicle under excitation of track irregularity, the displacements increase significantly with mud pumping length even if the track irregularity still exists. When the railway is under the normal state (mud pumping length equals to 0 m), the vertical displacements of rail, slab, and concrete base are around 0.75 mm, 0.2 mm, and 0.12 mm, respectively. However, when the length of mud pumping increases to 6.3 m, the displacements of rail, slab, and concrete base increase to 3.5 mm, 3 mm, and 2.75 mm, respectively. Meanwhile, when the mud pumping length is less than 5.04 m, the effect of train speed on displacement is not obvious, but when the mud pumping length equals to 6.3 m, the displacement will increase with train speed.
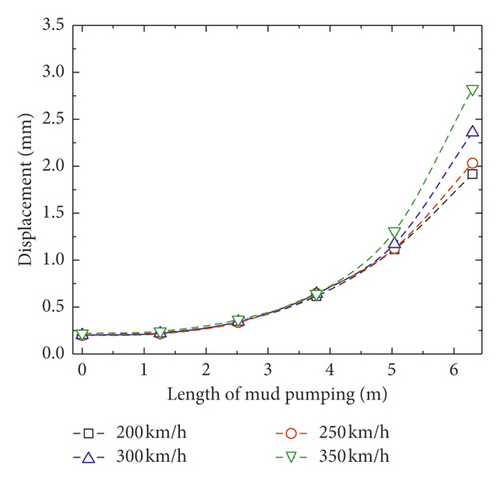
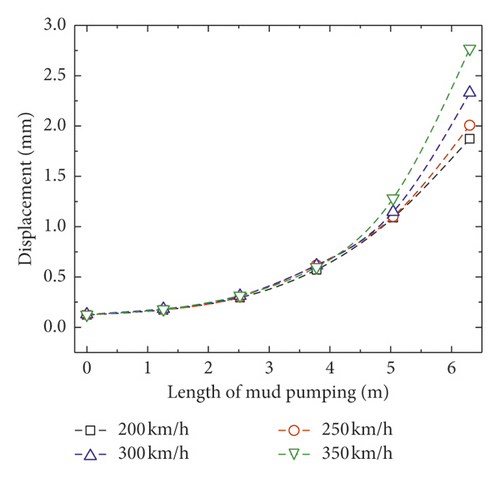
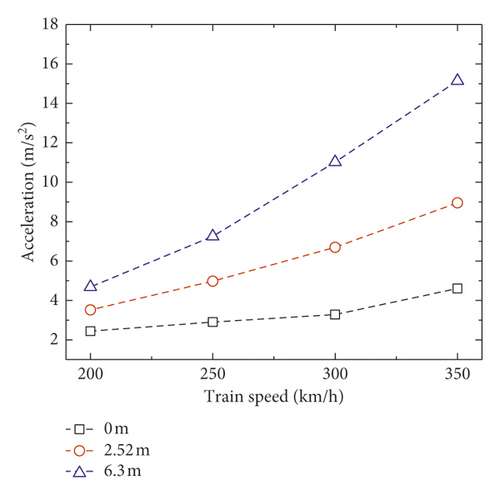
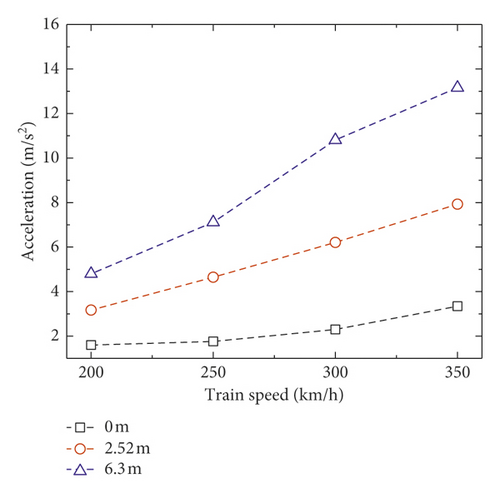
The vertical accelerations of the slab and concrete base obviously increase with the train speed, as shown in Figure 7. The accelerations also increase when the mud pumping length and train speed are increased. When the mud pumping length is 6.3 m, the maximum acceleration of slab is about 15 m/s2, and the maximum acceleration of the concrete base is about 13 m/s2.
4.1.3. Subgrade
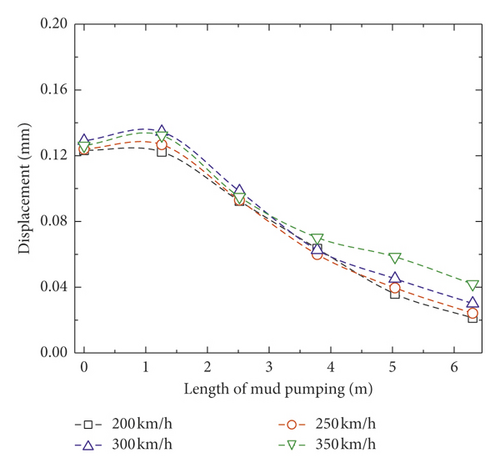
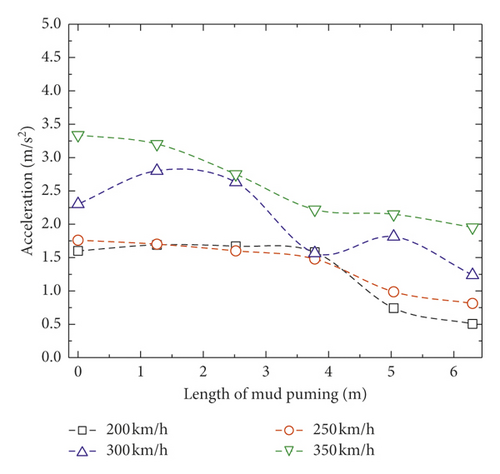
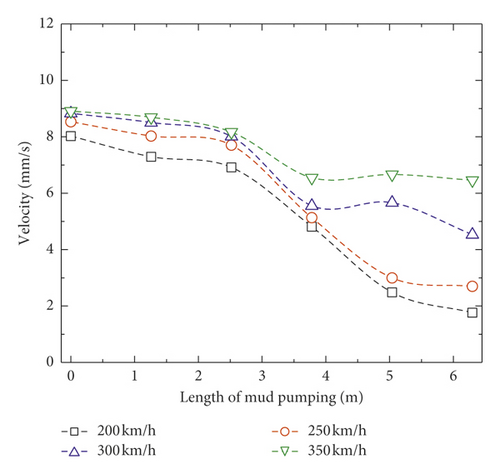
Unlike dynamic responses of slab track, the dynamic responses of subgrade obviously decrease when increasing the mud pumping length, as shown in Figure 8. When the train speed is 200 km/h, the minimum vertical displacement, acceleration, and velocity of subgrade are 0.02 mm, 0.5 m/s2, and 1.8 mm/s, respectively. The most likely reason is that there is contact loss between the concrete base and subgrade when mud pumping occurs, and dynamic energy cannot transfer to the degradation part of subgrade directly; thus, the dynamic responses of subgrade decrease with mud pumping length.
4.2. Assessment of Dynamic Responses under Mud Pumping Defect
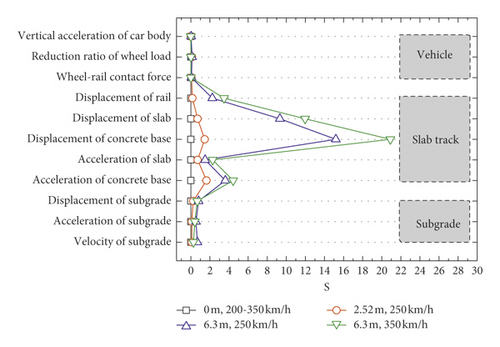
The assessment index of dynamic responses in high-speed railways is shown in Figure 9. The index increases when increasing the mud pumping length and train speed. Furthermore, the index of vehicle and subgrade does not change much when compared with the index of slab track. The vertical displacement of the concrete base exhibits the maximum value of S, followed by the vertical acceleration of the concrete base. When the mud pumping length is 6.3 m and the train speed is 350 km/h, the index S of vertical displacement and acceleration of concrete base are 20.9 and 4.4, respectively. Therefore, the mud pumping defect will have the greatest influence on the dynamic responses of the concrete base.
The Chinese code of technical regulations for dynamic acceptance for high-speed railways construction (TB10761-2013) has put forward several thresholds for assessing the dynamic responses of the vehicle, track, and subgrade, as shown in Table 2. When the dynamic responses overtake the thresholds, the running safety and stability of high-speed railway will be affected and this means the railway needs to be maintained. According to the thresholds, the limited length of mud pumping can be extracted from Figures 5–8. Most limited lengths are more than 6.3 m, which is the maximum mud pumping length in this simulation model. However, the lengths from vertical displacement of rail and slab are 5.23 m and 2 m, respectively. Therefore, the mud pumping length is suggested to be less than 2 m; otherwise, the mud pumping will affect the running quality of the railway.
| Items | Thresholds | Limited length of mud pumping (m) |
|---|---|---|
| Reduction ratio of the wheel load | 0.65 | >6.3 |
| Wheel-rail contact force | 170 kN | >6.3 |
| Vertical displacement of the rail | 2 mm | 5.23 |
| Vertical displacement of the slab | 0.3 mm | 2 |
| Vertical acceleration of the slab | 300 m/s2 | >6.3 |
| Vertical displacement of the upper layer of subgrade bed | 0.22 mm | >6.3 |
| Vertical acceleration of the upper layer of subgrade bed | 10 m/s2 | >6.3 |
| Vertical velocity of the upper layer of subgrade bed | 12 mm/s | >6.3 |
| Suggested value | 2 | |
5. Discussion
The amplitudes of vertical accelerations of the car body, the reduction ratio of wheel load, and the wheel-rail contact force do not change much when the random track irregularity exists, but they increase when there is no irregularity, as shown in Figure 5. The most likely reason is that the amplitude of vibration response induced by random irregularity during train running is still higher than the vibration response with increment induced by mud pumping, as shown in Figure 10. As long as the amplitude induced by random irregularity is the highest value, the maximum dynamic response of vehicle will not change with the mud pumping length. Therefore, the dynamic response of the vehicle is mainly determined by the random track irregularity in this simulation model, but it is worth noting that once the vibration response with increment induced by mud pumping overtakes the previous amplitude, the dynamic responses of the vehicle will undergo a great change when the mud pumping length is increased. Figures 6–8 show that the vibration responses of slab track and subgrade obviously change with mud pumping length even if the random track irregularity exists. This illustrates that the vibration response induced by mud pumping in slab track and subgrade overtakes the amplitude of vibration response induced by random irregularity.
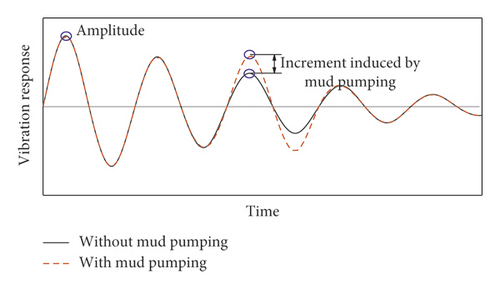
Moreover, the limited mud pumping length is suggested to be less than 2 m in this paper. Although this simulation model aims to predict the vibration response in practice, field tests under mud pumping defect still need to be carried out to verify this limited mud pumping length before it can be used in maintenance works in high-speed railways.
6. Conclusions
- (a)
The vertical acceleration of car body, the reduction ratio of wheel load, and wheel-rail contact force do not change much with mud pumping lengths, indicating that the dynamic responses of the vehicle are dominated by random track irregularity.
- (b)
Mud pumping will increase the vibration displacement and acceleration of slab track significantly but decrease the vibration responses of subgrade obviously.
- (c)
The concrete base is the part most sensitive to mud pumping defect in high-speed railways, so more attention should be paid to the vibration responses of the concrete base in practice when the mud pumping occurs.
- (d)
The limited mud pumping length is suggested to be less than 2 m, and once the mud pumping length overtakes this value, the running safety and stability of high-speed railways will be affected.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
This work was supported by the Key Research Development Program of China (nos. 2016YFC0802203-2 and 2016YFC0802203-3). And the authors gratefully acknowledge the financial support from China Scholarship Council.
Open Research
Data Availability
The data used to support the findings of this study are available from the corresponding author upon request.




