International Journal of Differential Equations

Volume 2019, Issue 1 9275051

Research Article

Open Access

Analysis of a Stochastic SIR Model with Vaccination and Nonlinear Incidence Rate

Amine El Koufi,

Corresponding Author

Amine El Koufi

[email protected]

orcid.org/0000-0001-6566-8181

Laboratory of Analysis Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O. Box 7955, Sidi Othman, Casablanca, Morocco uh2c.ac.ma

Search for more papers by this author

Jihad Adnani,

Jihad Adnani

orcid.org/0000-0002-5251-3495

Laboratory of Analysis Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O. Box 7955, Sidi Othman, Casablanca, Morocco uh2c.ac.ma

Search for more papers by this author

Abdelkrim Bennar,

Abdelkrim Bennar

Laboratory of Analysis Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O. Box 7955, Sidi Othman, Casablanca, Morocco uh2c.ac.ma

Search for more papers by this author

Noura Yousfi,

Noura Yousfi

orcid.org/0000-0001-8435-5981

Laboratory of Analysis Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O. Box 7955, Sidi Othman, Casablanca, Morocco uh2c.ac.ma

Search for more papers by this author

Amine El Koufi,

Corresponding Author

Amine El Koufi

[email protected]

orcid.org/0000-0001-6566-8181

Laboratory of Analysis Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O. Box 7955, Sidi Othman, Casablanca, Morocco uh2c.ac.ma

Search for more papers by this author

Jihad Adnani,

Jihad Adnani

orcid.org/0000-0002-5251-3495

Laboratory of Analysis Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O. Box 7955, Sidi Othman, Casablanca, Morocco uh2c.ac.ma

Search for more papers by this author

Abdelkrim Bennar,

Abdelkrim Bennar

Laboratory of Analysis Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O. Box 7955, Sidi Othman, Casablanca, Morocco uh2c.ac.ma

Search for more papers by this author

Noura Yousfi,

Noura Yousfi

orcid.org/0000-0001-8435-5981

Laboratory of Analysis Modeling and Simulation (LAMS), Faculty of Sciences Ben M’sik, Hassan II University, P.O. Box 7955, Sidi Othman, Casablanca, Morocco uh2c.ac.ma

Search for more papers by this author

First published: 21 August 2019

https://doi.org/10.1155/2019/9275051

Citations: 17

Academic Editor: Elena Kaikina

Share a link

Email
Wechat
Bluesky

Abstract

We expand an SIR epidemic model with vertical and nonlinear incidence rates from a deterministic frame to a stochastic one. The existence of a positive global analytical solution of the proposed stochastic model is shown, and conditions for the extinction and persistence of the disease are established. The presented results are demonstrated by numerical simulations.

1. Introduction

Mathematical models play an important role in the analysis and control of infectious diseases, and thus effective measures can be taken to reduce its transmission as much as possible. The study of mathematical models in epidemiology has received much attention from many scientists, and some novel results are obtained [1–4]. Recently, stochastic analysis has widely been applied in mathematical modeling in biology [5–9].

For compartmental mathematical models, the total population is divided into three classes, namely, susceptible population S(t), infected population I(t), and recover population R(t). For more details, see [10]. For some diseases, such as AIDS, rubella, varicella, hepatitis B, hepatitis, syphilis, and mumps, it is one of the main transmission modes that infected mothers infect their unborn or newborn offsprings, called vertical transmission [11]. Meng and Chen [12] proposed an SIR epidemic model with vaccination and vertical transmission mode as follows:

()

where b is the mortality rate in the susceptible and the recovered individuals and d is the mortality rate in the infective individuals. The constants p and q (p + q = 1) are vertical transmission rates, namely, p and q are, respectively, the proportion of the offspring of infective parents that are susceptible individuals and the rest are born infected. The arrival of newborns constitutes a recruitment rate of b(S + R) into the susceptible individuals and q dI into the infectious individuals. m(0 ≤ m ≤ 1) is the successful vaccination proportion to the newborn from S and R, r is the recover rate in the infective individuals into recovered individuals, and β is the contact rate. System (1) has a basic reproduction number R₀ defined by

()

On the contrary, environmental fluctuations have great influence on all aspects of real life. The aim of this work is to study the effect of these environmental fluctuations on the transmission rate β. We assume that the stochastic perturbations are of white noise type, that is,

, where B(t) is a Brownian motion and σ is the intensity. Then, the stochastic version corresponding to the deterministic model (1) with general incidence rate is as follows:

()

where B(t) is the independent standard Brownian motions defined on a complete probability space

with a filtration

satisfying the usual conditions (i.e., it is increasing and right continuous while ℱ₀ contains all P null sets).

g(S, I) = βSI/(1 + α₁S + α₂I + α₃SI) is the incidence rate, where α₁, α₂, α₃ ≥ 0. In addition, the incidence rate is the number of new infected situations by population in a determined time period. To model the disease transmission process, several authors employ the following bilinear incidence rate βSI, where β is a positive constant [13]. Yet, there exist many forms of nonlinear incidence rate and every form presents some advantages [14–16]. It is very important to note that g(S, I) = βSI/(1 + α₁S + α₂I + α₃SI) is a general form which represents mutual interference between S and I. in particular cases:

(1)
If α₁ = α₂ = α₃ = 0, g(S, I) becomes a bilinear incidence rate
(2)
If α₁ = α₂ = 0 or α₁ = α₃ = 0, g(S, I) becomes a saturated incidence rate [17]
(3)
If α₃ = 0, g(S, I) becomes a Beddington–DeAngelis functional response [18]
(4)
If α₃ = α₁α₂, g(S, I) becomes the Crowley–Martin functional response presented in [19]

Next, we consider the d-dimensional stochastic system:

()

where f(x, t) is a function in IR^d defined in [t₀, +∞) and g(x, t) is a d × m matrix, and f and g are locally Lipschitz functions in x. {B(t)}_t≥0 is a d-dimensional standard Wiener process defined on the above probability space.

Denote by

the family of all nonnegative functions U(x, t) defined on IR^d × [t₀, +∞) such that they are continuously twice differentiable in x and once in t. The differential operator ℒ [16] associated with (4) is defined by

()

If the differential operator ℒ acts on a function

, then

()

where U_t(x, t) = ∂U/∂t, U_x(x, t) = (∂U/∂x₁, …, ∂U/∂x_d), and U_xx(x, t) = (∂²U/∂x_i∂x_j).

The organization of this paper is as follows. In Section 2, we show the existence of unique positive global solution to the given SDE system. Extinction and persistence in mean results are explored in Section 3 and Section 4, respectively. In Section 5, the analytical results are illustrated with the support of numerical examples. Finally, we close the paper with conclusion and future directions.

2. Existence and Uniqueness of the Nonnegative Solution

As we are dealing with the population model, the positive solution of the model is of our interest. The coefficients of (3) are locally Lipschitz continuous and do not satisfy the linear growth condition, so the solution of (3) may explode at a finite time. The following theorem shows that the solution is positive and will not explode at a finite time.

We define a subset Δ of IR³ as follows:

()

Theorem 1. For any given initial value X₀ = (S(0), I(0), R(0)) ∈ Δ, there is a unique positive solution X(t) = (S(t), I(t), R(t)) of (3) on t ≥ 0, and the solution will remain in Δ with probability 1, namely, (S(t), I(t), R(t)) ∈ Δ for all t ≥ 0 almost surely (briefly a.s.).

Proof 1. Since the coefficients of system (3) are locally Lipschitz continuous, for any initial value (S(0), I(0), R(0)) ∈ Δ, there is a unique local solution on [0, τ_e), where τ_e is the explosion time. To show this solution is global, we need to show that τ_e = ∞ a.s. For this, we define the stopping time τ by

()

with the traditional setting inf ∅ = ∞ (as usual ∅ denotes the empty set). We have τ ≤ τ_e. If we can show that τ = ∞ a.s., then τ_e = ∞ a.s. and (S(t), I(t), R(t)) ∈ Δ for all t ≥ 0. In other words, to complete the proof, all we only need to show is that τ = ∞. Assume that this statement is false, then there exists a T > 0 such that P(τ < T) > 0. Define a

function U, by the expression

()

Using Itô’s formula, we get

()

Since f(S, I) ≥ 1, and S ≤ 1, I ≤ 1, we get,

()

where H = β + 2b + pd + r + σ². Then, we have

()

Note that some components of X(τ) equal 0; thus, lim_t⟶τU(X(t)) = +∞.

Letting t⟶τ in (12), we obtain

()

which contradicts our assumption. Then, τ = ∞ a.s. This completes the proof of theorem.

3. Extinction

In the following, we give a condition for the extinction of the disease. Let

()

Theorem 2. Let (S(t), I(t), R(t)) be the solution of system (3) with initial value (S(0), I(0), R(0)) ∈ Δ. Assume that

(i)
σ² > β²/(2(pd + r)) or
(ii)
R_s < 1 and σ² < β

Then,

()

Namely, I(t) tends to zero exponentially a.s., i.e., the disease dies out with probability 1.

Proof 2. Applying Itô’s formula to system (3) leads to

()

Integrating both sides of (16) from 0 to t, we get

()

where

, which is a local continuous martingale, and M(0) = 0. Moreover, its quadratic variation is

()

By the large number theorem for martingales [21], we obtain

()

If condition (i) is satisfied, dividing by t and taking the limit superior of both sides of (17), we get

()

If the condition (ii) is satisfied, note that

()

It follows that

()

Taking the superior limit of both sides of (22), we obtain

()

which implies that lim_t⟶+∞I(t) = 0.

Remark 1. From Theorem 1, we can get that the disease will die out if R_s < 1, and the white noise is not large such that σ² < β, while if the white noise is large enough such that condition (i) is satisfied, then the infectious disease of system (3) goes to extinction almost surely.

4. Persistence

Here, we investigate the condition for the persistence of the disease. The basic reproduction number R₀(see [20]), is the threshold between disease extinction and persistence, with extinction for R₀ ≤ 1 and persistence for R₀ > 1 in the deterministic model. In the stochastic model, we define the threshold of persistence for disease as

()

Definition 1. System (3) is said to be persistent in the mean if

()

We define

()

Theorem 3. If then the solution (S(t), I(t), R(t)) of system (3) with initial initial value (S(0), I(0), R(0)) ∈ Δ is persistent in mean. Moreover, we have

()

where χ = β(1 − m)(((r + dmp)/b)(1 − m) + ((α₂ + α₃)(pd + r)/β(1 − m))).

Proof 3. We have

()

Integrating from 0 to t and dividing by t > 0 the third equation of system (3), we get

()

From (28), one can get

()

where φ(t) = (R(t) − R(0))/t. From Itô’s formula and (3), we obtain

()

Integrating from 0 to t and dividing by t > 0 on both sides of yields

()

We can rewrite the inequality (32) as

()

where χ = β(1 − m)((r + dmp/b) − 1 + m + ((α₂ + α₃)(pd + r)/β(1 − m))). We can see that R(t) ≤ 1 and I(t) ≤ 1. Thus, one has lim_t⟶+∞R(t)/t = 0, lim_t⟶+∞I(t)/t = 0, and lim_t⟶+∞φ(t) = 0. Taking the inferior limit of both sides of (33) yields

()

This completes the proof of theorem.

5. Numerical Simulations

In order to illustrate our theoretical results, we give some numerical simulations. The values of m, σ, and β will be varied over the different examples.

Example 1. We choose the parameters in system (3) as follows:

()

By calculation, we have R₀ = 0.4902; in this case, the disease dies out as shown in Figure 1(a). By choosing m = 0.3, we obtain R₀ = 1.635, and we deduce that the disease persists in the population. Figure 1(b) illustrates this result.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Simulations of the path S(t), I(t), and R(t) for the corresponding deterministic system (1).

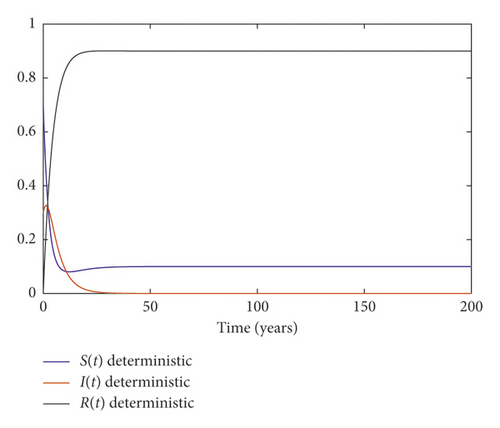
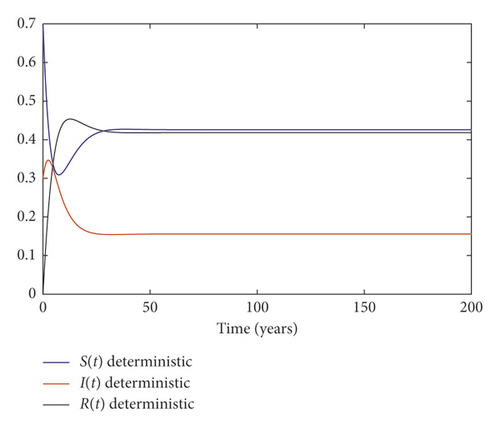
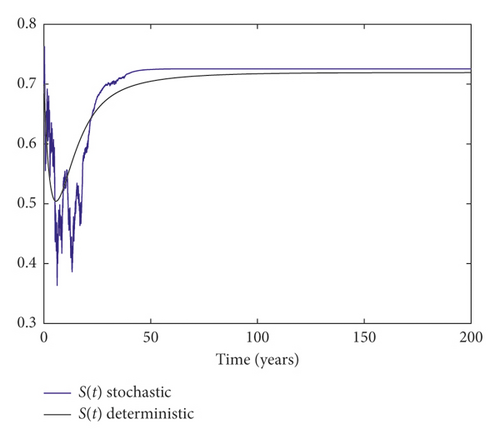
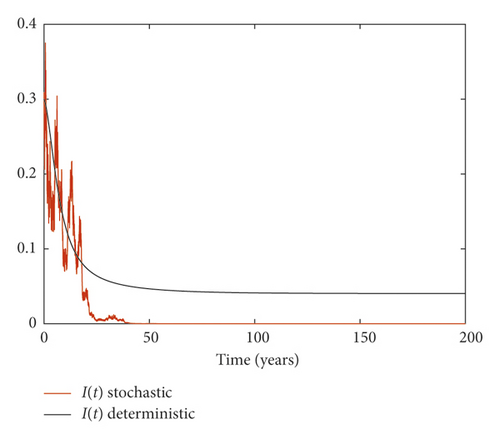
Example 2. We choose the parameters in system (3) as follows:

()

A simple computation shows that

()

It follows that the condition of Theorem 2 is satisfied. We conclude that the disease dies out; Figure 2 illustrates this result.

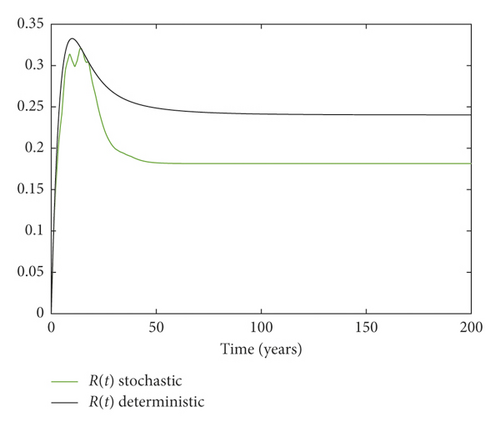
Example 3. On the contrary, we choose m = 0.05 and σ = 0.1 by simple calculation, and it can be found that which implies that the disease persists (Figure 3).

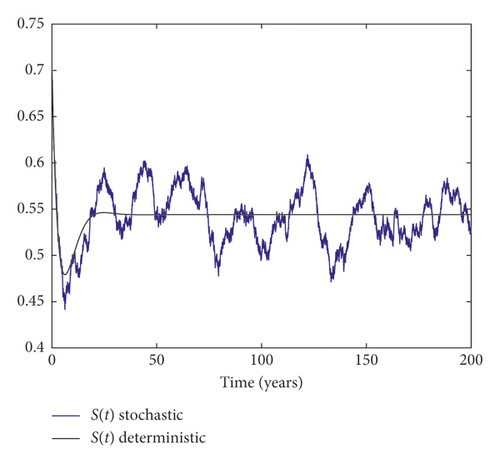
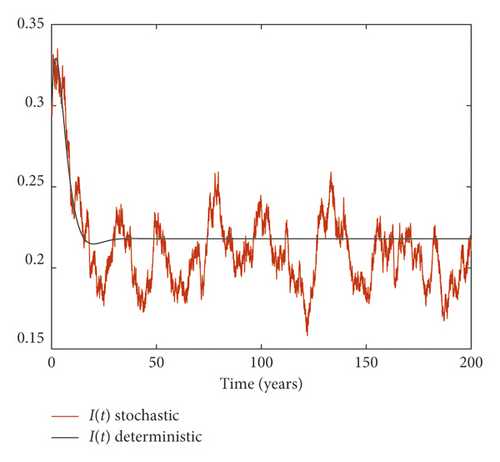
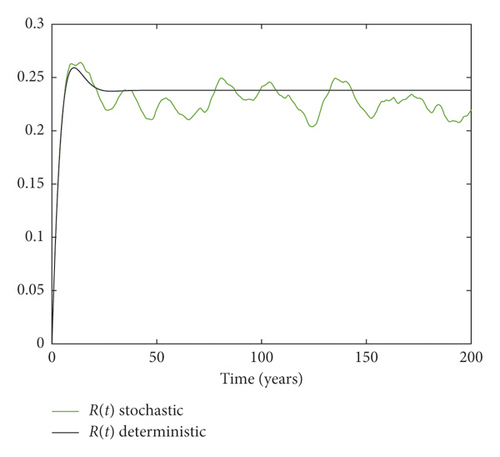
6. Conclusion

This article discusses a stochastic SIR epidemic model with vertical transmission and vaccination and nonlinear incidence rate. We have shown that when the noise is so small such that σ² < β, the extinction of the disease can be determined by the value of R_s, i.e., if R_s < 1, the disease dies out. Moreover, the disease dies out when the white noise is large enough such that σ² > (β²/2(pd + r)).

The persistence of the disease is determined by , i.e., if , the disease persists. We presented some numerical simulations to illustrate the obtained analytical results. To go further in this study, we can give a new dimension to the stochastic SIR epidemic model (3) by introducing a different type of noise which is the random telegraph noise (RTN), modeled by the Markov chain. We will investigate this case in our future works.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Zhang J. and Ma Z., Global dynamics of an SEIR epidemic model with saturating contact rate, Mathematical Biosciences. (2003) 185, no. 1, 15–32, https://doi.org/10.1016/s0025-5564(03)00087-7, 2-s2.0-0042828944.
10.1016/S0025-5564(03)00087-7
PubMed Web of Science® Google Scholar
2 Feng Z., Huang W., and Castillo-Chavez C., Global behavior of a multi-group SIS epidemic model with age structure, Journal of Differential Equations. (2005) 218, no. 2, 292–324, https://doi.org/10.1016/j.jde.2004.10.009, 2-s2.0-27744440076.
10.1016/j.jde.2004.10.009
Web of Science® Google Scholar
3 Tchuenche J. M., Nwagwo A., and Levins R., Global behaviour of an SIR epidemic model with time delay, Mathematical Methods in the Applied Sciences. (2007) 30, no. 6, 733–749, https://doi.org/10.1002/mma.810, 2-s2.0-33947105089.
10.1002/mma.810
Web of Science® Google Scholar
4 Hattaf K., Yousfi N., and Tridane A., Mathematical analysis of a virus dynamics model with general incidence rate and cure rate, Nonlinear Analysis: Real World Applications. (2012) 13, no. 4, 1866–1872, https://doi.org/10.1016/j.nonrwa.2011.12.015, 2-s2.0-84856533303.
10.1016/j.nonrwa.2011.12.015
Web of Science® Google Scholar
5 Cai Y., Kang Y., and Wang W., A stochastic SIRS epidemic model with nonlinear incidence rate, Applied Mathematics and Computation. (2017) 305, 221–240, https://doi.org/10.1016/j.amc.2017.02.003, 2-s2.0-85013657162.
10.1016/j.amc.2017.02.003
Web of Science® Google Scholar
6 Jiang D., Yu J., Ji C., and Shi N., Asymptotic behavior of global positive solution to a stochastic SIR model, Mathematical and Computer Modelling. (2011) 54, no. 1-2, 221–232, https://doi.org/10.1016/j.mcm.2011.02.004, 2-s2.0-79955469778.
10.1016/j.mcm.2011.02.004
Web of Science® Google Scholar
7 Adnani J., Hattaf K., and Yousfi N., Stability analysis of a stochastic SIR epidemic model with specific nonlinear incidence rate, International Journal of Stochastic Analysis. (2013) 2013, 4, 431257, https://doi.org/10.1155/2013/431257, 2-s2.0-84885651407.
10.1155/2013/431257
Google Scholar
8 El Koufi A., Adnani J., Bennar A., and Yousfi N., Dynamical behaviors of a stochastic SIRS epidemic model, Journal of Mathematical and Computational Science. (2018) 8, no. 3, 421–436, https://doi.org/10.28919/jmcs/3658.
10.28919/jmcs/3658
Google Scholar
9 El Koufi A., Naim M., Bennar A., and Yousfi N., Stability analysis of a stochastic SIS model with double epidemic hypothesis and specific nonlinear incidence rate, Communications in Mathematical Biology and Neuroscience. (2018) 2018, https://doi.org/10.28919/cmbn/3677, 2-s2.0-85055039717.
10.28919/cmbn/3677
Google Scholar
10 Zhien M., Zhou Y., and Wu J., Modeling and Dynamics of Infectious Diseases, 2009, 11, World Scientific, Singapore.
Google Scholar
11 Busenberg S. and Cooke K., Vertically Transmitted Diseases: Models and Dynamics, 2012, Springer Science & Business Media, Berlin, Germany.
Google Scholar
12 Meng X. and Chen L., The dynamics of a new SIR epidemic model concerning pulse vaccination strategy, Applied Mathematics and Computation. (2008) 197, no. 2, 582–597, https://doi.org/10.1016/j.amc.2007.07.083, 2-s2.0-39449119838.
10.1016/j.amc.2007.07.083
Web of Science® Google Scholar
13 Gomes M. G. M., White L. J., and Medley G. F., The reinfection threshold, Journal of Theoretical Biology. (2005) 236, no. 1, 111–113, https://doi.org/10.1016/j.jtbi.2005.03.001, 2-s2.0-20444502433.
10.1016/j.jtbi.2005.03.001
PubMed Google Scholar
14 Kaddar A., Stability analysis in a delayed SIR epidemic model with a saturated incidence rate, Nonlinear Analysis: Modelling and Control. (2010) 15, no. 3, 299–306.
10.15388/NA.15.3.14325
Web of Science® Google Scholar
15 Cui J., Sun Y., and Zhu H., The impact of media on the control of infectious diseases, Journal of Dynamics and Differential Equations. (2008) 20, no. 1, 31–53.
10.1007/s10884-007-9075-0
PubMed Web of Science® Google Scholar
16 Das P., Mukherjee D., and Sarkar A. K., Study of an SI epidemic model with nonlinear incidence rate: discrete and stochastic version, Applied Mathematics and Computation. (2011) 218, no. 6, 2509–2515, https://doi.org/10.1016/j.amc.2011.07.065, 2-s2.0-80053279829.
10.1016/j.amc.2011.07.065
Google Scholar
17 Liu X. and Yang L., Stability analysis of an SEIQV epidemic model with saturated incidence rate, Nonlinear Analysis: Real World Applications. (2012) 13, no. 6, 2671–2679, https://doi.org/10.1016/j.nonrwa.2012.03.010, 2-s2.0-84861937759.
10.1016/j.nonrwa.2012.03.010
Web of Science® Google Scholar
18 Beddington J. R., Mutual interference between parasites or predators and its effect on searching efficiency, The Journal of Animal Ecology. (1975) 44, no. 1, 331–340, https://doi.org/10.2307/3866.
10.2307/3866
Web of Science® Google Scholar
19 Crowley P. H. and Martin E. K., Functional responses and interference within and between year classes of a dragonfly population, Journal of the North American Benthological Society. (1989) 8, no. 3, https://doi.org/10.2307/1467324.
10.2307/1467324
Google Scholar
20 Driessche P. V. D. and Watmough J., Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences. (2002) 180, no. 1-2, 29–48, https://doi.org/10.1016/s0025-5564(02)00108-6, 2-s2.0-0036845274.
10.1016/S0025-5564(02)00108-6
PubMed Web of Science® Google Scholar
21 Mao X., Stochastic Differential Equations and Applications, 2007, Elsevier, Amsterdam, Netherlands.
10.1007/978-3-540-48831-6
Web of Science® Google Scholar

Citing Literature

All articles

Analysis of a Stochastic SIR Model with Vaccination and Nonlinear Incidence Rate

Abstract

1. Introduction

2. Existence and Uniqueness of the Nonnegative Solution

3. Extinction

4. Persistence

5. Numerical Simulations

6. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Analysis of a Stochastic SIR Model with Vaccination and Nonlinear Incidence Rate

Abstract

1. Introduction

2. Existence and Uniqueness of the Nonnegative Solution

3. Extinction

4. Persistence

5. Numerical Simulations

6. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information