Volume 2019, Issue 1 8480905

Research Article

Open Access

Analysis of the Main Factors Influencing the Dominant Frequency of Blast Vibration

Da Liu

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China whu.edu.cn

Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Wenbo Lu,

Corresponding Author

Wenbo Lu

[email protected]

orcid.org/0000-0002-3855-0409

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China whu.edu.cn

Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Yijia Liu,

Yijia Liu

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China whu.edu.cn

Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Ming Chen,

Ming Chen

orcid.org/0000-0002-1772-0288

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China whu.edu.cn

Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Peng Yan,

Peng Yan

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China whu.edu.cn

Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Pengchang Sun,

Pengchang Sun

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China whu.edu.cn

Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Da Liu,

Da Liu

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China whu.edu.cn

Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Wenbo Lu,

Corresponding Author

Wenbo Lu

[email protected]

orcid.org/0000-0002-3855-0409

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China whu.edu.cn

Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Yijia Liu,

Yijia Liu

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China whu.edu.cn

Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Ming Chen,

Ming Chen

orcid.org/0000-0002-1772-0288

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China whu.edu.cn

Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Peng Yan,

Peng Yan

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China whu.edu.cn

Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Pengchang Sun,

Pengchang Sun

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China whu.edu.cn

Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

First published: 2019

https://doi.org/10.1155/2019/8480905

Citations: 10

Academic Editor: Yuri S. Karinski

Share a link

Email
Wechat
Bluesky

Abstract

At present, the study on the dominant frequency of blasting vibration is still a worldwide problem. Compared with the mature research on the particle peak velocity of blasting vibration, the researches on the dominant frequency of blasting vibration are much less. In this paper, by analyzing the main influencing factors of the dominant frequency, an attenuation equation of the dominant frequency induced by blasting vibration has been proposed by dimensional analysis combined with the theory of radial spherical wave propagation. The proposed equation is applied to the fitting analysis on the dominant frequency measured in Zhoushan Green Petrochemical Base in China, which has obtained a favorable fitting correlation. Based on the fitting analysis, it has found that the correlation coefficient of radial vibration obtained by the proposed equation is higher than that of vertical vibration, which is resulted from the reason that the vibration in vertical is considered to be influenced most by the R-wave on the ground and perceived to be quite different from the radial vibration affected by P-wave. In generally, different components of blasting waves will affect the attenuation of dominant frequency.

1. Introduction

Blasting excavation has been widely used in mining, water and hydropower engineering, highway, municipal infrastructure construction, and other fields [1]. Although blasting is an indispensable, efficient, and economical excavation technology, it inevitably brings adverse effects on the surrounding buildings and environment. In order to control the blasting vibration, it is necessary to predict the vibration induced by blasting [2]. In recent years, the research on blasting vibration velocity has formed a mature system, and peak particle velocity (PPV) is often used as a criterion for evaluating blasting vibration safety [3]. By contrast, the study on the prediction of blasting vibration frequency is much less. In fact, more and more researches revealed that when the dominant frequency of blasting vibration is close to the natural frequency of the structure, it will produce resonance effect and easily cause damage to the structures, even if the PPV is in the range of safety standard [4, 5]. Therefore, it is also of great significance to study the attenuation law of the dominated frequency to keep the underprotected structure stability and safety.

The dominant frequency induced by blasting is affected by many factors, including characteristics of explosion source, distance away from explosion source, and physical-mechanical properties of rock [6]. Among them, Zhong et al. [7] have found that the dominant frequency band shifts from mid-high frequency to low frequency and the dominant frequency band become more concentrated with the increase of the distance away from explosion source, the charge weight per delay, and the decrease of the number of delay in millisecond detonation. Yang et al. [8] has found that the vibration frequency of breaking blasthole of full-face millisecond delay blasting in underground opening excavation increases as the burden decreases. Ling et al. [9] have studied the difference of energy distribution characteristics of blasting vibration signals in frequency domain under single-delay blasting and multidelay millisecond blasting by using wavelet analysis technology. Tripathy and Gupta [10] have indicated that the vibration induced by blasting is diversified with the rock and geological condition.

The majority of factors affecting the dominant frequency of blasting vibration can hardly be described quantitatively. As a result, it is very difficult to accurately obtain the attenuation law of the dominant frequency [11]. Generally speaking, the dominant frequency of blasting vibration decreases exponentially with the increase of the distance away from the explosion source due to the high-frequency filtering characteristics of rock [12]. In recent years, with the progress of the analysis technique of blasting vibration spectrum, many prediction formulas have been proposed by using the method of artificial neural network [13], support vector machine [14], and gene expression programming [15]. Although these formulas can obtain favorable fitting correlation, they are difficult to apply in engineer practice because of its too complex fitting parameters and calculation. Therefore, it is necessary to obtain a simple and practicable formula, which can reflect the changes of the dominant frequency with distance.

2. The Attenuation Equation of Dominant Frequency Induced by Blasting

2.1. Analysis of Main Influencing Factors of the Dominant Frequency

The explosive releases enormous energy in the process of blasting in rock, which mainly transforms into blasting shock wave, stress wave, and blasting gas. In the process of stress wave propagation in rock, due to the energy attenuation of wave and the damp absorption effect of rock, the properties and waveforms of stress wave will change correspondingly with distances. It will form the crushing zone, cracking zone, and elastic zone successively with the distance far from the blastholes [1]. In order to analyze the propagation and attenuation of blasting seismic wave by using elastic wave theory, the inelastic zone (crushing zone and cracking zone) near the blastholes is equivalent to the blasting source, and the blasting load is acted on the equivalent elastic boundary (cracking boundary, i.e., the outer boundary of the crushing zone). Therefore, the theoretical solution of the elastic wave excited by a spherical cavity in an elastic medium can be adopted, and the theoretical solution is given by Favreau [16].

Introducing potential function φ to represent radial displacement,

\begin{matrix} u = \frac{\partial φ (r, t)}{\partial r}, \end{matrix}

(1)

where u is the radial displacement, r represents the distance between blasting source with the measuring points, and t is the time.

Assuming the load function acting on the inner wall of the spherical cavity is p(t),

\begin{matrix} φ (r, t) = - \frac{a}{ρ ω r} \int_{0}^{s} p (s - t) e^{- η τ} \sin (ω τ) d τ, \end{matrix}

(2)

\begin{matrix} s = t - \frac{r - a}{C_{P}}, \end{matrix}

(3)

\begin{matrix} η = \frac{12 - ν}{1 - ν} \frac{C_{P}}{a}, \end{matrix}

(4)

\begin{matrix} ω = \frac{\sqrt{12 - ν}}{1 - ν} \frac{C_{P}}{a}, \end{matrix}

(5)

where p(t) is the blasting load acted on elastic cavity, λ and μ are the constant of Lame, ν is Poisson’s ratio, ρ is the density, C_P is the longitudinal wave velocity, a is the radius of elastic cavity (cracking zone), ω is the phase of function, φ is also the natural frequency of the equivalent system, and s and η are intermediate variables.

It is often assumed that the law of blasting load p(t) is used in the following form [17]:

\begin{matrix} p (t) = \{\begin{cases} 0, & t < - τ_{1}, \\ σ_{\max} (\frac{1 + t}{τ_{1}}), & - τ_{1} \leq t \leq 0, \\ σ_{\max} (\frac{1 - t}{τ_{2}}), & 0 \leq t \leq τ_{2}, \\ 0, & t > τ_{2}, \end{cases} \end{matrix}

(6)

where σ_max is the peak value of the blasting load, τ₁ is the rising time of the blasting load, and τ₂ is the time of blasting load reduction from peak to zero.

By means of the Fourier transform, the velocity spectrum of blasting vibration in the elastic rock mass can be obtained as follows [8, 17]:

\begin{matrix} F (ω) = \frac{|S_{σ} (j ω)| a ω C_{P} \sqrt{C_{P}^{2} + r^{2} ω^{2}}}{4 μ r^{2} \sqrt{{(C_{P} / a)}^{4} + [1 - (λ + 2 μ) / 2 μ] ω^{2} {(C_{P} / a)}^{2} + {[(λ + 2 μ) / 4 μ]}^{2} ω^{4}}}, \end{matrix}

(7)

\begin{matrix} |S_{σ} (j ω)| = \frac{σ_{\max}}{a_{e} b_{e} τ ω^{2}} {[122 + a_{e}^{2} + b_{e}^{2} + a_{e} b_{e} cos ω τ - (a_{e} cos b_{e} ω τ + b_{e} cos a_{e} ω τ)]}^{12 /}, \end{matrix}

(8)

where F(ω) is the velocity spectrum of blasting vibration, S_σ(ω) is the stress spectrum of blasting load, τ = τ₁ + τ₂, a_e = τ₁/τ, and b_e = τ₂/τ.

It can be concluded from equation (7) that the main influencing factors of velocity spectrum include three aspects: firstly, the distance away from blasting source r, secondly, the parameters of rock λ, μ, ν, and C_P, and finally, the parameters of blasting, such as the radius of elastic cavity (the cracking zone) a and load parameters a_e, b_e, and τ.

In practical, compared with spherical charge, cylindrical charge is used in open-pit blasting excavation more frequently, which is in advantage of its more uniform distribution of explosive energy in rock mass. Although the theoretical solution discussed previously is aiming at the spherical charge, in fact, analysis of the experimental data showed that blasts of cylindrical charges are similar to the processes observed in seismic investigations of blasts with spherical charges [17]. This is because spherical and cylindrical waves excited by spherical or cylindrical explosive sources can be regarded as plane waves when they propagate to the far region [1]. If the elastic cavity formed by cylindrical charge blasting is regarded as an equivalent blasting source, the blasting load will be applied to the boundary of the elastic cavity. The radius of the equivalent blasting source will be the radius of the boundary of the elastic cavity a, as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic diagram of single-hole blasting.

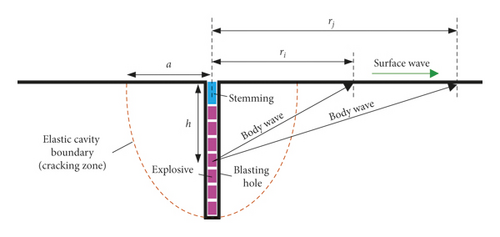
However, in the process of cylindrical charge blasting, some explosive energy will propagate in the form of stress wave in rock. According to the different propagation paths of wave, it can be divided into body wave and surface wave. The propagation of body wave in rock mass can be divided into compressive wave (P-wave) and shear wave (S-wave). In terms of the existence of the surface free surface, the surface wave (S-wave) will also appear on the surface free surface of the semi-infinite space, which is the most significant symbol different from the spherical charge blasting in infinite rock mass. In fact, studies have shown that, for vertical hole blasting, the P-wave is an important component for both near and far distance, and it mainly acts on the horizontal and radial vibrations; the S-wave is only the dominant wave in the near zone, and its role in the far zone can be neglected; the R-wave grows and develops gradually at a farther distance, and it will have a major impact on vertical vibration [2]. Therefore, if taking the elastic cavity formed by cylindrical blasting as a spherical blasting source, the radial vibration induced by the cylindrical blasting source will be closer to the vibration induced by the spherical blasting source than that of vertical direction, as shown in Figure 1.

Considering the condition of single-hole blasting, the multiple-hole blasting is equivalent to the elastic superposition of each single hole, as shown in Figure 2.

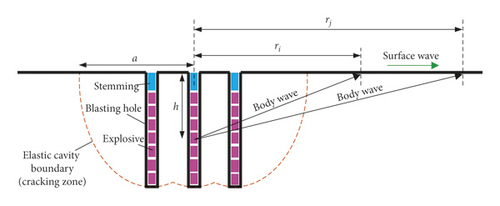
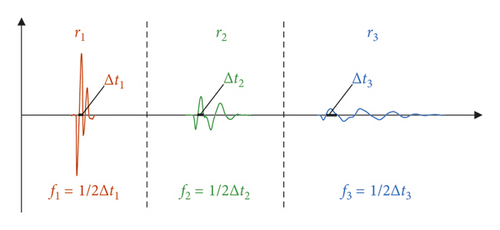
Figure 3 illustrates the changes of the dominant frequency of blasting vibration with distance, where the distance away from the blasting source is r₁ < r₂ < r₃ and the dominant frequency of each distance is f₁ > f₂ > f₃. The dominated frequency used to fitting analyzing in this paper is zero-crossing dominant frequency, which is also shown in Figure 3, and it is the most commonly used form of dominant frequency when the waveform has a clear peak [2].

2.2. Dimensional Analysis of the Dominant Frequency

It is known from the previous analysis that the vibration induced by elastic spherical cavity mainly depends on the longitudinal wave velocity C_P, the radius of the elastic cavity a, the density of the rock ρ, the charge weight Q, and the distance between the blasting source with the measuring points r, as shown in Table 1.

Table 1. Main influencing parameters and dimensions of dominant frequency.

Parameter	Unit (dimension)
Longitudinal wave velocity	m/s (LT⁻¹)
Radius of elastic cavity	m (L)
Distance between the blasting source with the measuring points	m (L)
Charge weight per delay	kg (M)
Density of rock	kg/m³ (ML⁻³)

Among all the parameters shown in Table 1, a, C_P, and ρ are independent with each other and include three basic dimensions of measurement: mass M, length L, and time T, which are selected as the main parameters of the dominated frequency by using the dimensional analysis method.

Based on the π-theorem, three nondimensional equations are established as follows [18]:

\begin{matrix} \{\begin{cases} π_{1} = a^{α_{1}} C_{P}^{β_{1}} ρ^{γ_{1}} f, \\ π_{2} = a^{α_{2}} C_{P}^{β_{2}} ρ^{γ_{2}} r, \\ π_{3} = a^{α_{3}} C_{P}^{β_{3}} ρ^{γ_{3}} Q . \end{cases} \end{matrix}

(9)

When the dimension of each physical quantity is substituted, according to the principle of dimension homogeneity, the dimensionless expression is obtained:

\begin{matrix} \{\begin{cases} π_{1} = \frac{f a}{C_{P}}, \\ π_{1} = \frac{Q}{a^{3} ρ}, \\ π_{3} = \frac{r}{a} . \end{cases} \end{matrix}

(10)

The functional relationship between dimensionless dimensions is as follows:

\begin{matrix} f = \frac{C_{P}}{a} {(\frac{Q^{13 /}}{r ρ^{13 /}})}^{α} {(\frac{r}{a})}^{β}, \end{matrix}

(11)

where α and β are coefficients.

Under the condition of spherical charge, the charge weight can be expressed as follows:

\begin{matrix} Q = \frac{4}{3} π q a^{3}, \end{matrix}

(12)

where q is the unit explosive consumption of rock.

Under the condition of cylindrical charge, the charge weight can be expressed as follows:

\begin{matrix} Q = \frac{1}{6} π q d^{3}, \end{matrix}

(13)

where d is the diameter of the blasthole.

It can be seen that a, d, and Q are not independent. Comparing equations (5) and (11) and considering the relationship between a, d, and Q in (12), the attenuation equation of blasting vibration dominant frequency induced by spherical explosion can be obtained:

\begin{matrix} f = ξ \frac{C_{P}}{Q^{13 /}} {(\frac{Q^{13 /}}{r})}^{β}, \end{matrix}

(14)

where ξ are β are coefficients.

In fact, ξ is a coefficient that included the effect of properties of rock. The longitudinal wave velocity C_P is also one of the parameters reflecting the properties of rocks. If the effect of C_P is included in the coefficient ξ and the dimensional consistency of (14) is not considered, the correlation coefficient of (14) will not be affected, and the equation can be further simplified as follows:

\begin{matrix} f = \frac{ζ}{Q^{13 /}} {(\frac{Q^{13 /}}{r})}^{β}, \end{matrix}

(15)

where ζ is the coefficient.

The charge weight of the cylindrical charge in bench blasting is

\begin{matrix} Q = q H S B, \end{matrix}

(16)

where Q is the charge weight, H is the bench height, S is the blastholes spacing, and B is the row spacing.

In mining bench blasting, bench height H is generally adopted as (1.5–2.0)B, stemming length is (0.7–1.0)B, drilling depth is 0.3B, blastholes spacing S = (1.0–2.0)B, and row spacing B and drilling diameter d have a relationship of B = (25–35)d [1]. So, according to the assumption in Section 2.1 and the proportional relationship among different blasting parameters mentioned above, equation (15) is still valid for cylindrical charge blasting.

Moreover, with the increase of the distance away from the blasting source, the wave front formed by the blasting seismic wave is cylindrical wave front. Revised from the theory of cylindrical waves in reference to the attenuation formula of PPV [19], equation (15) can be rewritten as follows:

\begin{matrix} f = \frac{α}{Q^{12 /}} {(\frac{Q^{12 /}}{r})}^{β}, \end{matrix}

(17)

where α and β are coefficients.

3. Fitting of Frequency Attenuation Law of Open-Pit Blasting in Zhoushan Petrochemical Base

3.1. Engineering Background

Zhoushan Green Petrochemical Base is located in Zhoushan City, Zhejiang Province, China. As shown in Figure 4, the project plans to reclaim 41 square kilometers of land area with Dayu Mountain as its core and build an island-type, modern, and ecological petrochemical base. The base is built in two phases where phase II is under excavation, as shown in Figure 5. The square quantity exploited by blasting is about 47 million cubic meters, and the open-pit excavation period is about 20 months in phase II.

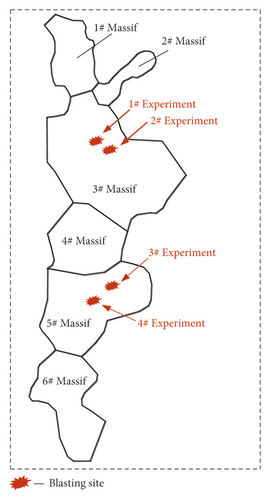
Two blasting sites have been arranged in phase II, as shown in Figure 6. There are two blasting experiments in each of the both blasting sites, which have been analyzed in order to verify the effectiveness of the proposed equation. The dominant frequency of the field measured blasting from 1# and 2# experiments in 3# massif to 3# and 4# experiments in 5# massif will be selected to fitting analyze. The vibration logging and analysis system used in field observation consists of three parts: three-axis velocity transducers, a blasting vibration intelligent monitor (Blast-UM), and computers installed with Blast-UM software used to withdraw and process test data. Typical blasting measuring points and devices are shown in Figure 7.

3.2. Experiments in 3# Massif

1# and 2# experiments are conducted in the platform with elevation of 16 m in 3# massif. 1# experiment is located on the northwest side of the platform, and 2# experiment is located on the north side of the platform. The diameter of the blasting holes is 115 mm, and the diameter of the explosive is 90 mm. The detailed blasting parameters of the two experiments are shown in Table 2.

Table 2. Drilling and blasting parameters for the blast in 3# massif.

Blast site	3# massif
Experiment	1#		2#
Blastholes	Multiple	Single	Multiple	Single
Blasthole diameter (mm)	115	115	115	115
Blasthole length (m)	13.2–14.9	14.8	12.7–14.7	14.2
Blasthole spacing (m)	4.5	—	4.5	—
Row spacing (m)	4.5	—	4.5	—
Charge diameter (mm)	70/90	90	70/90	90
Charge weight per hole (kg)	66–90	90	69–93	87
Stemming length (m)	4.0–5.5	4.0	4.5	4.5
Number of rows	4	—	4	—
Number of blastholes	116	1	126	1

In 1# and 2# experiment, a single-hole blasting was set in the last delay of the multiple-hole blasting to observe the dominant frequency attenuation law of single-hole blasting and multiple-hole blasting, respectively. Among them, six and eight surface blasting vibration measurement points were arranged in 1# and 2# experiment, respectively. The multiple-hole blasting is detonated by holes, MS3 detonators are used between holes, MS5 detonators are used between rows, and single-hole blasting and multiple-hole blasting are separated by the MS10 detonator. MS3/MS5/MS10 represent the millisecond with 50/110/650 ms, as shown in Figures 8 and 9. And a stereo sketch of the layout of measuring points is provided in the red-dotted frame.

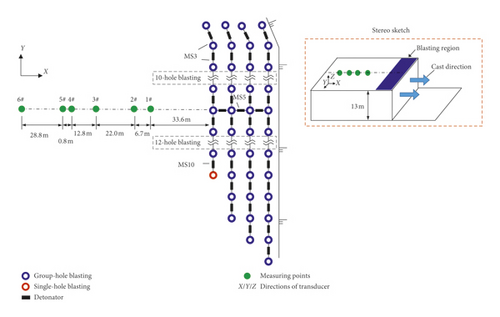
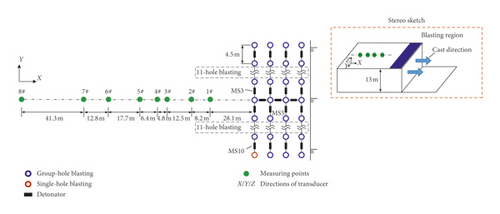
Figure 10 gives the typical time history curves of blasting vibration of the 1# measuring point in 1# experiment as an example. Blasting vibration is divided into two parts: the front part is multiple-hole blasting and the rear part is single-hole blasting. In order to facilitate observation, different colors are used to indicate the blasting vibration. The dominant frequency of the two parts is marked in the figure.

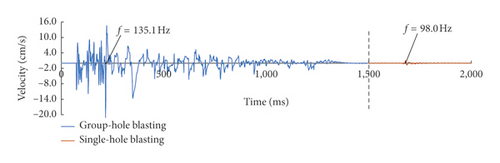
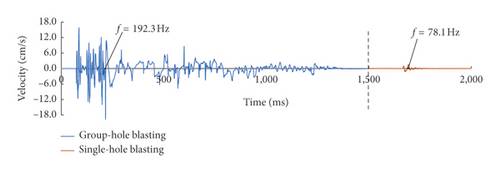
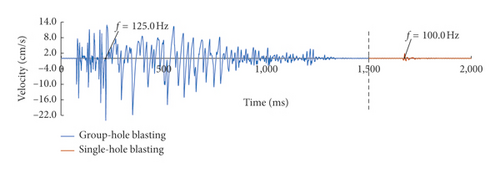
The values of dominant frequency of single-hole and multiple-hole blasting are given in Table 3.

Table 3. Dominant frequency of single vibration signals in 3# massif.

Experiment	Blasthole	Direction	Dominant frequency (Hz)
Experiment	Blasthole	Direction	1#	2#	3#	4#	5#	6#	7#	8#
1	Single	X	98.0	61.7	50.0	67.7	63.3	50.5	39.1	40.7
		Y	58.1	84.7	79.4	76.9	/	53.8	34.5	33.3
		Vertical	100.0	70.4	47.6	70.4	48.1	43.5	35.5	35.5
	Multiple	X	135.1	80.6	151.3	136.8	138.9	63.2	28.2	26.6
		Y	192.3	108.7	94.3	131.5	104.2	54.9	30.4	30.6
		Vertical	125.0	100.0	102.0	104.2	89.3	48.1	38.4	30.2

2	Single	X	83.3	89.3	84.7	54.6	47.6	52.6	—	—
		Y	111.1	89.3	53.5	35.2	53.2	52.1	—	—
		Vertical	72.5	83.3	72.5	35.5	44.2	43.5	—	—
	Multiple	X	166.7	108.7	113.6	84.3	68.5	42.6	—	—
		Y	156.3	200.0	83.3	33.3	58.8	58.8	—	—
		Vertical	92.9	89.3	65.8	46.9	48.1	48.1	—	—

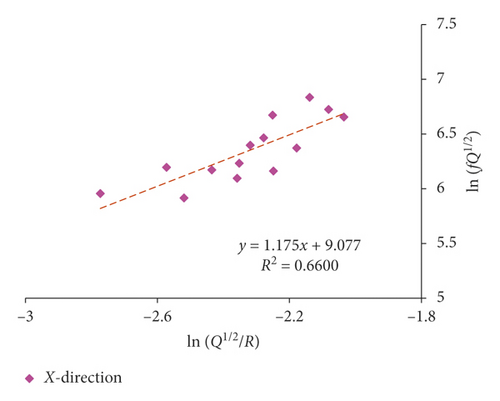
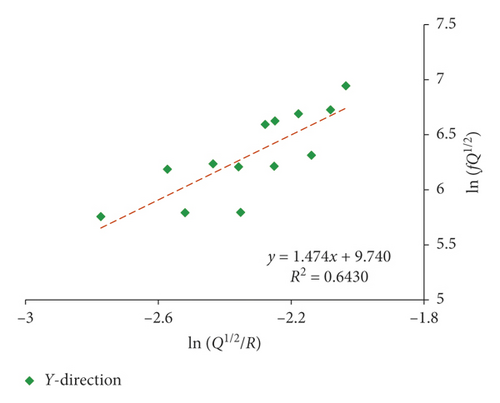
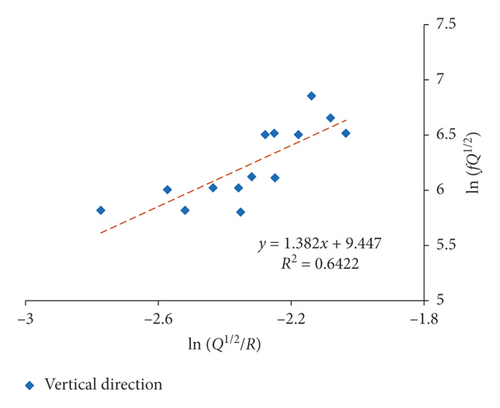
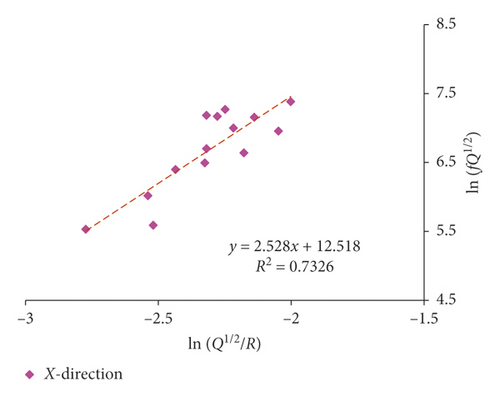
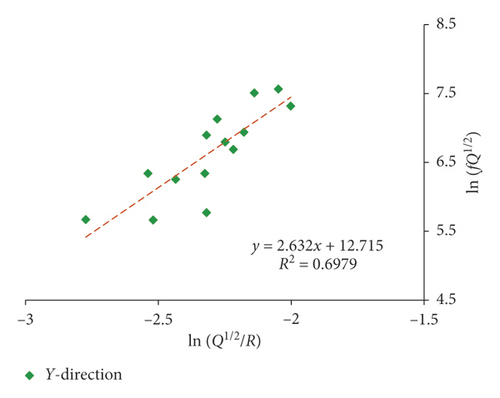
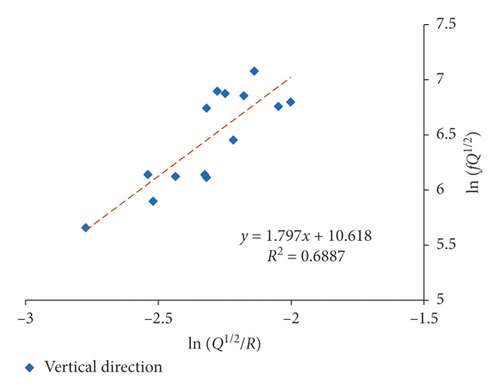
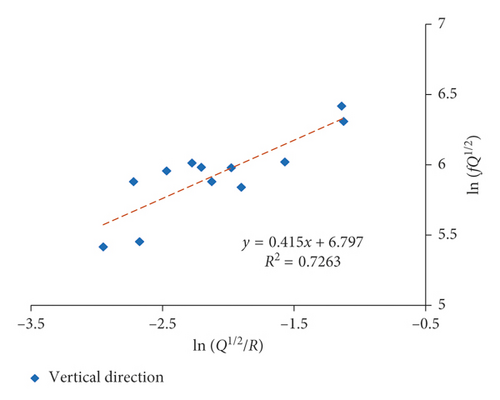
Since both 1# and 2# experiments were carried out in 3# massif, they were fitted together. Multiple-hole blasting is different from single-hole blasting in vibration waveform and spectrum characteristics due to the superposition and the influence of detonator delay. As a result, single-hole blasting and multiple-hole blasting are fitted separately. The fitting results of the attenuation rule for the dominant frequency of single-hole and multiple-hole blasting by equation (16) are presented in Figures 11 and 12 and Table 4.

Table 4. Fitting equation of the dominant frequency in 3# massif.

Equation	Blastholes	X-direction		Y-direction		Vertical
Equation	Blastholes	Equation	Correlation coefficient	Equation	Correlation coefficient	Equation	Correlation coefficient
(17)	Single	$f = ((8.753 E +) / Q^{12 /}) {(Q^{12 /} / r)}^{1.18}$	r² = 0.660	$f = ((1.704 E +) / Q^{12 /}) {(Q^{12 /} / r)}^{1.47}$	r² = 0.643	$f = ((1.274 E +) / Q^{12 /}) {(Q^{12 /} / r)}^{1.38}$	r² = 0.642
(17)	Multiple	$f = ((2.735 E +) / Q^{12 /}) {(Q^{12 /} / r)}^{2.53}$	r² = 0.733	$f = ((3.335 E +) / Q^{12 /}) {(Q^{12 /} / r)}^{2.63}$	r² = 0.698	$f = ((4.094 E +) / Q^{12 /}) {(Q^{12 /} / r)}^{1.80}$	r² = 0.689

The proposed equation (17) generally has obtained a favorably correlation coefficient in 3# massif. The dominant frequency of blasting vibration in multiple-hole blasting is decaying faster than that in single-hole blasting, which is also confirmed by Zhang et al. [20]. In addition, the fitting correlation coefficient of dominant frequency in X-direction is generally higher than that of the other two directions, and the vertical direction obtains the worst relevance, which is in compliance with previous discussion that the radial vibration is normally perceived to be related to the P-wave, while the vibration in vertical is normally considered to be influenced most by the R-wave reflected by the free face on the ground [2]. As a result, for surface vibration, the fitting correlation coefficient of radial vibration is higher than that of vertical vibration.

3.3. Experiments in 5# Massif

3# and 4# experiments are conducted in the platform with elevation of 30 m in 5# massif. 3# experiment is located on the northeast side of the platform, and 4# experiment is located on the north side of the platform. The diameter of the blasting holes is 115 mm, and the diameter of the explosive is 90 mm. The detailed blasting parameters of the two experiments are shown in Table 5.

Table 5. Drilling and blasting parameters for the blast in 5# massif.

Blast site	5# massif
Experiment	3#		4#
Blastholes	Multiple	Single	Multiple	Single
Blasthole diameter (mm)	115	115	115	115
Blasthole length (m)	10.6–13.3	13.0	14.4	14.8
Blasthole spacing (m)	6.0	—	6.1	—
Row spacing (m)	3.6	—	3.5	—
Charge diameter (mm)	90	90	90	90
Charge weight per hole (kg)	60–72	72	84/96/108	96
Stemming length (m)	4.5	4.5	5.0	5.0
Number of rows	5	—	6	—
Number of blastholes	40	1	54	1

In 3# and 4# experiment, besides the multiple-hole blasting, a single-hole blasting was also set up to observe the dominant frequency attenuation law of single-hole blasting and multiple-hole blasting, respectively. Among them, seven and five surface blasting vibration measurement points were arranged in 3# and 4# experiments, respectively. The multiple-hole blasting is detonated by holes, MS3 detonators are used between holes, MS5 detonators are used between rows, and single-hole blasting and multiple-hole blasting are separated by the MS10 detonator. MS3/MS5/MS13 represent the millisecond with 50/110/650 ms, as shown in Figures 13 and 14. And a stereo sketch of the layout of measuring points is also provided in the red-dotted frame.

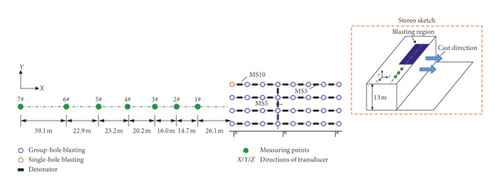
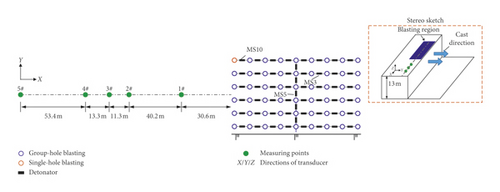
Figure 15 gives the typical time history curves of blasting vibration of the 3# measuring point in 3# experiment as an example. Blasting vibration is divided into two parts: the front part is multiple-hole blasting and the rear part is single-hole blasting. In order to facilitate observation, different colors are used to indicate the blasting vibration. The dominant frequency of the two parts is marked in the figure.

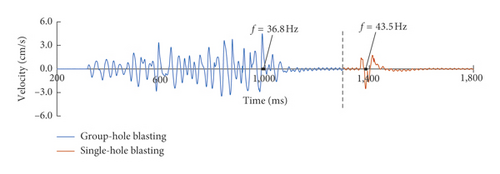
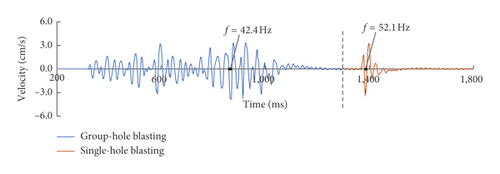
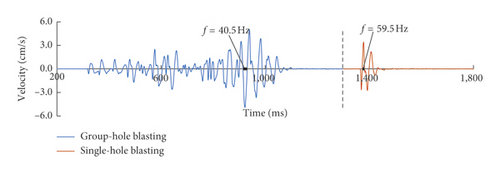
The values of dominant frequency of single-hole blasting and multiple-hole blasting are given in Table 6.

Table 6. Dominant frequency of single vibration signals in 5# massif.

Experiment	Blasthole	Direction	Measuring points number
Experiment	Blasthole	Direction	1#	2#	3#	4#	5#	6#	7#
3	Single	X	75.8	93.9	43.5	56.2	42.7	28.1	25.0
		Y	78.1	—	52.1	71.9	46.3	30.9	26.0
		Vertical	60.2	54.9	59.5	60.3	49.0	33.8	27.8
	Multiple	X	94.3	48.5	36.8	41.3	36.7	22.5	18.7
		Y	89.3	48.3	42.4	38.5	34.2	31.4	21.9
		Vertical	64.7	48.5	40.5	46.7	45.5	27.5	26.5

4	Single	X	68.5	56.8	34.7	45.9	36.8	—	—
		Y	73.5	54.3	45.5	36.5	37.0	—	—
		Vertical	66.7	54.9	54.3	49.5	37.2	—	—
	Multiple	X	84.7	45.9	36.0	32.5	37.7	—	—
		Y	78.1	63.3	53.8	31.1	34.5	—	—
		Vertical	62.5	40.3	36.5	41.7	36.5	—	—

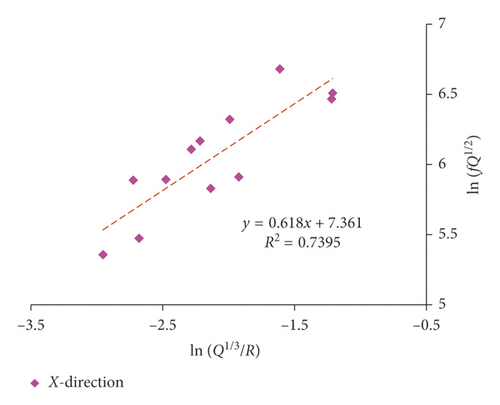
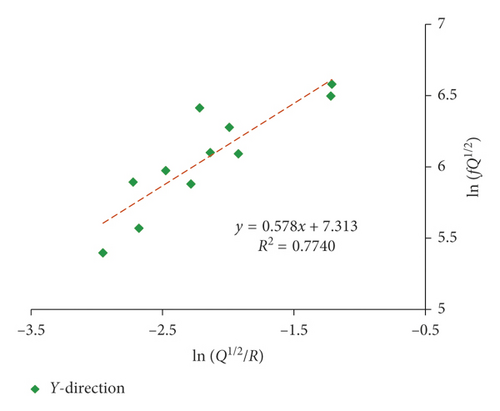
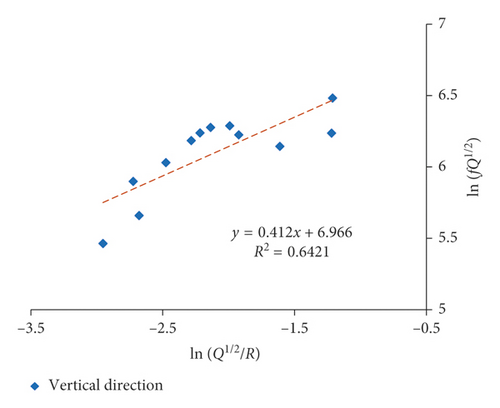
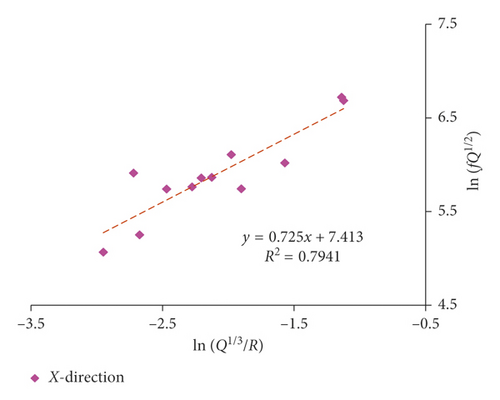
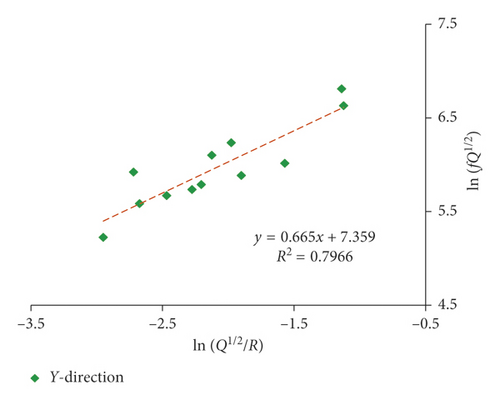
The fitting results of the dominant frequency by equation (17) are presented in Figures 16 and 17 and Table 7.

Table 7. Fitting equation of the dominant frequency in 5# massif.

Equation	Blastholes	X-direction		Y-direction		Vertical direction
Equation	Blastholes	Formula	Correlation coefficient	Formula	Correlation coefficient	Formula	Correlation coefficient
(17)	Single	$f = (1573 / Q^{12 /}) {(Q^{12 /} / r)}^{0.62}$	r² = 0.740	$f = (1500 / Q^{12 /}) {(Q^{12 /} / r)}^{0.58}$	r² = 0.774	$f = (1060 / Q^{12 /}) {(Q^{12 /} / r)}^{0.41}$	r² = 0.642
(17)	Multiple	$f = (1657 / Q^{12 /}) {(Q^{12 /} / r)}^{0.73}$	r² = 0.794	$f = (1570 / Q^{12 /}) {(Q^{12 /} / r)}^{0.67}$	r² = 0.797	$f = (859 / Q^{12 /}) {(Q^{12 /} / r)}^{0.42}$	r² = 0.726

The proposed equation (17) also has obtained a favorable correlation coefficient in 5# massif. And the fitting correlation coefficient of dominant frequency in X-direction is still higher than the vertical direction. Moreover, both of the amplitude and the attenuation speed of the dominant frequency in X-direction are larger than that in vertical direction, which is also in compliance with previous discussion that the radial vibration is more related to the P-wave, while the vibration in vertical is normally considered to be influenced most by the R-wave. In fact, the amplitude and attenuation speed of the P-wave are larger than that of the R-wave. It can be seen that different wave components have an important influence on the frequency.

4. Comparison with Other Formulas

In recent years, although the frequency of blasting vibration is being paid more attention and most of blasting vibration control standards are frequency-dependent, the prediction of frequency is still the most difficult in terms of the numerous influencing factors, which is difficult to quantify. But many scholars still have conducted quantities of in-depth studies. The blasting vibration frequency was initially put forward by Sadovskij [21], which is only considered the distance away from explosion source and ignored other factors:

\begin{matrix} f = {(k_{1} \log r)}^{- 1}, \end{matrix}

(18)

where f is the blast-induced dominant vibration frequency, k₁ is the nonnegative site specific fitting coefficient, and r is the distance between blasting source and measuring point.

Meng and Guo [22] have deduced the prediction formula of the dominant frequency of blasting seismic wave propagating in the viscoelastic medium as follows:

\begin{matrix} f = {(k_{1} Q^{13 /} + k_{2} r^{2})}^{- 1}, \end{matrix}

(19)

where k₁ and k₂ are uncertain parameters related to charge structures, and Q is the maximum explosive charge per delay.

Zhang and Yu [23] obtained the prediction formula of dominant frequency of blasting vibration by dimensional analysis as follows:

\begin{matrix} f = (\frac{k_{1}}{r}) {(\frac{Q^{13 /}}{r})}^{k_{2}}, \end{matrix}

(20)

where k₁ is defined as the site coefficient, which is related to rock properties and blasting parameters. k₂ is an attenuation coefficient of blasting vibration.

Jiao [24] proposed the formula for calculating the dominant frequency of ground particle vibration caused by blasting as follows:

\begin{matrix} f = k_{1} (\frac{C_{s}^{75 /}}{Q^{13 /}}) {(\frac{Q^{13 /}}{r})}^{25 /}, \end{matrix}

(21)

where k₁ is defined as the site coefficient, which is related to the dominant frequency of blasting vibration, and usually ranges from 0.01 to 0.3. C_s denotes the shear wave velocity in the rock.

Li et al. [25] has provided a prediction formula of blasting dominant frequency based on a combination of grey relational analysis and dimensional analysis as follows:

\begin{matrix} f = k_{1} (\frac{V^{k_{2}}}{Q^{13 /}}) {(\frac{Q^{13 /}}{r})}^{k_{3}} {(\frac{Q^{13 /}}{H})}^{k_{4}}, \end{matrix}

(22)

where k₁, k₂, k₃, and k₄ are nondimensional constants, which are related to the rock density and the wave velocity, H denotes the relative elevation, and V is the peak particle velocity.

In order to observe the difference of fitting effect between equation (17) and other formulas (18)–(22), the dominant frequency of blasting vibration measured in Zhoushan Green Petrochemical Base are fitted and compared with each other. As the length of the article is limited, Figure 18 only gives the fitting analysis curve of multiple-hole blasting of X-direction in 1# experiment. Table 8 gives a complete list of the fitting parameters and correlation coefficients of each experiment by each formula.

Table 8. The fitting results of different formulas.

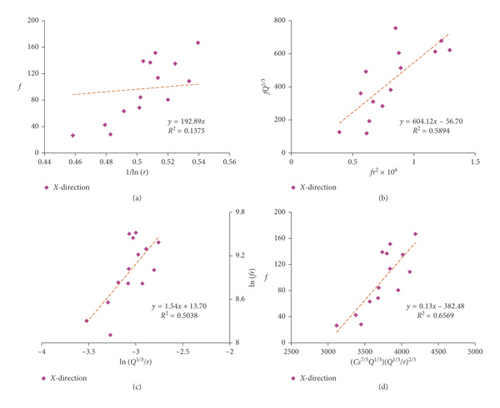
Equation	Blasthole	Direction	3# massif					5# massif
Equation	Blasthole	Direction	k₁	k₂	k₃	k₄	r²	k	k₁	k₂	k₄	r²
(18)	Single	X	95.75				0.212	125.88				0.461
		Y	95.66				0.178	125.40				0.540
		Z	94.01				0.176	114.57				0.595
	Multiple	X	85.15				0.138	192.89				0.463
		Y	89.51				0.116	192.50				0.489
		Z	79.90				0.155	147.05				0.691

(19)	Single	X	3.29E − 3	8.15E − 7			0.028	2.97E − 3	2.84E − 7			0.433
		Y	3.27E − 3	7.62E − 7			0.011	4.28E − 3	−3.53E − 7			0.519
		Z	3.52E − 3	6.06E − 7			0.007	4.45E − 3	−2.65E − 7			0.645
	Multiple	X	3.84E − 3	9.02E − 7			0.589	−1.76E − 2	1.07E − 5			0.266
		Y	3.58E − 3	8.64E − 7			0.679	−5.16E − 3	4.10E − 6			0.322
		Z	4.34E − 3	5.97E − 7			0.271	2.26E − 2	−1.01E − 5			0.435

(20)	Single	X	1.00E + 4	0.18			0.042	1176.71	−0.39			0.527
		Y	2.39E + 4	0.47			0.155	1085.72	−0.43			0.651
		Z	1.66E + 4	0.38			0.119	671.94	−0.60			0.805
	Multiple	X	8.94E + 5	1.54			0.504	1319.01	−0.28			0.381
		Y	1.19E + 6	1.65			0.475	1191.71	−0.35			0.530
		Z	7.78E + 4	0.81			0.312	573.17	−0.59			0.855

(21)	Single	X	0.047				0.642	0.017				0.360
		Y	0.057				0.636	0.017				0.303
		Z	0.049				0.596	0.016				0.299
	Multiple	X	0.026				0.240	0.011				0.645
		Y	0.026				0.204	0.011				0.652
		Z	0.020				0.272	0.010				0.780

(22)	Single	X	2.93	0.13	1.04	−7.87	0.683	1.62E + 4	0.00	0.71	2.46	0.862
		Y	5.20E + 7	−0.33	1.70	7.02	0.704	5.09E + 4	−0.20	0.86	2.89	0.925
		Z	3.00E + 8	0.10	1.30	10.11	0.673	9.54E + 3	−0.45	0.92	0.71	0.906
	Multiple	X	3.53	0.10	2.29	−11.67	0.758	3.01E + 3	0.74	−0.34	4.02	0.875
		Y	7.05E − 5	0.51	1.21	−18.45	0.890	1.16E + 3	−0.13	0.75	−0.50	0.782
		Z	7.39E − 8	0.26	1.29	−26.08	0.876	4.82E + 3	0.11	0.25	2.46	0.760

(17)	Single	X	8.75E + 3	1.18			0.660	1573	0.62			0.740
		Y	1.70E + 4	1.47			0.643	1500	0.58			0.774
		Z	1.27E + 4	1.38			0.642	1060	0.41			0.642
	Multiple	X	2.73E + 5	2.53			0.733	1657	0.73			0.794
		Y	3.33E + 5	2.63			0.698	1570	0.67			0.797
		Z	4.09E + 4	1.80			0.689	859	0.42			0.726

It can be seen from Table 8 that equation (17) generally performs better than most of other formulas, and the fitting correlation coefficient is only lower than equation (22). However, it is worth noting that although the fitting correlation coefficient obtained by equation (22) is generally the highest, it is difficult to apply in engineer practice in result of its too complex fitting parameters and calculation, which need four unknown parameters and multiple linear regression. In comparison, equation (17) can not only obtain a favorable fitting correlation but also simple and brief in form.

5. Conclusion

Based on the theoretical derivation of the attenuation equation of the dominant frequency induced by blasting and the fitting analysis of the dominant frequency in Zhoushan Green Petrochemical Base, the following conclusions can be drawn:

(1)
An equation reflecting the change of dominant frequency induced by blasting has been derived by dimensional analysis combined with the theory of radial spherical wave propagation. Based on the fitting analysis of dominant frequencies measured in Zhoushan Green Petrochemical Base, favorable correlation coefficients have been obtained, which proves the feasibility of the proposed equation. By comparing the different prediction formulas of dominant frequency with equation (17), it is found that equation (17) performs better in general, which can not only obtain a favorable fitting correlation but also simple and brief in form.
(2)
The fitting correlation coefficient of dominant frequency in radial direction is generally higher than the vertical direction, which is resulted from the existence of surface free surface in cylindrical charge blasting. The vibration in vertical is considered to be influenced most by the R-wave reflected by the free face on the ground, which is perceived to be quite different from the radial vibration affected by the P-wave. In other words, different types of waves will affect the dominant frequency of blasting vibration.

This paper has proposed an attenuation formula for dominant frequency, and it has found that the attenuation of dominant frequency is influenced by the component of the blasting wave. Although the proposed equation has obtained a favorable fitting correlation, it has adopted many simplified assumptions, such as that the rock is assumed to be linear elastic and the influence of free surface in semi-infinite space is neglected. Therefore, the proposed equation still needs to be further improved and optimized.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This work was supported by the National Natural Science Fund Project of China (51779190) and Hubei Province Technical Innovation Program (2017ACA102). The authors wish to express their thanks to all supporters.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Hustrulid W., Blasting principles for open pit mining, Mining Engineering. (2004) 1.
Google Scholar
2 Dowding C. H., Construction vibrations, Shock & Vibration. (1995) .
Google Scholar
3 Yang J. H., Lu W. B., Zhao Z. G., Yan P., and Chen M., Safety distance for secondary shotcrete subjected to blasting vibration in Jinping-II deep-buried tunnels, Tunnelling and Underground Space Technology. (2014) 43, no. 7, 123–132, https://doi.org/10.1016/j.tust.2014.04.008, 2-s2.0-84901296423.
10.1016/j.tust.2014.04.008
Web of Science® Google Scholar
4 Singh P. K. and Roy M. P., Damage to surface structures due to blast vibration, International Journal of Rock Mechanics and Mining Sciences. (2010) 47, no. 6, 949–961, https://doi.org/10.1016/j.ijrmms.2010.06.010, 2-s2.0-77955270377.
10.1016/j.ijrmms.2010.06.010
Web of Science® Google Scholar
5 Roy M. P., Singh P. K., Sarim M., and Shekhawat L. S., Blast design and vibration control at an underground metal mine for the safety of surface structures, International Journal of Rock Mechanics and Mining Sciences. (2016) 83, 107–115, https://doi.org/10.1016/j.ijrmms.2016.01.003, 2-s2.0-84953727586.
10.1016/j.ijrmms.2016.01.003
Web of Science® Google Scholar
6 Álvarez-Vigil A. E., González-Nicieza C., López Gayarre F., and Álvarez-Fernández M. I., Predicting blasting propagation velocity and vibration frequency using artificial neural networks, International Journal of Rock Mechanics & Mining Sciences. (2012) 55, no. 10, 108–116, https://doi.org/10.1016/j.ijrmms.2012.05.002, 2-s2.0-84864247513.
10.1016/j.ijrmms.2012.05.002
Web of Science® Google Scholar
7 Zhong G., Ao L., and Zhao K., Influence of explosion parameters on wavelet packet frequency band energy distribution of blast vibration, Journal of Central South University. (2012) 19, no. 9, 2674–2680, https://doi.org/10.1007/s11771-012-1326-5.
10.1007/s11771-012-1326-5
Web of Science® Google Scholar
8 Yang J. H., Lu W. B., Jiang Q. H., Yao C., and Zhou C. B., Frequency comparison of blast-induced vibration per delay for the full-face millisecond delay blasting in underground opening excavation, Tunnelling and Underground Space Technology. (2016) 51, 189–201, https://doi.org/10.1016/j.tust.2015.10.036, 2-s2.0-84946216318.
10.1016/j.tust.2015.10.036
Web of Science® Google Scholar
9 Ling T., Li X., Dai T., and Peng Z., Features of energy distribution for blast vibration signals based on wavelet packet decomposition, Journal of Central South University. (2015) 12, no. 1, 135–140, https://doi.org/10.1007/s11771-005-0387-0.
10.1007/s11771-005-0387-0
Google Scholar
10 Tripathy G. R. and Gupta I. D., Prediction of ground vibrations due to construction blasts in different types of Rock, Rock Mechanics and Rock Engineering. (2002) 35, no. 3, 195–204, https://doi.org/10.1007/s00603-001-0022-9, 2-s2.0-0036688017.
10.1007/s00603-001-0022-9
Web of Science® Google Scholar
11 González Nicieza C. and Alvarez Fernández M. I., Blasting propagation velocity, Rock Mechanics and Engineering, vol. 3 of Análysis, Modeling & Design, 2017, Taylor & Francis Online, London, UK.
Google Scholar
12 Zhou J., Lu W., Yan P., Chen M., and Wang G., Frequency-dependent attenuation of blasting vibration waves, Rock Mechanics and Rock Engineering. (2016) 49, no. 10, 4061–4072, https://doi.org/10.1007/s00603-016-1046-5, 2-s2.0-84978803764.
10.1007/s00603-016-1046-5
Web of Science® Google Scholar
13 Zhong Z. Y. and Xiaoguang J., Prediction of peak velocity of blasting vibration based on artificial neural network optimized by dimensionality reduction of FA-MIV, Mathematical Problems in Engineering. (2018) 2018, 12, 8473547, https://doi.org/10.1155/2018/8473547, 2-s2.0-85048557169.
10.1155/2018/8473547
Web of Science® Google Scholar
14 Khandelwal M., Kankar P., and Harsha S., Evaluation and prediction of blast induced ground vibration using support vector machine, Mining Science and Technology. (2010) 20, no. 1, 64–70, https://doi.org/10.1016/s1674-5264(09)60162-9, 2-s2.0-76249119416.
10.1016/s1674-5264(09)60162-9
Google Scholar
15 Faradonbeh R. S., Armaghani D. J., Majid M. Z. A. et al., Prediction of ground vibration due to quarry blasting based on gene expression programming: a new model for peak particle velocity prediction, International Journal of Environmental Science & Technology. (2016) 13, no. 6, 1453–1464, https://doi.org/10.1007/s13762-016-0979-2, 2-s2.0-84971602144.
10.1007/s13762-016-0979-2
Web of Science® Google Scholar
16 Favreau R. F., Generation of strain waves in rock by an explosion in a spherical cavity, Journal of Geophysical Research. (1969) 74, no. 17, 4267–4280, https://doi.org/10.1029/jb074i017p04267.
10.1029/JB074i017p04267
Web of Science® Google Scholar
17 Kuzmenko A. A., Vorobev V. D., Denisyuk I. I., and Dauetas A. A., Seismic Effects of Blasting in Rock, 1993, Routledge, London, UK.
Google Scholar
18 Lu W. B., Zhou J. R., and Chen M., Study on attenuation formula of dominant frequency of blasting vibration, Engineering Blasting. (2015) 21, no. 6, 1–6, in Chinese.
Google Scholar
19 Devine J. P. and Duvall W. I., Effect of charge weight on vibration levels for millisecond delayed quarry blasts, Earthquake Notes. (1963) 34, no. 2, 17–24.
Google Scholar
20 Zhang Z. Y., Luan L. F., Yin Z. Q. et al., Effects of detonation ways on energy distribution for different frequency bands of bench blasting, Blasting. (2008) 25, no. 2, 21–25, in Chinese.
Google Scholar
21 Sadovskij M. A., Evaluation of seismically dangerous zones in blasting, seismic institute of the academy of sciences. In: on the effects of blast-induced vibrations, Bulletin of Subalpina Mining Association. (1966) .
Google Scholar
22 Meng H. L. and Guo F., Experimental research on the master frequency of blasting seismic wave, Journal of Railway Engineering Society. (2009) 11, no. 11, 81–83, in Chinese.
Google Scholar
23 Zhang L. G. and Yu Y. L., Research on the relationship of main vibration frequency of blasting vibration and peak particle velocity, Nonferrous metals (Mine Section). (2005) 57, no. 4, 32–34, in Chinese.
Google Scholar
24 Jiao Y. B., Research on the standard of blasting seismic safety assessment, Blasting. (1995) 12, no. 3, 45–47, in Chinese.
Google Scholar
25 Li H., Li X., Li J., Xia X., and Wang X., Application of coupled analysis methods for prediction of blast-induced dominant vibration frequency, Earthquake Engineering and Engineering Vibration. (2016) 15, no. 1, 153–162, https://doi.org/10.1007/s11803-016-0312-6, 2-s2.0-84962921679.
10.1007/s11803-016-0312-6
Web of Science® Google Scholar

Citing Literature

All articles

Analysis of the Main Factors Influencing the Dominant Frequency of Blast Vibration

Abstract

1. Introduction

2. The Attenuation Equation of Dominant Frequency Induced by Blasting

2.1. Analysis of Main Influencing Factors of the Dominant Frequency

2.2. Dimensional Analysis of the Dominant Frequency