1. Introduction

In the dive phase, problems such as large Mach number variation range and large overload for a hypersonic vehicle are obvious. The translational and rotational aircraft dynamics are characterized by being fast time-varying, being nonlinear, having a strong coupling, and being uncertain [1]. The traditional aircraft guidance and the control system mainly separate the control and guidance subsystems, without utilizing the coupling information between subsystems based on engineering experience or singular perturbation theory. The integrated guidance control (IGC) system can make full use of the coupling information between the subsystems to improve the performance of the entire system. For the attitude control of hypersonic vehicles, Wang et al. proposed a hierarchical predictive control method [2] and developed a rapid generation method of multitarget entry trajectory [3] that could solve the problem of effective attitude controller and reentry guidance for the general hypersonic vehicle model. Hou and Duan proposed an integrated design method for guidance and control based on an adaptive dynamic surface which avoids the differential explosion problem of the traditional back-stepping method [4]. Wang et al. designed a method of the guidance control system based on banking turning control and dynamic surface control, and the uncertain term was estimated by the state observer and compensated by the control law [5]. Zhao et al. proposed a method of IGC for hypersonic vehicles that satisfies the terminal angular constraint based on the full-coupling model [6]. Then, Zhao et al. studied a method of IGC based on L2 gain interference consistency, which simplifies the structure and calculation of the IGC method [7]. Wang et al. studied the guidance control problem of hypersonic vehicles with composite constraints in the dive phase. The integrated model based on the sliding mode dynamic surface can realize the three-dimensional angle constraint of landing velocity [8].

For a hypersonic waverider aircraft, the intelligent morphing technology can effectively solve the problem that aerodynamic performance deteriorates sharply when deviating from the design state [9, 10]. When intelligent morphing technology is applied to the flying missile for the battlefield environment and combat mission changes, the accuracy, combat effectiveness, and cost-effectiveness ratio can greatly improve [11]. In 2004, Jae-Sung et al. studied the aerodynamic and aeroelastic properties of a variable span cruise missile similar to the shape of the Tomahawk and showed that the symmetrical increase in the span of the two wings can effectively reduce the drag and greatly improve the flight range [12]. In the modeling of morphing aircraft, Seigler et al. established a dynamic model of large-scale morphing flight for flight control problems and discussed various control methods [13]. Yang et al. developed dynamic modeling and dynamic response analysis of the variable sweep and variable span aircraft and proved that the combination of a suitable variant mode and variant velocity can reduce the workload of the flight control system [14]. Yue et al. analyzed the longitudinal multibody dynamics of the Z-wing morphing aircraft and showed that the variant of aerodynamic characteristics is the main factor affecting the dynamic characteristics of the aircraft during the folding process [15]. A joint simulation method based on Missile DATCOM and MATLAB proposed by Zhang Fair is applied to the study of variable wing dynamic characteristics of typical axisymmetric missiles [16]. Nobleheart et al. designed a time-varying system for a single-neural network adaptive controller for morphing aircraft [17]. In terms of the control of the morphing aircraft, Dong et al. studied the smooth-switching linear variable parameter (LPV) H∞ control problem for a class of variable span aircraft to ensure the stability and robustness of the aircraft system [18]. Gandhi et al. proposed a control scheme that used model identification to realize morphing control and keep the aircraft stable [19]. In terms of the ballistic design of the morphing missile, Huang et al. used the Radau pseudospectral method (RPM) to optimize the gliding trajectory of the variable sweep aircraft with the target of largest range [20]. Wei-Ming et al. designed a trajectory-attitude dual-loop adaptive sliding mode controller for the variable sweep missile to ensure the stability of the ballistic tracking to the optimal scheme when the wing is scheduled to be actuated [21].

Most of the above researches were aimed at the IGC system of the hypersonic vehicle and the stability control of the morphing aircraft. There were few reports on the control research of the hypersonic morphing missile and how to use the span variant to assist the ballistic control. The research in this paper is aimed at the IGC for a class of hypersonic variable span missiles. Based on the adaptive dynamic surface method, an IGC method in the dive phase with terminal angular constraint is designed and the span variant is skillfully applied to the auxiliary control of the IGC to enhance the control accuracy and reduce the workload of the control system. The variable span auxiliary control strategy was hardly studied for hypersonic missiles before. The results of simulation of the new method proposed in the paper show that the total flight time and the miss distance of the variable span are less than invariable span shown. The variety of span could adjust the lift-to-drag ratio of the missile so that it is easier to realize the terminal angular constraint, and the variable span reduces the workload for the attitude control system. At the same time, the robustness of a variable span missile is stronger than that of an invariable span missile.

In Section 2 in the paper, the geometric model, aerodynamic model, and 6 DOF motion model of the hypersonic deformation missile are established. In Section 3, the IGC model in the dive phase of the hypersonic morphing missile is established and the variable extension control method adapts to the IGC method. Section 4 displays the numerical simulation results and analyses of the IGC method. Section 5 is the conclusion for the paper.

2. The Motion Model of Hypersonic Variable Span Missile

2.1. The Shape and Parameters of Hypersonic Variable Span Missile

The outline of the shape of the variable-span hypersonic missile selected in this paper is shown in Figure 1.

The shape parameters and morphing modes are shown in Figure 2. The lift of the morphing missile was provided by a pair of horizontal front wings, and the four-rear wing was a +-shaped layout. The span variant of the wing is synchronously changed on both sides of the wings without differential changes. The synchronous or differential rotation of the four tails controls the rotational motion of the missile.

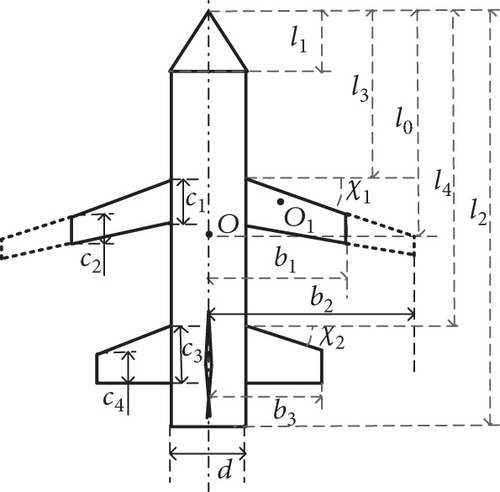
(1) Geometric Parameters of the Missile. l₁ is the length of the warhead. l₂ is the length of the total missile. d is the diameter of the main body and bottom of the warhead

(2) Variable Span Geometry. l₃ is the distance from the front end of the wing root to the nose of the warhead. c₁ is the chord length of the wing root. c₂ is the chord length of the wing tip. b₁ is the span of the wing. χ₁ is the sweep angle of the leading edge of the wing

(3) Geometric Parameters of the Tails. l₄ is the distance from the front end of the tail root to the nose of warhead. c₃ is the chord length of the tail root. c₄ is the chord length of the tail tip. b₃ is the span of the tail, and χ₂ is the sweep angle of the leading edge of the tail

b₁ is the span of the invariant wing, and b₂ is the maximum span of the variable span wing. When b is assumed as the span of the wing in a variable span state, the morphing rate of the wing span is defined as

$$ (1)

The missile characteristic parameters are shown: in Table 1, the mass of the missile is m, and the mass of the wing is m₁ and m₂ and m2. The moments of inertia are I_x, I_y, and I_z. The reference area is S₀. The longitudinal reference length is $$, and the lateral–directional reference length is $$.

Table 1. Missile characteristic parameter.

Name	Value	Name	Value	Name	Value
l1	3.43 m	c2	0.92 m	χ1	60∘
l2	8.00 m	b1	1.63 m	χ2	51.86∘
l3	4.70 m	b2	2.55 m	S0	5.66 m
l4	9.73 m	c3	1.70 m	$$	1.148 m
d	1.14 m	c4	0.85 m	$$	0.766 m
c1	2.12 m	b3	0.91 m	m	5000 kg
mi,  i = 1, 2	100 kg	Ix	15064 kg·m2	Iy, IZ	150646 kg·m2

3. IGC Method in the Dive Phase with Variable Span Auxiliary Control

3.1. IGC Model in the Dive Phase

In this paper, the IGC design of the dive phase of the hypersonic variable span missile is studied. The fixed point on the ground is selected as the target, and the IGC model in the dive phase with the terminal angular constraint is established.

3.1.1. Relative Motion of Variable Span Missile and Target

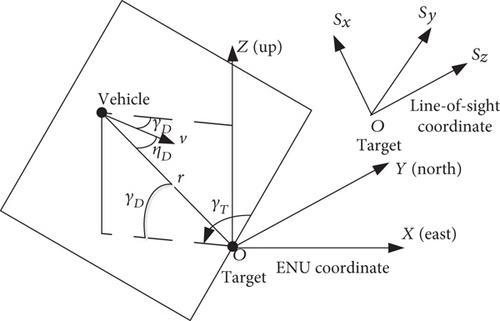
As shown in Figure 3, the East–North–Up (ENU) coordinate frame is formed by a plane tangential to the Earth’s surface and is attached to the target. The East axis is labeled X, the North axis is labeled Y, and the up axis is labeled Z. Define the line-of-sight (LOS) coordinate frame so that its origin is on the target where the S_x-axis points to the vehicle, the S_y-axis is in the horizontal plane of the target, and the S_z-axis is determined using the right-hand rule. η_D is the angle between the direction of velocity and the LOS, and γ_D is the longitudinal velocity azimuth in the dive plane. r_T is the distance between the center of mass of the variable span missile and the target point. λ_D and λ_T are the angles of elevation and azimuth of LOS.

The relative dynamic model of the variable span missile and the target point by the line-of-sight angles are expressed as [5]

$$ (19)

The relationship between the components in the LOS coordinate frame and the trajectory coordinate frame of the missile acceleration vector can be expressed as [6]

$$ (20)

where S_Hi,j(i, j = 1, 2, 3)are the elements in the conversion matrix of the trajectory coordinate frame to the LOS coordinate frame. i represents the row, and j represents the column.

To study the effect of the span variant on the IGC method, the hypersonic missile adopts the BTT control strategy in the dive phase to show the influence of the span variant more clearly. Therefore, the lateral force can be neglected. The influence of the lateral force in Equation (2) is regarded as the uncertainty term. Substituting Eq. (18) into Eq. (2) yields [6]

$$ (21)

where the uncertain items w_θ and w_σ can be expressed as [6]

$$ (22)

For missiles and fixed targets on the ground, the relative motion between them can be expressed as [6]

$$ (23)

then

$$ (24)

where γ_DF is the terminal angle. Because of |λ_D + γ_DF| < π/2 at the terminal time, it can be obtained as

$$ (25)

The terminal angle can be constrained by Eq. (25). By substituting Eq. (20) and Eq. (21) into Eq. (19), the relative dynamics of the target and the hypersonic variable span missile are denoted as

$$ (26)

In Eq. (26),

$$ (27)

3.1.2. Rotational Motion Model

The rotational motion model by the attack, sideslip, and bank angle is [7]

$$ (28)

Then, the rotational motion model that is available for control can be denoted as

$$ (29)

In Eq. (29),

$$ (30)

$$ (31)

In Eq. (31), the uncertainty can be expressed as [5]

$$ (32)

3.1.3. Processing of the Rotational Dynamic Model

When ignoring the Earth’s rotation, the launch coordinate frame is equivalent to the ground inertial system. By substituting Eq. (18) into Eq. (11), the simplified state equations with the input of fin deflections can be denoted as [7]

$$ (33)

Then, the rotational dynamic model that is available for control can be denoted as

$$ (34)

In Eq. (34) [5],

$$ (35)

$$ (36)

The variant rate of the three-axis moment of inertia caused by the variable span is difficult to calculate accurately, so it is regarded as an uncertainty in the Eq. (36).

By the combination of Eq. (26), (29), and (34), an IGC model for hypersonic variable span missiles with terminal angular constraints can be obtained as

$$ (37)

In Eq. (37), w₀, w₁, and w₂ are bounded function vectors for uncertain positions. Let us assume that there is a set of unknown constants e_i that satisfies [7]

$$ (38)

The method of solved x₁ by $$ will be introduced in Section 2.2.

3.2. The IGC Method in the Dive Phase with Variable Span Control

The IGC model in the dive phase guidance control with terminal angular constraint is shown in Eq. (37). The adaptive dynamic surface back-stepping control method is designed to make the system stable and make the output as close as possible to zero and make the system have strong robustness for uncertain factors.

3.2.1. Design of the Adaptive Dynamic Surface Back-Stepping IGC Method

To design an adaptive dynamic surface back-stepping control method, Eq. (37) is required to nonsingular [23] as

$$ (39)

Therefore, let us assume to make g₁ nonsingularity as

$$ (40)

in the whole dive phase. And Ω is the bounded closed set in $$, so Ω is a tight set.

The design steps of the adaptive dynamic surface back-stepping IGC method are as follows [6].

Step 1. Design the dynamic surface [5]

$$ (41)

where k_F is the angular error coefficient, of which the magnitude determines the weight of the terminal angular error in the dynamic surface.

The rate of change of the dynamic surface s₀ is designed according to the exponential approach law.

$$ (42)

where k₀₁ and k₀₂ are positive gain constants, ε₀₁ andε₀₂ are the gain-of-saturation function, and d₀₁ and d₀₂ are the boundary layer thickness. sat(s, d) is a saturation function which defined as [7]

$$ (43)

When the missile is far from the target point and r is large, the rate of approaching law in (42) will be slow so that the missile has a small overload in the initial stage. When the missile approaches the target point and r is small, the rate of approaching law in (42) increases so that $$ does not diverge to improve the accuracy of hitting. The selection of the saturation function can effectively eliminate the chattering of the first virtual control variable.

Deriving the dynamic surface s₀ and then combining (42) can get the first virtual control input x_1v as

$$ (44)

In Eq. (44), the result of deriving the terminal angle is

$$ (45)

In Eq. (44), k₀ = diag(k₀₁, k₀₂), ε₀ = diag(ε₀₁, ε₀₂), and $$.

According to $$, it can be translated as

$$ (46)

According to the aerodynamic model of the variable span missile, the structural form of the lift coefficient caused by the attack angle is

$$ (47)

It can be solved as

$$ (48)

In Eq. (48), take α_v as the main factor affecting for lift, and $$ is the previous moment attack angle.

Then,

$$ (49)

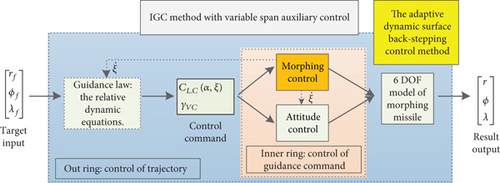
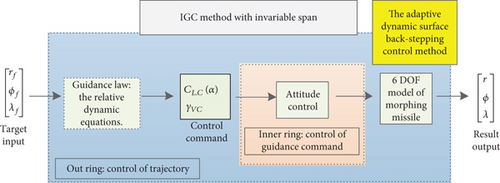
In order to exert the advantage of the variable span hypersonic missile, the morphing rate and attack angle of the wing are coordinated controls. The roadmap of the IGC method for a hypersonic morphing missile based on variable span auxiliary control is shown in Figure 4, while the IGC method with invariable span is shown in Figure 5.

The principle of coordinated control shown in Figure 4 is to translate the change of the lift coefficient into a change of the attack angle and the morphing rate, so that the span variant can withstand the change demand of the lift command and reduce the change demand of the attack angle control. While in the traditional IGC method with invariable span, the change demand of the lift command is only reached by the attack angle. It would improve the stability and velocity of missile IGC mission. That is,

$$ (50)

Solve Eq. (50) to get

$$ (51)

In Eq. (51), take α_v as the main factor affecting for lift; $$ is the previous moment value of each variable.

According to the model of the aerodynamic coefficient of the missile,

$$ (52)

where $$ is the coefficient matrix of $$ with respect to the morphing rate, and the expression is

$$ (53)

Let us substitute Eq. (53) into (3.35) and deriving on both sides to get

$$ (54)

Combining Eq. (51) and Eq. (54), the variation law of the morphing rate can be obtained as

$$ (55)

In order to prevent differential explosion, it will pass through the first-order filter as

$$ (56)

Step 2. Design the dynamic surface

$$ (57)

where $$, x_1d is the output value of the following first-order filter as

$$ (58)

where τ₁ = diag(τ₁₁, 0, τ₁₃) is the time constant of the filter.

Design the second virtual control input as

$$ (59)

where $$, k₁ = diag(k₁₁, k₁₂, k₁₃), and $$ is an estimate of the upper bound e₁ of the uncertainty w₁, which can be obtained by the following adaptive law

$$ (60)

where υ₁ and μ₁ are positive constants.

Step 3. Design the dynamic surface

$$ (61)

Similarly, x_2d is the output value of the following first-order filter as

$$ (62)

where τ₂ = diag(τ₂₁, τ₂₂, τ₂₃) is the time constant of the filter. The control input of the system is designed as

$$ (63)

where k₂ = diag(k₂₁, k₂₂, k₂₃) and $$ is an estimate of the upper bound e₂ of the uncertainty w₂, which can be obtained by the following adaptive law as

$$ (64)

where υ₂ and μ₂ are positive constants.

In summary, the adaptive dynamic surface back-stepping IGC method for variable span control of the system (3.20) can be expressed as

$$ (65)

3.2.2. Stability Analysis

The stability of the closed-loop system obtained using the control law in Eq. (65) is analyzed below.

Define the filter error b₁ and b₂, respectively, as

$$ (66)

Then, the derivative of the filtering error is

$$ (67)

Assuming $$, according to the assumption in Section 3.2.1, ‖B_i‖ is a tight set, then it has an upper bound as [7]

$$ (68)

We define the upper bound estimation error of the norm as [7]

$$ (69)

Then, its derivative is

$$ (70)

Substituting the parameter adaptive law (60) and Eq. (64) into Eq. (70) yields

$$ (71)

$$ can be defined as

$$ (72)

The derivative of s₀ is

$$ (73)

Substituting Eq. (44) into Eq. (73) yields

$$ (74)

The derivative of s₁ is

$$ (75)

Substituting Eq. (59) into Eq. (75) yields

$$ (76)

The derivative of s₂ is

$$ (77)

Now the expression of the control input u can be obtained by substituting Eq. (77) into Eq. (63) as

$$ (78)

In summary, the entire closed-loop system with the control law can be composed of the dynamic surface vector, the filtered error vector, and the upper bound estimation error of the uncertainty as

$$ (79)

The Lyapunov function is defined as

$$ (80)

where $$, $$, and $$.

The derivatives of the Lyapunov function (80) with respect to time are

$$ (81)

$$ (82)

$$ (83)

$$ (84)

$$ (85)

According to Young’s inequality, we can get [23]

$$ (86)

Since k_i, i = 0, 1, 2 is a diagonal matrix, the following inequality is established.

$$ (87)

where k_imin is the minimum value of the diagonal elements in each gain matrix k_i. Since the uncertainty w₀ satisfies the following inequality,

$$ (88)

e₀ is a positive constant. So, the following inequality is established [7]:

$$ (89)

and

$$ (90)

The follow inequality existed as

$$ (91)

if

$$ (92)

Then,

$$ (93)

Then

$$ (94)

Substituting Eq. (91) into Eq. (94) yields

$$ (95)

Substituting Eq. (91) into Eq. (95) yields

$$ (96)

Combining Eq. (90) with Eq. (96) yields

$$ (97)

Combining Eq. (89) and Eq. (97) yields

$$ (98)

Combining (88) and (90), the following inequalities are true:

$$ (99)

Substituting Eq. (86), Eq. (87), and (99) into Eq. (81) yields

$$ (100)

Then, using Young’s inequality again, we can get [7]

$$ (101)

and

$$ (102)

Substituting Eq. (87), Eq. (101), and Eq. (102) into Eq. (82) yields

$$ (103)

Considering that

$$ (104)

Substituting Eq. (87) and Eq. (104) into Eq. (83) yields

$$ (105)

Substituting Eq. (67) into Eq. (84) yields

$$ (106)

Substituting Eq. (71) into Eq. (85) yields

$$ (107)

The derivatives of the Lyapunov function like Eq. (100), (103), (105), (106), and (107) are summed to obtain [5]

$$ (108)

Let

$$ (109)

Then, c is a positive constant. Because ‖g₀‖ and ‖g₁‖ are a tight set, that is,

$$ (110)

Therefore, when parameter selection in the control law Eq. (65) and Eq. (92) satisfies the following inequalities:

$$ (111)

where γ is a positive constant. The derivatives of the Lyapunov function (80) with respect to time satisfies

$$ (112)

Then, the function satisfies the following inequality

$$ (113)

when

$$ (114)

$$ is negative. We select state variables as

$$ (115)

Then,

$$ (116)

That is, when $$, $$ was negative. For any given constant υ_i, i = 1, 2, as long as the selected element of k_i, i = 0, 1, 2 and μ_i, i = 1, 2 is large enough and the element of τ_i, i = 1, 2 is small enough, it can make γ large enough the same as $$ which is small enough, so that the final bounds of s₀, s₁, and s₂ are sufficiently small. So the boundaries of x_F, $$, $$, and β can be small enough. It indicates that the missile can eventually hit the target point at the required terminal angular and the side-slip angle remains near zero during the flight.

4. Simulation Analysis

4.1. Performance Analysis of IGC Method for a Variable Span Missile

In order to verify the effectiveness of the IGC method with a variable span auxiliary control in the dive phase of the hypersonic missile, the model is numerically simulated and the control group is set up to observe the effect of the IGC method under the condition of variable span and invariable span. The initial state is shown in Table 2.

Table 2. The initial state of the missile and the latitude and longitude of the target point.

Name	Value	Name	Value	Name	Value
v0 (m/s)	3000	α0 (°)	2	ϕ0 (°)	0
θ0 (°)	0	β0 (°)	0	ψ0 (°)	0
σ0 (°)	0	γV0 (°)	0	ϕT (°)	1
ωx0 ( o/s)	0	x (km)	0	ψT (°)	1
ωy0 ( °/s)	0	y (km)	30	ξ10	0.40
ωz0 ( ∘/s)	0	z (km)	0	ξ20	0.55
λF (°)	60

During the simulation process, it is necessary to control the amplitude and rate of change of the attack angle command and the rate of change of the bank angle command as follows.

$$ (117)

At the same time, the fin deflections of the missile are restricted as follows:

$$ (118)

The rate of change of the morphing rate of the wing is as follows.

$$ (119)

Firstly, the control parameters in Eq. (65) are optimized based on the genetic algorithm. The miss distance of the missile, the deviation of the terminal angular, the jitter of the attitude rates, and the jitter of fin deflections are optimized as fitness functions. The attitude rates and the jitter of the fin deflections can be expressed by the sum of the absolute values of their respective changes as

$$ (120)

where d_miss is the missile miss distance and t is the flight time of the missile in the dive phase. k_d, k_θ, k_ω, and k_δare the weight coefficients for measuring the miss distance, the error of the terminal angular, the jitter of rate of the angle, and the jitter of fin deflections. The initial population size is set to 60. After genetic optimization, the optimal controller parameters were obtained. The average fitness value changes with the genetic algebra as shown in Figures 6 and 7. The optimized parameter values are shown in Tables 2 and 3.

Table 3. Parameter optimization value of the IGC method for variable span missile.

Name	Value	Name	Value	Name	Value
k01	2.56	k11	10.12	k21	2.25
k02	0.51	k12	3.12	k22	2.78
ε01	0.62	k13	2.41	k23	5.32
ε02	0.33	τ11	0.71	τ21	0.44
d01	0.44	τ12	0.50	τ22	0.22
d02	0.27	υ1	50.11	τ23	1.3
kF	0.33	μ1	2.36	υ2	47.29
τξ	0.21			μ2	1.2

The simulation results are as follows.

Compare the simulation results obtained by the variable span missile with the invariable span missile as follows.

In Table 5, γ_D is the final terminal angular. V_t is the final velocity. T is the total flight time. Q_t is the final dynamic pressure. $$ are the average values of rolling, yawing, and pitching deflection angles, respectively.

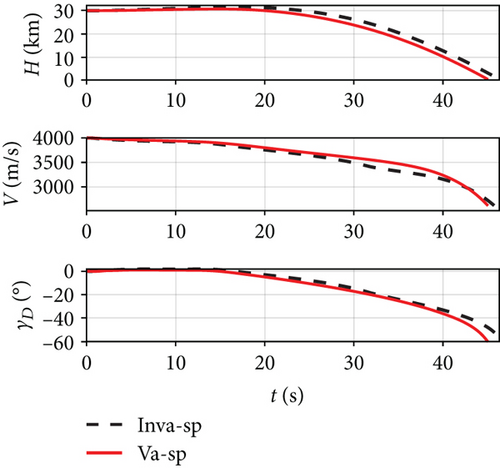
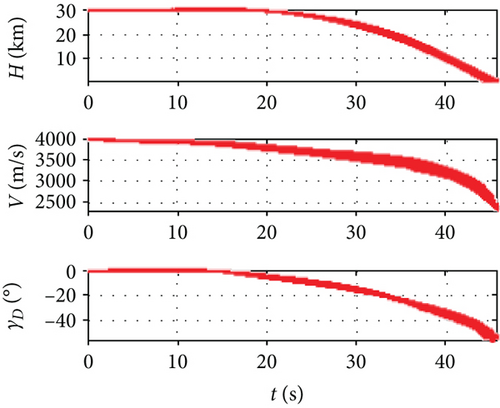
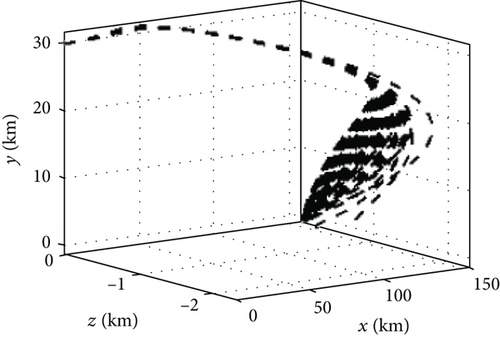
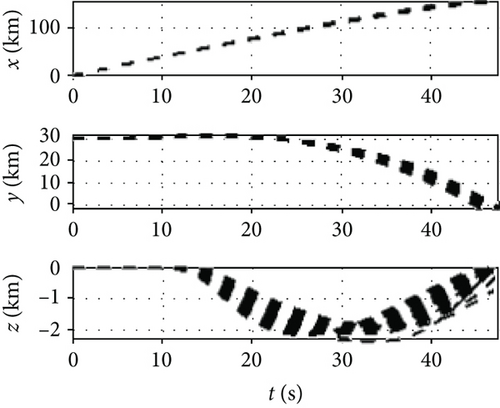
As shown in Figures 8 and 9, the IGC method designed by the adaptive dynamic surface method can well complete the falling point attack in the dive phase in the case of variable span and invariable span. The miss distance of the variable span missile is less than that of the variable span missile. In Figure 9, the total flight time and the lateral distance error of the trace of the variable span are less than those in the invariable span.

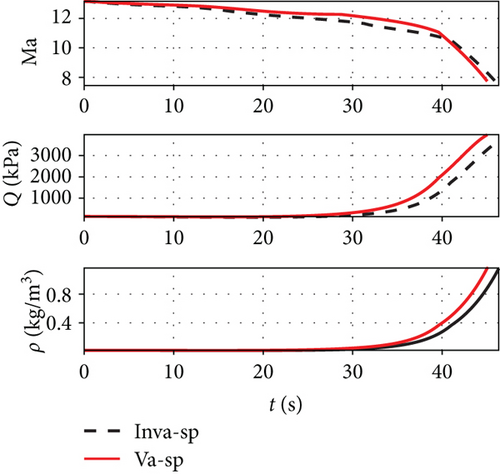
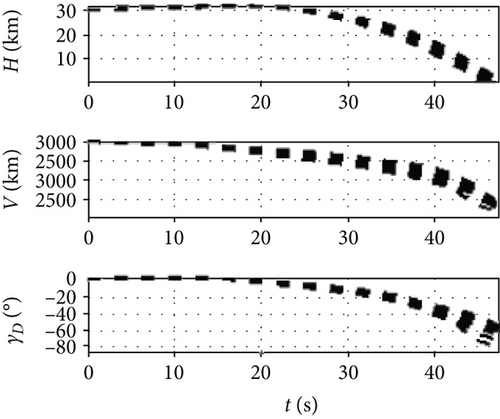
As shown in Figure 10, the trajectory height of the variable span in the dive phase is lower than that of the invariable span. The velocity and Mach number are larger than those of the invariable span. This is because the variable extension characteristic can adjust the lift-to-drag ratio of the missile, so that the resistance and velocity loss is smaller. At the same time, the terminal angular of the variable span missile is closer to the predetermined value than that of the invariable span missile which indicates that it is easier to realize the terminal angular constraint by the rapid change of lift due to the variable span. As shown in Figure 11, the final dynamic pressure of the variable span missile is much larger than that of the invariable span, which is caused by the difference in the final velocity. It demonstrates that the variable span characteristics are beneficial to achieving a fast and high-velocity attack in the dive phase and reduce the flight time.

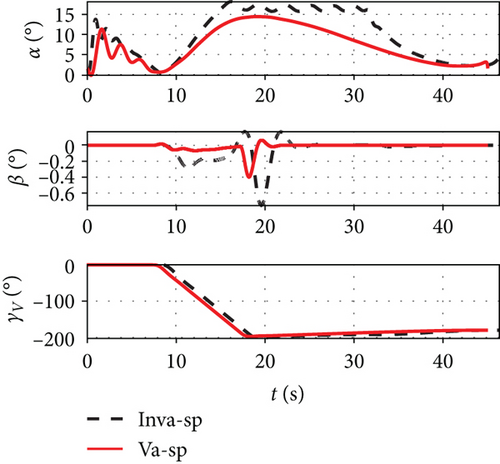
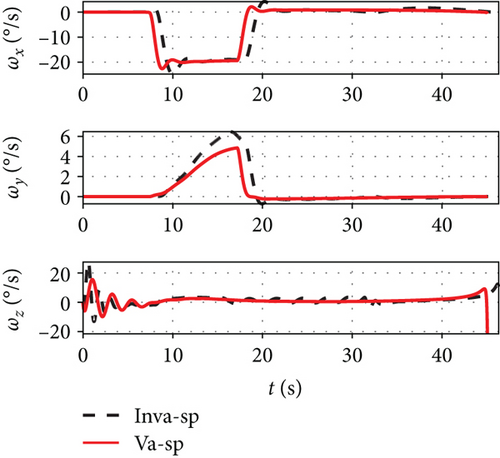
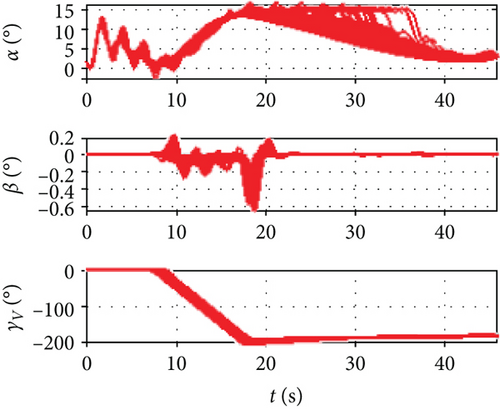
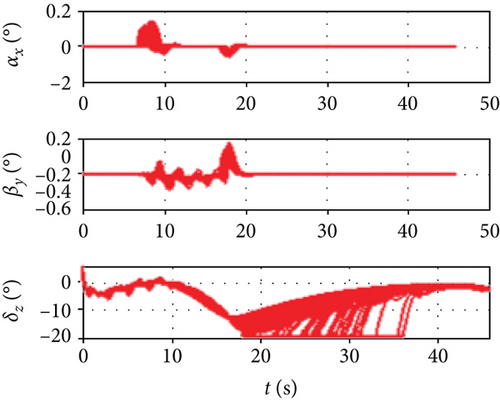
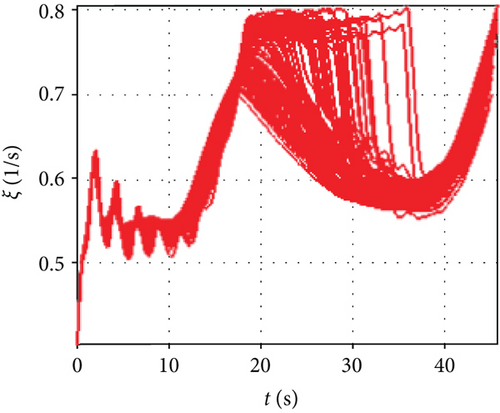
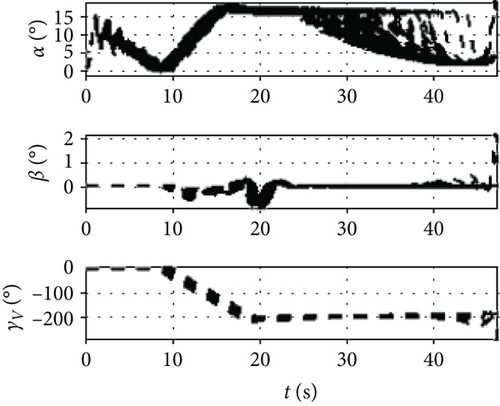
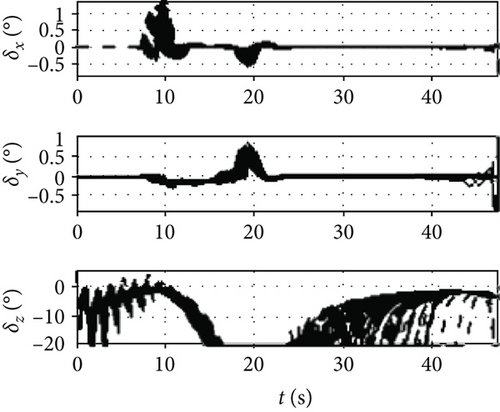
It can be seen from Figure 12 that the attack angle of the variable span in the dive phase is gentler than the invariant span and the total average value is smaller. Because the required change of the lift is performed by the change of span and attack angle, the change in the attack angle is gentler than the invariant span and the amplitude is also smaller. Because of the influence of the span variant on the aerodynamic coefficient, the changing amplitude of the side-slip angle under the variable span is smaller than the invariant span, while the changes in the bank angles of the two are more similar. It can be seen from Figure 13 that the rolling rate of the variable span has little difference from the invariable span while the yawing rate and the pitching rate have smaller amplitudes and smaller oscillation. As shown in Figure 14, the variation angle of the pitch fin deflections of the variable span is smaller than that of the invariant span which indicates that the variable span reduces the workload for the attitude control system. Figure 15 shows the morphing rate of the variable span missile in the dive phase. It can be seen that the variation of the span in the initial stage is more severe while in the middle and later stages the variation of the span is gentler, but the amplitude is increased. The combination of the change of span and attack angle achieves the change of lift request in the whole mission.

4.2. Robustness Analysis of the IGC Method for the Variable Span Missile

In order to verify the robust performance of the integrated guidance control method with variation of span, the influence of the aerodynamic coefficient uncertainty and the atmospheric density uncertainty of the system model is considered in the 6DOF simulation verification model. The distributions of the above uncertainties are as follows.

$$ (121)

where $$, $$, $$, $$, $$, $$, and $$ are, respectively, the nominal aerodynamic coefficient and atmospheric density. ν is the uncertainty parameter vector and satisfies

$$ (122)

The initial conditions and parameter settings are the same as those in Table 3 and Table 4. After 100 times of Monte Carlo simulation experiments, the results of the variable span missile are as follows.

Table 4. Parameter optimization value of the IGC method for the invariable span missile.

Name	Value	Name	Value	Name	Value
k01	3.22	k11	10.21	k21	2.14
k02	0.71	k12	2.14	k22	2.41
ε01	0.23	k13	1.75	k23	5.60
ε02	0.51	τ11	0.41	τ21	0.74
d01	0.13	τ12	0.56	τ22	0.44
d02	0.21	υ1	40.21	τ23	0.45
kF	0.35	μ1	0.75	υ2	75.30
				μ2	0.12

Table 5. Results of the adaptive dynamic surface IGC method.

Terms	Va_span	Inva_span
dmiss(m)	30.86	43.21
γD( ∘)	60.47	57.63
Vt(m/s)	2617	2518
T(s)	45.05	46.33
Qt(kPa)	3978	3660
$$	6.1843	9.9400
$$	0.1269	0.0880
$$	0.0605	0.0579

Table 6. Results of Monte Carlo simulation experiments.

Terms		Variable span	Invariable span
CEP (m)		51.31	77.20
dmiss(m)	μ	50.61	74.76
	σ	55.23	80.29
$$	μ	6.2196	9.9341
	σ	1.4145	1.4006
$$	μ	0.0344	0.0478
	σ	0.0056	0.0066
$$	μ	0.0370	0.0476
	σ	0.0076	0.0103

In Table 6, μ represents the mean value and σ represents the standard deviation. CEP in Table 6 is defined as the radius of the circle in which the center is the target point and the missile has a 50% probability of hitting the circle. The CEP could be calculated as follows.

$$ (123)

where σ_N and σ_E are the standard deviations of the north and east, respectively.

From Figures 16-25–26, it can be seen that the variable span missile can better meet the robust design requirements of the IGC method under the influence of the uncertainty. The side-slip angle is maintained in a small variation range in the dive phase and the attitude remains bounded which indicates that the designed IGC law can keep the state of the missile stable. In the case of variable span, the mean value of the miss distance is about 50.61 m, the standard deviation is about 55.23 m, and the CEP value is 51.31 m; these variables are smaller than the corresponding value of the invariable span. It indicates that the variable span missile has stronger robustness for the uncertainty aerodynamic caused by the aerodynamic coefficient and atmospheric density. The reason is that the change in the attack angle and span can better adjust the lift requested. In Figure 21, under the uncertainties, the change in morphing rate shows a large difference indicating that span variants can better offset the impact of uncertainties. The mean values of the pitching, yawing, and rolling fin deflections are 6.2196^∘, 0.0344^∘, and 0.0370^∘ with variable span which are less than those of the invariable span, respectively. It shows that fin deflection usage of the variable span is smaller than that of the invariant span, but the standard deviation of the two cases is similar.

5. Conclusion

In this paper, the IGC method for hypersonic variable span missiles under variable auxiliary control is studied. The physical model and deformation mode of the variable span missile are studied and the aerodynamic model is established by software. The aerodynamic model contains the influence of the morphing process on aerodynamics. In the case of fully considering the span variant of the wing, the motion model of the variable span missile is established which includes the influence of additional force and additional moment caused by the span variant. An IGC design model in the dive phase with terminal angular constraint is established. Based on the adaptive dynamic surface method, the IGC method is designed. At the same time, the stability of the system is proved by the Lyapunov theorem. By utilizing the variable span characteristics of the wing, the synergistic change of the span and the attack angle is completed to realize the control of the lift and achieve rapid and stable control of the centroid motion.

The parameters of the IGC method for span variant auxiliary control established above are optimized. The simulations of the variable span and invariable span are set for comparison. Results show that the adaptive dynamic surface method can well complete the motion mission of the dive phase of the hypersonic variable span missile. At the same time, the variable span missile has a smaller miss distance and flight time than the invariable span missile and the terminal angular is closer to the design value. The variations of the attack angle pitching fin deflection angle are smaller. The Monte Carlo simulation method is used to analyze the robustness of the IGC method for variable span missiles. Compared with the invariable span of the exhibition, the results show that the CEP of the variable span missile is less than that of the invariable span, which indicates that the robustness of the variable span missile is stronger than that of the invariable span missile.

In addition, in the study of the IGC method of hypersonic variable span missile, the accuracy of the hypersonic aerodynamic model needs more attention in the subsequent research.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Authors’ Contributions

Cunyu Bao and Peng Wang were contributed equally to this work.