1. Introduction

The hypersonic vehicle, typically traveling greater than Mach 5 in the near space, has developed rapidly in recent years, and their weaponization has accelerated. Compared with conventional missiles, hypersonic weapons show great advantages of diverse launching platforms, fast flight speed, and strong penetration capability. Aiming at time-sensitive and high-value targets, they pose severe challenges to the traditional antiaircraft or antimissile defense system. Hypersonic vehicles are going through intensive flight testing, for instance, the “Hypersonic Air-breathing Weapon Concept” and “Tactical Boost Glide” [1], the Russian “Zircon” hypersonic cruise missile [2], and the Chinese “DF-ZF” hypersonic glide vehicle [3, 4]. The defense system should be upgraded and prepared to meet the requirements of the future battlefield.

In order to eliminate the target in time, modern interceptors generally require the ability of beyond-visual-range air combat. Midcourse guidance is vital to the entire interception process. The purpose is to lead the interceptor to a desired position, where not only the target can be acquired but also a good initial angle is obtained for the terminal phase, thus to increase the interception rate. Midcourse guidances for intercepting conventional aviation targets or ballistic missiles are relatively mature. For example, concerning air-to-air missile, singular perturbation theory was applied to the derivation of near-optimal midcourse guidance in articles [5–7], but they did not consider the angle alignment constraints. Focusing on the optimal guidance problem with angular constraint, Indig et al. [8] proposed an analytic guidance law with a linear dynamic model, which would cause control saturation at the time of interception. Liu et al. [9] designed a biased proportional navigation guidance method with attitude constraint and line-of-sight angle rate control, but it mainly aimed at stationary ground target, not to mention the capability of energy management. Taking constant acceleration into consideration, Seo and Tahk [10] provided a closed-loop midcourse guidance law, but the terminal constraint can be fulfilled only under the assumption that the impact point was precisely predicted. To maximize the kill probability, Phillips and Drake [11] designed a two-tier approach for surface-to-air midcourse trajectory with an auxiliary constraint on an intersection approach angle. Three classes of midcourse guidance laws, namely, optimal fuel, optimal energy, and closed-loop explicit strategy, are proposed by Jalali-Naini and Pourtakdoust [12] with a zero-effort miss differential equation. Selecting different objectives and constraint functions, Reza and Abolghasem [13] solved an optimal interception problem with receding horizon control; commands are generated online by means of a differential flatness concept and nonlinear programming. Characterized by ultrafast speed and large-scale maneuverability, the requirements for hypersonic target interception become extremely strict, thus failing most of the existing midcourse guidance methods. New approaches must be found for these special targets, which can not only optimize trajectory online but also satisfy terminal-angle constraint.

To solve the real-time suboptimal problem with terminal constraints, Dwivedi et al. [14, 15] and Padhi and Kothari [16] put forward the model predictive static programming (MPSP) technique, which combines the “model predictive control” and “approximate dynamic programming” philosophies. With the qualities of accurate convergence and low computational cost, the MPSP technique has attracted extensive attention. Applying the MPSP algorithm, Oza and Padhi [17] presented a guidance law for air-to-ground missiles, which satisfies the constraint of terminal impact angle; superiority was demonstrated in comparison with augmented proportional navigation guidance and explicit linear optimal guidance. Halbe et al. [18] presented a robust suboptimal reentry guidance scheme for a reusable launch vehicle with the help of the MPSP algorithm. Apart from hard constraints of terminal conditions, soft constraints on path and control were also introduced through an innovative cost function, which consists of several components with various weighting factors. To solve the state variable inequality constraint, Bhitre and Padhi [19] converted the MPSP problem into an unconstrained but higher dimension one by means of a slack variable technique. Afterwards, the state constrained MPSP formulation was tested on an air-to-air engagement scenario. Considering the soft landing problem of a lunar craft during the powered descent phase, Sachan and Padhi [20] proposed a fuel optimal guidance law under the help of G-MPSP, where both terminal position and velocity were satisfied by adjusting the magnitude and angle of thrust. Bringing in sliding mode control, S. Li and X. Li [21] solved the divergence problem of the common MPSP algorithm caused by model inaccuracy; better robustness was proved when applied to maneuvering target interception. Moreover, Maity et al. [22, 23], Kumar et al. [24], and Guo et al. [25] also promoted the MPSP theory and applied it to the guidance design.

These aforementioned MPSP guidance laws in [15, 17] only lead the vehicle to a desired position defined by Y(X) and Z(X). However, when referring to a defense scenario, the optimal handover point changes with the maneuvering target, which requires additional prediction in every guidance cycle. In the process of midcourse guidance design for three-dimensional interception, the line-of-sight is not considered, which is vital to the flight trajectory and the startup of detection system. In addition, state-of-the-art guidance methods for intercepting hypersonic speed and large-scale maneuverable target are rarely researched to the best of the authors’ knowledge. To solve these problems, this paper adopts the line-of-sight coupled interception model and proposes a novel midcourse guidance method with the MPSP technique according to the characteristics of a specific target, which can optimize the interceptor’s trajectory and also meet the handover constraints.

The rest paper is organized as follows. In Section 2, the characteristics and technical requirements of midcourse guidance for hypersonic target interception are analyzed, and a three-dimensional interception model is established. In Section 3, suboptimal guidance law with constrained terminal line-of-sight or impact angle is derived utilizing the MPSP approach. The guidance scheme is validated in Section 4, considering a constant speed target and a typical boost-gliding target. Finally, the text is briefly summarized in Section 5.

2. Midcourse Guidance Problem

2.2. Coupled Line-of-Sight Dynamics

The kinematic relationship between the pursuer and evader in a three-dimensional space is shown in Figure 1, where M and T are centroids of the interceptor and target, respectively. MX₁Y₁Z₁ is the line-of-sight coordinate system. The axis MX₁ is aligned with the line-of-sight and points to target T. Staying in a vertical plane, the axis MY₁ is normal to MX₁ and points upward. The axis MZ₁ is defined by the right-hand rule and is normal to MX₁ and MY₁. AXYZ is the inertial reference coordinate system, and for clarity of illustration, its origin A is translated to coincide with the origin M. Hereafter, two Euler angles are introduced [30]. q_ε stands for the elevation line-of-sight, namely, the angle between the line-of-sight and horizontal plane ZAX. q_β is the azimuth line-of-sight, which acts on the horizontal plane with respect to reference direction AX. R represents the relative distance between the interceptor and target.

The unit vectors of the inertial reference coordinate AXYZ and the line-of-sight coordinate MX₁Y₁Z₁ are (i, j, k) and (i₁, j₁, k₁), respectively. Transformation from MX₁Y₁Z₁ to AXYZ can be done within two steps: clockwise rotate q_ε angle with respect to axis MZ₁ and then clockwise rotate q_β angle with respect to axis MY₁. In this way, we get

$$ (1)

where the transformation matrix is expressed as

$$ (2)

After then, the rotation angular velocity ω of the line-of-sight coordinate relative to the inertial reference coordinate is obtained by

$$ (3)

The range vector in the line-of-sight coordinate is R[R, 0, 0]^T. Applying the vector derivative method, the relative velocity between the interceptor and the target is given as

$$ (4)

Considering nonlinear point mass dynamics, the acceleration vectors of the interceptor and target on the line-of-sight coordinate system are denoted as $$ and $$, respectively. Applying the vector derivative method once again to relative velocity gives

$$ (5)

Substituting (3) and (4) to (5) and rearranging equations, the line-of-sight coupled 3D interception model is obtained:

$$ (6)

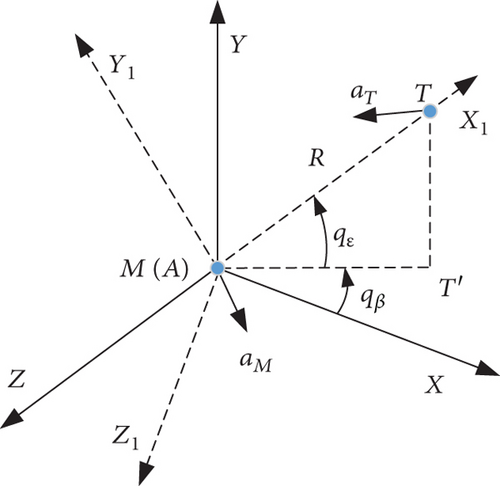
Generally, the thrust magnitude of the interceptor is designed previously according to the velocity characteristics, and the drag on the vehicle is closely related to its dynamic pressure. As a consequence, the term a_MR is difficult to be controlled during flight. In fact, like proportional navigation (PN) and most other guidance laws do, the control of a_MR is not necessary as long as $$. Thereby, the equation along the MX₁ direction can be ignored.

Defining the state variables x₁ = q_ε, $$, x₃ = q_β, and $$, the state transition equation for the line of sight and its rate can be written as

$$ (7)

The objective in the midcourse guidance design is to optimize the control history of a_Mε and a_Mβ, meanwhile satisfying the constraints in the guidance process and at the handover.

3. Angle Constrained MPSP Guidance

In this section, the suboptimal midcourse guidance law with a terminal-angle constraint is derived by means of the MPSP algorithm, in particular, the line-of-sight constrained MPSP guidance and the impact angle constrained MPSP guidance.

3.2. Impact Angle Constrained Guidance

As already mentioned in Section 2.1, the midcourse guidance with velocity angle alignment exhibits better handover properties if the target’s maneuver is somehow weak. However, only the line of sight and line-of-sight rate are involved while modeling the interception scenario. A solution can be found in [31], where the desired impact angle is able to be transferred into the final line-of-sight angle. For simplicity, the following process is done in the longitudinal plane and the lateral plane is similar.

The impact angle is defined as the angle between velocity vectors of the adversaries; particularly, we have

$$ (27)

where θ_imp is the impact angle in the longitudinal plane and θ_T and θ_M are the flight path angles of the target and interceptor, respectively. A perfect head-on interception scenario is formed by restricting θ_imp = π.

When the midcourse guidance comes to the end, the line-of-sight rate $$ has been driven to zero. The interceptor and target stay on an impact triangle geometry, as shown in Figure 2(a). Under this circumstance, the zero-effort miss can be guaranteed if both the interceptor and the target do not execute any further maneuvers from the instant time onward. Then, the relationship between the terminal line-of-sight angle and impact angle is given by

$$ (28)

where V_T and V_M are the velocities of the hypersonic target and interceptor, respectively, q stands for the line-of-sight in a 2D plane, and subscript f represents the final value in midcourse guidance.

Noting the target-to-missile speed ratio v = V_T/V_M, rearranging (28) yields

$$ (29)

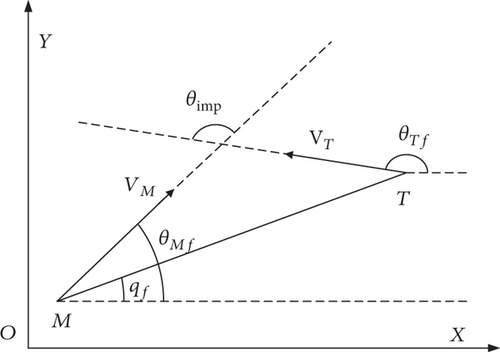
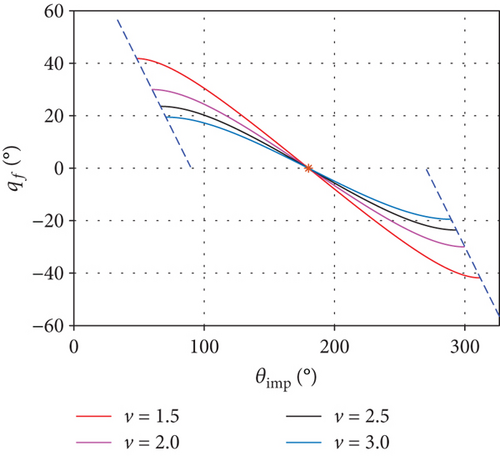
Different from the situation in [31], the interceptor no longer has velocity advantage, namely, v > 1; the singular problem is structurally avoided. One-to-one condition of q_f and θ_imp is further analyzed, in which a monotonous zone including head-on condition can be found. Considering an incoming target with θ_Tf = π, the relationship between q_f and θ_imp changes according to the speed ratio v, as shown in Figure 2(b). Since q_f is continuous, extreme points can be obtained by driving dq_f/dθ_imp = 0, which gives vcosθ_imp = 1. In conclusion, for any desired impact angle θ_imp ∈ (arccos(1/v), 2π − arccos(1/v)), a corresponding q_f can be calculated by (29).

Applying (29), the aforementioned line-of-sight constrained MPSP guidance is transferred into the impact angle constrained MPSP guidance, which actually constrains the final flight path angle for the interceptor in the midcourse phase. Note that the prediction of the target’s terminal flight path angle is required.

4. Simulation

Three different scenarios are presented to validate the effectiveness of the constrained MPSP midcourse guidance law. The first two scenarios refer to the cruising hypersonic target with a constant velocity in the longitudinal plane. Line-of-sight constrained and impact angle constrained midcourse guidance are applied, respectively; The last scenario considers the gliding target with a skipping trajectory in a three-dimensional space, and a full guidance scheme including midcourse is adopted.

4.2. Line-of-Sight Constrained Guidance

Interception confrontation scenario is presented to verify the proposed line-of-sight constrained MPSP midcourse guidance. The following conditions are set assuming the adversaries are in the longitudinal plane.

• (1)

  The initial position of the interceptor 0,17 km, the average velocity at 1200 m/s, 0° initial flight path angle, and 5 g maximum overload

• (2)

  The initial position of hypersonic target 400,35 km, the average velocity at 2400 m/s, 180.286° initial flight path angle, and without maneuver

• (3)

  Terminal handover distance is 60 km, simulation step of 20 ms, and the scheduled final line-of-sights are -5°, 0°, and 5°, respectively

• (4)

  Initial control guess utilizes the three-dimensional proportional guidance law

The results are shown in Table 1 and Figure 3.

Table 1. Convergence results of LOS constrained guidance.

		R(m)	qf( °)	$$	nyf(g)
qf = −5°	Default	60000	-5	0	-0.149
	Real	59960	-5.000	−5.908e − 5
qf = 0°	Default	60000	0	0	-0.052
	Real	59972	−8.377e − 6	−1.800e − 5
qf = 5°	Default	60000	5	0	-0.057
	Real	59940	5.000	−2.21e − 6

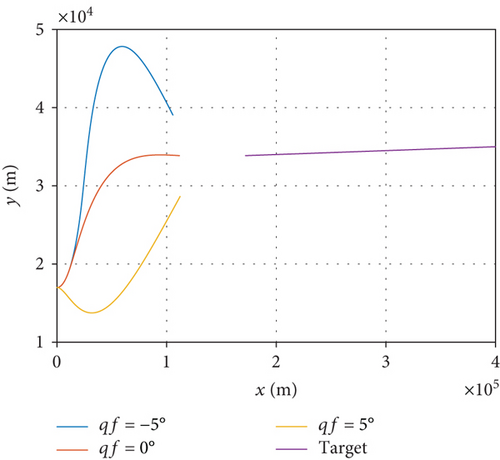
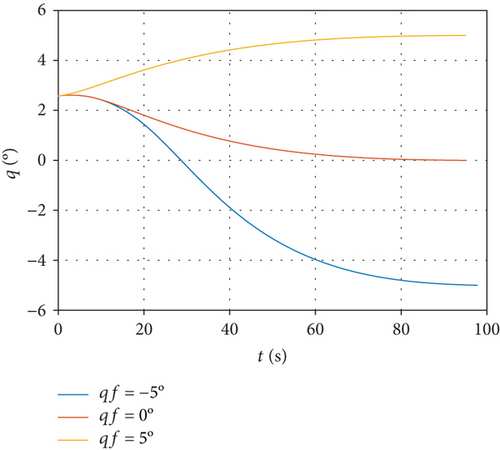
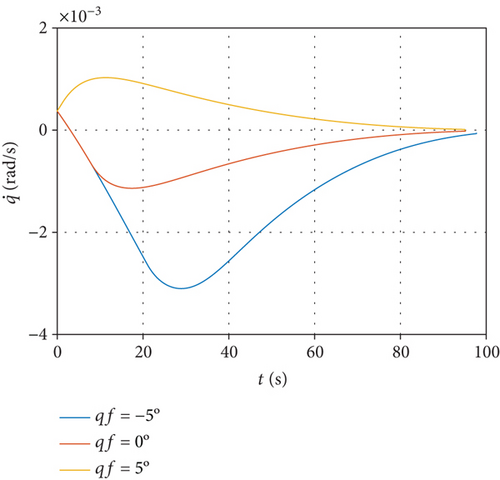
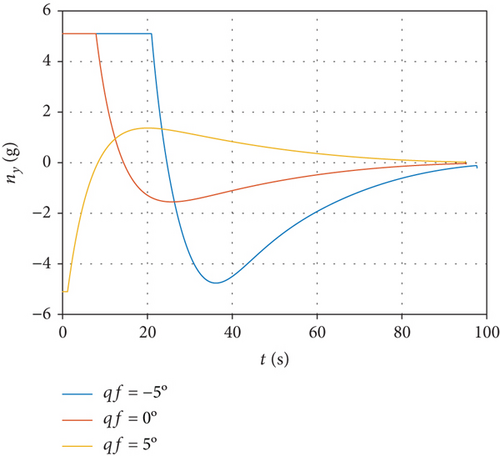
From Figure 3(a), we can see that the interceptor is able to reach the desired position under the command of the line-of-sight constrained MPSP guidance algorithm, right in the front of the hypersonic target. Figures 3(a) and 3(b) indicate that the terminal constraints of both line-of-sight and line-of-sight rate have been satisfied with high accuracy. In Figure 3(d), the overload command can gradually converge to zero, thus providing a favorable initial condition for the endgame interception.

4.3. Impact Angle Constrained Guidance

To validate the impact angle constrained MPSP midcourse guidance, the same simulation conditions are set as in Section 4.2, except that the required impact angles are 170°, 180°, and 190°, where 180° represents a typical head-on collision. The simulation results are shown in Table 2 and Figure 4.

Table 2. Convergence results of impact angle constrained guidance.

		R(m)	$$	θimp( °)	nyf(g)
θimp = 170°	Default	60000	0	170	0.015
	Real	59981	5.614e − 6	170.016
θimp = 180°	Default	60000	0	180	-0.051
	Real	59959	−1.465e − 5	179.958
θimp = 190°	Default	60000	0	190	-0.104
	Real	59945	−2.948e − 5	189.915

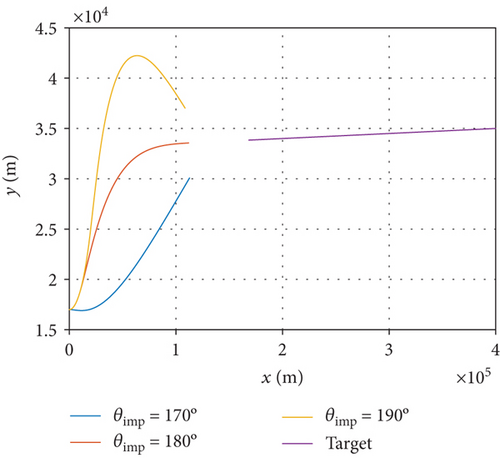
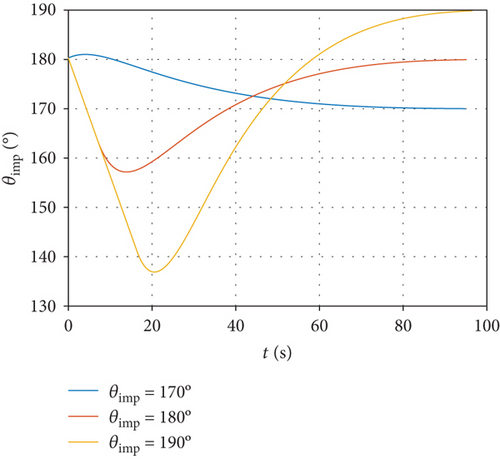
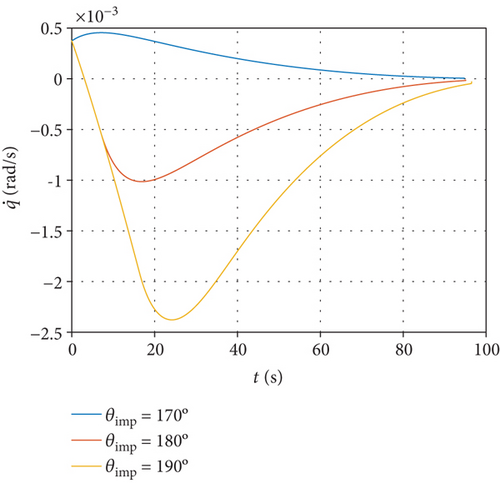
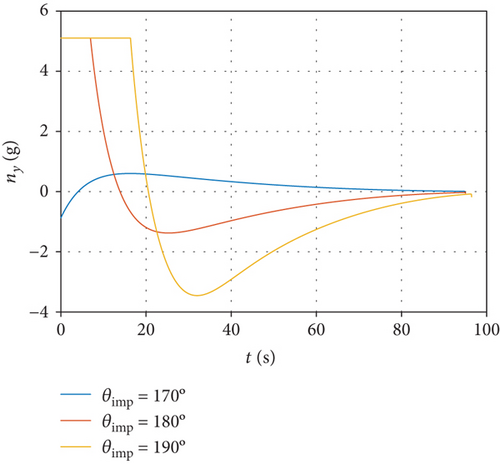
Similar conclusions can be made in contrast to the previous line-of-sight constrained MPSP guidance method. As shown in Figure 4(a), the interceptor is able to reach the desired position under the command of the impact angle constrained MPSP guidance algorithm. Figures 4(b) and 4(c) imply that the terminal constraints of both impact angle and line-of-sight rate have been satisfied. In Figure 4(d), the overload command gradually converges to zero and therefore provides a favorable initial condition for the endgame interception.

4.4. Full Trajectory Interception

To verify the effectiveness of full trajectory guidance scheme, parameters are set as follows:

• (1)

  Initial position of interceptor is 0,12,0 km, initial velocity is 360 m/s, and initial flight path angle and velocity azimuth angle are both 0°

• (2)

  The interceptor’s rocket works in two levels, the first level lasts 2 s and produces 30kN thrust, while the second level lasts 22 s and produces 8 kN thrust

• (3)

  The hypersonic target maintains pullup and pulldown gliding trajectory with an initial altitude of 60 km and speed of 5100 m/s

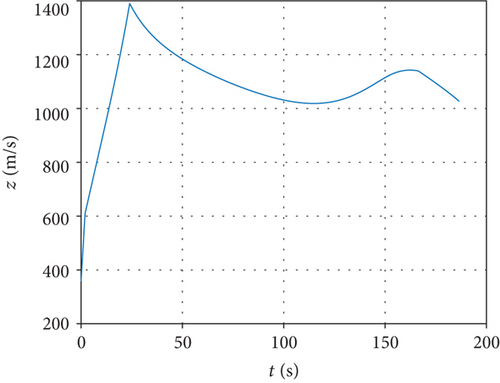
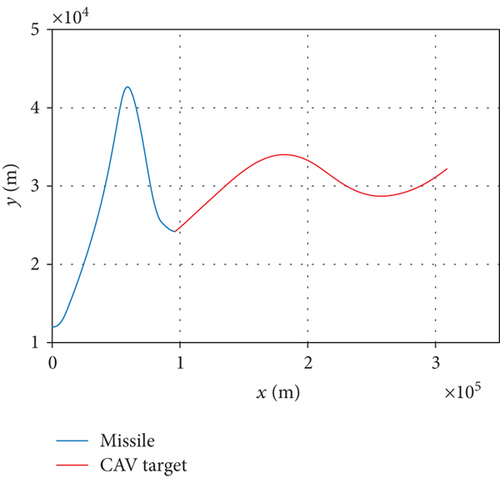
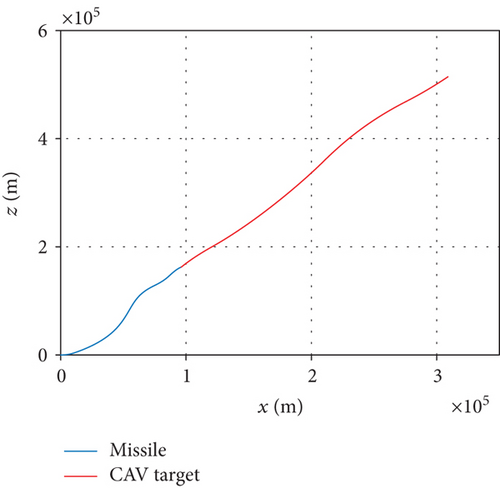
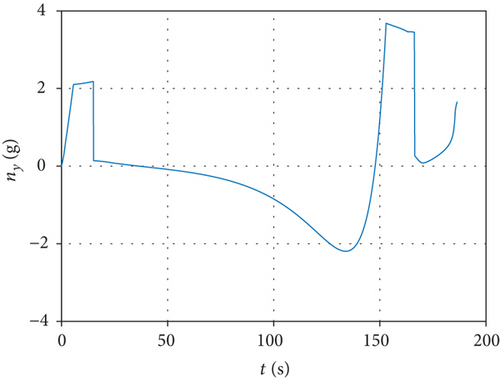
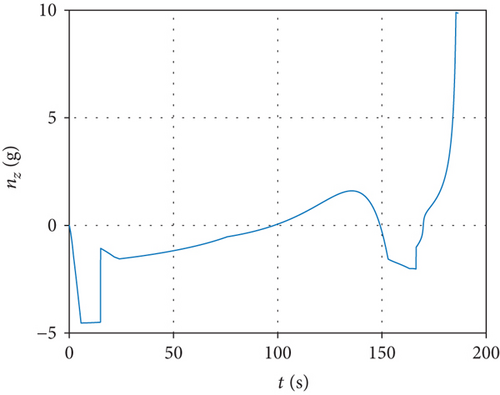
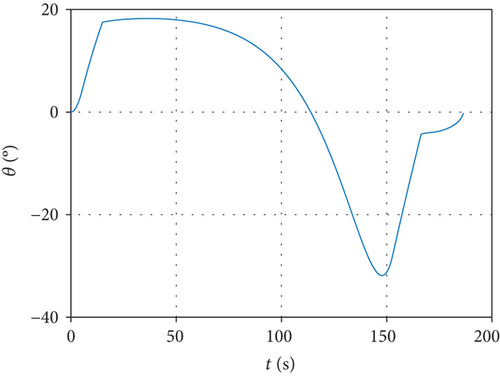
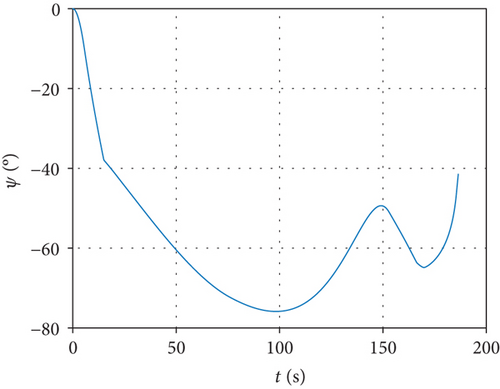
Assuming that the interceptor is released once the missile-target range meets the desired distance, simulation results are shown in Figure 5. From that, we can see the progress of the interceptor. After launching from an airborne platform, the interceptor climbs to upper air under trigonometric guidance. Until 15.00 s later, it turns to midcourse phase and keeps accelerating. A maximum speed of 1389.92 m/s is achieved when the rocket engine burns out at 24.00 s. The trajectory reaches a maximum altitude of 42.67 km after 113.36 s. Separation from booster rocket appears at 166.33 s when the handover range is reached and terminal guidance takes over. The final miss distance is 2.47 m after 186.44 s flight, which demonstrates the correctness of the proposed guidance strategy.

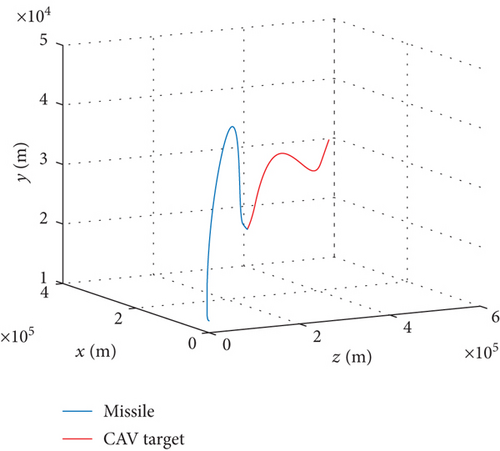
5. Conclusions

This paper proposes a novel midcourse guidance strategy for interceptors against near-space hypersonic targets. The characteristics of hypersonic weapon defense and the requirements of midcourse guidance design for interceptors are analyzed. The line-of-sight coupled interception model is established in a three dimensional space. Under the assumption that the closing velocity remains constant and the target maneuver is briefly negligible, a MPSP method-based suboptimal midcourse guidance law is derived for two different purposes that either satisfies the terminal line-of-sight angle constraint or satisfies the terminal impact angle constraint. Results indicate that the designed angle can be realized with maximum error less than 0°. In addition, the line-of-sight rate approaches zero at handover time, which implies that the final overload command can converge to a small value. In the interception of a hypersonic gliding target, the final miss distance turns out to be 2.47 m, which proves the effectiveness of this guidance law.

Conflicts of Interest

The authors declare that they have no conflicts of interest.