This article investigates a novel fuzzy-approximation-based nonaffine control strategy for a flexible air-breathing hypersonic vehicle (FHV). Firstly, the nonaffine models are decomposed into an altitude subsystem and a velocity subsystem, and the nonaffine dynamics of the subsystems are processed by using low-pass filters. For the unknown functions and uncertainties in each subsystem, fuzzy approximators are used to approximate the total uncertainties, and norm estimation approach is introduced to reduce the computational complexity of the algorithm. Aiming at the saturation problem of actuator, a saturation auxiliary system is designed to transform the original control problem with input constraints into a new control problem without input constraints. Finally, the superiority of the proposed method is verified by simulation.

1. Introduction

Air-breathing hypersonic vehicle (AHV) is a kind of high-velocity aircraft flying at more than 5 times the speed of sound and cruising at an altitude in the near space. With the increasing extension of human activities to space, high-velocity and high-altitude vehicles represented by air-breathing hypersonic vehicles will play an important role in the field of aerospace. The control system is the “nerve center” of an aircraft, and the design of the AHV control system has become one of the frontier issues in the field of control science [1].

Compared with traditional aircrafts, the flight environment of flexible air-breathing hypersonic vehicles is more complex, the flight envelope span is larger, and the aerodynamic characteristic change is more complex. These problems bring difficulties to the design of the FHV control system. At the same time, in the control theory, FHV has the characteristics of strong nonlinearity, strong coupling, fast time-varying, and uncertainty, which make FHV extremely sensitive to flight attitude in dynamic characteristics, and the design of the FHV control system is also subject to many constraints [2–4].

For the control of FHV, previous research has achieved fruitful results, for example, sliding mode variable structure control [5–8], neural network control [9–11], prescribed performance control [12–14], and fuzzy control [15, 16]. Hu et al. designed the FHV robust controller and the observers by means of sliding mode control in [6]. But in practical application, chattering problem exists in sliding mode control. In [7], the method of multimode switching between ordinary sliding surface and integral sliding surface is proposed to solve the chattering problem, but the switching between sliding surfaces is still relatively complex. In [8], Song et al. studied the double-loop sliding mode control method of HFV, unknown disturbances are observed by sliding mode observers, which enhanced the robustness of the control law. Bu et al. proposed an adaptive neural control method in [10]. The simulation results show that the control method can still guarantee the stable tracking of flight velocity and altitude to their respective reference inputs. In [11], the altitude subsystem of HFV is rewritten to a pure feedback form, and an adaptive neural control law is designed to ensure the realizability of the control law. By constructing the prescribed performance functions in [14], the velocity tracking error and altitude tracking error of FHV are guaranteed, and the prescribed transient performance and steady-state accuracy of the system are satisfied. In [16], unknown functions of FHV models are approximated online by using fuzzy systems, but the algorithm requires that the unknown functions be strictly positive and bounded. There are a lot of unknown functions in each subsystem, and computational costs are heavy.

Most of the above studies focus on the affine models of FHV, which require simplifying the nonaffine models of FHV to the complete affine forms of the control input under certain assumptions, and then conducting research [17]. However, in fact, many of the dynamic performances of FHV are nonlinear functions of rudder deflection, angle of attack, velocity, and altitude. Particularly in the hypersonic flight process of FHV, these nonaffine dynamic characteristics cannot be affine, so it is necessary to strengthen the study of nonaffine models of FHV. [18] designed a control law of FHV based on the Mean Value Theorem [19], which has achieved certain effects. In [20], for a class of high-order nonaffine nonlinear systems with completely unknown dynamics, Meng et al. developed a novel system transformation to transform the nonaffine system into an affine system. According to the idea expressed in [20, 21] combined the system transformation with prescribed performance control scheme, the simulation results verified the effectiveness of the method. In [22], the novel system transformation with a low-pass filter is applied to constrained systems.

Based on above research, a fuzzy-approximation-based novel back-stepping control scheme of FHV with nonaffine models is proposed in this article. The FHV’s nonaffine dynamics is decomposed into velocity subsystem and altitude subsystem to be controlled separately, and then nonaffine dynamics of FHV is processed by low-pass filters. A fuzzy approximator is introduced to approximate unknown function in each subsystem, and norm estimation approach [23] is introduced in the approximation of unknown functions. A novel back-stepping control method without virtual control law is designed. Considering the constraints of actuators, a new auxiliary system is designed to transform the control constraints into unconstrained ones. Finally, based on the simulation experiments, the performance of the control method is verified. The special contributions of this article are summarized as follows:

(1)
The traditional affine models need to simplify the nonaffine dynamics into fully affine forms. In this article, low-pass filters are used to solve the nonaffine dynamics of FHV
(2)
For each subsystem of FHV, only a fuzzy approximator is introduced to approximate the total uncertainties in the subsystem, which reduces the computational complexity of the system on the basis of ensuring the robustness of the controller. At the same time, the norm estimation approach is introduced in this article to ensure the computational speed compared with the previous fuzzy control method
(3)
Compared with the traditional back-stepping control method, all the virtual controllers proposed in this article are only used as intermediate variables for the stability analysis of the system and do not participate in the final solution and execution
(4)
An auxiliary system is introduced to transform the original control problem with input constraints into a new control problem without input constraints to solve the transient saturation problem in the control input

2. FHV Model and Preliminaries

2.1. FHV Model

Taking X-43A as the modeling objective, the longitudinal integration analytical model of FHV was established by Bolender and Doman [24]; Parker et al. ignored the weak coupling in the dynamic model and established the parameter fitting model of FHV [17].

(1)

(2)

(3)

(4)

(5)

(6)

(7)

where

(8)

where φ_f(∙) and φ_a(∙) are structural mode shapes; other variables and functions are given in [24].

The FHV models contain five rigid body states and two elastic modes. The five rigid body states are flight velocity V, flight altitude h, track angle γ, pitching angle θ, and pitch rate Q; η₁ and η₂ represent the two elastic modes of FHV; the distance between the vehicle and the earth’s center is expressed by r; m is the mass of FHV; moment of inertia is I_yy; define the flight angle of attack α = θ − γ. ς₁ and ς₂ represent the damping ratio, ω₁ and ω₂ represent the natural frequency for elastic modes, respectively; N₁ and N₂ are generalized forces; T, D, L, and M represent the thrust, resistance, lift, and pitching moment of FHV, respectively; where the approximations of T, D, L, M, N₁, and N₂ are designed as follows [17]:

(9)

with

(10)

The control inputs are fuel-air ratio Φ and elevator deflection angle δ_e; the average aerodynamic chord length of FHV is ; the reference area is S; represents the dynamic pressure of FHV; the air density at h is ρ; z_T is the coupling coefficient of thrust and moment; c_e represents rudder deflection coefficient; h₀ represents nominal altitude; the air density at nominal altitude is ρ₀; 1/h_s is the decay rate of air density.

Remark 1. In the following controller design, the rigid body states can be measured, and the elastic modes are usually regarded as the unknown dynamics, which are treated as the robustness of the controller [10, 25].

Remark 2. It can be seen from equation (10) that the FHV models are nonaffine for the control inputs, because the parameter fitting form of resistance D contains [17]. Therefore, in the subsequent control system design, based on the back-stepping control framework, in the case of uncertainties and nonaffine dynamics, fuzzy-approximation-based nonlinear tracking control laws Φ and δ_e are designed to achieve robust tracking of velocity and altitude commands V_ref and h_ref.

Remark 3. Because the fuel-air ratio Φ is related to thrust T, so the velocity V is mainly controlled by Φ. The elevator angle δ_e controls the change of altitude h by affecting the pitch rate Q, pitch angle θ, and track angle γ. Therefore, the FHV models can be decomposed into velocity subsystem (equation (1)) and altitude subsystem (equations (2)-(5)), and then the control laws are designed separately [26].

2.2. Theory of Fuzzy Approximation

In recent years, the universal approximation characteristics of the fuzzy system have been gradually discovered, proposed, and applied. Under sufficient rules of the fuzzy system, the fuzzy system can approximate the given nonlinear continuous function with arbitrary precision [27, 28]. The complete fuzzy system includes inference engine, knowledge base, fuzzification interface, and defuzzification interface. Compared with neural network and polynomial function approximation, the advantage of the fuzzy system is that it can effectively control based on fuzzy logic. Where the input of the system

, the output is

(11)

In the fuzzy system,

represents the parameter vector of ideal weight coefficient, fuzzy basis function

. Fuzzy basis functions are expressed as

(12)

In equation (12), is the jth (j = 1, ⋯, N) fuzzy rule corresponding to the ith (i = 1, ⋯, n) input point, N is the number of fuzzy rules, is the membership function, . In this article, the Gauss basis function is chosen as the membership function.

Lemma 1 [27]. Suppose that the real continuous function F(X) is an arbitrary function defined on compact set Ω. For any μ > 0, the fuzzy system can be obtained, and the following conditions are guaranteed:

(13)

2.3. Saturation Auxiliary System

In order to maintain the normal working mode of scramjet and the physical constraint of FHV by deflection angle, the actuators of control inputs Φ and δ_e are limited to some extent. The saturation problem of control input is described as follows:

(14)

(15)

where Φ_c denotes the fuel-air ratio in the case of input saturation, δ_ec denotes the elevator deflection in the case of input saturation, Φ_min and Φ_max are the lower and upper bounds of Φ, and δ_emin and δ_emax are the lower and upper bounds of δ_e. In this article, a saturation auxiliary system is designed under the condition of input saturation. The input constraints of the control system are transformed into unconstrained ones.

When the inputs of the saturated auxiliary system are Φ and δ_e, the sigmoid functions are used to approximate the outputs Φ_c and δ_ec of the auxiliary system.

(16)

According to equation (16) and the characteristic of the sigmoid function, whether Φ and δ_e take any value, the saturation auxiliary system can make Φ_c and δ_ec meet the constraints of equation (15).

Remark 4. In the controller design, the original control objective can be converted to design unconstrained Φ and δ_e such that velocity Vand altitude h track their reference commands V_ref and h_ref.

2.4. Controller Design

In the following section, the altitude subsystem and velocity subsystem of the controller are designed with the new fuzzy-approximation-based control scheme in this article.

2.4.1. Controller Design of the Altitude Subsystem

In the altitude subsystem, we design an altitude controller based on nonaffine dynamics and a fuzzy approximator to achieve stable tracking of reference altitude h_ref.

Define altitude tracking error

, the reference command of γ is chosen as

(17)

where k_h,1 ∈ R⁺ and k_h,2 ∈ R⁺ are design parameters.

If the design parameters k_h,1 > 0, k_h,1 > 0 and γ → γ_d, then can be regulated to zero exponentially [29]. In this way, the control objective of the altitude subsystem can be transformed to γ → γ_d by designing the appropriate control law δ_e.

According to the idea expressed in [20, 21], we define a set of newly state variables; the control input δ_e is also viewed as the newly defined state to deal with the nonaffine features. Define new state variables

(18)

Original nonaffine systems (3)-(5) can be rewritten to the following equivalent general nonaffine form according to equation (18).

(19)

where Ж₁(ψ_h,1, ψ_h,2) and Ж₃(ψ_h,1, ψ_h,2, ψ_h,3, ψ_h,4) are continuous differentiable nonlinear functions; u_h is an introduced variable, and it is regarded as the virtual control input of (19); the control inputs δ_e are generated by a low-pass filter “

” driven by u_h. “

” is input-to-state stable. y_h is the output of (19); τ_h ∈ R⁺is the design parameter.

From equations (3)-(5) together with previous studies [17], we have

(20)

Next, transform the nonaffine models.

Define υ₁ = ψ_h,1 = γ,

, combined with equation (19), the time derivative of υ₂⁠ is derived as

(21)

It can be noted that

(22)

We further define

. Taking time derivative of υ₃ and substituting (19)

(23)

Finally, define

. Invoking (19), the time derivative of υ₄ is derived as

(24)

where

(25)

Through model transformation, the nonaffine system (19) can be converted into affine form.

(26)

The fuzzy-approximation-based altitude subsystem controller is designed by using the transformed affine form.

Remark 5. According to the theory of input-to-state stability, when the input is bounded, the state of the system is also bounded. So we need to prove the boundedness of u_h.

Theorem 1. If the control inputs u_h are bounded, there must be fixed values u_hM, such that

(27)

Proof. Define the Lyapunov function

(28)

Taking time derivative along (28).

(29)

If τ_h > 1/2, ψ_h,4 will ultimately converge to the compact , where . That is, ψ_h,4 is bounded and the low-pass filter “” is stable when u_h is bounded.

Define tracking error e_h,1 as

(30)

Taking time derivative along (30) and employing (26), it leads to

(31)

Define intermediate variable υ_2d as

(32)

where λ_h,1 ∈ R⁺ is the design parameter.

Then, define tracking error e_h,2 as

(33)

Applying (26), the time derivative of e_h,2 is derived as

(34)

Define a new intermediate state variable υ_3d as

(35)

where λ_h,2 ∈ R⁺ is the design parameter.

Define tracking error e_h,3 as

(36)

Differentiating along (36) with respect to time and applying (26), we get

(37)

Then, the intermediate variable υ_4d is designed as

(38)

where λ_h,3 ∈ R⁺ is the design parameter.

Finally, define tracking error e_h,4 as

(39)

Taking the time derivative of e_h,4 and invoking (26) lead to

(40)

Define unknown function F_h as

(41)

where

. Since the function F_h is an unknown function, the fuzzy function approximator designed in the above part is used to approximate it. The estimated value

of the nonlinear function F_h can be expressed as

(42)

where

is the input vector to the unknown function, fuzzy basis function

is the ideal weight coefficient parameter vector, and the unknown function F_V can be expressed as

(43)

where μ_h represents the estimated error, and |μ_h| ≤ μ_hM; μ_hM is the upper bound of the estimated error.

Finally, the control law is devised as

(44)

where λ_h,4 ∈ R⁺ is the design parameter.

denotes the estimation of

; its adaptive law is selected as

(45)

where l₁ ∈ R⁺ is the design parameter.

Substitute equation (32) into equation (33) to obtain

(46)

Taking time derivative along (46),

(47)

By combining equations (26) and (35), equation (36) can be obtained.

(48)

Substituting equations (46) and (47) into equation (48), it yields

(49)

Taking time derivative along (49), we obtain

(50)

Substituting (26) and (38) into (39), e_h,4 is formulated as

(51)

Combining equations (46), (49), and (50), we can obtain

(52)

Substituting (49) and (52) into (44) leads to

(53)

Remark 6. Unlike the back-stepping control method proposed by Bu et al. [30], the presented altitude controller is exploited using an improved back-stepping framework, in which the virtual controller is transformed into intermediate variables and only the final actual control laws are needed to be implemented, which avoids repeated calculation and greatly reduces the computational pressure of the system.

Remark 7. Compared with the method in [16, 31, 32], each weight update requires a lot of calculation. In this article, only one online learning parameter is needed by using the norm estimation approach, which makes the online calculation of the system significantly reduced.

Theorem 2. Considering the closed-loop subsystem consisting of plant (26), with controller (53), and adaptive law (45). Then all the signals involved are semiglobally uniformly ultimately bounded.

Proof. Consider the following Lyapunov function:

(54)

with

Applying (31), (34), (37), (40), (41), and (45), is derived as

(55)

Considering (32), (35), and (38), becomes

(56)

Substituting (44) into (56) yields, we can get

(57)

From the fact that

(58)

we obtain

(59)

Thereby, equation (57) becomes

(60)

In this article, since , and applying (12), we know that 0 ≤ ξ_j(X) ≤ 1. There exists a constant, such that . Hence, we get

(61)

Then, (60) becomes

(62)

Let , , λ_h,2 > 0, λ_h,3 > 0, and l₁ > 0. And define the following compact sets

(63)

If or or or or , will be negative. It is clear that e_h,1, e_h,4, e_h,2, e_h,3 and are semiglobally uniformly ultimately bounded. This completes the proof.

2.5. Controller Design of Velocity Subsystem

For the velocity subsystem, its tracking target is to achieve the stable tracking of velocity V to reference velocity V_ref.

Define new state variables ψ_V,1 = V and ψ_V,2 = Φ. In order to ensure the control effect, the velocity subsystem should be changed into an equivalent general nonaffine form with ψ_V,1 and ψ_V,2.

(64)

where the transformation consists of a low-pass filter “

” and 2 newly defined state variables. Γ(ψ_V,1, ψ_V,2) is an unknown continuous differentiable nonlinear function, u_V is the input of (64), and y_V is the output of (64); τ_V ∈ R⁺ is the design parameter.

Then, define state variables ε₁ and ε₂. Where ε₁ = y_V,

, we can get

(65)

Where nonlinear continuous functions Y_V(ψ_V,1, ψ_V,2) and К_V are expressed as

(66)

Remark 8. Noting that α ∈ [−8.7rad, 8.7rad, ] × 10⁻²α ∈ [−8.7 rad, 8.7 rad] × 10⁻², so we can get the definitions of α² and α³ as α² ∈ [0 rad², 7.57 rad²] × 10⁻³ and α³ ∈ [−6.5850 rad³, 6.5850 rad³] × 10⁻⁴, respectively. And we can calculate that К_V > 0.

According to the above analysis, we can express the nonaffine model in the form of the affine model, as shown in equation (67).

(67)

Next, we need to prove the boundedness of u_V.

Theorem 3. If the control input u_V is bounded, there must be a fixed value u_VM, such that

(68)

Proof. Construct the Lyapunov function

(69)

Taking time derivative along (69)

(70)

If τ_V > (1/2), ψ_V,2 will ultimately converge to the compact . Where . As a result, the boundedness of u_h leads to the newly introduced system “” which is stable.

Define tracking error e_V,1 as

(71)

Taking time derivative along (71) and employing (67), it leads to

(72)

Define intermediate variable ε_2d as

(73)

where λ_V,1 ∈ R⁺ is the design parameter.

Define tracking error e_V,2 as

(74)

Utilizing (67) and (73), the time derivative of e_V,2 is derived as

(75)

where

. Since the function F_V is an unknown function, the fuzzy function approximator is used to approximate it. The estimated value

of the nonlinear function F_V can be expressed as

(76)

is the input vector of the unknown function; is the parameter vector of ideal weight coefficient, fuzzy basis function . The unknown function F_V can be expressed as

(77)

where μ_V stands for estimation error, |μ_V| ≤ μ_VM; μ_VM represents the upper bound of estimation error.

The velocity control law is designed as

(78)

where

, and its adaptive law is chosen to be

(79)

where l₂ ∈ R⁺ is the design parameter.

Substituting equations (67) and (73) into equation (74), we can obtain

(80)

Substitute equation (80) into equation (78) to get

(81)

Theorem 4. Considering the closed-loop subsystem consisting of plant (67), with controller (81) and adaptive law (79). Then, all the signals involved are semiglobally uniformly ultimately bounded.

Proof. Consider the following Lyapunov function candidate:

(82)

with

Applying (73), (74) into (72), is expressed as

(83)

Considering (75), (77), and (79), becomes

(84)

To simplify equation (84) and substituting (78) into (84) yields, we can get

(85)

From the fact that

(86)

we obtain

(87)

Thereby, equation (85) becomes

(88)

In this article, since, and applying (12), we know that 0 ≤ ξ_j(X) ≤ 1.There exists a constant, such that . Hence, we get

(89)

Then, (88) becomes

(90)

Let , , l₂ > 0. And define the following compact sets:

(91)

If or or , will be negative. Thus, e_V,1, e_V,2, and are semiglobally uniformly ultimately bounded. This is the end of the proof.

3. Simulation Results

To verify the effectiveness of the new control strategy proposed in this article, the proposed controller is tested in the simulation adopting the nonlinear models (1)-(7) implemented in MATLAB/SIMULINKs. The simulation step size is fixed, the step size is 0.01 s, and the simulation period is 100 s. The initial trim conditions of the FHV are shown in Table 1. The velocity step ΔV = 100 m/s, altitude step Δh = 200. Both the velocity and altitude reference inputs are given by a second-order reference model with a damping ratio of 0.95 and a natural frequency of 0.03rad/s. All the aerodynamic coefficients and parameters are the same as [17, 23].

Table 1. Initial trim conditions.

Item	Value	Units
V	2500	m/s
h	27000	m
γ	0	deg
θ	1.5295	deg
Q	0	deg/s
η₁	0.2857	—
η₂	0.2857	—

Design parameters are chosen as k_h,1 = 2, k_h,2 = 0.8, τ_h = 75, λ_h,1 = 45, λ_h,2 = 45, λ_h,3 = 53, λ_h,4 = 53, l₁ = 0.05, τ_V = 15, λ_V,1 = 10, λ_V,2 = 2, and l₂ = 0.05. In order to verify the robustness of the system, it is assumed that the aerodynamic coefficients of the FHV models have a perturbation of ±40%.

(92)

where C is the value of uncertain coefficient; C₀⁠ denotes the nominal value of C.

The fuzzy function approximators choose the Gauss basis functions as the membership functions, set the fuzzy set of each variable to 100. The input vectors are , . Where the fuzzy centers i_V, i_γ, i_θ, i_Q, i_Φ and i_δe of each fuzzy set are uniformly distributed on [2500 m, 2800 m], [−1.1^°, +1.1^°], [0^°, 11.5^°], [−5.7^°/s, +5.7^°/s], [0, 2], and [−23^°, +23^°], respectively. The membership functions of the above variables are shown in Table 2. To show the superiority of the proposed method, we do the simulation study compared with recent research methods of others. The following two different cases are considered.

Case 1. The method proposed in this paper (controller 1) is compared with the novel back-stepping control method (controller 2) in [33] without adding the saturation auxiliary system.

Table 2. Membership functions of variables.

V	γ	θ	Q	Φ	δ_e

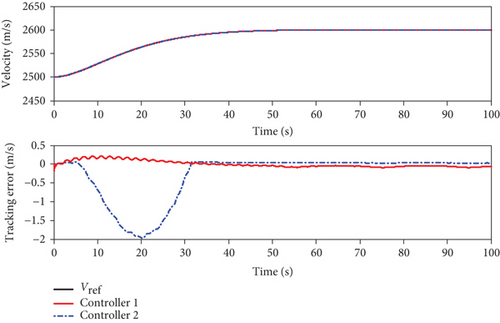
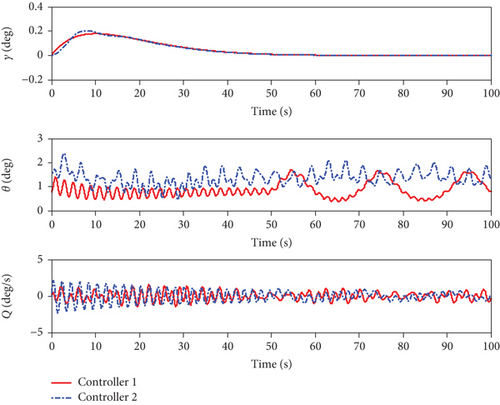
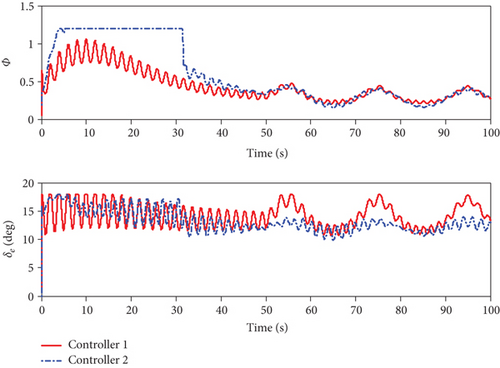
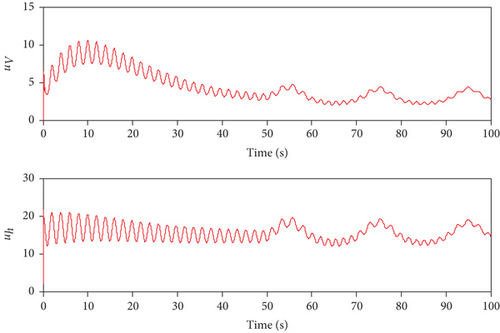
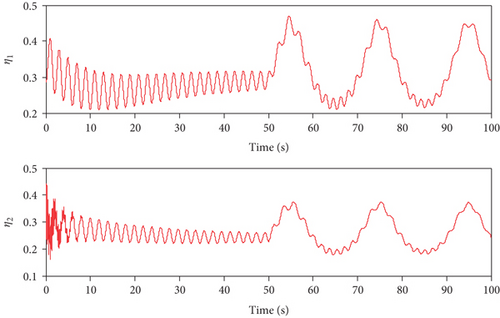
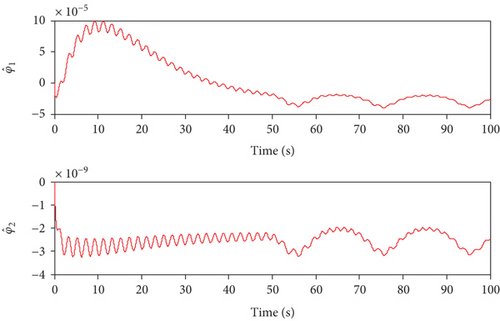
The obtained simulation results are shown in Figures 1–7. As can be seen from Figures 1 and 2, both of the two methods can achieve the desired tracking effects, but the tracking accuracy of controller 1 is higher than that of controller 2 in both altitude tracking effects and velocity tracking effects. According to Figure 3, the attitude angle changes of the two methods are roughly the same, but the change amplitude of controller 1 is less than that of controller 2. Figure 4 shows that the trend of Φ and δ_e are similar, the lines are relatively smooth, there is no high-frequency chattering phenomenon, and the amplitude of controller 1 is small. Figure 5 shows that u_V and u_h⁠ are bounded. Finally, variation curves of flexible states and the estimations of φ₁ and φ₂ are presented in Figures 6 and 7.

Case 2. Assuming that the actuators are subject to theoretical constraints: Φ ∈ [0.05,1.2], δ_e ∈ [−18^°, 18^°]. The closed-loop system simulation of FHV is carried out by using the method presented in this paper (controller 1) and the method of adaptive neural control with nonaffine dynamics (controller 2) in [34].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Altitude tracking performance.

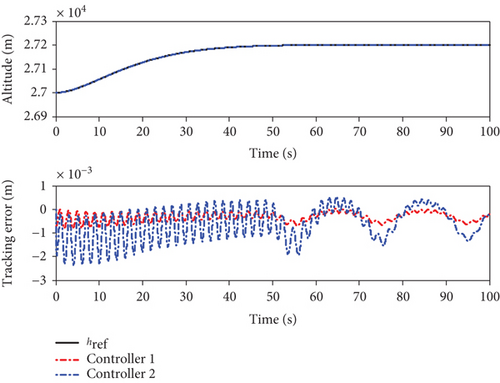
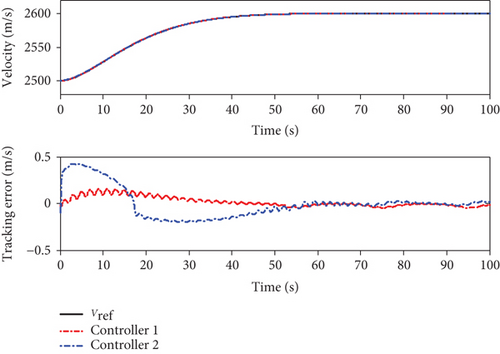
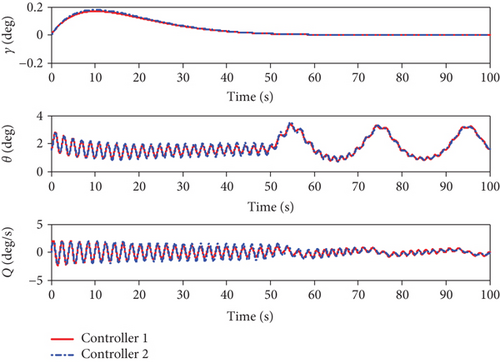
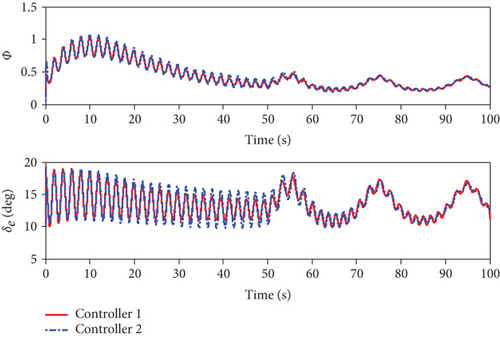
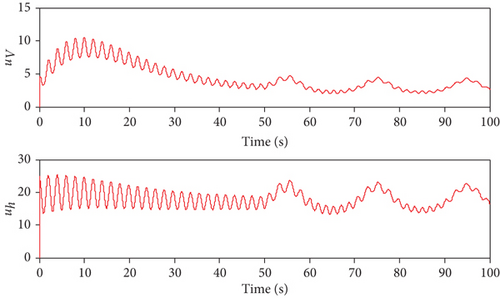
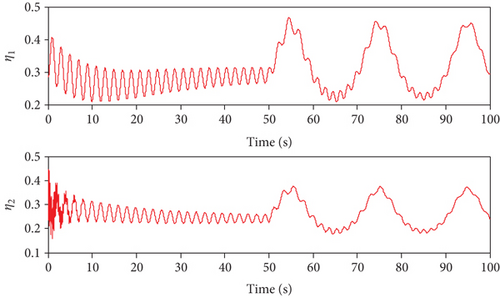
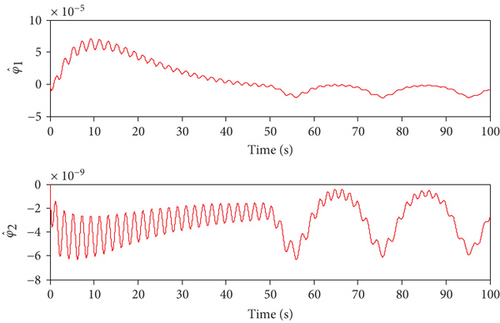
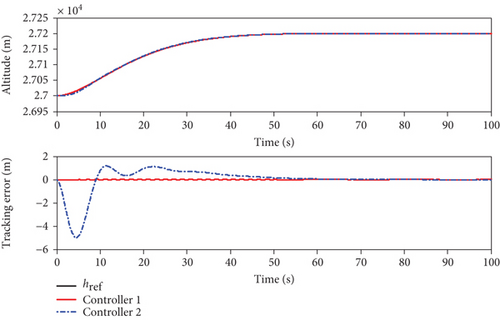
When the actuators are constrained, the simulation results using the two methods are shown in Figures 8–14. From Figures 8 and 9, it can be seen that both two methods can achieve stable tracking of reference altitude and velocity, but the altitude tracking error and velocity tracking error in controller 2 are relatively large, the maximum altitude tracking error is more than 4 m, and the maximum velocity tracking error is close to 2 m/s. At the same time, it can be seen from Figure 10 that the attitude angle changes of controller 1 are obviously smoother than that of controller 2. In Figure 11, although controller 2 can maintain the robustness of the system, the actuators are saturated for a long time. When controller 1 is saturated, it can also rely on the auxiliary system to maintain the stability of the system. In Figure 12, u_V and u_h⁠ are bounded. Variation curves of flexible states and the estimations of φ₁ and φ₂ are presented in Figures 13 and 14. To sum up, in both cases, the superiority of the proposed method can be demonstrated.

4. Conclusions

(1)
In this paper, a fuzzy-approximation-based novel back-stepping control method is proposed. The method does not need virtual control laws, but only needs a final actual control law, and the control algorithm is more simplified
(2)
For each subsystem of FHV, only a fuzzy approximator is needed to approximate the total uncertainties in the subsystem. Meanwhile, the norm estimation approach is introduced to directly estimate the norm of the weight vector in the fuzzy approximator, instead of the element itself, which reduces the computational complexity of the control algorithm and guarantees the real-time performance of the algorithm
(3)
The control method in this paper is based on nonaffine models and uses low-pass filters to deal with nonaffine dynamics, avoiding the loss of dynamic characteristics in affine models
(4)
The saturation problem of actuators in nonaffine models is discussed. By designing an auxiliary system, the original control problem with input constraints is transformed into a new control problem without input constraints
(5)
In two cases, the simulation results are compared with the recent methods to verify the advantages of the proposed method

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Acknowledgments

This work was supported by the Aeronautical Science Foundation of China (Grant No. 20175896023) and the National Natural Science Foundation of China (Grant Nos. 61603410, 61703424).

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Ouzts P., Soloway D., Moerder D., Wolpert D., and Benavides J., The role of guidance, navigation, and control in hypersonic vehicle multidisciplinary design and optimization, 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, October 2009, Bremen, Germany, https://doi.org/10.2514/6.2009-7329.
10.2514/6.2009-7329
Google Scholar
2 Korad A. S., Modeling, analysis, and control of a hypersonic vehicle with significant aero-thermo-elastic-propulsion interactions, and propulsive uncertainty, 2010, Arizona State University.
Google Scholar
3 Progress in control approaches for hypersonic vehicle, Science China Technological Sciences. (2012) 55, no. 10, 2965–2970, https://doi.org/10.1007/s11431-012-5036-x, 2-s2.0-84870371971.
10.1007/s11431-012-5036-x
Web of Science® Google Scholar
4 Xu B. and Shi Z., An overview on flight dynamics and control approaches for hypersonic vehicles, Science China Information Sciences. (2015) 58, no. 7, 1–19, https://doi.org/10.1007/s11432-014-5273-7, 2-s2.0-84933680171.
10.1007/s11432-015-5486-4
Web of Science® Google Scholar
5 Bu X., Wu X., Tian M., Huang J., Zhang R., and Ma Z., High-order tracking differentiator based adaptive neural control of a flexible air-breathing hypersonic vehicle subject to actuators constraints, ISA Transactions. (2015) 58, 237–247, https://doi.org/10.1016/j.isatra.2015.06.004, 2-s2.0-84943587471, 26142218.
10.1016/j.isatra.2015.06.004
PubMed Web of Science® Google Scholar
6 Hu X., Wu L., Hu C., and Gao H., Adaptive sliding mode tracking control for a flexible air-breathing hypersonic vehicle, Journal of the Franklin Institute. (2012) 349, no. 2, 559–577, https://doi.org/10.1016/j.jfranklin.2011.08.007, 2-s2.0-84856433471.
10.1016/j.jfranklin.2011.08.007
Web of Science® Google Scholar
7 Lai Z., Liu X., and Chen Z., Multi-mode time-varying sliding mode control of piezoceramic actuator based on inverse compensation, Electric Machines and Control. (2012) 16, no. 1, 92–96.
Google Scholar
8 Song C., Zhao G., and Chen J., Dual-loop sliding mode control for hypersonic aircraft with robust sliding mode observer, Journal of Solid Rocket Technology. (2012) 35, no. 4, 438–441.
Google Scholar
9 Xu B., Shi Z., Yang C., and Wang S., Neural control of hypersonic flight vehicle model via time-scale decomposition with throttle setting constraint, Nonlinear Dynamics. (2013) 73, no. 3, 1849–1861, https://doi.org/10.1007/s11071-013-0908-6, 2-s2.0-84880923540.
10.1007/s11071-013-0908-6
Web of Science® Google Scholar
10 Bu X., Wu X., Ma Z., and Zhang R., Novel adaptive neural control of flexible air-breathing hypersonic vehicles based on sliding mode differentiator, Chinese Journal of Aeronautics. (2015) 28, no. 4, 1209–1216, https://doi.org/10.1016/j.cja.2015.06.010, 2-s2.0-84938744637.
10.1016/j.cja.2015.06.010
Web of Science® Google Scholar
11 Xu B., Gao D., and Wang S., Adaptive neural control based on HGO for hypersonic flight vehicles, Science China Information Sciences. (2011) 54, no. 3, 511–520, https://doi.org/10.1007/s11432-011-4189-8, 2-s2.0-79952411343.
10.1007/s11432-011-4189-8
Web of Science® Google Scholar
12 Yang Q. and Chen M., Adaptive neural prescribed performance tracking control for near space vehicles with input nonlinearity, Neurocomputing. (2016) 174, 780–789, https://doi.org/10.1016/j.neucom.2015.09.099, 2-s2.0-84949681805.
10.1016/j.neucom.2015.09.099
Web of Science® Google Scholar
13 Wang Y. and Hu J., Improved prescribed performance control for air-breathing hypersonic vehicles with unknown deadzone input nonlinearity, ISA Transactions. (2018) 79, 95–107, https://doi.org/10.1016/j.isatra.2018.05.008, 2-s2.0-85047184639.
10.1016/j.isatra.2018.05.008
PubMed Web of Science® Google Scholar
14 Li Y., Wang C., and Hu Q., Adaptive control with prescribed tracking performance for hypersonic flight vehicles in the presence of unknown elevator faults, International Journal of Control. (2017) 1–10, https://doi.org/10.1080/00207179.2017.1406152, 2-s2.0-85036608298.
10.1080/00207179.2017.1406152
Google Scholar
15 Wang Y., Jiang C., and Wu Q., Attitude tracking control for variable structure near space vehicles based on switched nonlinear systems, Chinese Journal of Aeronautics. (2013) 26, no. 1, 186–193, https://doi.org/10.1016/j.cja.2012.12.009, 2-s2.0-84875211895.
10.1016/j.cja.2012.12.009
CAS Web of Science® Google Scholar
16 Gao D., Sun Z., and Luo X., Fuzzy adaptive control for hypersonic vehicle via backstepping method, Control Theory & Applications. (2008) 25, no. 5, 805–810.
Google Scholar
17 Parker J. T., Serrani A., Yurkovich S., Bolender M. A., and Doman D. B., Control-oriented modeling of an air-breathing hypersonic vehicle, Journal of Guidance, Control, and Dynamics. (2007) 30, no. 3, 856–869, https://doi.org/10.2514/1.27830, 2-s2.0-34249784843.
10.2514/1.27830
Web of Science® Google Scholar
18 Bu X., Wang Q., Zhao Y., and He G., Concise neural nonaffine control of air-breathing hypersonic vehicles subject to parametric uncertainties, International Journal of Aerospace Engineering. (2017) 2017, 16, 1374932, https://doi.org/10.1155/2017/1374932, 2-s2.0-85031932784.
10.1155/2017/1374932
Web of Science® Google Scholar
19 Du H. and Chen X., NN-based output feedback adaptive variable structure control for a class of non-affine nonlinear systems: a nonseparation principle design, Neurocomputing. (2009) 72, no. 7-9, 2009–2016, https://doi.org/10.1016/j.neucom.2008.12.015, 2-s2.0-61849179647.
10.1016/j.neucom.2008.12.015
Web of Science® Google Scholar
20 Meng W., Yang Q., Jagannathan S., and Sun Y., Adaptive neural control of high-order uncertain nonaffine systems: a transformation to affine systems approach, Automatica. (2014) 50, no. 5, 1473–1480, https://doi.org/10.1016/j.automatica.2014.03.013, 2-s2.0-84899992347.
10.1016/j.automatica.2014.03.013
Web of Science® Google Scholar
21 Bu X. and Wang Q., Neural network–based nonaffine control of air-breathing hypersonic vehicles with prescribed performance, International Journal of Advanced Robotic Systems. (2018) 15, no. 1, https://doi.org/10.1177/1729881418755246, 2-s2.0-85041410573.
10.1177/1729881418755246
Web of Science® Google Scholar
22 Meng W., Yang Q., Si J., and Sun Y., Adaptive neural control of a class of output-constrained nonaffine systems, IEEE Transactions on Cybernetics. (2016) 46, no. 1, 85–95, https://doi.org/10.1109/TCYB.2015.2394797, 2-s2.0-84960405079, 25667363.
10.1109/TCYB.2015.2394797
PubMed Web of Science® Google Scholar
23 Wang C. and Lin Y., Multivariable adaptive backstepping control: a norm estimation approach, IEEE Transactions on Automatic Control. (2012) 57, no. 4, 989–995, https://doi.org/10.1109/TAC.2011.2167815, 2-s2.0-84859731449.
10.1109/TAC.2011.2167815
Web of Science® Google Scholar
24 Bolender M. A. and Doman D. B., Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle, Journal of Spacecraft and Rockets. (2012) 44, no. 2, 374–387, https://doi.org/10.2514/1.23370, 2-s2.0-34248368556.
10.2514/1.23370
Google Scholar
25 Wilcox Z. D., MacKunis W., Bhat S., Lind R., and Dixon W. E., Lyapunov-based exponential tracking control of a hypersonic aircraft with aerothermoelastic effects, Journal of Guidance, Control, and Dynamics. (2010) 33, no. 4, 1213–1224, https://doi.org/10.2514/1.46785, 2-s2.0-77956359121.
10.2514/1.46785
Web of Science® Google Scholar
26 Fiorentini L. and Serrani A., Adaptive restricted trajectory tracking for a non-minimum phase hypersonic vehicle model, Automatica. (2012) 48, no. 7, 1248–1261, https://doi.org/10.1016/j.automatica.2012.04.006, 2-s2.0-84862871949.
10.1016/j.automatica.2012.04.006
Web of Science® Google Scholar
27 Wang L.-X. and Mendel J. M., Fuzzy basis functions, universal approximation, and orthogonal least-squares learning, IEEE Transactions on Neural Networks. (1992) 3, no. 5, 807–814, https://doi.org/10.1109/72.159070, 2-s2.0-0026928374, 18276480.
10.1109/72.159070
CAS PubMed Web of Science® Google Scholar
28 Wang L.-X., Stable adaptive fuzzy control of nonlinear systems, IEEE Transactions on Fuzzy Systems. (1993) 1, no. 2, 146–155, https://doi.org/10.1109/91.227383, 2-s2.0-0027591320.
10.1109/91.227383
Google Scholar
29 Zong Q., Wang F., Tian B., and Su R., Robust adaptive dynamic surface control design for a flexible air-breathing hypersonic vehicle with input constraints and uncertainty, Nonlinear Dynamics. (2014) 78, no. 1, 289–315, https://doi.org/10.1007/s11071-014-1440-z, 2-s2.0-84919877572.
10.1007/s11071-014-1440-z
Web of Science® Google Scholar
30 Bu X., Wu X., Zhang R., Ma Z., and Huang J., Tracking differentiator design for the robust backstepping control of a flexible air-breathing hypersonic vehicle, Journal of the Franklin Institute. (2015) 352, no. 4, 1739–1765, https://doi.org/10.1016/j.jfranklin.2015.01.014, 2-s2.0-84933279375.
10.1016/j.jfranklin.2015.01.014
Web of Science® Google Scholar
31 Chang Y., Jiang T., and Pu Z., Adaptive control of hypersonic vehicles based on characteristic models with fuzzy neural network estimators, Aerospace Science and Technology. (2017) 68, 475–485, https://doi.org/10.1016/j.ast.2017.05.043, 2-s2.0-85020892001.
10.1016/j.ast.2017.05.043
Web of Science® Google Scholar
32 Hu C., Zhou X., Sun B., Liu W., and Zong Q., Nussbaum-based fuzzy adaptive nonlinear fault-tolerant control for hypersonic vehicles with diverse actuator faults, Aerospace Science and Technology. (2017) 71, 432–440, https://doi.org/10.1016/j.ast.2017.10.002, 2-s2.0-85031019155.
10.1016/j.ast.2017.10.002
Web of Science® Google Scholar
33 Bu X., Wu X., Zhang R., Ma Z., and Huang J., A neural approximation-based novel back-stepping control scheme for air-breathing hypersonic vehicles with uncertain parameters, Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering. (2016) 230, no. 3, 231–243, https://doi.org/10.1177/0959651815622329, 2-s2.0-84958969503.
10.1177/0959651815622329
Web of Science® Google Scholar
34 Luo C., Lei H., Zhang D., and Zou X., Adaptive neural control of hypersonic vehicles with actuator constraints, International Journal of Aerospace Engineering. (2018) 2018, 15, 1284753, https://doi.org/10.1155/2018/1284753, 2-s2.0-85059101356.
10.1155/2018/1284753
Web of Science® Google Scholar

Citing Literature

All articles

Fuzzy-Approximation-Based Novel Back-Stepping Control of Flexible Air-Breathing Hypersonic Vehicles with Nonaffine Models

Abstract

1. Introduction

2. FHV Model and Preliminaries

2.1. FHV Model

2.2. Theory of Fuzzy Approximation

2.3. Saturation Auxiliary System

2.4. Controller Design

2.4.1. Controller Design of the Altitude Subsystem

2.5. Controller Design of Velocity Subsystem

3. Simulation Results

4. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Fuzzy-Approximation-Based Novel Back-Stepping Control of Flexible Air-Breathing Hypersonic Vehicles with Nonaffine Models

Abstract

1. Introduction

2. FHV Model and Preliminaries

2.1. FHV Model

2.2. Theory of Fuzzy Approximation

2.3. Saturation Auxiliary System

2.4. Controller Design

2.4.1. Controller Design of the Altitude Subsystem

2.5. Controller Design of Velocity Subsystem

3. Simulation Results

4. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information