Shock and Vibration
Volume 2019, Issue 1 2097164
Research Article
Open Access

Time-Delayed Feedback Tristable Stochastic Resonance Weak Fault Diagnosis Method and Its Application

Zhixing Li, 

Zhixing Li

School of Mechanical Engineering, University of Science & Technology Inner Mongolia, Baotou, China imust.cn

Search for more papers by this author
Songjiu Han, 

Songjiu Han

School of Mechanical Engineering, University of Science & Technology Inner Mongolia, Baotou, China imust.cn

Search for more papers by this author
Jianguo Wang, 

Corresponding Author

Jianguo Wang

School of Mechanical Engineering, University of Science & Technology Inner Mongolia, Baotou, China imust.cn

Search for more papers by this author
Xueping Ren, 

Xueping Ren

School of Mechanical Engineering, University of Science & Technology Inner Mongolia, Baotou, China imust.cn

Search for more papers by this author
Chao Zhang, 

Chao Zhang

School of Mechanical Engineering, University of Science & Technology Inner Mongolia, Baotou, China imust.cn

Search for more papers by this author
First published: 2019
https://doi.org/10.1155/2019/2097164
Citations: 6
Academic Editor: Stefano Marchesiello

Abstract

Pulses caused by rotating mechanical faults are weak and often submerged in strong background noise, which can affect the accuracy of fault detection. To solve this problem, we study the stochastic resonance phenomenon of a tristable potential system based on strong noise background and also investigate the influence of time-delayed feedback on this stochastic resonance model. The effects of time-delayed feedback strength on potential energy, steady-state probability density function, and signal-to-noise ratio (SNR) are discussed. The results show that stochastic resonance can be enhanced or suppressed by adjusting the delay time and feedback strength. Combined with bearing fault diagnosis simulation research and experimental verification evaluation, the proposed time-delayed feedback tristable stochastic resonance fault diagnosis method is more effective than the classical stochastic resonance method.

1. Introduction

In the early fault diagnosis of rotating machinery, the fault signal is often weak, and the working environment is mostly in the background of strong noise [1–3]. For example, in the early fault diagnosis of rolling bearings, the fault vibration signal itself is very weak, and it can easily be submerged in the surrounding noise, which causes interference in the identification of fault features [4]. Therefore, how to detect and extract weak fault signals from a background of strong noise is especially important for fault diagnosis of rotating machinery.

To solve the above problems, scholars have done considerable research on noise filtering and improvement of the signal-to-noise ratio (SNR) of useful signals and have proposed various methods. Traditional signal processing methods include wavelet analysis [5, 6], empirical mode decomposition [7, 8], Hilbert transform [9, 10], and singular value decomposition [11, 12]. Because noise plays a negative role in most cases, traditional methods mostly focus on filtering out noise. However, early fault signals tend to be weak, so filtering of useful signals can easily occur in the process of filtering out noise, which is very unfavorable to the detection results [13, 14]. In fact, noise is not harmful in all cases, and sometimes, it can enhance the strength of the useful signal, which is conducive to signal extraction and detection. For example, the ensemble empirical mode decomposition method adds a moderate amount of noise to each empirical mode decomposition to obtain multiple intrinsic mode functions and performs a lumped average for all intrinsic mode functions [15, 16]. Finally, the chaotic phenomenon of traditional empirical mode decomposition is solved, and the participation noise is reduced to a very low level [17]. The stochastic resonance used in this paper is another way to detect weak fault signals using noise. Stochastic resonance is the introduction of noise and periodic signals in nonlinear systems. With the aid of noise, the amplitude and power of the weak signal increase, and the particles transition in the potential well, enabling the detection of weak signals. Stochastic resonance was first proposed by Benzi et al. [18] and used in ancient meteorological problems and then used by scholars in various fields of research. In the field of fault diagnosis, early stochastic resonance research is mainly aimed at overcoming the small-parameter limitation problem. In other words, according to approximate adiabatic theory, the classical stochastic resonance theory requires the input signal frequency to be much less than 1. However, the characteristic frequencies in mechanical systems in practical applications are usually in the range of tens, hundreds of hertz, to several kilohertz, far exceeding the frequency range required by classical stochastic resonance theory [19]. To solve this problem, scholars use the frequency-shifted and scaling transform method to solve the small-parameter problem to achieve large-parameter stochastic resonance [20, 21]. Subsequently, in order to further study stochastic resonance, He et al. [22] proposed a new multiscale noise-tuning method that overcomes the limitations of the small parameters of classical stochastic resonance and improves the performance of classical stochastic resonance by using multiscale noise. Lei et al. [23] proposed an adaptive stochastic resonance method that utilizes the optimization ability of the ant colony algorithm to make more accurate diagnosis of faults. Lu et al. [24] proposed a sequence algorithm based on a multiscale noise-tuned stochastic resonance method to achieve signal demodulation, multiscale noise tuning, and bistable stochastic resonance sequences. Li and Shi [25] proposed a fault diagnosis method for rolling bearings based on strong background noise. This method not only overcomes the difficulty of selecting sensitive intrinsic mode function but also enhances the weak fault feature by combining it with adaptive stochastic resonance. Shi et al. [26] proposed a weak signal detection method based on adaptive stochastic resonance and analytical mode decomposition-ensemble empirical mode decomposition. This method can not only enhance the signal amplitude but also effectively detect the submerged weak multifrequency signal. Qiao et al. [27] proposed an adaptive unsaturated bistable stochastic resonance method that solved the problem of inherent output saturation in classical stochastic resonance.

Most of the above scholars’ research is directed toward the stochastic resonance of the classical bistable model. Classical bistable stochastic resonance has a single structure and cannot form a richer potential structure. The potential model cannot match the complex vibration signal, which limits the enhancement ability of weak signals. In order to further improve the extraction effect of stochastic resonance, some research scholars proposed the tristable stochastic resonance potential model. For example, Lu et al. [28] proposed a new method for enhancing the periodic fault signal of a rotating mechanical vibration using a tristable mechanical vibration amplifier. Lu et al. [29] proposed a new stochastic resonance method based on the Woods–Saxon potential model and used it for fault diagnosis of bearings. In summary, in most of the studies, although numerous tristable stochastic resonances and other models were studied, the effect of delay feedback on stochastic resonance was not considered. However, some scholars have studied the delay stochastic resonance. For example, Li et al. [30] proposed a weak signal detection method based on a time-delayed feedback monostable stochastic resonance system and adaptive minimum entropy deconvolution; this method achieves resonance detection of weak signals by selecting an appropriate time delay, feedback strength, and rescale ratio combined with a genetic algorithm. Lu et al. [31] proposed a nonstationary weak signal detection method based on a time-delayed feedback stochastic resonance model. This method is more suitable for detecting signals with strong nonlinear and nonstationary properties, as well as signals subjected to severe multiscale noise interference. Aiming at the problems existing in the above research, in this paper, we propose a new time-delayed feedback tristable stochastic resonance method and apply it to the diagnosis of weak bearing faults. The periodic signal and Gaussian white noise are introduced into the nonlinear tristable potential well, and the delay term (including feedback strength and delay time) is introduced. In the new potential system, through the adjustment and optimization of the potential function parameters and the delay term parameters, the potential function, the periodic signal, and the noise are optimally coupled to obtain the optimal SNR. Compared with the classical stochastic resonance method, the SNR is higher, the fault characteristics are more apparent, and the output effect is better than that of the classical stochastic resonance method.

The rest of the paper is organized as follows: In Section 2, the characteristics of the potential model are analyzed and the influence of each parameter on the potential model is discussed. In addition, a delay feedback term is introduced, the Fokker–Planck equation is given, and the SNR is derived. In Section 3, the process of fault detection and the simulation signal of fault extraction are studied. In Section 4, the experimental verification of the bearing inner ring is conducted to verify that the proposed method has higher SNR for an actual measurement, and the reliability of the proposed method is verified by using actual engineering data. Finally, the conclusions are drawn.

2. Potential Model and Time-Delayed Feedback Tristable Stochastic Resonance System

The process of SR detection of weak signals can be described by particle motion in the potential well. When the external drive is the periodic signal S(t), the particles oscillate slightly on the side of the potential well. When the noise ξ(t) is added to the system, the input signal becomes S(t) + ξ(t), and the noise energy will be partially transferred to the particle to overcome the barrier height of the system. When the external drive is too large, the particles in the system are too fast, called the overresonance. When the external drive is too small, the particles cannot break through the barrier and can only move in a potential well, which is called the underresonance. Since the periodic signal and noise are often fixed, in order to ensure the best stochastic resonance effect, it is necessary to adjust the potential model to make the particles move stably between the potential wells. Since the classical stochastic resonance is a bistable potential, the potential model has a single structure and cannot form a rich potential structure to match the complex vibration signal. Therefore, in this paper, the classical potential function is introduced [32]:
U x = x 2 b x 2 − c 2 + a x 2 , (1)
where a, b, and c are potential model parameters and are nonzero real numbers, used to adjust the potential structure. In a nonlinear system, noise and periodic signals work together to produce a synergistic effect, and a stochastic resonance phenomenon occurs. As shown in Figure 1, the particles transition between the potential wells under the action of noise and periodic signals. The higher the position of the particles in the ordinate, the larger the particle energy. In Figure 1(a), it can be seen that as a increases, the potential barrier of the intermediate potential well increases, and the positions of the potential wells on both sides are raised. In the synergy of the periodic signal and the noise, it is easy to jump from the potential wells on both sides to the intermediate potential well. In Figure 1(b), it can be seen that as b increases, the depth of the wells on both sides decreases, and the transition between the wells is easier and less energy is required; in Figure 1(c), it can be seen that as c increases, the barrier of the intermediate potential well increases, and it is difficult for the particles to transition between the three potential wells, and the required energy will increase.
Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Relationship between the three steady-state potential functions and x. Influence of (a) a, (b) b, and (c) c on the potential model.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Relationship between the three steady-state potential functions and x. Influence of (a) a, (b) b, and (c) c on the potential model.
Details are in the caption following the image
Figure 1 (c)
Open in figure viewerPowerPoint
Relationship between the three steady-state potential functions and x. Influence of (a) a, (b) b, and (c) c on the potential model.
The classic stochastic resonance method does not take into account the influence of historical information on the system, and it focuses on a short-term memory system. The historical information is introduced into the negative feedback of stochastic resonance to form a long-term memory system, and the detection effect of the weak signal can be improved. This long-term memory system is time-delayed feedback stochastic resonance. The classic bistable time-delayed system is as follows [33]:
d x t d t = x t − x 3 t + λ x t − τ + 2 D ξ t , (2)
where λ represents the feedback strength, τ represents the delay time, and both are often used as the tempering coefficients of the system itself; D represents the noise intensity; and ξ(t) represents the Gaussian white noise and satisfies 〈ξ(t)〉 = 0 and 〈ξ(t)ξ(t′)〉 = δ(t − t′). Equation (1) is substituted into equation (2). We can get a small delay tristable potential system driven by a weak periodic signal as follows [34]:
d x t d t = 682 b 2 x 5 t − b c x 3 t + c 2 + a x + λ x t − τ + A   cos Ω t + 2 D ξ t , (3)
where A represents the signal strength. Equation (2) is a non-Markov process, which is reduced to a Markov process by using the probability density method. The approximate time-delayed Fokker–Planck equation obtained is as follows [35]:
∂ p x , t ∂ t = ∂ h eff p x , t ∂ x + D ∂ 2 p x , t ∂ x 2 , (4)
where heff is the conditional average drift rate, given by
h eff = ∫ b a d x τ h x , x τ p x τ , t − τ ∣ x , t , (5)
where the integral boundaries a and b are ±∞, and p(xτ, t − τ|x, t) is the zero-order approximate Markov transition probability density, whose formula is
p x τ , t − τ ∣ x , t = 1 4 π D τ exp − x τ − x − h x τ 2 4 D τ , (6)
where h(x) = 6b2x5(t) − 8bcx3(t) + 2(c2 + a)x + λx  +  A cos(Ωt).
Equation (6) is substituted into equation (5) to obtain
h eff = 1 + λ τ 682 b 2 x 5 t − b c x 3 t + c 2 + a x + λ 1 + λ τ + 1 + λ τ A   cos Ω t . (7)
Furthermore, obtaining an effective Langevin equation relative to equation (4), we have
d x t d t = 682 b 2 x 5 t − b c x 3 t + c 2 + a x + λ x + A   cos Ω t + λ τ 682 b 2 x 5 t − b c x 3 t + c 2 + a x + λ x + A   cos Ω t + 2 D ξ t . (8)
Without considering the periodic signal and Gaussian noise, the equivalent time-delayed tristable potential corresponding to equation (8) can be derived as [36]
U e x = 1 + λ τ x 2 b x 2 − c 2 + a x 2 + 1 2 λ 1 + λ τ x 2 . (9)

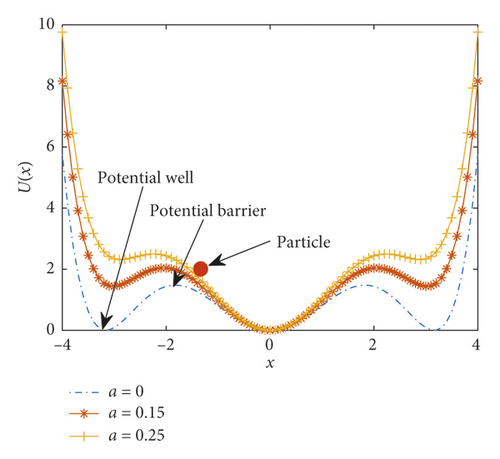
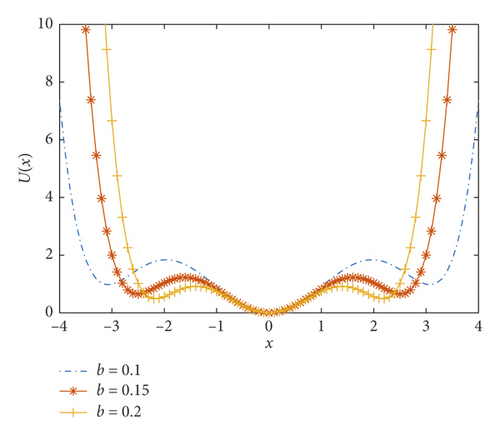
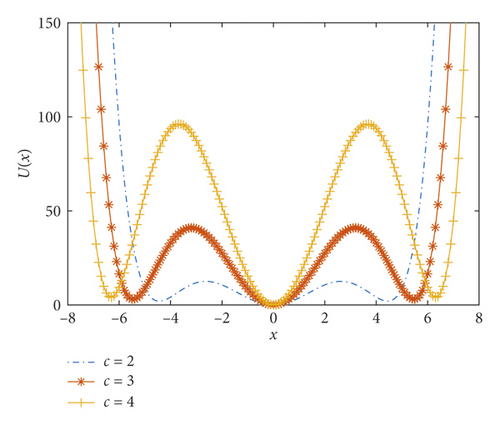
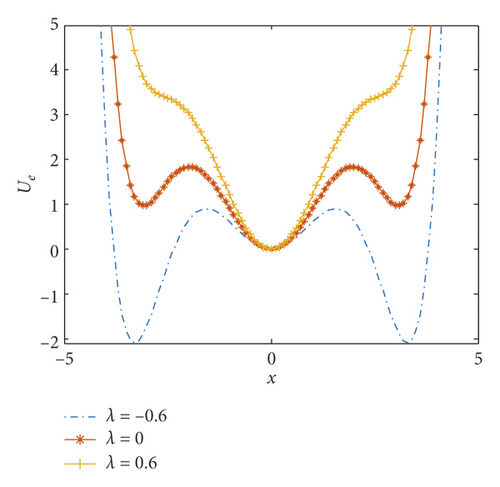
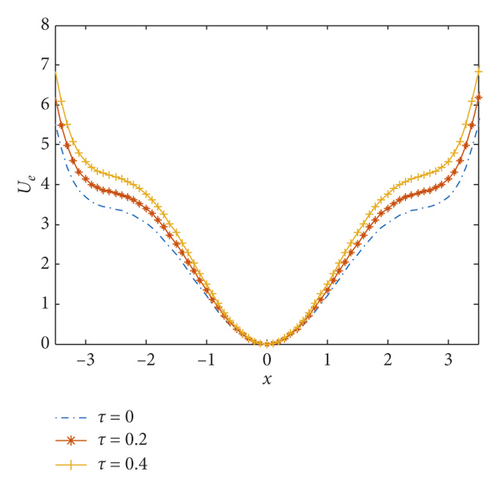
The effective potential function graph is shown in Figures 2(a) and 2(b).

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Potential energy and x when the parameters are as follows: (a) λ is taken as −0.6, 0, and 0.6 and a = 0.1, b = 0.1, c = 1, and τ = 0; (b) τ is taken as 0, 0.2, and 0.4 and a = 0.1, b = 0.1, c = 1, and λ = 0.6.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Potential energy and x when the parameters are as follows: (a) λ is taken as −0.6, 0, and 0.6 and a = 0.1, b = 0.1, c = 1, and τ = 0; (b) τ is taken as 0, 0.2, and 0.4 and a = 0.1, b = 0.1, c = 1, and λ = 0.6.
The time-delayed feedback stationary probability density function is expressed as
P st = N     exp − U e D , (10)
where N is a normalized constant, and the graph of Pst is shown in Figures 3(a) and 3(b).
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Relationship between the stationary probability density function and x with the corresponding parameters a = 0.4, b = 0.26, c = 0.45, A = 0, and D = 0.15 for (a) different delay strengths and (b) different time extensions.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Relationship between the stationary probability density function and x with the corresponding parameters a = 0.4, b = 0.26, c = 0.45, A = 0, and D = 0.15 for (a) different delay strengths and (b) different time extensions.
Then, the power spectral density function can be derived as
S ω = π 1 + λ M 2 2 N 2 + Ω 2 δ Ω − ω + δ Ω + ω + 1 − M 2 2 N 2 + Ω 2 2 1 + λ N N 2 + ω 2 , (11)
where Ω is the angular frequency (Ω = 2πf, that is, the product of the number of vibrations per unit time and 2π); ω is the output frequency [37]; S(ω) is the output power spectral density and is obtained by the Wiener–Khintchine theorem, which is the Fourier transform of the correlation function of the Langevin equation, independent of the frequency ω; N = 2 1 + λ 1 + λ τ / π exp − 1 + λ 2 1 + λ τ / 4 D ; and M = A / D 1 + λ τ 1 + λ N .
In equation (11), we are allowed to omit the last term ((M2)/(2(N2 + Ω2))), so S(ω) is only defined for positive Ω, and then equation (11) becomes [31]
S ω = S 1 ω + S 2 ω , S 1 ω = π 1 + λ M 2 2 N 2 + ω 2 δ Ω − ω , S 2 ω = 2 1 + λ N N 2 + ω 2 , (12)
where S1(ω) is the output power spectral density and there is no influence of the periodic signal in S2(ω), so S2(ω) is the noise power spectral density.
The SNR is given by
SNR = S 1 ω S 2 ω = 2 A 2 4 D 2 1 + λ 2 1 + λ τ 3 exp − 1 + λ 2 1 + λ τ 4 D . (13)

Taking dR/dD = 0, we can get D = (1/8)(1 + λ)2(1 + λτ) = (1/2)ΔU. When D/ΔU = 0.5, the SNR reaches a maximum.

Figure 2(a) shows that when other parameters are fixed and the feedback strength is too small, as shown by λ = −0.6, it is easier for the particles to jump from the potential wells on both sides to the middle potential well, and the required energy is low. However, the barrier value at this time is too high, which is not conducive to the transition of particles from the intermediate potential well to the potential wells on both sides, and the required energy is high. The excessive feedback strength is shown in the figure. When λ = 0.6, the minimum value of the potential wells on both sides is too low, which is also not conducive to the transition of the particles. It takes considerable energy for a particle to jump to the intermediate well. Figure 2(b) shows the effect of the delay time τ on the potential energy. As the delay time τ increases, the steepness of the potential wall of the potential well in the middle of the potential energy becomes lower, the position of the potential wells on both sides is reduced, and the particles can more easily transition among the three potential wells, requiring less energy. The adjustment of potential energy is achieved by adjusting the time-delayed feedback strength. When the external driving force is small, the potential energy can be increased by adjusting the delay parameter so that the particles can easily realize the transition between the potential wells, and vice versa, thereby achieving the best stochastic resonance effect.

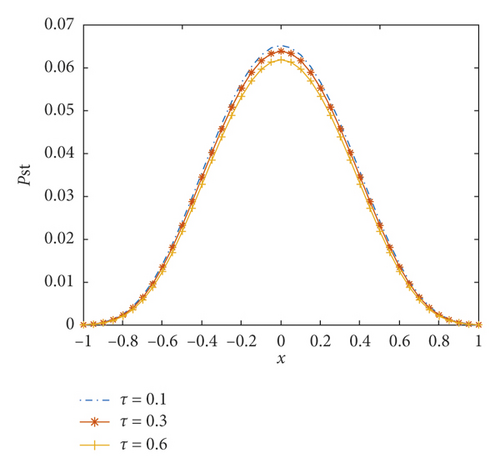
Figures 3(a) and 3(b) show the effect of delay strength and delay time on the probability density function, respectively. It can be seen in Figure 3(a) that as the intensity of the delay time increases, the peak of the probability density decreases, and the difference in value between the peaks is large. Figure 3(b) also shows that as the time extension increases, the probability density function peak decreases, but the difference in value between the peaks is small. Thus, comparing the two graphs, one can see that the feedback strength has a greater influence than the time extension on the probability density function. The larger the steady-state density function value, the more stable the transition of the particles between the potential wells, thus ensuring better stochastic resonance.

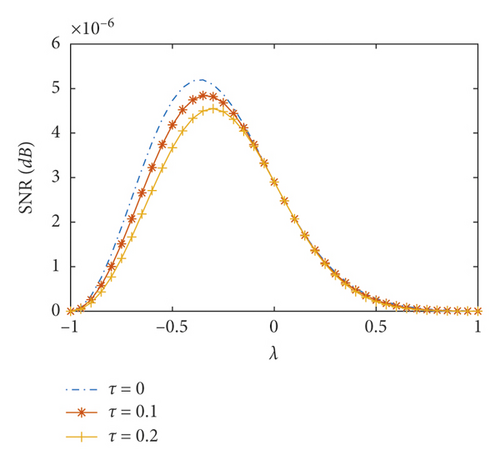
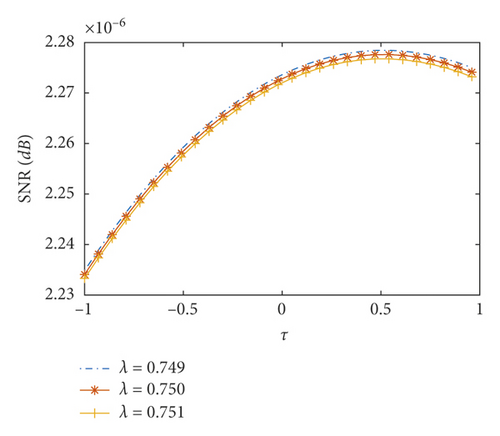
Figure 4(a) shows the effect of the feedback strength λ on the SNR. As shown in the figure, as the feedback strength λ increases, the SNR gradually increases to its peak value and then decreases. Figure 4(b) shows the effect of the delay time τ on the SNR; that is, as the delay time τ increases, the SNR increases and then decreases, while the feedback strength λ affects the SNR, and the value of the feedback strength λ becomes larger, and the value of the SNR peak is lower. From Figures 4(a) and 4(b), the influence of feedback strength λ and delay time τ on the SNR is obvious. At the same time, the effects of the two coefficients on the SNR are not synergistic but are mutually suppressed. Therefore, the optimal SNR of the time-delayed feedback tristable stochastic resonance needs to be obtained by adjusting the parameters. The SNR is used as an evaluation index for evaluating the output effect of the signal. The larger the SNR, the better the suppression noise and the signal extraction effect.

Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Delay feedback tristable stochastic resonance SNR: effect of (a) λ on SNR and (b) τ on SNR with parameters A = 0.001 and D = 1.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Delay feedback tristable stochastic resonance SNR: effect of (a) λ on SNR and (b) τ on SNR with parameters A = 0.001 and D = 1.

3. Simulation of Time-Delayed Feedback Tristable Stochastic Resonance

3.1. Signal Processing of Time-Delayed Tristable Stochastic Resonance

Because stochastic resonance theory is implemented under adiabatic approximation conditions, the above derivation is limited to small-parameter limits. In other words, the required frequency is much less than 1 Hz [19], and the fault frequency in engineering practice is usually tens of hertz or even hundreds of thousands of hertz. Therefore, we first use the frequency-shifted and scaling transform method to make the tristable stochastic resonance meet the small-parameter requirements, and then we use the fourth-order Runge–Kutta method to solve equation (3) as follows [24]:
K 1 = h − U ′ x n + λ x n − round τ × f s + S n + N n , K 2 = h − U ′ x n + K 1 2 + λ x n − round τ × f s + K 1 2 + S n + N n , K 3 = h − U ′ x n + K 2 2 + λ x n − round τ × f s + K 2 2 + S n + 1 + N n + 1 , K 4 = h − U ′ x n + K 3 + λ x n − round τ × f s + K 3 + S n + 1 + N n , x n + 1 = x n + K 1 + 22 K 2 + K 3 + K 4 6 , (14)
where fs is the sampling frequency and h is the calculation step.
In this paper, the ant colony algorithm is inspired by the behavior of ants searching for food in nature, and it is a group intelligent optimization algorithm. The ant colony algorithm is based on the study of the collective foraging behavior of real ant colonies in nature, simulating the real ant colony collaboration process. As a general stochastic optimization method, the ant colony algorithm [38] has been successfully applied to a series of combinatorial optimizations and achieved good results. The ant colony algorithm is used to optimize the parameters of the tristable stochastic resonance system. Output SNR is used as the evaluation index to evaluate the performance of the time-delayed feedback tristable stochastic resonance method for extracting weak fault signals. The expression is as follows:
SNR = 10   log 10   A d 2 ∑ i = 1 N / 2 A i 2 − A d 2 , (15)
where N is the signal length. A d 2 and ∑ i = 1 N / 2 A i 2 − A d 2 are the amplitudes corresponding to the drive frequency fd and the strongest interference frequency fn, respectively. The driving frequency refers to the fundamental frequency of the periodic signal, and the strongest interference frequency refers to the strongest noise frequency. The larger the SNR, the more obvious the difference between signal and noise. The specific process is as follows:
  • (1)

    Signal Preprocessing. Signal demodulation is used to detect the drive signal and the small-frequency-parameter limitation through frequency-shifted and scaling transform.

  • (2)

    Parameter Initialization. The parameter-matching algorithm is initialized, and the evaluation function of stochastic resonance is selected.

  • (3)

    Parameter Optimization. The structural parameters a, b, and c and the time-delayed parameters λ and τ are again optimized by the ant colony algorithm to obtain the optimal parameter combination. The optimal range is [0, 10].

  • (4)

    Output Calculation. Equation (2) is substituted into equation (14) to give the output waveform, and the SNR is calculated by using equation (15).

  • (5)

    Signal Postprocessing. The optimal parameters are substituted into the model for calculation, the spectrum is obtained, and the fault features are identified and diagnosed.

3.2. Simulation of Time-Delayed Tristable Stochastic Resonance

To verify the effect of the time-delayed feedback tristable stochastic resonance weak fault diagnosis method, the effect of the proposed method is analyzed by simulating the bearing fault signal. The simulated fault signal is as follows:
S t = A   sin 2 π f t ⋅ exp − d t − n t T d 2 , (16)
where A = 1 is the signal amplitude; t is the sampling time; f = 1 kHz is the carrier frequency; d = 6fs reflects the attenuation rate; fs = 10 kHz is the sampling frequency; n(t) = [t/Td](n(t) = floor(t/Td)) control pulse periods appear; Td = 1/fd = 0.014 is the pulse interval; fd = 72 kHz is the driving frequency; and the sampling time is 0.5 s. Figures 5(a) and 5(b) show the noiseless signal and the noisy signal, respectively. Figure 5(c) shows the spectrum of the Hilbert transform, and Figure 5(d) shows the envelope spectrum of the noisy signal. No information related to the driving frequency can be found in the spectrum or in the envelope spectrum because of noise interference. Therefore, by relying solely on the envelope signal, the identification and extraction of the fault signal cannot be achieved.
Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
Bearing simulation: (a) noiseless signal, (b) noisy signal, (c) spectrum, and (d) envelope spectrum.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
Bearing simulation: (a) noiseless signal, (b) noisy signal, (c) spectrum, and (d) envelope spectrum.
Details are in the caption following the image
Figure 5 (c)
Open in figure viewerPowerPoint
Bearing simulation: (a) noiseless signal, (b) noisy signal, (c) spectrum, and (d) envelope spectrum.
Details are in the caption following the image
Figure 5 (d)
Open in figure viewerPowerPoint
Bearing simulation: (a) noiseless signal, (b) noisy signal, (c) spectrum, and (d) envelope spectrum.

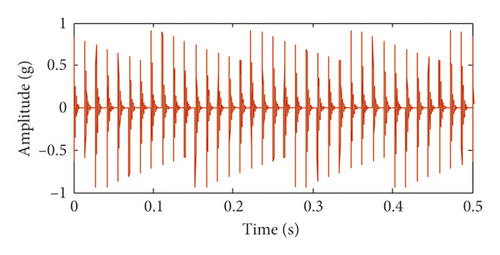
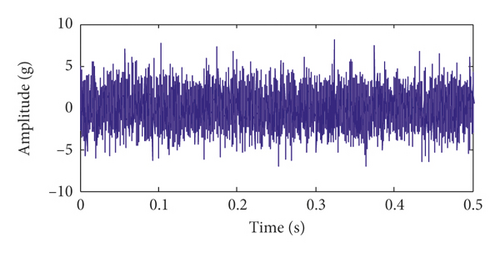
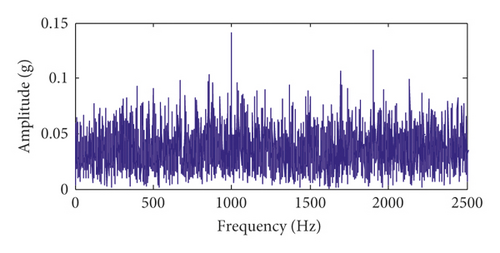
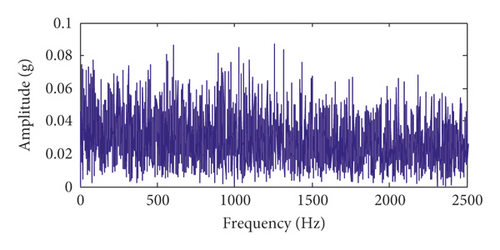
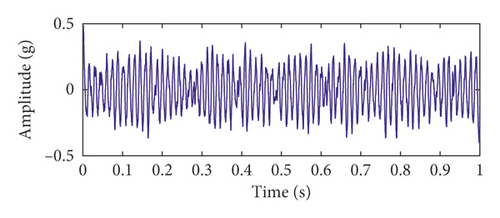
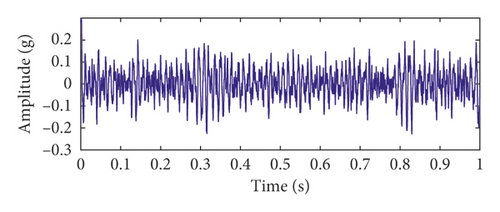
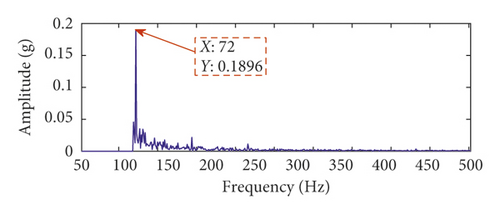
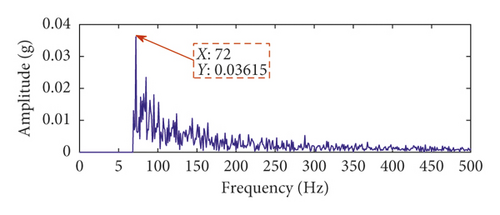
Figures 6(a) and 6(b) show the time-domain waveform and frequency spectrum of the time-delayed feedback tristable stochastic resonance method. Figures 6(c) and 6(d) show the time-domain waveform and frequency spectrum of the classical stochastic resonance method, respectively. It can be seen from Figures 6(a) and 6(c) that the pulse contour of the time-delayed feedback tristable stochastic resonance method is clearer. Meanwhile, the peak values of the proposed method and classical stochastic resonance method are 0.1896 and 0.03615. It can be seen that the proposed method better extracts the fault feature than the classical stochastic resonance method. In Figure 6(d), the noise is strong in the fault frequency band. The above analysis shows that the time-delayed feedback tristable stochastic resonance method has a greater effect on the weak fault signal than the classical stochastic resonance method.

Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
Bearing simulation. (a) Time-domain waveform and (b) spectrum of the time-delayed feedback tristable stochastic resonance method. (c) Time-domain waveform and (d) spectrum of the classical stochastic resonance method.
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
Bearing simulation. (a) Time-domain waveform and (b) spectrum of the time-delayed feedback tristable stochastic resonance method. (c) Time-domain waveform and (d) spectrum of the classical stochastic resonance method.
Details are in the caption following the image
Figure 6 (c)
Open in figure viewerPowerPoint
Bearing simulation. (a) Time-domain waveform and (b) spectrum of the time-delayed feedback tristable stochastic resonance method. (c) Time-domain waveform and (d) spectrum of the classical stochastic resonance method.
Details are in the caption following the image
Figure 6 (d)
Open in figure viewerPowerPoint
Bearing simulation. (a) Time-domain waveform and (b) spectrum of the time-delayed feedback tristable stochastic resonance method. (c) Time-domain waveform and (d) spectrum of the classical stochastic resonance method.

4. Experimental Verification

4.1. Experimental Verification of Time-Delayed Tristable Stochastic Resonance

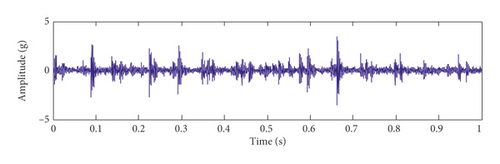
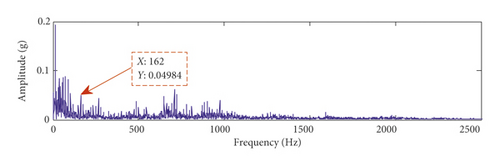
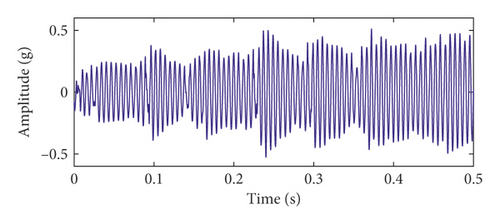
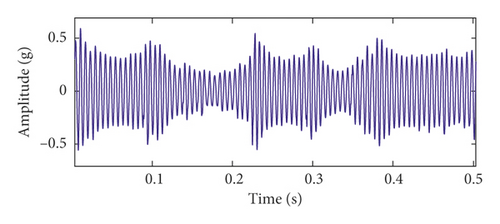
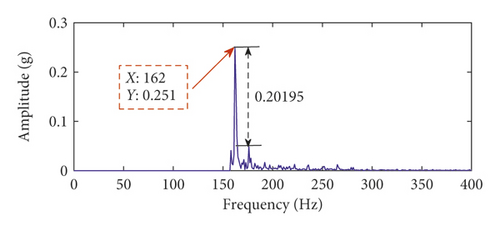
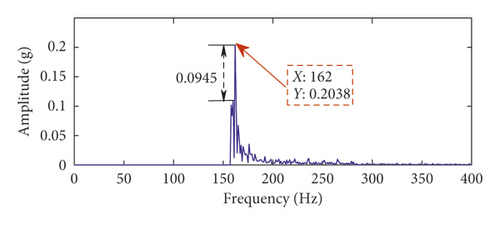
To verify the effectiveness of the time-delayed feedback tristable stochastic resonance method, the proposed method is applied to a fault characteristic frequency extraction experiment of slightly worn rolling bearings. Rolling bearings are an important part of rotating machinery and one of the more easily damaged parts. Therefore, a fault signal extraction experiment with slight wear of the inner ring of the rolling bearing is used to verify the effect of the proposed method. The test bench is a comprehensive experimental bench for mechanical equipment failure, as shown in Figure 7. The experimental data comprise a sampling frequency of 5120 Hz and a rotational speed of 1800 rpm. The bearing type used in the experiment is ER-16K, bearing diameter is 38.5/mm, and bearing contact angle α = 0. According to the vibration analysis theory, the bearing inner ring fault characteristic frequency is 162.69 Hz. The characteristic frequency in the figure is interfered by strong noise, so the fault features cannot be identified and extracted in the spectrum and the envelope spectrum in Figure 8. The time-delayed feedback tristable stochastic resonance method is applied to the extraction of the fault characteristic frequency of the rolling bearing. The time-domain waveform and spectrum of the output signal are shown in Figures 9(a) and 9(b), respectively. It can be seen from the spectrum that the maximum peak frequency is 162 Hz with a spectral peak of 0.251 and is close to the theoretical value of 162.69 Hz. In order to verify that the proposed method is superior to the traditional method, the experimental data used are applied to classical stochastic resonance and the time-domain waveform and spectrum of the output signal are shown in Figures 9(c) and 9(d). In Figure 9(c), the waveform profile is clearer. In Figure 9(d), the fault frequency is at 162 Hz and the spectral peak is 0.2038. Comparing the two methods, the proposed method in this paper is more effective. We define the difference between the frequency peak of the fault characteristic and the peak of the noise spectrum as the degree of recognition. The fault feature recognition degree of the proposed method is 0.20195, and the recognition degree of the classical bistable stochastic resonance method is 0.0495. Therefore, we can conclude that the proposed method is more effective.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Mechanical equipment failure comprehensive test bench.
Details are in the caption following the image
Figure 8 (a)
Open in figure viewerPowerPoint
Rolling bearing signal: (a) time-domain waveform, (b) spectrum, and (c) envelope spectrum.
Details are in the caption following the image
Figure 8 (b)
Open in figure viewerPowerPoint
Rolling bearing signal: (a) time-domain waveform, (b) spectrum, and (c) envelope spectrum.
Details are in the caption following the image
Figure 8 (c)
Open in figure viewerPowerPoint
Rolling bearing signal: (a) time-domain waveform, (b) spectrum, and (c) envelope spectrum.
Details are in the caption following the image
Figure 9 (a)
Open in figure viewerPowerPoint
Rolling bearing signal. (a) Time-domain waveform and (b) spectrum of the time-delayed feedback tristable stochastic resonance method. (c) Time-domain waveform and (d) spectrum of the classical stochastic resonance method.
Details are in the caption following the image
Figure 9 (b)
Open in figure viewerPowerPoint
Rolling bearing signal. (a) Time-domain waveform and (b) spectrum of the time-delayed feedback tristable stochastic resonance method. (c) Time-domain waveform and (d) spectrum of the classical stochastic resonance method.
Details are in the caption following the image
Figure 9 (c)
Open in figure viewerPowerPoint
Rolling bearing signal. (a) Time-domain waveform and (b) spectrum of the time-delayed feedback tristable stochastic resonance method. (c) Time-domain waveform and (d) spectrum of the classical stochastic resonance method.
Details are in the caption following the image
Figure 9 (d)
Open in figure viewerPowerPoint
Rolling bearing signal. (a) Time-domain waveform and (b) spectrum of the time-delayed feedback tristable stochastic resonance method. (c) Time-domain waveform and (d) spectrum of the classical stochastic resonance method.

4.2. Engineering Verification of Time-Delayed Tristable Stochastic Resonance

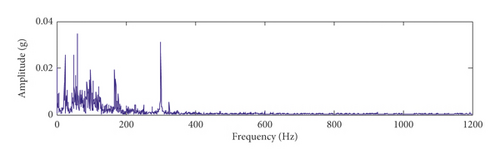
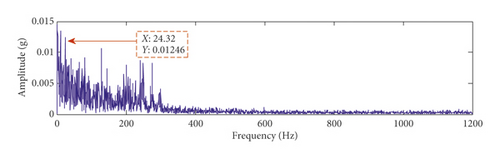
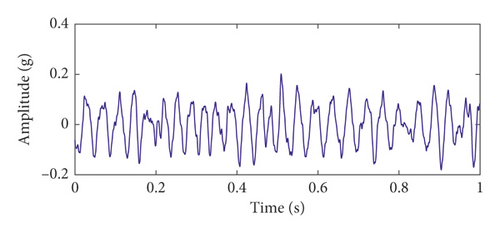
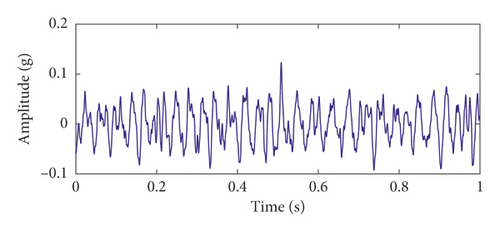
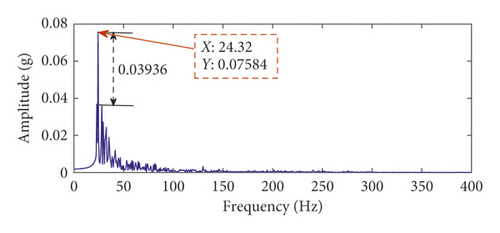
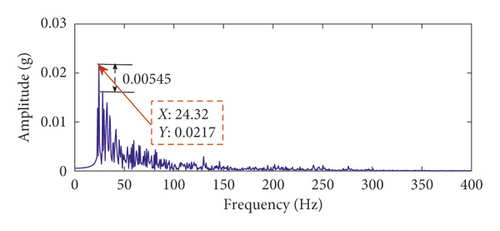
Based on the proposed method, the robust results are verified in the above experiment. The effect of the time-delayed tristable stochastic resonance in extracting the bearing weak fault signal is better than that of the classical stochastic resonance method, and the extracted fault features are more obvious. The noise interference is smaller. We apply the proposed method to the fault feature extraction experiment of the bearing inner ring of a steel mill to further verify the effectiveness of the proposed method. The experimental bearing is shown in Figure 10. The bearing inner ring fault characteristic frequency is 24 Hz, and the sampling frequency is 2560 Hz. The time-domain waveform, spectrum, and envelope spectrum of the original signal are shown in Figure 11. In the spectrum of Figure 11(b), it is difficult to find information related to the frequency of the fault characteristic because of the presence of the noise frequency. In the envelope spectrum of Figure 11(c), the fault characteristic frequency can be seen, but at the same time there are other strong noise frequencies. Therefore, the extraction of the bearing fault characteristics in actual engineering cannot be realized by using the envelope spectrum alone. To this end, the proposed method is applied to the experimental data, and Figures 12(a) and 12(b) are obtained. In the spectrum of Figure 12(b), it can be seen that the peak frequency of the highest spectrum is 24.32 Hz, which is very close to 24 Hz, so the proposed method can effectively extract the bearing fault characteristics in engineering practice. At the same time, the engineering experimental data taken are applied to the classical stochastic resonance method to obtain the time-domain waveform and spectrum, as shown in Figures 12(c) and 12(d), respectively. Comparing the two methods shows that the frequency of fault characteristics in the spectrum is the same, which verifies the accuracy of the proposed method. At the same time, the spectral peaks of the fault characteristics of the two methods are 0.07584 and 0.0217, respectively. The recognition degree of fault characteristics is 0.03936 and 0.00545, respectively; therefore, the fault characteristics extracted by the proposed method are more obvious. Moreover, the proposed method yields less in-band noise in the fault characteristic frequency. Therefore, the time-delayed feedback tristable stochastic resonance method is better when applied in engineering practice.

Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
Fault feature extraction of the bearing inner ring of a steel mill.
Details are in the caption following the image
Figure 11 (a)
Open in figure viewerPowerPoint
Engineering bearing signal. (a) Time-domain waveform, (b) spectrum, and (c) envelope spectrum.
Details are in the caption following the image
Figure 11 (b)
Open in figure viewerPowerPoint
Engineering bearing signal. (a) Time-domain waveform, (b) spectrum, and (c) envelope spectrum.
Details are in the caption following the image
Figure 11 (c)
Open in figure viewerPowerPoint
Engineering bearing signal. (a) Time-domain waveform, (b) spectrum, and (c) envelope spectrum.
Details are in the caption following the image
Figure 12 (a)
Open in figure viewerPowerPoint
Engineering bearing signal. (a) Time-domain waveform of the time-delayed feedback tristable stochastic resonance method. (b) Spectrum of the time-delayed feedback tristable stochastic resonance method. (c) Time-domain waveform of the classical stochastic resonance method. (d) Spectrum of the classical stochastic resonance method.
Details are in the caption following the image
Figure 12 (b)
Open in figure viewerPowerPoint
Engineering bearing signal. (a) Time-domain waveform of the time-delayed feedback tristable stochastic resonance method. (b) Spectrum of the time-delayed feedback tristable stochastic resonance method. (c) Time-domain waveform of the classical stochastic resonance method. (d) Spectrum of the classical stochastic resonance method.
Details are in the caption following the image
Figure 12 (c)
Open in figure viewerPowerPoint
Engineering bearing signal. (a) Time-domain waveform of the time-delayed feedback tristable stochastic resonance method. (b) Spectrum of the time-delayed feedback tristable stochastic resonance method. (c) Time-domain waveform of the classical stochastic resonance method. (d) Spectrum of the classical stochastic resonance method.
Details are in the caption following the image
Figure 12 (d)
Open in figure viewerPowerPoint
Engineering bearing signal. (a) Time-domain waveform of the time-delayed feedback tristable stochastic resonance method. (b) Spectrum of the time-delayed feedback tristable stochastic resonance method. (c) Time-domain waveform of the classical stochastic resonance method. (d) Spectrum of the classical stochastic resonance method.

The above analysis shows that the time-delayed tristable stochastic resonance system can get better signal output. From physical analysis, the time-delayed tristable stochastic resonance system has three potential wells and adjusts the potential structure with three parameters. Compared with the classical bistable stochastic resonance, the time-delayed tristable potential model can obtain a richer potential structure and match the complex vibration signal to achieve better stochastic resonance effect. Moreover, introducing a delay term in the potential model, the potential model can change the external driving energy to obtain a stable particle transition between the potential wells and finally get the best signal-to-noise ratio, which is the best signal enhancement effect. Therefore, it can be concluded that the signal output is better than the classical bistable stochastic resonance due to the existence of the tristable model and the delay term.

5. Conclusion

In this paper, we have studied the time-delayed feedback tristable stochastic resonance system. A method for time-delayed feedback tristable stochastic resonance weak faults is proposed. The main conclusions are as follows:
  • (1)

    The optimal potential energy, steady-state probability density function, and SNR can be obtained by adjusting the time-delayed and feedback strength. In other words, the optimal stochastic resonance effect can be obtained by adjusting the delay term.

  • (2)

    A new time-delayed feedback tristable stochastic resonance model is established. Compared with the classical bistable stochastic resonance model, the proposed model can obtain a richer structure by adjusting the system parameters, thus achieving matching with complex vibration signals.

  • (3)

    A new weak fault diagnosis method was proposed. The proposed method can not only extract the simulation and experimental signals of bearing faults, but also effectively extract the fault signals in the project. Compared with the classical stochastic resonance method, the weak fault features extracted by the proposed method have a good recognition.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China (NSFC) under Grants 51805275, 51865045, and 51565046 and in part by the Inner Mongolia Natural Science Foundation under Grant 2018ZD06.

    Data Availability

    The experiment is carried out on the mechanical failure comprehensive simulation test platform as shown in Figure 8. The signal is acquired by a Zonic Block/618 instrument connected to a computer. The experimental data can be obtained by sending an email to [email protected].

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.