We study the time evolution of the survival probability and the spin polarization of a dissipative nondegenerate two-level system in the presence of a magnetic field in the Faraday configuration. We apply the Extended Gaussian Orthogonal Ensemble approach to model the stochastic system-environment interaction and calculate the survival and spin polarization to first and second order of the interaction picture. We present also the time evolution of the thermal average of these quantities as functions of the temperature, the magnetic field, and the energy-levels density, for ρ(ϵ) ∝ ϵ^s, in the subohmic, ohmic, and superohmic dissipation forms. We show that the behavior of the spin polarization calculated here agrees rather well with the time evolution of spin polarization observed and calculated, recently, for the electron-nucleus dynamics of Ga centers in dilute (Ga,N)As semiconductors.

1. Introduction

The necessity to maintain the information for long periods of time and the efforts to control and manipulate the electronic spin degrees of freedom led to extensive research activities, such as, among others, the search for the best conditions to keep the spin polarization, as well as new mechanisms to enhance the spin coherence time [1–6]. In spite of abundant empirical knowledge of the spin depolarization rates and the spin coherence times, there is little knowledge of the explicit time evolution of these quantities, as functions of the relevant system-environment interaction parameters. In this paper, we focus on this problem and present a simple calculation of the time evolution of the spin polarization driven by the stochastic interaction of the system and its environment, with good results and few assumptions.

The physics of the two-state systems have been studied since the early days of the quantum theory, and various models and approaches have been proposed and published [7–18]. Attempts to solve completely the models for dissipative two-state systems are generally faced with mathematical complexities. Examples vary from entangled differential equations in master equation approaches [11, 19] to perturbative calculations in the ‘spin-boson’ [14] and the rotating-wave” approximation [16]. Recently the master equation approach [19] was applied to describe the evolution of the electronic and nuclear spin polarizations of interstitial gallium defects, which behave as paramagnetic centers in dilute (Ga,N)As semiconductor that selectively capture electrons with opposite spin, and block the recombination of conduction band electrons with the same spin (which lead to an increase of the lifetime of conduction electrons and bound electrons from picoseconds to nanoseconds). The intricacy of this approach expressed through almost a hundred of coupled nonlinear differential equations (with assumptions on the dissipative interactions) reminds us of the ‘much too intractable (intermediate results) of the spin-boson model’ [15]. In the physics of complex systems, it has been frequently found that some processes are insensitive to the details of the interaction, being only a few “gross properties” relevant to describe them. This feature, which is not new to many body problems, has often been used to construct successful and enlightening approaches in terms of ensembles of stochastic interactions [17, 20–27] that make possible satisfying evaluations of ensemble averages for relevant quantities. We will present here a Gaussian stochastic spin-environment interaction approach that strengthens this idea.

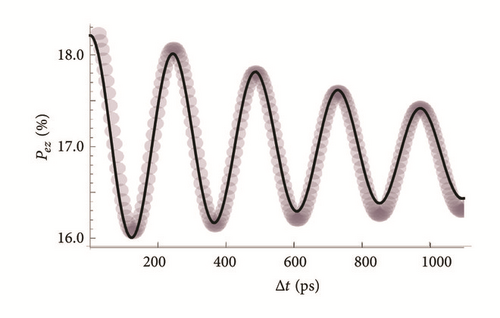
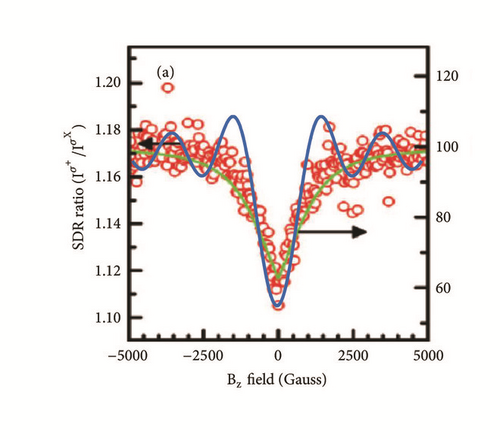
In the master equation approach in [28, 29], the electronic and nuclear spin dynamics, obtained through rather detailed calculations, oscillate as shown in Figure 1 (gray-circles curve). This behavior has been explained as caused by oscillations of the hyperfine interaction of bound electrons with the nuclei. In the stochastic interaction model presented here, we obtain, to second order of the interaction picture, the spin polarization oscillations shown also in Figure 1 and plotted with the continuous (black) curve on top of the gray-circles curve. The agreement of these results supports the suggestion that the loss of coherence and the oscillating time evolution of the spins might be caused by the stochastic nature of trapping and recombination. The complexity of the system makes it also difficult to establish to which extent the observed time evolution is a consequence of a new mechanism or of multiple stochastic and spin-field interactions. In Figure 2 we show the experimental results of the field effect, in the Faraday geometry, on the spin-dependent recombination ratio reported in [5], where the hyperfine interaction was uphold to explain this behavior when interstitial Ga²⁺ atoms are present in dilute (Ga,N)As semiconductors. On top of these data we plot also our results (see blue curve) for the spin polarization, as function of the magnetic field, driven by the stochastic interaction. The oscillatory behavior of our results might be behind the large dispersion of data in the experimental results shown in Figure 2.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The spin polarization calculated in [28] (gray circles) and our results (black curve), to second order of the interaction picture, for level density of the bath ρ_υ(ε) = 10⁹ϵ^s, with s = 0.28, and frequency ω_o = 2.73556 × 10¹⁰s⁻¹. The gray circles graph published with author’s permission.

We will show here that the gross properties of the spin dynamics and spin polarization oscillations, observed in the above mentioned examples, result when a two-state system interacts stochastically with its environment. To take into account the magnetic field in the Faraday configuration, we will consider the Hamiltonian,

(1)

where (1/2)ω_oσ_x represents a particle of spin 1/2 in the magnetic field

and H_E describes the environment (also referred as the bath), characterized by a level density ρ(ϵ). The potential σ_zV represents the system-environment interaction where the operator V represents the environment, with matrix elements modelled as statistically independent Gaussian variables. The Hamiltonians H_B and V belong to Gaussian orthogonal ensembles (GOEs) of random matrices with dimension N × N, large enough that the order relations in (14) are fulfilled. A similar Hamiltonian with the terms σ_x and σ_z interchanged with each other was studied before [18]. In that case, it was possible to evaluate the whole series of the survival probability and the spin polarization, in the interaction representation, for times much larger than the collision time t_coll and much smaller than the Poincarè recurrence time t_P. When the basis is chosen such that |1〉 and |−1〉 are the eigenstates of σ_x, the Hamiltonian describes the spin flip processes. If, instead, |1〉 and |−1〉 are the eigenstates of σ_z, the spin-flip processes are understood as tunneling process in the fictitious spin 1/2 picture [15]. Another system with a similar Hamiltonian σ_z/2 + H_e + λσ_zV, and the two-state system in an eigenstate of σ_x, at t = 0, was numerically studied in [30], showing also that the decoherence depends greatly on the nature of the random environment H_e and the interaction V. A result that agrees with the results obtained here and other previous papers where it was shown, analytically, that the survival probabilities depend explicitly on the density of levels ρ(ϵ) of the bath. The authors in [30] considered three cases: random matrices that belong to finite-dimension GOE, to BEGOE, and to FEGOE, being the last two embedded ensembles generated by k-body interactions of spinless fermions and bosons, respectively. The dynamics and complexity of this system are different from the ones studied here and in [18]. For the purpose of this paper it is good enough to calculate the survival and spin polarization to second order of the interaction picture, and for times t such that Δ_ot/ħ is of the order of 1. This means that when t≃ 1-10ns the magnetic fields are of the order of 10mT.

The Hamiltonian in (1) is similar to that of the spin-boson model for a two-state system in the fictitious spin 1/2 picture. In the spin-boson model the environment is modeled as a set of harmonic oscillators and the Hamiltonian describes effectively the tunneling between wells of a double well potential. Some quantities were calculated when appropriate approximations were introduced and the level density was assumed ∝E^s (which, depending on whether the exponent s is equal to 1, <1 or >1, corresponds to the so-called ohmic, subohmic and superohmic dissipation forms, respectively).

In the next section we will present the dissipative two-level model. We will present results for the first- and second-order terms of the interaction representation picture in Section 3. In Section 4 we will show some results for the survival probability and for the spin polarization. We discuss some conclusions at the end.

2. The Random Matrix Model and the Survival Probability

As mentioned before, we will consider the Hamiltonian in (1), where the environment interacts with a spin 1/2 particle. The interaction operator V is chosen such that its matrix elements are statistically independent Gaussian variables with zero mean and covariance given by [17, 21–23]

(2)

The angular brackets denote the ensemble average,

is the strength of the interaction, E_ab is the centroid of E_a and E_b, and

is a Lorentzian weight factor of width Δ_a. This means that the interaction connects states of the bath within an energy range of order of the Lorentzian width, which defines the collision time t_coll ~ ħ/Δ_a, i.e., the duration of each application of the spin-bath interaction that should be distinguished from the time between successive collisions. We will assume that at t ≤ 0 the system is held in the eigenstate |1〉 od σ_z, while the bath is in thermal equilibrium described by the canonical ensemble:

(3)

Here E_a denotes the energy eigenvalue of H_E in the state |a〉, with levels density ρ(E), and Z is the partition function. The states |aα〉, with |α〉 an eigenstate of σ_z, form a complete set. If, at time t = 0, the interaction is switched on, we pose the problem of calculating the probability P_1→1(t) that at time t > 0 the system remains in the state |1〉, regardless the state of the bath, i.e., the problem of calculating the thermal average of the survival probability,

(4)

where 〈⋯〉 stands for the ensemble average on the Gaussian variables and 〈⋯〉 _β for the thermal average. Concerning the Gaussian ensemble, it is worth mentioning that a wide research on random matrix ensembles underwent a rapid development leading to various modified versions, in particular the embedded ensembles (EE) generated by random k-body interactions, k = 2 being the most important; see [26, 27]. The statistical assumptions that we need in our calculations below are completely characterized by (2) and (12), which, according to [21], are compatible with the postulates of matrix elements given by the two-body random ensemble. Before we calculate these averages, we write the time evolution operator e^−iHt/ħ in the interaction representation as

(5)

Here

(6)

that can be written as

(7)

To simplify the notation, from here onwards we will define ε = E/ħ and ω_o = Δ_o/ħ. Using these quantities in (5), the amplitude of the survival probability becomes

(8)

This amplitude can straightforwardly be written as

(9)

Therefore,

(10)

For the calculation of the ensemble average of the survival probability P_1→1(t), we follow the procedure and the assumptions explained in detail in [17, 18, 21]. In the calculation of the average

(11)

using the statistical assumptions given in (2), one has to take into account that only the covariance of V_ab with itself or with V_ba is nonzero. This property implies that the average of a product factorizes into products of averages of pairs of matrix elements, more specifically into a number of configurations, such as

. The Lorentzian weight factor

in (2) is assumed to have the property

(12)

which, as mentioned above, restricts the scope of the interaction V to connect eigenstates of H_E within the energy interval

. Here

. The quantity

(13)

has time dimensions and as mentioned before is associated with the collision time, the duration of one application of the interaction V. We assume that Δ_a contains many band levels. In the following we will write Δ for Δ_a. If D is the mean level spacing of the energy eigenvalues of H_E, we will also assume that the characteristic tunneling frequencies, which are of the order of ω_o, are much larger than D. Therefore, the times involved in the calculation satisfy the inequalities

(14)

where t_P is the Poincarè recurrence time. Notice that, in the same way as ε and ω_o, the energies Δ, Δ_a, and D are in units of ħ. The assumptions in (14) are taken into account in the calculation of the ensemble average of (10). In this calculation, we meet with quantities like

(15)

which become

(16)

where

, and Δ are assumed to vary slowly with the energy. Since the product of

and

appear systematically and the energies ε_j and ε_j+1 vary almost continuously along the bath spectrum, we define the density ρ_υ(ε) = v²(ε)ρ(ε), in units of (E²/ħ²)(ħ/E) = 1/s. The values of m and n that determine the terms (m, n) of the sum in (10) determine also the order of the contribution to the survival probability, which is given by ν = (m + n)/2. For easy reference we write the survival probability as

(17)

with

(18)

3. Time Evolution of the Survival Probability and the Spin Polarization

In this section we present, in detail, results to zeroth and first order of the interaction picture (IP) of the survival probability described in previous section for a spin 1/2 system interacting with a magnetic field in the Faraday configuration and randomly with its environment. The second-order terms of the survival probability are calculated, in detail, in the appendix.

3.1. Survival and Spin Polarization to Zeroth Order of the IP

The zeroth order contribution describes the time evolution of the isolated spin 1/2 system in the Faraday geometry. This contribution is given by the term

in (18). The survival probability to zeroth order is then the well-known quantity

(19)

This means that the probability to find the isolated spin 1/2 system in the eigenstate | − 1〉 of σ_z, in the Faraday geometry, is

(20)

Therefore, as expected, the spin polarization of the isolated spin 1/2 system, is

(21)

It is clear that, in this case, the thermal average is

(22)

3.2. Survival and Spin Polarization to First Order of the IP

We calculate now the survival probability and spin polarization of the spin 1/2 system in the Faraday geometry, to first order of the interaction picture. In this calculation, we use the property

(23)

For the first-order contribution, we need to evaluate

, and

. The term

is given by

(24)

Neglecting terms of order 1/Δ and smaller, we have

(25)

The term (1,1) is given by

(26)

To order 1/Δ we have

(27)

Taking into account these contributions and the zeroth-order contribution

, we have, to first order of the interaction picture and for Δ ≫ ω_o, the survival probability

(28)

and the spin polarization

(29)

These quantities depend on the level density ρ_υ(ε) and, through the frequency ω_o, on the magnetic field. We show in Figure 3 the time evolution of the survival probability (upper panel) and of the spin polarization (lower panel), for two values of the density of levels ρ_υ(ε) each. For the blue curves we considered ρ_υ1(ε) = 2 × 10⁸ s⁻¹ while for the red curves we have ρ_υ2(ε) = 5 × 10⁸ s⁻¹. In all of these graphs, we consider the frequency ω_o = 2.73556 × 10¹⁰ s⁻¹. In Figure 4 we plot the thermal averages

(30)

and

(31)

assuming that the density of levels ρ_υ is proportional to ϵ^s. The graphs are plotted for T = 300K and for s = 0.2, s = 1 and s = 1.5, which correspond to the subohmic, ohmic, and superohmic dissipation forms, in the spin-boson model [15].

In Figure 5, we have the thermal average of the spin polarization calculated in [28, 29], and on top of it the thermal average of the spin polarization in (31). For this graph we considered ρ = 10⁹ × ϵ^ss⁻¹, with s=0.36 and ω_o = 2.58 × 10¹⁰s⁻¹. The agreement is good up to times of the order 500ps. In the appendix we obtain the polarization

(32)

whose thermal average

(33)

was plotted in Figure 1 on top of the spin polarization calculated in [19]. Our calculation of the spin polarization in Figure 1 was for T = 300K, ρ = 10⁹ × ϵ^ss⁻¹, with s = 0.28, and ω_o = 2.58 × 10¹⁰s⁻¹. As mentioned before, the agreement is rather good and strengthens the idea that in complex systems some processes are insensitive to the details of the interaction, and only few “gross properties” are relevant and can be described by suitable statistical models.

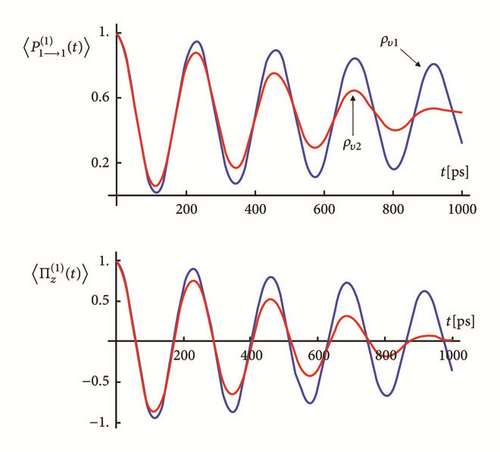
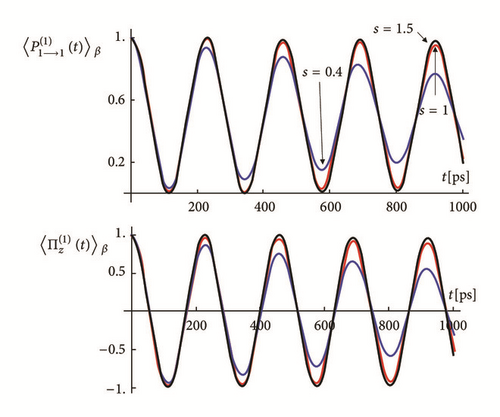
The analytical expressions of the survival probabilities and spin polarizations reported here allow also exploring the behavior of these quantities as functions of the magnetic field. This is the purpose in the next section.

4. The Field Effect on the Spin Polarization

A great amount of experimental research has been published to show the behavior of the spin polarization as function of the magnetic field. Nevertheless, we shall present here the behavior of the thermal averages of the survival probability and the spin polarization , as functions of the magnetic field and time.

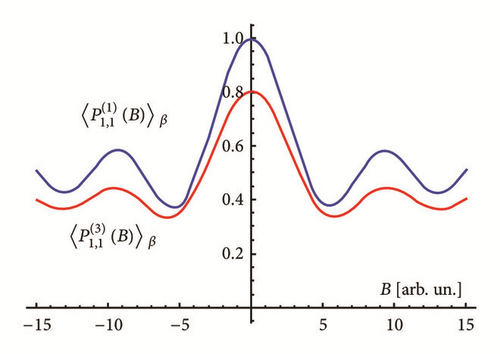
In Figure 6 we plot the magnetic field behavior of the survival probabilities and as functions of the magnetic field at t = 1.210⁻⁹ and for level density ρ_υ(ε) = 10⁹ϵ^s, with s = 0.2. As expected, the survival probability tends to a probability of 1/2 as the magnetic field increases.

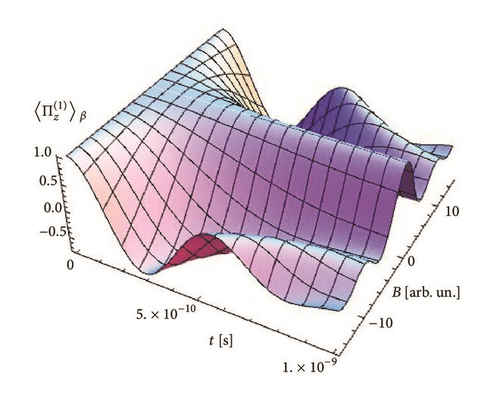
In Figure 7 we show the spin polarization as function of time and of the magnetic field for a level density ρ_υ(ε) = 10⁹ϵ^s, with s = 0.2. The oscillating behavior shown in this graph is compatible with the previous results, not only as function of time but also as function of the magnetic field.

5. Conclusions

We presented here a simple model to study the behavior of a two-level system interacting stochastically with its environment in the presence of a magnetic field in the Faraday configuration. We calculated the survival and spin polarization to first and second order of the interaction picture. We have shown the oscillating evolution of the thermal average of these quantities as function of time and the magnetic field, for different values of the temperature and for the level density ρ(ϵ) ∝ ϵ^s, in the subohmic, ohmic, and superohmic dissipation forms. We have shown that the spin polarization behavior agrees rather well with the time evolution of the spin polarization observed and calculated, recently, for the electron-nucleus dynamics of Ga centers in dilute (Ga,N)As semiconductors. The calculation of the higher order terms, in the interaction picture, is ongoing and we hope to obtain more accurate results and a better understanding of the oscillating behaviors reported here.

Conflicts of Interest

The author declares that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

I acknowledge useful comments and corrections of Herbert P. Simanjuntak and A. Robledo-Martinez.

Appendix

Survival Probability and Spin Polarization to Second Order

For the second-order contribution, one has to evaluate the following terms

, and

. For the term

we have to evaluate

(A.1)

with ensemble average

(A.2)

For the term

, there are two possible configurations for the pairing of the matrix elements V_ab that contribute to the same order in the leading order result. In Figure 8, we show graphically these pairing in configurations A and B. The corresponding averages are

(A.3)

(A.4)

Similarly, for the term

, the pairing of the matrix elements V_ab that contribute to the same order of the survival probability are shown in Figure 9, in configurations A and B. The corresponding averages are

(A.5)

(A.6)

Neglecting terms of order 1/Δ and higher, adding the contributions of all these terms and taking into account also the first-order term

, we have

(A.7)

Hence the probability that at time t the particle is in the spin state |−1〉 is

(A.8)

Therefore the polarization, to second order of the interaction picture, is given by

(A.9)

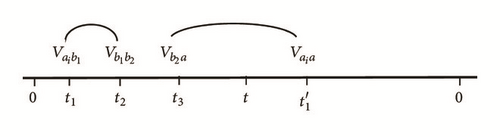
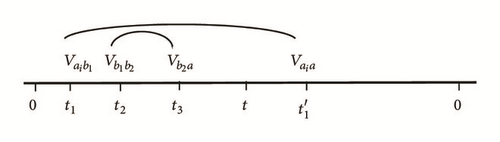
Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Fabian J., Matos-Abiague A., Ertlera C., Stano P., and Zutic′ I., Semiconductor spintronics, Acta Physica Slovaca. (2007) 57, no. 565.
Web of Science® Google Scholar
2 Johnston-Halperin E., Lofgreen D., Kawakami R. K., Young D. K., Coldren L., Gossard A. C., and Awschalom D. D., Spin-polarized Zener tunneling in (Ga,Mn)As, Physical Review B: Condensed Matter and Materials Physics. (2002) 65, no. 4, 041306, https://doi.org/10.1103/PhysRevB.65.041306.
10.1103/PhysRevB.65.041306
Google Scholar
3 Kohda M., Ohno Y., Takamura K., Matsukura F., and Ohno H., A spin Esaki diode, Japanese Journal of Applied Physics. (2001) 40, no. 12, L1274–L1276, https://doi.org/10.1143/JJAP.40.L1274, 2-s2.0-0035698922.
10.1143/JJAP.40.L1274
CAS Web of Science® Google Scholar
4 Kalevich V. K., Afanasiev M. M., Shiryaev A. Y., and Egorov A. Y., Amplification of spin-filtering effect by magnetic field in GaAsN alloys, Physical Review B: Condensed Matter and Materials Physics. (2012) 85, no. 3, 035205, https://doi.org/10.1103/PhysRevB.85.035205.
10.1103/PhysRevB.85.035205
Google Scholar
5 Puttisong Y., Wang X. J., Buyanova I. A., and Chen W. M., Effect of hyperfine-induced spin mixing on the defect-enabled spin blockade and spin filtering in GaNAs, Physical Review B. (2013) 87, 125202.
10.1103/PhysRevB.87.125202
Web of Science® Google Scholar
6 Sandoval-Santana C., Balocchi A., Amand T., Harmand J. C., Kunold A., and Marie X., Room-temperature optical manipulation of nuclear spin polarization in GaAsN, Physical Review B: Condensed Matter and Materials Physics. (2014) 90, no. 11, 115205, https://doi.org/10.1103/PhysRevB.90.115205.
10.1103/PhysRevB.90.115205
Google Scholar
7 Rosen N. and Zener C., Double stern-gerlach experiment and related collision phenomena, Physical Review A: Atomic, Molecular and Optical Physics. (1932) 40, no. 4, article 502, https://doi.org/10.1103/PhysRev.40.502, Zbl0004.42704.
10.1103/PhysRev.40.502
Google Scholar
8 Gamow G., Zur quantentheorie des atomkernes, Zeitschrift für Physik. (1928) 51, no. 3-4, 204–212.
10.1007/BF01343196
CAS Google Scholar
9 Weisskopf V. F. and Wigner E. P., Berechnung der natürlichen linienbreite auf grund der diracschen lichttheorie, Zeitschrift für Physik. (1930) 63, no. 1-2, 54–73.
10.1007/BF01336768
CAS Google Scholar
10 Weisskopf F. and Wigner E. P., Über die natürliche Linienbreite in der Strahlung des harmonischen Oszillators, Zeitschrift für Physik. (1930) 65, no. 1-2, 18–29.
10.1007/BF01397406
CAS Google Scholar
11 van Hove L., The approach to equilibrium in quantum statistics: a perturbation treatment to general order, Physica. (1957) 23, no. 1-5, 441–480.
10.1016/S0031-8914(57)92891-4
Web of Science® Google Scholar
12 Pirc R. and Gosar P., Green′s function approach to paraelastic relaxation, Physik der kondensierten Materie. (1969) 9, no. 4, 377–398.
10.1007/BF02422918
Google Scholar
13 Sander L. M. and Shore H. B., Theory of paraelectric resonance and relaxation, Physical Review B: Condensed Matter and Materials Physics. (1969) 3.
Google Scholar
14 Chakravarty S. and Legget A. J., Dynamics of the two-state system with ohmic dissipation, Physical Review Letters. (1984) 52, no. 5.
10.1103/PhysRevLett.52.5
Web of Science® Google Scholar
15 Legget A. J., Chakravarty S., Dorsey A. T. et al., Dynamics of the dissipative two-state system, Reviews of Modern Physics. (1987) 59, no. 1.
Web of Science® Google Scholar
16 Cohen-Tannoudji C., R. Balian, S. Haroche, and S. Lieberman, Atoms in strong magnetic fields, in Frontiers in Laser Spectroscopy, Frontiers in Laser Spectroscopy, 1977, 1, Amsterdam, Holland.
Google Scholar
17 Mello P. A., Pereyra P., and Kumar N., A soluble random-matrix model for relaxation in quantum systems, Journal of Statistical Physics. (1988) 51, no. 1-2, 77–94, https://doi.org/10.1007/BF01015321, MR952747.
10.1007/BF01015321
Web of Science® Google Scholar
18 Pereyra P., Random matrix model for dissipative two-level systems, Journal of Statistical Physics. (1991) 65, no. 3-4, 773–792, https://doi.org/10.1007/BF01053754, MR1137434, Zbl0943.82574.
10.1007/BF01053754
Web of Science® Google Scholar
19 Azaizia S., Carrère H., Sandoval-Santana J. C. et al., Electron-nuclear coherent spin oscillations probed by spin-dependent recombination, Physical Review B: Condensed Matter and Materials Physics. (2018) 97, no. 15, 155201.
10.1103/PhysRevB.97.155201
CAS Google Scholar
20 Brody T. A., Flores J., French J. B., Mello P. A., Pandey A., and Wong S. S., Random-matrix physics: spectrum and strength fluctuations, Reviews of Modern Physics. (1981) 53, no. 3, 385–479, https://doi.org/10.1103/RevModPhys.53.385, MR619406.
10.1103/RevModPhys.53.385
CAS Web of Science® Google Scholar
21 Agassi D., Weidenmüller H. A., and Mantzouranis G., The statistical theory of nuclear reactions for strongly overlapping resonances as a theory of transport phenomena, Physics Reports. (1975) 22, no. 3, 145–179.
10.1016/0370-1573(75)90028-9
Google Scholar
22 Agassi D., Ko C. M., and Weidenmüller H. A., Transport theory of deeply inelastic heavy-ion collisions based on a random-matrix model. i. derivation of the transport equation, Annals of Physics. (1977) 107, no. 1-2, 140–167, https://doi.org/10.1016/0003-4916(77)90207-X.
10.1016/0003-4916(77)90207-X
CAS Web of Science® Google Scholar
23 Weidenmüller H. A., K. W. McVoy and W. A. Friedman, Transport theory of deeply inelastic heavy-ion reactions, Theoretical Methods in Medium-Energy and Heavy-Ion Physics, 1978, Plenum Press, New York, NY, USA.
10.1007/978-1-4613-2877-3_4
Google Scholar
24 Mello P. A., Pereyra P., and Seligman T. H., Information theory and statistical nuclear reactions. I. general theory and applications to few-channel problems, Annals of Physics. (1985) 161, no. 2, 254–275, https://doi.org/10.1016/0003-4916(85)90080-6, MR793815.
10.1016/0003-4916(85)90080-6
CAS Web of Science® Google Scholar
25 Mello P. A., Pereyra P., and Kumar N., Macroscopic approach to multichannel disordered conductors, Annals of Physics. (1988) 181, no. 2, 290–317, https://doi.org/10.1016/0003-4916(88)90169-8.
10.1016/0003-4916(88)90169-8
Web of Science® Google Scholar
26 Kota V. K. B. and Chavda N. D., Random k-body ensembles for chaos and thermalization in isolated systems, Entropy. (2018) 20, no. 7, article 541, https://doi.org/10.3390/e20070541.
10.3390/e20070541
PubMed Web of Science® Google Scholar
27 Borgonovi F., Izrailev F. M., Santos L. F., and Zelevinsky V. G., Quantum chaos and thermalization in isolated systems of interacting particles, Physics Reports. (2016) 133, article 122, 1–58, https://doi.org/10.1016/j.physrep.2016.02.005, MR3478934.
10.1016/j.physrep.2016.02.005
Google Scholar
28 Sandoval-Santana J. C., Detección del flip-flop de los centros paramagnéticos del GAAsN mediante bombeo óptico en régimen pulsado, 2018, Universidad Autónoma Metropolitana, Mexico City, Mexico.
Google Scholar
29 Sandoval-Santana J. C., Electron-nuclear spin dynamics of Ga centers in GaAsN dilute nitride semiconductors probed by pump-probe spectroscopy, The European Physical Journal Plus. (2018) 133, no. 122, https://doi.org/10.1140/epjp/i2018-11957-4.
10.1140/epjp/i2018-11957-4
Web of Science® Google Scholar
30 Vyas M. and Seligman Th. H., Random matrix ensembles for many-body quantum systems, AIP Conference Proceedings. (2017) 1950, no. 1, https://doi.org/10.1063/1.5031701.
10.1063/1.5031701
Google Scholar

All articles

Spin Polarization Oscillations and Coherence Time in the Random Interaction Approach

Abstract

1. Introduction

2. The Random Matrix Model and the Survival Probability

3. Time Evolution of the Survival Probability and the Spin Polarization

3.1. Survival and Spin Polarization to Zeroth Order of the IP

3.2. Survival and Spin Polarization to First Order of the IP

4. The Field Effect on the Spin Polarization

5. Conclusions

Conflicts of Interest

Acknowledgments

Appendix

Survival Probability and Spin Polarization to Second Order

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Spin Polarization Oscillations and Coherence Time in the Random Interaction Approach

Abstract

1. Introduction

2. The Random Matrix Model and the Survival Probability

3. Time Evolution of the Survival Probability and the Spin Polarization

3.1. Survival and Spin Polarization to Zeroth Order of the IP

3.2. Survival and Spin Polarization to First Order of the IP

4. The Field Effect on the Spin Polarization

5. Conclusions

Conflicts of Interest

Acknowledgments

Appendix

Survival Probability and Spin Polarization to Second Order

Open Research

Data Availability

References

Figures

References

Related

Information