Formulation of a Linearized Model for Vehicle-Track Interactions
Abstract
In this paper, a fundamental wheel-rail interaction (WRI) element accompanied by its coupling matrices with other vehicle-track components have been derived taking into consideration the aspect of linearization. The key to the presented formulation is the use of the geometrical relationships of relative motions between degrees of freedom (DOFs) and energy principle. To the WRI element, both of the conditions of wheel-rail contacts and wheel-rail separations are allowed in the numerical computations; besides, the effects of the linear creepage and the gravitational restoring are considered in the description of wheel-rail interactions. By comparing with an advanced three-dimensional nonlinear model, the capability of the linear model in characterizing the response amplitude and frequency characteristic of vehicle-track systems is demonstrated. Moreover, the method for the random vibration analysis of the linear model is presented by treating the creep coefficients as the random sources, through which the safety margin of system response can be predicted well. From the numerical examples, it is, additionally, concluded that the lateral creep coefficient holds significant influence on wheel-rail lateral interactions and track vibrations, especially for the responses at low frequency ranges.
1. Introduction
To ensure a comfortable, safe, and efficient transportation, it was critical to scientifically assess the dynamic performance of vehicle-track systems under varying loads; consequently, a vehicle-track interaction system was formulated. The vehicle-track interactions are essentially nonlinear, while for lowering the modelling complexity, increasing the computational efficiency, and broadening the model application, it was rather popular to simplify the vehicle-track systems as a coupled and linearized system.
In the last decades, the models aiming at describing the vehicle-track interactions have experienced a rapid development from the earliest two-dimensionally vertical models [1–8] to more advanced three-dimensionally spatial ones. Concerning the system nonlinearity, Sun et al. [9] presented a 3D wagon-track system dynamics model, where a wagon system with 37 degrees of freedom (DOFs), a four-layer track, and the wheel-rail interfacial contacts were comprehensively considered; Zhai et al. [10] presented a theoretical framework and methodologies for characterizing the 3D nonlinear vehicle-track interactions; recently, Xu and Zhai [11, 12] made pioneering and the most advanced work in developing temporal-spatial stochastic models for train-track (bridge) interactions, in which the finite element method (FEM) and random theory were introduced to construct the track systems and to achieve the random vibration analysis, respectively.
With the development of nonlinear models, the methodologies are constantly developed to mathematically investigate the vehicle-track (bridge) interactions in the field of linearization modelling. See for instance, Zeng and Guo [13] made pioneering work on building a train-bridge time-dependent model by an application of the principle of a stationary value of total potential energy of dynamic system [14]; Yang and Wu [15] proposed a versatile element that is capable of considering various vehicle-bridge interaction (VBI) effects; however, the condition of wheel-rail separation is neglected in both of the these two models. Some other related researches can be consulted in [16, 17]. Moreover, Zhang et al. [18] regarded the vehicle as a spring-mass-damper system and the track as an infinitely long substructural chain consisting three layers of rail, sleeper, and ballast, and the vehicle and the tracks were coupled by linear springs; based on this developed model, the pseudoexcitation method (PEM) was introduced to achieve the high-efficient frequency characteristic analysis for system indices. Nguyen et al. [19] presented simulations for vehicle-substructure dynamic interactions and wheel movements, where the two compatibilities, i.e., force equilibrium and geometrical relation, are satisfied in the wheel-rail interfaces.
Additionally, the train-track dynamic simulations under transient conditions also show remarkable significance to railway maintenance, assessment, rolling fatigue, safety, etc. See for instance, Handoko and Dhanasekar [20] pointed out that the traction and braking forces are seldom considered in the practice of wagon dynamics simulation, although these forces will greatly modify the wheel-rail contact parameters and then the wheelset dynamics; Liu et al. [21] also studied the mechanism of wheelset longitudinal vibration by analysing the process of wheel/rail rolling contact; generally, the track defects can cause profound effects to the dynamics of the railway wagon; Zhang and Dhanasekar [22] noticed this problem and published a model for the dynamics of wagons subject to braking/traction torques on a perfect track by explicitly considering the pitch degree of freedom for wheelsets [23, 24] and extended this model for cases of lateral and vertical track geometry defects and worn railhead and wheel profiles; Grossoni et al. [25] examined the dynamic behaviour at a rail joint using a two-dimensional vehicle-track coupling model, where the influence of the number of layers and the number of elements between two sleepers and the beam model are investigated. Laterally, Zong and Dhanasekar [26] considered the gap between rail joints to account for thermal movement and to maintain electrical insulation for the control of signals and/or broken rail detection circuits; besides, railhead can provide high stresses due to the passage of heavily loaded wheels through a very small contact patch [27], and a multibody dynamic model was developed in [28] to accurately model and analyse the track dynamic behaviour in vicinity of rail discontinuities; recently Zong and Dhanasekar [29] provided a idea of simplifying the design of the IRJs consisting of only two pieces of insulated rails embedded into a concrete sleeper; Ling et al. [30] presented a formulation for a passive road-rail crossing involving stiffened edges of the raised road pavement to minimise the risk of failure of wheel-rail contact using a nonlinear three-dimensional multibody dynamics model; additionally, a series of work on impact derailment due to lateral collisions between heavy road vehicles and passenger trains at level crossings and the associated derailments had also been conducted in [31–34].
In the above presentations, though the nonlinear and linear vehicle-track interaction, models have been established by many researchers, while the applicability of the linear model and its comparison to the nonlinear model have rarely been reported. In this paper, a contribution, which is not beneficial to train-track dynamic to severe transient impact/rolling issues, was made to develop a highly practical and efficient model, and fully deriving the equation of motion for the linearized vehicle-track interactions. The coupling mechanism between a railway vehicle and the tracks in relation to wheel-rail interactions and system responses that are of great interest to railway engineers will be revealed.
- (1)
In section 2, a general wheel-rail interaction (WRI) element is presented, in which the jumping of the vehicle off the rail, the linear creepage, and gravitational restoring actions are properly considered.
- (2)
In section 3, the coupling matrices for building the physical-mechanical connections between system components and WRI element are elaborately illustrated and finally the unified equation of motion for the vehicle-track system is established.
- (3)
In section 4, numerical examples, including comparisons with the nonlinear model and a practice of random vibration analysis, are conducted to validate the reliability and feasibility of the proposed model.
- (4)
In section 5, some conclusions are drawn accordingly.
2. WRI Element
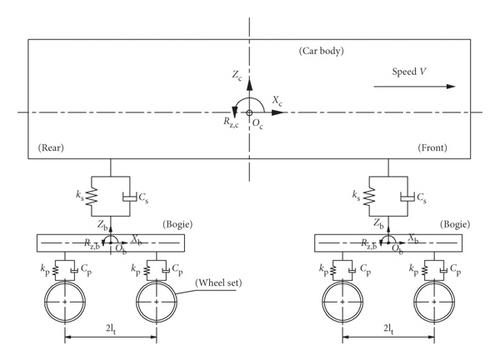
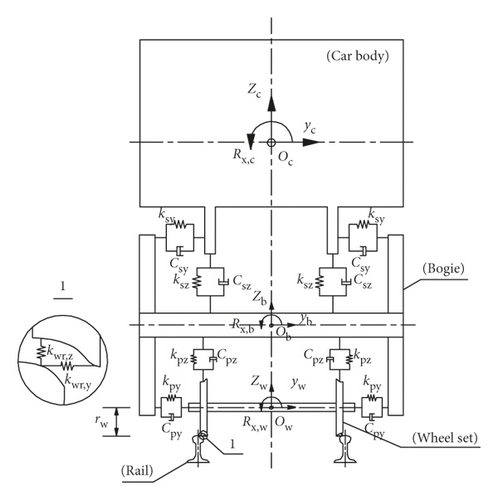
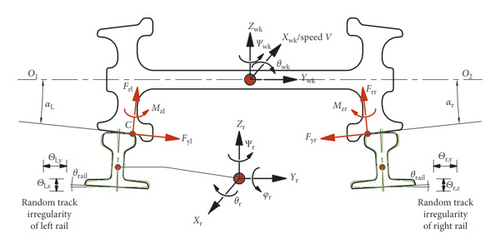
In the whole vehicle-track model presented in Figure 1, the wheel-rail interactions play a key role in determining the dynamic trajectories of vehicle/track behaviours. In this part, a wheel-rail interaction (WRI) element will be developed to depict the wheel-rail interaction mechanism from aspect of linearization.

2.1. Displacement Vector
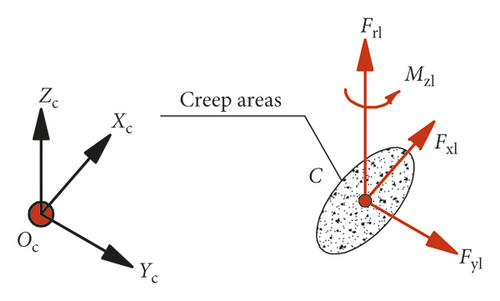
2.2. Wheel-Rail Coupling Matrices
In most of the running conditions, the wheels constantly keep contact with the rails, thus the wheel-rail coupling matrices that consider the wheelset’s vertical displacement as nonindependent will be presented here as an emphasis. The wheel-rail coupling matrices are marked by subscript “wr” with order of .
Using the same strategy, the damping matrix, stiffness matrix, and load vector over the extensive displacement vector, i.e., Cwr, Kwr, and Fwr, can be derived in the same way as Mwr.
3. Vehicle-Track Interaction Model
As illustrated in Figure 1, a ballastless track system was formulated with a moving vehicle subjected to constant velocity. The railway vehicle was modelled as a four-axle mass-spring-damper system, which consisted of a car body, two bogie frames, four wheelsets, and two stage suspensions. The car body and bogie frames have 6 DOFs each including motions of longitudinal X, transverse Y, bounce Z, roll Φ, yaw ψ, and pitch β with respect to their mass centroids, respectively, while for the wheelsets, only the motions of longitudinal, transverse, vertical, and yaw were considered. The total number of DOFs of vehicle system was therefore 34. The vehicle proceeded with velocity v in the longitudinal direction.
In the track system, the rails were modelled as spatial Bernoulli–Euler beam supported by discrete viscoelastic supported with finite length, and the rail pads were assumed as linear spring-damper elements. Moreover, slab tracks were assumed to be thin plate elements connected to subgrade through cement asphalt mortar (CA mortar) layer, which was regarded as continuous plane springs and dashpots.
3.1. Equation of Motion for the Vehicle-Track Interaction Systems
The wheel-rail coupling matrices, namely, Mwr, Cwr, and Kwr, were core terms in Equation (23). In Equation (23), the elements in the wheel-rail coupling matrices can be partitioned and inserted into different positions based on the “set-in-right-position” rule [37]. The submatrices of the slab track accompanied by their interactions with the rail elements can be found in [38], here not given for brevity.
The submatrices of vehicle systems, the coupling submatrices between vehicle systems and wheel-rail interaction element and the force vectors will be elaborated in the following sections.
3.2. The “Set-in-Right-Position” Rule
It is obvious that Equation (25) denotes the i-th equilibrium equation of this dynamic system. Herein, δγi denotes the i-th row in the matrix; besides, there are displacement parameters γj, j = 1, 2, …, n derived from ∂ ∏ /∂γi. In the dynamic matrices, the serial number j denotes the j-th column. Hence, the coefficient multiplied by δγi and γj should be set in the cross position of the matrix at the i-th row and the j-th column.
3.3. Matrices for the Vehicle Systems
The damping matrix, i.e., Cvv, with the same order of Kvv, can be obtained by substituting the stiffness coefficient k in Kvv with damping coefficient c.
3.4. Matrices for the Vehicle-WRI Element Interactions
The coupling matrices for vehicle-WRI element interactions were marked with the subscript ‘v-wr’ or ‘wr-v’. Before deriving the matrices Kv−wr, Kwr−v, Cv−wr, and Cwr−v, one can deduce the interaction matrices between the vehicle and the rails at first, namely, Kvr and Cvr.
The damping matrix, i.e., Cvr, with the same order of Kvr, can be obtained by substituting the stiffness coefficient k in Kvr with damping coefficient c.
The damping matrices Cv−wr and Cwr−v had the same expression as Kv−wr and Kwr−v, respectively, by merely substituting the stiffness coefficient k with damping coefficient c.
3.5. Force Vectors
All elements in the load vector of the slab track Fs are zero.
Till now, all details about the construction of this linear vehicle-track dynamic model had been illustrated. Since the shape functions, i.e., NR,z in Equation (2) and the differentiation with respect to the local coordinate ξw are time-dependent, the dynamic matrices and force vectors in Equation (23) should be updated in each time-step. Moreover, unlike the most vehicle-track models presented in Refs. [3, 39], no iteration procedures are required to guarantee the response stability of the dynamic model.
Equation (23) can be solved by the step-by-step integration method to obtain simultaneously the dynamic responses of vehicle-track systems even using relatively large integration-steps.
4. Numerical Examples
In the numerical examples, it is assumed that a railway vehicle runs with a constant velocity of 350 km/h on the ballastless slab-tracks. For constructing the vehicle-track model, a track segment element is taken between two adjacent rail pads [40]; moreover, a cyclic calculation model proposed by Xu et al. [41] is applied to increase the computational efficiency lowered by the high DOFs of the long track finite element model, and the boundary effect of the tracks can be reduced fairly well.
The physical parameters of the vehicle and the tracks can be referred in Tables 1 and 2. The track irregularity, as the excitation of the wheel-rail interactions, is obtained by a track irregularity probabilistic model [42] where the measured track irregularities from a high-speed line of China are used as the data sources.
| Notation | Parameter | Values |
|---|---|---|
| Mc | Car body mass (kg) | 34500 |
| Mt | Bogie mass (kg) | 3500 |
| Mw | Wheelset mass (kg) | 2200 |
| Icx | Mass moment of inertia of car body about the X axis (kg m2) | 124304 |
| Icy | Mass moment of inertia of car body about the Y axis (kg m2) | 1560400 |
| Icz | Mass moment of inertia of car body about the Z axis (kg m2) | 1521000 |
| Itx | Mass moment of inertia of bogie about the X axis (kg m2) | 2522 |
| Ity | Mass moment of inertia of bogie about the Y axis (kg m2) | 1722 |
| Itz | Mass moment of inertia of bogie about the Z axis (kg m2) | 3100 |
| Iwx | Mass moment of inertia of wheelset about the X axis (kg m2) | 730 |
| Iwy | Mass moment of inertia of wheelset about the Y axis (kg m2) | 84 |
| Iwz | Mass moment of inertia of wheelset about the Z axis (kg m2) | 990 |
| Kpx | Stiffness coefficient of primary suspension along the X axis (MN/m) | 11.68 |
| Kpy | Stiffness coefficient of primary suspension along the Y axis (MN/m) | 7.40 |
| Kpz | Stiffness coefficient of primary suspension along the Z axis (MN/m) | 1.173 |
| Ksx | Stiffness coefficient of secondary suspension along the X axis (MN/m) | 0.1790 |
| Ksy | Stiffness coefficient of secondary suspension along the Y axis (MN/m) | 0.1790 |
| Ksz | Stiffness coefficient of secondary suspension along the Z axis (MN/m) | 0.61 |
| Cpz | Damping coefficient of primary suspension along the Z axis (kN s/m) | 19.60 |
| Csy | Damping coefficient of secondary suspension along the Y axis (kN s/m) | 54.80 |
| Csz | Damping coefficient of secondary suspension along the Z axis (kN s/m) | 9.80 |
| Lc | Semilongitudinal distance between bogies (m) | 8.75 |
| Lt | Semilongitudinal distance between wheelsets in bogie (m) | 1.25 |
| R0 | Wheel radius (m) | 0.43 |
| Notation | Parameter | Values |
|---|---|---|
| E | Elastic modulus of rail (N/m2) | 1970400 |
| ρ | Density of rail (kg/m3) | 7.16 × 103 |
| I0 | Torsional inertia of rail (m4) | 3.731 × 10−5 |
| Iy | Rail second moment of area about the Y axis (m4) | 3.257 × 10−5 |
| Iz | Rail second moment of area about the Z axis (m4) | 5.20 × 10−6 |
| GK | Rail torsional stiffness (N m/rad) | 1.9587 × 105 |
| Kpv | Fastener stiffness in vertical direction (N/m) | 2.9 × 107 |
| Kph | Fastener stiffness in lateral direction (N/m) | 1.5 × 107 |
| Chp | Fastener damping in vertical direction (N s/m) | 5 × 104 |
| Ch | Fastener damping in lateral direction (N s/m) | 5 × 104 |
| Es | Elastic modulus of rail (N/m2) | 3.6 × 1011 |
| μ | Poisson ratio of slab | 0.25 |
| Ms | Mass per unit volume of slab (kg/m3) | 2400 |
| Hs | Height of slab (m) | 0.19 |
| Ls | Length of slab (m) | 4.95 |
| Ws | Width of slab (m) | 2.40 |
| KvCA | Equivalent vertical stiffness coefficient of CA layer (N/m) | 6.0 × 107 |
| CvCA | Equivalent vertical damping coefficient of CA layer (N/m) | 9.0 × 104 |
| KhCA | Equivalent vertical stiffness coefficient of CA layer (N/m) | 1.03 × 106 |
| ChCA | Equivalent vertical damping coefficient of CA layer (N/m) | 1.0 × 106 |
4.1. Comparison between the Linear Model and the Nonlinear Model
To investigate the efficiency and feasibility of this presented model, a comparative analysis is conducted against the nonlinear model developed by Xu and Zhai [11]. In the nonlinear model, the three-dimensional wheel-rail nonlinear contacts are considered comprehensively.
Figures 3 and 4 show the comparisons on the lateral and vertical accelerations of the car body. As seen from these two figures, though there exists unavoidable discrepancy between the models on response amplitudes, the tendency of the time-domain responses of the linear model coincides well with that of the nonlinear model; moreover, the dominant frequencies of the car body accelerations drawn from these two models are almost the same. For the vertical acceleration of the car body, the absolute maximum values are 1.6 m/s2 and 1.41 m/s2; with respect to the nonlinear model and linear model, the dominant frequencies are 1.17 Hz and 6.25 Hz. While for the lateral acceleration, the absolute maximum values of the nonlinear and linear model are 0.145 m/s2 and 0.144 m/s2, respectively; besides, the domain frequencies for these two models are 1.72 Hz, 5.46 Hz, and 10.94 Hz and are similar, but there exists a slight difference in spectral densities inevitably.
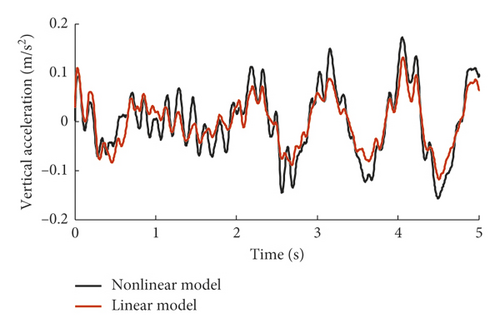
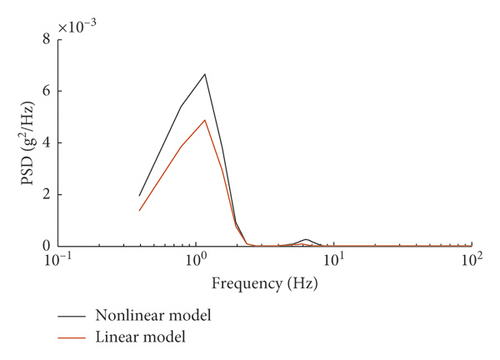
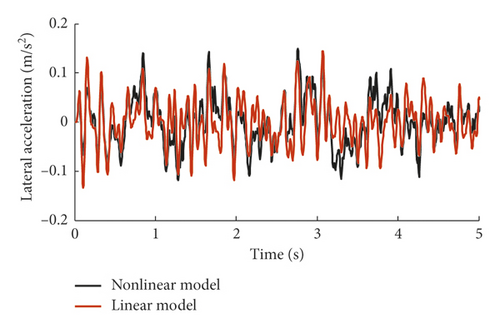
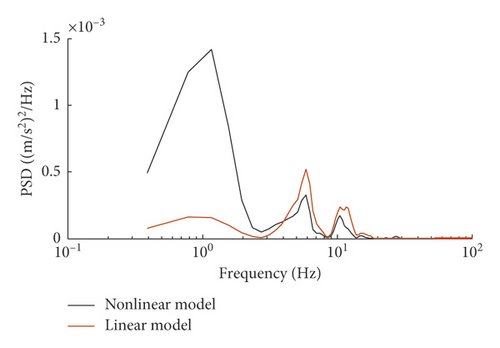
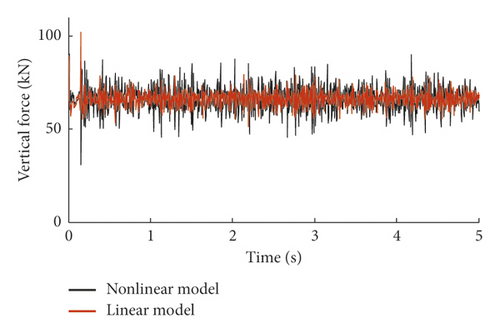
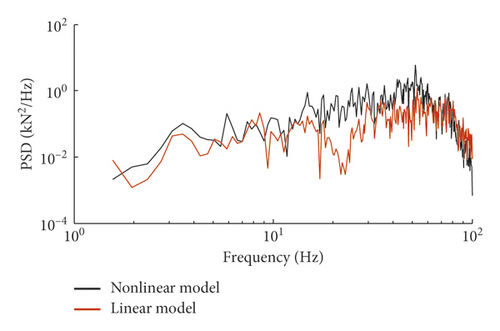
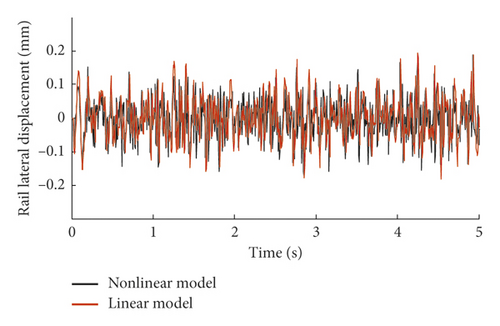
Figure 5 illustrates the discrepancy of the wheel-rail vertical force between the nonlinear model and the linear model due to the implementation of different wheel-rail coupling models. As observed from Figure 4, there is a significant correlation between the results of these two models; see for instance, the sections possessing violent wheel-rail interactions are almost the same, but the forces derived by the nonlinear model are locally larger than those of the linear model, especially at high frequency ranges shown in Figure 5(b), because the time interval of integration of the nonlinear model should be greatly smaller than the linear model for guaranteeing the stability of time integration. Moreover, Figure 6 shows the dynamic responses of the rail lateral displacement at both time and frequency domains, from which one can observe that the results of these two models coincide well with each other. The linear model has accurately characterized the dominant frequencies of rail lateral displacement in the whole frequency range of 1–200 Hz though there are differences in spectral values.
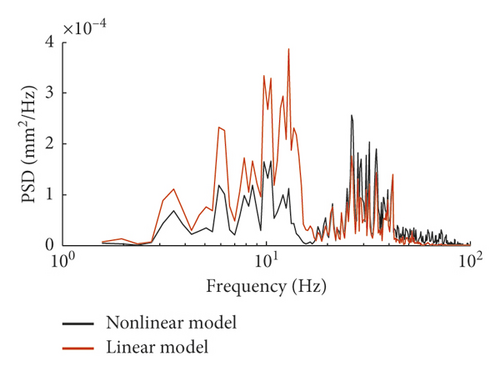
In the numerical calculation, if the railway vehicle moves on the track for one second, the computation time for the linear model is 15 sec, while for the nonlinear model, it is 156 sec in MATLAB®, and thus the computational efficiency has been significantly improved.
4.2. Random Vibrations concerning Randomness of Creep Coefficients
Creep coefficient possesses key influence on wheel-rail tangential interactions. Through numerical investigations, it is noticed that the lateral creep coefficient CY in the linearized model will majorly determine the vehicle-track lateral dynamics under irregular excitations. Undoubtedly, the creep coefficients are time-dependent and show randomicity. For obtaining more complete results, there is a necessity to treat the model as an ergodic dynamical system where the most influential parameters, e.g., creep coefficient, should be considered with an ergodicity.
- (2)
Since the PDF of CY denoted by pCy is obtained in the above step, the methods for random parameters selection presented in Ref. [5] can be implemented to get the represented random field of CY, that is, ΩCy.
- (3)
Set H(·) as the operator of vehicle-track interaction model and loading ΩCy and track irregularity vector TIrre into H(·), the random vibration of vehicle-track systems Rindi can be calculated out consequently, that is,
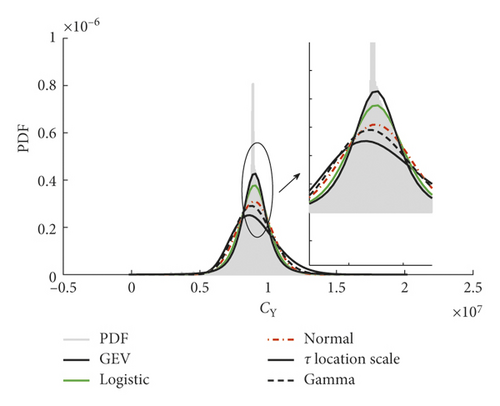
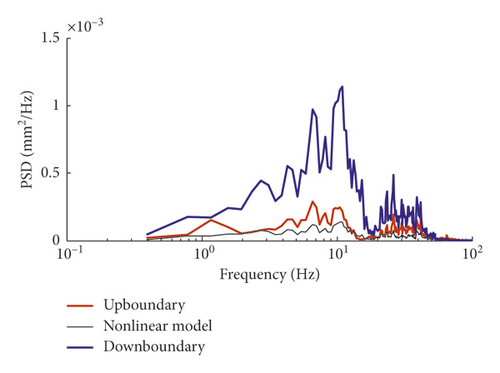
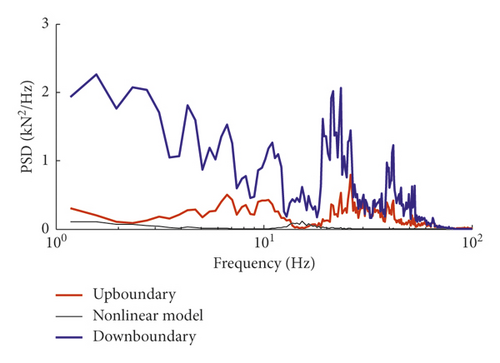
It is obvious that time-domain responses of the linear model will inevitably envelop those of the nonlinear model. Therefore, with an implementation of the random vibration analysis, the results derived by the linear model can be provided as a reference to guarantee the safety margin of the vehicle-track dynamic behaviours.
However, it should be noted that though the linear model is capable of characterizing the characteristic frequencies of dynamic indices, the chosen of the creep coefficient will exert significant influence on the response amplitude; moreover, the responses of wheel-rail lateral force at low frequency of 10 Hz below will increase violently, which should be treated as one of the deficiencies of the linear model with an emphasis. It is therefore a rather important work to choose the creep coefficient optimally.
5. Conclusions
- (1)
The linearized model can give approachable results to the nonlinear model regarding the response amplitudes and the main dominant frequencies characterized by these two models are also similar. However, there exist obvious differences in frequency spectrum amplitude.
- (2)
This presented model possesses higher computational stability due to the linearization. However, this linearization might lead to acceptable deviations in engineering practice comparing to the nonlinear model.
- (3)
In this dynamic condition, the system responses at low frequency range of 0–16.5 Hz will be significantly enlarged by the increase of the lateral creep coefficient.
- (4)
This current work shows limitations for dynamics problems related to transients, discrete joints, derailment, etc.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this article.
Acknowledgments
This work was supported by the National Key Research and Development Program of China (grant no. 2016YFB120050).
Appendix
A. Matrix Formulation for Vehicle System
B. Matrix Formulation for Vehicle-WRT Coupled System
Open Research
Data Availability
The data we used in this paper for calculation, analysis, and formula derivation are included in this paper or can be found in the references listed in this paper.




