Considering the microstructure of tooth surface and the dynamic characteristics of the vibration responses, a compound dynamic backlash model is employed for the gear transmission system. Based on the fractal theory and dynamic center distance, respectively, the dynamic backlash is presented, and the potential energy method is applied to compute the time-varying meshing stiffness, including the healthy gear system and the crack fault gear system. Then, a 16-DOF coupled lateral-torsional gear-rotor-bearing transmission system with the crack fault is established. The fault characteristics in the time-domain waveform and frequency response and statistics data are described. The effect of crack on the time-varying meshing stiffness is analyzed. The vibration response of three backlash models is compared. The dynamic response of the system is explored with the increase in crack depth in detail. The results show that the fault features of countershaft are more obvious. Obvious fluctuations are presented in the time-domain waveform, and sidebands can be found in the frequency domain responses when the tooth root crack appears. The effect of compound dynamic backlash on the system is more obvious than fixed backlash and backlash with changing center distance. The vibration displacement along meshing direction and dynamic meshing force increases with the increase in crack depth. Backlash and variation of center distance show different tendencies with increasing crack depth under different rotational speeds. Amplitude of the sidebands increases with crack depth increasing. The amplitude of multiplication frequency of rotational frequency has an obvious variation with growing crack depth. The sidebands of the multiplication frequency of meshing frequency show more details on the system with complex backlash and crack fault.

1. Introduction

The gear transmission systems are widely used in many machinery fields, which are employed for transmitting power and changing speed. The steady operation is a necessary condition for the gear system. Therefore, the mechanism and dynamic characteristics of gear failure are a major subject in the dynamic field.

The gearbox failure is closely related to gear tooth, including spalling, pitting, crack, and broken tooth, which potentially lead to a complete damage. In order to clearly detect and diagnose in the gear transmission system, the vibration responses and fault features of the gear transmission system with fault are developed [1–3].

The typical kinds of damage are crack failure and spalling failure. The vibration responses of the gear system are closely related to the time-varying meshing stiffness (TVMS) of the gear pair. Yang and Lin [4] calculated TVMS by the potential energy method considering axial compressive energy, Hertzian energy, and bending energy. Tian [5] further investigated TVMS of a gear pair with crack. Govind et al. [6] studied TVMS, crack propagation behaviour, and the vibration responses of spur gear. Chen et al. [7] presented two improved calculation models for gear tooth fillet-foundation stiffness. When a gear pair appeared a large crack length, the computational accuracy of the two models was compared. Chen and Shao [8] developed a gear pair meshing stiffness calculation method considering tooth profile modification and tooth root crack.

Many outstanding scholars have made great contributions to the research of healthy gear system. Zhou et al. [9] presented a coupled lateral-torsional 16-DOF gear-rotor-bearing system considering piecewise periodic stiffness, friction, and eccentricity, and the motion states and frequency variations were analyzed in detail. In addition, the backlash is an important factor to ensure smooth and reliable operation. Chen et al. [10] investigated the dynamic backlash with the fractal feature and the effect of the dynamic backlash on the 2-DOF gear system. Li et al. [11] researched TVMS that was affected by tooth profile changes and developed bifurcation characteristics of the gear system. Xiang and Gao [12] calculated the differential equation of the gear transmission model with dynamic friction, TVMS, and dynamic backlash on the basis of the 4th order Runge–Kutta method and observed the effect of dynamic backlash and gear eccentricity under different rotational speeds.

Many scholars had made a mountain of work for the gearbox with crack fault. Saxena et al. [13] studied the influences of the meshing stiffness and damping on the flexible rotor-shaft system. They explored vibration responses and frequency characteristics in detail. Mohammed and Rantatalo [14] established a 6-DOF dynamic gear model to study the natural frequency and time-frequency with different crack sizes. Saeed et al. [15] researched vibration responses in the presence of single- and multi-tooth simultaneous crack using the finite element method (FEM). Ma et al. [16] established a perforated gear system with different degree cracks. The gear crack propagation paths, frequency components, and frequency values were analyzed in detail. Ma et al. [17] built a meshing stiffness model for a cracked gear system, and the influences of the crack depth and initial position were analyzed by FEM. Chen et al. [18] presented a meshing stiffness calculation method for the nonuniform tooth root crack along the tooth width. The meshing stiffness and vibration response calculated by three different algorithms were compared. Ma and Chen [19] established a 4-DOF gear system to investigate the dynamic characteristics and vibration responses with local failure and explore the failure mechanism. Hu et al. [20] presented a finite element node dynamic model for gear with crack. The RMS (root-mean-square) of the gear system parameters, vibration waveform, and frequency spectra were analyzed. Chen and Shao [21] investigated the effect of crack on a planetary gear system. Liu et al. [22] studied vibration characteristics of the planetary gear system when sun gear appeared a tooth root crack.

For the research of crack, some scientists devoted to establish a simple gear model, such as simplifying backlash as a fix value, employing a periodic meshing stiffness, and establishing a few-DOF model. In this paper, a 16-DOF coupled lateral-torsional gear-rotor-bearing transmission system considering compound-type dynamic backlash, TVMS, eccentricity, and friction force is established. The compound dynamic backlash on the basis of the microstructure characteristics and vibration features is defined. TVMS is calculated by the potential energy method. This complex model is employed for investigating the effect of crack faults and researching crack failure features. The vibration responses of the gear system are researched by analyzing influences of the rotational speed and crack depth value variation. The differential equations of motion are solved using the Runge–Kutta numerical method. The simulation results, including time-domain waveforms, frequency-domain spectra, and waterfall plots, are shown. We focus on the effect of the crack depth growing on a complex gear system. The amplitude statistics of sideband supply an effective reference for the condition monitoring and fault diagnosis of the gear-rotor-bearing system.

2. Dynamic Model of the Gear-Rotor-Bearing System

2.1. Lumped Mass Model of the Gear System

The lumped mass model of the gear system is consisted of input, gears, shafts, bearing, and output. This model is described in Figure 1. O₁(x₁, y₁) and O₂(x₂, y₂) are the centers of two gears. G₁(x_g1, y_g1) and G₂(x_g2, y_g2) are the barycenters of two gears. m_i (i = 1, 2) are quality of gears. J₁ and J₂ represent the moments of gear inertial. m_bi (i = 1, 2, 3, 4) represent quality of bearing. J_d and J_g are equivalent rotational inertia of input and output terminals. The torsional stiffness and damping of shaft are given by k_ti and c_ti (i = 1, 2). k_si and c_si (i = 1, 2) are, respectively, lateral stiffness and damping. c_bi (i = 1, 2, 3, 4) are equivalent bearing damping, including x direction and y direction. In the x and y directions, F_xi and F_yi (i = 1, 2, 3, 4) are defined as nonlinear bearing forces. ρ_i (i = 1, 2) represent the eccentricity. φ_i (i = 1,2, d, g) are, respectively, angle displacements of gear, pinion, input, and output, and the angle displacements are composed of an angle displacement ω_it (i = 1, 2) and microscopic displacement θ_i(t). According to the geometrical relationship, the equations for the displacement of gears and input/output are given by

\begin{matrix} φ_{1} = ω_{1} t + θ_{1}, \\ φ_{2} = ω_{2} t + θ_{2}, \\ φ_{d} = ω_{1} t + θ_{d}, \\ φ_{g} = ω_{2} t + θ_{g} . \end{matrix}

(1)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The gear system model.

Because of the eccentricity of gears, the rotating geometrical centers O₁(x₁, y₁) and O₂(x₂, y₂) and the barycenters G₁(x_g1, y_g1) and G₂(x_g2, y_g2) are at different positions. The relationship equations are found as

\begin{matrix} x_{g 1} = x_{1} + ρ_{1} \cos φ_{1}, \\ y_{g 1} = y_{1} + ρ_{1} \sin φ_{1}, \\ x_{g 2} = x_{2} + ρ_{2} \cos φ_{2}, \\ y_{g 2} = y_{2} + ρ_{2} \sin φ_{2} . \end{matrix}

(2)

In the xoy plane, elastic deformation of the shafts can be determined as

\begin{matrix} δ_{x 1} = x_{1} - ξ_{1} x_{b 1} - ξ_{2} x_{b 2}, \\ δ_{y 1} = y_{1} - ξ_{1} y_{b 1} - ξ_{2} y_{b 2}, \\ δ_{x 2} = x_{2} - ξ_{3} x_{b 4} - ξ_{4} x_{b 3}, \\ δ_{y 2} = y_{2} - ξ_{3} y_{b 4} - ξ_{4} y_{b 3}, \end{matrix}

(3)

where ξ_i can be computed as

\begin{matrix} ξ_{i} = \frac{l_{b i}}{l_{j}}, i = 1,2,3,41,2; j =, \end{matrix}

(4)

where l_bi represents the distances between the gear’s centers and centers of bearing and l_j is the length of shafts. The deformation between two gears along the meshing direction δ(t) is given by

\begin{matrix} δ (t) = (r_{b 1} φ_{1} - r_{b 2} φ_{2}) + (y_{g 1} - y_{g 2}) - e (t), \\ = (r_{b 1} θ_{1} - r_{b 2} φ_{2}) + (y_{1} - y_{2} + ρ_{1} \sin φ_{1} - ρ_{2} \sin φ_{2}) - e {(t)}^{}, \end{matrix}

(5)

where static transmission error e(t) is caused by manufacture and assembly, and r_b1 and r_b2 are gear base circle radii. This error can be treated as a sinusoidal function e(t) = e₀ + e_rsin(ω_mt + φ_m) [9], where e₀ and e_r severally represent mean and amplitude of the error, and φ_m and ω_m are, respectively, initial phase and meshing frequency. ω_m meshing frequency is expressed as ω_m = 2πn₁z₁/60(2πn₂z₂/60). z₁ and z₂ are the gears’ teeth. n₁ and n₂ are the gears’ rotating velocity.

The dynamic meshing force (DMF) F_m (j = 1, 2) can be determined as

\begin{matrix} F_{m} = \sum_{i = 1}^{j} F_{m i} = \sum_{i = 1}^{j} k_{t i} f (δ (t)) + c_{m} \dot{δ} (t), \end{matrix}

(6)

where the state is the single-tooth meshing at j = 1, while the state is double-tooth meshing at j = 2. k_ti (i = 1, 2) and c_m are TVMS and meshing damping, respectively. f(δ) is the backlash function in the gear system, which is given by [23]

\begin{matrix} f (δ) = \{\begin{cases} δ (t) - (1 - ψ) b_{h} (t), & δ (t) > b_{h} (t), \\ ψ b_{h} (t), & - b_{h} (t) < δ (t) < b_{h} (t), 01 \leq ψ \leq, \\ δ (t) + (1 - ψ) b_{h} (t), & δ (t) < - b_{h} (t), \end{cases} \\ c_{m} = 2 ξ_{m} \sqrt{\frac{k_{t}}{(1 / m_{1}) + (1 / m_{2})}}, \end{matrix}

(7)

where b_h(t) is the gear dynamic backlash and ψ is a nonlinear coefficient. Meshing damping is given by c_m. b_h(t) is presented in Section 2.3.

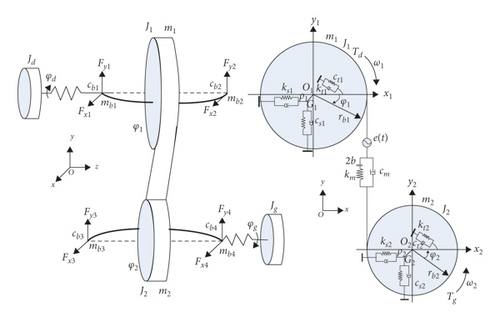
2.2. Time-Varying Meshing Stiffness for Gears with Tooth Crack

The meshing stiffness model of a gear pair with a tooth root crack was described by Tian in 2004. The energy method was used to solve the mathematical modeling problem of the gear meshing stiffness. On the basis of the research, we further investigated the gear system with a tooth root crack with time-varying meshing stiffness. The schematic graph of tooth crack is shown in Figures 2(a) and 2(b).

The potential energy of the meshing gear teeth is shown as follows [21]:

\begin{matrix} U_{b} = \int_{0}^{d} \frac{F_{b} {[(d - x) - F_{a} h]}^{2}}{2 E I_{x}} d x, \\ U_{s} = \int_{0}^{d} \frac{1.2 F_{b}^{2}}{2 {GA}_{x}} d x, \\ U_{a} = \int_{0}^{d} \frac{F_{a}^{2}}{2 {EA}_{x}} d x . \end{matrix}

(8)

I_x and A_x are equivalent to the area moment of inertia and the area of the section, respectively [5], and G represents the shear modulus. They are determined as

\begin{matrix} I_{x} = \frac{1}{12} {(2 h_{x})}^{3} L, \\ A_{x} = (2 h_{x}) L, \\ G = \frac{E}{2 (1 + υ)}, \end{matrix}

(9)

where h_x is the distance between the point on the tooth’s curve and the tooth’s central line [5].

For the single-tooth-pair meshing process, the overall meshing stiffness for the gears with tooth crack could be given by

\begin{matrix} k_{t} = \frac{1}{(1 / k_{h}) (+ 1 / k_{b 1}) + (1 / k_{s 1}) + (1 / k_{a 1}) + (1 / k_{b 2}) + (1 / k_{s 2}) + (1 / k_{a 2})}, \end{matrix}

(10)

where k_h is the Hertzian contact stiffness, k_s is the shear stiffness, k_b is the bending stiffness, and k_a is the axial compression stiffness. And k_h can be given by

\begin{matrix} k_{h} = \frac{π E L}{4 (1 - v^{2})} . \end{matrix}

(11)

where E is Young’s modulus and L is the tooth face width. F_f = μλ(v_S)F_m represents Poisson’s ratio. In addition, k_b, k_s, and k_a can be expressed as

\begin{matrix} \frac{1}{k_{b}} = \int_{- α_{1}}^{α_{2}} \frac{3 {\{1 + \cos α_{1} [(α_{2} - α) \sin α - \cos α]\}}^{3} (α_{2} - α) \cos α}{E (2 L {[\sin α + (α_{2} - α) \cos α]}^{3})} d α, \\ \frac{1}{k_{s}} = \int_{- α_{1}}^{α_{2}} \frac{1.2 (1 + v) (α_{2} - α) \cos α \cos^{2} α_{1}}{E (L [\sin α + (α_{2} - α) \cos α])} d α, \\ \frac{1}{k_{a}} = \int_{- α_{1}}^{α_{2}} \frac{(α_{2} - v) \cos α \sin^{2} α_{1}}{E (2 L [\sin α + (α_{2} - α) \cos α])} d α . \end{matrix}

(12)

For the double-tooth-pair meshing process, the overall meshing stiffness for the gears with tooth crack could be given by

\begin{matrix} k_{t} = k_{t 1} + k_{t 2} = \sum_{i = 1}^{2} \frac{1}{(1 / k_{h, i}) + (1 / k_{b 1, i}) + (1 / k_{s 1, i}) + (1 / k_{a 1, i}) + (1 / k_{b 2, i}) + (1 / k_{s 2, i}) + (1 / k_{a 2, i})}, \end{matrix}

(13)

where i (i = 1, 2) are the first or second pair of meshing teeth.

When the gear pair appears a tooth root crack, I_xc and A_xc are expressed as

\begin{matrix} I_{x c} = \{\begin{cases} \frac{1}{12} {(h_{c} + h_{x})}^{3} L, & if x \leq g_{c}, \\ \frac{1}{12} {(2 h_{x})}^{3} L = \frac{2}{3} h_{x}^{3} L, & if x > g_{c}, \end{cases} \\ A_{x c} = \{\begin{cases} (h_{c} + h_{x}) L, & if x \leq g_{c}, \\ 2 h_{x} L, & if x > g_{c}, \end{cases} \end{matrix}

(14)

where h_c represents the distance between the root the crack and the central line of the tooth. The other parameters and formulas are given in [4, 5, 21].

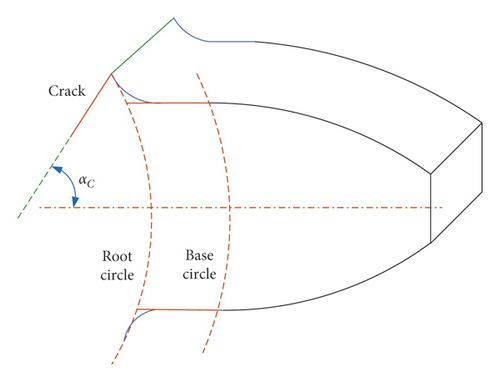
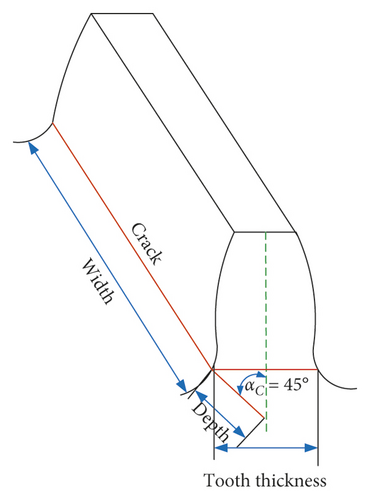
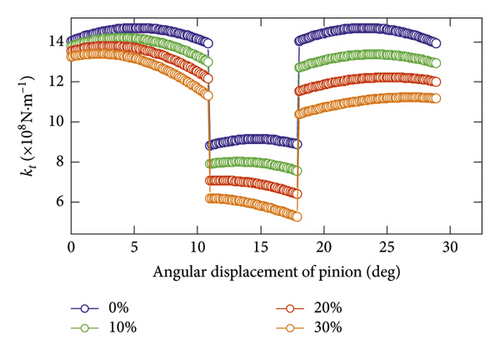
The overall effective meshing stiffness is given by the equations. Crack position is a tooth root of pinion. Equation (14) is input into equation (8), and then TVMS can be calculated. The time-varying meshing stiffness can be provided as shown in Figure 3.

2.3. Dynamic Backlash

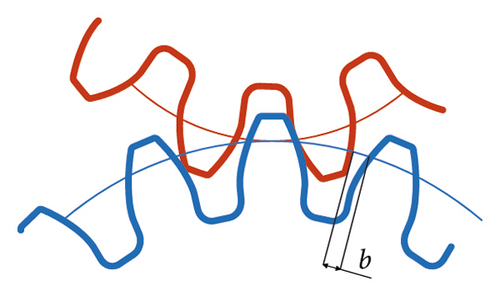
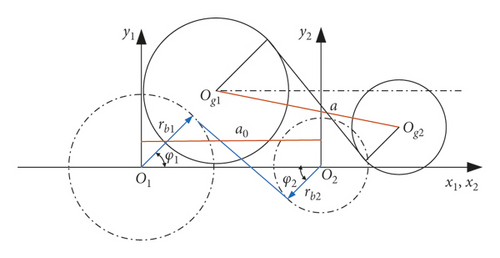
In the gear mesh process, the backlash is one of the most important factors. The backlash is the distance between two tooth profiles. In order to prevent the gears from getting stuck and ensure lubrication of gears, the backlash must exist. Rough tooth surfaces are not considered as an inherent characteristic. In the section, the compound dynamic backlash model is established considering rough tooth surface and vibration characteristic of the gear system. The sketch of backlash is shown in Figure 4. The relative displacement is generated when two rough teeth surface gears mesh.

The dynamic backlash b_h(t) is consisted of the microscopic backlash Δb(t) and vibration variation backlash b(t). In order to approximate rough tooth surfaces, the W-M fractal function is employed. The microscopic backlash Δb(t), which represents the inherent characteristic of the rough tooth surface, can be determined as [24–26]

\begin{matrix} Δ b (t) = L_{s} {(\frac{G_{c}}{L_{s}})}^{D - 1} \sum_{n = 0}^{n_{\max}} \frac{\cos (2 π γ^{n} t / L_{s})}{γ^{(2 - D) n}}, (121 < D <, γ >), \end{matrix}

(15)

where L_s is the sampling width, γⁿ represents space frequency of flank profile, G_c is the characteristic scale coefficient, and D represents the fractal dimension controlling the complexity of the fractal curve. The relationship between G_c and R_q is given by

\begin{matrix} R_{q} = {[\frac{G_{c}^{2 (D - 1)}}{2 \ln γ} \frac{1}{42 - D} (\frac{1}{ω_{k}^{(42 - D)}} \frac{1}{ω_{h}^{(42 - D)}})]}^{0.5}, \end{matrix}

(16)

where ω_k and ω_h are, respectively, equivalent to lower cutoff frequency and upper cutoff frequency. When the gear system appeared vibration, the center distance of gears is changed. By changing the center distance of gears, the backlash must be generated with volatility. The vibration variation backlash b(t) and dynamic center distance a can be determined as [27, 28]

\begin{matrix} a = \sqrt{{(a_{0} \cos α_{0} + x_{2} - x_{1})}^{2} + {(y_{2} - y_{1} - a_{0} \sin α_{0})}^{2}}, \\ b (t) = (a - a_{0}) \tan φ_{1} + b_{0}, \end{matrix}

(17)

where a₀ represents initial center distance, α₀ is the pressure angle, and b₀ represents fixed backlash. The simplified center distance model is shown in Figure 5(a).

When crack occurs on the teeth surfaces, the dynamic center distance a is increased. The dynamic backlash with crack is given by

\begin{matrix} b_{h} (t) = b (t) + Δ b (t) . \end{matrix}

(18)

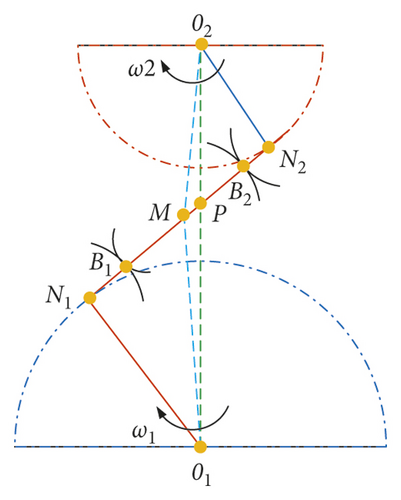
2.4. The Friction Force

Due to the meshing contact points located in different positions, the direction of friction force must be different. Thus, the frictional force changes periodically with the changing of contact points. Friction is given by

\begin{matrix} F_{f} = \sum_{i = 1}^{j} μ λ_{i} (ν_{s}) F_{m i}, j = 1,2, \\ λ (ν_{s}) = \{\begin{cases} 1, & ν_{s} > 0, \\ 0, & ν_{s} = 0, \\ - 1, & ν_{s} < 0, \end{cases} \end{matrix}

(19)

where the state is the single tooth meshing at j = 1, while the state is double tooth meshing at j = 2. λ(v_s) is the direction coefficient of the friction force, μ is the friction coefficient of the gear surface, and F_mi is the dynamic meshing force.

v_s represents relative sliding velocity of the meshing point M of the tooth pairs in Figure 5(b), which can be determined as

\begin{matrix} ν_{S} = ν_{M 1} \sin φ_{1} - ν_{M 2} \sin φ_{2}, \end{matrix}

(20)

where v_M1 and v_M2 are, respectively, on the meshing point M and are described as follows:

\begin{matrix} ν_{M 1} = ω_{1} \bar{O_{1} M}, \\ ν_{M 2} = ω_{1} \bar{O_{2} M} . \end{matrix}

(21)

Friction torque is determined as

\begin{matrix} T_{f 1} = F_{f} \bar{N_{1} M}, \\ T_{f 2} = F_{f} \bar{N_{2} M}, \end{matrix}

(22)

where

\bar{N_{1} M}

and

\bar{N_{2} M}

are, respectively, the friction arms and are defined as

\begin{matrix} \bar{N_{1} M} = (r_{b 1} + r_{b 2}) \tan α - \sqrt{r_{a 2}^{2} - r_{b 2}^{2}} + r_{b 1} ω_{1} t, \\ \bar{N_{2} M} = (r_{b 1} + r_{b 2}) \tan α - \bar{N_{1} M} . \end{matrix}

(23)

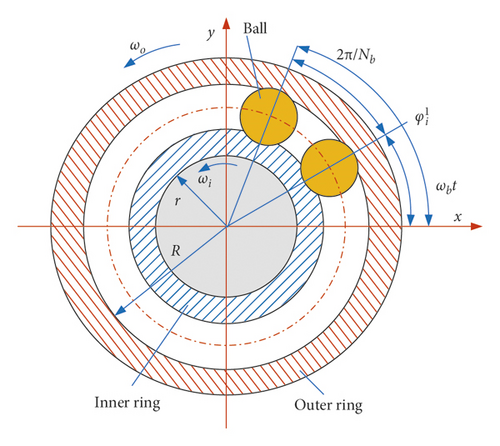
2.5. Ball Bearing Model

In Figure 6, the ball bearing model is shown. The outer ring is fastened to the bearing chock. The inner ring is fastened to the shaft. The rolling elements are evenly distributed between inner and outer rings. v_i and v_o representing the contact point velocities between the rolling elements and inner/outer rings are given by

\begin{matrix} ν_{i} = ω_{i} \cdot r, \\ ν_{o} = ω_{o} \cdot R, \end{matrix}

(24)

where R and r are radii of inner and outer rings, and the angular velocities of inner and outer rings are ω_i and ω_o. The velocity of cage is expressed as

\begin{matrix} v_{b} = \frac{(v_{o} + v_{i})}{2} = \frac{(ω_{o} R + ω_{i} r)}{2} . \end{matrix}

(25)

Due to ω_i = ω and ω_o = 0, the angular velocity of cage ω_b is given by

\begin{matrix} ω_{b} = \frac{2 v_{b}}{(R + r)} = \frac{ω_{i} \cdot r}{(R + r)} . \end{matrix}

(26)

The momentary angular displacement

φ_{i}^{1}

of the ith rolling element is given by

\begin{matrix} φ_{i}^{1} = ω_{b} \cdot t + \frac{2 π (i - 1)}{N_{b}}, i = 1,2,3, \dots, N_{b}, \end{matrix}

(27)

where N_b is the number of rolling balls and ω_b is the angular velocity of the cage.

The deformation of the ith rolling ball can be described by

\begin{matrix} δ_{i}^{1} = x \cos φ_{i}^{1} + y \sin φ_{i}^{1} - γ_{0}, \end{matrix}

(28)

where γ₀ represents bearing clearance. The Hertz contact theory is employed for computing contact force. Contact force of the ith rolling element f_i can be determined as

\begin{matrix} f_{i} = K_{b} {(x \cos φ_{i}^{1} + y \sin φ_{i}^{1} - γ_{0})}^{32 /} \cdot H (x \cos φ_{i}^{1} + y \sin φ_{i}^{1} - γ_{0}), \end{matrix}

(29)

where K_b is the Hertz contact stiffness and H(x) is the Heaviside function. So, the bearing forces are given by

\begin{matrix} F_{x j} = \sum_{i = 1}^{N_{b}} f_{i} \cos φ_{i}^{1} = F \cos φ_{i}^{1}, \\ F_{y j} = \sum_{i = 1}^{N_{b}} f_{i} \sin φ_{i}^{1} = F \sin φ_{i}^{1}, \\ j = 1,2,3,4. \end{matrix}

(30)

2.6. Mathematical Model of the GRBS

The nonlinear differential equation (33) of the GRBS are evolved from Lagrange’s equation.

c_t₁, c_t₂, c_s₁, and c_s₂ are torsion and bending damping, respectively, and are given by

\begin{matrix} c_{t 1} = 2 ξ_{t} \sqrt{\frac{k_{t 1}}{(1 / I_{d}) + (1 / I_{1})}}, \\ c_{t 2} = 2 ξ_{t} \sqrt{\frac{k_{t 2}}{(1 / I_{2}) + (1 / I_{g})}}, \end{matrix}

(31)

\begin{matrix} c_{s 1} = 2 ξ_{s} \sqrt{\frac{k_{s 1}}{(1 / m_{b 1}) + (1 / m_{1})}}, \\ c_{s 2} = 2 ξ_{s} \sqrt{\frac{k_{s 2}}{(1 / m_{b 3}) + (1 / m_{2})}}, \end{matrix}

(32)

\begin{matrix} J_{d} {\ddot{θ}}_{d} + c_{t 1} ({\dot{θ}}_{d} - {\dot{θ}}_{1}) + k_{t 1} (θ_{d} - θ_{1}) = T_{d}, \\ m_{1} {\ddot{x}}_{1} + c_{s 1} ({\dot{x}}_{1} - ξ_{2} {\dot{x}}_{b 1} - ξ_{1} {\dot{x}}_{b 2}) + k_{s 1} (x_{1} - ξ_{2} x_{b 1} - ξ_{1} {\dot{x}}_{b 2}) \\ = m_{1} ρ_{1} {\ddot{θ}}_{1} \sin (ω_{1} t + θ_{1}) + m_{1} ρ_{1} {(ω_{1} + {\dot{θ}}_{1})}^{2} \cos (ω_{1} t + θ_{1}) - F_{f}, \\ m_{1} {\ddot{y}}_{1} + c_{s 1} ({\dot{y}}_{11} - ξ_{2} {\dot{y}}_{b 1} - ξ_{1} {\dot{y}}_{b 2}) + k_{s 1} (y_{1} - ξ_{2} y_{b 1} - ξ_{1} y_{b 2}) \\ = m_{1} ρ_{1} {(ω_{1} + {\dot{θ}}_{1})}^{2} \sin (ω_{1} t + θ_{1}) - m_{1} ρ_{1} {\ddot{θ}}_{1} \cos (ω_{1} t + θ_{1}) - F_{m} - m_{1} g, \\ (J_{1} + m_{1} ρ_{1}^{2}) {\ddot{θ}}_{1} + c_{t 1} ({\dot{θ}}_{1} - {\dot{θ}}_{d}) + k_{t 1} (θ_{1} - θ_{d}) \\ = m_{1} ρ_{1} \sin (ω_{1} t + θ_{1}) {\ddot{x}}_{1} - m_{1} ρ_{1} \cos (ω_{1} t + θ_{1}) {\ddot{y}}_{1} - F_{m} r_{b 1} + T_{f 1}, \\ m_{2} {\ddot{x}}_{2} + c_{s 2} ({\dot{x}}_{2} - ξ_{4} {\dot{x}}_{b 3} - ξ_{3} {\dot{x}}_{b 4}) + k_{s 2} (x_{2} - ξ_{4} x_{b 3} - ξ_{3} x_{b 4}) \\ = m_{2} ρ_{2} {\ddot{θ}}_{2} \sin (ω_{2} t + θ_{2}) + m_{2} ρ_{2} {(ω_{2} + {\dot{θ}}_{2})}^{2} \cos (ω_{2} t + θ_{2}) + F_{f}, \\ m_{2} {\ddot{y}}_{2} + c_{S 2} ({\dot{y}}_{2} - ξ_{4} {\dot{y}}_{b 3} - ξ_{3} {\dot{y}}_{b 4}) + k_{s 1} (y_{2} - ξ_{4} y_{b 3} - ξ_{3} y_{b 4}) \\ = m_{2} ρ_{2} {(ω_{2} + {\dot{θ}}_{2})}^{2} \sin (ω_{2} t + θ_{2}) - m_{2} ρ_{2} {\ddot{θ}}_{2} \cos (ω_{2} t + θ_{2}) - F_{m} - m_{2} g, \\ (J_{2} + m_{2} ρ_{2}^{2}) {\ddot{θ}}_{2} + c_{t 2} ({\dot{θ}}_{2} - {\dot{θ}}_{g}) + k_{t 2} (θ_{2} - θ_{g}) \\ = m_{2} ρ_{2} \sin (ω_{2} t + θ_{2}) {\ddot{x}}_{2} - m_{2} ρ_{2} \cos (ω_{2} t + θ_{2}) {\ddot{y}}_{2} - F_{m} r_{b 2} - T_{f 2}, \\ m_{b 1} {\ddot{x}}_{b 1} + c_{s 1} ξ_{2} (- {\dot{x}}_{1} + ξ_{2} {\dot{x}}_{b 1} + ξ_{1} {\dot{x}}_{b 2}) + c_{b x 1} {\dot{x}}_{b 1} + k_{s 1} ξ_{2} (- x_{1} + ξ_{2} x_{b 1} + ξ_{1} x_{b 2}) = F_{x 1}, \\ m_{b 1} {\ddot{y}}_{b 1} + c_{s 1} ξ_{2} (- {\dot{y}}_{1} + ξ_{2} {\dot{y}}_{b 1} + ξ_{1} {\dot{y}}_{b 2}) + c_{b y 1} {\dot{y}}_{b 1} + k_{s 1} ξ_{2} (- y_{1} + ξ_{2} y_{b 1} + ξ_{1} y_{b 2}) = F_{y 1} - m_{b 1} g, \\ m_{b 2} {\ddot{x}}_{b 2} + c_{s 1} ξ_{1} (- {\dot{x}}_{1} + ξ_{2} {\dot{x}}_{b 1} + ξ_{1} {\dot{x}}_{b 2}) + c_{b x 2} {\dot{x}}_{b 2} + k_{s 1} ξ_{1} (- x_{1} + ξ_{2} x_{b 1} + ξ_{1} x_{b 2}) = F_{x 2}, \\ m_{b 2} {\ddot{y}}_{b 2} + c_{s 1} ξ_{1} (- {\dot{y}}_{1} + ξ_{2} {\dot{y}}_{b 1} + ξ_{1} {\dot{y}}_{b 2}) + c_{b y 2} {\dot{y}}_{b 1} + k_{s 1} ξ_{1} (- y_{1} + ξ_{2} y_{b 1} + ξ_{1} y_{b 2}) = F_{y 2} - m_{b 2} g, \\ m_{b 3} {\ddot{x}}_{b 3} + c_{s 2} ξ_{4} (- {\dot{x}}_{2} + ξ_{4} {\dot{x}}_{b 3} + ξ_{3} {\dot{x}}_{b 4}) + c_{b x 3} {\dot{x}}_{b 3} + k_{s 2} ξ_{4} (- x_{2} + ξ_{4} x_{b 3} + ξ_{3} x_{b 4}) = F_{x 3}, \\ m_{b 3} {\ddot{y}}_{b 3} + c_{s 2} ξ_{4} (- {\dot{y}}_{2} + ξ_{4} {\dot{y}}_{b 3} + ξ_{3} {\dot{y}}_{b 4}) + c_{b y 3} {\dot{y}}_{b 3} + k_{s 2} ξ_{4} (- y_{2} + ξ_{4} y_{b 3} + ξ_{3} y_{b 4}) = F_{y 3} - m_{b 3} g, \\ m_{b 4} {\ddot{x}}_{b 4} + c_{s 2} ξ_{3} (- {\dot{x}}_{2} + ξ_{4} {\dot{x}}_{b 3} + ξ_{3} {\dot{x}}_{b 4}) + c_{b x 4} {\dot{x}}_{b 4} + k_{s 2} ξ_{3} (- x_{2} + ξ_{4} x_{b 3} + ξ_{3} x_{b 4}) = F_{x 4}, \\ m_{b 4} {\ddot{y}}_{b 4} + c_{s 2} ξ_{3} (- {\dot{y}}_{2} + ξ_{4} {\dot{y}}_{b 3} + ξ_{3} {\dot{y}}_{b 4}) + c_{b y 4} {\dot{y}}_{b 4} + k_{s 2} ξ_{3} (- y_{2} + ξ_{4} y_{b 3} + ξ_{3} y_{b 4}) = F_{y 4} - m_{b 4} g, \\ J_{g} {\ddot{θ}}_{g} + c_{t 2} ({\dot{θ}}_{g} - {\dot{θ}}_{2}) + k_{t 2} (θ_{g} - θ_{2}) = - T_{g}, \end{matrix}

(33)

where k_s₁, k_s₂, k_t₁, and k_t₂ represent bending stiffness and torsion stiffness of the shafts. c_bij (i = x, y) (j = 1, 2, 3, 4) are equivalent bearing damping in the directions x and y.

The gear-rotor-bearing model with strong nonlinear and time-varying characteristics is established. The dynamic backlash and time-varying meshing stiffness with crack are included in the system. The main parameters are shown in Tables 1 and 2.

Table 1. Parameters of the gear-bearing system.

Parameter	Symbol	Numerical value
Pressure angle	α	20°
Moment of inertia	J₁/J₂	7.1 × 10⁻³/1.39 × 10⁻⁴ kg·m²
Moment of inertia of input/output	J_d/J_g	1.25 × 10⁻⁴/5.75 × 10⁻⁴ kg·m²
Mass	m₁/m₂	2.6/0.9 kg
Stiffness of bearings	k₁/k₂	2/2 × 10⁸ N·m⁻¹
Teeth	z₁/z₂	30/20
Module	m	4 mm
Tooth width	L	0.03 m
Mean/amplitude of the transmission error	e₀/e_r	2 × 10⁻⁵/3 × 10⁻⁵ m
Eccentricity	ρ₁/ρ₂	3 × 10⁻⁵/2 × 10⁻⁵ m
Driving torque	T_l	270 N·m
Loading torque	T_d	160 N·m
Damping ratio of gear meshing	ξ_m	0.02
Damping ratio of shaft	ξ_s/ξ_t	0.1/0.1

Table 2. Model parameters of the bearing.

Parameter	Symbol	Numerical value
Outer ring radius of bearing	R₁/R₂	0.031/0.021 m
Inner ring radius of bearing	r₁/r₂	0.02/0.015 m
Contact stiffness	K_b1/K_b2	13.34 × 10⁹/10.56 × 10⁹ Nm^3/2
Bearing clearance	γ₀₁/γ₀₂	3 × 10⁻⁵/2 × 10⁻⁵ m
Ball number	N₁/N₂	14/18

3. Dynamic Response and Discussion

3.1. Comparison of Three Backlash Models

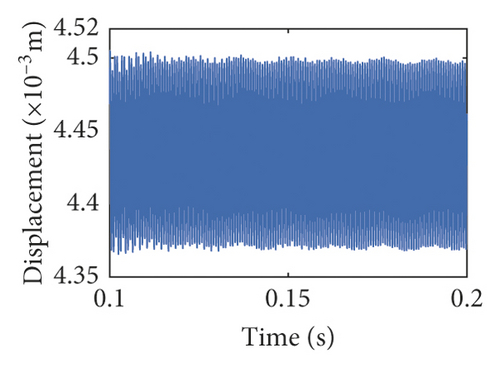
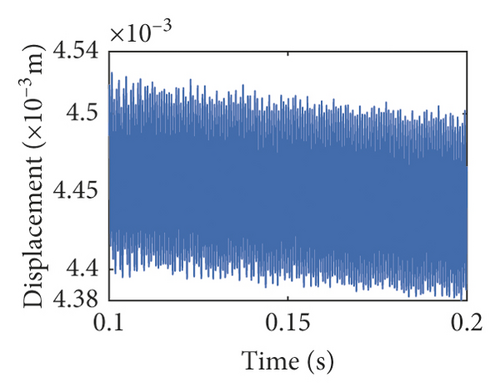
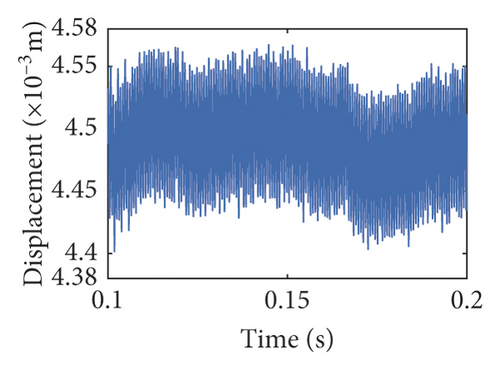
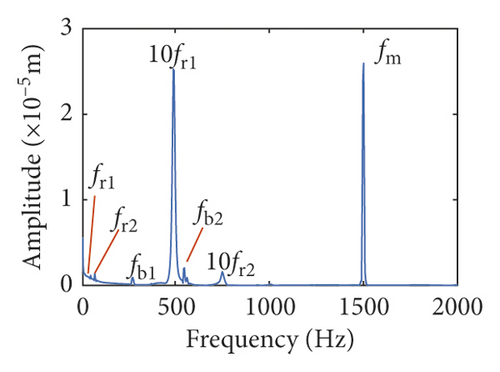
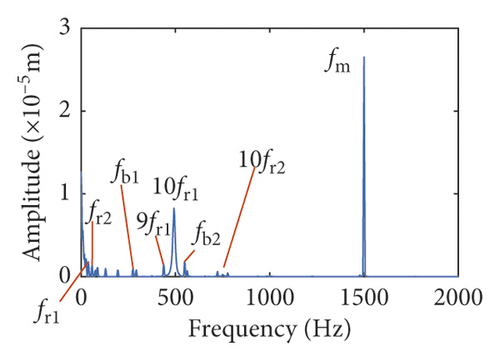
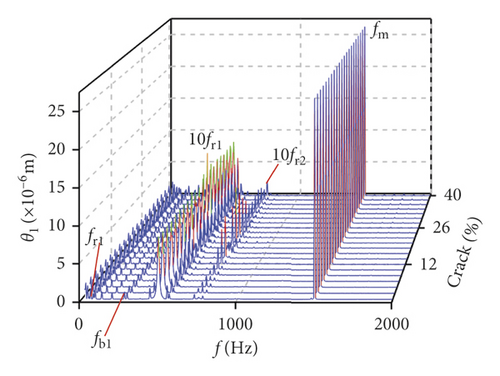
In the section, the three models about backlash are explored by the same parameters. The time-domain waveforms and frequency spectra are shown in Figures 7 and 8. The waveform of fixed backlash is stable, as is shown in Figure 7(a). The vibration waveform of dynamic backlash based on the dynamic center distance model produces significant fluctuations in Figure 7(b). It is clearly seen that the vibration displacement fluctuations of the compound dynamic backlash model are the biggest in Figure 7(c). In addition, the amplitude of 10f_r1 has an obvious difference among Figures 8(a)–8(c). The frequency components of compound dynamic backlash are more than the others. It is distinct that the waveforms, frequency components, and amplitude are most different for the three models.

3.2. Dynamic Response of the Gear System with a Tooth Root Crack

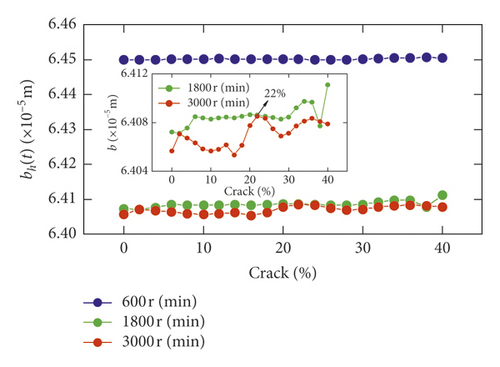
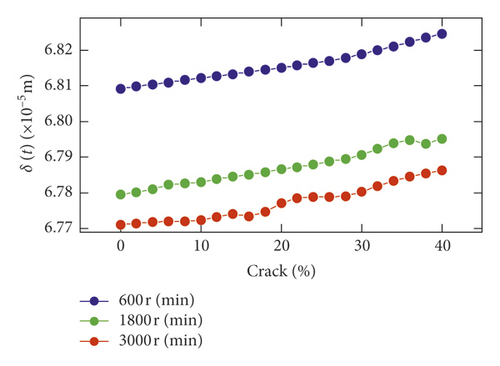
On the basis of the gear transmission system model equation (30), the vibration responses of the gear system with different crack depths are listed to investigate the effect on the system. Fractal dimension D is assumed to be 1.5, and friction coefficient μ = 0.05. The crack depth is set from zero to forty percent of the tooth thickness. Considering the different spindle speeds, such as 600 r/min, 1800 r/min, and 3000 r/min, the response characteristics are investigated under the different crack depths. In Figures 9(a)–9(d), the RMS of each significant parameter is presented, including the dynamic meshing force F_m, variation of dynamic center distance of gears Δa, the comprehensive elastic deformation δ(t), and the backlash b_h(t) of the gear. Apparently, in Figure 7(a), it is stationary for the 600 r/min of the blue line with increasing crack depth. Within the limits of 0–30%, the RMS green curve of b_h(t) is little different. When the rotational speed is 3000 r/min, the maximum value of the red line of b_h(t) is crack 22%.

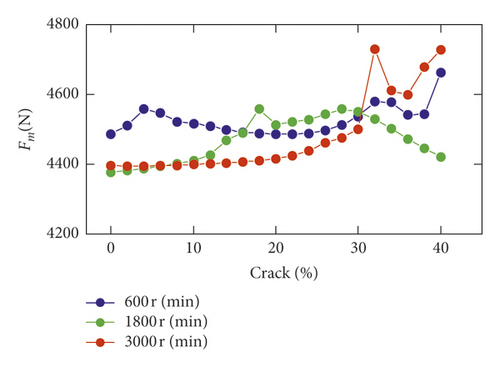
The dynamic meshing force F_m increases with the increase in crack depth in the range of 0% and 30% in Figure 9(b), setting to 1800 r/min or 3000 r/min. It indicates that F_m increases with crack depth within the limits of high speed. But, it slightly decreases in the range of low speed. When the crack is severe in the range of 30% and 40%, F_m of 600 r/min and 3000 r/min has a rapid, fluctuating increase. However, F_m of 1800 r/min is a rapid fall.

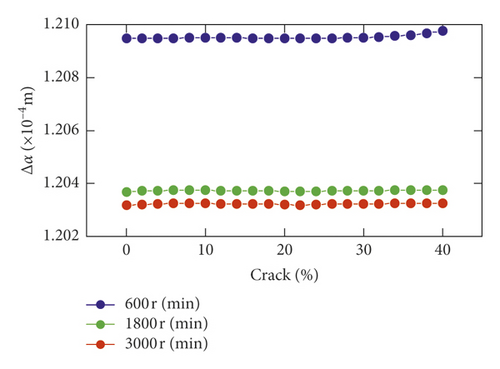
The RMS of comprehensive elastic deformation δ(t) speed increases with the increase in crack depth in Figure 9(c). But it is a fall with the increase in speed. The variation of center distance Δa(Δa = a − a₀) is shown in Figures 9(d) and 10(a)–10(c). The larger the speed set, the smaller the variation value of center distance. An enlarged view of each speed is shown in Figure 10.

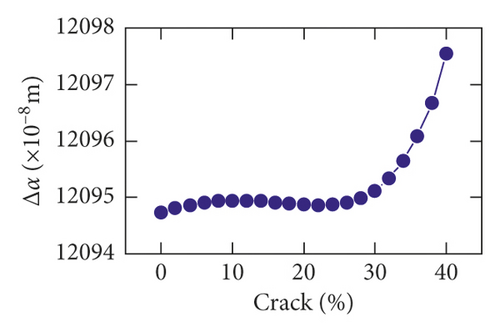
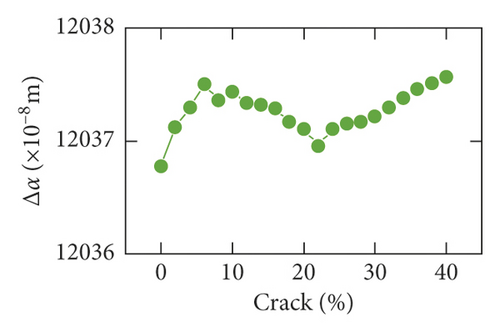
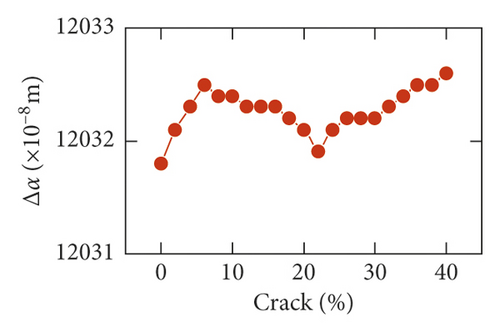
When the speed is low, the RMS of Δa slowly increases in the range of 0% and 30%, and it grows rapidly within the limit of 30% and 40%. With increasing speed, an increase in volatility is shown in Figures 10(b) and 10(c). The value corresponding to the crack 22% is the minimum value. The value corresponding to the crack 40% is the maximum value.

3.3. Vibration Responses and Frequency Characteristics with Different Crack Depths

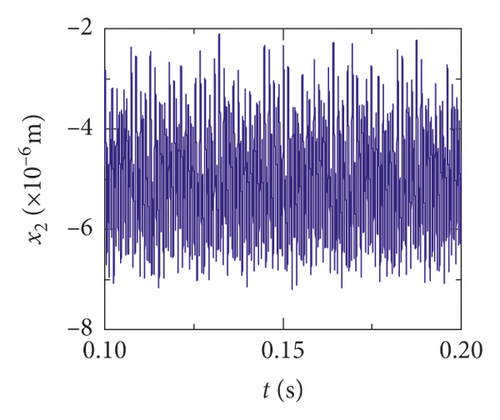
In order to study the effect of crack on dynamic responses of the system, the time-domain waveform and frequency-domain response are shown with different crack depths. The rotational speed is set to 3000 r/min. The crack depth is set to 0%, 10%, and 30% of the tooth thickness. Figures 11(a)–11(e), 12(a)–12(e), and 13(a)–13(e) display the vibration displacements of the gears and the bearings, which are, respectively, at 0%, 10%, and 30% of the tooth thickness. Figures (14)–(16) show the frequency domain responses at the different crack depths.

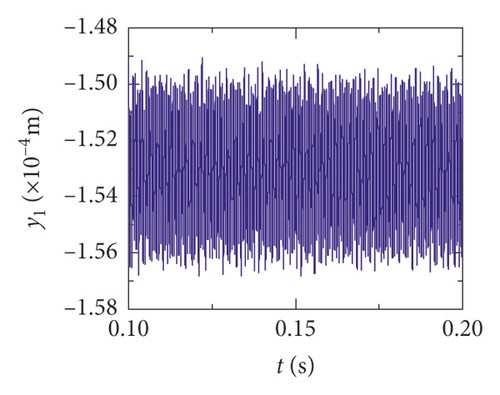
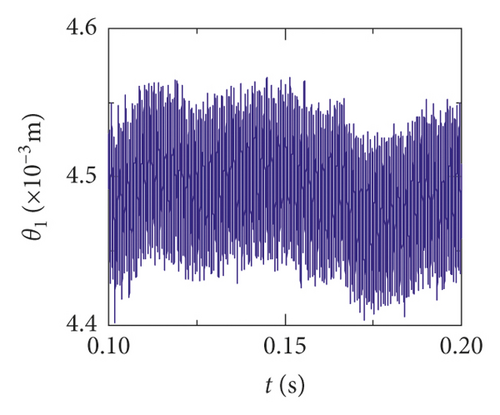
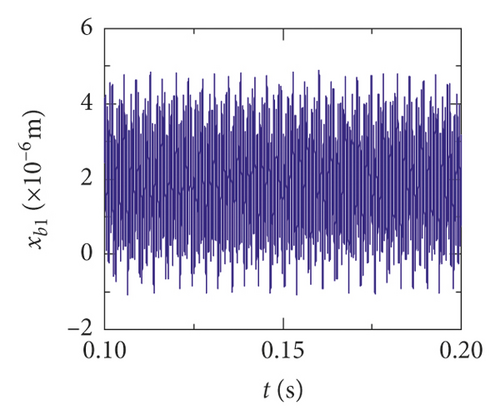
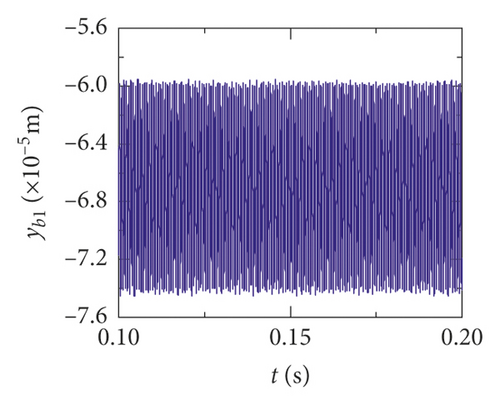
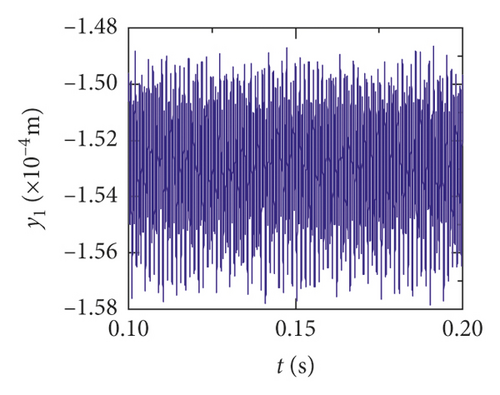
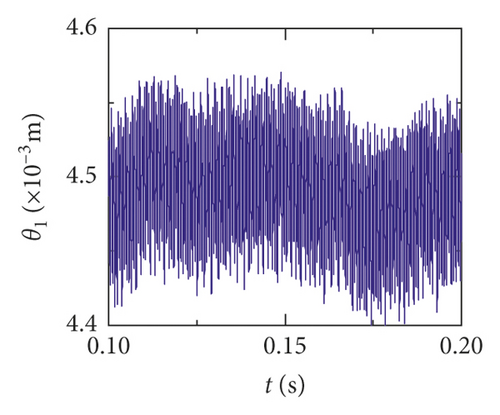
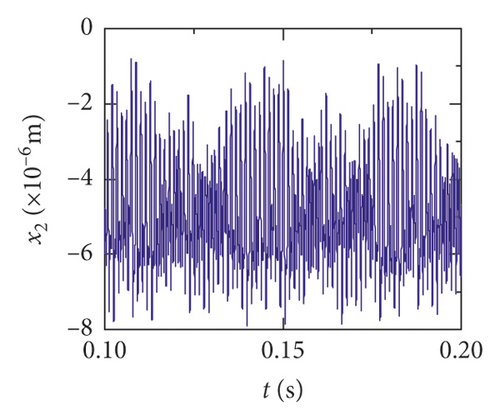
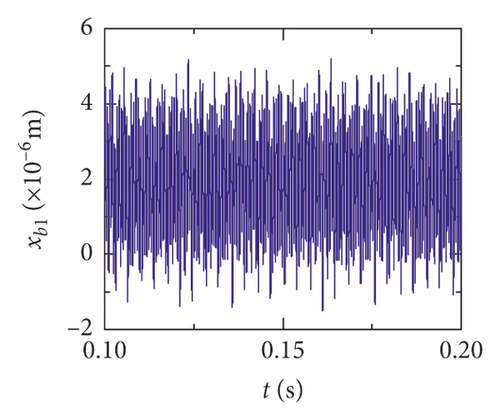
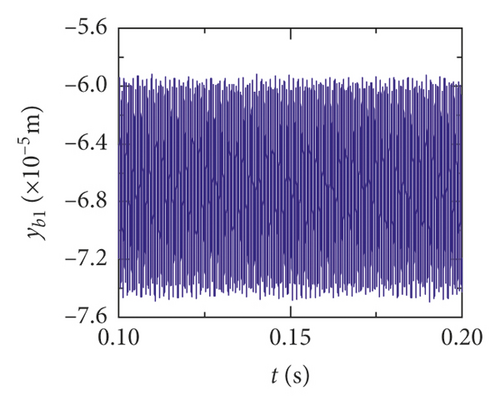
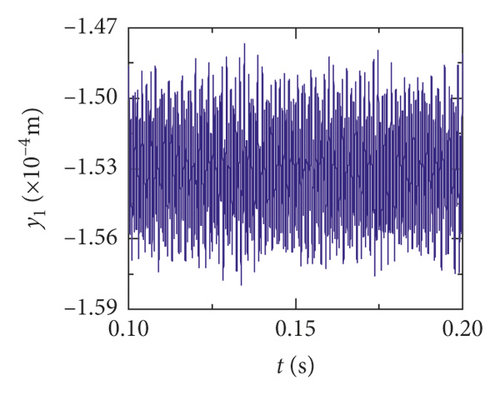
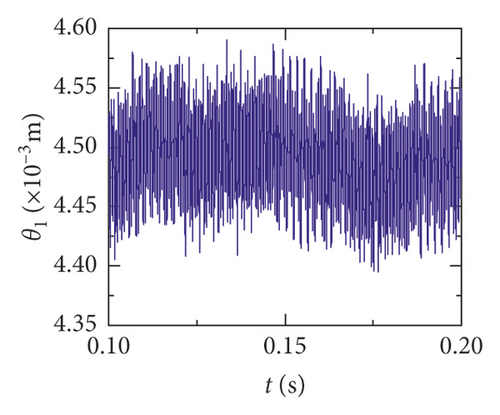
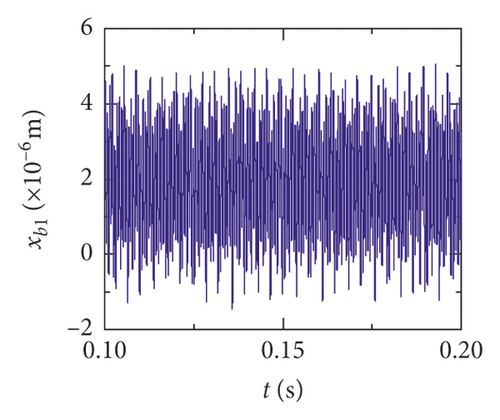
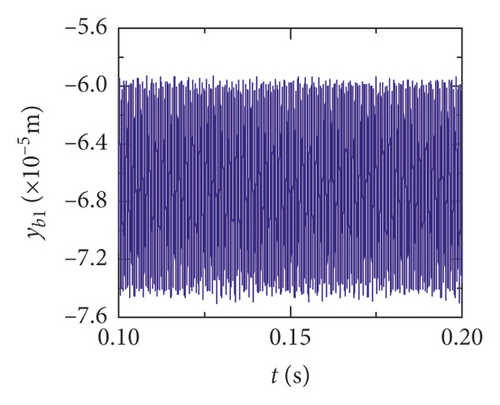
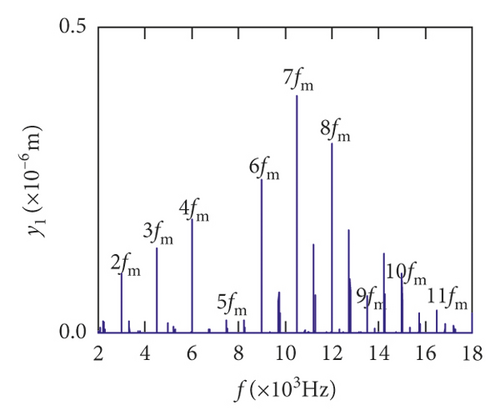
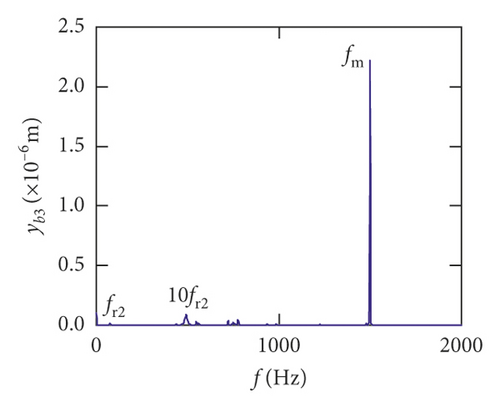
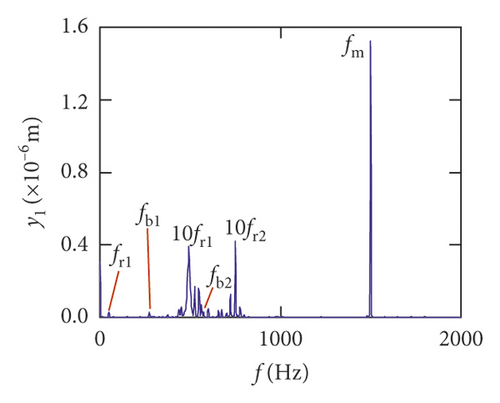
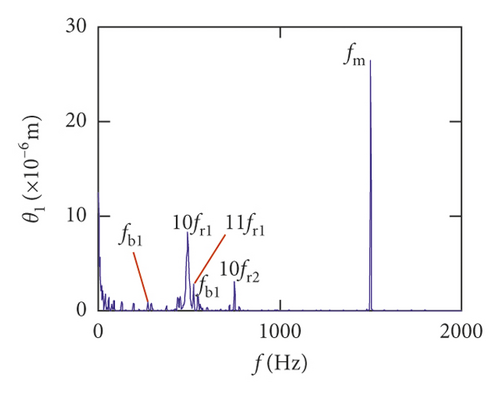
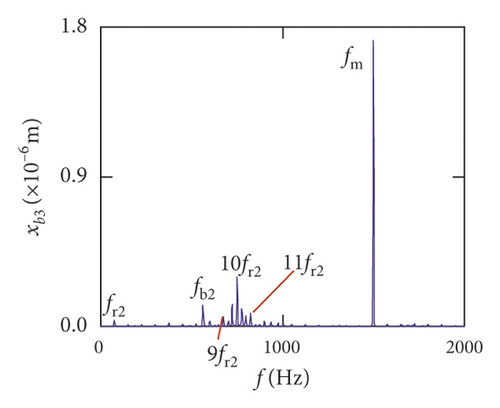
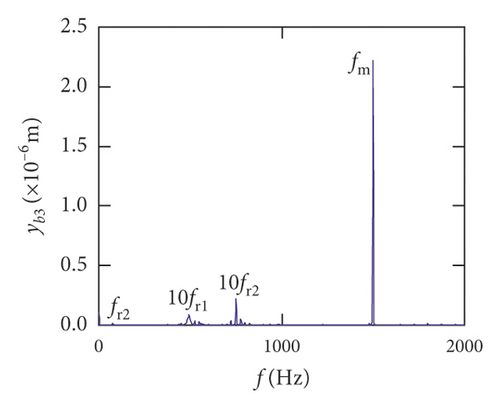
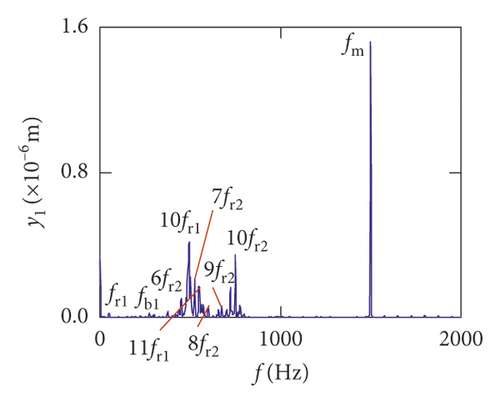
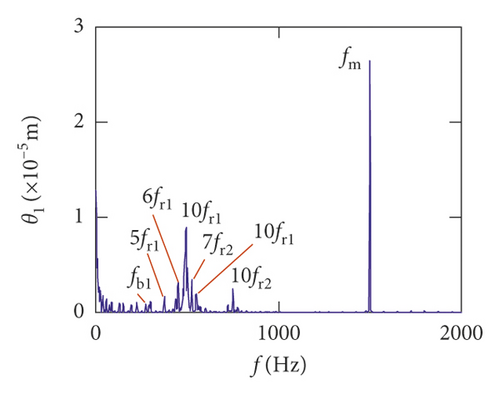
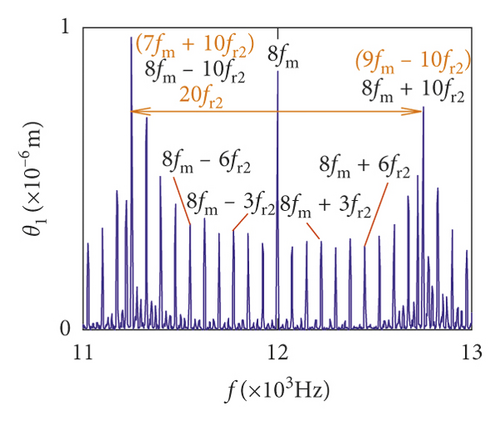
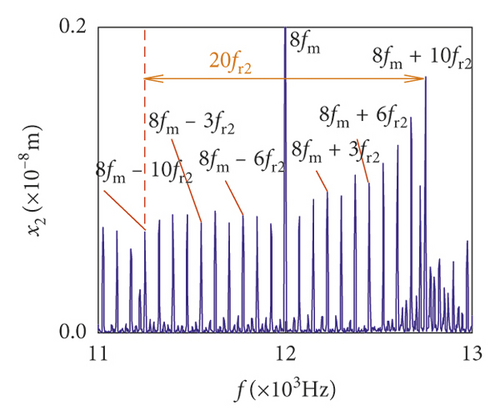
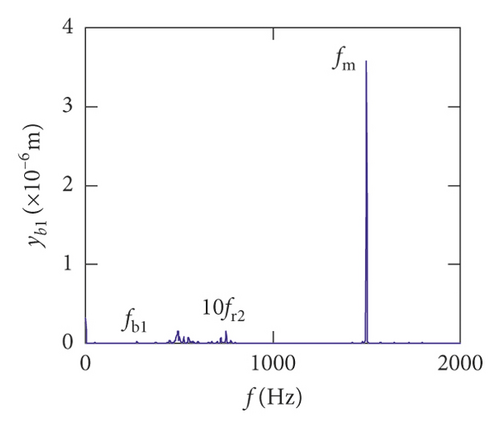
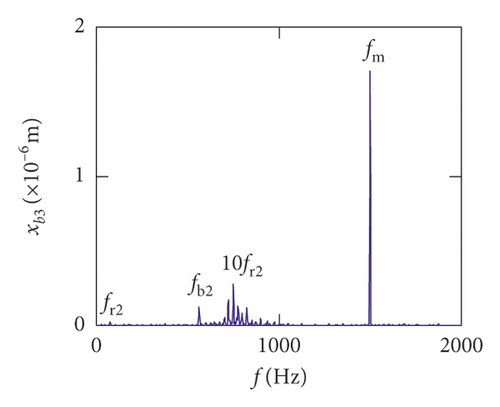
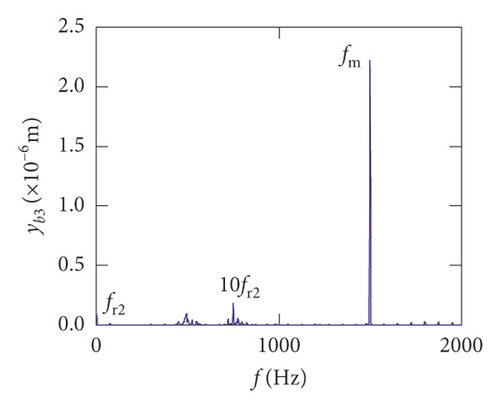
For the healthy gear system shown in Figure 11(b), the fluctuation of the vibration displacement in torsional direction (θ₁) is more obvious than others. It indicates that the vibration response in torsional direction (θ₁) is more sensitive to nonlinear factors and excitation. In Figure 11(e), those factors have less impact on the vibration of the bearing.

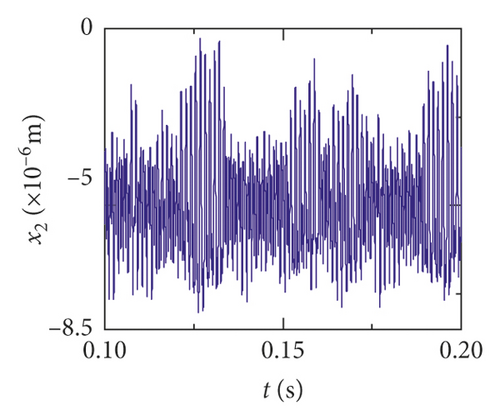
The time-domain waveform will exist as a pulse in theory when a tooth root crack appears. Though the variation of waveform in all directions is obvious in Figures 12 and 13, a pulse is covered with the fluctuation caused by other excitation factors. So, the pulse form that should have been generated is not so obvious. The amplitude of the pinion in x₂ direction is distinctly increased because of the crack fault, and the change of waveform is also obvious in Figures 12(c) and 13(c). In addition, the amplitude of the other directions has a slight increase, as is shown in Figures 12(a), 12(b), 13(a), and 13(b). The vibration response of the bearing is among those least affected in Figures 12(d), 12(e), 13(d), and 13(e).

Obviously, the effect of a tooth root crack on vibration response of the gear system components is different. In the case of vibration response in x₂ direction, the statistic datum from the results shows that the amplitude of crack 10% increases by 1.428 times than the healthy system. The amplitude increases by 1.735 times than the healthy system. But the rate of increase of vibration amplitude on the bearing does not exceed 15%. In addition, the time-domain waveform fluctuates more intense in x₂ direction. For transverse (x_b1) and longitudinal (y_b1) vibrations of the bearing, the vibration waveforms become more disordered because a tooth root crack appears, as is shown in Figures 12(d), 12(e), 13(d), and 13(e). But the amplitudes of vibration are less changed.

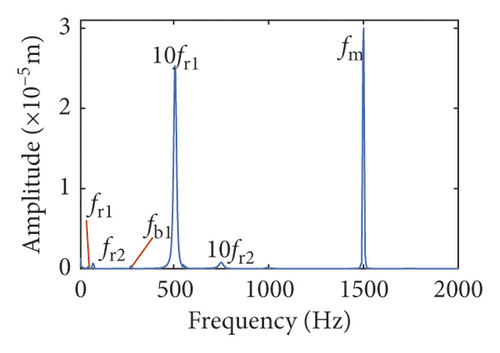
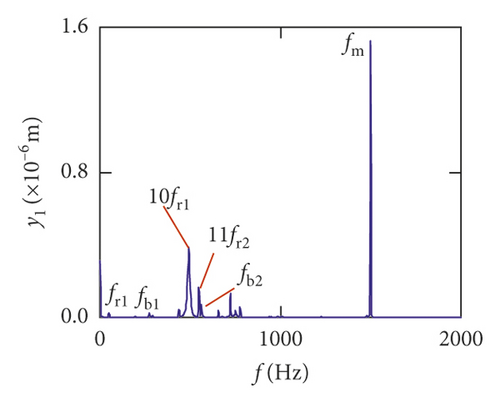
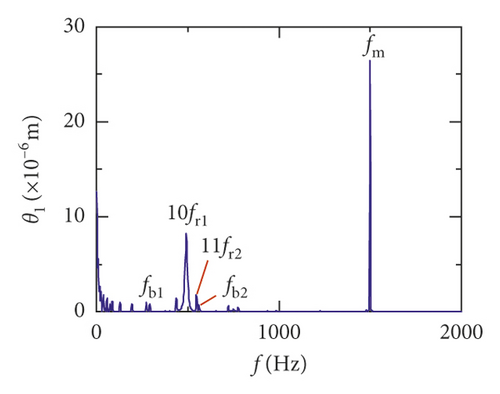
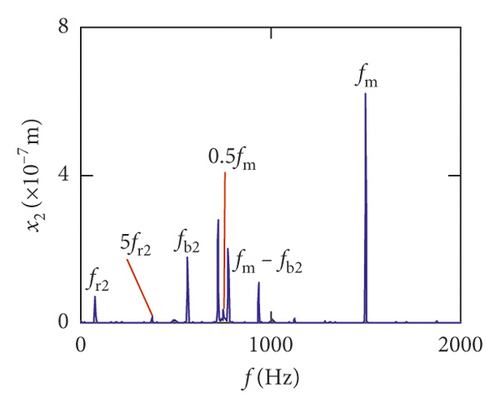
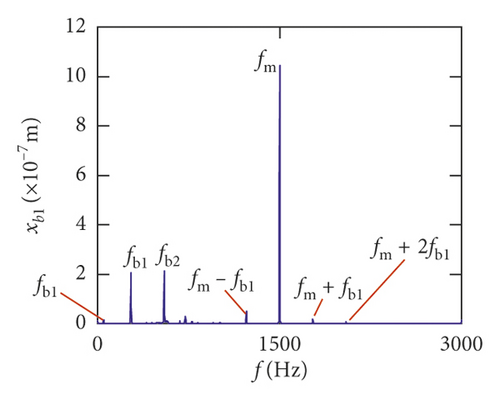
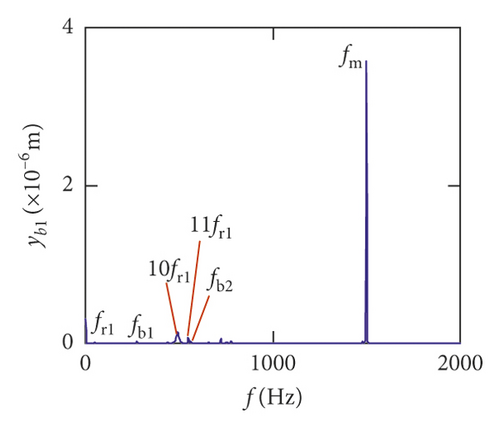
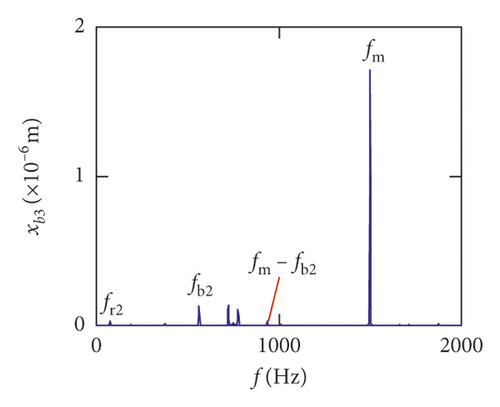
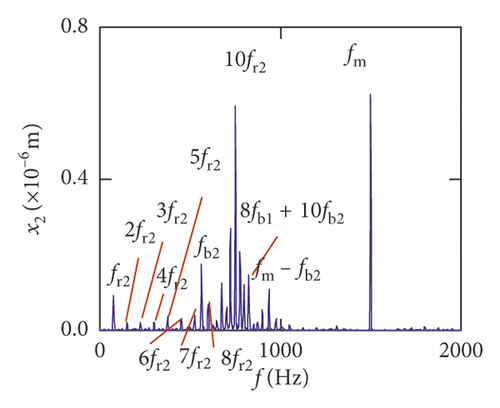
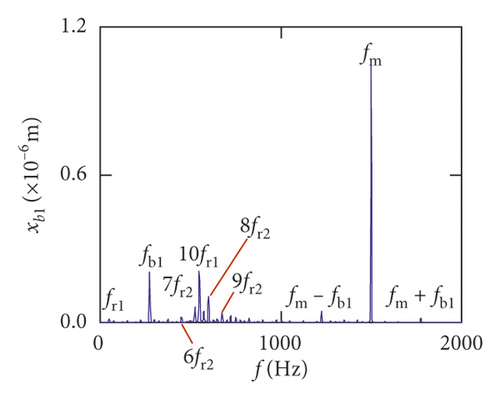
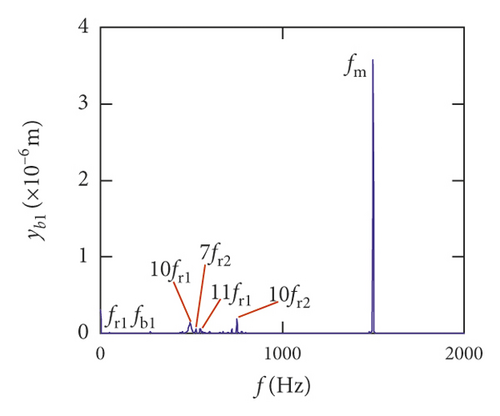
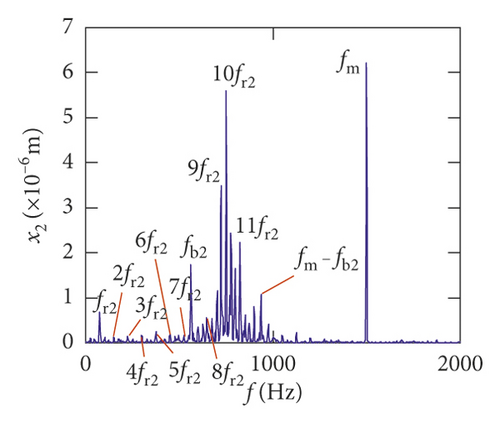
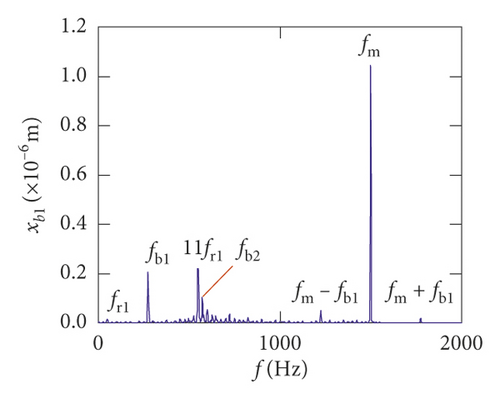
Figures (14)–(16) display, respectively, the frequency spectra of the healthy gear system, gear system with crack 10%, and gear system with crack 30%. The vibration frequency on the healthy gear system is explained in Figures 14(a)–14(i). In the healthy frequency spectra, it is obviously shown that the rotating frequency f_r1 (f_r1 = n₁/60 = 50 Hz) and the mesh frequency f_m (f_m = n₁z₁/60 = 1500 Hz) are presented in Figure 14. However, besides f_r1 and f_m, the rotating frequency f_r2 (f_r2 = n₂/60 = 75 Hz), variable stiffness frequencies f_b1 (f_b1 = N₁r₁n₁/60(R₁ + r₁) = 274.3 Hz) and f_b2 (f_b1 = N₂r₂n₂/60(R₂ + r₂) = 563.4 Hz), and combination frequency 0.5f_m(10f_r2), 2f_m, 3f_m, f_m − f_b1, f_m + f_b1, and f_m − f_b2 can be observed in the frequency spectra.

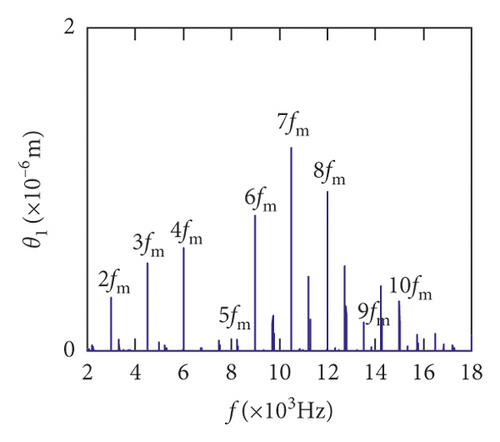
The meshing frequency f_m is the highest amplitude and the (0.5f_m)10f_r1 is the second highest in y₁ and θ₁ direction, as is shown in Figures 14(a) and 14(b). Besides, multiplication frequency of meshing frequency f_m can be seen in Figures 14(d) and 14(e), including 2f_m, 3f_m, 4f_m, 5f_m, 6f_m, 7f_m, 8f_m, 9f_m, 10f_m, and 11f_m. In order to further explore the bearing vibration frequency, Figures 14(f)–14(i) are presented. It is clearly observed that f_m are the highest amplitude frequency. But the frequency components of the transverse (x_b1, x_b3) are more abundant than longitudinal (y_b₁, y_b₃).

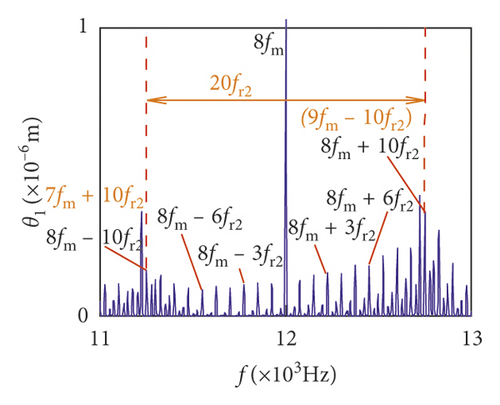
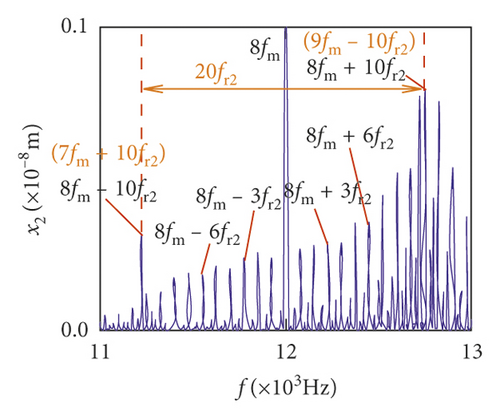
For crack 10%, the sidebands near multiplication frequency components can be found in Figures 15(b) and 15(d). The range of the whole sideband of 8f_m is 20f_r2. In addition, it is a significant phenomenon for the early cracked gear system that obvious multiplication frequency of f_r2 (75 Hz) is observed in Figures 15(f)–15(i). This phenomenon is not found from the healthy gear system. In bearing frequency spectra, sidebands in x_b1 and x_b3 directions are more obvious than in y_b1 and y_b3 directions. In addition, 0.5f_m(10f_r2) amplitude increases in all directions.

As the crack depth increases, the changes in the amplitudes of meshing frequency and the multiplication frequency are not obvious. But sidebands of the multiplication frequency of f_m are distinctly changed by the crack. In Figures 15(c), 15(e), 16(c), and 16(e), the amplitude of the sideband gradually increases with the increase in crack depth. For crack 30%, the frequency component becomes more complex than early crack (10%) and healthy system. 0.5f_m(10f_r2) and f_m are the dominant frequencies in all directions.

The statistics data of the sidebands are shown in Tables 3 and 4. In Tables 3 and 4, the amplitudes of sideband sharply increase when the crack depth changes from 10% to 20%. From 20% to 30%, the variations will become a slow increase or decrease.

Table 3. Amplitude of the sideband in θ₁ direction.

Crack depth (%)	8f_m − 6f_r2 (Hz)	Amplitude (×10⁻⁶ m)	8f_m − 3f_r2 (Hz)^(a)	Amplitude (×10⁻⁶ m)	8f_m + 3f_r2 (Hz)^(a)	Amplitude (×10⁻⁶ m)	8f_m + 6f_r2 (Hz)^a	Amplitude (×10⁻⁶ m)
0	11550	≈0	11775	≈0	12225	≈0	12450	≈0
10	230.4% 16.2%	0.0913	172.0% 10.0%	0.1103	159.6% −24.5%	0.1489	130.0% −43.3%	0.1741
20		0.3017		0.3009		0.3866		0.4004
30		0.3503		0.3309		0.2918		0.2270

^aThe first line is the frequency of sideband, respectively, and the other lines indicate the growth rate when every crack 10% increases.

Table 4. Amplitude of the sideband in x₂ direction.

Crack depth (%)	8f_m − 6f_r2 (Hz)	Amplitude (×10⁻⁸ m)	8f_m − 3f_r2 (Hz)^(a)	Amplitude (×10⁻⁸ m)	8f_m + 3f_r2 (Hz)^(a)	Amplitude (×10⁻⁸ m)	8f_m + 3f_r2 (Hz)^a	Amplitude (×10⁻⁸ m)
0	11550	≈0	11775	≈0	12225	≈0	12450	≈0
10	192.9% 34.3%	0.0183	132.4% 38.7%	0.0238	189.7% 9.0%	0.0292	192.7% −6.7%	0.0358
20		0.0536		0.0553		0.0846		0.1048
30		0.0720		0.0767		0.0922		0.0978

^aThe first line is the frequency of sideband, respectively, and the other lines indicate the growth rate when every crack 10% increases.

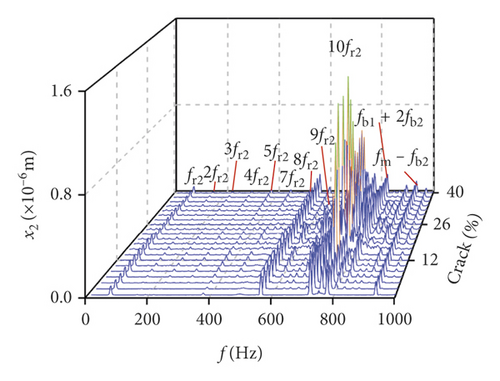
In order to further research the influences of a tooth root crack, waterfall maps of different crack depths in all directions can be seen in Figure 17. The amplitude of 0.5f_m(10f_r2) in y₁ direction increases in the range of (0%, 22%) in Figure 17(a). When the crack depth is 22%, the amplitude of 0.5f_m(10f_r2) is the biggest. Then the amplitude decreases in the range of (24%, 40%). The amplitude of 10f_r1 only appears a slight fluctuation near crack 22%. The amplitude of f_m shows less variation. In Figure 17(b), the multiplication frequency of f_m is shown, including 5f_m, 6f_m, …, 10f_m. The sidebands appear near multiplication frequency. These sidebands are irregular, and the amplitude of sidebands is different. The change rules of 0.5f_m(10f_r2), f_m, and 10f_r1 in θ₁ direction are similar to those in y₁ direction, as is shown in Figure 17(c). In addition, some noise frequency occurs in the lower frequency. In x₂ direction, f_r2 and its multiplication frequency 2f_r2, 3f_r2, …, 10f_r2 appear and some compound frequencies f_b1+ f_b2, f_m − f_b2 also exist in Figure 17(e). The multiplication frequency of f_m in x₂ direction is different from that in y₁ and θ₁ directions (compare Figure 17(f) with Figures 17(b) and 17(d)). The amplitude of sidebands increases with crack growing in all directions, as is shown in Figures 17(b), 17(d), and 17(f).

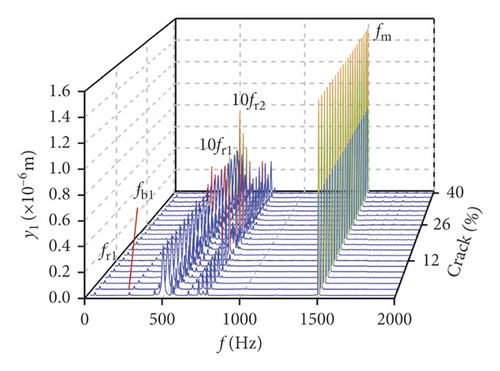
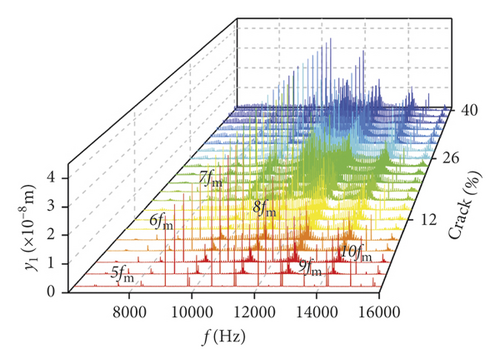
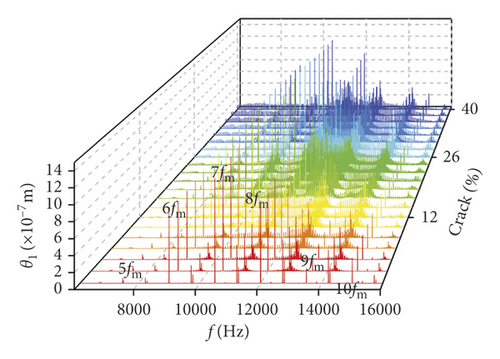
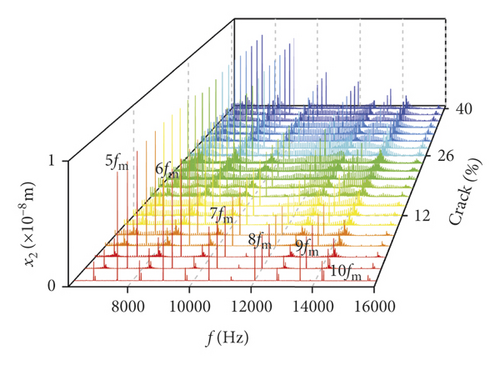
Influences of crack growing on the bearing is shown in Figures 18(a)–18(d). It can be seen that the frequency changes of transverse (x_b1, x_b3) vibrations are more violent than those of the longitudinal (y_b1, y_b3) vibrations. f_b₁, f_b₂, 0.5f_m, and f_m are found from the bearings in x_b3 direction, and the amplitude of 0.5f_m(10f_r2) is changed as the crack depth increases, as is shown in Figure 18(a). The number of noise frequencies in the spectra of transverse vibration is more than that in the frequency spectra of longitudinal vibration.

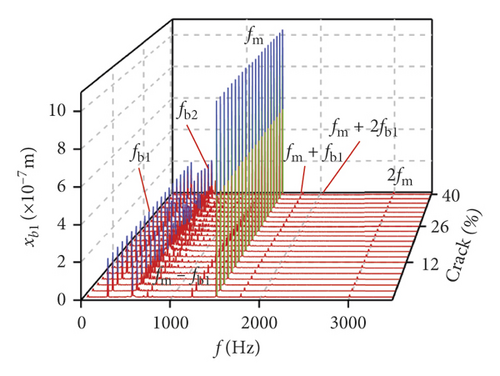
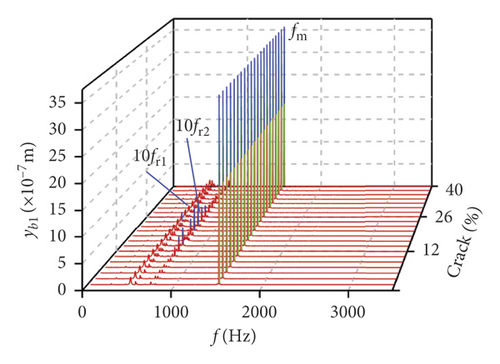
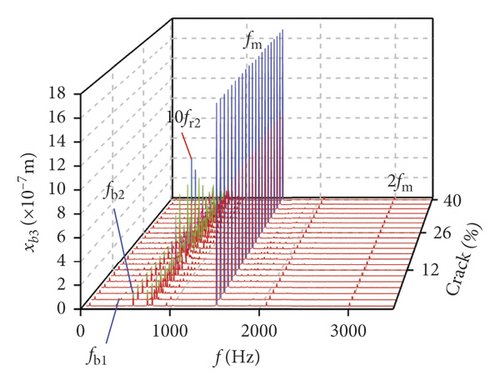
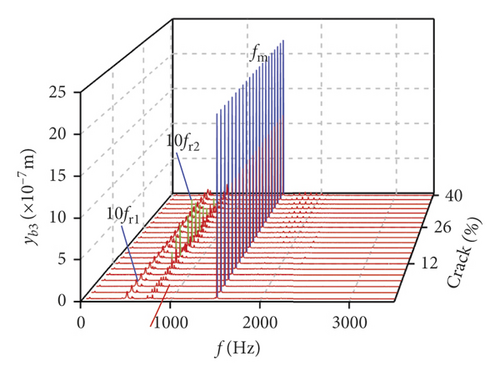
In Figures 18(b) and 18(d), the frequency components include 0.5f_m(10f_r2), 10f_r1, and f_m.

For the comprehensive comparison, the impact in the transverse vibration is more dramatic than that in the longitudinal vibration from the change of the crack, whether the bearings or the gears. Moreover, besides the sidebands, 0.5f_m(10f_r2) and the noise frequency, the amplitude variation of other frequency components is inconspicuous, as shown in Figure 18.

4. Conclusion

A nonlinear model with the crack fault, compound backlash, and dynamic stiffness has been built to investigate the coupled lateral-torsional fault features of the 16-DOF gear-rotor-bearing system. The potential energy method is employed for analyzing effective meshing stiffness, and assumed that the dynamic backlash is time varying. This time-varying backlash is composed of two parts. One is the dynamic backlash with fractal characteristics based on the microstructure of the tooth surface. The other is time-varying center distance based on the gear vibration characteristics. The comparison between the healthy gear system and crack fault system, including time-domain waveforms and frequency-domain responses, is analyzed in detail. The analysis results are shown as follows:

(1)
The effect of crack growing on meshing force of the gear system is distinct at high rotational speed. With the increase in crack, different crack degrees show different vibration responses. In addition, for high speed, the meshing force slowly increases in the range of crack (0, 30%). But the meshing force rapidly increases within the limits of 30% and 40% when the rotational speeds are 600 r/min and 3000 r/min. The meshing force declines in the range of 30% and 40% when the speed is 1800 r/min. The comprehensive elastic deformation δ(t) and the variation of center distance Δaare mainly affected by rotational speed. In addition, δ(t) and Δa slowly increase with growing crack depth. Moreover, the dynamic backlash RMS exhibits peak at crack 22% when the speed is 3000 r/min. The backlash is a main reason causing the amplitude variation of 0.5f_m(10f_r1).
(2)
The shaft frequency and multiplication frequency of the dominant frequency can be found in the frequency domain spectra when the gear system appears crack fault. And the amplitudes of these sidebands and the amplitudes of part multiplication frequency go up with the growing of the crack depth, yet the amplitude of frequency components is not changed. For this spur gear model, the pinion and shaft 2 show more obvious fault characteristics due to which sideband effect and time-domain waveforms are more complex as the crack increases.

Nomenclature

A_x:: Area of the tooth cross section at point x
A_xc:: After appearing crack, area of the tooth cross section at point x
b(t):: Dynamic backlash
Δb(t):: Microscopic backlash
b_h(t):: Vibration variation backlash
c_bij:: i = x, y, and j = 1–4, bearing damping in x and y directions
c_m:: Mesh damping
c_si:: i = 1-2, bending damping
c_ti:: i = 1-2, torsion damping
D:: Fractal dimension controlling the complexity of the fractal curve
E:: Young’s modulus
e(t):: Static transmission error
e₀:: Mean error
e_r:: Amplitude error
F_f:: Friction
f_i:: i = 1–N, contact force of the ith rolling element
F_mj:: j = 1-2, dynamic force
F_xj:: Bearing force in x direction
F_yj:: Bearing force in y direction
G:: Shear modulus
G_c:: Characteristic scale coefficient
H:: Heaviside function
h_c:: Distance between the root the crack and the central line of the tooth
h_x:: Distance between the point on the tooth’s curve and the tooth’s central line
I_x:: Area moment of inertia of the tooth cross section at point x
I_xc:: After appearing crack, area moment of inertia of the tooth cross section at point x
k_a:: Axial compression stiffness of gear
k_b:: Bending stiffness of gear
k_h:: Hertzian contact stiffness of gear
k_s:: Shear stiffness of gear
k_si:: i = 1-2, bending stiffness of shafts
k_t:: TVMS
k_ti:: i = 1-2, torsion stiffness of shafts
L:: Width of tooth
L_s:: Sampling width
l_bi:: i = 1–4, distances between gear’s centers and centers of bearing
l_j:: j = 1-2, length of shafts
$\bar{N_{1} M}$ :: Friction arm
$\bar{N_{2} M}$ :: Friction arm
r_b1:: Basic circle of gear
r_b2:: Basic circle of pinion
R_q:: RMS roughness
T_f1:: Friction torque
T_f2:: Friction torque
U_a:: Axial compression energy
U_b:: Bending energy
U_s:: Shear energy
v_b:: Velocity of cage
v_i:: Contact point velocities between the rolling elements and inner ring
v_o:: Contact point velocities between the rolling elements and outer ring
v_M1:: Velocity on the meshing point of gear
v_M2:: Velocity on the meshing point of pinion
v_s:: Relative sliding velocity of the meshing point M of the tooth pairs
x_gi:: Abscissa of centers of mass
y_gi:: Ordinate of centers of mass
φ_i:: i = 1,2, d, g angle displacement
$φ_{i}^{1}$ :: i = 1–N, rotational angle of the ith rolling ball
δ(t):: Deformation between two gears along meshing direction
δ_xi:: Elastic deformations of the shaft in x direction
δ_yi:: Elastic deformations of the shaft in y direction
$δ_{i}^{1}$ :: Deformation of the ith rolling ball
λ(vs):: Direction coefficient
ω_b:: Angular velocity of cage
ω_h:: Upper cutoff frequency
ω_i:: Angular velocity of the inner ring
ω_o:: Angular velocity of the outer ring
ω_k:: Lower cutoff frequency
ω_m:: Meshing frequency
ρ_i:: i = 1-2, eccentricity
ξ_m:: Meshing damping ratio
γⁿ:: Space frequency of flank profile
μ:: Friction coefficient.

Conflicts of Interest

No potential conflicts in this paper are declared by the authors about research, relationship, and publication.

Acknowledgments

This work was funded by the Natural Science Foundation of China (no. 51675350), and Key project of Natural Science Foundation of Science and Technology Department of Liaoning Province (20170540673).

Open Research

Data Availability

All the data are included within the manuscript, and all parameters are valid. Interested researchers can obtain the numerical solution files by contacting the authors via mail ([email protected]).

References

1 McFadden P. D., Examination of a technique for the early detection of failure in gears by signal processing of the time domain average of the meshing vibration, Mechanical Systems and Signal Processing. (1987) 1, no. 2, 173–183, https://doi.org/10.1016/0888-3270(87)90069-0, 2-s2.0-45949124245.
10.1016/0888-3270(87)90069-0
Web of Science® Google Scholar
2 Mcfadden P. D., Low frequency vibration generated by gear tooth impacts, NDT International. (1985) 18, no. 5, 279–282, https://doi.org/10.1016/0308-9126(85)90008-2, 2-s2.0-0022145269.
10.1016/0308-9126(85)90008-2
Web of Science® Google Scholar
3 Belsak A. and Flasker J., Detecting cracks in the tooth root of gears, Engineering Failure Analysis. (2007) 14, no. 8, 1466–1475, https://doi.org/10.1016/j.engfailanal.2007.01.013, 2-s2.0-34250695042.
10.1016/j.engfailanal.2007.01.013
Web of Science® Google Scholar
4 Yang D. C. H. and Lin J. Y., Hertzian damping, tooth friction and bending elasticity in gear impact dynamics, Journal of Mechanisms Transmissions and Automation in Design. (1987) 109, no. 2, 189–196, https://doi.org/10.1115/1.3267437, 2-s2.0-85024596996.
10.1115/1.3267437
PubMed Web of Science® Google Scholar
5 Tian X. H., Dynamic simulation for system response of gearbox including localized gear faults, 2004, University of Alberta, Edmonton, Canada, M.S. thesis.
Google Scholar
6 Govind V. J., Sachin K., and Kumar K. P., Crack growth modeling in spur gear tooth and its effect on mesh stiffness using extended finite element method, Engineering Failure Analysis. (2018) 94, 109–120.
10.1016/j.engfailanal.2018.07.032
Web of Science® Google Scholar
7 Chen Z., Zhang J., Zhai W., Wang Y., and Liu J., Improved analytical methods for calculation of gear tooth fillet-foundation stiffness with tooth root crack, Engineering Failure Analysis. (2017) 82, 72–81, https://doi.org/10.1016/j.engfailanal.2017.08.028, 2-s2.0-85028721042.
10.1016/j.engfailanal.2017.08.028
Web of Science® Google Scholar
8 Chen Z. and Shao Y., Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack, Mechanism and Machine Theory. (2013) 62, 63–74, https://doi.org/10.1016/j.mechmachtheory.2012.10.012, 2-s2.0-84871898835.
10.1016/j.mechmachtheory.2012.10.012
Web of Science® Google Scholar
9 Zhou S., Song G., Sun M., and Ren Z., Nonlinear dynamic response analysis on gear-rotor-bearing transmission system, Journal of Vibration & Control. (2016) 24, no. 9, 1–20, https://doi.org/10.1177/1077546316667178, 2-s2.0-85045443966.
10.1177/1077546316667178
CAS Web of Science® Google Scholar
10 Chen Q., Ma Y., Huang S., and Zhai H., Research on gears’ dynamic performance influenced by gear backlash based on fractal theory, Applied Surface Science. (2014) 313, 325–332, https://doi.org/10.1016/j.apsusc.2014.05.210, 2-s2.0-84904806092.
10.1016/j.apsusc.2014.05.210
CAS Web of Science® Google Scholar
11 Li X., Xu J., Pan W. et al., Dynamics of gear transmission system with fractal meshing stiffness on tooth surface, Journal of Harbin Institute of Technology. (2019) 51, no. 7, 56–62.
Google Scholar
12 Xiang L. and Gao N., Coupled torsion-bending dynamic analysis of gear-rotor-bearing system with eccentricity fluctuation, Applied Mathematical Modelling. (2017) 50, 569–584, https://doi.org/10.1016/j.apm.2017.06.026, 2-s2.0-85028010795.
10.1016/j.apm.2017.06.026
Web of Science® Google Scholar
13 Saxena A., Chouksey M., and Parey A., Effect of mesh stiffness of healthy and cracked gear tooth on modal and frequency response characteristics of geared rotor system, Mechanism and Machine Theory. (2017) 107, 261–273, https://doi.org/10.1016/j.mechmachtheory.2016.10.006, 2-s2.0-85008600461.
10.1016/j.mechmachtheory.2016.10.006
Web of Science® Google Scholar
14 Mohammed O. D. and Rantatalo M., Dynamic response and time-frequency analysis for gear tooth crack detection, Mechanical Systems and Signal Processing. (2015) 66, 612–624.
Web of Science® Google Scholar
15 Saeed M. A., Sadok S., and Mohammad R. P., Model-Based analysis of spur gears’ dynamic behavior in the presence of multiple cracks, Shock and Vibration. (2018) 2018, 20, 1913289, https://doi.org/10.1155/2018/1913289, 2-s2.0-85048174814.
10.1155/2018/1913289
Web of Science® Google Scholar
16 Ma H., Pang X., Zeng J., Wang Q., and Wen B., Effects of gear crack propagation paths on vibration responses of the perforated gear system, Mechanical Systems and Signal Processing. (2015) 62-63, 113–128, https://doi.org/10.1016/j.ymssp.2015.03.008, 2-s2.0-84928644769.
10.1016/j.ymssp.2015.03.008
Web of Science® Google Scholar
17 Ma H., Song R., Pang X., and Wen B., Coupled model of artificial neural network and grey model for tendency prediction of labor turnover, Mathematical Problems in Engineering. (2014) 2014, 22, 832192, https://doi.org/10.1155/2014/832192, 2-s2.0-84904097853.
10.1155/2014/832192
Web of Science® Google Scholar
18 Chen Z., Zhai W., Shao Y. et al., Analytical model for mesh stiffness calculation of spur gear pair with non-uniformly distributed tooth root crack, Engineering Failure Analysis. (2016) 66, 502–514.
10.1016/j.engfailanal.2016.05.006
Web of Science® Google Scholar
19 Ma R. and Chen Y., Research on the dynamic mechanism of the gear system with local crack and spalling failure, Engineering Failure Analysis. (2012) 26, no. 12, 12–20, https://doi.org/10.1016/j.engfailanal.2012.05.022, 2-s2.0-84865299198.
10.1016/j.engfailanal.2012.05.022
Web of Science® Google Scholar
20 Hu Z., Tang J., Zhong J., and Chen S., Frequency spectrum and vibration analysis of high speed gear-rotor system with tooth root crack considering transmission error excitation, Engineering Failure Analysis. (2015) 60, 405–441.
10.1016/j.engfailanal.2015.11.021
Web of Science® Google Scholar
21 Chen Z. and Shao Y., Dynamic simulation of planetary gear with tooth root crack in ring gear, Engineering Failure Analysis. (2013) 31, 8–18, https://doi.org/10.1016/j.engfailanal.2013.01.012, 2-s2.0-84874428028.
10.1016/j.engfailanal.2013.01.012
Web of Science® Google Scholar
22 Liu J., Zhang L., Zhao S. et al., Dynamic characteristics of wind turbine planetary set with crack in sun gear, Acta Energiae Solaris Sinica. (2019) 40, no. 1, 192–198.
Google Scholar
23 Kahraman A. and Singh R., Interactions between time-varying mesh stiffness and clearance non-linearities in a geared system, Journal of Sound and Vibration. (1991) 146, no. 1, 135–156, https://doi.org/10.1016/0022-460x(91)90527-q, 2-s2.0-0026419565.
10.1016/0022-460X(91)90527-Q
Web of Science® Google Scholar
24 Majumdar A. and Tien C. L., Fractal characterization and simulation of rough surfaces, Wear. (1990) 136, no. 2, 313–327, https://doi.org/10.1016/0043-1648(90)90154-3, 2-s2.0-0025015774.
10.1016/0043-1648(90)90154-3
Web of Science® Google Scholar
25 Wang S. and Komvopoulos K., A fractal theory of the interfacial temperature distribution in the slow sliding regime: Part I-elastic contact and heat transfer analysis, Journal of Tribology. (1994) 116, no. 4, 812–822, https://doi.org/10.1115/1.2927338, 2-s2.0-0028532320.
10.1115/1.2927338
Web of Science® Google Scholar
26 Shirong G. and Tonder K., The Fractal behavior and fractal characterization of rough surfaces, Tribology. (1997) 17, no. 1, 73–80.
Google Scholar
27 Siyu C., Jinyuan T., Caiwang L., and Qibo W., Nonlinear dynamic characteristics of geared rotor bearing systems with dynamic backlash and friction, Mechanism and Machine Theory. (2011) 46, no. 4, 466–478, https://doi.org/10.1016/j.mechmachtheory.2010.11.016, 2-s2.0-79251595540.
10.1016/j.mechmachtheory.2010.11.016
Web of Science® Google Scholar
28 Luo Y., Baddour N., and Liang M., Effects of gear center distance variation on time varying mesh stiffness of a spur gear pair, Engineering Failure Analysis. (2017) 75, 37–53, https://doi.org/10.1016/j.engfailanal.2017.01.015, 2-s2.0-85010960627.
10.1016/j.engfailanal.2017.01.015
Web of Science® Google Scholar

Citing Literature

All articles

Frequency and Vibration Characteristics of High-Speed Gear-Rotor-Bearing System with Tooth Root Crack considering Compound Dynamic Backlash

Abstract

1. Introduction

2. Dynamic Model of the Gear-Rotor-Bearing System

2.1. Lumped Mass Model of the Gear System

2.2. Time-Varying Meshing Stiffness for Gears with Tooth Crack

2.3. Dynamic Backlash

2.4. The Friction Force

2.5. Ball Bearing Model

2.6. Mathematical Model of the GRBS

3. Dynamic Response and Discussion

3.1. Comparison of Three Backlash Models

3.2. Dynamic Response of the Gear System with a Tooth Root Crack

3.3. Vibration Responses and Frequency Characteristics with Different Crack Depths

4. Conclusion

Nomenclature

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Frequency and Vibration Characteristics of High-Speed Gear-Rotor-Bearing System with Tooth Root Crack considering Compound Dynamic Backlash

Abstract

1. Introduction

2. Dynamic Model of the Gear-Rotor-Bearing System

2.1. Lumped Mass Model of the Gear System

2.2. Time-Varying Meshing Stiffness for Gears with Tooth Crack

2.3. Dynamic Backlash

2.4. The Friction Force

2.5. Ball Bearing Model

2.6. Mathematical Model of the GRBS

3. Dynamic Response and Discussion

3.1. Comparison of Three Backlash Models

3.2. Dynamic Response of the Gear System with a Tooth Root Crack

3.3. Vibration Responses and Frequency Characteristics with Different Crack Depths

4. Conclusion

Nomenclature

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information