Computational Studies on the Molecule 1-(2-Hydroxyethyl)-5-Fluorouracil in Gas Phase and Aqueous Solution and Prediction of Its Confinement inside Capped Nanotubes
Abstract
Density functional theory (DFT) calculations were performed on a fluorouracil derivative at the B3LYP/6−31+G(d) level. Furthermore, the ONIOM method was performed to investigate the possibility of its confinement inside capped nanotubes. The results found of the structural parameters of the optimized molecule are in good agreement with experimental data. The analysis of thermodynamic properties leads us to predict that the confinement of the studied molecule inside capped nanotubes SWCNT(12,0), SWCNT(14,0), and SWCNT(16,0) is possible. The large Eg values found suggest a good stability for the studied molecule. The predicted nonlinear optical (NLO) properties of the studied molecule are much greater than those of urea. Thereby, it is a good candidate as second-order NLO material. The calculated ∆Gsol values suggest that the studied molecule is more soluble than the 5-FU molecule. The results of quantum molecular descriptors show that the studied molecule is hard electrophile and strongly reactive.
1. Introduction
Experimental and theoretical studies have been previously done on the molecule uracil and its derivatives [1], especially the anticarcinogenic drug 5-fluorouracil (5-FU) [2] employed for treating solids tumors, especially those of gastrointestinal tract, brain, breast, pancreas, and liver [3]. One of the 5-FU derivatives recently characterized by X-ray diffraction is the molecule 1-(2-hydroxyethyl)-5-fluorouracil [4]. A good understanding of properties of molecules with therapeutic effects is very crucial, as well as their direct delivery to the right target. The study of interactions between nanostructures and therapeutic molecules is very important for the carrying and targeted delivery of drugs and other biomolecules. Various types of hybrid nanostructures modeled by the interaction of therapeutic molecules or chemical substances with nanometric structures such as phagraphene [5], fullerenes [6], and boron nitride nanoparticles [7] have been reported in the literature. These nanostructures can also be very important for applications such as the design of sensor systems [8] and energy storage devices [9]. The carbon nanotube is one of the most popular nanostructures used as nanocarrier on the basis of interactions with chemical compounds.
The confinement of molecules inside carbon nanotubes remains a big challenge. The confinement of therapeutic molecules inside nanotubes is very interesting due to the fact that the nanotube protects the biologically active molecule from degradation, and the hybrid nanostructure formed by the nanotube and the confined molecule can overcome the resistance of mechanical, physicochemical, and enzymatic barriers. Nanotubes can even cross biological barriers [10], thus offering the possibility of using them in gene therapy. Zare et al. [11] have reported a research work on the comparison of drug delivery systems. They have shown that carbon nanotubes deliver the 5-FU molecule better than the p-sulfonatocalix-[4]-arene. Carbon nanotubes have a great potential to carry molecules. Many studies on medical and biomedical applications [12, 13] of carbon nanotubes have been reported in the literature. Robinson et al. [14] have developed a generalized numerical method for generating the atomic coordinates of nanotube caps.
Many computational methods [15] have been developed to investigate the properties of molecules. Density functional theory (DFT) is greatly used in molecular computational study. This computational method reproduces very well the experimental properties of molecules such as geometrical structures, vibrational properties, and nonlinear and electronic properties [16, 17]. Recently, it has been reported that the van der Waals interactions play a major role in the encapsulation of molecules inside carbon nanotubes [18]. The van der Waals interactions can be taken into consideration in the modeling of hybrid nanostructures using the quantum mechanics (QM)/molecular mechanics (MM) calculations, especially the ONIOM method. The ONIOM method [19] has proved to be a powerful tool in combining quantum mechanics and molecular mechanics calculations. Chung et al. [20] have reported a review on the ONIOM method and its applications. In their review, many theoretical investigations using ONIOM methods on the encapsulation of molecules inside carbon nanotubes and other nanostructures have been reported. In particular, Garcia et al. [21] have studied the confinement of β-carotene inside carbon nanotubes using an ONIOM method. Ahmadi et al. [22] have studied the adsorption of ammonia molecules inside aluminum nitride nanotubes using an ONIOM method. To experimentally encapsulate a drug into a capped carbon nanotube, the first step is to synthesize the carbon nanotube [23]. As the synthesized nanotubes are usually closed by domes, at least one end must be opened before incorporation of the drug. The opening of the nanotube can be done by chemical oxidation [24] or thermal oxidation [25]. Yudasaka et al. [26] have developed two different methods, called nanoextraction and nanocondensation, to incorporate guest molecules into single-walled carbon nanotubes in liquid phases. Ren et al. [27] have applied the nanoextraction method to incorporate the antitumor agent hexamethylmelamine into carbon nanotubes. Recently, Wu et al. [28] have also used the nanoextraction method to incorporate the antitumor agent oxaliplatin into multiwalled carbon nanotubes. Satishkumar et al. [24] have reported experimental methods for closing carbon nanotubes. They have experimentally shown that uncapped nanotubes can be closed by the reaction at high temperature with benzene vapour in a reducing atmosphere of hydrogen and argon.
To the best of our knowledge, this is the first theoretical study on the molecule 1-(2-hydroxyethyl)-5-fluorouracil published. The aim of this work is to investigate the properties of the molecule 1-(2-hydroxyethyl)-5-fluorouracil in gas phase and aqueous solution. Furthermore, the changes occurring in the molecular geometrical structure and the thermodynamic stability when it is confined inside the hollow space of capped nanotubes SWCNT(12,0), SWCNT(14,0), and SWCNT(16,0) by considering mainly the van der Waals interaction have been investigated. This study is performed to predict the encapsulation of this molecule into carbon nanotubes; the long-term objective is to perform a targeted delivery of this molecule in cancer cells following the model proposed by Hilder et al. [29]. In this study, the molecular structure analysis of the studied molecule has been performed in gas phase and aqueous solution by a DFT method and inside the nanotube cavity by an ONIOM(DFT:MM) method. The thermodynamic properties of the studied molecule and the thermodynamic stability study of the optimized hybrid nanostructures have been investigated at different temperatures. The vibrational analysis, the nonlinear and electronic properties, the Gibbs free energy of solvation, and the quantum molecular descriptors of the studied molecule have been investigated in gas phase and aqueous solution.
2. Computational Methodology
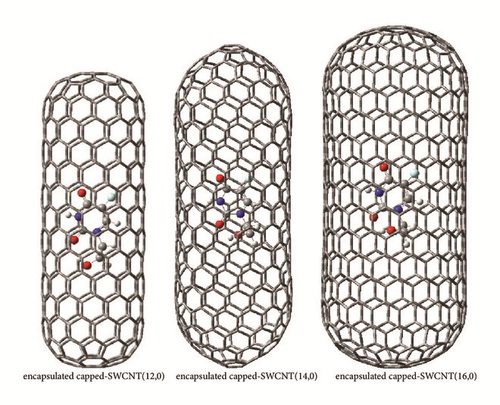
Density functional theory (DFT) was performed for the calculations of properties of the studied molecule in gas phase and aqueous solution, while the ONIOM(DFT:MM) method was performed to study the hybrid nanostructures. The hybrid nanostructures were obtained by the confinement of the studied molecule inside the nanotube cavities. We used capped nanotubes SWCNT(12,0), SWCNT(14,0), and SWCNT(16,0) of 336, 428, and 488 carbon atoms, respectively. The diameters of these nanotubes are 9.402 Å, 10.968 Å, and 12.536 Å. These nanotubes were chosen to point up the diameter range of carbon nanotubes that allow the studied molecule to be confined without any significant molecular geometry alteration. The uncapped nanotubes SWCNT(12,0), SWCNT(14,0), and SWCNT(16,0) have a finite length of 17.39 Å, and they have 204, 238, and 272 carbon atoms, respectively. Each cap of these nanotubes was formed with pentagonal defects. The 2D projections of the capped nanotubes are shown in Figure 1(a). The full geometry optimizations were performed on the studied molecule and the hybrid nanostructures using Gaussian 09 W program [30]. The results of simulations were visualized by GaussView 5 program [31]. We used the functional B3LYP with the 6−31+G(d) basis set to implement DFT calculations. The polarizable continuum model with a conductor solvent model (CPCM) was applied to account for solvation effects. In our calculations, water (dielectric constant (ε) of 78.4) was used as solvating medium. The Gibbs free energy of solvation was calculated by taking the difference between the total electronic energy in water after polarized continuum model (PCM) corrections using the SMD continuum model [32] and the total electronic energy in gas phase.
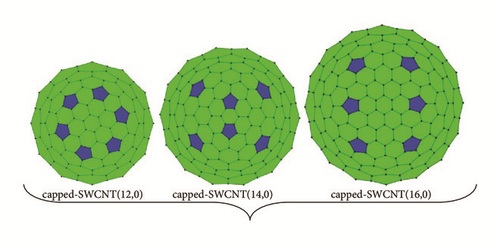
The inclusion of van der Waals (vdW) interactions [18] for an accurate description of the molecular structure of nanostructures designed by encapsulation of molecule inside the hollow space of nanotube is indispensable. The combination of DFT with the united force field (UFF) has been widely used [33, 34]. The noncovalent interactions were applied during the optimization of the hybrid nanostructures with the ONIOM method by combining the B3LYP/6−31+G(d) level with the united force field (UFF). The stability constant and thermodynamic quantities such as enthalpy, Gibbs free energy, and entropy were computed to analyze the stability of the optimized hybrid nanostructures. The use of localized basis sets reduces the amount of computational work required. However, calculations using finite basis sets are susceptible to basis set superposition errors (BSSEs). The changes of energies in all complexes nanostructures were corrected by calculating the basis set superposition error using the counterpoise method [35]. In this method, the BSSE is calculated using the mixed basis sets, and the error is then subtracted a posteriori from the uncorrected energy. The mixed basis sets are realized by introducing “ghost orbitals” (basis set functions which have no electrons or protons).
3. Results and Discussion
3.1. Optimized Structure
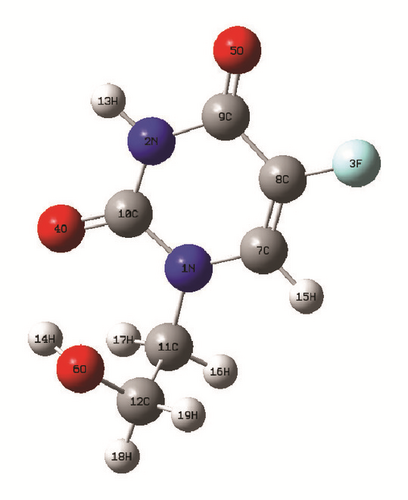
The optimized geometrical parameters of the studied molecule in gas phase, aqueous solution, and the hollow space of the capped nanotubes SWCNT(12,0), SWCNT(14,0), and SWCNT(16,0) are gathered in Table 1. The molecular structure of the studied molecule and the optimized hybrid nanostructures are shown in Figures 1(b) and 1(c), respectively. The computed bond lengths of the studied molecule in gas phase and aqueous solution and inside the capped nanotubes change slightly in comparison to experimental values of the crystal structure [4]. The changes of structural parameters of the studied molecule in aqueous solution in comparison to those in gas phase are induced by the dipolar interaction between it and the solvating medium. Inside the nanotube cavity, the van der Waals interactions applied between the confined molecule and the nanotube contribute mainly to the changes of structural parameters of the studied molecule in comparison to those in gas phase.
Gas Phase |
Aqueous solution |
Inside capped-SWCNT(12,0) |
Inside capped-SWCNT(14,0) |
Inside capped-SWCNT(16,0) |
Experimental [4] |
|
|---|---|---|---|---|---|---|
B3LYP 6−31+G(d) |
B3LYP 6−31+G(d) |
ONIOM (B3LYP/6−31+G(d):UFF) |
ONIOM (B3LYP/6−31+G(d):UFF) |
ONIOM (B3LYP/6−31+G(d):UFF) |
||
| Bond lengths (Å) | ||||||
| N1-C10 | 1.392 | 1.388 | 1.382 | 1.393 | 1.391 | 1.373(3) |
| N1-C7 | 1.382 | 1.377 | 1.381 | 1.381 | 1.382 | 1.376(3) |
| N1-C11 | 1.471 | 1.476 | 1.481 | 1.470 | 1.472 | 1.479(3) |
| N2-C10 | 1.384 | 1.385 | 1.380 | 1.385 | 1.384 | 1.374(3) |
| N2-C9 | 1.407 | 1.397 | 1.405 | 1.407 | 1.408 | 1.385(3) |
| F3-C8 | 1.345 | 1.352 | 1.343 | 1.345 | 1.344 | 1.355(3) |
| O4-C10 | 1.228 | 1.231 | 1.228 | 1.227 | 1.228 | 1.228(3) |
| O5-C9 | 1.219 | 1.230 | 1.218 | 1.219 | 1.219 | 1.225(3) |
| O6-C12 | 1.415 | 1.426 | 1.410 | 1.416 | 1.415 | 1.418(3) |
| C7-C8 | 1.349 | 1.350 | 1.348 | 1.348 | 1.349 | 1.329(4) |
| C8-C9 | 1.459 | 1.449 | 1.453 | 1.459 | 1.459 | 1.431(4) |
| C11-C12 | 1.534 | 1.530 | 1.543 | 1.534 | 1.533 | 1.511(4) |
| Bond angles (°) | ||||||
| C10-N1-C7 | 121.315 | 121.328 | 120.132 | 121.284 | 121.266 | 121.2(2) |
| C10-N1-C11 | 117.662 | 118.194 | 118.819 | 118.043 | 117.666 | 119.9(2) |
| C7-N1-C11 | 120.947 | 120.473 | 120.966 | 120.457 | 120.997 | 118.9(2) |
| C10-N2-C9 | 128.872 | 128.384 | 130.159 | 129.067 | 128.910 | 128.2(2) |
| C8-C7-N1 | 122.075 | 121.679 | 123.498 | 122.288 | 122.084 | 121.3(2) |
| C7-C8-F3 | 120.673 | 120.775 | 120.968 | 120.711 | 120.725 | 120.6(2) |
| C7-C8-C9 | 121.770 | 121.941 | 121.267 | 121.611 | 121.742 | 122.5(2) |
| F3-C8-C9 | 117.557 | 117.281 | 117.765 | 117.667 | 117.533 | 116.9(2) |
| O5-C9-N2 | 121.874 | 121.850 | 121.863 | 121.909 | 121.865 | 120.8(2) |
| O5-C9-C8 | 126.769 | 126.316 | 127.708 | 126.747 | 126.814 | 127.3(2) |
| N2-C9-C8 | 111.357 | 111.833 | 110.428 | 111.341 | 111.319 | 111.9(2) |
| O4-C10-N2 | 122.497 | 121.976 | 122.404 | 122.560 | 122.546 | 121.6(2) |
| O4-C10-N1 | 122.957 | 123.204 | 123.087 | 123.128 | 122.909 | 123.4(2) |
| N2-C10-N1 | 114.543 | 114.820 | 114.509 | 114.311 | 114.543 | 114.9(2) |
| N1-C11-C12 | 113.368 | 113.328 | 115.139 | 113.407 | 113.723 | 111.5(2) |
| O6-C12-C11 | 113.637 | 113.499 | 114.512 | 113.704 | 113.940 | 111.9(2) |
The maximum difference between the theoretical and experimental bond lengths is found at C8−C9 bond. The bond lengths N1−C10, N1−C7, N2−C10, N2−C9, and C8−C9 in the gas phase and aqueous solution and inside nanotubes are close to the experimental values of the studied molecule and slightly lower than the corresponding experimental bonds of the 5-fluorouracil (5-FU) molecule [2]. The bonds O4−C10 and O5−C9 are very close to the experimental values of the studied molecule and slightly greater than the corresponding experimental bonds of the 5-FU molecule [2].
As illustrated in Table 1, most computed angles are slightly different from experimental ones. In comparison to experimental bond angles, the maximum shifts occur at C10−N1−C11 bond angle in gas phase and at N1−C11−C12 bond angle in aqueous solution and inside nanotubes. The most discrepancy between the studied fluorouracil derivative and the 5-FU molecule occurs at the N2−C9−C8 bond angle. Thus, the replacement of the hydrogen atom in the 5-FU molecule at the position N1 by the 1-(2-hydroxyethyl) fragment induces changes of molecular geometrical parameters of the pyrimidine ring. The dihedral angles N1−C11−C12−06 of the confined molecule are 94.223°, 52.307°, and 51.057, and the dihedral angles C11−C12−06−H14 are −54.497°, 41.838°, and 35.051° inside SWCNT(12,0), SWCNT(14,0), and SWCNT(16,0), respectively. Clearly, the structure of the studied molecule can be affected by the confinement into the capped nanotube SWCNT(12,0) because the dihedral angles N1−C11−C12−06 and C11−C12−06−H14 of the isolated molecule are 50.822° and 37.769°, respectively. When the studied molecule is confined inside the nanotube SWCNT(14,0) or SWCNT(16,0), its structural parameters are not evidently affected by the nanotube. The geometries of the confined molecule inside SWCNT(14,0) and SWCNT(16,0) are very similar to those of the isolated molecule. The confined molecule approximately locates in the middle axis of SWCNT(12,0) and SWCNT(14,0), but it is in the side of SWCNT(16,0). We can conclude that any nanotube whose diameter is greater than 10.968 Å will have no significant influence on the geometry of the studied molecule. However, nanotubes whose diameter is less than 9.402 Å can significantly change or destroy the molecular structure of the confined molecule. The results found for structural parameters of the studied molecule are in good agreement with X-ray crystallographic data [4].
3.2. Thermodynamic Properties of the Studied Molecule and Thermodynamic Stability Study of the Optimized Hybrid Nanostructures
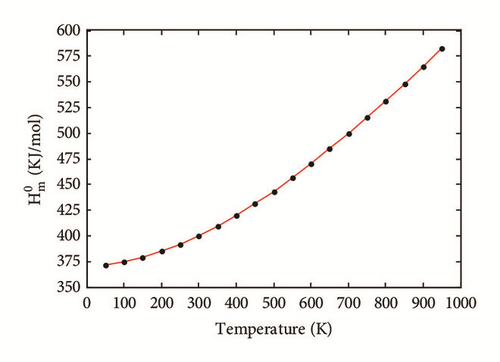
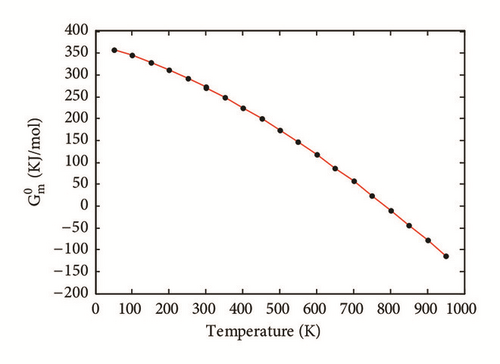

The two-layered ONIOM method has been used to study the confinement of the studied molecule inside capped nanotubes SWCNT(12,0), SWCNT(14,0), and SWCNT(16,0). In this work, the ONIOM method is implemented by treating the full system at the low level of theory (a molecular mechanics method) and the interesting part of the system at high level of theory (a quantum mechanics method). The enthalpy change, ∆HT, and the change of Gibbs free energy, ∆GT, for the confinement reaction between the studied molecule and the nanotubes were estimated on the basis of the confinement energy found in the literature [34, 40, 41]. The entropy change was derived from ∆HT and ∆GT. The enthalpy change ∆HT, the entropy change ∆ST, the change of Gibbs free energy ∆GT and the stability constant logK for the confinement reaction leading to the optimized hybrid nanostructures are reported in Supplementary Material S2. As illustrated in Figure 3(a), the ∆HT values are negative and increase at any temperature from 100 to 900 K. Hence, the formation of optimized hybrid nanostructures is an exothermic process. The thermodynamic quantity ∆ST provides information about the order or disorder of optimized hybrid nanostructures. The ∆ST values are negative at any temperature from 100 to 900 K. Thus, the formation of optimized hybrid nanostructures is done in an ordered way. However, as illustrated in Figure 3(b), a reduction of the degree of organization of hybrid nanostructures is done with the increasing temperature because the ∆ST values increase. As shown in Figure 3(c) the ∆GT values increase in the range of 100-900 K. In addition, the ∆GT values under 900 K are negative (see Supplementary Material S2), which implies that the confinement of the studied molecule inside the hollow space of capped nanotubes SWCNT(12,0), SWCNT(14,0), and SWCNT(16,0) is possible. Thus, the formation process of optimized hybrid nanostructures is spontaneous and thermodynamically favorable for temperatures under 900 K. As shown in Figure 3(d), the stability constant logK values decrease with the increasing temperature. This implies that the interaction between the confined molecule and each capped nanotube decreases with the increasing temperature. At low temperatures, the interaction between the confined molecule and the nanotube is relatively weak.
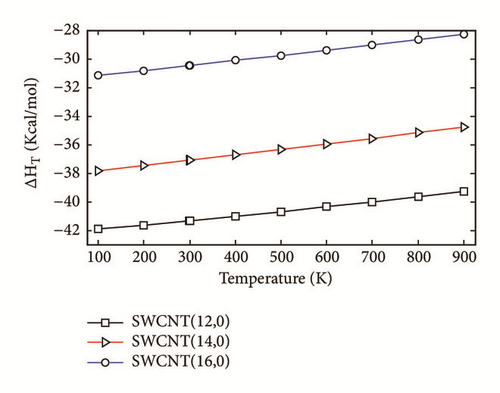
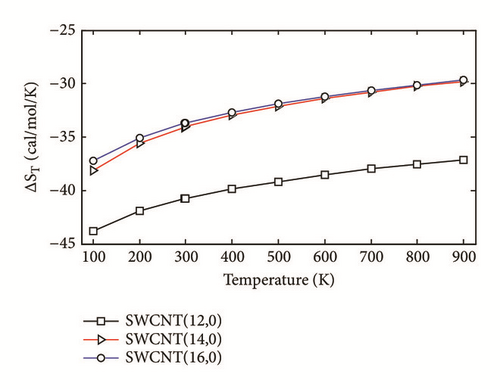
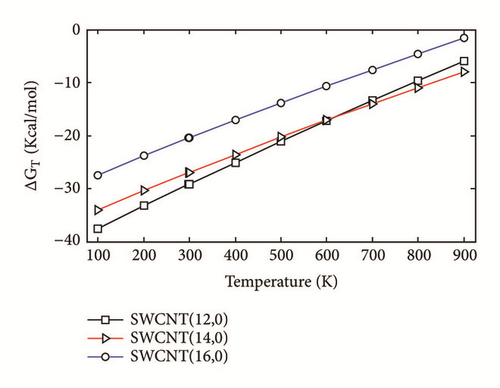
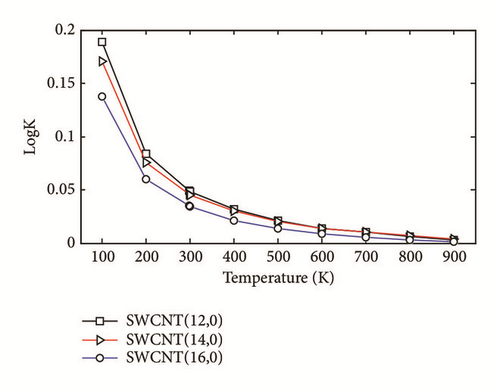
According to the thermodynamic properties and the stability constant computed, the confinement of the studied molecule inside capped nanotubes SWCNT(12,0), SWCNT(14,0), and SWCNT(16,0) is possible and the formation of optimized hybrid nanostructures is thermodynamically favorable.
3.3. Vibrational Analysis of the Studied Molecule in Gas Phase and Aqueous Solution
Vibrational results are useful to better characterize the studied molecule. The quantities of interest in vibrational spectra are frequencies and intensities. The PCM model has been extended to vibrational studies [42]. In aqueous solution, the reaction field of water perturbs the molecular potential energy surface (PES) and induces changes of vibrational frequencies. The vibrational frequencies, IR intensities, Raman activities, and assignments of strong vibrational modes of the studied molecule in gas phase and aqueous solution are reported in Table 2. Most modes are not pure but contain significant contributions of other modes. The IR intensity and Raman activity spectra are shown in Figure 4.
| Gas phase | Aqueous solution | ASSIGNMENTS a,b | ||||
|---|---|---|---|---|---|---|
| Frequency | IR intensity | Raman activity | Frequency | IR Intensity | Raman activity | |
| 3693.369 | 69.061 | 44.508 | 3705.977 | 87.657 | 98.192 | ν(06 − H) |
| 3586.430 | 75.248 | 74.241 | 3577.938 | 115.905 | 149.567 | ν(N2 − H) |
| 3238.231 | 2.895 | 77.440 | 3251.219 | 6.661 | 182.559 | ν(C7 − H) |
| 3141.099 | 6.603 | 42.173 | 3160.495 | 8.380 | 106.641 | νas(CH2, C11 and C12) |
| 3084.940 | 33.197 | 113.127 | 3111.124 | 43.204 | 166.701 | νs(CH2, C11) + νas(CH2, C12) |
| 3081.124 | 23.687 | 97.655 | 3104.464 | 21.819 | 312.681 | νs(CH2, C11) + νas(CH2, C12) |
| 3000.562 | 74.151 | 202.427 | 3031.451 | 86.618 | 368.806 | νs(CH2, C12) |
| 1789.169 | 538.145 | 99.162 | 1740.087 | 421.750 | 127.385 | ν(C = 0, C9 and C10) + δ(N2 − H) |
| 1762.630 | 717.354 | 5.220 | 1707.784 | 1468.833 | 235.994 | ν(C10 = O) + δ(N2 − H) |
| 1711.453 | 101.079 | 51.197 | 1699.171 | 818.283 | 54.809 | ν(C7 = C8) + δ(C7 − H) |
| 1529.037 | 1.166 | 9.056 | 1519.870 | 1.880 | 16.642 | δ(CH2, C12, scissoring) |
| 1500.104 | 20.636 | 13.178 | 1496.912 | 43.736 | 27.878 | δ(CH2, C11, scissoring) |
| 1482.282 | 55.577 | 3.273 | 1489.073 | 93.803 | 13.530 | ν(ring, C − C and C − N strechting) + γ(CH2, C11, twisting) |
| 1448.190 | 45.498 | 9.248 | 1443.952 | 60.681 | 26.451 | δ(O6 − H) + γ(CH2, C12, overtone) |
| 1427.302 | 23.576 | 7.779 | 1427.587 | 3.0543 | 20.827 | δ(N2 − H) + γ(CH2, C12, overtone) |
| 1421.510 | 3.616 | 1.511 | 1423.682 | 23.509 | 6.940 | δ(N2 − H, C7 − H) + γ(CH2, C11, overtone) |
| 1390.505 | 118.205 | 7.611 | 1387.181 | 119.856 | 11.122 | γ(C − H, C11 and C12) + δ(O6 − H) |
| 1380.598 | 38.196 | 40.217 | 1380.309 | 114.269 | 131.649 | δ(O6 − H, C7 − H, ) + γ(CH2, C11, twisting) |
| 1347.554 | 83.164 | 7.909 | 1349.457 | 129.749 | 13.904 | δ(O6 − H, C7 − H, N2 − H) + γ(C − H, C11 and C12) |
| 1281.458 | 44.323 | 17.485 | 1284.076 | 103.003 | 28.210 | γ(CH2, C12, twisting) + γ(C − H, C11) + δ(C7 − H) |
| 1256.870 | 106.831 | 7.770 | 1240.649 | 71.580 | 45.139 | ν(C8 − F, N2 − C10) + δ(C7 − H) + γ(CH2, C12, twisting) |
| 1225.483 | 75.439 | 2.778 | 1231.243 | 282.155 | 6.081 | γ(CH2, C11 and C12, twisting)+ δ(O6 − H, C7 − H, N2 − H) |
| 1171.275 | 71.265 | 6.885 | 1178.572 | 74.246 | 37.119 | ν(ring, C − N strechting) + δ(O6 − H, C7 − H, N2 − H) + γ(C − H, C11 and C12) |
| 1152.566 | 18.908 | 10.654 | 1144.897 | 77.474 | 17.510 | ν(C11 − N) + δ(O6 − H, C7 − H) + γ(C − H, C11) |
| 1114.000 | 40.616 | 3.788 | 1092.868 | 41.455 | 9.179 | ν(C12 − O) + δ(C7 − H) |
| 1078.303 | 39.558 | 0.562 | 1065.832 | 121.038 | 1.764 | δ(O6 − H) + ρ(CH2, C11 and C12) |
| 950.975 | 14.994 | 4.003 | 957.424 | 26.819 | 6.760 | ν(C11 − C12) + δ(N2 − H, C7 − H) |
| 901.949 | 24.808 | 3.319 | 926.124 | 33.394 | 8.721 | γ(C7 − H) |
| 888.823 | 16.915 | 2.971 | 888.838 | 38.112 | 6.208 | δ(N2 − H, C7 − H) + ρ(CH2, C11 and C12) + ν(C11 − C12) |
| 856.699 | 12.157 | 6.746 | 856.464 | 28.472 | 12.028 | δ(N2 − H) + ρ(CH2, C11) + ν(C11 − C12) |
| 777.597 | 11.367 | 16.247 | 782.228 | 10.639 | 48.556 | δ(ring, CNC, NCN bending) |
| 751.894 | 0.787 | 0.694 | 752.374 | 0.591 | 2.834 | γ(ring, O4N1N2C10, O5N2C8C9 out of plane deformation) |
| 741.280 | 68.559 | 0.783 | 737.753 | 95.416 | 1.452 | γ(N2 − H, wagging) + γ(ring, O4N1N2C10, O5N2C8C9 out of plane deformation) |
| 689.145 | 18.744 | 4.013 | 689.745 | 33.709 | 6.088 | ρ(CH2, C12) + ν(N1 − C11) + δ(ring, N2C10N1 bending) |
| 673.146 | 41.930 | 1.197 | 668.088 | 2.271 | 6.203 | γ(N2 − H, wagging) |
| 667.305 | 1.219 | 2.541 | 654.352 | 93.406 | 1.226 | ρ(CH2, C11) + δ(ring, O5C9N2, O4C10N2, F3C8C7 bending) |
| 563.675 | 9.497 | 2.281 | 563.724 | 11.316 | 5.625 | δ(NCC, N1C11C12 bending) + ρ(CH2, C12) |
| 501.458 | 1.490 | 9.674 | 503.295 | 3.892 | 19.791 | δ(CCO, C11C12O6 bending) + δ(ring, C8C7N1, O4C10N2 bending) |
| 436.878 | 83.784 | 2.489 | 435.560 | 35.623 | 7.042 | γ(O6 − H, wagging) + δ(ring, N2C10N1, C11N1C7 bending) |
| 408.328 | 127.290 | 1.384 | 409.922 | 9.849 | 1.315 | γ(O6 − H, wagging) + γ(ring, C8C7N1C10 out of plane deformation) |
- a: limited to the description of strong vibrational modes of the studied molecule and the reported vibrational modes are those of the studied molecule in gas phase although many descriptions are identical in the two media (in gas and water).
- b: ν, νs, and νas, stretching (simple, symmetric, and asymmetric); δ: in plane bending (simple, scissoring); γ: out of plane bending (twisting, overtone, wagging, deformation); ρ: rocking.
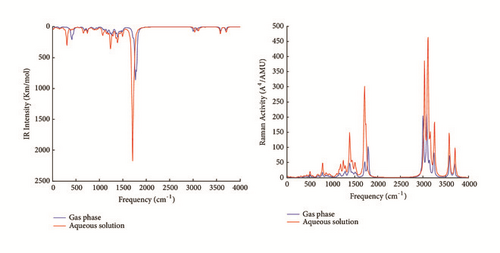
The solvation of the studied molecule produces greater shifts between the computed values in gas phase and aqueous solution of IR intensities and Raman activities. The maximum IR intensities are 717.354 and 1468.833 Km/mol and are observed in gas phase and aqueous solution at 1762.630 and 1707.784 cm−1, respectively. Similarly, the maximum Raman activities are 202.427 and 368.806 A4/AMU and are observed in gas phase and aqueous solution at 3000.562 and 3031.451 cm−1, respectively. Identical vibrational modes contribute to the maximum IR intensities and Raman activities in gas phase and aqueous solution but with different intensities. The stretching vibrational mode of the bond C10=O and the bending vibrational mode of angles formed with the N2−H bond in the plane of the pyrimidine ring constitute two contributions to maximum IR intensities of the studied molecule in gas phase and aqueous solution. The symmetric stretching vibrational modes of the −CH2 group at position C12 contribute to maximum Raman activities of the studied molecule in gas phase and aqueous solution. The first three maximum unscaled vibrational frequencies are found at 3693.369, 3586.430, and 3238.231 cm−1 in gas phase and 3705.977, 3577.938, and 3251.219 cm−1 in aqueous solution and correspond to the O−H stretching vibration, N2−H stretching vibration, and C7−H stretching vibration, respectively. The scaling factor 0.95 is appropriated to compute vibrational frequencies at B3LYP/6−31+G level [43]. The maximum vibrational frequencies found with the scaling factor 0.95 are 3508.701, 3407.109, and 3076.319 cm−1 in gas phase and 3520.678, 3399.041, and 3088.658 cm−1 in aqueous solution, respectively. The maximum vibrational modes of the studied molecule have been observed experimentally at 3520, 3410, and 2994 cm−1 [4]. The O−H stretching vibration usually occurs in the region 3300−3600 cm−1 [44]. The vibrational stretching modes N2−H and C7−H have been experimentally observed in the molecule 5-FU at 2992 and 2815 cm−1 [4] and theoretically observed without scaling factor with the 3P86/6−31G(d,p) level at 3640 and 3258 cm−1 [2], respectively. In the uracil molecule, the N2−H and C7−H vibrational modes have been experimentally observed at 3160 and 3090 cm−1 [1] and theoretically observed without scaling factor with the B3LYP/6−311++G(d,p) basis at 3597 and 3244 cm−1 [1], respectively. Thereby, with the scaling factor 0.95, the computed vibrational frequencies at B3LYP/6−31+G(d) are in good agreement with the experimental IR frequencies values [4].
3.4. Nonlinear and Electronic Properties, Gibbs Free Energy of Solvation, and Quantum Molecular Descriptors of the Studied Molecule
The nonlinear optical (NLO) properties of organic molecules are extensively investigated with density functionals [45]. The values of the computed NLO properties are gathered in Table 3. The following relations have been used to convert the mean polarizability (αm) and the static first-order hyperpolarizability (βm) in electrostatic units (esu): 1 a.u. of α = 0.148x10−24 esu and 1 a.u. of β = 8.639x10−33 esu. In aqueous solution, the values of μtot, αm, and βm increase. When the studied molecule is solvated, the reaction field of water modifies the nonlinear responses. The calculated dipole moment is 5.117 D in gas phase. The computed μtot value of the urea molecule is 4.590 D with the B3LYP/6−31+G(d) method. Gester et al. [46] have reported a μtot value of 3.93 D in gas phase and 5.91 D in aqueous solution for the 5-FU molecule. The polarizability tensor (αij) is dominated by the diagonal components and the highest value is obtained for the component αxx. In this direction, the found value is 19.249 Å3 in gas phase and 25.071 Å3 in aqueous solution. The αm value of the studied molecule is greater than that of urea (αurea = 4.181 Å3 at B3LYP/6−31+G(d) level). Basis sets have effects on the hyperpolarizability. Fernando et al. [47] have shown that the inclusion of diffuse functions into basis sets is crucial to obtain accurate results of the hyperpolarizability. Therefore, diffuse basis sets give acceptable values of the hyperpolarizability. The urea molecule is a well-known NLO material and is widely used to predict good NLO material on the basis of the static first-order hyperpolarizability. The βm value of urea computed at the B3LYP/6−31+G(d) level is 0.526 × 10−30cm5/esu. This value is slightly lower than the value reported in the literature at B3LYP/6−31++G(d,p) level (βm = 0.770 × 10−30cm5/esu) [48]. The βm value of the studied molecule is 1.487 × 10−30cm5/esu, which is theoretically 2.82 times greater than that of urea at B3LYP/6−31+G(d) level. These results show that the studied molecule is a good candidate as second-order NLO material.
| Gas phase | Aqueous solution | |
|---|---|---|
| CPCM | ||
| Properties | B3LYP/6−31+G(d) | B3LYP/6−31+G(d) |
| μtot | 5.117 | 7.292 |
| αm | 14.298 | 18.725 |
| βm | 1.487 | 1.576 |
| Eg | 5.167 | 5.165 |
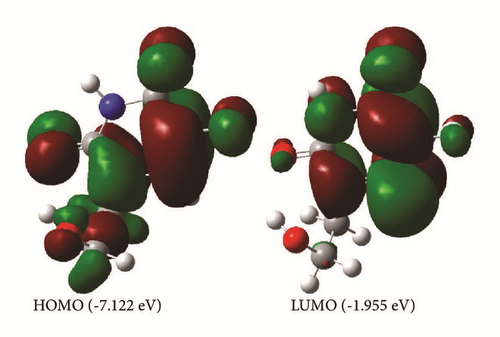
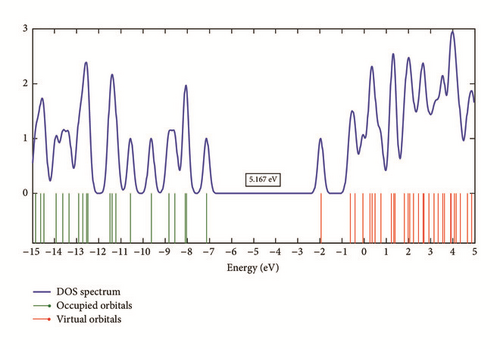
The analysis of electronic properties of organic molecules is usually related to frontier orbitals [17]. The HOMO and LUMO orbitals and the density of states (DOS) plot of the studied molecule are shown in Figures 5 and 6. The LUMO orbital is mainly localized on the pyrimidine ring, while the HOMO orbital is localized on the whole molecule. The HOMO and LUMO values are −7.122 eV and −1.955 eV in gas phase and −6.947 eV and −1.782 eV in aqueous solution. The solvation modifies slightly the band structure of the studied molecule. The results of the energy gap (Eg) gathered in Table 3 show that the solvation decreases slightly the Eg value when the studied molecule is moved from the gas phase to aqueous solution. The large Eg values found refer to high excitation energies for many excited states and suggest a good stability for the studied therapeutic molecule.
Pienko et al. [49] have reported in the literature that the solubility is a crucial parameter for bioavailability prediction of therapeutic molecule. The Gibbs free energy of solvation (∆Gsol) is a physicochemical parameter related to the solubility, which can be derived from quantum mechanical calculations. From thermodynamic consideration, negative values of ∆Gsol mean that the process of solvation is spontaneous. The more negative the ∆Gsol value, the higher the degree of solubility. The computed ∆Gsol value of the studied molecule is −18.524 Kcal/mol. Therefore, the dissolution in water of the studied molecule is spontaneous. The computed ∆Gsol value of the 5-FU molecule is −15.950 Kcal/mol with the CPCM/B3LYP/6−31+G(d) method. This shows that the studied molecule is more soluble than the 5-FU molecule. The increase in the degree of solubility in water of the studied molecule in comparison to 5-FU molecule is probably induced by the presence of the 1-(2-hydroxyethyl) fragment. Recently, Zafar et al. [50] have estimated the range of Gibbs free energy of solvation in drug design; they have reported that the ∆Gsol value of quality drug candidates should be less than −12 Kcal/mol. the ∆Gsol value of the studied molecule is much less than −12 Kcal/mol. Therefore, the studied molecule is a promising quality drug candidate.
Table 4 shows the calculated quantum molecular descriptors of the studied molecule in gas phase and aqueous solution. When the studied molecule is moved from the gas phase to aqueous solution, the values of EA, IP, χ, μ, η, and ω decrease.
| Gas phase | Aqueous solution | |
|---|---|---|
| Quantum molecular | CPCM | |
| Descriptors | B3LYP/6−31+G(d) | B3LYP/6−31+G(d) |
| EA (eV) | 1.955 | 1.782 |
| IP (eV) | 7.122 | 6.947 |
| χ (eV) | 4.539 | 4.365 |
| μ (eV) | −4.539 | −4.365 |
| η (eV) | 2.584 | 2.583 |
| S (eV−1) | 0.387 | 0.387 |
| ω (eV) | 3.986 | 3.688 |
The computed values of the electron affinity (EA) and the ionization potential (IP) of the 5-FU molecule are 1.955 and 7.276 eV with the B3LYP/6−31+G(d) method, respectively. The IP value of the studied molecule decreases in comparison to that of the 5-FU molecule. However, the EA value does not change because the LUMO orbital, which is directly related to the electron affinity, is localized on the pyrimidine ring. Furthermore, the values of χ and μ of the 5-FU molecule are 4.615 and −4.615 eV, respectively. These results show that the reactivity of the studied molecule is improved because its IP value decreases, while its μ value increases in comparison to those of the 5-FU molecule. The harness of a molecule refers to its resistance toward deformation in presence of an electric field. Usually, a soft molecule has a small energy gap, while a hard molecule has a large energy gap. The studied molecule is hard because its harness is greater than its softness. This result is in agreement with the large energy gap found. The computed values of η and S of the 5-FU molecule are 2.660 eV and 0.375 eV−1 with the B3LYP/6−31+G(d) method, respectively. The comparison of the harness and softness of the studied molecule with those of the 5-FU molecule indicates that the studied molecule is more soft and less hard than the 5-FU molecule. Schwöbel et al. [51] have reported a review of experimental and theoretical methods of measurement and estimation of electrophilic reactivity. It appears that the electrophilicity index is a good descriptor to measure the electrophilic reactivity of chemical compounds. Parthasarathi et al. [52] have reported in the literature a study on the biological activity prediction with the electrophilicity index. Their results show that the biological activity of chemical compounds may be effectively described with the electrophilicity index. Furthermore, Roy et al. [53] have reported research work on the toxicity prediction with the electrophilicity. They showed that the electrophilicity is a promising descriptor for toxicological prediction considering the case of aliphatic compounds. The ω value of the studied molecule varies very slightly in comparison to 5-FU molecule (ω = 4.003 eV with the B3LYP/6−31+G(d) method). This molecule is hard electrophile.
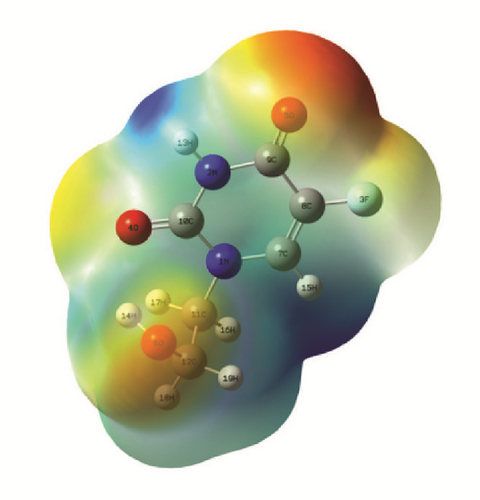
The sites for nucleophilic and electrophilic reactions have been determined with the molecular electrostatic potential (MEP). Figure 7 shows the total electron density surface mapped with electrostatic potential of the studied molecule. Potential increases in the order red < orange < yellow < green < blue. Atoms localized in the red regions are negative potential sites and participate in electrophilic reactions, while atoms localized in the blue regions are positive potential sites and participate in nucleophilic reactions. The V(r) values near the atoms O5, O6, O4, and F of the studied molecule are −0.052, −0.041, −0.033, and −0.022 au, respectively. These sites are the most negative potential sites and are involved in electrophilic reactions. The most positive potential sites are localized near the C7−H and N2−H bonds. The V(r) values near the C7−H and N2−H bonds are 0.055 and 0.052 au, respectively. These sites are involved in nucleophilic reactions. These results provide information of sites where the studied molecule can have intermolecular interactions with other compounds (as a nanotube during the confinement process and water during the solvation process) and covalent bonding with toxic proteins in the inhibition process of their activities.
4. Conclusions
Density functional theory calculations have been performed on the molecule 1-(2-hydroxyethyl)-5-fluorouracil in gas phase and aqueous solution, and the ONIOM method has been performed to investigate the possibility of its confinement inside capped carbon nanotubes SWCNT(12,0), SWCNT(14,0), and SWCNT(16,0). The results found for structural parameters of the studied molecule are in good agreement with the X-ray crystallographic data. The solvation and the confinement inside nanotubes of the studied molecule change slightly its molecular geometrical parameters. Correlation equations have been obtained to predict the standard thermodynamics properties , , and of the studied molecule at any temperatures. The analysis of the thermodynamic properties ∆HT, ∆ST, and ∆GT and the stability constant logK leads to the prediction that the confinement of the studied molecule inside these nanotubes is possible and the formation of optimized hybrid nanostructures is thermodynamically favorable. Vibrational analysis has been performed to better characterize the optimized molecule in gas phase and aqueous solution. The solvation of the studied molecule produces greater shifts between the computed values in gas phase and aqueous solution of IR intensities and Raman activities. The predicted nonlinear properties of the studied molecule are much greater than those of urea. The studied molecule is a good candidate as second-order NLO material. The large Eg values found suggest a good stability for the studied molecule. The calculated ∆Gsol values suggest that the studied molecule is more soluble than the 5-FU molecule. Frontier molecular orbital (FMO) energies have been employed to study the quantum molecular descriptors according to Koopmans theorem. The solvation decreases the values of EA, IP, χ, μ, η, and ω. The results of EA and IP show that the studied molecule has the same tendency to accept electrons as the 5-FU molecule from a donor and its reactivity is higher than that of the 5-FU molecule. The μ value of this fluorouracil derivative confirms that its reactivity is improved in comparison to that of the 5-FU molecule. The studied molecule is more soft and less hard than the 5-FU molecule. The ω value of the studied molecule changes very slightly in comparison to that of the 5-FU molecule. We hope that these results will be helpful for other researches on new organic materials, drugs, and hybrid nanostructures.
Conflicts of Interest
The authors declare that there are no conflicts of interest as concerns this article.
Acknowledgments
We are thankful to the Council of Scientific and Industrial Research (CSIR), India, forfinancial support through Emeritus Professor scheme (grant no. 21(0582)/03/EMR-II) to Late Prof. A.N. Singh of the Physics Department, Bahamas Hindu University, India, which enabled him to purchase the Gaussian Software. We are most grateful to Late Emeritus Prof. A.N. Singh for donating this software to one of us, Dr. Geh Wilson Ejuh, and to the Materials Science Laboratory of the University of Yaoundé I for enabling us to use their computing facilities.
Open Research
Data Availability
The data used to support the findings of this study are included within the article.




