This paper presents a method to control the rotor speed of wind turbines in presence of gearbox efficiency fault. This kind of faults happens due to lack of lubrication. It affects the dynamic of the principal shaft and thus the rotor speed. The principle of the fault tolerant control is to find a bloc that equalizes the dynamics of the healthy and faulty situations. The effectiveness decrease impacts on not only the dynamics but also the steady state value of the rotor speed. The last reason makes it mandatory to add an integral term on the steady state error to cancel the residual between the measured and operating point rotor speed. The convergence of the method is proven with respect to the rotor parameters and its effectiveness is evaluated through the rotor speed.

1. Introduction

The wind turbine is an electromechanical device to extract the energy from the wind and feed it to the customer through the grid. The wind turbine is composed of several interconnected components. First, the rotor transforms the aerodynamic torque defined by (1) into mechanical torque. The latter is transformed into electricity through a conventional generator. The bond between the rotor and the generator is performed by the bias of a mechanical gearbox. The role of the gearbox is to maintain the same power from rotor to generator through a transformation ratio Ng [1]. Figure 1 summarizes the different components of a modern wind turbine.

()

The wind turbine (WT) operates in two distinct regions. The first region is called moderate winds (<7 s/m). In this interval, the WT is controlled through the generator torque to maximize the extraction of the energy contained in the wind. The second region is called high winds region (>7 m/s) in which the objective is to maintain a constant power at the nominal value. This is achieved through controlling three actuators existing in each blade. Those actuators are called pitch because they let the blade turn a pitch angle about its longitudinal axis. By this pitching movement, the blade is exposed (0° pitch) or not (90° pitch) to the wind and then the rotor speed is accelerated or decelerated [2]. An overview of the modelling and control of the wind turbine systems could be found in [3].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The composition of a wind turbine system.

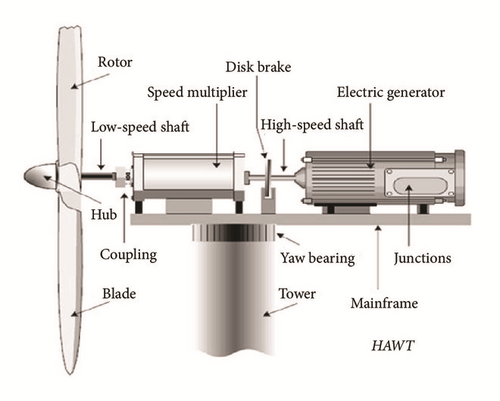
However, the dusty and wet environment induces degradation in some critical components such as the blades, the shafts, the sensors, the generator, and the mechanical components such as the gearbox. Moreover, the challenging situations in which the wind turbines operate (high winds and turbulences, faults on the sensors, and actuators [4]) require highly available systems. For this reason, fault tolerant control strategies [5] are elaborated to prevent the damaging effect of faults and failures on the turbine structure [6]. Most of the FTC methods are composed of two blocs. The first bloc estimates the fault and provides information about the amplitude and the shape of the fault. The last information is then provided to the FTC bloc to build a new control law suitable for the faulty situation. The production of the new control law could be performed either by changing the regulator’s parameters or by adding a new term to the old control law to compensate the fault term. More details on faults in the wind turbines and their FTC could be found in [7], where different types of faults and their corresponding severities are cited. Leakage fault in the hydraulic actuators which is of high severity could not be resolved and the only solution is to shut down the wind turbine for possible maintenance.

In the present paper, the considered fault is the degradation of the efficiency of the gearbox linking the rotor to the generator. It is a fault of medium severity which impacts the dynamics of the rotor and then deteriorates the result of the speed regulation. It will be demonstrated that the fault could be considered an internal fault and a suitable fault tolerant strategy is then applied.

2. The Wind Turbine Model

The considered nominal objective of the wind turbine control is to regulate the rotor speed about the operating value of 40 rpm. The chosen operating wind speed is 18 m/s with 30% of variations according to Kaimal distribution.

The blade pitch operating angle is 9°. This operating point belongs to the high wind region where the only objective is to regulate the power by regulating the rotor speed. This prevents the wind turbine from exceeding the nominal values and from being damaged due to high winds. The parameters of the wind turbine are extracted through linearization from the software FAST [8]. FAST is industrial software developed by the National Renewable Energy Laboratory in Colorado to test and validate the control laws on the wind turbines before physical implementation.

The considered control objective requires considering the rotor and the gearbox models.

2.1. The Rotor Speed Model

The rotor model of the wind turbine is extracted by applying the first law of mechanics to the turbine and is given by

()

where ∂T_a/∂ω = α; ∂T_a/∂Ω_r = γ et ∂T_a/∂β = ξ. T_a is the aerodynamic torque applied by the wind on the blades and defined by (1). δω is the variation of the wind speed, δβ is the variation of the pitch angle, and δΩ_r is the variation of the rotor speed, about the operating point. J_t is the total inertia of the wind turbine. The linearization about the chosen operating point gives γ = −0.1039 J_t; ξ = − 2.5727 J_t; and α = 0.61141 J_t.

2.2. The Gearbox Model

The gearbox is used to adapt the low speeds (40 rpm) of the rotor to the high speeds of the generator (1500 rpm) while maintaining the same power between the two nodes. This relationship could be modelled by the following equation:

()

Ω_g is the generator speed, J_g is the generator inertia, T_g is the generator torque, T_lss,e is the principle shaft torque, and η_gbx and N_g are, respectively, the efficiency and the multiplication ratio of the gearbox. The variation of the parameter η_gbx induces a variation of the generator speed. This variation is also transmitted to the rotor due to N_g:

()

The torque T_lss,e is a picture of the aerodynamic torque. The torque should be carefully estimated as in [9].

2.3. Aerodynamic Torque Estimation

The aerodynamic torque could be estimated from the drive train model.

2.3.1. Drive Train Model

The drive train is composed of a low speed shaft (rotor side) interconnected with a high-speed shaft (generator side) through a mechanical gearbox with a ratio Ng. The drive train is modelled by the following differential equations:

()

J_r is the rotor inertia, J_g is the generator inertia, and X is the restoring force applied on the low speed shaft. The shaft is driven by the aerodynamic torque. The generator torque about the equivalent low speed shaft N_gT_g is used to accelerate or decelerate the shaft. D_lss,e and K_lss,e are the damping and stiffness coefficients of the principle shaft.

2.3.2. Torque Estimation Loop

In literature, many approaches have been proposed for aerodynamic torque estimation. Authors in [10] proposed a PI based observer to estimate aerodynamic torque. In [11] authors used the Kalman filter to reconstruct the aerodynamic torque Fourier coefficients. In this paper, the proposed method is based on the transfer function between the aerodynamic torque T_a and the rotor speed Ω_r. However, in most cases, the rotor speed cannot be measured; the measured generator speed about low speed shaft could be considered as a good approximation to the rotor speed. In fact, after transients, the rotor and generator speed about the equivalent low speed shaft are the same, in the case of a rigid equivalent shaft, or when damping the torsional modes of the mechanical shaft.

The transfer function F(s) between the aerodynamic torque T_a and generator speed Ω_r is obtained after manipulations of (5) as follows:

()

where a = D_lss,e/J_rJ_g; b = K_lss,e/J_rJ_g; c = ((J_r + J_g)/J_rJ_g)D_lss,e; and d = K_lss,e((J_r + J_g)/J_rJ_g).

The idea is to keep the model speed Ω_gm sufficiently close to the measured one, Ω_g, by acting on the model with an adequate aerodynamic torque . This could be performed through a feedback estimation loop as presented in Figure 2. In contrast to authors in the previous works, and since the transfer function F(s) already contains an integrator term, and assuming that the mean of Ω_g is sufficiently low frequency, only a proportional action is needed to estimate T_a. After transients, the model output Ω_gm converges to Ω_g and its input converges to the actual torque T_a. Finally, can be considered as an estimation of the actual aerodynamic torque T_a. The proportional torque estimator gain is chosen in such way that the slowest pole of the closed loop of the transfer function F(s) is cancelled.

Figure 3 shows the actual and estimated aerodynamic torque. The actual aerodynamic torque represented in Figure 3 by the blue color is obtained for comparison by the following equation:

()

J_r is the rotor inertia about the shaft of the turbine. The shaft torque (KNm) and the rotor acceleration (deg/sec²) can be obtained from FAST software as outputs. In the industrial wind turbines, a strain gauge is installed on the mechanical shaft of the wind turbine to measure the shaft torque. The rotor acceleration is measured by an accelerometer.

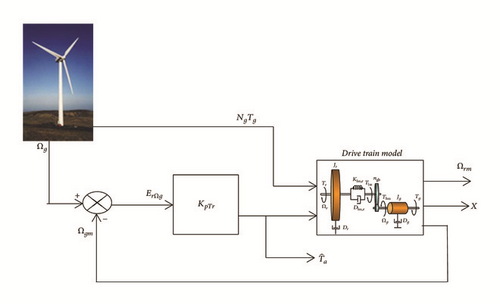
Note that K_pTr is the proportional torque estimator gain; E_rΩg is the speed tracking error, T_g is the generator torque about the high-speed shaft, N_g is the gearbox ratio, and the term N_gT_g is the generator torque about the low speed shaft; Ω_gm is the model generator speed about low speed shaft; Ω_g is the measured generator speed; X is the restoring force of the low speed shaft; Ω_rm is the model rotor speed; is the estimated aerodynamic torque.

Define the mean convergence error between actual aerodynamic torque T_a and estimated aerodynamic torque

along N samples of data:

()

In the present case of simulation, we obtain a relative error of 1.8%. The torque estimation could then be considered sufficiently accurate.

2.4. Estimated Aerodynamic Torque Filtering

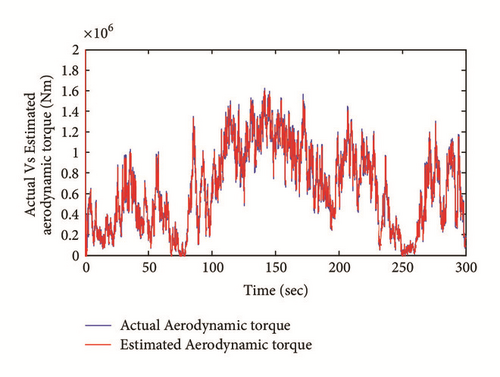
In this section, a spectral analysis is performed to identify the frequencies of the wind speed transmitted to the torque and those resulting from the mechanical vibration. The objective is to reconstruct the frequencies specific to the wind speed. Figures 4 and 5 show the power spectral density of the wind profile and aerodynamic torque, respectively.

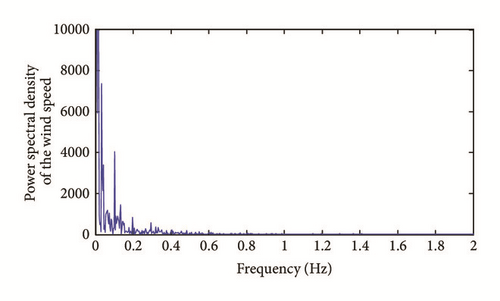
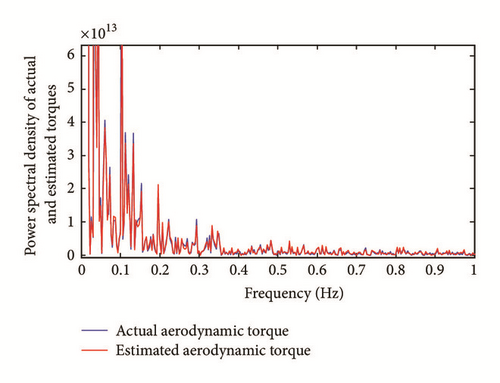
One can notice that the frequencies contained in the wind and having a significant effect on the torque of the rotor resides in the low frequency range (<0.12 Hz). The peaks that occur beyond this area are the result of vibrations of the mechanical structure as a result of excitations caused by the wind. The estimated aerodynamic torque, which will be used for reconstitution of the wind speed, should therefore be filtered according to the previous remark. In the case of our system, we chose a low pass filter of 0.4 Hz bandwidth. Figure 6 shows the power spectral density of filtered and the nonfiltered torque.

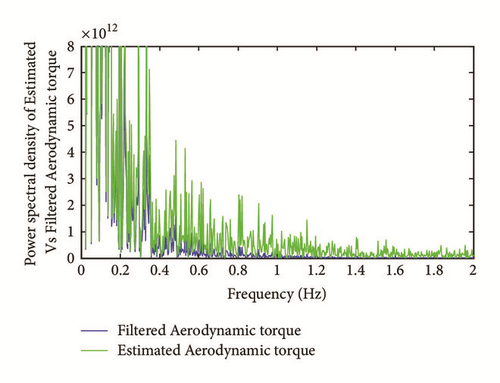
From Figure 6, one can notice that frequencies above 0.4 Hz have been attenuated and filtered.

2.5. Gearbox Efficiency Estimation

After estimation of the principal shaft torque, the gearbox efficiency variations η_gbx could be estimated through (3) as in [12] by the following manipulations:

()

Figure 7 shows the fault detection scheme of the gearbox efficiency.

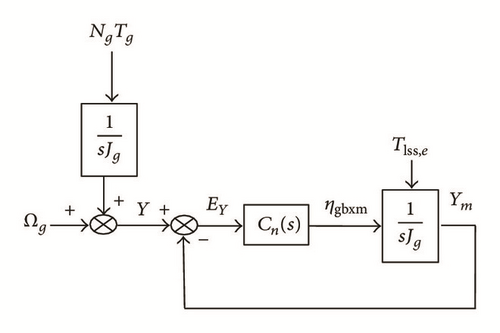
Ω_g is the measured generator speed, E_Y is the tracking error loop, η_gbxm is the estimated drive train efficiency, N_gT_g is the generator torque about the low speed shaft, and T_lss,e is the previously estimated shaft torque. Y is the measured variable to be tracked by the model’s output. C_n(s) is the proportional action transfer function used for the estimation. C_n(s) is a constant gain M.

In the present case, the proportional gain M is fixed at lower values and progressively increases until we have got good estimation results. For this turbine, we found optimal K at 0.9.

Figure 8 represents different results of estimation for different gearbox efficiencies. The estimate of η_gbx constitutes a fault residual, given by (10), used in the activation of the fault tolerant control if a gearbox fault happens. In fact, when r ≠ 1, it means that the efficiency of the gearbox decreases and the fault tolerant control bloc should be activated.

()

Since the fault in η_gbx affects the generator speed as in (3), and the generator speed is linked to the rotor speed through (4), it can be concluded that this fault affects only the dynamics of the rotor represented by the parameter γ/J_t in (3). This conclusion is verified only under the assumption that no actuator fault neither sensor faults are present at the same time with the gearbox loss of efficiency fault.

2.6. Gearbox Efficiency Impact on the Eigenvalues of the Dynamic Matrix

Figure 9 illustrates the variation of the eigenvalues of the dynamic matrix with respect to the gearbox efficiency. For efficiencies less than 20%, the variations of the eigenvalues are fast with a gradient of 0.62 in absolute values. This gradient becomes slower with 0.1633 for values more than 20% of efficiencies. This means that, for values less than 20%, it is easy to reach eigenvalues near the instability (near 0) than for values more than 20%. The algebraic equation representing the curve in Figure 9 is given by

()

where a = −0.3203; b = 0.0604; c = 0.3124.

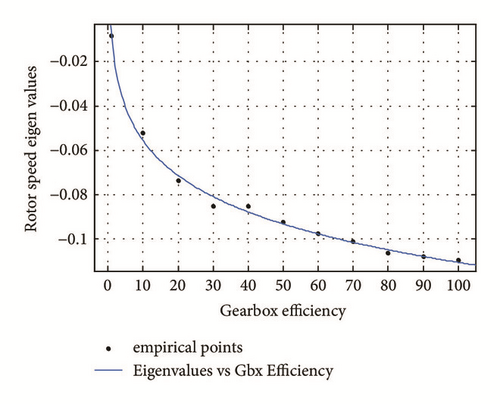
This paragraph shows that the efficiency fault impacts the stability of the system. Hence, the fault tolerant control becomes necessary.

3. The Fault Tolerant Control Strategy

3.1. Dynamics Equalization Gain

The fault tolerant bloc to be computed should satisfy the following condition:

()

where A, B, and C represent the dynamic, input action, and measurement matrix of the healthy system. A_f represents the dynamic matrix affected by the fault and K is the bloc to be computed, where

()

The resolution of (12) with respect to K while applied on the model of the wind turbine in (2) gives the value of K:

()

where γ and ξ are turbine dependent coefficients defined in (2) of the healthy model of the rotor. γ_f is the coefficient γ but in the faulty situation.

The new control law is then given by

()

3.2. Convergence of the Dynamics Equalization Method

Let us define the healthy system by (2) and the faulty system by

()

And the error between the faulty rotor speed and the healthy rotor speed is defined by

()

The dynamics of the error are given by

()

By taking K as in (14), the error dynamics become

()

Since γ/J_t is negative (by the nature of the rotor), the error dynamics converges to zero as the time evolves. It can be concluded that the stability of the method depends on the stability of the initial system and any deviation from the healthy speed will be caused only by the imperfections of the model.

3.3. Steady State Reconfiguration by Residual Integration

The gearbox efficiency impacts also the steady state of the rotor speed. For this, an integral part is needed to cancel the static error between 40 rpm and the real time measured rotor speed. The global fault tolerant control law is given by

()

In this simulation, a good value of N is −0.03.

3.4. Convergence of the Integrated Strategy

We take K as in (14), the error dynamics using control law in (20) becomes

()

This means that

()

The dynamics in (22) are stable, if the eigenvalues of the matrix

are of negative real parts. The eigenvalues of the matrix are given by λ₁ and λ₂ in (23) as

()

To obtain eigenvalues with negative real parts, one should resolve inequality λ_1,2≺0.

()

While ξ is negative and J_t is positive, N should be fixed negative N < 0 to have stability of the integrated method.

3.5. Robustness Considerations

Let define a robustness level θ which should robustify the method (represented by the error e) against the wind disturbance ω. The inequality to be verified is given by

()

where e = δΩ_rf − δΩ_r and δΩ_r = δΩ_{r_ref} = 0 rpm deviation from the operating rotor speed. After applying the FTC method, the closed loop rotor system becomes

()

In the present paper, the desired rotor speed reference δΩ_{r_ref} is 0 rpm deviation from the operating speed 40 rpm. Equation (26) could be simplified to

()

And the error becomes equivalent to e = δΩ_rf. So the inequality to be verified becomes

()

The objective is to extract the transfer function between the turbulence δω and the rotor speed δΩ_rf. For this aim, the Laplace transform is applied to

()

If the disturbance effect is considered, the transfer function could be obtained by

()

If the Laplace operator s is replaced by jτ, where j is the complex number and τ is the pulsation (2πf). The module of the transfer function is then given by

()

By replacing (31) in (28), inequality (28) becomes equivalent to

()

The inequality symbol change between the two last lines of (32) comes because the term ξ/J_tτ² is inferior to 0.

Finally,

()

Then, to ensure robustness level θ, and given a pulsation τ = 2πf (rad/s) the design parameter N should verify inequality (33). It is recommended to take the maximal frequency contained in the wind equal to 1 Hz as in Section 2, Figure 4.

4. Results and Discussions

Figure 10 illustrates the rotor speed in the nominal, faulty, and fault tolerant cases. In order to evaluate the effectiveness of the method, the distance (according to the ordinates axis) between two points on the curve is considered. The first point is P1 with abscissa 143 seconds and the second point P2 with 90.34 seconds of abscissa. In the nominal situation, the difference between the ordinates of P1 and P2 is of 8.1 rpm; this value becomes 11.5 rpm in the faulty situation. By using the fault tolerant control strategy, this value is reduced to 9.2 rpm. As shown in the same Figure 10, not only the dynamics are impacted but also the steady state value of the rotor speed which become closer to 40 rpm operating point due to the integral term N∫(δΩ_rf − δΩ_r) in the control law.

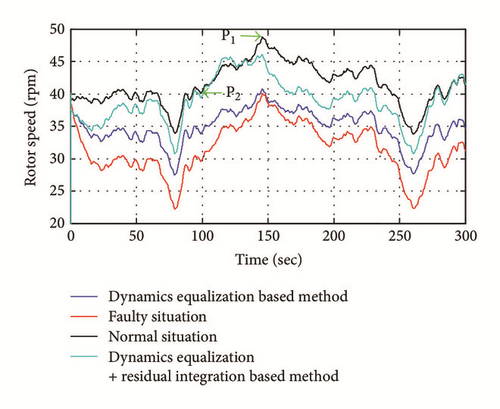
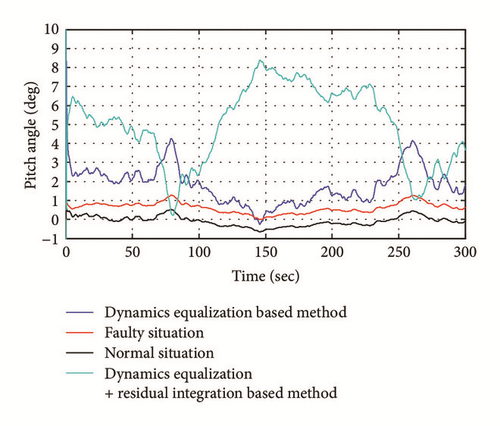
Figure 11 illustrates the pitch angle in the three situations. It can be stated that, in the faulty situation (red), the nominal regulator “tries” to beat the deviation in the speed by generating some pitch angles but without satisfactory results. By adding the term KδΩ_rf to the old control signal, the efforts become bigger and the difference between the points P1 and P2 is reduced. In the integrated method, the efforts become bigger and the integral part is evidently impacting the pitch angles to cancel the steady state error.

Compared to other methods, the proposed strategy reconstructs the rotor speed while keeping the generated power constant as before the fault occurrence. In fact, another way to do is to decrease the operating point generator torque in (3) to maintain the same generator speed variations and then the same rotor speed variations

. This could be done by multiplying the generator torque input by the estimated gearbox efficiency. This method helps keeping the rotor speed as it was but impacts the generator torque and then the generated power whose expression is given by

()

The method of this paper uses pitch actuators instead of generator torque and this helps keeping the generated power constant and then satisfies continuously the customer demand of electricity.

5. Conclusion

In this paper, a fault tolerant control method composed of several steps is proposed to deal with the loss of gearbox efficiency. This fault occurs due to the dusty environment of the modern large scale wind turbines. The first step is to estimate the shaft torque through a suitable transfer function between the rotor speed and the shaft torque. The last torque is used to estimate in real time the gearbox efficiency through a suitable loop. The estimated efficiency is used to select a corresponding eigenvalue from Figure 9. A design coefficient K is computed so the dynamics of the prefault and postfault cases are equalized. The rotor speed steady state is reconstructed by adding an integral part of the residual between the measured and reference rotor speed (zero deviation from operating point is desired).

On the other hand, a performance based conditions were given to help choosing the design integration parameter N. Based on the fact that the residual should not be impacted by the wind disturbance; a performance level θ has been proposed to verify |e|≺θ|ω|. The last inequality helps to give a negative (because ξ is by construction negative) inferior limit to N function of θ as .

The method is characterized by its ease of elaboration and parameters design and especially helps keeping a continuous production of the power in contrast to the generator torque based method.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

References

1 Wang H. P., Pintea A., Christov N., Borne P., and Popescu D., Modelling and recursive power control of horizontal variable speed wind turbines, Control Engineering and Applied Informatics. (2012) 14, no. 4, 33–41, 2-s2.0-84876438560.
Web of Science® Google Scholar
2 Magar K. T., Balas M. J., and Frost S. A., Smooth transitioning of wind turbine operation between region II and region III with adaptive disturbance tracking control, Wind Engineering. (2014) 38, no. 3, 337–348, 2-s2.0-84901769401, https://doi.org/10.1260/0309-524X.38.3.337.
10.1260/0309-524X.38.3.337
Google Scholar
3 Song Y.-D., Li P., Uu W., and Qin M., An overview of renewable wind energy conversion system modeling and control, Measurement + Control. (2010) 43, no. 7, 203–208, 2-s2.0-84863338422, https://doi.org/10.1177/002029401004300703.
10.1177/002029401004300703
Web of Science® Google Scholar
4 Ribrant J. and Bertling L. M., Survey of failures in wind power systems with focus on Swedish wind power plants during 1997–2005, IEEE Transactions on Energy Conversion. (2007) 22, no. 1, 167–173, https://doi.org/10.1109/tec.2006.889614, 2-s2.0-33947670511.
10.1109/TEC.2006.889614
Web of Science® Google Scholar
5 Rezaei V. and Salmasi F. R., Robust adaptive fault tolerant pitch control of wind turbines, Wind Engineering. (2014) 38, no. 6, 601–612, 2-s2.0-84913621214, https://doi.org/10.1260/0309-524X.38.6.601.
10.1260/0309-524X.38.6.601
Google Scholar
6 Odgaard P. F., Stoustrup J., and Kinnaert M., Fault-tolerant control of wind turbines: A benchmark model, IEEE Transactions on Control Systems Technology. (2013) 21, no. 4, 1168–1182, 2-s2.0-84879936035, https://doi.org/10.1109/TCST.2013.2259235.
10.1109/TCST.2013.2259235
Web of Science® Google Scholar
7 Li P., Song Y., Liu W., and Qin M., Monitoring of Wind Turbines: A Bio-Inspired Fault Tolerant Approach, Measurement + Control. (2011) 44, no. 4, 111–115, https://doi.org/10.1177/002029401104400403.
10.1177/002029401104400403
PubMed Web of Science® Google Scholar
8 Jonkman J. M. and Buhl M. L., FAST User′s Guide - Updated August 2005, 2005, no. NREL/TP-500-38230, https://doi.org/10.2172/15020796.
10.2172/15020796
Google Scholar
9 Ait Elmaati Y., El Bahir L., and Faitah K., An integrator based wind speed estimator for wind turbine control, Wind and Structures, An International Journal. (2015) 21, no. 4, 443–460, 2-s2.0-84947928326, https://doi.org/10.12989/was.2015.21.4.443.
10.12989/was.2015.21.4.443
Google Scholar
10 Østergaard K. Z., Brath P., and Stoustrup J., Estimation of effective wind speed, Journal of Physics: Conference Series. (2007) 75, no. 1, https://doi.org/10.1088/1742-6596/75/1/012082, 012082, 2-s2.0-34548177974.
10.1088/1742-6596/75/1/012082
Web of Science® Google Scholar
11 Hafidi G. and Chauvin J., Wind speed estimation for wind turbine control, Proceedings of the 2012 IEEE International Conference on Control Applications, CCA 2012, October 2012, Croatia, 1111–1117, 2-s2.0-84873102260, https://doi.org/10.1109/CCA.2012.6402654.
10.1109/CCA.2012.6402654
Google Scholar
12 Ait Elmaati Y., El Bahir L., and Faitah K., Residual generation for the gearbox efficiency drop fault detection in the NREL 1.5WindPact turbine, Proceedings of the 1st International Conference on Electrical and Information Technologies, ICEIT 2015, March 2015, Morocco, 77–81, 2-s2.0-84945297442, https://doi.org/10.1109/EITech.2015.7162939.
10.1109/EITech.2015.7162939
Google Scholar

Citing Literature

All articles

Fault Tolerant Control of Internal Faults in Wind Turbine: Case Study of Gearbox Efficiency Decrease

Abstract

1. Introduction