Hand Detection Using Cascade of Softmax Classifiers
Abstract
Sliding-window based multiclass hand posture detections are often performed by detecting postures of each predefined category using an independent detector, which makes it lack efficiency and results in high postures confusion rates in real-time applications. To tackle such problems, in this work, an efficient cascade detector that integrates multiple softmax-based binary (SftB) models and a softmax-based multiclass (SftM) model is investigated to perform multiclass posture detection in parallel. The SftB models are used to distinguish the predefined postures from the background regions, and the SftM model is applied to discriminate among all the predefined hand posture categories. Another usage of the cascade structure is that it could effectively decompose the complexity of background pattern space and therefore improve the detection accuracy. In addition, to balance the detection accuracy and efficiency, the HOG features of increasing resolutions will be adopted by classifiers of increasing stage-levels in the cascade structure. The experiments are implemented under various scenarios with complicated background and challenging lightings. Results show the superiority of the proposed SftB classifiers over the traditional binary classifiers such as logistic regression, as well as the accuracy and efficiency improvements brought by the softmax-based cascade architecture compared with the noncascade multiclass softmax detectors.
1. Introduction
Hand detection refers to determining the hands location and their shapes. It works as a prerequisite step for various hand gesture recognition systems [1, 2] that have been widely studied, due to their potential application in entertainment and virtual reality [3], medical systems, and assistive technologies, as well as in crisis management and disaster relief [4]. However, hand detection is never an easy task due to the hand deformation [5], the sensitivity of skin colors to lighting conditions [6], and the complicated environments for practical applications. As a result, robust and efficient hand detection remains a challenging task in computer vision community.
Multiclass hand posture detection is worthy of investigation for several reasons: different users may be habituated to using different postures for interaction, many application systems require multiple postures to realize different functions, and robust detection of human hand from multiple viewpoints can be achieved through multiclass hand detection by letting different posture categories represent postures captured under different viewpoints. One way to deal with multiclass hand detection is first to locate the human hand and then to determine the hand shape by classification. Such methods are usually of low accuracy. For example, to locate human hand using skin color cues can be easily affected by the lighting condition and the skin-like background, which will lead to high miss and false rates and will degrade the follow-up classification accuracy/speed in detection. Another example is to train binary classifier for sliding-window-based hand localization, in which all predefined postures are treated as a positive class and the background is regarded as negative class. In this method, the difference in posture shapes increases the pattern complexity of positive space and resultantly leads to low excluding rate for background. Another way for multiclass hand detection is to build independent detector for each predefined posture and perform multiposture detection by sequentially detecting each of the predefined postures with the corresponding posture detectors [7, 8]. The disadvantage of such practice contains several aspects: (a) the computing cost is high, because multiple rounds of detections are required to find the postures of multiple categories; (b) a window image may be predicted into multiple posture categories, which would result in heavy overlapping detection results; and (c) the multiple detectors are trained independently rather than jointly and in collaboration, which causes confusion detection between different postures easily.
- (1)
A softmax-based cascade architecture is proposed to perform multiclass hand postures detection in parallel and meanwhile to decompose the complexity of background pattern space to improve the detection accuracy.
- (2)
The SftB classifier is proposed to better distinguish the predefined postures from the background regions, since it could decompose the complexity of multiclass posture pattern space by the multiclass decision boundaries that are learned jointly.
- (3)
The cascade is designed to take low-resolution HOG features at the lower stages and to use HOG features of higher resolutions for stage-classifiers of higher levels, which helps to balance between the detection accuracy and efficiency.
The remainder of this paper is organized as follows. Section 2 briefly reviews the existing work on vision-based human hand detection problem. The proposed softmax-based cascade architecture is described in Section 3 in detail. Experimental results and discussions are provided in Section 4. Conclusions and future work are offered in Section 5.
2. Related Work
The vision-based hand detection methods can generally be separated into two groups: the appearance-based methods and the 3D-model-based methods [2, 7]. The appearance methods carry out the detection by directly comparing the image features with prebuilt appearance models. These methods are usually of high efficiency, but their performance can be easily affected by viewpoint variation and hand deformation. The 3D methods adopt a kinematic model with high degree of freedom [5, 8]. Such methods offer a richer hand description and therefore could deal with more posture categories, but they are usually computationally expensive due to the complex model matching algorithms. Here in this work, an appearance method is explored to perform the multiclass hand posture detection in parallel.
The key of appearance methods is to seek effective features for hand posture representation as well as to develop an efficient and expressive posture classification model. The frequently used appearance features include the Haar-like [2, 7, 9], HOG [10–12], SIFT [13, 14], and BRIEF [14, 15]. However, such features are seriously affected by the cluttered backgrounds that introduce noise to features encodings. For this reason, recently there are trends to adopt the combination of multiple feature descriptions, such as the integration of HOG and skin features in [16] and the association of Haar-like and HOG in [2]. However, the accuracy improvements for such multifeature methods are usually gained at the expense of considerable increase in computing cost. To improve the efficiency, a classifier of two levels is presented in [1], in which the possible presence of hands is determined from a global perspective in the first level, and then hand regions are precisely delineated at pixel level by a probabilistic model in the second level. And, in [17], the saliency map generated by a Bayesian model is firstly thresholded to localize the hand regions, and then shape and texture features are extracted from the saliency map of hand regions for hand posture recognition. More recently, the deep learning (DL) methods are also investigated for hand posture detection, such as the integration of CNN scheme with fast candidate generation [18], the multiscale deep feature approach [19], and the deep architecture with three networks of sharing convolution layers [20]. However, the speeds of DL-based methods are much lower than those of the classical methods if the algorithms are running on a machine without advanced GPUs.
Multiclass posture detection problem is often addressed by two-stage methods [20–23], in which hand region proposals are firstly obtained by techniques like skin, motion, or saliency detection which are robust to hand deformation and viewpoint variation, and then these regions are classified by multiple binary models or single multiclass model to achieve the final posture recognition. For such methods, precise region proposals are prerequisite to achieve satisfactory recognition rates, while obtaining precise proposals is never an easy job in itself if no specific posture models are utilized. As a result, the misdetection is often relatively high for such methods. The sliding-window-based methods usually perform the multiclass posture detection with multiple posture-specific detectors [9, 24]. Such methods may have relatively high recall rates. But they lack efficiency since each window needs to be classified by multiple detectors and suffer from heavy confusion detections because the detectors for different categories are trained independently rather than in a coordinated manner. Besides, there are works that adopt tree-type structure [7], but practical experiments show that there is no significant improvement in accuracy or efficiency. Here in this work, we propose a softmax-based cascade detector to perform multiclass hand posture detection simultaneously rather than category by category. Moreover, owing to the multiclass objective function, the decision boundaries are essentially obtained by seeking a balance among all categories and therefore can help reduce the confusion rates among different posture categories.
3. The Proposed Methodology
In this section, the softmax model is firstly presented for multiclass classification. Then, the softmax-based cascade architecture is introduced for multiclass hand posture detection. And, finally, we will show how to apply multiresolution features to the cascade architecture to balance the detection accuracy and efficiency.
3.1. Multiclass Hand Posture Classification by Softmax Regression
3.2. Softmax-Based Cascade Architecture for Human Hand Detection
In the experimental part, k0 is set at 2. For ease of understanding, the flowchart for the window image classification is provided in Figure 1.
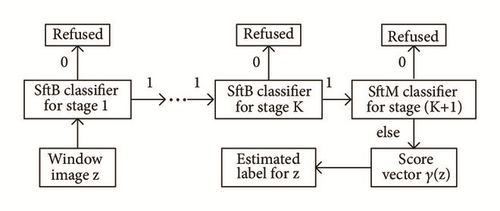
3.3. Multiresolution HOG Feature for Different Stage-Classifiers
For sliding-window-based hand detection, there are tens of thousands window images to be classified in single frame, which makes the detection system lack efficiency. To improve the efficiency, here in this work, the multiresolution HOG features are adopted for posture representations [24]. The cascade is designed so that the HOG features with low resolutions are utilized by classifiers of lower stage-levels, and HOG features with high resolutions are utilized by classifiers of higher stage-levels. The varied feature resolutions can be achieved by adjusting the density of cell splits in window images as discussed in [24]. With such multiresolution scheme, a large number of background windows can be excluded by the classifiers using low-resolution HOG features. And only few difficult background windows need to be further classified by the HOG features of high resolutions which are more discriminative and more computationally costly. In this way, the detection speed can be greatly improved without sacrificing the detection accuracy. Concretely, let Jk denote the time consumption for single window classification with Bk(·), and denote the percentage of windows through the kth stage as follows: ρk = number of windows through the first k stage-classifiers/number of all windows generated from the full-sized image. Then, based upon the proposed multiresolution and cascade scheme, the average time expense for classifying one window image is . However, if the detection system adopts a single softmax with HOG features of the highest resolution, the time expense would be JK+1, which is usually several times as much as E1.
To promote the understanding, details of the training process for the proposed method are described in Algorithm 1. In Step (1), the training data is prepared and some hyperparameters are defined to control the training process. In Step (2), the first stage-classifier is trained, while the rest of stage-classifiers are trained one by one in Step (3). During training of the first stage, the initial Nt negatives are randomly cropped, and all the rest are acquired using hard example mining techniques (Step (2.4)). Such strategy could enhance the discriminative ability of the first stage-classifier. For stage larger than 1, all the NT negatives are directly mined based upon the previous stage-classifier (Step (3.2)). In the kth stage, the multiclass softmax model is firstly learned, and then based upon the predefined pass-rate hyperparameters βk, the modified SftB classifiers Bk(·) and Ck(·) can be generated. Once the stage reaches the predefined K + 1, the procedure could stop and return the set of cascade components .
-
Algorithm 1: The procedure of training softmax-based cascade.
-
(1) Prepare multiclass posture example set and the full-sized background images set . Specify the control factors {Nt, NT},
-
the stage number K + 1, the HOG resolutions for different stages, the posture samples pass-rates for the first k stages ,
-
and the size of train samples w × h. Set the current stage level as k = 1, the set of stage-classifiers as . Note that,
-
all sub-images cropped from full-sized background images are of size w × h in training process.
-
(2) Train the first stage classifier as follows:
-
(2.1) Set , Z = {Nt sub-images randomly cropped from images in , and S = ⌀.
-
(2.2) Train a softmax model with sample sets X, Z and HOG of specified resolution, and modify the model into two SftB
-
classifiers B1(⋅) (Eq. (7)) and C1(⋅) (Eq. (8)) based upon the pass-rate β1.
-
(2.3) Add B1(⋅) and C1(⋅) to . If |Z| > NT, go to step (3). Otherwise, go to step (2.4). Here |Z| represents the number of
-
examples in Z.
-
(2.4) Randomly crop sub-image z from an image I queried from . Add z to S if . Repeat this process until |S|
-
reaches to Nt.
-
(2.5) Reset Z = Z ∪ S and S = ⌀. And go to step (2.2).
-
(3) Train the remaining k stage classifiers:
-
(3.1) Set example sets X and Z as: , Z = ⌀.
-
(3.2) Randomly crop z from image . Add z to S if . Repeat this process until |Z| reaches to the
-
predefined NT.
-
(3.3) Train a softmax model with sample sets X, Z and HOG of specified resolution.
-
Then, modify this model into SftB classifiers Bk+1(⋅) and Ck+1(⋅) based on pass-rate βk+1, if k + 1 ≤ K.
-
(3.4) Add Bk+1(⋅) and Ck+1(⋅) to , and let k = k + 1.
-
(3.5) If k ≤ K, go to (3.1). Otherwise, cascade training has been finished and the procedure could be stopped.
4. Experimental Results and Discussions
The proposed method is evaluated on a dataset that is collected under various scenarios with complex background and challenging light conditions. In this section, we firstly describe the dataset and experimental settings. Then, performances of the proposed SftB classifier and softmax-based cascade are evaluated. And, finally, influences of the settings for posture example pass-rates are discussed.
4.1. Datasets and Experimental Settings
4.1.1. Datasets
The experimental dataset comprises four predefined posture categories. For each category, there are around 2000 positive examples with normalized size of 80 × 80 pixels. The samples are obtained by cropping hand regions from the full images that are collected from ten subjects under various backgrounds and lighting conditions. The negative samples are generated during training process by randomly cropping image regions from 500 extra complicated pictures of full size. These full-sized images comprise various undefined hand postures but contain no hand posture of predefined categories. Except for the training samples, we also prepare 4000 full-sized images to evaluate the performance of the proposed method, and each image contains at least one predefined posture instance. Examples for the defined posture categories are presented in Figure 2.

4.1.2. Experimental Settings
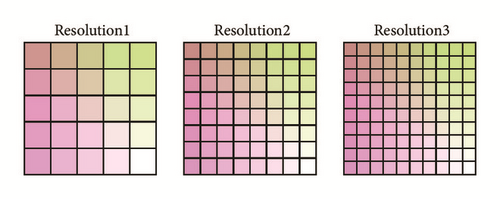
In the experiment, training samples are normalized into the resolution of 80 × 80 pixels. HOG features of various resolutions are utilized for classification, where different resolutions are achieved by adopting different cell splits. Cell splits for the adopted 3 resolutions are illustrated in Figure 3. Parameters for HOG features of all resolutions are fixed as unsigned gradient orientation, 9 equally distributed angle bins, 2 × 2 cells per block, and block steps equaling to cell size. Totally four stages-classifiers are incorporated into the softmax structure. The first three are SftB classifiers, and the last one is SftM classifier. Feature configuration for each stage-classifier is presented in Table 1. In addition, to improve the detection efficiency, changing window size is employed for multiscale search rather than resizing the image itself (e.g., we could take window size of 64 × 64, 80 × 80, 96 × 96, and 120 × 120 to detect hands of different scales in the frame. For window size of s × s, the region of cell c(i, j) will be taken as [x + x1, x + x2, y + y1, y + y2], where (x, y) are the top left coordinates of this window image, x1 = floor((i − 1)∗s/rc) + 1, x2 = ceil(i∗s/rc), y1 = floor((j − 1)∗s/rc) + 1, y2 = ceil(j∗s/rc), and rc is the cell number at horizontal or vertical direction (totally rc∗rc cells as shown in Figure 3). To sum up, the cell size changes with the window size. Although such calculation for cell location is not so accurate when s is not divisible by rc, the feature is still effective. In video-based detection, if the application scenario requires the users to be near the camera, the window sizes should be larger, while if the users are required to stay far away from the camera, the window sizes should be smaller) and the window step is set as 0.05 times of the window size. For live hand detection, the web-camera is set so that image with 320 × 240 resolution could be captured. All experiments are conducted on a PC equipped with Intel(R) Pentium(R) G3220 @3.00GHz CPU, 4.00GB RAM, and under the visual studio 2013 platform.
Cascade stage |
Cell split |
Block layout |
Feature dimension |
Output domain |
|---|---|---|---|---|
| Stage 1 | 5×5 | 4×4 | 576 | {0,1} |
| Stage 2 | 8×8 | 7×7 | 1764 | {0,1} |
| Stage 3 | 10×10 | 9×9 | 2916 | {0,1} |
| Stage 4 | 10×10 | 9×9 | 2916 | {0, ⋯, P} |
4.2. Effectiveness of the Proposed SftB Classifiers
To evaluate the proposed SftB classifier, we, respectively, use the softmax and logistic regression (LR) techniques to train the first three binary stage-classifiers to produce the final four-stage cascade. During the SftB cascade training period, all samples prepared for the pth stage-classifiers C(p,SftB)(·) are divided into the training set and the testing set . C(p,SftB)(·) is learned from dataset , and ROC curve for C(p,SftB)(·) is calculated based on the testing set (the ROC describes the variation relation between false positive rates (FPR) and true positive rates (TPR). Different TPR of are achieved by adjusting the value of threshold ζk. And varying ζk can in return produce varying FPR on . In this way, the ROC curve for SftB can be produced). Similarly, we can train C(p,LR)(1 ≤ p ≤ 3). In this way, totally six ROC curves are produced based upon . In addition, an extra ROC curve is also generated for a SftB classifier based upon and using HOG features of the first resolution. All the seven ROC curves are displayed in Figure 4, where the notations “stage2&Reso2&LR” and “stage2&Reso2&SftB,” respectively, represent the LR and SftB classifiers trained with HOG features of the second resolution. Other notations can be explained in a similar way.
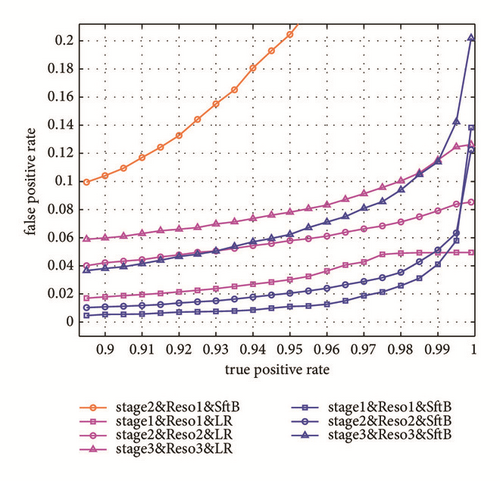
From Figure 4, we can see that, with the same HOG resolution and for fixed TPR (Table 4), the FPR (Table 4) under SftB classifier is much smaller than that calculated with LR classifier. This is because that the SftB is modified from a multiclass classifier, which essentially provides the decision boundaries among different posture categories and therefore can decompose the complex space formed by multiclass posture examples. Moreover, we find that the classifier “Stage2&Reso1&SftB” seriously underperforms the others, which indicates that increasing the resolution of HOG features is crucial to guarantee the classification accuracy.
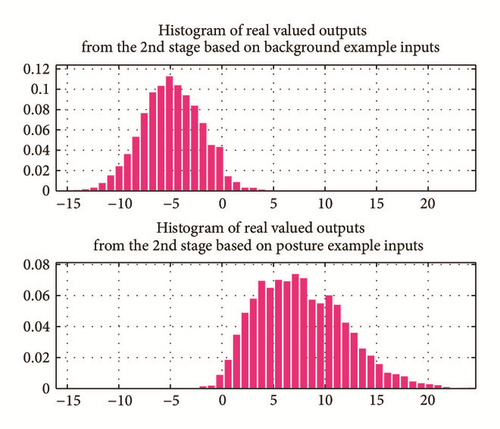
In addition, the histograms for outputs from (see (8)) are calculated and presented in Figure 5, so that more knowledge can be gained about the proposed softmax-based binary classification. In the illustration, the upper histogram is calculated based upon the background examples and the bottom one is calculated based upon the predefined hand posture examples.
4.3. Effectiveness of the Proposed Softmax-Based Cascade Detector
The four confusion matrices corresponding to the four detectors are presented in Table 2, where the Softmax+Resolution1, Softmax+Resolution2, and Softmax+Resolution3, respectively, represent the confusion matrix computed from the three noncascade detectors. Note that the confusion matrix here is different from that for classification problem. In fact, for sliding-window-based detection, one target instance may be covered by many windows, and the postprocessing is only applied to windows that are classified into the same category. As a result, one region can be finally predicted into more than one posture category. For this reason, the sum of elements in each row does not necessarily equal to one.
| Softmax+Resolution1 | Softmax+Resolution2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BK | vict | close | open | fist | BK | vict | close | open | fist | |
| BK | 0.7104 | 0.1480 | 0.1211 | 0.0628 | 0.1469 | 0.8205 | 0.0843 | 0.0291 | 0.0326 | 0.1145 |
| vict | 0.0420 | 0.9136 | 0.2006 | 0.2157 | 0.2585 | 0.0706 | 0.9001 | 0.0492 | 0.0856 | 0.1776 |
| close | 0.0272 | 0.5438 | 0.9251 | 0.5447 | 0.4443 | 0.0017 | 0.4477 | 0.9626 | 0.4077 | 0.4911 |
| open | 0.0532 | 0.3291 | 0.2181 | 0.9070 | 0.3531 | 0.0630 | 0.1987 | 0.0532 | 0.9055 | 0.2234 |
| fist | 0.0183 | 0.7114 | 0.4862 | 0.5146 | 0.9233 | 0.0342 | 0.4370 | 0.1935 | 0.2494 | 0.9391 |
| Softmax+Resolution3 | The Proposed Softmax Cascade | |||||||||
| BK | vict | close | open | fist | BK | vict | close | open | fist | |
| BK | 0.8369 | 0.0889 | 0.0090 | 0.0287 | 0.0983 | 0.9884 | 0.0061 | 0.0022 | 0.0033 | 0.0053 |
| vict | 0.0761 | 0.8993 | 0.0214 | 0.0928 | 0.2292 | 0.0547 | 0.9294 | 0.0032 | 0.0389 | 0.0151 |
| close | 0.0026 | 0.4323 | 0.9574 | 0.3872 | 0.4655 | 0.0153 | 0.0383 | 0.9838 | 0.1319 | 0.0502 |
| open | 0.0862 | 0.1717 | 0.0187 | 0.9033 | 0.2219 | 0.0300 | 0.0682 | 0.0090 | 0.9700 | 0.0787 |
| fist | 0.0350 | 0.3361 | 0.0984 | 0.1435 | 0.9299 | 0.0609 | 0.1093 | 0.0459 | 0.0300 | 0.8957 |
From Table 2, we can see that the hand detection with noncascade softmax detectors may cause high false detection rates at the background areas and high confusion rates among different posture categories. By contrast, the proposed softmax-based cascade could significantly suppress all kinds of false detections without sacrificing the recall rates. This is because the complexity of background space can be effectively decomposed by the usage of multiple stage-classifiers, and therefore it becomes much easier for the final multiclass softmax model to discriminate among the predefined postures and the minorities of remaining backgrounds.
To make more direct and intuitional comparisons, multiple performance values based on summary measures are also computed and provided in Table 3. The measures mean recall rate and mean correct rate, respectively, represent the averaged recall rates and the averaged confusion rates among the four predefined posture categories. For the definition of FPPI and mean correct rate, please refer to Table 4.
| Mean recall rate | Mean confusion rate | FPPI | Mean correct rate | Time consumption for 240×320 picture |
|
|---|---|---|---|---|---|
| Softmax+Resolution1 | 0.9172 | 0.4017 | 0.4788 | 0.3548 | 25.16ms |
| Softmax+Resolution2 | 0.9268 | 0.2512 | 0.2605 | 0.4812 | 63.39ms |
| Softmax+Resolution3 | 0.9225 | 0.2182 | 0.2248 | 0.5155 | 99.45ms |
| The proposed softmax cascade | 0.9448 | 0.0515 | 0.0169 | 0.8475 | 27.17ms |
| FPPI |
|
|---|---|
| FPPW |
|
| Mean correct rate |
|
| Detection rate |
|
| Case1 | the case in which pass-rate of higher stage is larger than the pass-rate of lower stage |
| Case2 | the case in which the pass-rate of higher stage is smaller than the pass-rate of lower stage |
| TPR | the abbreviation of true positive rate |
| FPR | the abbreviation of false positive rate |
| LR | the abbreviation of logistic regression |
From Table 3, we can see that the detection accuracy with Softmax+Resolution3 is the highest among the three noncascade classifiers. However, by comparison, the proposed multiclass cascade detector further improves the mean recall rate from 0.9225 to 0.9448 and boosts the mean correct rate from 0.5155 to 0.8475. Meanwhile, the mean confusion rate is reduced from 0.2182 to 0.0515, and the FPPI is reduced from 0.2248 to 0.0169. In addition, the proposed detector is faster than Softmax+Resolution3 by almost 4 times.
Figure 6 shows some hand posture detection result based on a normal web-camera. From the results, we can see that the proposed method can detect the defined hand postures under various environments. And the system can reach a real-time running speed of 27 FPS under our experimental setup.


4.4. The Influences of the Settings for Posture Example Pass-Rates
Performance of the proposed cascade is directly affected by the thresholds ζk of its stage-classifiers as shown in (8). The thresholds affect not only the detection results but also the training process, since the background samples for the pth stage are acquired by the previous (p-1) stage-classifiers. These thresholds are determined based upon the settings for pass-rates of posture samples (for Hk(·), could be computed based upon the posture examples set which is used for learning Θk. Sort in ascending order to produce vector , and take the value ξk = χ(floor((1 − βk)Nps)) as threshold, where βk are the preset posture examples pass-rates for the kth stage SftB during training period) which are set at the training stage to control the training process. To acquire better cascade detector, we prepare multiple groups of settings for the pass-rates and then train the four-stage cascade classifier with each group of settings. After that, the FPPW and detection rate (Table 4) are computed based upon each of these cascade detectors, and the best group of settings is selected by comparing the values of all FPPW and detection rates. Note that the detection rate does not necessarily equal to the mean correct rate, since confusion detections may exist among different posture categories.
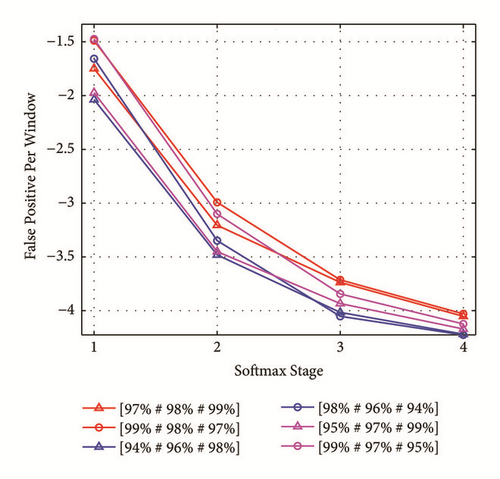
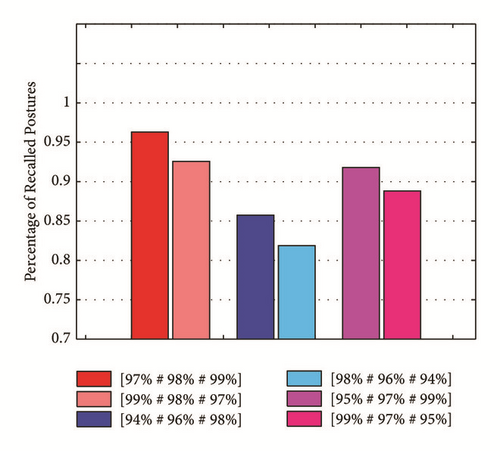
The six groups of pass-rates being compared are, respectively, [97%#98%#99%], [99%#98%#97%], [94%#96%#98%], [98%#96%#94%], [95%#97%#99%], and [99%#97%#95%]. The notation [97%#98%#99%] means that, for the first three stage-classifiers, the pass-rate of posture examples is successively set to 97%, 98%, and 99%. Each group contains exact three pass-rate settings because there are exact four stage-classifiers in each cascade detector, while the fourth stage is a multiclass softmax model that will not be modified. The curves for variation relations of FPPW with the stage-level are presented in Figure 7, and the detection rates are illustrated in Figure 8. Except that FPPW and detection rate are both increasing with the product of three pass-rates, we have another important observation. That is, when the product of the three pass-rates is fixed, the detection rate in Case1 (Table 4) is significantly higher than that in Case2 (Table 4), while the FPPW in both cases are very close. This indicates that the detectors trained in Case1 are more discriminative than those trained in Case2. This observation suggests that, to achieve good performance, it is better to set low pass-rates for classifiers at low stages and set higher pass-rates for classifiers at higher stages.
5. Conclusion and Future Work
In this work, a softmax-based cascade detector is proposed to perform the multiclass hand posture detection in parallel. The cascade contains several SftB classifiers used for distinguishing all predefined postures from the backgrounds and a SftM classifier mainly used to discriminate among all predefined hand postures. Moreover, the HOG features of increasing resolutions are adopted by stage-classifiers with increasing stage-levels so as to further reduce the efficiency without sacrificing the detection accuracy. Experimental comparison of ROC curves demonstrates the superiority of the proposed SftB classifier. And evaluation results on a challenging dataset indicate that the proposed model structure could improve both the accuracy and efficiency as compared with the noncascade multiclass posture detection methods. In the future work, we will replace the softmax-based stage-classifiers in the cascade with more expressive classification model, such as the convolutional neural networks, to further improve the accuracy of single-stage classification.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Acknowledgments
This work was supported in part by the National Key R&D Program of China (no. 2017YFB1103602), the National Natural Science Foundation of China (nos. 51705513, U1613213, and U1713213), Shenzhen Science Plan (KQJSCX20170731165108047 and JCYJ20170413152535587), and Shenzhen Engineering Laboratory for 3D Content Generating Technologies (no. [2017]476).
Appendix
Acronyms, Definitions, and Terminology
See Table 4.




