Dynamic Modeling and Coupling Characteristic Analysis of Two-Axis Rate Gyro Seeker

1. Introduction

The radar seeker has many advantages, such as high-range, all-weather detection capability, compared with traditional photoelectric seeker [1]. Therefore, a radar seeker can be a more effective choice in developing military power or upgrading missile systems than traditional photoelectric seeker [2]. Radar seeker servo system is a key part of a precise, stable target tracking system. The core of the radar seeker is a precise electromechanical servo device that compensates for the missile body disturbance to the beam axis of the seeker [3, 4] and maintains the beam-pointing stability in space, thus tracking the line of sight quickly. Two major types of stable servo seeker in history [5], namely, dynamic gyro and rate gyro stabilization modes, are used to meet different needs. In [6], the dynamic modeling and simulation of the dynamic gyro-type seeker were conducted, and the influence of the missile disturbance on the servo control system of the seeker was analyzed; however, the disadvantages of the dynamic gyro seeker include low load capacity, large forward torque, and delayed response. In [7], the stability tracking principle of rate gyroscope-stabilized laser seeker was investigated; the stability of the seeker load is high, and the reaction speed is fast.

When a radar system for tracking and measuring target is accommodated on a moving carrier, a line of sight stabilization system is the basis for high-precision tracking. In order to eliminate the influence of the carrier, a stable platform is usually available to achieve the stability of the line of sight; according to different stable objects and stability requirements, there can be various ways of stability [8–10]. In order to precisely control the line of sight of the detection system and make it track the target motion accurately while isolating the missile body disturbance, some scholars adopted a variety of stable platform schemes and control methods [11–13]. Unlike the airborne or ground-based tracking radar case, the radar seeker will output line of sight (LOS) angle rate for terminal guidance of homing missile using proportional navigation [14]. In [15], a stable platform control loop of a seeker was designed and the effect of disturbance moment on LOS tracking was analyzed. The guidance accuracy of the homing missile will be affected by the LOS rate output accuracy because the output error of the LOS rate caused by servo platform disturbance torque would induce the disturbing rate rejection, thereby resulting in its parasitical loop. In [16–18], the effect of disturbing rate rejection caused by spring and damping torques on the stability of the guidance system was analyzed. Any deviation in the course of the seeker control loop will make the body attitude angle couple into the LOS rate output, because the missile will be subject to airflow, disturbance torque in the flight process, thereby affecting the stability and tracking of the radar seeker beam axis and reducing the missile guidance accuracy [19–22]. Therefore, the two-channel rate gyro servo platform-type seeker-coupled model must be studied by using the platform kinematic [23, 24] and dynamic models [25].

The current study is aimed at building a dynamic model of two-axis rate gyro radar seeker and analyze the coupling characteristics between the two channels. The rest of this paper is organized as follows: Section 2 introduces the rate gyro stabilization platform tracking principle. Section 3 builds a dynamic model of two-axis platform radar seeker, including mass imbalance, disturbance torque, and cross-coupling. Section 4 introduces a frequency domain servo motor transfer function identification method, which provides reasonable design parameters for the seeker control system. Section 5 designs the lag compensation network parameters for tracking loop and stability loop, respectively, analyzes the characteristic in frequency domain and at the same time analyzes the influence of the missile motion on the angle of the gimbal, disturbance rate rejection characteristic and coupling effect between the two gimbals by simulation. Section 6 concludes the study.

2. Rate Gyro Stabilization Platform Tracking Principle

The radar seeker servo device consists of a gyro assembly, DC torque motor, angular position sensor, radar signal processing system, and yaw and pitch gimbals [26]. Figure 1 illustrates the schematic of two-axis rate gyro stability platform. The outer gimbal is the pitch gimbal, the inner gimbal is the yaw gimbal, and they are connected by the bearing; thus, the ring gimbal can rotate around each other. The outer gimbal shaft is mounted on two brackets through the bearing gimbal, and the bracket and the base are fixed together. The torque motor is mounted on one end of the shaft to enable the rotation of the shaft. The potentiometer gauge is mounted on the other end of the shaft to measure the rotation angle of the gimbal relative to the base. The inner gimbal passes through the bearing gimbal on the outer gimbal. The torque motor is also mounted on one end of the inner gimbal shaft, and the potentiometer is mounted on the other end. The two rate gyros are mounted on the inner gimbal to measure the rotation angle rate of the inner gimbal relative to the inertial space. The measured value is equal to the true LOS angle rate and can be used to guide the missile. The radar antenna is also mounted on the inner gimbal.

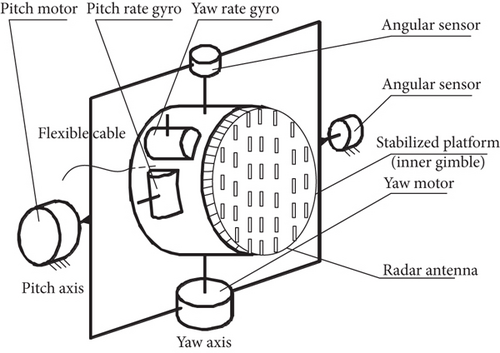
The radar antenna and inertial device (rate gyro) are mounted on the inner gimbal of the stable platform. Any movement of the platform in inertial space will be sensed by the inertial devices. The real antenna beam off-centered angle signals are sent to the corresponding electric motor to control the platform back to the initial reference orientation in the inertial space, which is a function of the seeker stability loop. The radar seeker antenna measures the angle error between the beam direction and the true LOS to track the target, thus forming negative angle feedback to achieve closed loop tracking control by angle tracking loop.

3. Dynamic Model of Two-Axis Platform Radar Seeker

3.1. Coordinate System Definition and Transformation

Figure 2 depicts the geometric schematic between the seeker gimbal and missile body coordinates. The coordinate systems are defined as follows.

• (1)

  Inertial coordinate system Ox_iy_iz_i: the Ox_i-axis points to the earth plane flat, and the Oy_i-axis points along the vertical direction. The Oz_i-axis direction can be obtained by the right-hand rule. The subscript i denotes the inertial

• (2)

  Missile body coordinate system $$: the $$-axis coincides with the longitudinal axis of the missile and points to the front of the missile. The $$-axis is located within the missile longitudinal symmetry plane and is perpendicular to the $$-axis pointing up. The $$-axis direction is obtained by the right-hand rule. A point is the missile center of mass; O point is the gimbal rotating center, which coincides with the center of the antenna beam. Ox_by_bz_b is the new coordinate system obtained by translating the missile body coordinate system $$ from A point to O point. The subscript b denotes the missile body

• (3)

  Outer gimbal coordinate system Ox_wy_wz_w: the Ox_w-axis is perpendicular to the outer gimbal plane and points to the target. The Oz_w-axis coincides with the Oz_b-axis of the missile body coordinate system. Oy_w-axis is located within the Ox_by_b plane and can be obtained by the right-hand rule. The subscript w denotes the outer gimbal

• (4)

  Inner gimbal coordinate system Ox_ny_nz_n: the Ox_n-axis points to the target and coincides with the beam direction. The Oy_n-axis coincides with the Oy_w-axis of the outer gimbal coordinate system. Oz_n-axis is located within the Ox_wz_w plane and can be obtained by the right-hand rule. The subscript n denotes the inner gimbal

• (5)

  LOS coordinate system Ox_sy_sz_s: the Ox_s-axis points to the target. The Oy_s-axis is located within the vertical plane that contains the Ox_s-axis and is perpendicular to theOx_s-axis pointing up. The Oz_s-axis direction can be obtained by the right-hand rule. The subscript s denotes the LOS

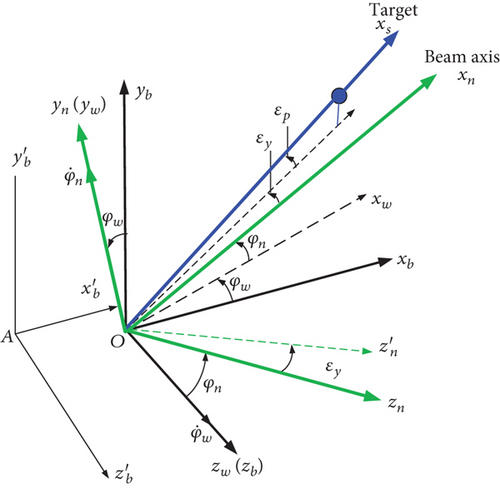
According to the coordinate systems above, from Ox_by_bz_b to Ox_wy_wz_w, Oz_b-axis is the axis of rotation; φ_w is the angle of rotation. From Ox_wy_wz_w to Ox_ny_nz_n, Oy_w-axis is the axis of rotation; φ_n is the angle of rotation. From Ox_ny_nz_n to Ox_sy_sz_s, first, the axis of rotation is Oy_n-axis and the angle of rotation is ε_y, and then, the axis of rotation is $$-axis (transition axis), and the axis of rotation is ε_p.

Figure 3 displays the coordinate transformation relationship.

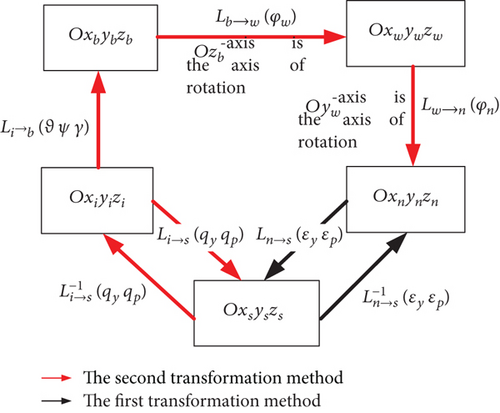
According to the coordinate systems above, from Ox_iy_iz_i to Ox_by_bz_b, ψ, ϑ, and γ denote the missile body yaw, pitch, and roll angles; the axis of rotation is Oy_i-axis, $$-axis (transition axis), and $$-axis (transition axis), respectively. From Ox_iy_iz_i to Ox_sy_sz_s, q_y and q_p are the LOS angles in the yaw and pitch directions; the axis of rotation is Oy_i-axis, and $$-axis (transition axis), respectively. From Ox_by_bz_b to Ox_ny_nz_n, φ_w and φ_n are the gimbal angles in the pitch and yaw directions; the axis of rotation is Oz_b-axis and Oy_w-axis, respectively. From Ox_ny_nz_n to Ox_sy_sz_s, ε_y and ε_p are the seeker antenna beam off-centered angles in the yaw and pitch directions; the axis of rotation is Oy_n-axis and $$-axis (transition axis), respectively.

The transformation matrix of the missile body coordinate system to the outer gimbal coordinate system can be written as follows:

$$ (1)

The transformation matrix of the outer gimbal coordinate system to the missile body coordinate system can be written as follows:

$$ (2)

where L_b→w denotes the transformation matrix from Ox_by_bz_b to Ox_wy_wz_w, $$ denotes the transformation matrix from Ox_wy_wz_w to Ox_by_bz_b, $$ is the inverse of the matrix L_b→w, and the transformation angle is φ_w. The other coordinate transformation relationships are similar.

3.2. Model of the Antenna Beam Off-Centered Angle

Figure 4 presents the geometric relationship for beam off-centered angle calculation. The antenna boresight unit vector in Ox_sy_sz_s is [1 0 0]^T when the unit vector $$ is along with the line of sight, which can be projected to Ox_ny_nz_n directly, which is denoted as $$ in Ox_ny_nz_n.

$$ (3)

where $$ denotes the transformation matrix from Ox_sy_sz_s to Ox_ny_nz_n; the transformation angles are ε_y and ε_p. The subscript n1 denotes the unit vector $$ which is transformed to the n frame with the first transformation method.

At the same time, the unit vector $$ can be projected to Ox_iy_iz_i, then be projected to Ox_by_bz_b, and finally be projected to Ox_ny_nz_n, which is denoted as $$ in Ox_ny_nz_n.

$$ (4)

where $$ denotes the transformation matrix from Ox_sy_sz_s to Ox_iy_iz_i, L_i→b denotes the transformational matrix from Ox_iy_iz_i to Ox_by_bz_b, and L_b→n denotes the transformational matrix from Ox_by_bz_b to Ox_ny_nz_n. The subscript n2 denotes the unit vector $$ which is transformed to the n frame with the second transformation method.

$$ (5)

Due to $$, the antenna beam off-centered angle calculation formula is expressed as follows:

$$ (6)

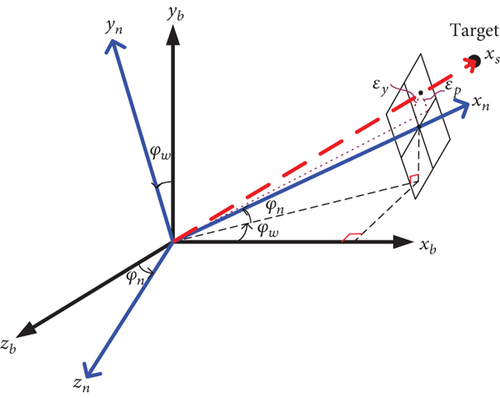
3.3. Dynamic Derivation of the Seeker Platform

The projection of the missile angular rate with respect to the inertial space in the missile body frame is

$$ (7)

where the superscript i denotes inertial coordination system, b/i denotes missile body with respect to the inertial space, and the subscript b denotes the projection in the missile system.

The rotation relationship of the missile coordinate system to the inner gimbal coordinate system can be expressed as follows:

$$ (8)

where $$ denotes the inner gimbal angular rate with respect to the missile body, $$ coincides with the Oy_w-axis, and $$ coincides with the Oz_b-axis.

The inner gimbal angular rate with respect to the missile body in the inner gimbal coordinate system can be expressed as follows:

$$ (9)

The missile body angular rate with respect to the inertial space in the inner gimbal coordinate system can be expressed as follows:

$$ (10)

The inner gimbal angular rate with respect to the inertial space in the inner gimbal coordinate system can be obtained by (9) and (10).

$$ (11)

where

$$ (12)

The missile body angular rate with respect to the inertial space in the outer gimbal coordinate system can be expressed as follows:

$$ (13)

The outer gimbal angular rate with respect to the inertial space in the outer gimbal coordinate system can be expressed as follows:

$$ (14)

We obtain (15) by substituting (14) into (12).

$$ (15)

A derivative of (15) is as follows:

$$ (16)

where

$$ (17)

Applying Newton’s laws to the inner gimbal, the dynamic equation of the inner gimbal according to the theorem of the momentum of the rigid body rotating about a moving point o can be expressed as follows:

$$ (18)

where moving point o is the intersection of the inner gimbal and outer gimbal (rotating center of the gimbal), $$ denotes the angular momentum of the inner gimbal about the point o, J_n denotes the inertia terms of the inner gimbal about the point o, $$ is the cross product of the moment arm from the point o to the center of mass of the inner gimbal assembly and the mass of the inner gimbal times the specific force acceleration of the inner gimbal at the point o, $$ denotes the moment arm from the point o to the center of mass of the inner gimbal, $$ denotes the specific force acceleration of the inner gimbal at the point o, and m_n denotes the inner gimbal system mass.

Since the inner gimbal only has rotational freedom about the Oy_n, the second component M_ny of (11) is taken. The external torque M_ny is equal to the applied commanded torque from the inner gimbal controller torque $$, minus the spring or cable torque K_Snφ_n, minus the viscous torque $$, and minus the Coulomb friction torque $$.

$$ (19)

where K_Sn, K_Vn, and K_couln denote the spring, viscous, and Coulomb friction torque factors, respectively. The disturbance torque between the missile body and the seeker will affect the stability of the seeker. Therefore, the influence of the disturbance torque must be suppressed by the design of the seeker.

Now applying Newton’s laws to the outer gimbal, the dynamic equation can be expressed as follows:

$$ (20)

where $$ denotes the angular momentum of the outer gimbal about the point o, J_w denotes the inertia terms of the outer gimbal about the point o, $$ is the cross product of the moment arm from the point o to the center of mass of the outer gimbal assembly and the mass of the outer gimbal times the specific force acceleration of the outer gimbal at the point o, $$ denotes the moment arm from the point o to the center of mass of the outer gimbal, $$ denotes the specific force acceleration of the outer gimbal at the point o, and m_w denotes the outer gimbal system mass.

Since the outer gimbal only has rotational freedom about the Oz_w, the second component M_wz of (13) is taken. The external torque M_wz is equal to the applied commanded torque from the outer gimbal torque $$, minus the spring or cable torque K_Swφ_w, minus the viscous torque $$, minus the Coulomb friction torque $$, and minus the reaction torque of the inner gimbal on the outer gimbal.

$$ (21)

where

$$ (22)

We obtain (23) by substituting M_nx and M_nz into (21).

$$ (23)

Note that (23) and M_ny contain the common terms $$ and $$. It is these terms that need to be solved for using these two equations. These two equations can be put into the form of a matric equation as shown below.

$$ (24)

The solutions for $$ and $$ are found by inverting the matrix and multiplying by the vector containing the F₁ + M_ny and F₂ + M_cc terms.

$$ (25)

According to (25), $$ and $$ can be written as follows:

$$ (26)

If the inertia product and the mass imbalance moment are zero, then the parameters $$, $$, F₁, F₂, and J_eq can be simplified as follows:

$$ (27)

correspondingly.

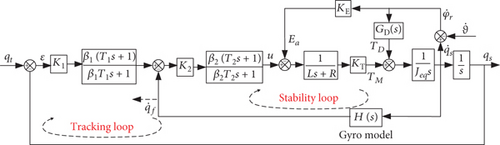
Figure 5 demonstrates the LOS rate extraction model for the two-gimbal-coupled system. The model starts from the antenna beam off-centered angles computed by (6) and the corrective network using the lag compensation network to increase open loop gain with lag compensation coefficient β and time constant T; L is inductance and R is resistance in the motor model. First, through the antenna beam off-centered angle model, the ε_y and ε_p can be obtained, and then the off-centered angles can be amplified by the gain K₁ or K₃ to be LOS angle rate signal; the LOS angle rate error ($$) can be amplified by the gain K₂ or K₄ to be voltage signal. The lag compensation network in the tracking loop (which is an angle position loop; its main function is to receive the off-centered angle signal, control the movement of the seeker platform, and realize the closed loop tracking to the target) can reduce the tracking error. The lag compensation network in the stability loop (which is an angle rate loop; its main function is to isolate the missile body motion and keep the beam stable in inertial space) can increase the open loop gain. The voltage signal through the motor model, moment coefficients K_T1 or K_T2, and load moment of inertia J_eq can output gimbal angular acceleration signal; gimbal angular rate can be obtained by integrating the gimbal angular acceleration signal. Finally, the gimbal angular rate feedback to the input point of the stability loops through the rate gyro model. The objective of the controller in Figure 5 is to align the antenna boresight with the LOS and eliminate the ε_y and ε_p promptly and in a stable way.

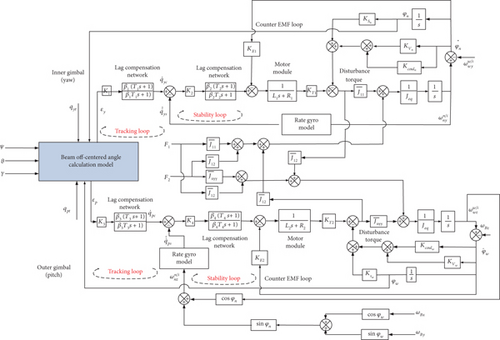
4. Dynamic Model Identification of the Seeker Control Loop

The analysis of the transfer function of the seeker platform and the inertial device is necessary before designing the seeker control system. The mathematical model of the transfer function is typically obtained through the system parameter identification method. The transfer function in frequency domain can be obtained by measuring the frequency characteristics of the inertial device to identify the system. In a sufficiently wide frequency range, the frequency of the input signal of the inertial device is continuously changed, the ratio of the output characteristic of the inertial device to the input characteristic is measured, and the decibel number for identifying the logarithmic amplitude-frequency characteristics is obtained.

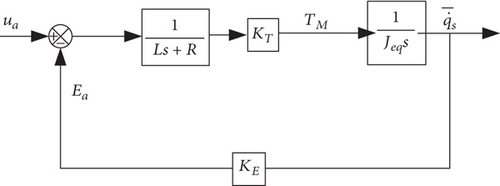
In this study, in order to validate the method, we assume that the transfer function of the torque motor is a second-order model, which contains the motor model 1/(Ls + R), moment coefficient K_T, back EMF coefficient K_E, and moment of inertia J_eq. The torque motor model is shown in Figure 6.

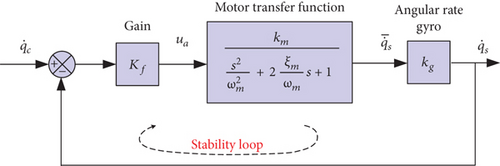
Setting $$, k_m = 1/K_E, and $$, the stability loop can be shown in Figure 7.

Data fitting results are obtained for the experimental data at different input frequencies. Thus, we can measure the angle rate ratio $$. We can identify the value of the system parameters k_n, t_n, and ξ_n by using (31)–(33), and the values of the torque motor parameters k_m, t_m, and ξ_m can be calculated by (30).

The input signal is the angular velocity signal obtained by differentiating the angular position signal, where the amplitude is 0.2°, and the frequency is 1.25–15.7 rad/s, with the inner gimbal as the measured object. The closed loop frequency characteristic of the seeker can be obtained by accessing the data processing. Figure 8 presents the frequency characteristic curve, where the dotted line is the measured data, and the solid line is the magnitude-frequency characteristics of the second order.

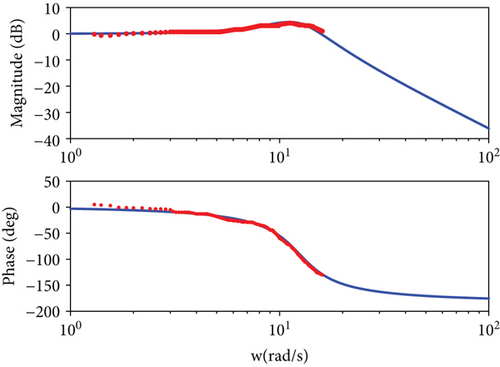
Then, we can obtain ω_n = 12.42 rad/s (1.99 Hz), ξ_n = 0.315; the closed loop bandwidth is 17.9 rad/s (2.8 Hz).

Using the parameters K_f = 1.6, k_g = 1, and J_eq = 0.0025995 in the stability loop, we can obtain the torque motor parameters k_m = 1.87, ω_m = 6.2 rad/s, and ξ_m = 0.63 by using (30); they are matched with the true motor model; the frequency of the stability loop is nearly 2 times that of the motor model.

5. Simulation Analysis of the Seeker Two-Axis-Coupled Dynamic Model

Equations (19), (21), and (32) and Figure 5 reflect the complexity of the two-gimbal platform seeker system. The dynamic model includes not only the cross-coupling and mass imbalance but also the disturbance torque from the spring, viscous, and Coulomb friction torque factors. Moreover, the body attitude angle will couple into the seeker LOS rate output. We can simulate the tracking performances and coupling characteristics of the seeker according to the two-gimbal-coupled system block diagram illustrated in Figure 5. We assume that the inertia product and the mass imbalance moment are zero to verify the accuracy and availability of the seeker dynamic model. According to the test model of the seeker in laboratory, the dynamic parameters are summarized in Table 1.

Figure 9 shows the open loop Bode diagram of tracking loop with and without the lag compensation.

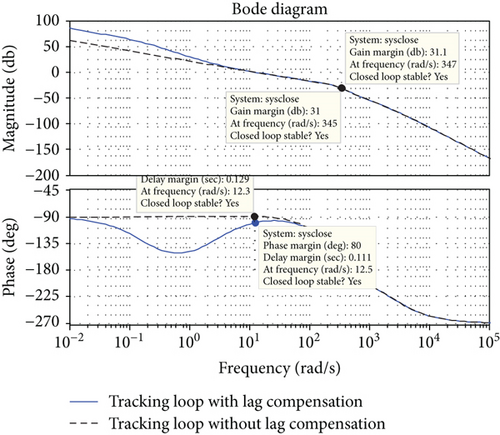
Figure 10 shows the open loop Bode diagram of stability loop with and without the lag compensation.

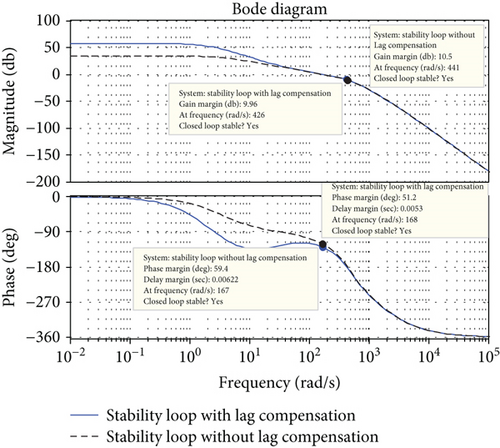
If the missile and the target are stationary and the relative distance is fixed, then the yaw angle is a constant value of the LOS angle input, and the missile body yaw angle is the positive rotation signal input. Figure 11 displays the simulation curve with body yaw direction input. The yaw gimbal will swing in the opposite direction when the missile body is yaw swinging to ensure the stability of the LOS because the LOS angle input has the constant value of 0. Therefore, the LOS angle output is near zero in the case of missile yaw disturbances, and the swing is not large. The lag compensation network can increase the open loop gain 15 times. The closed loop Bode diagram of tracking loop is shown in Figure 12, and the closed loop bandwidth is 12.37 rad/s (1.97 Hz), which is close to the frequency of oscillation (2 Hz). The open loop Bode diagram is shown in Figure 10; we can find that the lag compensation increases the open loop gain. The closed loop Bode diagram about stability loop is shown in Figure 13: the closed loop bandwidth is 370 rad/s (59 Hz), which is larger than the tracking loop and the frequency of oscillation and can improve the disturbance rejection capability.

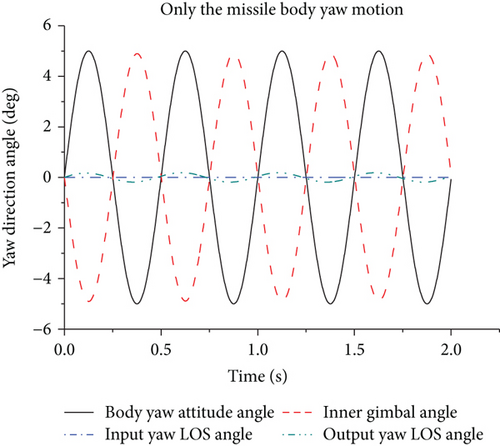
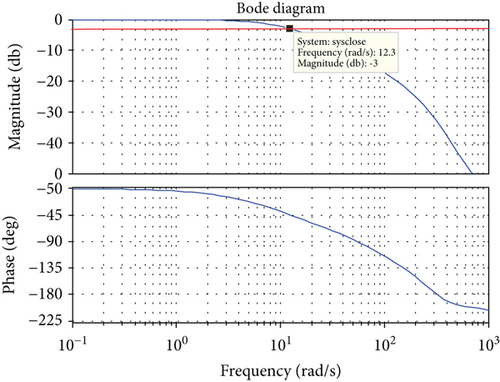
Figure 14 demonstrates the coupling swing curve of the pitch gimbal caused by the missile yaw movement. The missile yaw movement causes not only the yaw gimbal swing but also the pitch gimbal coupling swing.

Figure 15 depicts the simulation curve with body pitch attitude angle input signal. The pitch gimbal will swing in the opposite direction when the body is swinging to ensure the stability of the LOS. The output pitch LOS angle is close to the input pitch LOS angle (which is zero). The closed loop bandwidth is greater than the frequency of oscillation. The frequency characteristic is the same as of the yaw gimbal.

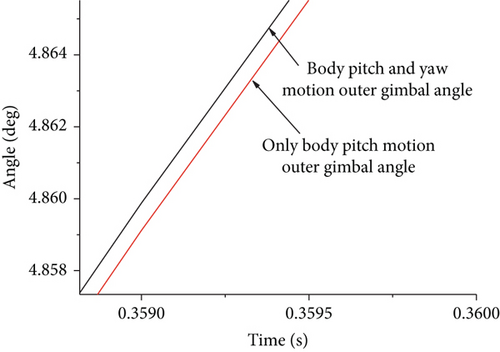
Figure 16 depicts the simulation curve with body pitch angle and yaw angle input. The pitch gimbal will swing in the opposite direction of the body pitch motion; the yaw gimbal will swing in the opposite direction of the body yaw motion, when the missile body pitch and yaw is swinging to ensure the stability of the LOS. Figure 17 presents the outer gimbal simulation curve with body pitch and yaw angle input or only the pitch angle input. We find that the outer gimbal angle swing amplitude is higher with body pitch and yaw input than only the pitch angle input given the coupling between the gimbal and the missile body and the coupling effect between the inner and outer gimbals.

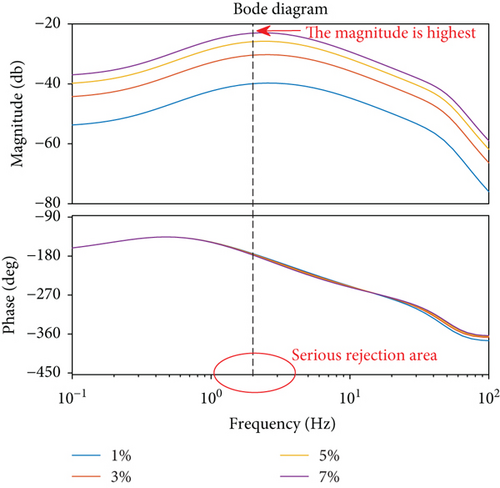
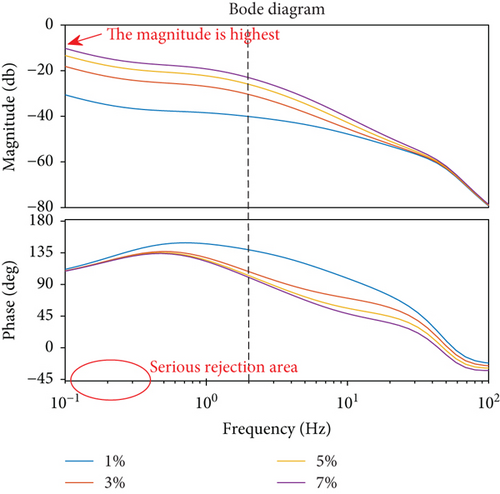
Figures 19 and 20 illustrate the disturbing rate rejection transfer function in frequency domain caused by viscous and spring torques, respectively. The disturbing rate rejection amplitudes are 1%, 3%, 5%, and 7% when the frequency is 2 Hz. In Figure 19, we find that the maximum value of the amplitude of the disturbing rate rejection transfer function is located near 2 Hz, where the operating frequency of the seeker is maximized and has a significant influence on the parasitic loop. In Figure 20, we find the serious rejection area under the action of spring torque which is located in the low-frequency band and presents the integral link characteristic. Spring and viscous torques will affect the tracking accuracy of the seeker.

6. Conclusions

The two-axis rate gyro-stabilized platform dynamic model-based seeker with cross-coupling, mass unbalance, and disturbance torque is built according to the two-axis rate gyro stabilization platform tracking principle, applying the torque motor drive and seeker servo control theory and combining the platform framework kinematics theory and spatial coordinate transformation method. Simultaneously, two-gimbal-coupled system block diagram is built. The frequency domain method is used to identify the seeker sensor transfer function. This study comprehensively considers the conditions of the disturbance moment of the platform, coupling characteristics, and gimbal angle changing curve analyzed in different missile body inputs. Furthermore, the disturbing rate rejection caused by spring and viscous torque factors is analyzed. On the basis of the analysis, the coupling effect of the missile body to the gimbal is strong given the presence of disturbance torque. The missile motion is coupled to the seeker output, but the seeker servo stable platform can reduce the influence of the missile disturbance by swinging in the opposite direction. The coupling effect between the inner and outer gimbals is evident. The serious segregation area is located in the middle- and low-frequency band by analyzing the function frequency characteristics of disturbing rate rejection transfer caused by spring and viscous torque factors. Spring and viscous torque factors will affect the tracking accuracy of the seeker.

The results of this study can support the equivalence demonstration of the seeker servo control system in the closed loop simulation test and actual work conditions and thus uphold the study of the seeker servo control system and semiphysical simulation.

Conflicts of Interest

The authors declare that there is no conflict of interests regarding the publication of this article.