The interaction effects, arising at partial contact of rigid multisinusoidal wavy surface with an elastic half-plane, are considered in the assumption of continuous contact configuration. The analytical exact and asymptotic solutions for periodic and nonperiodic contact problems for wavy indenters are derived. Continuous contact configuration, appearing at small ratios of amplitude to wavelength for cosine harmonics, leads to continuous oscillatory contact pressure distribution and oscillatory relations between mean pressure and a contact length. Comparison of periodic and nonperiodic solutions shows that long-range elastic interaction between asperities does not depend on a number of cosine wavelengths.

1. Introduction

Real rough surfaces are three-dimensional and multiscale. Besides fully random rough surfaces [1] there are natural and technical surfaces, having quasiregular character of asperities on several scales (e.g., periodic anisotropic waviness) [2]. For these surfaces the geometric model of two-dimensional wavy 2D profile can be applied as a first approximation. Also, in some fields of engineering, the wavy textures of different shapes are used (e.g., in optical devices and MEMS) [3]. Considering the elastic contact processes, occurring for soft materials (polymers and biological materials), the various analytical methods of plane elasticity can be applied. In the case of full contact, when the gap between surfaces is filled, the problem can be easily solved by Fourier transform method [4]. However, the very high applied pressure is required to reach the full contact condition even for soft materials, so partial contact is the more often case. Partial contact between wavy surfaces is a problem with mixed boundary conditions, which was solved by different mathematical techniques.

The classic periodic contact problem in plane elasticity is an old problem [5, 6]. Concerning geometry of a wavy surface, considered in the previous studies, the cosine [7, 8], the squared cosine [9], and evenly spaced parabolic or wedge stamps [10, 11] were generally used. The analytical solution of the pointed problem for those surface geometries was obtained by different methods. For the cosine profile they are complex stress function [7], dual series equation [12], intercontact gaps method [13], variable transform method [11], and fracture mechanics approach [14].

Taking into account simple wavy geometry (cosine or squared cosine) the contact problems with more complicated boundary conditions were studied: sliding problem with friction [15, 16], with a fluid lubricant [17], with a partial slip [11, 18], with adhesion and sliding friction [19], for viscoelastic material [20], for Winkler model of viscoelastic material and adhesion [21], for elastic layer with presence of friction and wear [22], and dynamic problem for anisotropic half-plane [23].

The normal elastic problem for a two-dimensional nonsinusoidal wavy profile, where a shape of a waveform is controlled by a parameter, was solved analytically [24]. It was established that the pressure distribution is highly sensitive to the shape of a wavy surface, especially at large loads.

The presence of several scales of a wavy surface leads in general to a multizone periodic contact problem [9, 25]. The asymptotic approximate solution for initial contact for a two-scale wavy surface was obtained [24]. It was shown that even for initial contact the interplay between harmonics exists. Considering the problem in a wide range of applied loads it is necessary to use a numerical procedure. Such studies were performed by different techniques: Fourier series and cotangent transform [26], full contact solution and iteration procedure [27], FFT and variational principle [28], nonlinear boundary integral equation [29], boundary element method [30], and finite element method [31]. The equations for internal stresses for sinusoidal pressure distributions in 2D and 3D cases were also derived [32]. The results of these studies show that multiscale character of a wavy surface at partial contact with an elastic half-plane leads to multiple peaks of high pressure. The pressure distribution is jagged in this case, and a load-area dependence tends to proportionality at large number of harmonics [31].

In cases, considered in the previous studies, the contact was partial at all scales, because the amplitudes of different harmonics were comparable. This situation leads to a discontinuous (discrete) contact configuration [33]. Besides numerical methods, the other way to solve these problems is usage of multiasperity contact models. Based on the nature of the surfaces models can be deterministic and statistical. Review of statistical models, based on individual asperity contact, in comparison with the Persson’s model and numerical simulations, is performed in [34]. For the nearly complete contact case, when the ratio of the real area of contact to the nominal contact area approaches unity, the statistical model, based on fracture mechanics approach, was developed [35]. For deterministic multiscale surfaces, (e.g., multisinusoidal self-affine surfaces), the Archard’s approach was successfully implemented [36, 37].

However, if at a certain scale amplitude of the cosine harmonic is much smaller than its period, full contact on this scale occurs, and a continuous oscillating pressure distribution on a larger scale will be observed [33, 38]. For distinguishing these cases the Johnson parameter, coupling an amplitude, a period of cosine harmonic, and a reduced modulus of elasticity with Hertzian pressure at the point, where maximum pressure occurs, is used [33]. In the present study the continuous contact configuration, observed at small amplitudes of subsequent cosine harmonics, is analyzed analytically for periodic and nonperiodic multisinusoidal rigid indenters in contact with an elastic half-plane.

2. Problem Formulation and Assumptions

The general scheme of the problem on the single period λ₁ for one, two, and three cosine harmonics profile is presented in Figure 1.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Contact of a cosine wavy profile, having one (a), two (b), and three (c) harmonics with an elastic half-plane.

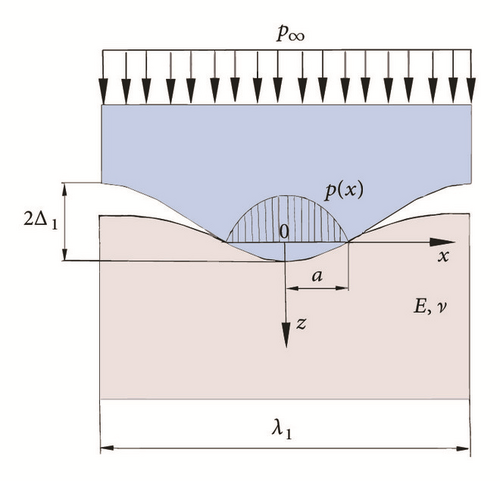
The wavy surface is assumed to be rigid, and the elastic half-plane is an isotropic semi-infinite body with two elastic constants: Young’s modulus E and Poisson’s coefficient ν. Also the plain strain condition is applied. The amplitudes of cosine harmonics are much smaller than their periods (Δ_i ≪ λ_i, where i = 1, 2 … N is a harmonic sequence number). This condition makes it possible to apply the linear elasticity theory. The Johnson parameter χ = πEΔ_i/2p_hλ_i (where p_h = 2p_∞λ_i/πa, p_∞ is an applied mean pressure, and a is a contact half-width) should be χ < 1 [33] for preserving the continuous contact configuration.

The two different problems with similar geometry of a rigid surface are considered. For the problem with periodic boundary conditions the integral equation with Hilbert kernel is used [11]:

()

where h(x) is an initial gap between surfaces, and p(x) is a contact pressure distribution.

For a nonperiodic indenter the integral equation with Cauchy kernel is used [10]:

()

Choosing for simplicity the largest wavelength λ₁ = 2π, one can write the expression for the gap function derivative for the ith cosine harmonic:

()

where δ is a contact approach and n_i = λ₁/λ_i. In the given formulation of the problem .

So, on the basis of the superposition principle and taking into account the assumed continuous contact configuration the total contact pressure distribution can be obtained as a sum of distributions of separate cosine harmonics:

()

where N is a number of wavelengths and p_i(x) is a component of pressure distribution for the ith wavelength.

The vertical elastic displacements can be obtained via the following expression [9, 10]:

()

where C is a constant depending on the selected datum point and are the surface vertical displacements for the ith wavelength.

The mean (nominal) pressure p_∞ is determined by invoking the equilibrium equation:

()

where p_∞i is a component of mean pressure corresponding to the ith wavelength.

3. Solutions of the Problem for the ith Harmonic

3.1. Solution for a Periodic Wavy Surface

Following equations (1) and (3) the integral equation for the ith harmonic is as follows:

()

The analytical solution for the contact pressure distribution for the ith harmonic can be obtained via the reduction of equation (7) to the integral equation with Cauchy kernel using the following variable transform [11]:

()

Considering the symmetry of the profile the integral equation (7) is reduced to

()

where

– is a Chebyshev polynomial of the second kind with a degree n_i [39].

Taking into account the considered assumptions the solution of equation (9) can be obtained by means of the Chebyshev expansion of the left side and the known spectral relations for the Chebyshev polynomials (Appendix). In initial variables the contact pressure distribution for the ith harmonic is determined by

()

where

()

where T_j – is a Chebyshev polynomial of the first kind with a degree j [39].

The total pressure distribution is obtained by using equation (4). For numerical calculations it is necessary to hold finite terms of the infinite series in equation (10). For the arbitrary period, the variables x and a in equations (10) and (12) should be multiplied on 2π/λ₁. The mean pressure p_∞i and the vertical displacements can be obtained using numerical integration in equations (5) and (6). The maximum pressure is determined as the pressure at the point x = 0.

3.2. Solution for a Wavy Rigid Nonperiodic Indenter

Following equations (2) and (3) the integral equation for the ith harmonic is

()

The solution of the equation (13) can be obtained, using an inversion without singularities on both endpoints [8, 11] and the Chebyshev expansion of the left side [39], which can be written explicitly:

()

where J_j(t) is the Bessel function of the first kind of the integer order j and the argument t [39].

The displacements within the contact zone x ∈ [−a, a] can be determined analytically using equation (5) and the relations for Chebyshev polynomials [40]. For the ith harmonic the final relation is

()

where sign ∑^/ identifies the sum of terms with odd j only.

According to equation (6) the mean pressure for the ith harmonic p_∞i is calculated by integration of equation (14) and resulting in a simple expression:

()

The approximate close-form relation for the contact pressure distribution can be obtained assuming that the largest values of pressure are concentrated near the point x = 0. Then equation (14) can be represented as

()

where sign ∑^/ identifies the sum of terms with odd j only.

Using the known relations for the Chebyshev polynomials [41] the following expression can be written:

()

With the use of an approximate relation between zeros of Bessel functions of integer order [42] the following expression can be written:

()

Then, applying the Jacobi-Anger expansion [42], the close-form relation is

()

The close-form integral relation for a maximum pressure (x = 0) can be determined exactly from equation (18):

()

4. Results and Discussion

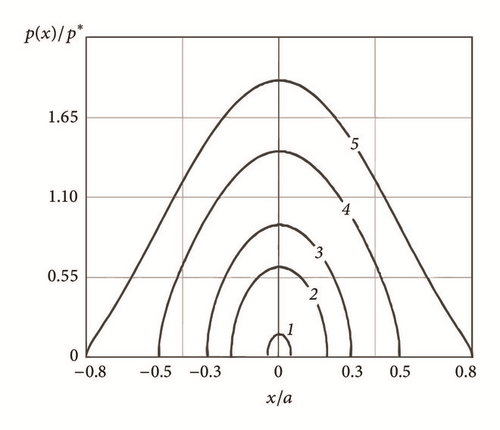
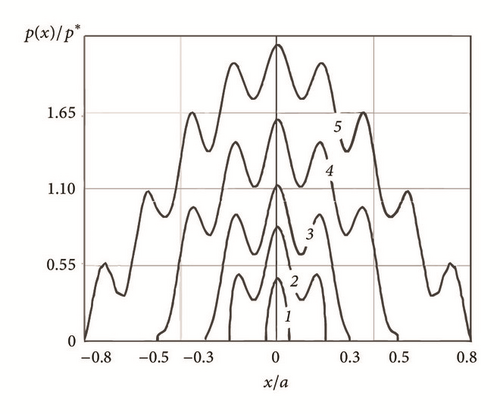
The evolution of the dimensionless contact pressure distribution p(x)/p ∗ (p ∗ = πEΔ₁/λ₁) for a periodic problem (equations ((6) and (10)-(12)), λ₁ = 2π, Δ₁ = 0.5) for various contact lengths (2a) and two different profiles f(x) is shown in Figure 2.

The exact (solid lines, equation (14)) and the approximate (dotted lines, equation (20)) graphs of the dimensionless contact pressure p(x)/p ∗ for different profiles of a nonperiodic wavy indenter are shown in Figure 3.

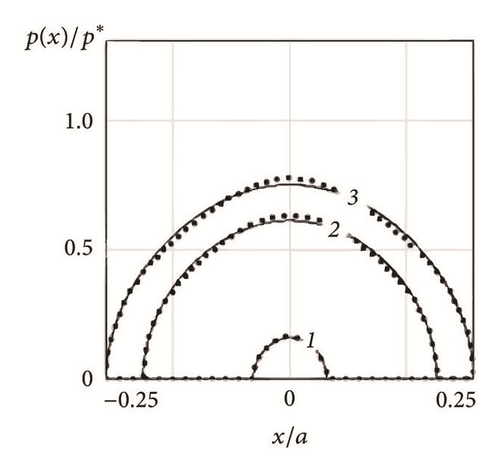
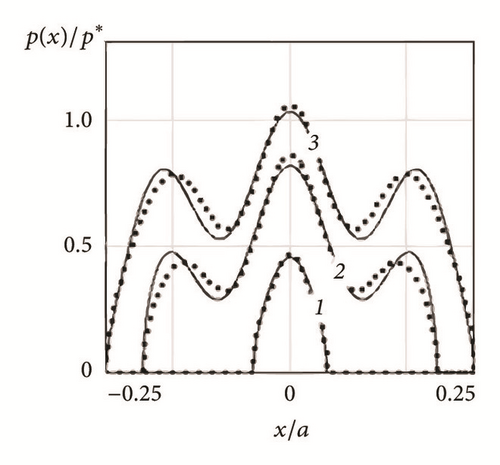
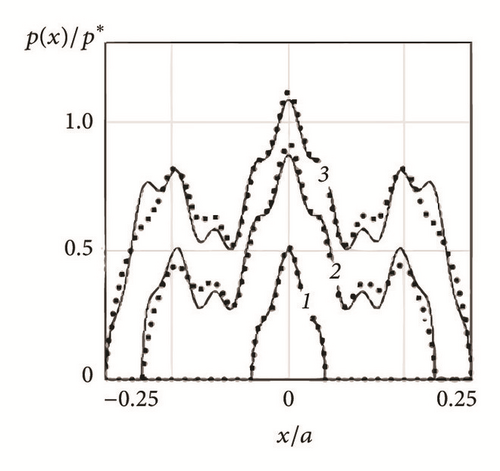
Figures 2 and 3 illustrate that, with increasing the number of harmonics, the pressure distribution becomes more complex and the maximum pressure grows significantly. For a single-scale periodic cosine profile (Figure 2(a)) the Westergaard’s solution is recovered. For a single-scale nonperiodic indenter (Figure 3(a)) the Hertz solution is observed, as the cosine function is very close to the quadratic parabola. Thereby, the distributions, presented in Figures 3(b) and 3(c), correspond to wavy cylinder problem at small waviness [38]. Comparison of the exact and the approximate values of pressure for a single indenter (Figure 3) shows that equation (20) satisfactorily describes the behavior of the pressure distribution.

Comparing the periodic and the nonperiodic solutions the elastic interaction effect is of interest. The mean pressure – contact length curves for two profiles, calculated from periodic and nonperiodic solutions, are presented in Figure 4.

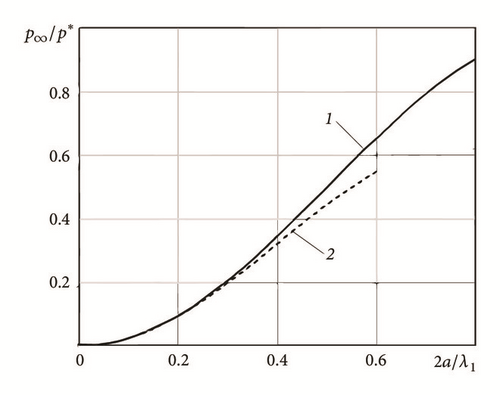
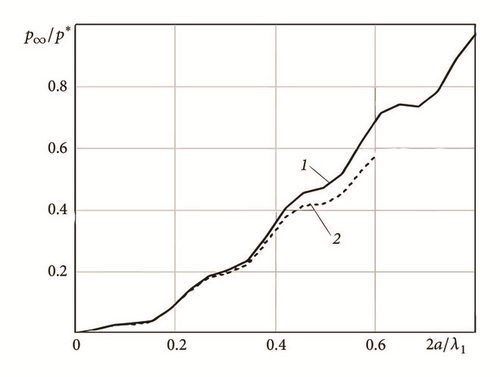
Figure 4 shows that, at small contact lengths (2a < 0.25λ₁), the solutions are close. The piece of graphs agreement does not depend on profile geometry. With increase of load the periodic solution gives the smaller contact length due to elastic interaction on the largest scale. For the profile with two cosine harmonics and continuous contact configuration, presented in this study, the oscillations of mean pressure – contact length curves are observed (Figure 4(b)). Curves in Figure 4(a) correspond to Westergaard’s (curve 1) and Hertz (curve 2) solutions, recovered for profile with one wavelength.

Graphs of the mean and the maximum pressures versus contact length on the interval 2a < 0.25λ₁ for different profiles of a wavy nonperiodic indenter are shown in Figure 5.

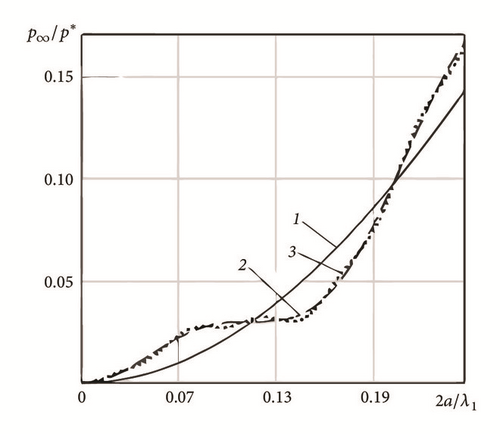
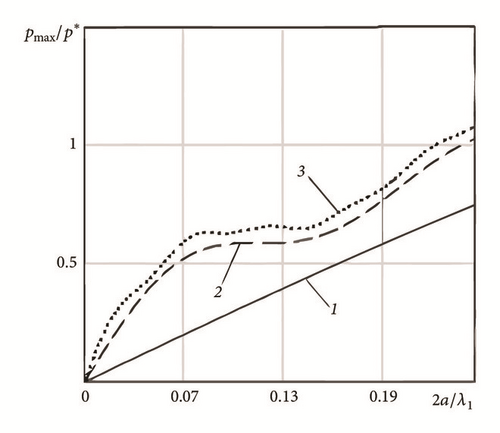
Figure 5 shows that the maximum pressure depends on profile geometry stronger than the mean pressure. However, adding the third harmonic leads to insignificant change of the graphs character. Continuous contact configuration at the presence of several cosine wavelengths leads to oscillatory character of the mean and the maximum pressure graphs. Combining these two graphs numerically one can obtain the dependence of peak pressure from mean pressure (Figure 6).

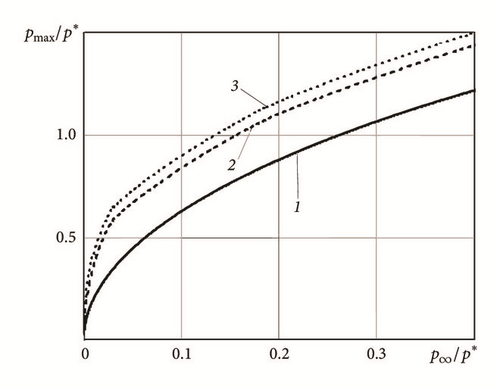
Figure 6 shows that dependences of the maximum pressure from the mean pressure are not oscillatory for the profiles with two and three wavelengths, and additional cosine harmonics change the graph considerably in value but not in character. This statement can be useful in the analysis of contact surfaces fracture processes [33].

5. Conclusions

The continuous contact configuration is one of the two possible configurations, arising at indentation of a multisinusoidal 2D wavy surface into an elastic half-plane. This configuration leads to continuous oscillatory contact pressure distribution. Comparison of the derived periodic and nonperiodic solutions shows that the long-range elastic interaction between asperities does not depend on a number of cosine wavelengths and can be neglected at small loads (contact lengths) for arbitrary wavy profile geometry. The assumption of neglecting the long-range periodicity leads to exact equations for determining the remote and the maximum pressures from the contact length, described by oscillatory functions. However, the dependences of the maximum pressure from the mean pressure are not oscillatory for the profiles with two and three wavelengths and resemble those for a simple cosine profile of indenter. The influence of the additional cosine harmonics on the maximum pressure is significantly larger than on the mean pressure for the same contact zone length. The derived equations can be used at the analysis of contact characteristics of deterministic profiles of arbitrary geometry and also at the validation of more complex numerical models of rough surfaces contact.

Conflicts of Interest

The author declares that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

The research was supported by RSF (project no. 14-29-00198).

Appendix

Derivation of Contact Pressure Distribution for the Periodic Problem

The main integral equation of the considered contact problem for the ith harmonic in transformed variables (8) is

()

where U_n is a Chebyshev polynomial of a second kind with a degree n_i.

The appropriate inversion of this integral equation has to be nonsingular on both endpoints [11]:

()

By introducing the new variables,

()

the expression (A.2) can be written in the following form:

()

where the function φ_i(s) is

()

Since the integrand function is defined on the interval [-1; 1] and satisfies the Hölder condition, it can be represented as an expansion in Chebyshev polynomials of the first kind [41].

()

where T_j is a Chebyshev polynomial of the first kind with a degree j [39].

The coefficients A_ij in equation (A.6) are defined by the following expression [43]:

()

With the use of integral relation between the Chebyshev polynomials of the first and the second kind [41]

()

and equation (A.4) the expression for the contact pressure distribution for the ith harmonic is

()

Returning to the original variables, and bearing in mind positive pressures notation, one can obtain

()

Open Research

Data Availability

No data were used to support this study.

References

1 Persson B. N. J., Theory of rubber friction and contact mechanics, The Journal of Chemical Physics. (2001) 115, no. 8, 3840–3861, 2-s2.0-0035934290, https://doi.org/10.1063/1.1388626.
10.1063/1.1388626
CAS Web of Science® Google Scholar
2 Rodríguez Urribarrí A. C., van der Heide E., Zeng X., and de Rooij M. B., Modelling the static contact between a fingertip and a rigid wavy surface, Tribology International. (2016) 102, 114–124, 2-s2.0-84983591279, https://doi.org/10.1016/j.triboint.2016.05.028.
10.1016/j.triboint.2016.05.028
Web of Science® Google Scholar
3 Adnan A. S., Ramalingam V., Ko J. H., and Subbiah S., Nano texture generation in single point diamond turning using backside patterned workpiece, Manufacturing Letters. (2013) 2, no. 1, 44–48, 2-s2.0-84899081027, https://doi.org/10.1016/j.mfglet.2013.10.004.
10.1016/j.mfglet.2013.10.004
Google Scholar
4 Ju Y. and Farris T. N., Spectral Analysis of Two-Dimensional Contact Problems, Journal of Tribology. (1996) 118, no. 2, https://doi.org/10.1115/1.2831303.
10.1115/1.2831303
Web of Science® Google Scholar
5 Sadowski M. A., Zwiedimensionale probleme der elastizitatshtheorie, ZAMM—Zeitschrift für Angewandte Mathematik und Mechanik. (1928) 8, no. 2, 107–121, https://doi.org/10.1002/zamm.19280080203.
10.1002/zamm.19280080203
Google Scholar
6 Muskhelishvili N. I., Some Basic Problems of the Mathematical Theory of Elasticity, 1977, Springer, Dordrecht, Netherlands.
10.1007/978-94-017-3034-1
Google Scholar
7 Westergaard H. M., Bearing pressures and cracks, Journal of Applied Mechanics. (1939) 6, 49–53.
10.1115/1.4008919
Google Scholar
8 Johnson K. L., Contact Mechanics, 1987, Cambridge University Press, Cambridge, UK.
Google Scholar
9 Schtaierman I. Y., Contact Problem of Theory of Elasticity, 1949, Gostekhizdat, Moscow, Russia.
Google Scholar
10 Galin L. A., Contact problems, 2008, Springer, Netherlands, Dordrecht.
Google Scholar
11 Block J. M. and Keer L. M., Periodic contact problems in plane elasticity, Journal of Mechanics of Materials and Structures. (2008) 3, no. 7, 1207–1237, 2-s2.0-70350397843, https://doi.org/10.2140/jomms.2008.3.1207.
10.2140/jomms.2008.3.1207
Web of Science® Google Scholar
12 Dundurs J., Tsai K. C., and Keer L. M., Contact between elastic bodies with wavy surfaces, Journal of Elasticity. (1973) 3, no. 2, 109–115, 2-s2.0-0003051543, https://doi.org/10.1007/BF00045817.
10.1007/BF00045817
Google Scholar
13 Krishtafovich A. A., Martynyak R. M., and Shvets R. N., Contact between anisotropic half-plane and rigid body with regular microrelief, Journal of Friction and Wear. (1994) 15, 15–21.
Google Scholar
14 Xu Y. and Jackson R. L., Periodic Contact Problems in Plane Elasticity: The Fracture Mechanics Approach, Journal of Tribology. (2018) 140, no. 1, https://doi.org/10.1115/1.4036920.
10.1115/1.4036920
Web of Science® Google Scholar
15 Kuznetsov E. A., Periodic contact problem for half-plane allowing for forces of friction, Soviet Applied Mechanics. (1976) 12, no. 10, 1014–1019, 2-s2.0-34250298283, https://doi.org/10.1007/BF00885047.
10.1007/BF00885047
Google Scholar
16 Nosonovsky M. and Adams G. G., Steady-state frictional sliding of two elastic bodies with a wavy contact interface, Journal of Tribology. (2000) 122, no. 3, 490–495, 2-s2.0-0034480584, https://doi.org/10.1115/1.555391.
10.1115/1.555391
CAS Web of Science® Google Scholar
17 Kuznetsov Y. A., Effect of fluid lubricant on the contact characteristics of rough elastic bodies in compression, Wear. (1985) 102, no. 3, 177–194, 2-s2.0-0022043425, https://doi.org/10.1016/0043-1648(85)90217-0.
10.1016/0043-1648(85)90217-0
Web of Science® Google Scholar
18 Ciavarella M., The generalized Cattaneo partial slip plane contact problem. {II}. Examples, International Journal of Solids and Structures. (1998) 35, no. 18, 2363–2378, https://doi.org/10.1016/S0020-7683(97)00155-8, MR1614373.
10.1016/S0020-7683(97)00155-8
Web of Science® Google Scholar
19 Carbone G. and Mangialardi L., Adhesion and friction of an elastic half-space in contact with a slightly wavy rigid surface, Journal of the Mechanics and Physics of Solids. (2004) 52, no. 6, 1267–1287, 2-s2.0-1642586403, https://doi.org/10.1016/j.jmps.2003.12.001, Zbl1079.74587.
10.1016/j.jmps.2003.12.001
Web of Science® Google Scholar
20 Menga N., Putignano C., Carbone G., and Demelio G. P., The sliding contact of a rigid wavy surface with a viscoelastic half-space, Proceedings of the Royal Society A Mathematical, Physical and Engineering Sciences. (2014) 470, no. 2169, 20140392–20140392, https://doi.org/10.1098/rspa.2014.0392, Zbl1348.74256.
10.1098/rspa.2014.0392
Web of Science® Google Scholar
21 Goryacheva I. G. and Makhovskaya Y. Y., Modeling of friction at different scale levels, Mechanics of Solids. (2010) 45, no. 3, 390–398, 2-s2.0-77955412210, https://doi.org/10.3103/S002565441003009X.
10.3103/S002565441003009X
Web of Science® Google Scholar
22 Soldatenkov I. A., The contact problem for an elastic strip and a wavy punch under friction and wear, Journal of Applied Mathematics and Mechanics. (2011) 75, no. 1, 85–92.
10.1016/j.jappmathmech.2011.04.013
Google Scholar
23 Zhou Y.-T. and Kim T.-W., Analytical solution of the dynamic contact problem of anisotropic materials indented with a rigid wavy surface, Meccanica. (2017) 52, no. 1-2, 7–19, https://doi.org/10.1007/s11012-016-0386-2, MR3578052, Zbl1369.74070.
10.1007/s11012-016-0386-2
Web of Science® Google Scholar
24 Tsukanov I. Y., Effects of shape and scale in mechanics of elastic interaction of regular wavy surfaces, Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology. (2017) 231, no. 3, 332–340, 2-s2.0-85011827517, https://doi.org/10.1177/1350650116657699.
10.1177/1350650116657699
Web of Science® Google Scholar
25 Goryacheva I. G., Contact mechanics in tribology, 1998, 61, Kluwer Academic Publishers, Dordrecht, MR1663852, Zbl0947.74002.
10.1007/978-94-015-9048-8
Google Scholar
26 Manners W., Partial contact between elastic surfaces with periodic profiles, Proceedings of the Royal Society. (1998) 454, no. 1980, 3203–3221, https://doi.org/10.1098/rspa.1998.0298, MR1664302.
10.1098/rspa.1998.0298
Google Scholar
27 Chekina O. G. and Keer L. M., A new approach to calculation of contact characteristics, Journal of Tribology. (1999) 121, no. 1, 20–27, 2-s2.0-0033066124, https://doi.org/10.1115/1.2833804.
10.1115/1.2833804
Web of Science® Google Scholar
28 Stanley H. M. and Kato T., An fft-based method for rough surface contact, Journal of Tribology. (1997) 119, no. 3, 481–485, 2-s2.0-0031190183, https://doi.org/10.1115/1.2833523.
10.1115/1.2833523
Web of Science® Google Scholar
29 Borodich F. M. and Galanov B. A., Self-similar problems of elastic contact for non-convex punches, Journal of the Mechanics and Physics of Solids. (2002) 50, no. 11, 2441–2461, https://doi.org/10.1016/S0022-5096(02)00031-5, MR1925362, Zbl1100.74605, 2-s2.0-0036833201.
10.1016/S0022-5096(02)00031-5
Web of Science® Google Scholar
30 Ciavarella M., Demelio G., and Murolo C., A numerical algorithm for the solution of two-dimensional rough contact problems, Journal of Strain Analysis for Engineering Design. (2005) 40, no. 5, 463–476, 2-s2.0-23844478211, https://doi.org/10.1243/030932405X15936.
10.1243/030932405X15936
Web of Science® Google Scholar
31 Paggi M. and Reinoso J., A variational approach with embedded roughness for adhesive contact problems, 2018, https://arxiv.org/abs/1805.07207.
Google Scholar
32 Tripp J. H., Van Kuilenburg J., Morales-Espejel G. E., and Lugt P. M., Frequency response functions and rough surface stress analysis, Tribology Transactions. (2003) 46, no. 3, 376–382, 2-s2.0-0141638636, https://doi.org/10.1080/10402000308982640.
10.1080/10402000308982640
CAS Web of Science® Google Scholar
33 Paulin C., Ville F., Sainsot P., Coulon S., and Lubrecht T., Effect of rough surfaces on rolling contact fatigue theoretical and experimental analysis, Tribology and Interface Engineering Series. (2004) 43, 611–617, 2-s2.0-17644371418.
10.1016/S0167-8922(03)80089-5
Google Scholar
34 Jackson R. L. and Green I., On the modeling of elastic contact between rough surfaces, Tribology Transactions. (2011) 54, no. 2, 300–314, 2-s2.0-84857704722, https://doi.org/10.1080/10402004.2010.542277.
10.1080/10402004.2010.542277
Web of Science® Google Scholar
35 Xu Y., Jackson R. L., and Marghitu D. B., Statistical model of nearly complete elastic rough surface contact, International Journal of Solids and Structures. (2014) 51, no. 5, 1075–1088, 2-s2.0-84892432109, https://doi.org/10.1016/j.ijsolstr.2013.12.005.
10.1016/j.ijsolstr.2013.12.005
Web of Science® Google Scholar
36 Ciavarella M., Murolo G., Demelio G., and Barber J. R., Elastic contact stiffness and contact resistance for the Weierstrass profile, Journal of the Mechanics and Physics of Solids. (2004) 52, no. 6, 1247–1265, 2-s2.0-1642602151, https://doi.org/10.1016/j.jmps.2003.12.002, Zbl1079.74589.
10.1016/j.jmps.2003.12.002
Web of Science® Google Scholar
37 Jackson R. L., An Analytical solution to an archard-type fractal rough surface contact model, Tribology Transactions. (2010) 53, no. 4, 543–553, 2-s2.0-77954097685, https://doi.org/10.1080/10402000903502261.
10.1080/10402000903502261
CAS Web of Science® Google Scholar
38 Hills D. A., Nowell D., and Sackfield A., Mechanics of elastic contacts, 1993, Butterworth-Heinemann, Oxford, UK.
Google Scholar
39 Gradshteyn I. S. and Ryzhik I. M., Table of Integrals, Series, and Products, 2015, 8th edition, Elsevier.
Google Scholar
40 Arzhang A., Derili H., and Yousefi M., The approximate solution of a class of Fredholm integral equations with a logarithmic kernel by using Chebyshev polynomials, Global Journal of Computer Sciences. (2013) 3, no. 2, 37–48.
Google Scholar
41 Mason J. C. and Handscomb D. C., Chebyshev Polynomials, 2003, Chapman and Hall, London, UK.
Google Scholar
42 Oldham K., Myland J., and Spanier J., An Atlas of Functions, 2008, 2nd edition, Springer, New York, NY, USA, https://doi.org/10.1007/978-0-387-48807-3, MR2466333, Zbl1167.65001.
Google Scholar
43 Elliott D., The evaluation and estimation of the coefficients in the Chebyshev series expansion of a function, Mathematics of Computation. (1964) 18, 274–284, https://doi.org/10.2307/2003301, MR0166903, 2-s2.0-84968502841.
10.1090/S0025-5718-1964-0166903-7
Web of Science® Google Scholar

Citing Literature

All articles

Partial Contact of a Rigid Multisinusoidal Wavy Surface with an Elastic Half-Plane

Abstract

1. Introduction

2. Problem Formulation and Assumptions

3. Solutions of the Problem for the ith Harmonic

3.1. Solution for a Periodic Wavy Surface

3.2. Solution for a Wavy Rigid Nonperiodic Indenter

4. Results and Discussion

5. Conclusions

Conflicts of Interest

Acknowledgments

Appendix

Derivation of Contact Pressure Distribution for the Periodic Problem

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Partial Contact of a Rigid Multisinusoidal Wavy Surface with an Elastic Half-Plane

Abstract

1. Introduction

2. Problem Formulation and Assumptions

3. Solutions of the Problem for the ith Harmonic

3.1. Solution for a Periodic Wavy Surface

3.2. Solution for a Wavy Rigid Nonperiodic Indenter

4. Results and Discussion

5. Conclusions

Conflicts of Interest

Acknowledgments

Appendix

Derivation of Contact Pressure Distribution for the Periodic Problem

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information