Volume 2018, Issue 1 8213950

Research Article

Open Access

M-Polynomials and Degree-Based Topological Indices of Triangular, Hourglass, and Jagged-Rectangle Benzenoid Systems

Young Chel Kwun,

Young Chel Kwun

orcid.org/0000-0002-5028-0640

Department of Mathematics, Dong-A University, Busan 49315, Republic of Korea donga.ac.kr

Search for more papers by this author

Ashaq Ali,

Ashaq Ali

Department of Mathematics and Statistics, The University of Lahore, Lahore, Pakistan uol.edu.pk

Search for more papers by this author

Waqas Nazeer,

Corresponding Author

Waqas Nazeer

[email protected]

orcid.org/0000-0002-5488-0467

Division of Science and Technology, University of Education, Lahore 54000, Pakistan ue.edu.pk

Search for more papers by this author

Maqbool Ahmad Chaudhary,

Maqbool Ahmad Chaudhary

Department of Mathematics and Statistics, The University of Lahore, Lahore, Pakistan uol.edu.pk

Search for more papers by this author

Shin Min Kang,

Corresponding Author

Shin Min Kang

[email protected]

orcid.org/0000-0002-5294-4447

Department of Mathematics and Research Institute of Natural Science, Gyeongsang National University, Jinju 52828, Republic of Korea gnu.ac.kr

Center for General Education, China Medical University, Taichung 40402, Taiwan cmu.edu.cn

Search for more papers by this author

Young Chel Kwun,

Young Chel Kwun

orcid.org/0000-0002-5028-0640

Department of Mathematics, Dong-A University, Busan 49315, Republic of Korea donga.ac.kr

Search for more papers by this author

Ashaq Ali,

Ashaq Ali

Department of Mathematics and Statistics, The University of Lahore, Lahore, Pakistan uol.edu.pk

Search for more papers by this author

Waqas Nazeer,

Corresponding Author

Waqas Nazeer

[email protected]

orcid.org/0000-0002-5488-0467

Division of Science and Technology, University of Education, Lahore 54000, Pakistan ue.edu.pk

Search for more papers by this author

Maqbool Ahmad Chaudhary,

Maqbool Ahmad Chaudhary

Department of Mathematics and Statistics, The University of Lahore, Lahore, Pakistan uol.edu.pk

Search for more papers by this author

Shin Min Kang,

Corresponding Author

Shin Min Kang

[email protected]

orcid.org/0000-0002-5294-4447

Department of Mathematics and Research Institute of Natural Science, Gyeongsang National University, Jinju 52828, Republic of Korea gnu.ac.kr

Center for General Education, China Medical University, Taichung 40402, Taiwan cmu.edu.cn

Search for more papers by this author

First published: 12 September 2018

https://doi.org/10.1155/2018/8213950

Citations: 23

Academic Editor: Marjana Novic

Share a link

Email
Wechat
Bluesky

Abstract

Chemical graph theory is a branch of mathematical chemistry which has an important effect on the development of the chemical sciences. The study of topological indices is currently one of the most active research fields in chemical graph theory. Topological indices help to predict many chemical and biological properties of chemical structures under study. The aim of this report is to study the molecular topology of some benzenoid systems. M-polynomial has wealth of information about the degree-based topological indices. We compute M-polynomials for triangular, hourglass, and jagged-rectangle benzenoid systems, and from these M-polynomials, we recover nine degree-based topological indices. Our results play a vital role in pharmacy, drug design, and many other applied areas.

1. Introduction

Mathematical chemistry provides tools such as polynomials and functions to capture information hidden in the symmetry of molecular graphs and thus predict properties of compounds without using quantum mechanics. A topological index is a numerical parameter of a graph and depicts its topology. Topological indices describe the structure of molecules numerically and are used in the development of qualitative structure activity relationships (QSARs). Most commonly known invariants of such kinds are degree-based topological indices. These are actually the numerical values that correlate the structure with various physical properties, chemical reactivity, and biological activities [1–5]. It is an established fact that many properties such as heat of formation, boiling point, strain energy, rigidity, and fracture toughness of a molecule are strongly connected to its graphical structure.

Hosoya polynomial, Wiener polynomial [6], plays a pivotal role in distance-based topological indices. A long list of distance-based indices can be easily evaluated from Hosoya polynomial. A similar breakthrough was obtained recently by Deutsch and Klavžar [7], in the context of degree-based indices. Deutsch and Klavžar [7] introduced M-polynomial in, 2015, to play a role, parallel to Hosoya polynomial to determine closed form of many degree-based topological indices [8–11]. The real power of M-polynomial is its comprehensive nature containing healthy information about degree-based graph invariants. These invariants are calculated on the basis of symmetries present in the 2d-molecular lattices and collectively determine some properties of the material under observation. Benzenoid hydrocarbons play a vital role in our environment and in the food and chemical industries.

Benzenoid molecular graphs are systems with deleted hydrogens. It is a connected geometric figure obtained by arranging congruent regular hexagons in a plane so that two hexagons are either disjoint or have a common edge.

This figure divides the plane into one infinite (external) region and a number of finite (internal) regions. All internal regions must be regular hexagons. Benzenoid systems are of considerable importance in theoretical chemistry because they are the natural graph representation of benzenoid hydrocarbons. A vertex of a hexagonal system belongs to, at most, three hexagons. A vertex shared by three hexagons is called an internal vertex [12].

In this paper, we study three benzenoid systems, namely, triangular, hourglass, and jagged-rectangle benzenoid systems.

2. Basic Definitions and Literature Review

Throughout this article, we assume G to be a connected graph, V (G) and E (G) are the vertex set and the edge set, respectively, and d_v denotes the degree of a vertex v.

Definition 1. The M-polynomial of G is defined as M(G, x, y) = ∑_{δ≤i≤j≤Δ}m_ij(G)xⁱy^j where δ = Min{d_v | v ∈ V(G)}, Δ = Max{d_v | v ∈ V(G)} and m_ij(G) is the edge vu ∈ E(G) such that where ≤j [7].

Wiener Index and its various applications are discussed in [13–15]. Randić Index, R_−1/2(G), was introduced by Milan Randić in 1975, defined as . For general details about R_−1/2(G) and its generalized Randić Index, refer [16–20], and the Inverse Randić Index is defined as . Clearly, R_−1/2(G) is a special case of R_α(G) where α = −(1/2). This index has many applications in diverse areas. Many papers and books such as [21–23] are written on this topological index as well. Gutman and Trinajstić introduced two indices defined as M₁(G) = ∑_uv∈E(G)(d_ud_v) and M₂(G) = ∑_uv∈E(G)(d_ud_v). The modified second Zagreb Index is defined as ^mM₂(G) = ∑_uv∈E(G)(1/d(u)d(v)). We refer [24–28] to the readers for comprehensive details of these indices. Other famous indices are Symmetric Division Index: SDD(G) = ∑_uv∈E(G){(min(d_u, d_v)/max(d_u, d_v)) + (max(d_u, d_v)/min(d_u, d_v))}, Harmonic Index: H(G) = ∑_vu∈E(G)(2/d_u + d_v), Inverse Sum Index: I(G) = ∑_vu∈E(G)(d_ud_v/d_u + d_v), and Augmented Zagreb Index: [29, 30].

Tables presented in [7–10] relate some of these well-known degree-based topological indices with M-polynomial with the following reserved notations:

(1)

3. Computational Results

In this section, we give our computational results. In terms of chemical graph theory and mathematical chemistry, we associate a graph with the molecular structure where vertices correspond to atoms and edges to bonds. The triangular benzenoid system is shown in Figure 1. In the following theorem, we compute M-polynomial of the triangular benzenoid system.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Triangular benzenoid.

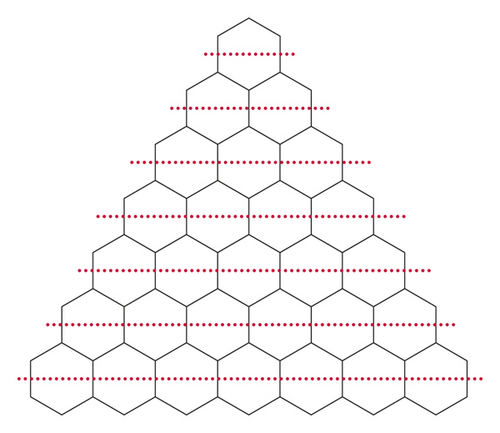
Theorem 1. Let T_pbe a Triangular benzenoid system where p shows the number of hexagons in the base graph and total no. of hexagons inT_pis(1/2)p(p + 1). Then,

(2)

Proof. Let T_p be a triangular benzenoid. Then from Figure 1, we have

(3)

The edge set of T_p has the following three partitions:

(4)

Now,

(5)

Thus, the M-polynomial of T_p is

(6)

Now, we derive formulas for many degree-based topological indices using M-polynomial.

Proposition 2. Let T_pbe a triangular Benzenoid.

Then,

(1)
M₁(T_p) = 9p² + 21p − 6
(2)
M₂(T_p) = (27/2)p² + 45p − 12
(3)
^mM ₂(T_p) = (1/6)p² + (5/6)p + (1/2)
(4)
R_α(T_p) = (3^2α+1/2)p² + (2^α+1 · 3^α+1 − (3^2α+1/2))p + (3 · 2^2α+1 − 2^α+1 · 3^α+1)
(5)
RR_α(T_p) = (1/2 · 3^2α−1)p² + ((1/2^α−1 · 3^α−1) + (1/2 · 3^2α−1))p + ((3/2^2α−1) − (1/2^α−1 · 3^α−1))
(6)
SSD(T_p) = 3p² + 24p − 9
(7)
H(T_p) = (1/2)p² + (19/10)p + (3/5)
(8)
I(T_p) = (9/4)p² + (99/20)p − (6/5)
(9)
A(T_p) = (2187/128)p² + (46965/128)p − 336

Proof. Let

(7)

Then,

(8)

(1)
First Zagreb Index:
(9)
(2)
Second Zagreb Index:
(10)
(3)
Modified second Zagreb Index:
(11)
(4)
Generalized Randic Index:
(12)
(5)
Inverse Randic Index:
(13)
(6)
Symmetric Division Index:
(14)
(7)
Harmonic Index:
(15)
(8)
Inverse Sum Index:
(16)
(9)
Augmented Zagreb Index:
(17)

Topological indices of T_p for specific values of p are given in Table 1.

Our next target is the benzenoid hourglass system which is obtained from two copies of a triangular benzenoid T_p by overlapping their external hexagons and shown in Figure 2. In Theorem 3, we compute M-polynomial of the benzenoid hourglass system.

Table 1. Topological indices of triangular benzenoid for different values of p.

Name of index	p = 1	p = 2	p = 3	p = 4	p = 5
M-polynomial	6x²y²	6x²y² + 6x²y³ + 3x³y³	6x²y² + 12x²y³ + 9x³y³	6x²y² + 18x²y³ + 18x³y³	6x²y² + 24x²y³ + 30x³y³
First Zagreb Index	24	72	138	222	324
Second Zagreb Index	46.50000000	132	244.5000000	384	550.5000000
Modified second Zagreb Index	1.500000000	2.833333333	4.500000000	6.500000000	8.833333333
Randić Index for α = 1/2	17.39387692	41.09081537	73.78775383	115.4846923	166.1816308
Inverse Randić Index for α = 1/2	2.898979486	7.348469229	12.79795897	19.24744872	26.69693846
Symmetric Division Index	18	5	90	135	186
Harmonic Index	3	6.400000000	10.80000000	16.20000000	22.60000000
Inverse Sum Index	6	17.70000000	33.90000000	27.30000000	39.90000000
Augmented Zagreb Index	48	466.1718750	918.5156250	1405.031250	1925.718750

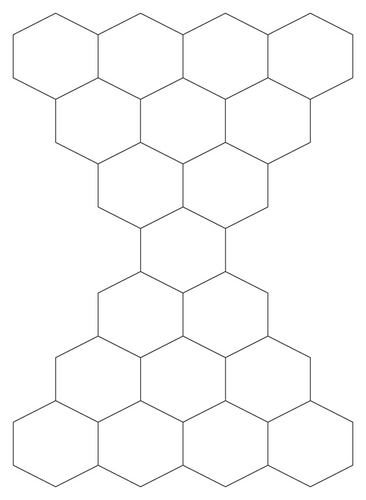
Theorem 3. Let X_pdenotes the Benzenoid Hourglass. Then, its M-polynomial is

(18)

Proof. Let X_p denotes the benzenoid hourglass which is obtained from two copies of a triangular benzenoid T_p by overlapping their external hexagons. Then, we have

(19)

The edge set of X_p has the following three partitions:

(20)

Now,

(21)

Thus, the M-polynomial of X_p is

(22)

Now, we derive formulas for many degree-based topological indices using M-polynomial.

Proposition 4. Let X_pbe a Benzenoid Hourglass.

Then,

(1)
M₁(X_p) = 6(3p² + 7p − 4)
(2)
M₂(X_p) = 27p² + 45p − 28
(3)
^mM ₂(X_p) = (1/3)p² + (5/3)p − (2/9)
(4)
R_α(X_p) = 3^2α+1p² + (2^α+2 · 3^α+1 − 3^2α+1)p + (2^2α+3 − 2^α+4 · 3^α + 4 · 3^2α)
(5)
RR_α(X_p) = (1/3^2α−1)p² + ((1/3^α−1 · 2^α−2) − (1/3^2α−1))p + ((1/2^2α−3) − (1/3^α⋅2^α−4) + (4/3^2α))
(6)
SSD(X_p) = 6p² + 20p − 32/3
(7)
H(X_p) = p² + 19/5p − 16/15
(8)
I(X_p) = 9/2p² + 99/10p − 26/5
(9)
A(X_p) = (2187/64)p² + (3957/64)p − (295/16)

Topological indices of X_p for specific values of p are given in Table 2.

Table 2. Topological indices of benzenoid hourglass for different values of p.

Name of index	p = 1	p = 2	p = 3	p = 4	p = 5
M-polynomial	8x²y² − 4x²y³ + 4x³y³	8x²y² + 8x²y³ + 10x³y³	8x²y² + 20x²y³ + 22x³y³	8x²y² + 32x²y³ + 40x³y³	8x²y² + 44x²y³ + 64x³y³
First Zagreb Index	36	132	264	432	636
Second Zagreb Index	44	170	350	584	872
Modified second Zagreb Index	1.777777778	4.444444444	7.777777778	11.77777778	16.44444444
Randić Index for α = 1/2	92.81601318	198.9976439	323.1792746	465.3609054	625.5425361
Inverse Randić Index for α = 1/2	3.648129059	8.097618797	14.54710855	22.99659829	33.44608803
Symmetric Division Index	15.33333333	53.33333333	103.3333333	165.3333333	239.3333333
Harmonic Index	3.733333333	10.53333333	19.33333333	30.13333333	44.26666667
Inverse Sum Index	9.200000000	32.60000000	65	106.4000000	156.8000000
Augmented Zagreb Index	77.56250000	241.9062500	474.5937500	775.6250000	1145

Now, we study benzenoid jagged-rectangle shown in Figure 3.

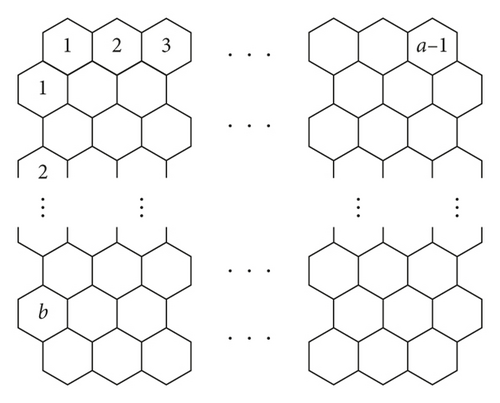
Theorem 5. Let B_p,qdenotes a Jagged-rectangle Benzenoid system for allp, q ∈ N − 1.

Then,

(23)

Proof. Let B_p,q denotes a benzenoid system jagged-rectangle for all p, q ∈ N − 1. A benzenoid jagged-rectangle forms a rectangle and the number of benzenoid called in each chain alternate p and p − 1.

The edge set of B_p,q has the following three partitions:

(24)

Now,

(25)

Thus, the M-polynomial of B_p,q is

(26)

Proposition 6. Let B_p,qdenotes a Jagged-rectangle Benzenoid system for allp, q ∈ N − 1.

Then,

(1)
M₁(B_p,q) = 2(13p − q + 18pq − 14)
(2)
M₂(B_p,q) = 33p − 13q − 44
(3)
^mM ₂(B_p,q) = (7/9)p + (11/18)q + (2/3)pq − (1/9)
(4)
R_α(B_p,q) = (3^α · 2^α+2 + 3^2α)p + (2^2α+1 + 3^α · 2^α+2 − 5 · 3^2α)q + 6 · 3^2αpq + (2^2α+2 − 3^α · 2^α+2 − 4 · 3^2α)
(5)
RR_α(B_p,q) = ((1/3^α · 2^α−2) + (1/3^2α))p + ((1/2^2α−1) + (1/3^α · 2^α−2) − (5/3^2α))q + (6/3^2α)pq + ((1/2^2α−2) − (1/3^α⋅2^α−2) − (4/3^2α))
(6)
SSD(B_p,q) = (32/3)p + (8/3)q + 12pq − (26/3)
(7)
H(B_p,q) = (29/15)p + (14/15)q + 2pq − (14/15)
(8)
I(B_p,q) = (63/10)p − (7/10)q + 9pq − (34/5)
(9)
A(B_p,q) = (2777/64)p − (573/64)q + (2187/32)pq − 729/16.

Topological indices of B_p,q for specific values of p and q are given in Table 3.

Table 3. Topological indices of jagged-rectangle benzenoid system for different values of p and q.

Name of index	p = 1, q = 1	p = 2, q = 11	p = 3, q = 11	p = 4, q = 11	p = 5, q = 11
M-polynomial	6x²y² + 4x²y³ − 2x³y³	6x²y² + 8x²y³ + 4x³y³	6x²y² + 12x²y³ + 12x³y³	6x²y² + 16x²y³ + 16x³y³	6x²y² + 20x²y³ + 22x³y³
First Zagreb Index	12	54	96	138	180
Second Zagreb Index	−24	9	42	75	108
Modified second Zagreb Index	1.944444444	3.388888889	4.833333333	6.277777778	7.722222222
Randic Index for α = 1/2	15.79795897	46.59591794	77.39387692	108.1918359	138.9897949
Inverse Randic Index for α = 1/2	3.966326495	7.932652990	11.89897949	15.86530598	19.83163248
Symmetric Division Index	16.66666667	39.33333333	62	84.66666667	107.3333333
Harmonic Index	3.933333333	7.866666667	11.80000000	15.73333333	19.66666667
Inverse Sum Index	9.200000000	24.50000000	39.80000000	55.10000000	70.40000000
Augmented Zagreb Index	57.21875000	168.9531250	280.6875000	392.4218750	504.1562500

4. Conclusion

In this paper, we computed M-polynomials for triangular, hourglass, and jagged-rectangle benzenoid systems. From these M-polynomials, we recover first Zagreb, second Zagreb, modified second Zagreb, Randić, inverse Randić, symmetric division, inverse sum, and harmonic and augmented Zagreb indices of triangular, hourglass, and jagged-rectangle benzenoid systems. Note that there are no benzenoid molecules having the triangular graphs and hourglass graphs as their skeleton. It is important to mention here that some of these topological indices are calculated directly by using formulas in the literature.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This study was supported by research funds from Dong-A University.

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Rücker G. and Rücker C., On topological indices, boiling points, and cycloalkanes, Journal of Chemical Information and Computer Sciences. (1999) 39, no. 5, 788–802, https://doi.org/10.1021/ci9900175, 2-s2.0-0041037845.
10.1021/ci9900175
CAS Web of Science® Google Scholar
2 Klavžar S. and Gutman I., A comparison of the Schultz molecular topological index with the Wiener index, Journal of Chemical Information and Computer Sciences. (1996) 36, no. 5, 1001–1003, https://doi.org/10.1021/ci9603689, 2-s2.0-0041822789.
10.1021/ci9603689
CAS Web of Science® Google Scholar
3 Brückler F. M., Došlić T., Graovac A., and Gutman I., On a class of distance-based molecular structure descriptors, Chemical Physics Letters. (2011) 503, no. 4-6, 336–338, https://doi.org/10.1016/j.cplett.2011.01.033, 2-s2.0-79952899557.
10.1016/j.cplett.2011.01.033
CAS Web of Science® Google Scholar
4 Deng H., Yang J., and Xia F., A general modeling of some vertex-degree based topological indices in benzenoid systems and phenylenes,”, Computers and Mathematics with Applications. (2011) 61, no. 10, 3017–3023, https://doi.org/10.1016/j.camwa.2011.03.089, 2-s2.0-79955843627.
10.1016/j.camwa.2011.03.089
Web of Science® Google Scholar
5 Zhang H. and Zhang F., The Clar covering polynomial of hexagonal systems I, Discrete Applied Mathematics. (1996) 69, no. 1-2, 147–167, https://doi.org/10.1016/0166-218x(95)00081-2, 2-s2.0-0012312027.
10.1016/0166-218X(95)00081-2
Web of Science® Google Scholar
6 Gutman I., Some properties of the Wiener polynomial, Graph Theory Notes New York. (1993) 125, 13–18.
Google Scholar
7 Deutsch E. and Klavžar S., M-polynomial and degree-based topological indices, 2014, https://arxiv.org/abs/1407.1592.
Google Scholar
8 Munir M., Nazeer W., Rafique S., and Kang S. M., M-polynomial and related topological indices of nanostar dendrimers, Symmetry. (2016) 8, no. 9, https://doi.org/10.3390/sym8090097, 2-s2.0-84990062914.
10.3390/sym8090097
Web of Science® Google Scholar
9 Munir M., Nazeer W., Rafique S., Nizami A. R., and Kang S. M., M-polynomial and degree-based topological indices of titania nanotubes, Symmetry. (2016) 8, no. 11, https://doi.org/10.3390/sym8110117, 2-s2.0-84994201959.
10.3390/sym8110117
Web of Science® Google Scholar
10 Kwun Y., Munir M., Nazeer W., Rafique S., and Kang S. M., M-polynomial and degree-based topological indices of V-phenylenic nanotubes and nanotori, Scientific Reports. (2017) 7, no. 1, https://doi.org/10.1038/s41598-017-08309-y, 2-s2.0-85027853177.
10.1038/s41598-017-08309-y
PubMed Web of Science® Google Scholar
11 Munir M., Nazeer W., Rafique S., Nizami A. R., and Kang S. M., Some computational aspects of triangular boron nanotubes, Symmetry. (2016) 9, no. 1, https://doi.org/10.3390/sym9010006, 2-s2.0-85011664704.
10.3390/sym9010006
Web of Science® Google Scholar
12 Munir M., Nazeer W., Rafique S., and Kang S. M., M-polynomial and degree-based topological indices of polyhex nanotubes, Symmetry. (2016) 8, no. 12, https://doi.org/10.3390/sym8120149, 2-s2.0-85004045153.
10.3390/sym8120149
Web of Science® Google Scholar
13 Ali A., Nazeer W., Munir M., and Kang S. M., M-Polynomials and topological indices of zigzag and rhombic benzenoid systems, Open Chemistry. (2018) 16, no. 1, 73–78, https://doi.org/10.1515/chem-2018-0010, 2-s2.0-85043322362.
10.1515/chem-2018-0010
Web of Science® Google Scholar
14 Wiener H., Structural determination of paraffin boiling points, Journal of the American Chemical Society. (1947) 69, no. 1, 17–20, https://doi.org/10.1021/ja01193a005, 2-s2.0-8544254107.
10.1021/ja01193a005
CAS PubMed Web of Science® Google Scholar
15 Dobrynin A. A., Entringer R., and Gutman I., Wiener index of trees: theory and applications, Acta Applicandae Mathematicae. (2001) 66, no. 3, 211–249, https://doi.org/10.1023/a:1010767517079, 2-s2.0-0035329265.
10.1023/A:1010767517079
Web of Science® Google Scholar
16 Gutman I. and Polansky O. E., Mathematical concepts in organic chemistry, 2012, Springer Science and Business Media, Berlin, Germany.
Google Scholar
17 Randić M., On characterization of molecular attributes, Acta Chimica Slovenica. (1998) 45.
Web of Science® Google Scholar
18 Bollobás B. and Erdös P., Graphs of extremal weights, Ars Combinatoria. (1998) 50, 225–233.
Web of Science® Google Scholar
19 Amić D., Bešlo D., Lučić B., Nikolić S., and Trinajstić N., The vertex-connectivity index revisited, Journal of Chemical Information and Computer Sciences. (1998) 38, no. 5, 819–822, https://doi.org/10.1021/ci980039b, 2-s2.0-0000709092.
10.1021/ci980039b
CAS Web of Science® Google Scholar
20 Hu Y., Li X., Shi Y., Xu T., and Gutman I., On molecular graphs with smallest and greatest zeroth-order general Randic index, MATCH Communications in Mathematical and in Computer Chemistry. (2005) 54, no. 2, 425–434.
Web of Science® Google Scholar
21 Caporossi G., Gutman I., Hansen P., and Pavlović L., Graphs with maximum connectivity index, Computational Biology and Chemistry. (2003) 27, no. 1, 85–90, https://doi.org/10.1016/s0097-8485(02)00016-5, 2-s2.0-0345702209.
10.1016/S0097-8485(02)00016-5
CAS Web of Science® Google Scholar
22 Li X. and Gutman I., Mathematical chemistry monographs no. 1, Kragujevac. (2006) 330.
Google Scholar
23 Kier L., Molecular Connectivity in Chemistry and Drug Research, 2012, 14, Elsevier, New York, NY, USA.
Google Scholar
24 Kier L. B. and Hall L. H., Molecular Connectivity in Structure-Activity Analysis: Research Studies, 1986, Chemometrics Research Studies Press, 1st edition.
Google Scholar
25 Gutman I. and Furtula B., Recent Results in the Theory of Randić Index, 2008, University of Kragujevac and Faculty of Science Kragujevac, Kragujevac, Serbia.
Google Scholar
26 Nikolić S., Kovačević G., Miličević A., and Trinajstić N., The Zagreb indices 30 years after, Croatica Chemica Acta. (2003) 76, no. 2, 113–124.
CAS Web of Science® Google Scholar
27 Gutman I. and Das K. C., The first Zagreb index 30 years after, MATCH Communications in Mathematical and in Computer Chemistry. (2004) 50, no. 1, 83–92.
CAS Google Scholar
28 Das K. C. and Gutman I., Some properties of the second Zagreb index, MATCH Communications in Mathematical and in Computer Chemistry. (2004) 52, no. 1, 3–1.
Google Scholar
29 Trinajstić N., Nikolić S., Miličević A., and Gutman I., About the Zagreb Indices, Kemija u Industriji: Časopis Kemičara i Kemijskih Inženjera Hrvatske. (2010) 59, no. 12, 577–589.
CAS Google Scholar
30 Vukičević D. and Graovac A., Valence connectivity versus Randić, Zagreb and modified Zagreb index: a linear algorithm to check discriminative properties of indices in acyclic molecular graphs, Croatica Chemica Acta. (2004) 77, no. 3, 501–508.
CAS Web of Science® Google Scholar

Citing Literature

All articles

M-Polynomials and Degree-Based Topological Indices of Triangular, Hourglass, and Jagged-Rectangle Benzenoid Systems

Abstract

1. Introduction

2. Basic Definitions and Literature Review

3. Computational Results

4. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

M-Polynomials and Degree-Based Topological Indices of Triangular, Hourglass, and Jagged-Rectangle Benzenoid Systems

Abstract

1. Introduction

2. Basic Definitions and Literature Review

3. Computational Results

4. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information