For the future information confrontation, a single jamming mode is not effective due to the complex electromagnetic environment. Selecting the appropriate jamming decision to coordinately allocate the jamming resources is the development direction of the electronic countermeasures. Most of the existing studies about jamming decision only pay attention to the jamming benefits, while ignoring the jamming cost. In addition, the conventional artificial bee colony algorithm takes too many iterations, and the improved ant colony (IAC) algorithm is easy to fall into the local optimal solution. Against the issue, this paper introduces the concept of jamming cost in the cognitive collaborative jamming decision model and refines it as a multiobjective one. Furthermore, this paper proposes a tabu search-artificial bee colony (TSABC) algorithm to cognitive cooperative-jamming decision. It introduces the tabu list into the artificial bee colony (ABC) algorithm and stores the solution that has not been updated after a certain number of searches into the tabu list to avoid meeting them when generating a new solution, so that this algorithm reduces the unnecessary iterative process, and it is not easy to fall into a local optimum. Simulation results show that the search ability and probability of finding the optimal solution of the new algorithm are better than the other two. It has better robustness, which is better in the “one-to-many” jamming mode.

1. Introduction

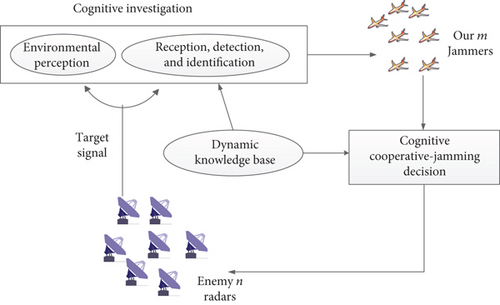
With the advent of net-defender technology, information confrontation has played a more and more important role in the modern war, and multiattackers in various patterns have been the main way as electronic attack. The conventional jamming resource allocation algorithms based on point-to-point allocation are not suitable for modern war due to its low efficiency. Cognitive cooperative jamming will become a trend in the information confrontation due to the ability of cognitive technology for autonomous environment perception and real-time optimization of operating parameters [1, 2]. Cognitive confrontation is a closed-loop learning processing system based on the dynamic knowledge base of perception-recognition decision-making action-perception, and it is used to improve the combat effectiveness of electronic equipment under a complex electromagnetic environment [3]. Decision-making plays a vital role in this closed-loop system, directly affecting combat effectiveness and benefits [4–6].

One major goal of decision-making is to improve the jamming benefit, which is mainly measured by power, frequency, jamming space, and jamming patterns in the existing research [7–11]. These studies, however, which cannot reflect the real battlefield situation, only considered how to maximize the jamming benefit from the attacker and ignore the jamming cost. Literature [12] takes the jamming cost in to account, but it is rather vague. In order to be closer to the actual application scenario, this paper takes the jamming benefit and jamming cost into account together and selects the detection probability as the attacker cost to measure the attacker effect with power, frequency, jamming space, and jamming patterns.

Decision-making is a nonlinear integer combinatorial optimization problem [13, 14]. At present, intelligent algorithms such as genetic algorithms (GA), improved ant colony (IAC) algorithms, and particle swarm optimization (PSO) are widely used to solve this problem. Literature [15] used a genetic algorithm to solve multi-UAV (unmanned aerial vehicle) mission planning problems. Literature [16] proposed a quantum genetic algorithm that uses a qubit to encode communication parameters. It used quantum rotation gates to update the population and assign nonlinear characteristics to the algorithm. However, this algorithm is high in complexity and slow in convergence. Literature [17] introduced the ant colony algorithm to the intelligent decision problem and improved the speed of convergence. Literature [18] proposed an IAC algorithm to optimize the allocation of multitarget defender jamming resources and accelerate the speed of searching optimization. Literature [19] uses particle swarm optimization for decision-making. However, most intelligent algorithms need many complicate parameters, and there still is some room for improvement to convergence speed. To this issue, literature [20] applied the artificial bee colony algorithm to make antijamming communication decisions, which reduces the number of parameters and intensified convergence. However, the conventional ABC algorithm is easy to fall into the local maximum with poor robustness. This paper combines the ABC algorithm with the tabu search algorithm and proposes a new rule for searching new solutions. The optimization probability of the algorithm is improved while ensuring fewer parameters and fast convergence.

2. The Model of Multiobjective Cognitive Collaborative Jamming Decision

Suppose there are m attackers to jam n defenders, shown in Figure 1. The matrix X used to represent the jamming decision scheme can be achieved by the artificial intelligence algorithm, where x_ij = 1 means the attacker is assigned to jam the defender; otherwise, x_ij = 0. Different from the previous research, we propose the concept of jamming cost and convert the traditional model into the multiobjective collaborative jamming decision-making model.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Cognitive confrontation scene description.

2.1. Jamming Benefit and Jamming Cost

In this paper, the jamming benefit is measured by four elements (power suppression benefit, frequency alignment benefit, jamming coverage space benefit, and jamming pattern benefit), which can be represented by vector Q = [q_1ij, q_2ij, q_3ij, q_4ij].

(1) Power Suppression Benefit. Firstly, we apply the ratio of jamming and signal (JSR) to describe the power suppression benefit which represents the suppressing effect to defender R_j(j = 1, 2, …, n) from attacker u_i(i = 1, 2, …, m). The power suppression benefit function can be expressed as q_1ij. Only when the ratio of the power of the received interference power and the power of the echo signal is greater than the minimum JSR is it deemed that the jamming of the attacker is effective. The power of the attacker signal and the effective echo signal power received by the defender R_j are shown in

(1)

where P_s and P_j separately represent the transmission power of the defender and attacker, G_t is the defender main lobe gain, G_A is the gain of the attacker, σ is the scattering area of the self-defense aircraft, A is the equivalent receiving area of the defender antenna, and R is the distance between defender and attacker.

K_j denotes the minimum ratio of jamming and signal, which indicates defender R_j required for normal work. Therefore, we can derive the decision-making criterions. After normalization, q_1ij can be expressed as

(2)

(2) Frequency Alignment Benefit. Then, the frequency alignment benefit function q_2ij is addressed to report the jamming suppression effect of attacker u_i(i = 1, 2, …, m) on defender R_j(j = 1, 2, …, n). The attacker u_i can only jam the defender R_j if the attacker’s jamming frequency overlaps with the defender’s operating frequency. (f_i1, f_i2) denotes the operating frequency of the attacker, and (f_j1, f_j2) denotes the operating frequency of the defender. Consequently, q_2ij can be expressed as

(3)

(3) Jamming Coverage Space Benefit. After that, we introduce the jamming coverage space benefit function q_3ij to represent the jamming coverage space benefit which represents the jamming suppression effect on the coverage space of attacker u_i(i = 1, 2, …, m) on defender R_j(j = 1, 2, …, n). The maximum jamming energy intensity EN of the attacker and its corresponding effective jamming radius satisfy the relation in

(4)

where ε is the lowest energy intensity threshold that affects the defender. If the distance between the attacker and the target exceeds the jamming radius, the jamming is invalid. Otherwise, q_3ij is inversely proportional to d². q_3ij can be expressed as

(5)

(4) Jamming Pattern Benefit. Finally, the jamming pattern benefit function q_4ij is adopted to describe the jamming pattern benefit which represents the jamming suppression effect of attacker u_i(i = 1, 2, …, m) on defender R_j(j = 1, 2, …, n). Suppose that each defender (possibly of different system types) have valid m types of jamming patterns and have been sorted according to the advantages and disadvantages of theoretical jamming effects. If attacker u_i contains the jamming patterns which are effective for defender R_j, then the higher the jamming pattern is in ranking, the greater the value of the jamming pattern benefit function is. Otherwise, q_4ij = 0. q_4ij can be expressed as

(6)

The weight vector of the four indicators is calculated as ε = [ε₁, ε₂, ε₃, ε₄] using the analytic hierarchy process. Hence, the jamming benefit can be expressed as

(7)

All of the above indicators are for maximizing the m jamming benefits and ignoring the jamming cost. According to the jamming effect factors mentioned above, this paper will form a multiobjective cognitive collaborative jamming decision model. Thus, the purpose is to maximize the jamming benefits while minimizing the probability that the attacker is discovered.

The jamming cost that we mainly consider in this paper is the probability that the attacker was detected by the defender. The probability of the attacker being discovered by the defender should be minimized as much as possible to ensure the jamming benefit. The probability expression that the defender discovers the attacker from t₁ to t₂ is defined as

(8)

where r(t) = (θ_0.5/φ)f_re^−y0S_N(t) indicates the instantaneous probability density of the attacker found by the defender.

Hence, the jamming cost can be expressed as

(9)

2.2. Objective Functions and Constraints

In the multiobjective cognitive cooperative jamming decision task, we intend to obtain the maximum jamming benefit, as well as the minimum jamming cost, where minimizing f_cost can also be considered as maximizing (−f_cost), just as

(10)

Obtaining the greatest jamming benefits and paying the smallest jamming costs are equally important in multiobjective cognitive collaborative jamming decision tasks. Therefore, the fitness function can be expressed as

(11)

where x_ij is the decision variable, x_ij = 0 means attacker u_i does not jam defender R_j, and x_ij = 1 means attacker u_i jams defender R_j. Decision matrix X is constituted by x_ij. ω_j means the importance of defender R_j.

We obtain different decision-making schemes corresponding to different decision matrixes X through simulation. Finally, the decision matrix X that maximizes the objective function is selected as the final decision-making scheme.

Since the number of defenders that can be jammed at one time is limited, as well as the total number of attackers and defenders, the objective function should be restricted as

(12)

where (1) means one defender should be jammed by one attacker at list and (2) means one attacker can jam at most α_i defenders at one time to ensure the jamming effect on the defender network.

3. Tabu Search-Bee Colony Algorithm

In recent years, intelligent algorithms, such as genetic algorithm (GA) [15, 16], improved ant colony (IAC) algorithm [17, 18], and particle swarm optimization (PSO) [19], are widely used to solve the jamming decision-making problem. Among them, the IAC algorithm is the most widely used because it can greatly improve the optimization speed and reduce the running time to achieve the best decision-making. However, the parameters in the IAC algorithm depend heavily on manual selection which lack objectivity and credibility. Aimed to this issue, we propose the artificial bee colony (ABC) algorithm to solve the jamming decision-making problem because the ABC algorithm needs only fewer parameters and owns higher objectivity [21]. The using steps of making jamming decisions using the ABC algorithm are as follows:

(1)
Initialize bee populations. There are three population parameters:
- (a)
  The total number of bees: N (bees produce nectar as jamming decision matrix)
- (b)
  Maximum iterations: maxCycle
- (c)
  The single largest number of searching for each food source: limit
Because all bees are scouts with no prior information, the algorithm randomly generates N jamming decision matrix X overall situation corresponding to N food sources. The jamming effect of every decision scheme is its profitability f_fit.
At this time, all bees are scouts with no prior information. The algorithm randomly generates N jamming decision matrix X overall situation corresponding to N food sources. The jamming effect of every decision scheme is its profitability f_fit.
(13)
(2)
Divide all bees into employed foragers and onlookers according to the jamming effect of every decision matrix X in step (1). Among them, the N/2 bees with a higher f_fit value are employed foragers, and the other N/2 bees are onlookers. Onlookers select employed foragers to follow according to the probability P of the f_fit value of the former N/2 decision matrix.

(14)

(3)
Every employed forager searches for a new decision matrix around the old one and calculates its profitability. If it is greater than the old, then replace it according to the greedy criterion. The search formula is in
(15)
where
(16)
rand 1, and rand 2 are unequal random integers between [1, n].
(4)
Onlookers change the distribution mode of the attacker corresponding to employed foragers to get a new decision matrix after selecting them to follow, similar as in step (3).
(5)
If employed foragers and onlookers search more than limited times for a decision matrix and find no decision scheme with better profitability, then give up this decision matrix, turn the role of the bee into scouts, and generate a new decision matrix that satisfies the constraints.
(6)
Record the decision matrix of the maximum jamming effect and turn to step (2), until the maximum iteration number maxCycle is satisfied. The decision matrix which makes the profitability maximal is the decision scheme with the best jamming effect.

The jamming decision based on the ABC algorithm can not only ensure the optimization speed of the algorithm but also solve the problem that the IAC algorithm requires a large number of early parameters depending on manual selection. It is an effective improvement of the IAC algorithm.

However, there are some major problems faced by the ABC algorithm. When the optimization domain is large or in a flat area, the new solution sometimes overlaps with the already searched solution and further results in unnecessary repeated searches. As a result, the global search ability of the algorithm is reduced, and it is sometimes easy to fall into the local maximum. Due to the limitation of the taboo table in the tabu search algorithm, the probability of falling into the local optimal solution can be greatly reduced [22–24]. In order to avoid the algorithm falling into the local optimum and increase the probability of getting the optimal solution, we introduce the tabu search algorithm to the jamming decision-making field and introduce the new tabu search-artificial bee colony (TSABC) algorithm to the problem of jamming decision-making.

It is the first time that the TSABC algorithm is introduced to the problem of jamming decision-making. The elements in the taboo table are the decision matrices corresponding to different decision schemes, and the Euclidean distance cannot be calculated. Due to this, the conventional method of using the Euclidean distance between elements to represent the threshold has lost its significance in jamming decisions. We propose a new method for calculating the threshold value and a novel strategy to generate a new solution. The specific improvements are as follows.

If employed foragers and onlookers search more than limited times for a decision matrix and find no decision scheme with better profitability, then add the solution to the taboo list, convert the bee character into the scouts, and randomly generate a new solution that satisfies the constraint conditions. The element number of the taboo list is limited. In order to expand the search space, we consider the solution whose gap with the elements in the taboo list is less than the threshold value which is also in the taboo range. Since the elements in the taboo table are decision matrices corresponding to different decision schemes, the Euclidean distance cannot be calculated. Considering that the purpose of the decision-making is to obtain the maximum jamming benefit in the jamming decision problem, we propose the minimum value of the difference between the fitness of every two solutions in the taboo list as a threshold. It can be calculated as

(17)

where i, j = 1, 2, …, n; n is the number of elements in the taboo list.

If the difference of the fitness between the new solution and the solution in the taboo list is smaller than the threshold, we think that this new solution is in the range of the taboo list, and the new solution will be repeatedly generated until it is out of the taboo list.

The application of tabu search in the ABC algorithm in the jamming decision is shown in Algorithm 1.

Algorithm 1: The application of tabu search in ABC algorithm in jamming decision.

1: send employed foragers
2: calculate the jamming effect of the current decision matrices
3: if optimal solution updated after limit times
then
4: keep the updated solution
5: else
6: update tabu list
7: search for new solution through the Tabu Search Algorithm
8: while distance ≤ thresholdvalue do
9: keep the solution as the new solution
10: end while
11: end if
12: send onlookers
13: repeat

4. Simulation Analysis

To verify the robustness and the ability of the improved tabu search-artificial bee colony algorithm for multiobjective collaborative jamming decision-making, we set two different jamming modes named “one-to-one” and “one-to-many” for simulation verification using the above objective function.

“One-to-one” jamming mode: suppose that the number of attackers is m = 10, and the number of defenders is n = 10. Each attacker can jam one defender. Calculate the weighted sum of the jamming benefit and jamming cost of attacker u_i(i = 1, 2, …, m) to defender R_j(j = 1, 2, …, n); the jamming effect matrixes are then shown in (18) and (19).

“One-to-many” jamming mode: suppose that the number of attackers is m = 5, and the number of defenders is n = 8. Each attacker can jam multiple defenders. Calculate the weighted sum of the jamming benefit and jamming cost of attacker u_i(i = 1, 2, …, m) to defender R_j(j = 1, 2, …, n); the jamming effect matrixes are then shown in (20) and (21).

(18)

(19)

(20)

(21)

We design two sets of experiments to verify the optimization speed and optimization probability of the tabu search artificial bee colony algorithm. In the two experiments, NP = 40, limit = 100, and maxCycle = 100.

Experiment 1: the IAC algorithm, ABC algorithm, and TSABC algorithm are used to simulate the jamming decision in the “one-to-one” and “one-to-many” modes, which verifies that the optimization ability of the TSABC algorithm is better than that of the IAC algorithm and ABC algorithm. Then, the comparison of the simulation results of the three algorithms is exhibited in Figures 2 and 3.

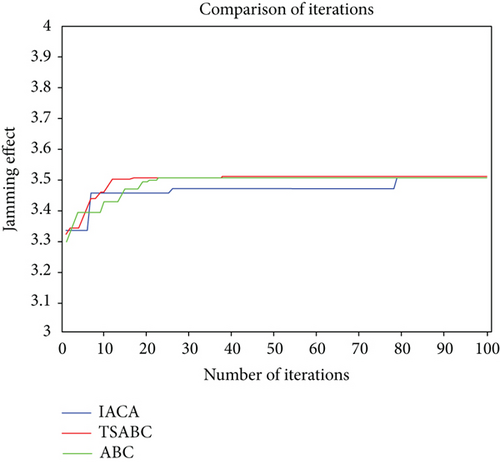
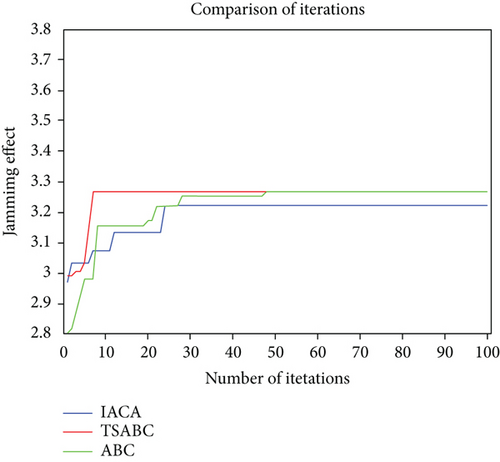
It can be seen from Figures 2 and 3 that the IAC algorithm requires more iterations in the “one-to-one” mode. Although it is reduced in the “one-to-many” mode, the search ability is reduced too. The TSABC algorithm need not repeat the search process in the ABC algorithm because of the tabu list, which helps reach the optimal value with fewer iterations. The above results show that the optimization ability of the TSABC algorithm is better.

Next, we can obtain the respective optimal decision matrixes X in two modes through the simulation. The corresponding jamming decision schemes are shown in Tables 1 and 2.

Table 1. Jamming decision scheme in the “one-to-one” mode.

Rader number	1	2	3	4	5	6	7	8	9	10
Attacker number	4	9	1	2	7	6	3	10	8	5

Table 2. Jamming decision scheme in the “one-to-many” mode.

Defender number	1	2	3	4	5	6	7	8
Attacker number	1	4	3	5	2	1	4	2

Tables 1 and 2 show the jamming matching schemes. It can be seen from the tables that each defender has a corresponding attacker to jam. The number of defenders jammed per attacker is 1 in the one-to-one mode and does not exceed 2 in the “one-to-many” mode, which meets the constraint set.

In order to avoid the fortuity of a single optimization, we introduce Monte Carlo simulation to perform the decision-making process under the two modes 100 times, respectively, and record the average number of iterations after each operation. The optimization ability of three algorithms in two modes is shown in Figures 4 and 5.

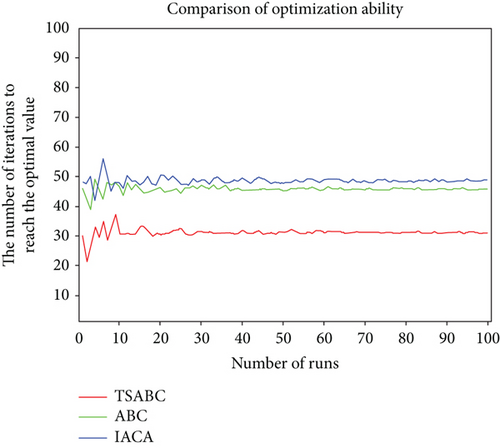
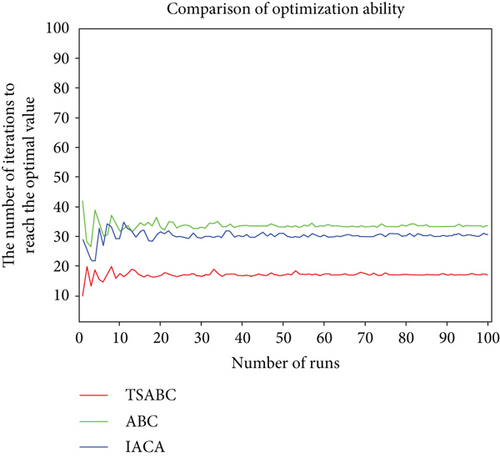
It is obviously seen in Figures 4 and 5 that the number of iterations fluctuates around a fixed value. The number of iterations of the TSABC algorithm is less than the other two, which further indicates that the TSABC algorithm has a stronger optimization ability.

Experiment 2: Monte Carlo simulation is ulteriorly used to perform the decision-making process in the two modes 100 times, respectively, and record the average optimized value and the optimization probability of each algorithm after each decision. The average optimized values in two modes are shown in Figures 6 and 7.

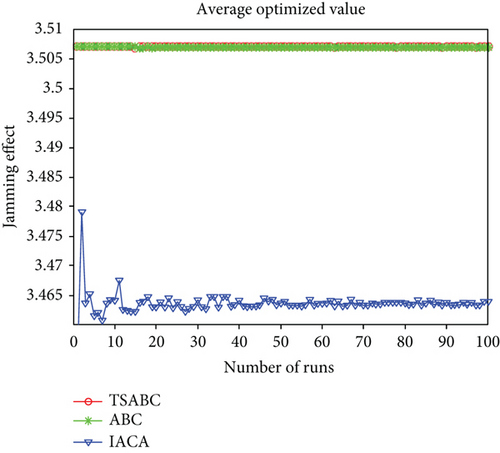
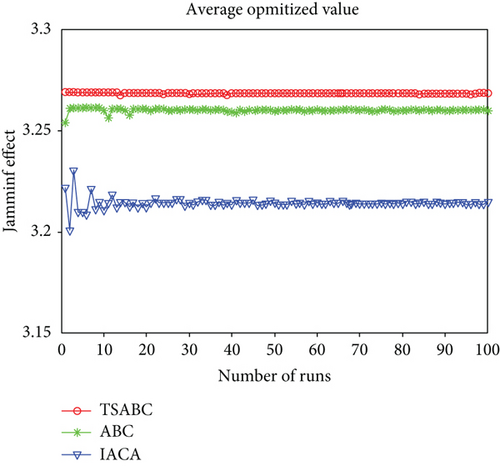
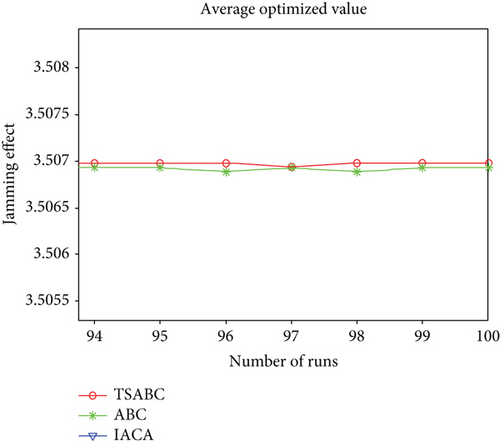
The difference of the average optimized value in the one-to-one mode is small between the TSABC algorithm and ABC algorithm, and partial enlargement is shown in Figure 8.

It can be seen from Figures 5 and 6 that the optimization probability of the TSABC algorithm is better than that of the IACA algorithm and ABC algorithm. This phenomenon indicates that compared with the other two algorithms, the TSABC algorithm can jump out of the local optimum more effectively to find the optimal solution and improve the search probability. Thus, the robustness of the proposed algorithm is verified.

To further demonstrate the superiority of the proposed algorithm, the performance comparison of the three algorithms is shown in Table 3.

Table 3. The performance comparison of three algorithms.

	IACA	ABC	TSABC	IACA	ABC	TSABC
	One-to-one			One-to-many
Average optimized value	3.46498	3.50676	3.50688	3.22874	3.26611	3.26794
The average number of iterations to obtain the optimal value	50	48	31	31	34	19
Optimization probability	0.72	0.94	0.97	0.65	0.84	0.95

In Table 3, we take the weighted sum of the jamming benefit and jamming cost as the objective function of the multiobjective cognitive cooperative jamming decision, which ensures that the simulation solution can pay a very small jamming cost while obtaining great jamming benefits. It can be seen from Table 3 that the average number of iterations of the TSABC algorithm is less than the other two algorithms. Most importantly, the probability of the TSABC algorithm getting the optimal solution is far greater than the other two, which means its optimization probability is greater. Apparently, the optimization ability and the optimization probability of the proposed algorithm are both enhanced. In addition, the TSABC algorithm has better robustness. The advantages are more obvious in one to many modes.

5. Conclusion

In the modern war, information confrontation plays an increasingly important role where cognitive cooperative jamming will become a trend due to the ability of cognitive technology for autonomous environment perception and real-time optimization of operating parameters. Jamming decision-making plays a vital role in the closed loop of cognitive confrontation. Aiming at the problem of maximizing the jamming benefit as the decision target in the existing jamming decision model, in this paper, two objective functions as jamming benefit and jamming cost are proposed to measure the jamming effects, and the calculation methods of specific indicators and their revenue values are given, respectively. The increase in the objective function transformed the collaborative jamming decision-making problem into a multiobjective optimization problem and refined the model of multiobjective cognitive collaborative jamming decision. In the aspect of the decision algorithm, aiming at the deficiency of the improved ant colony algorithm in the jamming decision-making problem, this paper introduces the tabu search artificial bee colony algorithm to the jamming decision-making problem, and the superiority of the algorithm is proved by simulation. The simulation results show that the improved TSABC algorithm is greater than comparison methods both in the optimization ability and the optimization probability and has better robustness and higher application value in cognitive confrontation.

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Acknowledgments

This paper is funded by the National Natural Science Foundation of China (Grant No. 61701134), the National Key Research and Development Program of China (Grant No. 2016YFF0102806), the Natural Science Foundation of Heilongjiang Province, China (Grant No. F2017004), and the Fundamental Research Funds for the Central Universities of China (No. HEUCFM180802).

Open Research

Data Availability

The research data and software code used to support the findings of this study are available from the corresponding author upon request.

References

1 Zhang K., Zhang X., and Jin J., A preliminary study of cognitive electronic warfare, Space Electronic Warfare. (2013) 29, no. 1, 53–56.
Google Scholar
2 Sabatini R., Moore T., and Hill C., Avionics-based GNSS integrity augmentation for unmanned aerial systems sense-and-avoid, Proceedings of the 27th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2014), September 2014, Tampa, FL, USA, 3600–3617.
Google Scholar
3 Fan Z., Zhu G., and Hu Y., Overview of cognitive electronic warfare, Electronic information countermeasure Technology. (2015) 30, no. 1, 33–38.
Google Scholar
4 Lu X., Xu D., Xiao L., Wang L., and Zhuang W., Anti-jamming communication game for UAV-aided VANETs, GLOBECOM 2017 - 2017 IEEE Global Communications Conference, December 2017, Singapore, 1–6, https://doi.org/10.1109/glocom.2017.8253987, 2-s2.0-85046481766.
10.1109/glocom.2017.8253987
Google Scholar
5 Sun Q., Tian Y., and Diao M., Cooperative localization algorithm based on hybrid topology architecture for multiple mobile robot system, IEEE Internet of Things Journal. (2018) https://doi.org/10.1109/JIOT.2018.2812179, 2-s2.0-85042867766.
10.1109/JIOT.2018.2812179
PubMed Web of Science® Google Scholar
6 Niu C., Li Y., Hu R., and Ye F., Fast and efficient radio resource allocation in dynamic ultra-dense heterogeneous networks, IEEE Access. (2017) 5, 1911–1924, https://doi.org/10.1109/access.2017.2653798, 2-s2.0-85015799948.
10.1109/access.2017.2653798
Web of Science® Google Scholar
7 Xue Y., Zhuang Y., and Zhang Y., Multi-UCAV cooperative jamming air combat decision based on heuristic adaptive discrete differential evolution algorithm, Journal of Astronautics. (2013) 34, no. 2, 343–351.
Google Scholar
8 Li M., Research on multi-ECAV cooperative jamming resource optimization allocation problem, [M.S. thesis], 2013, National University of Defense Technology.
Google Scholar
9 Ming Z., Lingling Z., Xiaohong S., Peijun M., and Yanhang Z., Improved discrete mapping differential evolution for multi-unmanned aerial vehicles cooperative multi-targets assignment under unified model, International Journal of Machine Learning and Cybernetics. (2017) 8, no. 3, 765–780, https://doi.org/10.1007/s13042-015-0364-3, 2-s2.0-85019222213.
10.1007/s13042-015-0364-3
Web of Science® Google Scholar
10 Jiang H., Zhang Y., and Xu H., Optimal allocation of cooperative jamming resource based on hybrid quantum-behaved particle swarm optimisation and genetic algorithm, IET Radar, Sonar & Navigation. (2017) 11, no. 1, 185–192, https://doi.org/10.1049/iet-rsn.2016.0119, 2-s2.0-85017408679.
10.1049/iet-rsn.2016.0119
Web of Science® Google Scholar
11 Gupta P., Mehlawat M. K., and Mittal G., A fuzzy approach to multicriteria assignment problem using exponential membership functions, International Journal of Machine Learning and Cybernetics. (2013) 4, no. 6, 647–657, https://doi.org/10.1007/s13042-012-0122-8, 2-s2.0-84885929647.
10.1007/s13042-012-0122-8
Web of Science® Google Scholar
12 Lou Y., Zhuang Y., and Gu J., Task scheduling method based on IMOABC in collaborative jamming environment, Computer Technology and Development. (2017) 27, no. 11, 46–51.
Google Scholar
13 Huang S., Zhu L., and Liu S., Based on virtual beamforming cooperative jamming with Stackelberg game for physical layer security in the heterogeneous wireless network, EURASIP Journal on Wireless Communications and Networking. (2018) 2018, no. 1, https://doi.org/10.1186/s13638-018-1081-x, 2-s2.0-85044757853.
10.1186/s13638-018-1081-x
Google Scholar
14 Gao Q., Zou H., Zhang X., and Zhou L., New relaxation algorithm for three-dimensional assignment problem, IEEE Conference Anthology, January 2013, China, 1–4, https://doi.org/10.1109/anthology.2013.6784972, 2-s2.0-84899422729.
10.1109/anthology.2013.6784972
Google Scholar
15 Ramirez-Atencia C., Bello-Orgaz G., R-Moreno M. D., and Camacho D., Solving complex multi-UAV mission planning problems using multi-objective genetic algorithms, Soft Computing. (2017) 21, no. 17, 4883–4900, https://doi.org/10.1007/s00500-016-2376-7, 2-s2.0-84989859000.
10.1007/s00500-016-2376-7
Web of Science® Google Scholar
16 Lu T.-C., Yu G.-R., and Juang J.-C., Quantum-based algorithm for optimizing artificial neural networks, IEEE Transactions on Neural Networks and Learning Systems. (2013) 24, no. 8, 1266–1278, https://doi.org/10.1109/TNNLS.2013.2249089, 2-s2.0-84880899852, 24808566.
10.1109/TNNLS.2013.2249089
PubMed Web of Science® Google Scholar
17 Zhao N., Li S., and Wu Z., Cognitive radio engine design based on ant colony optimization, Wireless Personal Communications. (2012) 65, no. 1, 15–24, https://doi.org/10.1007/s11277-011-0225-7, 2-s2.0-84861726962.
10.1007/s11277-011-0225-7
Web of Science® Google Scholar
18 He F., Qi S., Xie G., and Wu T., Improved ant colony algorithm for optimal allocation of jamming resources of multiple targets radar, Fire Control and Command Control. (2014) 39, no. 5, 111–114.
CAS Google Scholar
19 Zhang Y.-Z., Li J.-W., Hu B., and Zhang J.-D., An improved PSO algorithm for solving multi-UAV cooperative reconnaissance task decision-making problem, 2016 IEEE International Conference on Aircraft Utility Systems (AUS), October 2016, Beijing, China, 434–437, https://doi.org/10.1109/aus.2016.7748089, 2-s2.0-85006826308.
10.1109/aus.2016.7748089
Google Scholar
20 Hui X., Chen J., and Niu Y., An initial population optimization-based particle swarm algorithm for anti-jamming communication decision engines, 11th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM 2015), 2016, Shanghai, China, https://doi.org/10.1049/cp.2015.0696.
10.1049/cp.2015.0696
Google Scholar
21 Ye F., Che F., and Tian H., Cognitive cooperative-jamming decision method based on bee colony algorithm, 2017, 2017 Progress in Electromagnetics Research Symposium - Fall (PIERS - FALL), November 2017, Singapore, 531–537, https://doi.org/10.1109/piers-fall.2017.8293195, 2-s2.0-85045337966.
10.1109/piers-fall.2017.8293195
Google Scholar
22 Paprocka I., Gwiazda A., and Baczkowicz M., Robustness of schedules obtained using the Tabu search algorithm based on the average slack method, International Conference on European Transnational Education, 2016, Springer International Publishing, 426–434.
Google Scholar
23 Zheng W., Qiaoqiao L., Hongtao T., and Jianxun L., Multiple task planning based on TS algorithm for multiple heterogeneous unmanned aerial vehicles, Proceedings of 2014 IEEE Chinese Guidance, Navigation and Control Conference, August 2014, Yantai, China, 630–635.
Google Scholar
24 Li F., Feng J., Liu J., and Lu S., Defect profile reconstruction from MFL signals based on a specially-designed genetic taboo search algorithm, Insight - Non-Destructive Testing and Condition Monitoring. (2016) 58, no. 7, 380–387, https://doi.org/10.1784/insi.2016.58.7.380, 2-s2.0-84978906092.
10.1784/insi.2016.58.7.380
Google Scholar

Citing Literature

All articles

Multiobjective Cognitive Cooperative Jamming Decision-Making Method Based on Tabu Search-Artificial Bee Colony Algorithm

Abstract

1. Introduction

2. The Model of Multiobjective Cognitive Collaborative Jamming Decision

2.1. Jamming Benefit and Jamming Cost

2.2. Objective Functions and Constraints

3. Tabu Search-Bee Colony Algorithm

4. Simulation Analysis

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Multiobjective Cognitive Cooperative Jamming Decision-Making Method Based on Tabu Search-Artificial Bee Colony Algorithm

Abstract

1. Introduction

2. The Model of Multiobjective Cognitive Collaborative Jamming Decision

2.1. Jamming Benefit and Jamming Cost

2.2. Objective Functions and Constraints

3. Tabu Search-Bee Colony Algorithm

4. Simulation Analysis

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information