A Selective-Awakening MAC Protocol for Energy-Efficient Data Forwarding in Linear Sensor Networks
Abstract
We introduce the Selective-Awakening MAC (SA-MAC) protocol which is a synchronized duty-cycled protocol with pipelined scheduling for Linear Sensor Networks (LSNs). In the proposed protocol, nodes selectively awake depending on node density and traffic load conditions and on the state of the buffers of the receiving nodes. In order to characterize the performance of the proposed protocol, we present a Discrete-Time Markov Chain-based analysis that is validated through extensive discrete-event simulations. Our results show that SA-MAC significantly outperforms previous proposals in terms of energy consumption, throughput, and packet loss probability. This is particularly true under high node density and high traffic load conditions, which are expected to be common scenarios in the context of IoT applications. We also present an analysis by grade (i.e., the number of hops to the sink, which is located at one end of the LSN) that reveals that LSNs exhibit heterogeneous performance depending on the nodes’ grade. Such results can be used as a design guideline for future LSN implementations.
1. Introduction
Internet of Things (IoT) is a network paradigm that is playing a key role in the development of smart environments where everyday objects are augmented with computational capabilities and Internet connectivity [1, 2], so that they can interact with each other in order to share information about the environment, coordinate actions autonomously, and fulfill other specific purposes such as target tracking, medical supervision of patients, and animal monitoring [3–5].
IoT has been proposed as a core technology for establishing what it is known as Advanced Measurement Infrastructures (AMI) which are responsible for monitoring public distribution networks of water, electricity, or gas [6–8]. With this technology, it is possible to identify leaks along lines or pipelines and optimize the operation of these distribution networks.
IoT applications have also been identified as a mean for fostering smart mobility. In these scenarios, a set of sensors are located along the road infrastructure in order to coordinate urban transport, monitor events that affect mobility, or manage transit through dynamic coordination of traffic lights [9, 10]. The objective is to extend the lifetime of the road infrastructure, improve safety, decrease commuters’ travel time, and diminish air pollution in densely populated cities.
As in the previous examples, when the sensing devices are deployed along linear structures, the resulting wireless sensor network (WSN) is usually denoted as a Linear Sensor Network (LSN) [11]. In particular, when the node density is high, as it is commonly the case when a wide variety of variables are being sensed [3], the LSN is named a thick LSN [12]. As in any WSN, one of the main goals when designing an LSN is to provide high throughput in an energy-efficient way [13], which could be achieved by defining appropriate Medium Access Control (MAC) protocols.
Among the large body of work devoted to designing efficient MAC protocols that improve energy consumption, synchronized duty-cycling protocols [14] have been shown to be particularly effective in the context of MANETs [15], WSNs [16–18], and LSNs [3, 19, 20]. Building on the success of duty-cycling, complementary techniques have been proposed to further improve the performance of LSN; for instance, Tong et al. introduced the PRI-MAC protocol [19] which implements a pipelined scheduling as a complement for a duty-cycled protocol that is based on S-MAC [21].
In pipelined scheduling, nodes are classified according to their grade (distance in hops to the sink node) and nodes with the same grade share the same schedule; namely, they synchronously enter the different modes in the following sequence: one reception slot, one transmission slot, and ξ sleeping slots. Grade schedules are arranged in such a way that packets can be forwarded from one grade to another in a pipelined fashion. This way, a packet can traverse a source-to-sink path in a single cycle if there are no other packets at the queues of the nodes along its path, which is the main advantage of this strategy over other proposals.
- (i)
During a transmission slot, nodes that are candidates to contend for the channel awake with probability p(i), where i is the nodes’ grade. This probability is selected in order to maximize the LSN throughput.
- (ii)
During a reception slot, nodes with saturated buffers do not awake.
As shown in Section 7, the first rule simultaneously reduces node energy consumption and the probability of having a packet collision, without reducing throughput or requiring extra signaling. The second rule also reduces energy consumption without affecting any of the network performance metrics, because it avoids wasting energy to receive a packet that will be dropped. To the best of our knowledge, these strategies, as well as their analysis and evaluation, have not been previously reported in the context of LSN or IoT applications.
In concordance with previous work (e.g., [16, 19, 21]), our proposed protocol is specifically designed to operate in an LSN with a single sink node at one end of the network, and the remaining nodes can both generate new packets and act as relays for other nodes without performing any data processing or aggregation. In addition, data packets are transferred between nodes located in adjacent grades by means of unicast transmissions. A detailed description of the assumptions and operation scenarios is presented in Section 3.
In order to evaluate the performance of SA-MAC, we developed a mathematical model of the nodes’ queue length based on a Discrete-Time Markov Chain (DTMC). From the steady-state probabilities of this DTMC, we developed expressions for the main system performance metrics, namely, energy consumption, throughput, packet loss probability, and source-to-sink delay. This analysis is similar to those presented in [16–19] and is validated through extensive discrete-event simulations.
Our numerical results show that SA-MAC clearly outperforms previous work in terms of energy consumption, packet loss probability, and throughput, at the cost of a moderate increase in source-to-sink delay. This is particularly true under high node density and high traffic load conditions, which are expected to be a possible scenario in the context of IoT applications [1].
Lastly, it is important to mention that our analysis is intended to evaluate not only the general performance of the network, but also the performance at each grade. This detailed analysis reveals that the network performance is not homogeneous and makes it possible to identify those specific grades that may compromise the whole network lifetime and reliability. This is another major contribution of this paper because it provides a guideline for the design of pipelined LSN.
The rest of the paper is organized as follows. In Section 2 we discuss a representative sample of previous work in duty-cycled MAC protocols for multihop WSNs and LSNs. In Section 3 we present a general overview of the proposed protocol. Then, in Section 4 we derive the DTMC that models our system. In Section 5 we present expressions for the network performance metrics. In Section 6 we provide criteria to select the awakening probability. Lastly, we discuss relevant numerical results and present our conclusions in Sections 7 and 8, respectively.
2. Related Work
Synchronized duty-cycled protocols for WSNs have been extensively studied because of their energy efficiency, which is achieved by reducing idle listening and overhearing. In these schemes, nodes synchronously wake up in order to transmit/receive one or several packets during a cycle. One example of this kind of protocol is Sensor MAC (S-MAC), which was proposed by Ye et al. [21]. In S-MAC, a fully connected group of nodes share the same schedule; namely, all the nodes synchronously enter the transmission/reception mode to exchange information and, then, all of them synchronously enter sleeping mode to save energy. One disadvantage of S-MAC is that it substantially increases source-to-sink delay because nodes may wait a complete cycle in order to attempt a transmission; moreover, this disadvantage is accentuated when multiple hops are required because the delay accumulates at each hop.
Yang and Heinzelman [16] provide a model, based on a DTMC, to evaluate the performance of duty-cycled protocols. In their model, the Markov chain states represent the nodes’ queue length; and the chain solution is used to evaluate throughput, delay, and power consumption. This kind of analysis has been utilized in subsequent works (e.g., [17, 18]); however, the analysis in [16] is restricted to one-hop WSNs, whereas more recent works, including [19] and our work, have extended the analysis to study LSNs.
On the other hand, in recent years, multiple works have proposed synchronized duty-cycled protocols for multihop WSNs, including [17, 18, 22–24]. In the following paragraphs, we present a brief overview of each of them.
Guntupalli and Li [17] propose another synchronized duty-cycled protocol for multiple packet transmission per cycle. In this scheme, which is called DW-MAC, multiple packet transmission is enabled by means of competition-based reservations established during a particular time interval, called the data period. The authors present a DTMC-based analysis that characterizes the energy consumption and the lifetime of the network. It must be noticed that although their study includes multiple hops, it is limited to a scenario where there is only one relay between the source node and the sink node. In [18], Guntupalli et al. extended the analysis presented in [17] to incorporate a four-dimensional DTMC; this analysis, however, does not consider multiple hops.
Singh and Chouhan [22] present a protocol called CROP-MAC that optimizes pipelined flows with the help of staggered sleep/wake scheduling, efficient synchronization, and appropriate use of routing layer information. Based on CROP-MAC, Singh et al. [23] developed a protocol that provides multipacket transmission per cycle (JRAM protocol). In this protocol, a node has more than one opportunity to transmit, and the sink is able to receive packets from multiple nodes in the same cycle. JRAM accomplishes this by dividing the network into disjoint sets of nodes, by proposing a new cycle structure, and by reducing the size of periodical synchronization packets. Their results indicate that JRAM works best in scenarios with high-rate events occurrence.
Additionally, Khaliq and Henna [24] present a protocol called HE-PRMAC that uses cross-layer information for the transmission of packets through multiple hops in a single duty cycle. As a result, packet latency is reduced. In order to decrease the overhead when traffic load is high, HE-PRMAC introduces a new message called Ready To Receive (RTR), which is used to transmit how many packets a destination node can receive from a source node.
Even though many of the above-mentioned works analyze multihop WSNs, their protocols were not designed to take advantages of particular topologies. By contrast, in [3, 19, 20] the authors proposed synchronized duty-cycled MAC protocols specifically for LSNs.
Wang et al. [3] introduce a Utility-based Adaptive Duty-Cycle (UADC) algorithm to increase energy efficiency, reduce transmission delay, and improve network lifetime of WSNs with linear topology. The main idea of this algorithm is to select the relay node that maximizes the utility of the system, which is defined as a function of the nodes’ energy consumption.
Tong et al. [19] propose PRI-MAC, a synchronized duty-cycled protocol that incorporates a pipelined scheduling for LSN. The authors evaluated the performance of the network in terms of throughput, node’s radio activity per cycle, and delivered packet latency. Khanh et al. [20] introduce the RP-MAC protocol, which is based on PRI-MAC. In RP-MAC the authors define a new cycle structure and a new state, called overhearing, which eliminates the need of transmitting the Request To Send (RTS) message, hence reducing the end-to-end delay and energy consumption, in comparison with PRI-MAC.
Similar to [19, 20], we also analyze a pipelined scheduling for LSN; however, we introduce a novel MAC protocol, where nodes selectively awake, depending on node density and traffic load in the network.
From this review, we would like to highlight the main contributions of our work: (i) none of previous proposals are designed for dense LSNs, which can be widely applicable in the context of IoT; (ii) unlike previous protocols, our proposed protocol does not aggregate new control messages or node states during a cycle; (iii) even though the performance experienced by a node in an LSN is highly dependent on its distance to the sink, previous grade analyses are limited and fail to provide detailed performance models. In contrast, our model allows the analysis of both the complete LSN and each grade in the system, as it is described in the next sections.
3. Selective-Awakening MAC Protocol
In this section, we provide a general overview of the proposed protocol. We first present a brief description of one of its main components: the pipeline scheduling (Section 3.1). Then, in Section 3.2, we provide the basis of traditional synchronized duty-cycled MAC protocols ([16, 19, 21]). Later, in Section 3.3, we describe the main features of our proposed MAC protocol as well as its advantages over previous work.
3.1. Pipelined Scheduling
As in [19], we assume that the LSN has a unique sink node which is located at one end of the network. The remaining nodes generate packets with information provided by their respective sensors and can act as relays. Nodes are classified according to their grade, namely, their distance in hops to the sink node. Figure 1 illustrates this type of network. The grade of a node is denoted by i, and the total number of grades in the LSN is denoted by I. By definition, the sink node has grade zero; hence i ∈ [0, I]. As in [19, 25], we also assume that the process of determining the node’s grade and the next node on the way to the sink was previously performed during an initialization stage, where a different layer of the protocol stack fills a Next Hop table; in other words, we are assuming unicast transmissions.
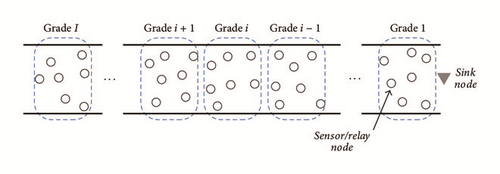
Multihop transmissions are accomplished through a pipelined scheduling where newly generated packets are relayed from a node at grade i to a node at grade i − 1 until they reach the sink. During the pipelined scheduling, nodes operate according to the frame depicted in Figure 2. In this frame, the nodes at grade i + 1 with packets to transmit synchronously awake to contend for the channel, following the MAC protocol described in Section 3.2. During this same time slot, nodes at grade i also synchronously awake to be able to receive a packet from grade i + 1. In the next slot, nodes at grade i act as transmitters, while nodes at grade i − 1 act as receivers. This process continues until nodes at grade 1 become transmitters and the sink node becomes the receiver.
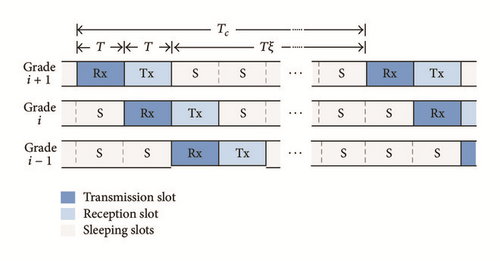
After the reception and transmission slots, all the nodes at a particular grade go to sleep for ξ slots (see Figure 2), in order to save energy. According to this description, the cycle duration, denoted by Tc, is equal to (ξ + 2)T, where T is the duration of every slot. Also note that since the schedules between adjacent grades are staggered, it is possible for a packet to travel through the whole LSN in only one cycle.
3.2. Synchronized Duty-Cycled MAC Protocol
Similar to PRI-MAC [19], we assume that, at the beginning of every transmission slot, awake nodes at grade i with packets to transmit synchronously initiate a backoff counter (see Figure 3), whose value w is a uniform random variable in [0, W − 1]. This backoff counter generates a contention window whose duration is equal to σw, where σ is the length of one minislot.
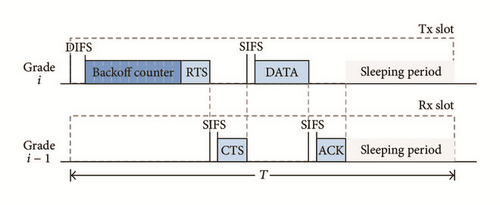
Contending nodes keep listening to the channel during their backoff time and if they detect a transmission from other nodes, they go to the sleeping mode. Otherwise, they initiate an RTS/CTS/DATA/ACK handshake with a receiver at grade i − 1 (recall that we assume unicast transmissions). Figure 3 illustrates the handshake process for the case where a data packet is successfully transmitted.
When there is a tie in the smallest backoff counter generated by the contending nodes, an RTS collision occurs, and none of the winners receive the corresponding CTS message. When these nodes detect the lack of this message, they go to sleep; consequently, no data packet is transmitted from grade i during that particular cycle. From now on, we will refer to the smallest backoff time generated by a contending node as the winner backoff time.
Note that it is possible to have a sleeping period after the exchange of frames within a transmission slot because the winner backoff time can be smaller than W (see Figure 3). However, the slot duration is always equal to T in order to maintain synchronization. Also, note that, in this protocol, at most one packet can be transmitted per cycle from one grade to the following one. Thus, since this is also true for the communication between grade 1 and the sink node, the maximum throughput in the LSN is 1/Tc packets/sec.
3.3. Selective Awakening
Unlike previous proposals (e.g., PRI-MAC) where all the nodes at grade i, with packets to transmit, awake to contend for the channel during their transmission slot, in the proposed protocol, nodes at grade i wake up with probability p(i). The rationale behind this proposal is that if there are many awake nodes at each grade, a lot of collisions may occur, degrading the throughput performance. Moreover, even if the collision probability is kept small (e.g., by utilizing a large contention window), a lot of energy is unnecessarily wasted, since, among the awake nodes, at most one of them will successfully transmit a packet. It is important to point out that the values of the probabilities p(i) have to be carefully selected because if they are excessively small, it will be common to have situations where none of the nodes wake up at the transmission slots, reducing the network throughput. Considering this, we propose to set the values of the probabilities p(i) in such a way as to maximize the network throughput as a function of the traffic load.
In Section 6, we describe the criteria to select these probabilities. The main intuition behind our proposal is that, due to the nature of an LSN, the traffic load at lower grades is higher because nodes at those grades receive the accumulated traffic generated at higher grades. Our numerical results show that, by following these criteria, the energy consumption is significantly reduced in comparison with PRI-MAC, without degrading network throughput.
We also propose to consider the state of the data queues when deciding whether to awake a node during a reception slot. More specifically, in SA-MAC nodes with full data queues remain in sleeping state during reception slots. This simple functionality substantially increases energy efficiency without affecting the system throughput or any other performance metric because it avoids wasting energy to receive a packet that will be dropped.
In the following sections, we develop a mathematical analysis of the performance of the proposed protocol based on a Discrete-Time Markov Chain (DTMC). In this analysis, we assume that the only reason for transmission errors is packet collisions, similar to previous works, such as [16, 19]. Therefore, the channel is assumed to be ideal, without effects such as multipath fading, shadowing, and signal capture. In order to make the following sections more readable, we summarize the main variables used throughout our analyses in the Notations section.
4. Analytical Model
As it has been proposed in several works (e.g., [16–19]), we model the behavior of the nodes by means of a unidimensional DTMC whose states represent the length of a node’s queue at the beginning of the transmission slot. Let K be the maximum queues’ length (in packets) and m any of the possible states for this chain; hence, m ∈ [0, K]. In Figure 4, we illustrate the possible transitions from one of these states.
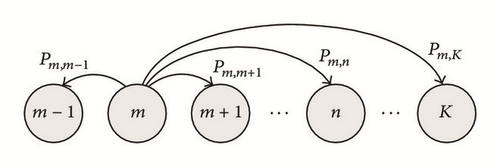
In addition, we denote by the transition probabilities from state m to state n in one cycle, for a node in grade i. As we show in Figure 4, the chain cannot transit from state m to a state n ≤ m − 2 because the nodes can transmit (eliminate from its queue) at most one packet during one cycle. By contrast, transitions to any higher state are possible as a result of the new-packet generation process in each node.
As it was mentioned before, a node at grade i has to relay packets from nodes belonging to higher grades (besides transmitting the locally generated packets); hence, the DTMC steady-state probabilities at grade i depend on the behavior of the higher grades.
In order to obtain these steady-state probabilities at each grade, we adapted the method described in [19] to our proposal. This method consists in solving the DTMC for the grade i and then using these results to calculate the probability of having a successful transmission at this grade, which in turn is used to solve the DTMC at grade i − 1, and so on. Notice that the steady-state probabilities at grade I do not depend on other grades (since nodes at this grade do not relay packets), and hence, the method proceeds by first solving the Markov chain for this latter case.
The presentation of the analysis is organized as follows. In Section 4.1 we calculate the probabilities of transmitting or receiving a packet in each cycle. These probabilities are required to establish the transition probabilities for the DTMC. Since the DTMC sampling points are the beginnings of the transmission slots, all the probabilities in Section 4.1 refer to such points. In Section 4.2, we establish the transition probabilities for the DTMC and we provide a detailed description of the method mentioned in the previous paragraph. Considering that the evaluation of some performance parameters depends on the probability of having a saturated queue at the beginning of the reception slot, we obtain such probability in Section 4.3.
4.1. Probabilities of Transmitting and Receiving a Packet
This means that nodes at grade i will wake up only if they have packets to transmit.
In the proposed protocol, nodes contend for the channel by generating a backoff counter w, which is a uniform random variable in [0, W − 1]. Given a value of the backoff counter w, the probability of winning the contention is the same as the probability of having the smallest backoff counter among the contending nodes. Since the probability of having a backoff timer smaller than another node is (W − w)/W, the probability of having the smallest backoff counter in a group of n contenders equals ((W − w)/W)n. This probability includes the case when more than one contender obtains the smallest backoff timer.
Notice that we calculate ps(i) from the point of view of a contending node at grade i; hence, for an external observer (e.g., a receiver in the next grade), the probability of having a successful packet transmission from a node at grade i is pa(i)ps(i).
4.2. Markov Chain Model
The proposed DTMC has K + 1 states that represent a node’s queue length, where K is the queue size. The sampling points of this Discrete-Time Markov Chain are placed at the beginning of the transmission slots, which also implies that the chain’s time step is equal to the cycle duration (Tc).
Because the chain transition probabilities depend on p(i), pt(i), and pr(i), as well as their complements, here, we define q(i) = 1 − p(i), qt(i) = 1 − pt(i), and qr(i) = 1 − pr(i) in order to simplify some of the subsequent expressions.
It is important to point out that the chain transition probabilities depend on the probability pt(i) of winning the contention (with or without collision). This is because, as in previous works, we assume that the packet at the head of the queue is removed when the node wins the contention, even if a collision occurs. This strategy implies that every packet has only one chance to be transmitted from one grade to the next one.
- (i)
Because a node with an empty queue has 0 probability of awaking or transmitting, does not depend on p(i) or pt(i), as can be seen in (13) and (14).
- (ii)
Since a node can transmit one packet, at most, during a cycle, its queue length cannot be reduced by two or more units during this period of time; therefore, for n ≤ m − 2 is zero, as can be seen in (15).
- (iii)
In general, is expressed as the sum of two main terms: (a) one term that represents the transitions when the node is awake during the transmission slot, and, hence, it depends on both pt(i) and pr(i); (b) one term that represents the transitions when the node is asleep during such slot; therefore, it only depends on pr(i). This was made explicit in (17) and (18).
Now, in order to evaluate the performance of the whole LSN, the previous DTMC has to be solved for each grade to find the steady-state probabilities, for 0 ≤ m ≤ K, which represent a unique solution, because the DTMC is irreducible and aperiodic. Given that the solution at grade i depends on the solutions of higher grades, firstly, we proceed by solving the DTMC for grade I because the probability of receiving a packet from a higher grade equals 0 (pr(I) = 0).
In general, can be found by substituting p(i), pr(i), pt(i), and ak in (13)–(19) and then numerically solving the resulting system of linear equations. Except for pt(i), all the probabilities that are involved in (13)–(19) are known at this point: p(i) can be previously selected according to the criteria of Section 6, pr(i) is equal to zero (for i = I) or can be calculated according to (9) (for i < I), and ak is defined in (12).
- (1)
Propose an initial value for pe(i) and use it to calculate pt(i), according to (3)–(5) and (7).
- (2)
Substitute pt(i), as well as p(i), pr(i), ak, and so on, in (13)–(19), and solve the DTMC, for example, through the Gauss-Seidel method [26].
- (3)
Make .
- (4)
Repeat Steps (2) and (3) until pe(i) has converged according to certain criteria (e.g., mean squared error within a certain threshold value).
- (5)
Compute pr(i − 1) according to (9), because this value will be required when computing the solution for the next grade.
In the Appendix, we present a convergence analysis of this iterative method.
4.3. Probability of Having a Full Queue at the Beginning of the Reception Slot
- (i)
The node removes one packet from its queue and generates K − m + 1 or more new packets.
- (ii)
The node generates K − m or more new packets, without removing packets from its queue.
Notice that can also be interpreted as relayed-packet drop probability at grade i, given a successful transmission at grade i + 1.
5. Performance Metrics
Based on the steady-state probabilities of the previously described Markov chain, in this section, we determine expressions for the following performance metrics: energy consumption, packet loss probability, throughput, and source-to-sink delay. Initially, all the expressions are formulated in terms of the nodes’ grade and, subsequently, the general performance of the network is obtained.
5.1. Energy Consumption
For the sake of finding expressions for Tb, Tc, and Ts, recall that, in the proposed MAC protocol, a contending node uses a backoff counter whose value w is a uniform random variable in [0, W − 1]. Hence, the backoff time is equal to σw, where σ is the duration of one minislot. In addition, recall that τdifs, τrts, τcts, τdata, τack, and τsifs are the duration of the messages and interframe spaces involved in the protocol.
5.2. Throughput and Packet Loss Probability
In an LSN, a packet that was generated at grade i has to accomplish i successful hops in order to reach the sink node; hence, the packet loss probability depends on this index. As it is expected, this probability is closely related to the network throughput; hence, in this subsection we analyze both of these parameters.
As we have explained in Section 4.1, pa(i) is the awakening probability for a node at grade i at the beginning of the transmission slot and pt(i) is the probability of winning the contention given that the node is awake (see (3) and (7), resp.). According to this, the product pa(i)pt(i) represents the probability of removing one packet from the node’s queue, in one cycle (recall that when a node wins the contention, it removes the packet from the head of its queue, even if a collision occurs). Notice that this product can also be interpreted as the rate at which packets leave a node at grade i, in packets per cycle.
Additionally, we define pr(i) as the packet reception probability for a node at grade i and as the probability of having a saturated queue at the beginning of the reception slot (see (9) and (21), resp.); therefore, we can interpret the product as the rate at which packets from higher grades enter the queue of a node at grade i, in packets per cycle.
We assume that the generation packet rate per node in packets/cycle is λTc. However, because of the finite queue length, the new-packet admission rate per node, rq(i), can be smaller than λTc; that is, some packets are dropped in its source node.
In order to give a deeper insight on the relation between Th and pPL(i), in the following, we propose an alternative way to calculate rs(i).
5.3. Delay
- (i)
dh(1) is the average delay from the instant when the packet arrives at grade h to the beginning of the next cycle;
- (ii)
dh(2) is the average delay from the beginning of the first cycle after the arrival, to the instant when the packet reaches the head of the queue.
- (iii)
dh(3) is the average delay from the instant when the packet reaches the head of the queue to the instant it is transmitted to the next grade.
Notice that dh(3) depends not only on p(i)pt(i), but also on the probability of successful transmission in one cycle, p(i)ps(i).
6. Criteria for Selecting the Awakening Probabilities
As we mentioned in Section 3, if an excessively small value of p(i) is selected, it is probable that none of the nodes wakes up in some of the transmission slots, hence reducing the network throughput. On the other hand, if we simply select p(i) = 1 (or select a large value), possibly, a lot of collisions will occur and the network throughput will be also diminished. On the basis of these considerations, we propose to select p(i) in such a way that the throughput in the corresponding grade is maximized.
By solving (49) in terms of p(i), we can obtain the awakening probability that maximizes Th(i). However, this cannot be directly calculated, since pe(i) depends on p(i) (see Section 4.2). In order to overcome this problem, we propose to calculate an approximation for pe(i), which will only be used to solve (49). This approximation is denoted by and must be substituted into (49) instead of pe(i).
As it was mentioned above, p(i) must be selected in order to avoid collisions. Hence, our approximation considers each node at grade i as a K-length queue with one server, where packets arrive at rate λTc + pr(i) packets per cycle, and the mean service time is N cycles. Notice that the latter of these assumptions is a direct consequence of considering that the probability of collision is very close to zero.
Lastly, it is important to notice that depends on the behavior of nodes in higher grades, since pr(i) = pa(i + 1)p(i + 1). Therefore, for the purpose of calculating and consequently p(i), the higher grades must be previously solved, according to the method described in the end of Section 4.2.
7. Numerical Results and Discussion
The DTMC evaluation is carried out through the numerical solution explained in Section 4.2. As we have mentioned before, this solution involves the application of the Gauss-Seidel method; we have evaluated it with 5 × 104 iterations, with an approximation error of 5 × 10−4.
In addition, we have developed a discrete-event simulation for SA-MAC to validate our analyses, which was implemented in Matlab and executed over 1 × 105 cycles. In every cycle, we simulated all the events that are included in the staggered schedules of the grades, and we provide a brief description of them in the following paragraph.
At the beginning of a transmission slot, we identify all nodes that have packets to transmit, and these nodes wake up with probability p(i). Subsequently, we generate a backoff counter for every awake node and, then, we carry on the contention process. Once this process is over, we update statistics related to the packet transmission. Simultaneously, we simulate the reception slot for the next grade. In this case, we identify which nodes have nonsaturated queues and we execute for them the reception events, and we also update statistics about the packet reception. We simulate the transmission/reception between every couple of adjacent nodes, including the process between grade 1 and the sink node. It is important to mention that, along these processes, nodes are generating new packets at a rate λ. In all the transmission/reception events, we consider an ideal channel.
In this section, we first present numerical evaluations for the awakening probability selection: in terms of traffic load, from low to high load with λ ∈ {0.001,0.003,0.01,0.03}, in a dense network (N = 20), and in terms of network density, from low to high node density with N ∈ {10,20,30}, and λ = 0.003.
Second, we evaluate SA-MAC performance in terms of throughput, power consumption, average source-to-sink delay, and new-packet drop probability. In order to highlight the advantages of SA-MAC over previous proposals, we compare its performance with PRI-MAC under different scenarios. This helps us to recognize how the number of nodes per grade and traffic load affect these performance parameters.
Finally, we present results on the grade analysis, where we can highlight that packet loss probability and source-to-sink delay are not the same for every grade, whereas average power consumption is different for remote grades.
In all our numerical evaluations, we select I = 7 (number of grades in the network) and K = 15 (queue’s length), and we take from [16, 19] the rest of the network parameter values, which are shown in Table 1.
| Parameter | Value |
|---|---|
| ξ | 18 |
| σ | 1 ms |
| τack | 11 ms |
| τcts | 11 ms |
| τdata | 43 ms |
| τdifs | 10 ms |
| τrts | 11 ms |
| τsifs | 5 ms |
| Prx | 59.9 mW |
| Psp | 0 mW |
| Ptx | 52.2 mW |
| W | 64 |
7.1. Awakening Probability Evaluation
In Figure 5, we show the selected awakening probability for a node with packets to transmit, p(i), as a function of the grade number i and for different values of the packet generation rate (λ) when N = 20. In Figure 6, we also show this probability, but in terms of the number of nodes per grade (N) for the case when λ = 0.003. These results were obtained through the approximation method described in Section 6.
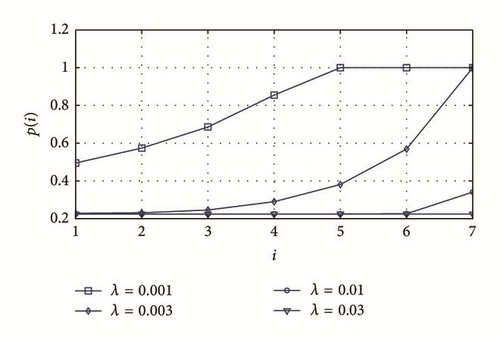
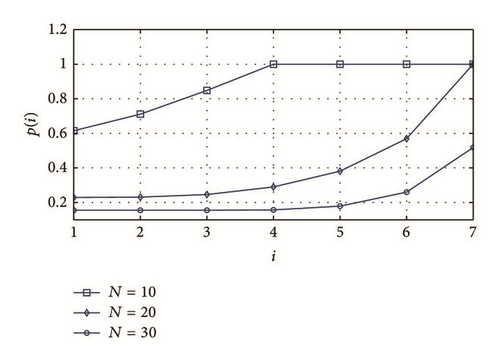
From Figure 5, we can observe that if λ increases, the selected p(i) must decrease because the higher the value of λ, the higher the probability that multiple nodes have packets to transmit; therefore, it is necessary to avoid collisions by reducing the number of contenders. Similarly, large values of N require the selection of small values of p(i), as it can be observed in Figure 6.
Additionally, it is interesting to point out that, in both Figures, p(i) is smaller for nodes closer to the sink (small values of i). This is a consequence of the fact that these nodes accumulate packets from higher grades. As a result, their probability of having packets to transmit is higher, and collisions must be avoided by awaking a small proportion of them in each cycle, that is, selecting a small value of p(i).
We also analyze the effect of using the proposed approximation method for determining p(i) on the system throughput by exhaustively evaluating Thi over the whole domain of p(i). These results are shown in Figure 7, where the triangles indicate the points (p(i), Thi) computed by the approximation method. In this scenario (λ = 0.003 and N = 30), Thi exhibits the same performance for i ∈ [3,6] and, hence, we only show the results for Th6.
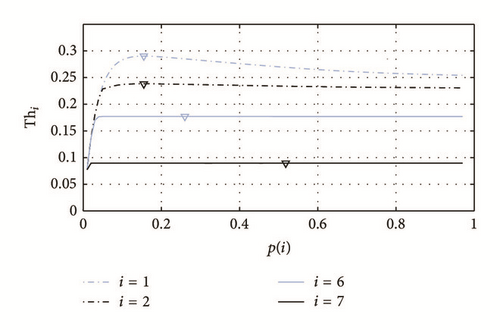
In this scenario, the throughput in remote grades (e.g., i = 7) reaches its maximum over a wide range of values of p(i). This is because the arrival packet rate is so low that small values of p(i) do not create bottlenecks and large values do not generate collisions. By contrast, in grades where the traffic load is much higher, the throughput reaches its maximum only if p(i) is adequately selected.
These results show that, independently of the traffic load per grade, the proposed method is capable of finding the values of p(i) that maximize the throughput. On the basis of this observation, in the remaining numerical evaluations, we use the approximation method for selecting the values of p(i).
Additionally, it is important to point out that the wide range of values of p(i) that provide the maximum throughput will allow, in future work, to select this probability in such a way as to optimize not only the throughput, but also other performance parameters. For example, further energy savings could be achieved, but they must be constrained by target levels of source-to-sink delay or packet loss probability. Another approximation may include the selection of the awakening probabilities as a function of the queue’s length of nodes, so that the packet loss probability or the source-to-sink delay can also be optimized, while satisfying energy consumption constraints.
These new proposals may require redefining equations in Section 6; however, the DTMC and performance parameters definitions would suffer small changes.
7.2. SA-MAC Protocol Evaluation
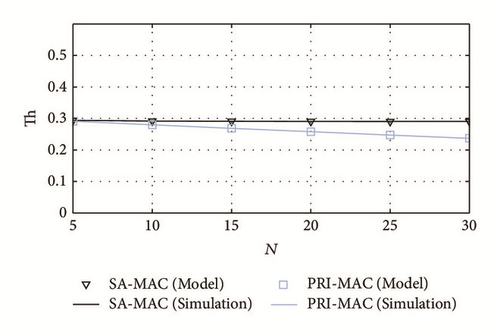
In Figure 8 we show the network throughput attained by SA-MAC and PRI-MAC. In SA-MAC, the throughput is almost constant in spite of the increase in N. The explanation for this performance is that p(i) is selected to maximize the throughput (it must be noticed that, given the network parameters in Table 1, the maximum throughput, 1/Tc, is 0.31 packets/sec). By contrast, since PRI-MAC does not consider a selective awakening, that is, p(i) = 1 regardless of the network parameters, a lot of collisions occur for large values of N in the grades which are closer to the sink, and, as a result, the throughput performance is degraded. Consequently, it can be concluded that SA-MAC is better suited for high-density networks than PRI-MAC.
In Figure 9 we show the average power consumption for both protocols. It can be observed that a significant reduction of power consumption can be achieved with SA-MAC, in comparison with that of PRI-MAC; and it must be highlighted that this reduction is quite notorious for large values of N. This performance is achieved in SA-MAC because the energy wasted in collisions is very small; moreover, further savings are achieved by avoiding the awakening of multiple nodes in a network that is able to transmit only one packet per contention. Besides, in SA-MAC, the wasted energy is also reduced because the nodes with a saturated queue do not awake in the reception mode.
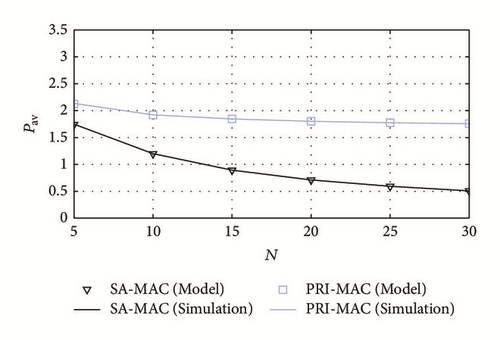
Notice that the joint analysis of throughput and power consumption reveals the main advantage of SA-MAC: its adaptation to different levels of traffic load allows it to save a lot of energy (hence, extending the network lifetime), without sacrificing the throughput performance.
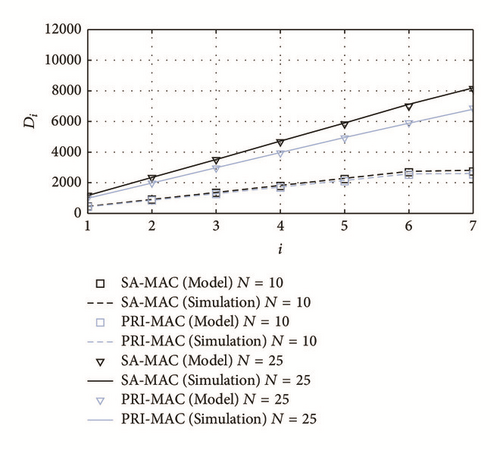
It is also important to notice that, in some scenarios, this advantage comes with a moderate degradation of the source-to-sink delay, as it is shown in Figure 10. This was expected because our proposal reduces collisions by probabilistically turning off nodes with packets to transmit, which increments the waiting time experienced by the packets in the sleeping nodes. This degradation is more apparent for large values of N, as we can observe in Figure 10. This is because the larger the value of N, the smaller the value of p(i). Therefore, on average, nodes will have to wait for longer periods of time to attempt a transmission.
This increase in delay also affects the new-packet drop probability, pND(i), because large delays reduce the space in the buffers to admit new generated packets. Since delay is larger for SA-MAC in comparison with PRI-MAC, pND(i) is also slightly larger for the former, as it is shown in Figure 11. A similar situation occurs in terms of N: when this parameter increases, pND(i) also increases in both schemes.
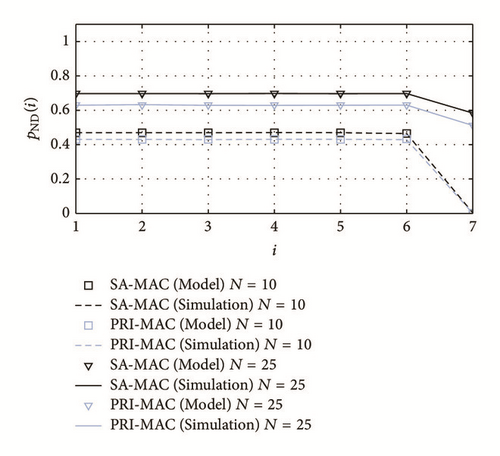
When pND(i) is analyzed in terms of the grade i, a special case arises for the last grade (i = 7 in our experiments), where buffers are dedicated only to admit the locally generated packets; therefore, pND(7) is lower in comparison with other grades.
From this analysis, it is possible to identify network conditions where both protocols exhibit similar performance for throughput, source-to-sink delay, and drop probability, but where SA-MAC significantly outperforms PRI-MAC in terms of energy consumption; for instance, when N = 10 the power consumption incurred by SA-MAC is around 63% of that of PRI-MAC.
7.3. Per-Grade Network Performance
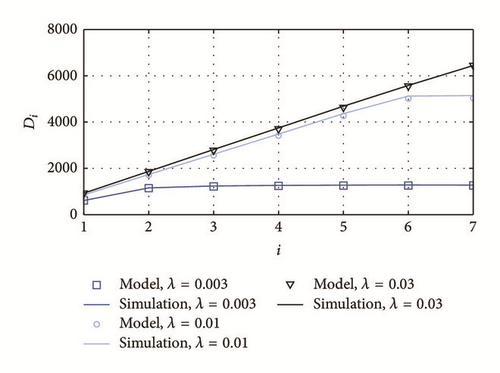
In Figures 12, 13, and 14 we show the analysis by grade for packet loss probability pPL(i), average power consumption P(i), and source-to-sink delay Di, respectively, under different scenarios.
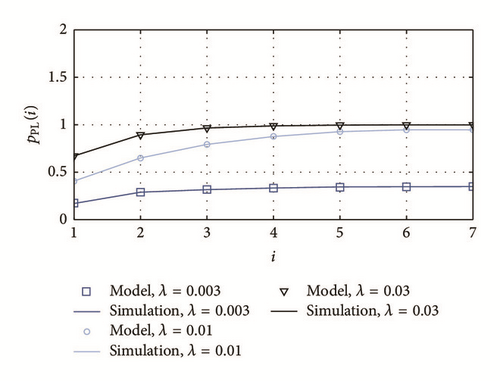
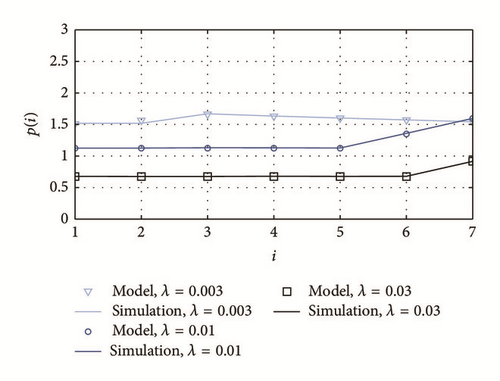
As it was expected, the packet loss probability increases as the distance from the sink also increases, because a packet generated in a remote node needs to overcome a large number of hops. This observation leads to the conclusion that prioritization schemes must be proposed in future works for packets generated in remote nodes. In addition, it is interesting to observe that this probability exhibits smooth variations in terms of i for small traffic loads (e.g., λ = 0.003).
In Figure 13 we can observe that, in general, power consumption increases as the traffic load decreases. This effect is a direct consequence of the strategy used to turn off nodes during the reception slot: since a node goes to sleep when its queue is full, under low traffic loads, nodes stay awake most of the time. On account of these observations, it is clear that in future works a node must go to sleep (during the transmission slot) not only when its queue is saturated, but also when the traffic load is very low.
In order to interpret the power consumption in each grade, we highlight that as i increases, the transmission power consumption decreases (since the nodes have less packets to relay), while the reception power consumption increases (since the nodes keep awake because their queues are not saturated). For λ = 0.003, the decreasing component (i.e., the transmission power consumption) is dominant when i ≥ 3, whereas the opposite occurs otherwise; as a result, grade 3 is the least power efficient in the whole network (see Figure 13). Notice that the less efficient grade will depend on traffic load; it can even be grade I when the traffic load is high (e.g., λ = 0.01), or grade 1 when the traffic load is very low.
The previous observations also lead us to identify that the network lifetime is not determined by the average power consumption in the whole network, but by the average power consumption in the less efficient grade.
Lastly, in Figure 14, it is possible to appreciate that, under low traffic loads, the source-to-sink delay is almost the same, regardless of the packet source (e.g., λ = 0.003). This phenomenon is a consequence of the pipelined scheduling, which makes possible for a packet to go through the whole network in less than one cycle, when such packet finds an empty queue in every node (which is only possible under very low traffic loads). Under moderate traffic loads (e.g., λ = 0.01), the previously described phenomenon occurs only in the most remote grades (where multiple hops are possible during one cycle), but in the closest grades to the sink, a significant extra delay is accumulated for each accomplished hop. When the traffic load is large, this significant extra delay is accumulated in all the hops; therefore, the average delay is directly proportional to the number of hops to reach the sink.
8. Conclusions and Future Work
In this paper, we have introduced SA-MAC, an energy-efficient MAC protocol for dense LSN with applications to IoT. SA-MAC is a synchronized duty-cycle MAC protocol with a pipelined scheduling where nodes selectively awake based on the node density per grade and on the state of their data queues.
As part of SA-MAC, we introduced a set of awakening probabilities that maximizes the throughput per grade by reducing the number of packet collisions. Our numerical evaluations showed that, in order to select appropriate values for these probabilities, the network designer should also consider the grade, the data packet generation rate, and the number of nodes per grade.
Additionally, we have developed a DTMC-based analytical model for the performance of SA-MAC that was validated by means of extensive discrete-event simulations. The results obtained from simulations and mathematical analysis show that SA-MAC outperforms previous work in terms of energy efficiency, packet loss probability, and throughput. The latter is particularly true under certain IoT-like conditions, where both high node density and high traffic load are possible scenarios.
Another contribution of this work is the first per-grade detailed analysis of the performance of an LSN. This deeper analysis revealed, among other things, that there is a set of specific grades that have a larger impact over the network lifetime and reliability.
We believe that the analysis per grade deserves further investigation, for instance, to include other objective functions besides throughput, such as packet drop probability, source-to-sink delay, or energy consumption. It is even possible to formulate the problem as a multiobjective optimization problem where two or more performance metrics are jointly optimized. Other extensions of this work also include prioritization schemes for QoS provisioning and new schemes for selecting the awakening probabilities as a function of the queue’s length that also optimize the main network performance parameters. This new scheme may lead to further reductions in the number of contending nodes and to the design of new mechanisms for assigning priorities to data packets that can also help reducing the packet loss probability and the source-to-sink delay, all this while preserving energy in order to increase the network lifetime.
-
- ak:
-
- Probability that a node generates k packets during a cycle
-
- Al:
-
- Probability that a node generates l or more packets during a period of time
-
- Cn(i):
-
- Probability of n contenders besides the node of interest in grade i
-
- Di:
-
- Average source-to-sink delay for a packet that is generated at grade i
-
- I:
-
- Number of grades in the LSN
-
- K:
-
- Maximum number of packets that a node can buffer
-
- N:
-
- Number of nodes in each grade
-
- p(i):
-
- Awaking probability given a nonempty queue
-
- pa(i):
-
- Unconditional awaking probability
-
- pb(i):
-
- Probability of detecting a busy channel (for an awake node of interest)
-
- pc(i):
-
- Probability of collision (for an awake node of interest)
-
- pe(i):
-
- Probability of empty queue
-
- :
-
- Probability of transition from state m to state n
-
- pND(i):
-
- New-packet drop probability
-
- ppl(i):
-
- Packet loss probability
-
- pr(i):
-
- Packet reception probability
-
- ps(i):
-
- Probability of successful packet transmission (for an awake node of interest)
-
- pt(i):
-
- Probability of winning the contention (for an awake node of interest)
-
- P(i):
-
- Average power consumption of a node in grade i
-
- Pav:
-
- Average power consumption of a node
-
- Prx:
-
- Average power consumption for a node in reception mode
-
- Psp:
-
- Average power consumption for a node in sleeping mode
-
- Ptx:
-
- Average power consumption for a node in transmission mode
-
- rs(i):
-
- Rate at which the generated packets at grade i reach the sink node
-
- Rs(i):
-
- Rate at which the generated packets at grades i to I reach the sink node
-
- sn:
-
- Probability of successful packet transmission given n additional contenders
-
- T:
-
- Slot duration
-
- Tc:
-
- Cycle duration
-
- :
-
- Period of time between the beginning of a transmission slot and the beginning of the next reception slot
-
- tn:
-
- Probability of winning the contention (with or without collision) given n additional contenders
-
- Th:
-
- Network throughput
-
- Thi:
-
- Throughput at grade i
-
- W:
-
- Maximum backoff counter
-
- λ:
-
- Packet generation rate per node
-
- ξ:
-
- Number of slots that a node spends in sleeping mode per cycle
-
- :
-
- DTMC steady-state probabilities
-
- :
-
- Relayed-packet drop probability at grade i
-
- σ:
-
- Duration of one minislot.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Appendix
Convergence Analysis of the Iterative Method to Compute pe(i) and pt(i)
In Section 4.2 we propose a method to iteratively find pe(i) and pt(i). In this appendix, we analyze the convergence of such a method. In order to simplify our nomenclature, we omit the dependence on i from , pe(i), and pt(i).
Firstly, we define pt = f(pe) and pe = g(pt), where f(pe) represents (3)–(5) and (7), while g(pt) is implicit in the DTMC solution (recall that pe is equal to π0, the steady-state probability of an empty queue). The problem that our method solves is to find a pair that simultaneously satisfy these functions.
To analyze this problem in terms of only one variable, instead of pe = g(pt), we use the equivalent expression pt = g(−1)(pe), where g(−1)(x) is the reciprocal function of g(x). Therefore, the problem can be restated as finding a value that satisfies . In the following, we provide some arguments to show that a unique solution exists for this problem.
- (i)
Even if the contenders (besides the node of interest) always have packets to transmit (pe = 0), there exists a probability that the node of interest wins the contention; hence
(A.1) - (ii)
Only if the contenders (besides the node of interest) never have packets to transmit (pe = 1), the node of interest wins the contention with certainty (f(1) = 1); hence,
(A.2)
- (i)
If an awaken node never wins the contention (pt = 0), the probability of an empty queue has to be zero; hence,
(A.3) - (ii)
Even if a node transmits every time it awakens (pt = 1), this node may accumulate packets while sleeping; hence,
(A.4)
- (i)
According to (3)–(5) and (7), if the probability of empty queue increases (pe), then, the probability that a node of interest wins the contention also increases; that is, f(pe) is monotonically increasing.
- (ii)
According to the DTMC, if the probability that a node transmits a packet (pt) increases, then, the probability of empty queue also increases; that is, g(pt) is monotonically increasing, which also implies that g(−1)(pe) is monotonically increasing.
On the other hand, the convexity of f(pe) is also demonstrable because the second derivative of (7) is positive. Unfortunately, we have not yet developed an analytical expression for g(−1)(pe); however, according to extensive numerical evaluations, we identify that this function is also convex in .
In the following, we analyze our iterative method under the assumption that f(pe) and g(−1)(pe) satisfy all the characteristics discussed above. However, it is clear that a deeper study on the features of g(−1) must be accomplished in future work in order to analytically demonstrate its convexity.
In Figure 15, we illustrate three iterations of this method for a specific scenario (i = 7, λ = 0.01, and N = 20).
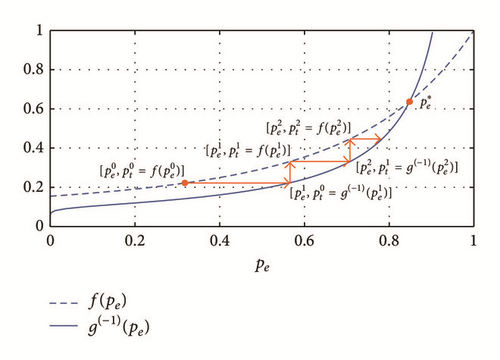
Considering this definition, we execute our method for an extremely small target error (e.g., 1 × 10−15) and we assume that , where L is the number of iterations that provide this target error. Then, we estimate r and C, for k ≫ 1 and k ≪ L, that is, for values of k that satisfy the limit in (A.11) but provide large errors in comparison with L.
We find that our method always converges linearly (r = 1); however, the asymptotic error constant can vary for different sets of parameters values, as we summarize in Table 2.
| N | p | Error | L |
|
C |
|---|---|---|---|---|---|
| 10 | 1.000 | 1 × 10−15 | 20 | 0.961 | 0.167 |
| 20 | 0.341 | 1 × 10−12 | 31 | 0.848 | 0.416 |
| 30 | 0.165 | 1 × 10−9 | 107 | 0.357 | 0.843 |




