In view of the problems of low efficiency, poor anticavitation performance, and curve hump for current centrifugal pump in the process of desulfurization and dust removal, the desulfurization dust removal centrifugal pump was designed. The velocity coefficient method was used for hydraulic design of centrifugal pump, and the three-dimensional modeling and numerical simulation of flow field of centrifugal pump were carried out by using computational fluid dynamics technology (CFD). The optimal mathematical model with the highest efficiency and the lowest pump net positive suction head (NPSH_r) as the objective function was established under the condition of no curve hump. The immune particle swarm optimization algorithm was used to optimize the multiobjective function, and the optimal combination of the main parameters was obtained. The simulation results showed that, compared with the traditional centrifugal pump, the performance of the optimized centrifugal pump had been greatly improved, which eliminated the phenomenon of curve hump. Based on IH model chemical pump to build a prototype test platform, the experimental results of the external characteristics of the prototype pump and the optimization pump under different working conditions were obtained. At the rated flow rate, the optimization pump efficiency was increased by 13.30%, the head was increased by 11.52%, and NPSH_r was decreased by 10.14%. The experimental results showed that the optimized indexes met the design requirements and improved the performance of centrifugal pump. At the same time, the accuracy of the immune particle swarm control method was verified, which provided some reference for the design of desulfurization dust removal centrifugal pump.

1. Introduction

Centrifugal pump is a widely used general machinery, mainly used in petrochemical, urban water supply and drainage, aerospace, and other fields [1]. At present, there are some problems in centrifugal pumps, such as low efficiency, poor anticavitation performance, and curve hump, especially in low speed centrifugal pumps. The early centrifugal pump development is mainly based on the Euler theory, univariate theory, binary theory, and flow similarity theory and other methods for hydraulic design and model conversion, whether the designer has a wealth of engineering experience is the key to determine the success of centrifugal pump design [2–8]. Industries, in order to achieve the function of desulfurization, usually to improve the chemical pump, but the improved efficiency of the chemical pump was low, could not meet the requirements of energy saving and environmental protection, and the operating conditions were not suitable for the desulfurization dust removal pump requirements. Aiming at the shortage of traditional centrifugal pump in this aspect, the structure design of desulfurization dust removal centrifugal pump was carried out by CFD technology, with the highest efficiency, the NPSH_r as the objective function, and the no curve hump as the constraint conditions for multiobjective optimization, and the immune particle swarm control algorithm was used to optimize the calculation, so as to get a centrifugal pump with good performance.

2. Calculation of Mathematical Model for Desulfurization Dust Removal Centrifugal Pump

2.1. Hydraulic Design

The hydraulic design of desulfurization dust removal centrifugal pump is carried out by the velocity coefficient method [9], in which rotational speed n = 1450 r/min, flow rate Q = 50 m³/h, and head H = 20 m.

The design of desulfurization dust removal centrifugal pump is a single suction impeller: pump specific speed , hydraulic efficiency η_h = 1 + 0.0835lg(Q/n)^1/3 = 0.860, volumetric efficiency , and mechanical efficiency .

2.2. Impeller Design

Considering that the fluid in the desulfurization dust removal centrifugal pump is alkaline medium, the rigid polyvinyl chloride with good corrosion resistance and high mechanical strength is selected as the material of impeller.

(1)
Calculation of the suction port and outlet diameter of centrifugal pump

Pump inlet flow rate V_S = 2.76 m/s, pump suction port diameter

, and pump outlet diameter D_d = (1−0.7)D_S = 80–56 mm.

(2)
Determination of impeller inlet diameter D₁

Impeller equivalent diameter is

(1)

where k₀ is the impeller inlet coefficient, taking into account the cavitation and efficiency of centrifugal pump, and k₀ takes 4.0.

Hub diameter is

(2)

in which pump shaft diameter d = 20 mm.

Impeller inlet diameter

(3)
Determination of impeller outlet diameter D₂

Impeller outlet diameter is

(3)

where

(4)
Determination of impeller outlet width b₂

The calculation formula of impeller outlet width is [9]

(4)

where

(5)
Determination of impeller inlet width b₁

First, the impeller inlet velocity v₀ is determined, and then the impeller inlet width b₁ is calculated:

(5)

where

Impeller inlet width is b₁ = η_vQ/πD_jv₀ = 22.9 mm.

(6)
Determination of blade inlet and outlet angle

The recommended blade inlet angle is , and the impact angle is Δβ = 3^∘–15^∘.

Due to , the selected inlet angle is β₁ = 30^∘.

Considering that the value of β₂ is usually within the range of 16^∘–40^∘, the outlet angle β₁ = 30^∘ for this design is selected.

(7)
Determination of the number of blades Z

(6)

(8)
Calculation of blade thickness and selection of blade packing angle

Calculation of blade thickness is

(7)

where the coefficient A is related to specific speed and material, and A = 4.5 is desirable by look-up table [9].

Generally, the value range of the blade angle φ is 90^∘–120^∘ because the specific speed of the pump is lower, and φ takes 120^∘.

(9)
Determination of impeller structure parameters

In summary, the main structural parameters of impeller are shown in Table 1.

Table 1. The main structural parameters of impeller.

Parameters	Calculation results	Final results
D_S (mm)	80	80
D_d (mm)	56–80	65
D₁ (mm)	89.4	90
D₂ (mm)	256.6	260
b₁ (mm)	12.1	12.5
b₂ (mm)	22.9	23
β₁ (°)	23–40	30
β₂ (°)	16–40	30
Z	5.2	6
S (mm)	2.13	3
φ (°)	90–120	120

2.3. Calculation of Main Structural Parameters of Vortex Chamber

(1)
Calculation of base circle diameter and vortex chamber inlet width

Since the base circle diameter calculation formula is: D₃ = (1.03–1.08)D₂ = 267.8–280.8 mm, the selected base circle diameter D₃ = 270 mm.

Vortex chamber inlet width is b₃ = b₂ + 0.05D₂ = 25.5 mm.

(2)
Calculation of each section area of vortex chamber

For convenience of calculation and drawing, circular vortex chamber and 8 equal parts are selected. The average velocity v₃ of the vortex chamber is

(8)

in which the velocity coefficient k₃ = 0.46.

The calculation formula of each section area is

(9)

where i takes 1 to 8, respectively.

The calculation results of each section area of vortex chamber are shown in Table 2.

Table 2. Vortex section area.

Section	1	2	3	4	5	6	7	8
Area(cm²)	1.91	3.81	5.72	7.63	9.53	11.44	13.34	15.25

3. Three-Dimensional Modeling and Flow Field Analysis of Desulfurization Dust Removal Centrifugal Pump

3.1. Centrifugal Pump Three-Dimensional Model

CFturbo is a professional impeller and volute design software, easy to operate, widely used in centrifugal pumps, centrifugal fans, turbines, and other rotating machinery designs [10–12]. The above design parameters are introduced into the CFturbo 10.0 software, and the three-dimensional model of centrifugal pump is shown in Figure 1 through the parameter setting.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Centrifugal pump three-dimensional model.

3.2. Grid Division

Pumplinx is a software developed for the hydraulic simulation and calculation of pump, which provides engineers with fast and accurate calculation results. The three-dimensional model of centrifugal pump is imported into the Pumplinx 3.4 software, and the Cartesian grid is divided, as shown in Figure 2; a total of 78668 grids are obtained.

In order to further verify the effect of grid number on the numerical simulation performance of centrifugal pump, six groups of grid numbers are selected to simulate the changes of centrifugal pump η, H, and NPSH_r under the same working conditions. Grid independence analysis is shown in Table 3 [13].

Table 3. Grid independence analysis.

Schemes	Grid numbers	η(%)	H(m)	NPSH_r(m)
1	60000	81.63	16.76	1.03912
2	65000	81.75	18.65	1.03961
3	70000	82.23	19.24	1.04022
4	75000	82.25	19.28	1.04026
5	80000	82.27	19.32	1.04033
6	85000	82.29	19.33	1.04035

As can be seen from Table 3, when the number of grids is between 60000 and 70000, the number of grids has a great influence on each index of centrifugal pump. When the number of grids is between 70000 and 85000, the variation range of each index is small. Therefore, when the number of grids is more than 70000, the sensitivity of the external characteristics of centrifugal pump to the number of grids is small, and each index value tends to be stable. Visible, the number of selected impeller grids is reasonable.

3.3. Boundary Condition Setting

Before the flow field simulation, the boundary conditions are set. The rotating speed of impeller is n = 1450 r/min, the flow rate of pump is Q = 50 m³/h, the fluid medium is selected by water, and the turbulence model is selected as the k−ε model. The interface coupling between impeller and volute is coupled with dynamic-static interface. The inlet adopts the speed inlet boundary condition, the outlet boundary adopts the free outlet, and the surface of the solid wall has no slip.

3.4. Flow Field Simulation

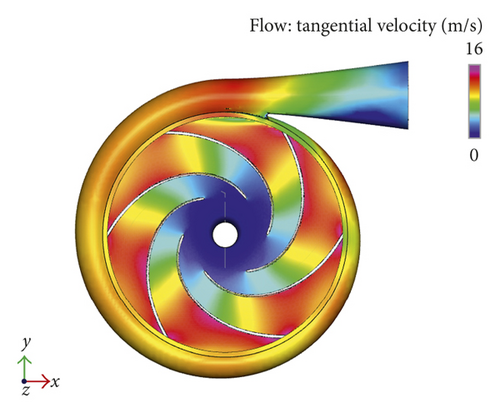
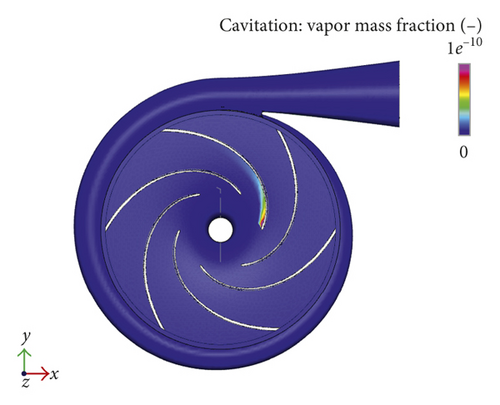
After setting the parameters, the flow field is simulated by Pumplinx 3.4 software. Figure 3 shows the pressure contour diagram, velocity contour diagram, and cavitation contour diagram of desulfurization dust removal centrifugal pump, respectively.

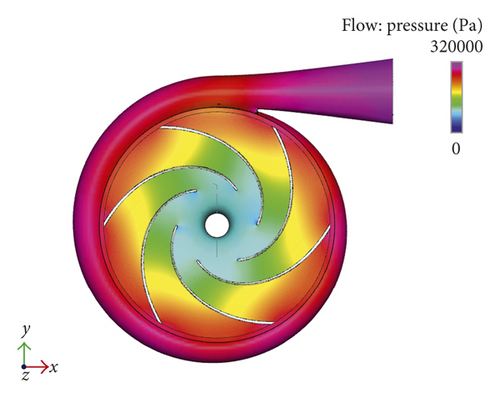
According to Figure 3(a), the pressure from the center of the impeller to the volute is gradually increased, reaching the maximum at the volute outlet, so that the fluid has enough energy to reach the specified head. However, the uneven pressure distribution on the volute and the reaction to the impeller may cause the vortex phenomenon among the blades.

As shown in Figure 3(b), the velocity from the center of the impeller to the outlet of the impeller is gradually increasing, the velocity distribution of impeller near the volute wall is uneven, and the vortex phenomenon is easy to appear, which affects the normal flow of fluid.

As shown in Figure 3(c), there is a large range of cavitation in the blades near the impeller inlet. This is because the impeller inlet pressure is very low, to reach the critical pressure of fluid at room temperature, resulting in cavitation phenomenon.

4. Centrifugal Pump Optimization Mathematical Model Establishment

In view of the above flow field simulation, with the highest efficiency and the lowest NPSH_r as the objective function, the centrifugal pump was optimized with the constraint conditions of no curve hump.

4.1. Maximum Efficiency Model of Centrifugal Pump

According to the Stodola formula, when the inlet has no prerotating, the theoretical head of the centrifugal pump is [14]

(10)

where σ = 1 − π/Zsinβ₂, σ denotes the slip coefficient, and ψ₂ denotes the impeller outlet exclusion coefficient.

The total efficiency of centrifugal pump is expressed as

(11)

where P_m is the centrifugal pump mechanical loss and S₁ is the hydraulic loss.

When η is the largest, 1/η is the smallest, and the highest efficiency objective function is

(12)

4.2. Centrifugal Pump Minimum NPSH_r Model

The expression of centrifugal pump NPSH_r is [15]

(13)

where λ is the inlet pressure drop coefficient of the blade, and k₁ and k₂ are the coefficients.

Centrifugal pump NPSH_r objective function is

(14)

In summary, the total objective function is

(15)

where ω_i is the weight coefficient and

is the ideal value of corresponding subobjective function.

4.3. Constraint Conditions

In order to avoid the problem of curve hump in centrifugal pump, according to empirical function, the following should be satisfied [16]:

(16)

According to the requirements of optimization design, the scope of design variables is adjusted appropriately, and other constraints can be obtained:

(17)

5. Immune Particle Swarm Control Algorithm Design

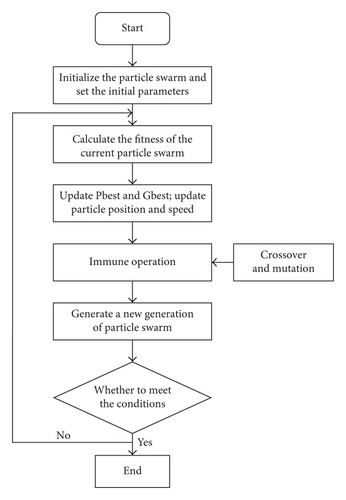
The immune particle swarm algorithm is a new improved particle swarm algorithm based on the immune mechanism of the biological system. The control effect is obvious, which has the characteristics of fast convergence speed, high convergence precision, and strong adjustment ability. In this paper, Matlab 7.0 software is used to write immune particle swarm optimization algorithm to optimize the multiobjective function.

Determine the optimal solution for the parameter selection:

(18)

where e(t) is the system error, u(t) is the output of the immune controller, and t is the time.

In order to avoid the overshoot phenomenon, using the penalty function, the optimal solution is

(19)

where ey(t) = y(t) − y(t − 1) and y(t) is the system output.

Fitness function f = 1/J, and the greater the fitness, the higher the accuracy of particles.

The parameter optimization process is shown in Figure 4 [17, 18].

6. Optimization Design of Desulfurization Dust Removal Centrifugal Pump

6.1. Parameter Determination

By calculating, the constraints could be obtained as follows: 63.7 mm < D₁ < 95.6 mm, 21.6 mm < b₁ < 32.4 mm, 235.4 mm < D₂ < 274.6 mm, 9.0 mm < b₂ < 13.5 mm, 23° < β₁ < 40°, 10° < β₂ < 40°, 90° < φ < 130°, and 4 < Z < 9.

Particle size N = 60, maximum number of iterations max DT = 200, learning factor c₁ = c₂ = 1.624, inertia weight coefficient ω = 0.628, crossover probability p_c = 0.576, mutation probability p_m = 0.01 − [1 : 1 : N]∗0.01/N, and weight ω₁ = 0.003, ω₂ = 0.87, andω₃ = 96.

6.2. Analysis of Results after Optimization

The immune particle swarm algorithm is programmed by Matlab 7.0 software, and the iterative result of optimal solution is shown in Figure 5.

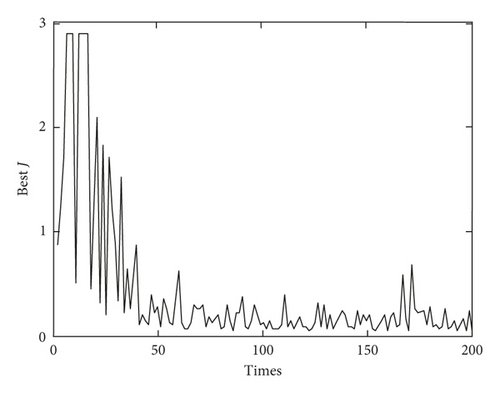
The optimized parameters of impeller are shown in Table 4.

Table 4. Impeller parameter optimization results.

Parameters	D₁ (mm)	b₁ (mm)	D₂ (mm)	b₂ (mm)	β₁ (°)	β₂ (°)	φ (°)	Z
Prototype pump	90	23	260	12.5	30	30	120	6
Optimization pump	94	26	262	11	28	18	110	6

6.3. Simulation of Flow Field after Optimization

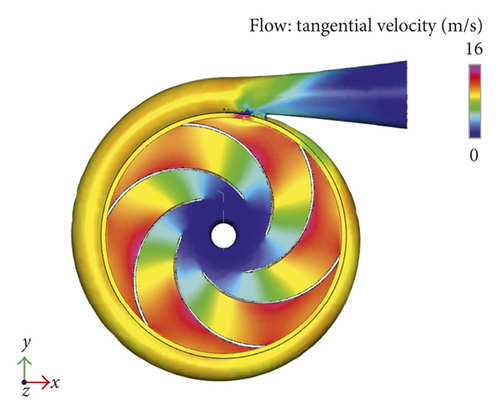
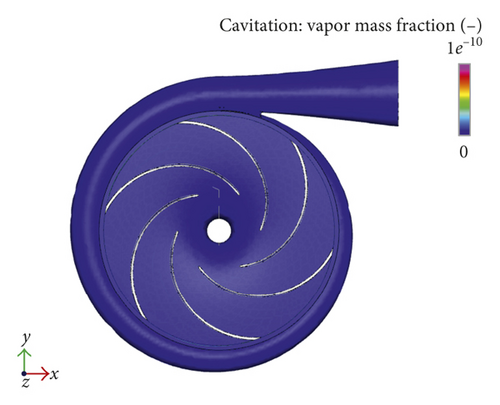
According to the optimized parameters, the parameters are remodeled, and the CFD analysis is carried out, as shown in Figure 6.

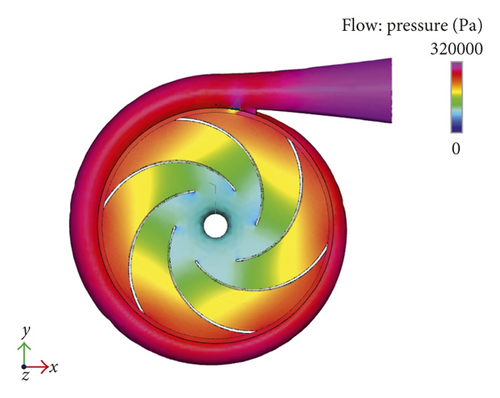
As can be seen from Figure 6(a), the pressure distribution on the volute of the optimization pump is relatively uniform, the energy loss in the volute is small, and the vortex phenomenon between blades is avoided.

As can be seen from Figure 6(b), the velocity of the fluid near the volute wall of the optimization pump is relatively uniform, and the vortex phenomenon is avoided.

As can be seen from Figure 6(c), the cavitation near the inlet of the impeller of the optimization pump is obviously reduced, and the cavitation phenomenon is basically eliminated.

From the optimized pressure contour diagram, velocity contour diagram, and cavitation contour diagram, it can be seen that the effect of the initial design structure of centrifugal pump has been significantly improved, and the overall performance of centrifugal pump has a certain promotion.

6.4. Simulation of External Characteristics

In order to verify the feasibility of the optimization scheme, the external characteristics of the prototype pump and the optimization pump under rated operating conditions are simulated respectively (where rated flow Q_d = 50 m³/h), and the simulation results are shown in Table 5.

Table 5. Simulation results of external characteristics.

Optimization index	Prototype pump	Optimization pump	Optimization rate (%)
η(%)	82.28	92.23	12.09
H(m)	19.31	21.43	10.98
NPSH_r(m)	1.04030	0.94876	8.80

According to the simulation results of the external characteristics, the optimization pump efficiency is improved by 12.09%, the head is increased by 10.98%, and NPSH_r is reduced by 8.80%. At the same time, β₂Z^0.773 before and after optimization are 119.85 and 71.91, respectively, and the curve hump is eliminated.

7. Experimental Verification

In order to verify the accuracy of immune particle swarm optimization, an external characteristic test bench is built with IH model horizontal stainless steel chemical centrifugal pump, as shown in Figures 7 and 8, respectively. IH model chemical pump is mainly composed of pump body, shaft key, impeller nut, packing ring, brake pad, packing gland, shaft, pump cover, and suspension bearing components. The chemical pump has the advantages of reasonable and reliable layout of water conservancy, small size, light weight, good anticavitation performance, low power consumption, easy maintenance, and high work efficiency.

Based on the optimized impeller structure parameters given in Table 4, the impeller is made as shown in Figure 9, and the impeller material is made of transparent rigid polyvinyl chloride. The internal flow field of centrifugal pump is measured under 6 working conditions of 0.2Q_d, 0.4Q_d, 0.6Q_d, 0.8Q_d, 1.0Q_d, and 1.2Q_d. Figure 10 shows the external characteristic curves of the prototype pump and the optimization pump.

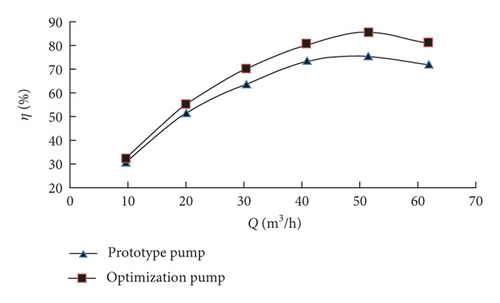
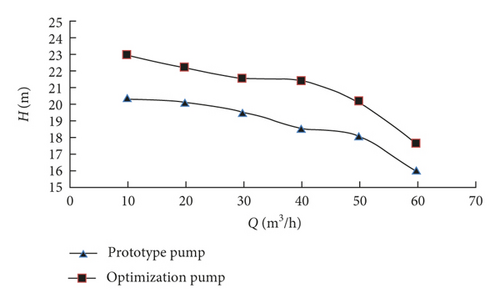
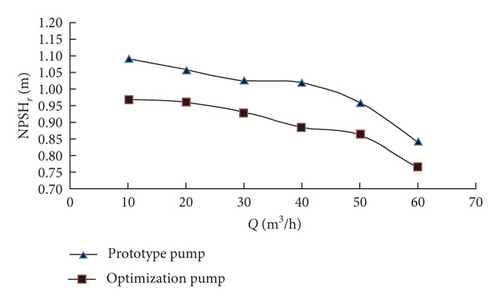
According to the pump characteristic curves, the experimental values of the optimization pump and the prototype pump are in good agreement, which can accurately reflect the change trend of η, H, and NPSH_r with the variation of flow rate.

There is a small error between the simulation value and the experimental value; the main reason is that, in the numerical simulation experiment of centrifugal pump hydraulic design, the leakage of impeller sealing ring, volume loss caused by axial force, and mechanical loss caused by centrifugal pump in the working process is not considered.

The experimental results of each index of prototype pump and optimization pump under different working conditions are extracted from Figure 10, as shown in Table 6.

Table 6. Experimental results of prototype pump and optimization pump.

Indexes	Q(m³/h)
Indexes	10	20	30	40	50	60
Prototype pump η(%)	32.12	51.77	63.36	72.69	74.43	71.24
Optimization pump η(%)	33.46	55.06	69.44	79.17	84.33	79.71
Δη(%)	4.17	6.36	9.60	8.91	13.30	11.89
Prototype pump H(m)	20.36	20.11	19.49	18.53	18.06	15.97
Optimization pump H(m)	22.97	22.22	21.55	21.41	20.14	17.64
ΔH(%)	12.82	10.49	10.57	15.54	11.52	10.46
Prototype pump NPSH_r(m)	1.09198	1.05678	1.02558	1.01914	0.95987	0.84287
Optimization pump NPSH_r(m)	0.97007	0.9584	0.92943	0.88455	0.86255	0.76461
ΔNPSH_r(%)	11.16	9.31	9.38	13.21	10.14	9.28

As can be seen from Table 6, under different working conditions, the optimization pump efficiency and head are all larger than the prototype pump, and the optimization pump NPSH_r is less than the prototype pump. At the rated flow rate, the optimization pump efficiency is increased by 13.30%, the head is increased by 11.52%, and NPSH_r is decreased by 10.14%, which achieve the desired optimization goal.

In summary, every index of the optimization pump has been significantly improved, and it can be concluded that the immune particle swarm optimization algorithm is feasible; the control strategy is further verified by the centrifugal pump external characteristic test.

8. Conclusion

(1)
The hydraulic design of desulfurization dust removal centrifugal pump was carried out by the velocity coefficient method, and the main structural parameters of impeller and volute were obtained. The three-dimensional model of centrifugal pump was established by CFturbo 10.0 software, and the centrifugal pump was numerically simulated and analyzed by Pumplinx 3.4 software.
(2)
An optimization mathematical model with the highest efficiency and the lowest NPSH_r as the objective function was established under the condition of no curve hump. A total of eight indexes of D₁, b₁, D₂, b₂, β₁, β₂, φ, and Z were optimized by the immune particle swarm algorithm.
(3)
Through the simulation and analysis of the optimization results, the optimization pump efficiency was increased from 82.28% to 92.23%, the head was increased from 19.31 m to 21.43 m, and NPSH_r was decreased from 1.04030 m to 0.94876 m; the curve hump problem was eliminated. The overall performance of centrifugal pump was improved significantly, and the feasibility of immune particle swarm optimization was verified.
(4)
Based on the IH model chemical pump, the external characteristic test bench was built, and the external characteristic curves of each index parameter of centrifugal pump under different working conditions were obtained. The variation law of experimental values of all index parameters was basically consistent before and after optimization, and compared with the prototype pump, the experimental values of the optimization pump were significantly improved. The accuracy of the immune particle swarm optimization control strategy was verified, which provided some reference value for the structural optimization design of desulfurization dust removal centrifugal pump in the future.
(5)
Taking centrifugal pump as the research object, the main indexes of centrifugal pump were optimized by immune particle swarm optimization algorithm, which improved the hydraulic performance of centrifugal pump. Due to the limitation of research conditions, this paper only studied the optimization of pump efficiency, head, and NPSH_r, without considering the optimization of other indicators. In the following research work, based on immune particle swarm optimization control strategy, the influence of the main geometric parameters of centrifugal pump on the pump characteristics will be considered comprehensively, in order to improve the working performance of centrifugal pump.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This project was supported by Key Project of Natural Science Research in Colleges and Universities of Anhui Province, China (KJ2017A450), Anhui Province University Outstanding Young Talent Support Program Project, China (gxyq2017071), and Natural Science Foundation of Chaohu University, China (XLZ-201503).

References

1 Wang W. J., Yuan S. Q., Pei J., Zhang J. F., Yuan J. P., and Mao F. L., Two-point hydraulic optimization of pump impeller based on kriging model and neighborhood cultivation genetic algorithm, Journal of Mechanical Engineering. (2015) 51, no. 15, 33–38, https://doi.org/10.3901/jme.2015.15.033, 2-s2.0-84941012079.
10.3901/JME.2015.15.033
Google Scholar
2 Tan L., Cao S., Wang Y., and Zhu B., Direct and inverse iterative design method for centrifugal pump impellers, Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy. (2012) 226, no. 6, 764–775, https://doi.org/10.1177/0957650912451411, 2-s2.0-84871821898.
10.1177/0957650912451411
Web of Science® Google Scholar
3 Kim S., Choi Y. S., Lee K. Y., and Yoon J. Y., Design optimization of centrifugal pump impellers in a fixed meridional geometry using DOE, International Journal of Fluid Machinery & Systems. (2009) 2, no. 2, 172–178, https://doi.org/10.5293/ijfms.2009.2.2.172.
10.5293/IJFMS.2009.2.2.172
Google Scholar
4 Sakthivel N. R., Sugumaran V., and Nair B. B., Automatic rule learning using roughset for fuzzy classifier in fault categorization of mono-block centrifugal pump, Applied Soft Computing. (2012) 12, no. 1, 196–203, https://doi.org/10.1016/j.asoc.2011.08.053, 2-s2.0-81155123062.
10.1016/j.asoc.2011.08.053
Web of Science® Google Scholar
5 Derakhshan S., Pourmahdavi M., Abdolahnejad E., Reihani A., and Ojaghi A., Numerical shape optimization of a centrifugal pump impeller using artificial bee colony algorithm, Computers & Fluids. (2013) 81, no. 9, 145–151, https://doi.org/10.1016/j.compfluid.2013.04.018, 2-s2.0-84878190819.
10.1016/j.compfluid.2013.04.018
Web of Science® Google Scholar
6 Minemura K. and Uchiyama T., Three-dimensional calculation of air-water two-phase flow in centrifugal pump impeller based on a bubbly flow model, Journal of the Acoustical Society of America. (1993) 115, no. 1, 4–8.
Google Scholar
7 Shojaeefard M. H., Boyaghchi F. A., and Ehghaghi M. B., Experimental study and three-dimensional numerical flow simulation in a centrifugal pump when handling viscous fluids, International Journal of Industrial Engineering & Production Research. (2006) 17, no. 4, 53–60.
CAS Google Scholar
8 Xu Y., Tan L., Cao S. L., Cao S., and Qu W., Multiparameter and multiobjective optimization design of centrifugal pump based on orthogonal method, Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science. (2016) 231, no. 14, 2569–2579, https://doi.org/10.1177/0954406216640303, 2-s2.0-85023739521.
10.1177/0954406216640303
Web of Science® Google Scholar
9 Guan X. F., Theory and Design of Pump, 2011, Aerospace Press, Beijing, China.
Google Scholar
10 Guo J. P., Gao Z. X., Qin D. Q., and Xing H., Hydraulic design optimization of centrifugal pump with high head and large capacity by using CFD, Journal of Drainage and Irrigation Machinery Engineering. (2013) 31, no. 3, 220–224.
CAS Google Scholar
11 Wang Z. J., Tong L., Li L. L., and Zheng J. S., Numerical simulation of three-dimensional flow in centrifugal pump and performance prediction based on CFD, Fluid Machinery. (2012) 40, no. 6, 14–18.
Google Scholar
12 Zhu R. S. and Ou M. X., Simulation of reverse flow in low specific speed double suction centrifugal pump, Transactions of the Chinese Society for Agricultural Machinery. (2009) 40, no. 4, 82–85.
Google Scholar
13 Mou J. G., Dai D. S., Gu Y. Q., Liu J., and Wu D., Influences of impeller ring structure on performance and flow field of centrifugal pump, Journal of Central South University. (2017) 48, no. 6, 1522–1529.
Google Scholar
14 Ma F. H., Tang L. F., Xu B. X., and Wan P., Optimization of structure parameters of centrifugal pump based on CFD, Journal of Chongqing University of Arts and Sciences. (2016) 35, no. 5, 49–56.
Google Scholar
15 Nie S. H., Zhu B. L., Liao S. T., and Xu E. T., Optimization design of centrifugal pump based on genetic algorithm, Journal of Machine Design. (2013) 30, no. 12, 19–22.
Google Scholar
16 Liao F. and Zhang H., Optimization design of lower speed pump based on genetic algorithm, Journal of Chinese Agricultural Mechanization. (2016) 37, no. 2, 233–236.
Google Scholar
17 Wang Y. Q., Optimization design of single inverted pendulum based on immune PID control, Key Engineering Materials. (2015) 670, 259–265.
Google Scholar
18 Sun X., Zhang W. G., Yin W., and Li A. J., Optimization of flight controller parameters based on PSO-immune algorithm, Journal of System Simulation. (2007) 19, no. 12, 2765–2767.
Google Scholar

Citing Literature

All articles

Multiobjective Optimization Design and Experimental Study of Desulfurization Dust Removal Centrifugal Pump Based on Immune Particle Swarm Algorithm

Abstract

1. Introduction